

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-20-011 ; CERN-EP-2022-181 | ||
| Search for a heavy composite Majorana neutrino in events with dilepton signatures from proton-proton collisions at $ \sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 6 October 2022 | ||
| Phys. Lett. B 843 (2023) 137803 | ||
| Abstract: Results are presented of a search for a heavy Majorana neutrino $ \mathrm{N}_{\ell} $ decaying into two same-flavor leptons $ \ell $ (electrons or muons) and a quark-pair jet. A model is considered in which the $ \mathrm{N}_{\ell} $ is an excited neutrino in a compositeness scenario. The analysis is performed using a sample of proton-proton collisions at $ \sqrt{s} = $ 13 TeV recorded by the CMS experiment at the CERN LHC, corresponding to an integrated luminosity of 138 fb$ ^{-1} $. The data are found to be in agreement with the standard model prediction. For the process in which the $ \mathrm{N}_{\ell} $ is produced in association with a lepton, followed by the decay of the $ \mathrm{N}_{\ell} $ to a same-flavor lepton and a quark pair, an upper limit at 95% confidence level on the product of the cross section and branching fraction is obtained as a function of the $ \mathrm{N}_{\ell} $ mass $ m_{\mathrm{N}_{\ell}} $ and the compositeness scale $ \Lambda $. For this model the data exclude the existence of $ \mathrm{N}_{\mathrm{e}} $ ($ \mathrm{N}_{\mu} $) for $ m_{\mathrm{N}_{\ell}} $ below 6.0 (6.1) TeV, at the limit where $ m_{\mathrm{N}_{\ell}} $ is equal to $ \Lambda $. For $ m_{\mathrm{N}_{\ell}} \approx $ 1 TeV, values of $ \Lambda $ less than 20 (23) TeV are excluded. These results represent a considerable improvement in sensitivity, covering a larger parameter space than previous searches in pp collisions at 13 TeV. | ||
| Links: e-print arXiv:2210.03082 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
The fermion interaction as a sum of gauge (center) and contact (right) contributions. |

png pdf |
Figure 2:
Feynman diagrams for the decay of a heavy composite Majorana neutrino to $ \ell\mathrm{q}\overline{\mathrm{q}}^\prime $. |
png pdf |
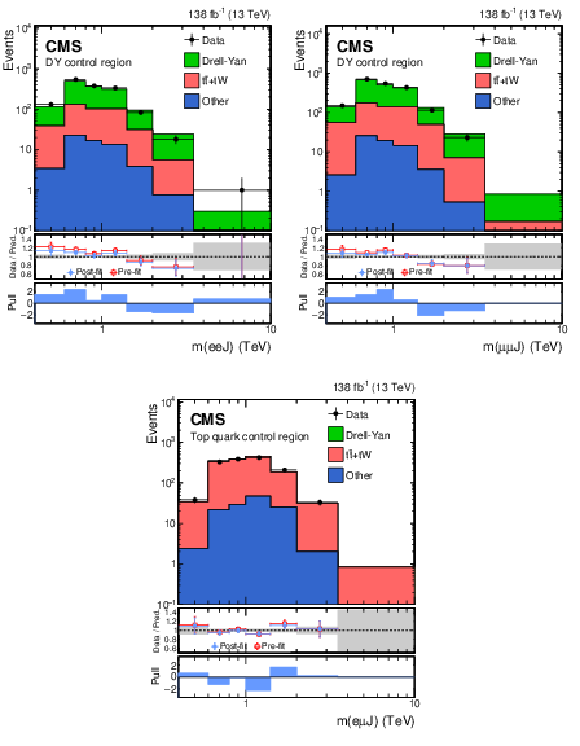
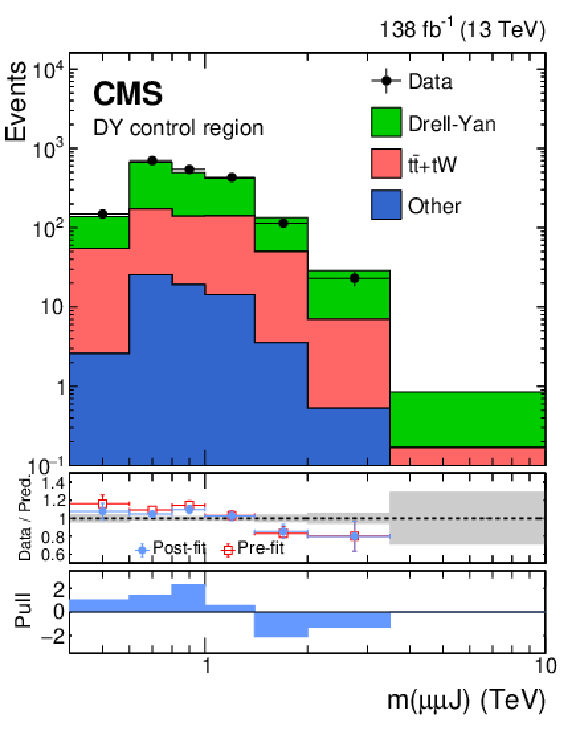
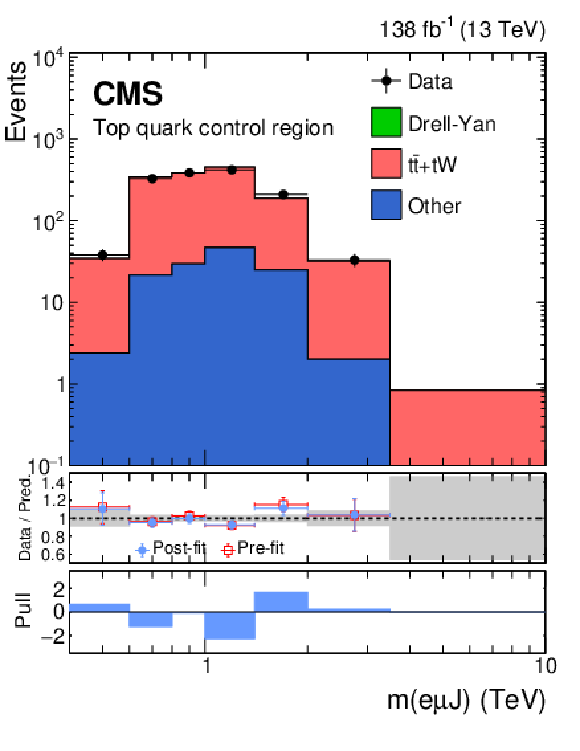
Figure 3:
Distribution of $ m(\ell\ell\,\mathrm{J}) $ in the DY-enriched CR for the electron (upper left) and muon (upper right) flavors, and of $ m(\mathrm{e}\mu \mathrm{J}) $ in the top-quark-enriched CR (lower). Data points are overlaid on the post-fit background (stacked histograms). The overflow is included in the last bin. The middle panels show ratios of the data to the pre-fit background prediction and post-fit background yield as red open squares and blue points, respectively. The gray band in the middle panels indicates the systematic component of the post-fit uncertainty. The lower panels show the distributions of the pulls, defined in the text. |

png pdf |
Figure 3-a:
Distribution of $ m(\ell\ell\,\mathrm{J}) $ in the DY-enriched CR for the electron flavor. Data points are overlaid on the post-fit background (stacked histograms). The overflow is included in the last bin. The middle panel shows ratios of the data to the pre-fit background prediction and post-fit background yield as red open squares and blue points, respectively. The gray band in the middle panel indicates the systematic component of the post-fit uncertainty. The lower panel shows the distributions of the pulls, defined in the text. |
png pdf |
Figure 3-b:
Distribution of $ m(\ell\ell\,\mathrm{J}) $ in the DY-enriched CR for the muon flavor. Data points are overlaid on the post-fit background (stacked histograms). The overflow is included in the last bin. The middle panel shows ratios of the data to the pre-fit background prediction and post-fit background yield as red open squares and blue points, respectively. The gray band in the middle panel indicates the systematic component of the post-fit uncertainty. The lower panel shows the distributions of the pulls, defined in the text. |
png pdf |
Figure 3-c:
Distribution of $ m(\mathrm{e}\mu \mathrm{J}) $ in the top-quark-enriched CR. Data points are overlaid on the post-fit background (stacked histograms). The overflow is included in the last bin. The middle panel shows ratios of the data to the pre-fit background prediction and post-fit background yield as red open squares and blue points, respectively. The gray band in the middle panel indicates the systematic component of the post-fit uncertainty. The lower panel shows the distributions of the pulls, defined in the text. |

png pdf |
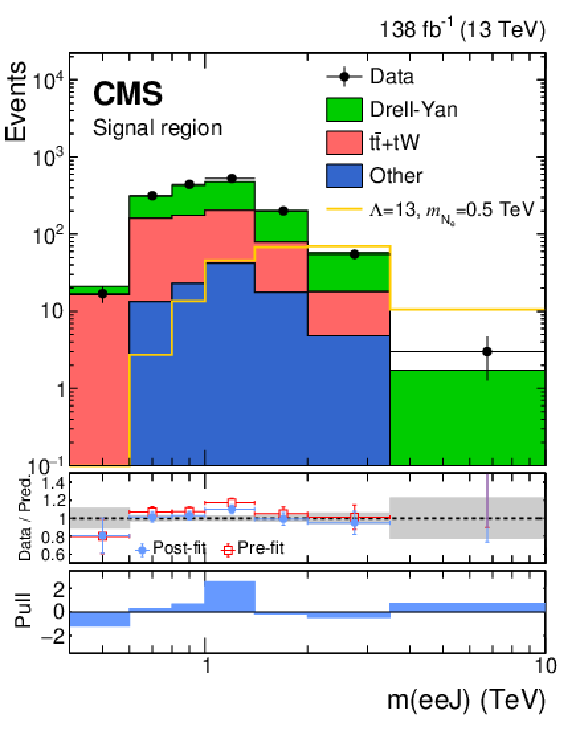
Figure 4:
Distributions of $ m(\ell\ell\,\mathrm{J}) $ for the data, and the post-fit backgrounds (stacked histograms), in the SRs of the $ \mathrm{e}\mathrm{e}\mathrm{q}\overline{\mathrm{q}}^\prime $ (left) and the $ \mu\mu\mathrm{q}\overline{\mathrm{q}}^\prime $ (right) channels. The template for one signal hypothesis is shown overlaid as a yellow solid line. The overflow is included in the last bin. The middle panels show ratios of the data to the pre-fit background prediction and post-fit background yield as red open squares and blue points, respectively. The gray band in the middle panels indicates the systematic component of the post-fit uncertainty. The lower panels show the distributions of the pulls, defined in the text. |
png pdf |
Figure 4-a:
Distribution of $ m(\ell\ell\,\mathrm{J}) $ for the data, and the post-fit backgrounds (stacked histograms), in the SRs of the $ \mathrm{e}\mathrm{e}\mathrm{q}\overline{\mathrm{q}}^\prime $ channel. The template for one signal hypothesis is shown overlaid as a yellow solid line. The overflow is included in the last bin. The middle panel shows ratios of the data to the pre-fit background prediction and post-fit background yield as red open squares and blue points, respectively. The gray band in the middle panel indicates the systematic component of the post-fit uncertainty. The lower panel shows the distributions of the pulls, defined in the text. |
png pdf |
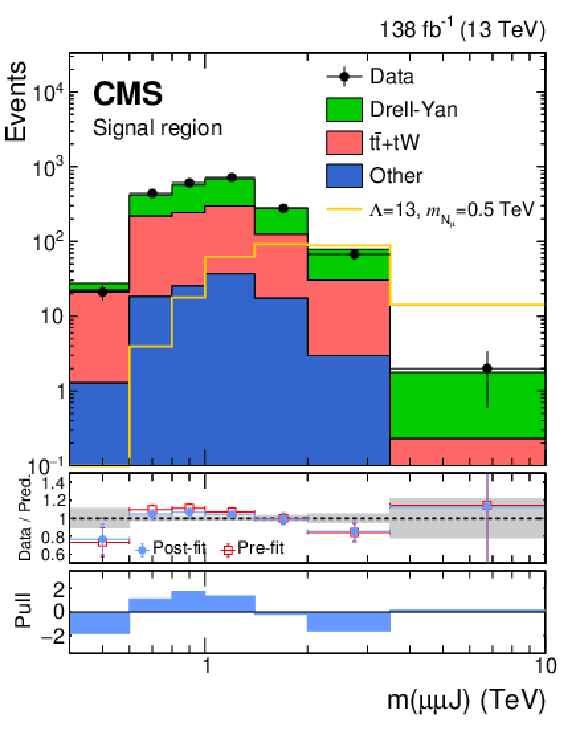
Figure 4-b:
Distribution of $ m(\ell\ell\,\mathrm{J}) $ for the data, and the post-fit backgrounds (stacked histograms), in the SRs of the $ \mu\mu\mathrm{q}\overline{\mathrm{q}}^\prime $ channel. The template for one signal hypothesis is shown overlaid as a yellow solid line. The overflow is included in the last bin. The middle panel shows ratios of the data to the pre-fit background prediction and post-fit background yield as red open squares and blue points, respectively. The gray band in the middle panel indicates the systematic component of the post-fit uncertainty. The lower panel shows the distributions of the pulls, defined in the text. |

png pdf |
Figure 5:
Expected (black dashed lines with green dark and yellow light bands) and observed (solid blue lines) limits on the product of cross section and branching fraction for the $ \mathrm{e}\mathrm{e}\mathrm{q}\overline{\mathrm{q}}^\prime $ (left) and $ \mu\mu\mathrm{q}\overline{\mathrm{q}}^\prime $ (right) channels. The uncertainty bands account for the post-fit statistical and systematic uncertainty. The magenta dot-dashed lines denote the model cross sections for the benchmark scale parameter $ \Lambda = $ 13 TeV. |

png pdf |
Figure 5-a:
Expected (black dashed lines with green dark and yellow light bands) and observed (solid blue lines) limits on the product of cross section and branching fraction for the $ \mathrm{e}\mathrm{e}\mathrm{q}\overline{\mathrm{q}}^\prime $ channel. The uncertainty band accounts for the post-fit statistical and systematic uncertainty. The magenta dot-dashed line denotes the model cross sections for the benchmark scale parameter $ \Lambda = $ 13 TeV. |

png pdf |
Figure 5-b:
Expected (black dashed lines with green dark and yellow light bands) and observed (solid blue lines) limits on the product of cross section and branching fraction for the $ \mu\mu\mathrm{q}\overline{\mathrm{q}}^\prime $ channel. The uncertainty band accounts for the post-fit statistical and systematic uncertainty. The magenta dot-dashed line denotes the model cross sections for the benchmark scale parameter $ \Lambda = $ 13 TeV. |
png pdf |
Figure 6:
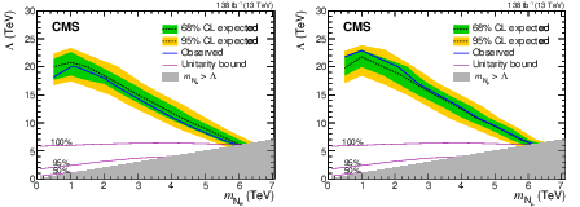
Expected (black dashed lines with green dark and yellow light bands) and observed (solid blue lines) limits in the ($ m_{\mathrm{N}_{\ell}} $, $ \Lambda $) plane of the composite model for the $ \mathrm{e}\mathrm{e}\mathrm{q}\overline{\mathrm{q}}^\prime $ (left) and $ \mu\mu\mathrm{q}\overline{\mathrm{q}}^\prime $ (right) channels. The gray shading indicates the region where $ m_{\mathrm{N}_{\ell}} $ would exceed $ \Lambda $, the EFT scale parameter, and the three solid magenta lines in the lower part of the plots represent the fraction of the signal-model phase space that satisfies the unitarity condition in the EFT approximation. |
png pdf |
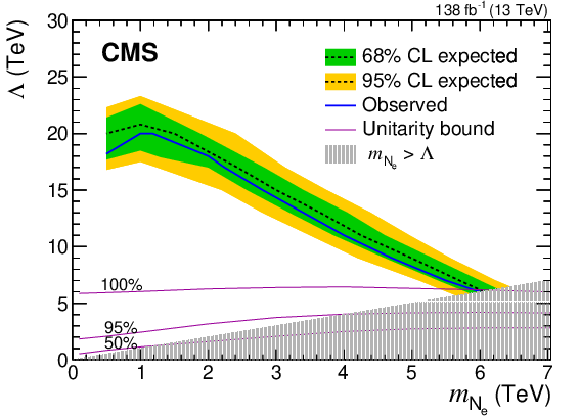
Figure 6-a:
Expected (black dashed lines with green dark and yellow light bands) and observed (solid blue lines) limits in the ($ m_{\mathrm{N}_{\ell}} $, $ \Lambda $) plane of the composite model for the $ \mathrm{e}\mathrm{e}\mathrm{q}\overline{\mathrm{q}}^\prime $ channel. The gray shading indicates the region where $ m_{\mathrm{N}_{\ell}} $ would exceed $ \Lambda $, the EFT scale parameter, and the three solid magenta lines in the lower part of the plot represent the fraction of the signal-model phase space that satisfies the unitarity condition in the EFT approximation. |
png pdf |
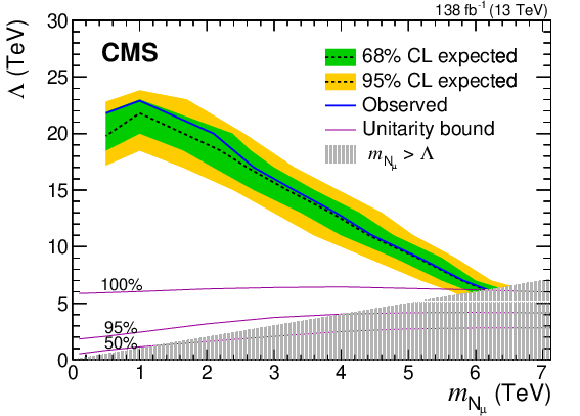
Figure 6-b:
Expected (black dashed lines with green dark and yellow light bands) and observed (solid blue lines) limits in the ($ m_{\mathrm{N}_{\ell}} $, $ \Lambda $) plane of the composite model for the $ \mu\mu\mathrm{q}\overline{\mathrm{q}}^\prime $ channel. The gray shading indicates the region where $ m_{\mathrm{N}_{\ell}} $ would exceed $ \Lambda $, the EFT scale parameter, and the three solid magenta lines in the lower part of the plot represent the fraction of the signal-model phase space that satisfies the unitarity condition in the EFT approximation. |
| Tables | |
png pdf |
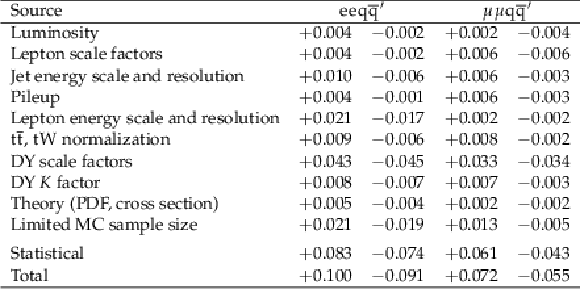
Table 1:
The impact of each systematic uncertainty on the signal strength $ \mu $ as extracted from the ML fit, for the $ \mathrm{N}_{\ell} $ signal point with $ m_{\mathrm{N}_{\ell}} = $ 0.5 TeV and $ \Lambda = $ 13 TeV. Upper and lower uncertainties are given, for both electron and muon channels. |
| Summary |
| A search is reported for a heavy composite Majorana neutrino $ \mathrm{N}_{\ell} $, where the flavor $ \ell $ corresponds to an electron or muon, that appears in composite fermion models. In the specific model considered, the $ \mathrm{N}_{\ell} $ is produced in association with a lepton and subsequently decays into a same-flavor lepton plus two quarks, leading to a signature with two same-flavor leptons and at least one large-radius jet. The analysis is performed using a sample of proton-proton collisions at $ \sqrt{s} = $ 13 TeV recorded by the CMS experiment at the CERN LHC, corresponding to an integrated luminosity of 138 fb$ ^{-1} $. The data are found to be in agreement with the standard model expectations. In the context of an effective field theory with compositeness scale parameter $ \Lambda $, an upper limit at 95% CL is established on $ \sigma(\mathrm{p}\mathrm{p}\to\ell\mathrm{N}_{\ell})\mathcal{B}(\mathrm{N}_{\ell}\to\ell\mathrm{q}\overline{\mathrm{q}}^\prime) $ as a function of $ \Lambda $ and the $ \mathrm{N}_{\ell} $ mass $ m_{\mathrm{N}_{\ell}} $. Masses less than 6.0 (6.1) TeV are excluded for $ \ell =\mathrm{e}\,(\mu) $, at the limit $ m_{\mathrm{N}_{\ell}} = \Lambda $. For $ m_{\mathrm{N}_{\ell}} \approx $ 1 TeV, values of $ \Lambda $ less than 20 (23) TeV are excluded. The present search represents a considerable improvement in sensitivity, covering a larger parameter space than previous searches in pp collisions at 13 TeV. |
| References | ||||
| 1 | J. C. Pati, A. Salam, and J. A. Strathdee | Are quarks composite? | PLB 59 (1975) 265 | |
| 2 | J. C. Pati and A. Salam | Supersymmetry at the preonic or prepreonic level and composite supergravity | NPB 214 (1983) 109 | |
| 3 | H. Harari | Composite models for quarks and leptons | Phys. Rep. 104 (1984) 159 | |
| 4 | O. W. Greenberg and C. A. Nelson | Composite models of leptons | PRD 10 (1974) 2567 | |
| 5 | P. A. M. Dirac | The evolution of the physicist's picture of nature | Sci. Am. 208 (1963) 45 | |
| 6 | H. Terazawa, K. Akama, and Y. Chikashige | Unified model of the Nambu-Jona-Lasinio type for all elementary particle forces | PRD 15 (1977) 480 | |
| 7 | E. Eichten and K. D. Lane | Dynamical breaking of weak interaction symmetries | PLB 90 (1980) 125 | |
| 8 | E. Eichten, K. D. Lane, and M. E. Peskin | New tests for quark and lepton substructure | PRL 50 (1983) 811 | |
| 9 | U. Baur, M. Spira, and P. M. Zerwas | Excited quark and lepton production at hadron colliders | PRD 42 (1990) 815 | |
| 10 | U. Baur, I. Hinchliffe, and D. Zeppenfeld | Excited quark production at hadron colliders | Int. J. Mod. Phys. A 2 (1987) 1285 | |
| 11 | H. Terazawa | t quark mass predicted from a sum rule for lepton and quark masses | PRD 22 (1980) 2921 | |
| 12 | N. Cabibbo, L. Maiani, and Y. Srivastava | Anomalous Z decays: excited leptons? | PLB 139 (1984) 459 | |
| 13 | O. Panella and Y. N. Srivastava | Bounds on compositeness from neutrinoless double beta decay | PRD 52 (1995) 5308 | hep-ph/9411224 |
| 14 | O. Panella, C. Carimalo, Y. N. Srivastava, and A. Widom | Neutrinoless double beta decay with composite neutrinos | PRD 56 (1997) 5766 | hep-ph/9701251 |
| 15 | O. Panella, C. Carimalo, and Y. N. Srivastava | Production of like sign dileptons in pp collisions through composite majorana neutrinos | PRD 62 (2000) 015013 | hep-ph/9903253 |
| 16 | S. Biondini et al. | Complementarity between neutrinoless double beta decay and collider searches for heavy neutrinos in composite-fermion models | 11, 2021 | 2111.01053 |
| 17 | M. Fukugita and T. Yanagida | Baryogenesis without grand unification | PLB 174 (1986) 45 | |
| 18 | S. Davidson, E. Nardi, and Y. Nir | Leptogenesis | Phys. Rept. 466 (2008) 105 | 0802.2962 |
| 19 | D. Zhuridov | Baryogenesis from leptomesons | PRD 94 (2016) 035007 | 1604.07740 |
| 20 | S. Biondini and O. Panella | Leptogenesis and composite heavy neutrinos with gauge mediated interactions | EPJC 77 (2017) 644 | 1707.00844 |
| 21 | R. Leonardi et al. | Hunting for heavy composite Majorana neutrinos at the LHC | EPJC 76 (2016) 593 | 1510.07988 |
| 22 | CMS Collaboration | Search for a heavy composite Majorana neutrino in the final state with two leptons and two quarks at $ \sqrt{s}= $ 13 TeV | PLB 775 (2017) 315 | CMS-EXO-16-026 1706.08578 |
| 23 | S. Biondini, R. Leonardi, O. Panella, and M. Presilla | Perturbative unitarity bounds for effective composite models | PLB 795 (2019) 644 | 1903.12285 |
| 24 | CMS Collaboration | HEPData record for this analysis | link | |
| 25 | ATLAS Collaboration | Search for excited leptons in proton-proton collisions at $ \sqrt{s} = $ 7 TeV with the ATLAS detector | PRD 85 (2012) 072003 | 1201.3293 |
| 26 | ATLAS Collaboration | Search for excited electrons and muons in $ \sqrt{s} = $ 8 TeV proton-proton collisions with the ATLAS detector | New J. Phys. 15 (2013) 093011 | 1308.1364 |
| 27 | CMS Collaboration | Search for excited leptons in pp collisions at $ \sqrt{s}= $ 7 TeV | PLB 720 (2013) 309 | CMS-EXO-11-034 1210.2422 |
| 28 | CMS Collaboration | Search for excited leptons in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JHEP 03 (2016) 125 | CMS-EXO-14-015 1511.01407 |
| 29 | CMS Collaboration | Search for excited leptons in $ \ell\ell\gamma $ final states in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 04 (2019) 015 | CMS-EXO-18-004 1811.03052 |
| 30 | CMS Collaboration | Search for an excited lepton that decays via a contact interaction to a lepton and two jets in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 05 (2020) 052 | CMS-EXO-18-013 2001.04521 |
| 31 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 32 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 33 | CMS Collaboration | The CMS Experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 34 | A. Belyaev, N. D. Christensen, and A. Pukhov | CalcHEP 3.4 for collider physics within and beyond the Standard Model | Comput. Phys. Commun. 184 (2013) 1729 | 1207.6082 |
| 35 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 36 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 37 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 38 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 39 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: $ s $- and $ t $-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 40 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 41 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 42 | J. M. Lindert et al. | Precise predictions for V+jets dark matter backgrounds | EPJC 77 (2017) 829 | 1705.04664 |
| 43 | CMS Collaboration | Measurements of differential Z boson production cross sections in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 12 (2019) 061 | CMS-SMP-17-010 1909.04133 |
| 44 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 45 | CMS Collaboration | Search for new physics in final states with an energetic jet or a hadronically decaying W or Z boson and transverse momentum imbalance at $ \sqrt{s}= $ 13 TeV | Phys. Rev. D 97 ), no.~9, 0, 2018 link |
CMS-EXO-16-048 1712.02345 |
| 46 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 47 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 48 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 49 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA 8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 50 | GEANT4 Collaboration | GEANT 4---A simulation toolkit | NIM A 506 (2003) 250 | |
| 51 | T. Melia, P. Nason, R. Rontsch, and G. Zanderighi | W$ ^+ $W$ ^- $, WZ and ZZ production in the POWHEG BOX | JHEP 11 (2011) 078 | 1107.5051 |
| 52 | M. Beneke, P. Falgari, S. Klein, and C. Schwinn | Hadronic top-quark pair production with NNLL threshold resummation | NPB 855 (2012) 695 | 1109.1536 |
| 53 | M. Cacciari et al. | Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation | PLB 710 (2012) 612 | 1111.5869 |
| 54 | P. Bärnreuther, M. Czakon, and A. Mitov | Percent level precision physics at the Tevatron: first genuine NNLO QCD corrections to $ \mathrm{q}\overline{\mathrm{q}}\to{\mathrm{t}\overline{\mathrm{t}}}$+X | PRL 109 (2012) 132001 | 1204.5201 |
| 55 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels | JHEP 12 (2012) 054 | 1207.0236 |
| 56 | M. Czakon and A. Mitov | NNLO corrections to top pair production at hadron colliders: the quark-gluon reaction | JHEP 01 (2013) 080 | 1210.6832 |
| 57 | M. Czakon, P. Fiedler, and A. Mitov | Total top-quark pair-production cross section at hadron colliders through $ O(\alpha_\mathrm{S}^4) $ | PRL 110 (2013) 252004 | 1303.6254 |
| 58 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order | Comput. Phys. Commun. 182 (2011) 2388 | 1011.3540 |
| 59 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 60 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 61 | CMS Collaboration | ECAL 2016 refined calibration and Run2 summary plots | CMS Detector Performance Summary CMS-DP-2020-021, 2020 CDS |
|
| 62 | CMS Collaboration | Performance of the reconstruction and identification of high-momentum muons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P02027 | CMS-MUO-17-001 1912.03516 |
| 63 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 64 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 65 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 66 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 67 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 68 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 69 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2018 link |
CMS-PAS-LUM-17-004 |
| 70 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 link |
CMS-PAS-LUM-18-002 |
| 71 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 72 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 73 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 74 | R. J. Barlow and C. Beeston | Fitting using finite Monte Carlo samples | Comput. Phys. Commun. 77 (1993) 219 | |
| 75 | J. S. Conway | Incorporating nuisance parameters in likelihoods for multisource spectra | in PHYSTAT, 2011 link |
1103.0354 |
| 76 | T. Junk | Confidence level computation for combining searches with small statistics | NIM A 434 (1999) 435 | hep-ex/9902006 |
| 77 | A. L. Read | Presentation of search results: The $ \text{CL}_s $ technique | JPG 28 (2002) 2693 | |
| 78 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|