CMS-B2G-20-009

CMS-B2G-20-009 ; CERN-EP-2022-152
Search for new heavy resonances decaying to WW, WZ, ZZ, WH, or ZH boson pairs in the all-jets final state in proton-proton collisions at $ \sqrt{s}= $ 13 TeV
CMS Collaboration
30 September 2022
Phys. Lett. B 844 (2023) 137813
Abstract: A search for new heavy resonances decaying to WW, WZ, ZZ, WH, or ZH boson pairs in the all-jets final state is presented. The analysis is based on proton-proton collision data recorded by the CMS detector in 2016-2018 at a centre-of-mass energy of 13 TeV at the CERN LHC, corresponding to an integrated luminosity of 138 fb$^{-1}$. The search is sensitive to resonances with masses above 1.3 TeV, decaying to bosons that are highly Lorentz-boosted such that each of the bosons forms a single large-radius jet. Machine learning techniques are employed to identify such jets. No significant excess over the estimated standard model background is observed. A maximum local significance of 3.6 standard deviations, corresponding to a global significance of 2.3 standard deviations, is observed at masses of 2.1 and 2.9 TeV. In a heavy vector triplet model, spin-1 Z' and W' resonances with masses below 4.8 TeV are excluded at the 95% confidence level (CL). These limits are the most stringent to date. In a bulk graviton model, spin-2 gravitons and spin-0 radions with masses below 1.4 and 2.7 TeV, respectively, are excluded at 95% CL. Production of heavy resonances through vector boson fusion is constrained with upper cross section limits at 95% CL as low as 0.1 fb.
Links: e-print arXiv:2210.00043 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; Physics Briefing ; CADI line (restricted) ;

Figures & Tables	Summary	Additional Figures	References	CMS Publications

Figures
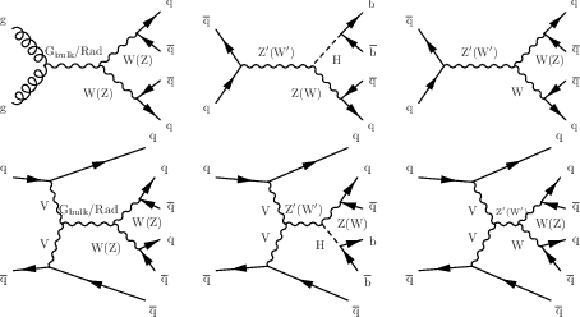
png pdf	Figure 1: Feynman diagrams of the signal processes ggF or DY produced (upper) and VBF produced (lower): (left) graviton or radion decaying to WW or ZZ; (center) Z' and W' decaying to ZH and WH, respectively; (right) Z' and W' decaying to WW and WZ, respectively.
png pdf	Figure 1-a: Example Feynman diagram of signal process: DY produced graviton or radion decaying to WW or ZZ.
png pdf	Figure 1-b: Example Feynman diagram of signal process: DY produced Z' and W' decaying to ZH and WH, respectively.
png pdf	Figure 1-c: Example Feynman diagram of signal process: DY produced Z' and W' decaying to WW and WZ, respectively.
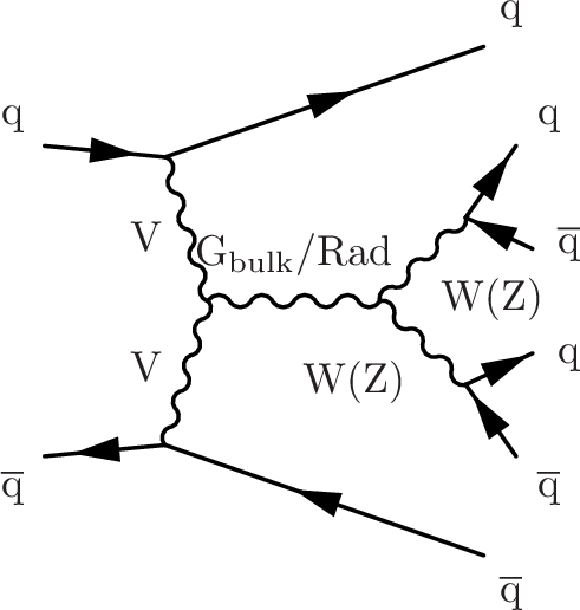
png pdf	Figure 1-d: Example Feynman diagram of signal process: VBF produced graviton or radion decaying to WW or ZZ.
png pdf	Figure 1-e: Example Feynman diagram of signal process: VBF produced Z' and W' decaying to ZH and WH, respectively.
png pdf	Figure 1-f: Example Feynman diagram of signal process: VBF produced Z' and W' decaying to WW and WZ, respectively.
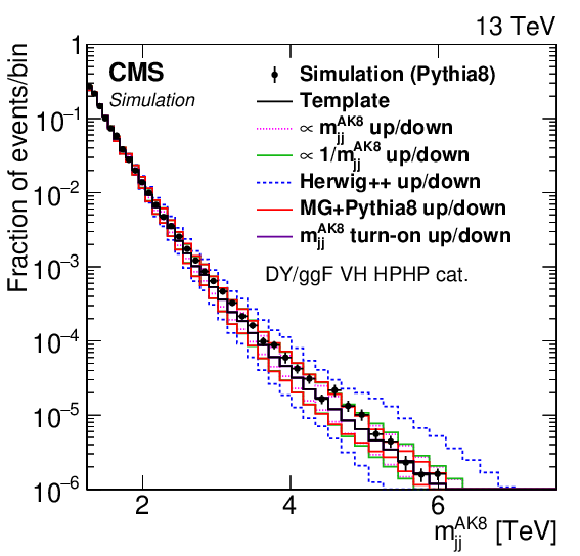
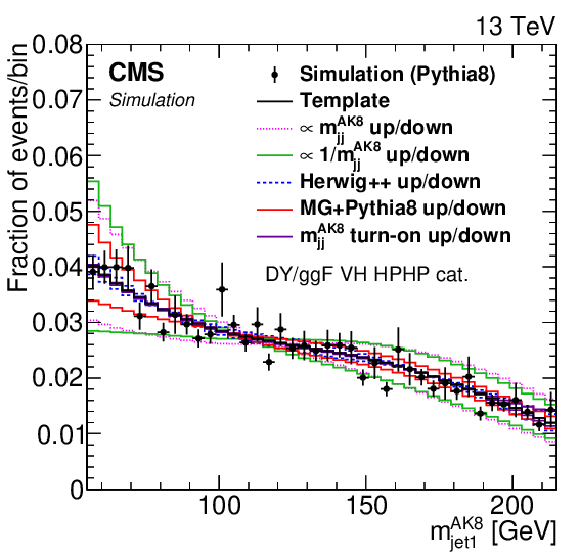
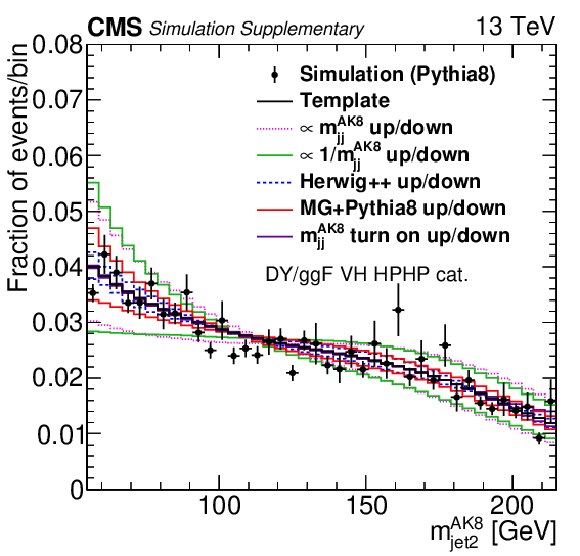
png pdf	Figure 2: Distributions of $ m_\mathrm{jj}^{ \mathrm{AK8} } $ (left) and $ m_\text{jet1}^{ \mathrm{AK8} } $ (right) in the nominal QCD multijet simulation using PYTHIA 8 (black markers) and three-dimensional templates (black solid line) in the DY/ggF VH HPHP category. Superimposed are the normalized up and down variations of five alternative shapes corresponding to shape nuisance parameters in the fit model. Each of the variations has a characteristic dependence on $ m_\text{jet}^{ \mathrm{AK8} } $ to allow the necessary flexibility in the fit for the template to adapt to the data. We also allow an overall variation of the rate in the fit.
png pdf	Figure 2-a: Distribution of $ m_\mathrm{jj}^{ \mathrm{AK8} } $ in the nominal QCD multijet simulation using PYTHIA 8 (black markers) and three-dimensional templates (black solid line) in the DY/ggF VH HPHP category. Superimposed are the normalized up and down variations of five alternative shapes corresponding to shape nuisance parameters in the fit model. Each of the variations has a characteristic dependence on $ m_\text{jet}^{ \mathrm{AK8} } $ to allow the necessary flexibility in the fit for the template to adapt to the data. We also allow an overall variation of the rate in the fit.
png pdf	Figure 2-b: Distribution of $ m_\text{jet1}^{ \mathrm{AK8} } $ in the nominal QCD multijet simulation using PYTHIA 8 (black markers) and three-dimensional templates (black solid line) in the DY/ggF VH HPHP category. Superimposed are the normalized up and down variations of five alternative shapes corresponding to shape nuisance parameters in the fit model. Each of the variations has a characteristic dependence on $ m_\text{jet}^{ \mathrm{AK8} } $ to allow the necessary flexibility in the fit for the template to adapt to the data. We also allow an overall variation of the rate in the fit.
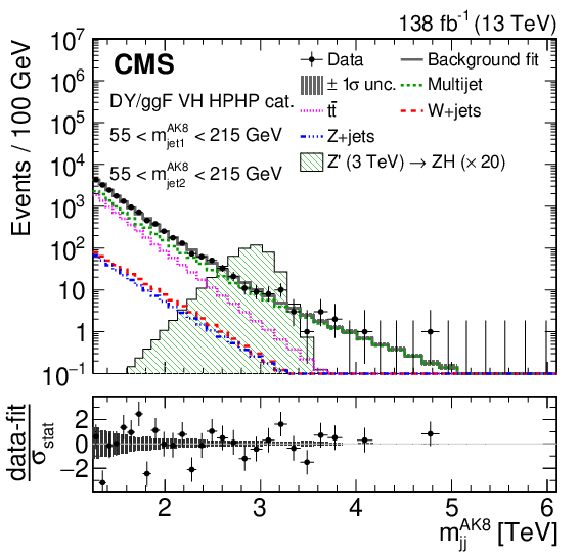
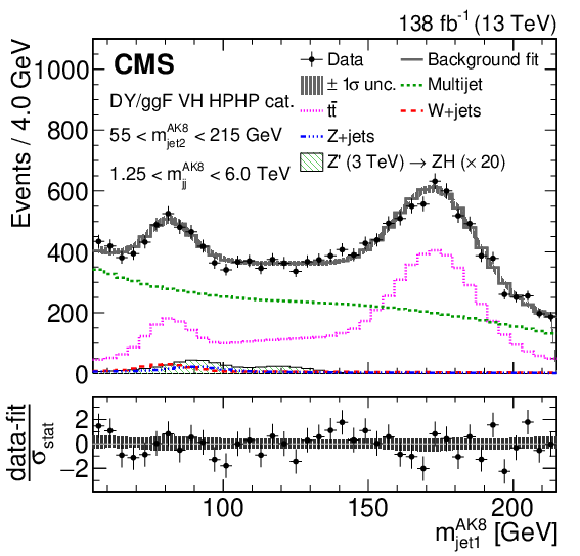
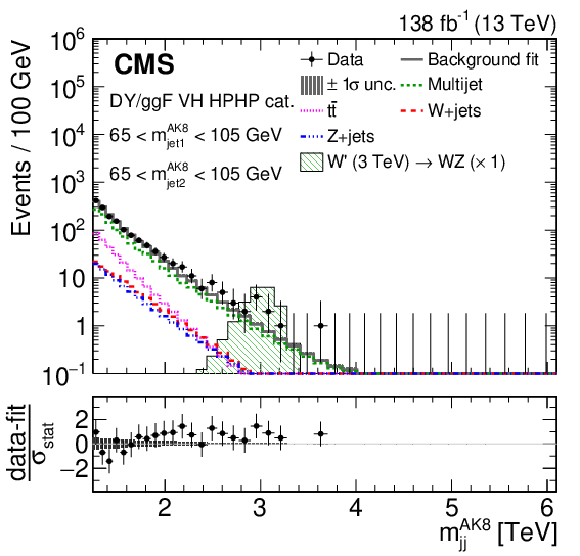
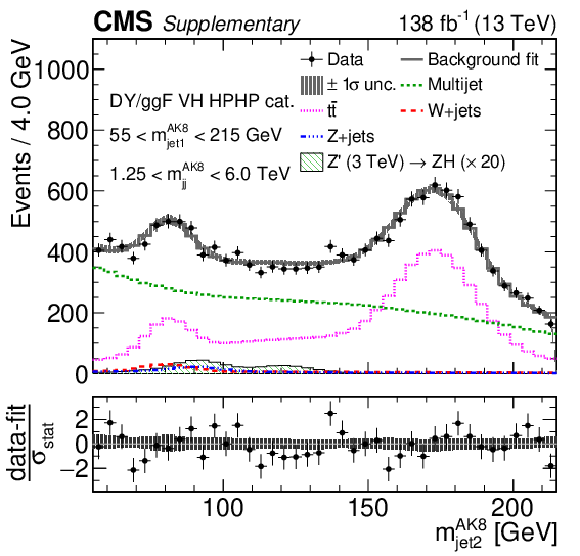
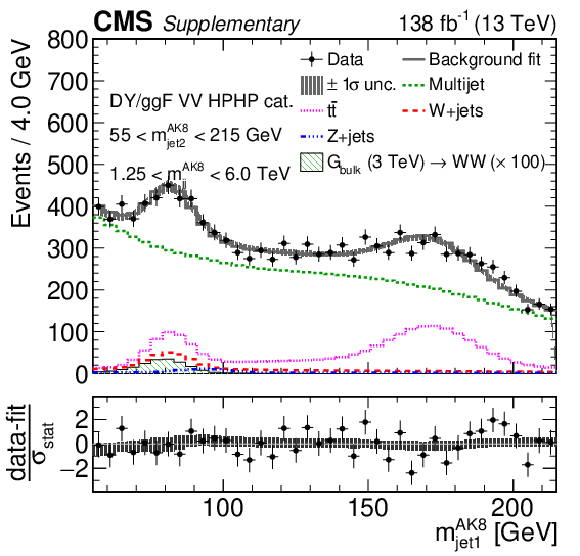
png pdf	Figure 3: Comparison between the background post-fit and the data distributions of $ m_\mathrm{jj}^{ \mathrm{AK8} } $ (left) and $ m_\text{jet1}^{ \mathrm{AK8} } $ (right) in the DY/ggF VH HPHP category. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are represented as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor of 20. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Figure 3-a: Comparison between the background post-fit and the data distributions of $ m_\mathrm{jj}^{ \mathrm{AK8} } $ in the DY/ggF VH HPHP category. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are represented as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor of 20. Shown below the plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Figure 3-b: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{ \mathrm{AK8} } $ in the DY/ggF VH HPHP category. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are represented as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor of 20. Shown below the plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
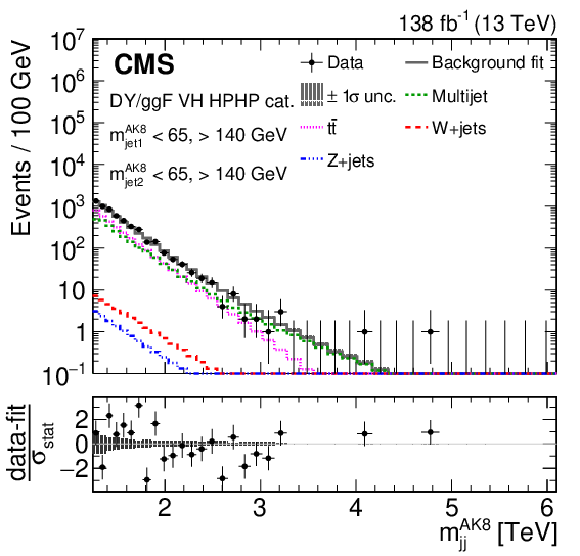
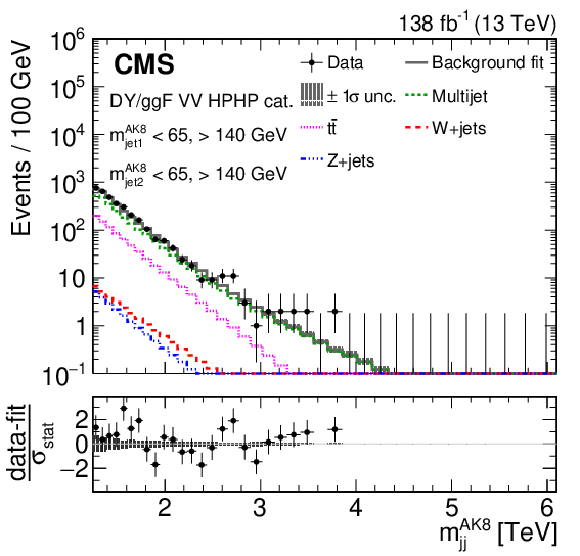
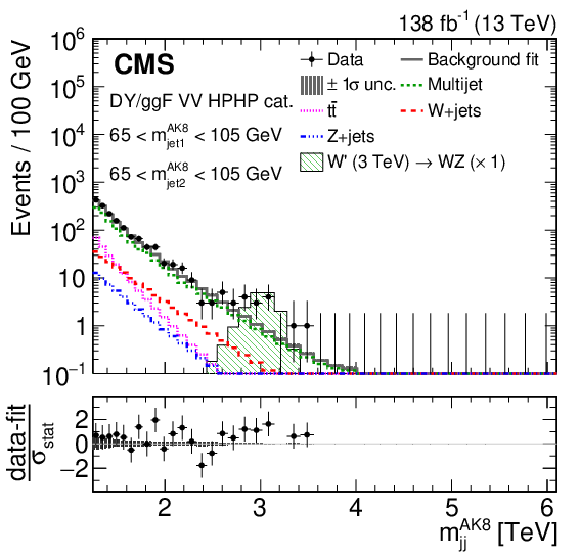
png pdf	Figure 4: Projections of the data and background post-fit distributions onto the $ m_\mathrm{jj}^{ \mathrm{AK8} } $ dimension in regions enriched in background ($ m_\text{jet1}^{\mathrm{AK8}} < $ 65 or $ > $140 GeV, and $ m_\text{jet2}^{\mathrm{AK8}} < $ 65 or $ > $140 GeV), for the HPHP VH (left) and VV (right) DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Figure 4-a: Projection of the data and background post-fit distributions onto the $ m_\mathrm{jj}^{ \mathrm{AK8} } $ dimension in regions enriched in background ($ m_\text{jet1}^{\mathrm{AK8}} < $ 65 or $ > $140 GeV, and $ m_\text{jet2}^{\mathrm{AK8}} < $ 65 or $ > $140 GeV), for the HPHP VH DY/ggF category. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below the plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Figure 4-b: Projection of the data and background post-fit distributions onto the $ m_\mathrm{jj}^{ \mathrm{AK8} } $ dimension in regions enriched in background ($ m_\text{jet1}^{\mathrm{AK8}} < $ 65 or $ > $140 GeV, and $ m_\text{jet2}^{\mathrm{AK8}} < $ 65 or $ > $140 GeV), for the HPHP VV DY/ggF category. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below the plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
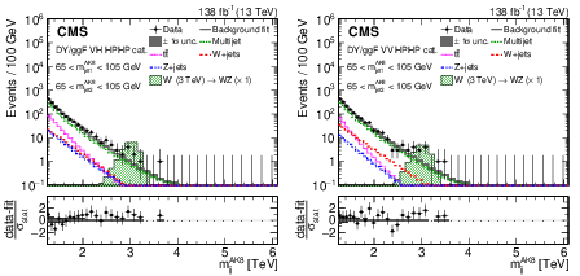
png pdf	Figure 5: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{ \mathrm{AK8} } $ dimension in regions enriched in signal from DY/ggF VV ( 65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV) for the HPHP VH (left) and VV (right) DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Figure 5-a: Projection of data and background post-fit distributions onto the $ m_\mathrm{jj}^{ \mathrm{AK8} } $ dimension in regions enriched in signal from DY/ggF VV ( 65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV) for the HPHP VH DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid. Shown below the plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Figure 5-b: Projection of data and background post-fit distributions onto the $ m_\mathrm{jj}^{ \mathrm{AK8} } $ dimension in regions enriched in signal from DY/ggF VV ( 65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV) for the HPHP VV DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid. Shown below the plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
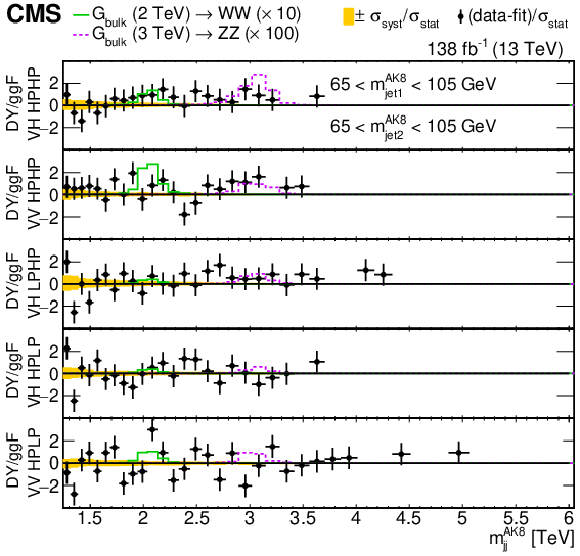
png pdf	Figure 6: Distributions of the difference between the data and the background-only fit divided by the statistical uncertainty in the data. The total uncertainty in the background estimate fitted to data divided by the statistical uncertainty in the data is shown as a band. It should be noted that these two uncertainties are partially correlated. Three projections of the 3D phase space are shown in regions enriched in signal from DY/ggF VV (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV) (upper left), DY/ggF VH (65 $ < m_\text{jet1/2}^{\mathrm{AK8}} < $ 105 GeV, 110 $ < m_\text{jet2/1}^{\mathrm{AK8}} < $ 140 GeV) (upper right) and VBF VV/VH (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 140 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 140 GeV) (lower). Examples of expected signal shapes added to the fit are overlaid, where the number of expected events is scaled by an arbitrary normalization factor stated in the legend.
png pdf	Figure 6-a: Distribution of the difference between the data and the background-only fit divided by the statistical uncertainty in the data. The total uncertainty in the background estimate fitted to data divided by the statistical uncertainty in the data is shown as a band. It should be noted that these two uncertainties are partially correlated. The projection of the 3D phase space is shown in the 65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV region. Examples of expected signal shapes added to the fit are overlaid, where the number of expected events is scaled by an arbitrary normalization factor stated in the legend.
png pdf	Figure 6-b: Distribution of the difference between the data and the background-only fit divided by the statistical uncertainty in the data. The total uncertainty in the background estimate fitted to data divided by the statistical uncertainty in the data is shown as a band. It should be noted that these two uncertainties are partially correlated. The projection of the 3D phase space is shown in the DY/ggF VH (65 $ < m_\text{jet1/2}^{\mathrm{AK8}} < $ 105 GeV, 110 $ < m_\text{jet2/1}^{\mathrm{AK8}} < $ 140 GeV region. Examples of expected signal shapes added to the fit are overlaid, where the number of expected events is scaled by an arbitrary normalization factor stated in the legend.
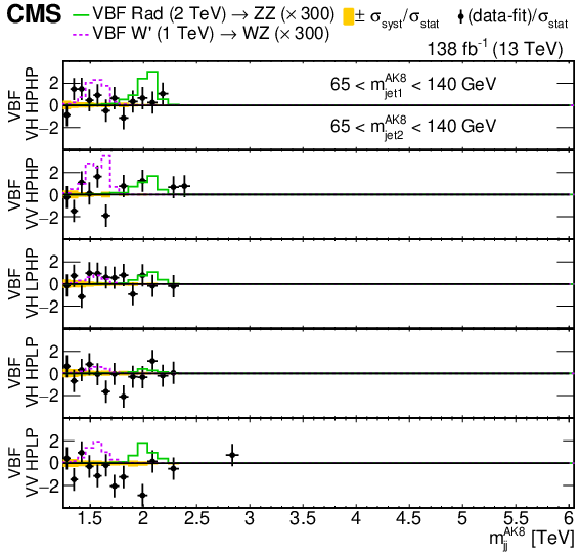
png pdf	Figure 6-c: Distribution of the difference between the data and the background-only fit divided by the statistical uncertainty in the data. The total uncertainty in the background estimate fitted to data divided by the statistical uncertainty in the data is shown as a band. It should be noted that these two uncertainties are partially correlated. The projection of the 3D phase space is shown in the VBF VV/VH (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 140 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 140 GeV region. Examples of expected signal shapes added to the fit are overlaid, where the number of expected events is scaled by an arbitrary normalization factor stated in the legend.
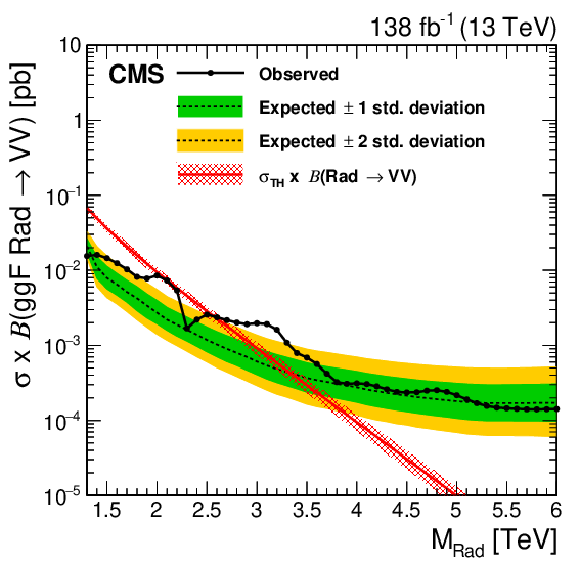
png pdf	Figure 7: Observed and expected 95% CL upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ of data at $ \sqrt{s}= $ 13 TeV, for $ \text{Rad}\to\mathrm{V}\mathrm{V} $ (upper left), $ \mathrm{G}_{\text{bulk}}\to\mathrm{V}\mathrm{V} $ (upper right), HVT model B $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{V} $+ VH (lower left), HVT model C $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{V} $+ VH (lower right) signals. For each signal scenario the theoretical prediction and its uncertainty associated with the choice of PDF set is shown.
png pdf	Figure 7-a: Observed and expected 95% CL upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ of data at $ \sqrt{s}= $ 13 TeV, for $ \text{Rad}\to\mathrm{V}\mathrm{V} $ signals. The theoretical prediction and its uncertainty associated with the choice of PDF set is shown.
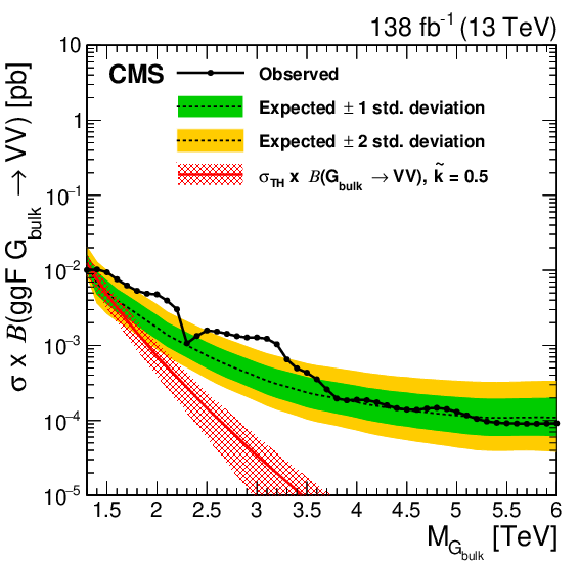
png pdf	Figure 7-b: Observed and expected 95% CL upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{G}_{\text{bulk}}\to\mathrm{V}\mathrm{V} $ signals. The theoretical prediction and its uncertainty associated with the choice of PDF set is shown.
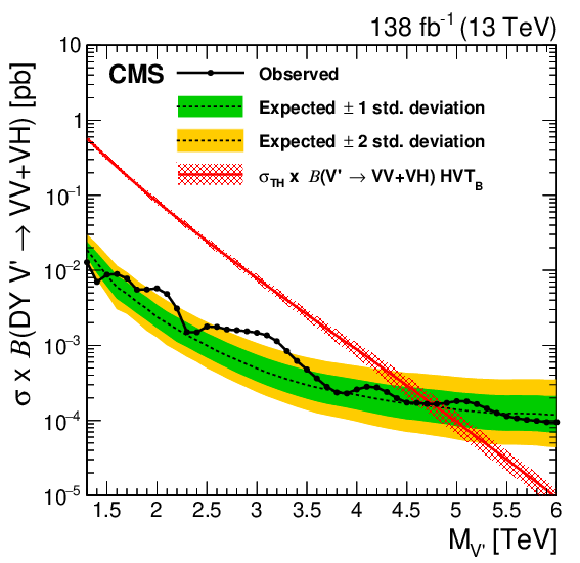
png pdf	Figure 7-c: Observed and expected 95% CL upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ of data at $ \sqrt{s}= $ 13 TeV, for HVT model B $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{V} $+ VH signals. The theoretical prediction and its uncertainty associated with the choice of PDF set is shown.
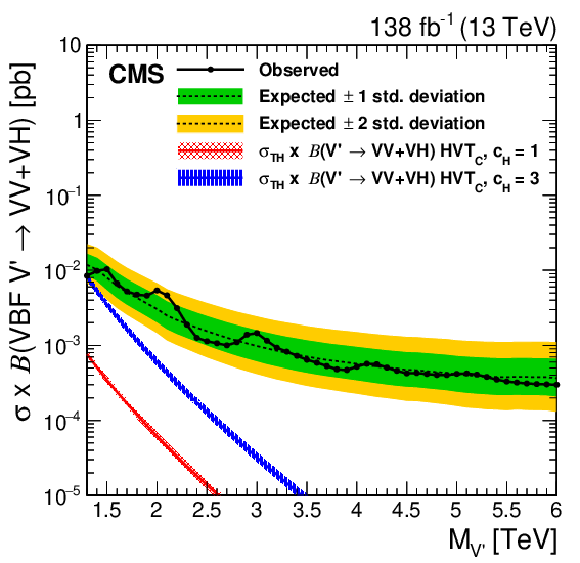
png pdf	Figure 7-d: Observed and expected 95% CL upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ of data at $ \sqrt{s}= $ 13 TeV, for HVT model C $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{V} $+ VH signals. The theoretical prediction and its uncertainty associated with the choice of PDF set is shown.

Tables
png pdf	Table 1: Summary of the event category definitions. The categories are listed from the highest to the lowest sensitivity in each production mode. The percentages correspond to the maximum misidentification rate associated with the high (HP) and low (LP) purity working points.
png pdf	Table 2: Summary of the exclusion limits on the resonance masses for the considered models. The numbers show the lower limit at 95% CL, with the exception of the ones given in parentheses quoting the ranges of exclusion.

Summary

A search has been presented for resonances with masses above 1.3 TeV that decay to WW, WZ, ZZ, WH, or ZH boson pairs. Each of the two boson decays is clustered into one large-radius jet, yielding a dijet final state from Drell--Yan and gluon fusion production, complemented by two additional jets for vector boson fusion production. The hadronic decays of H, W, and Z bosons are identified using machine learning-based jet taggers that reduce the background from quantum chromodynamics multijet production. No evidence of a departure from the expected background is found. A maximum local significance of 3.6 standard deviations from the standard model prediction, corresponding to a global significance of 2.3 standard deviations, is observed at masses of 2.1 and 2.9 TeV. Upper limits at 95% confidence level on the resonance production cross section are set as a function of the resonance mass. In a heavy vector triplet model, spin-1 Z' and W' resonances with masses below 4.8 TeV are excluded. These limits are the most stringent to date. In a bulk graviton model, spin-2 gravitons and spin-0 radions with masses below 1.4 and 2.7 TeV, respectively, are excluded. Furthermore, the exclusive production of new heavy resonances through the vector boson fusion mode is constrained with upper cross section limits as low as 0.1 fb.

Additional Figures
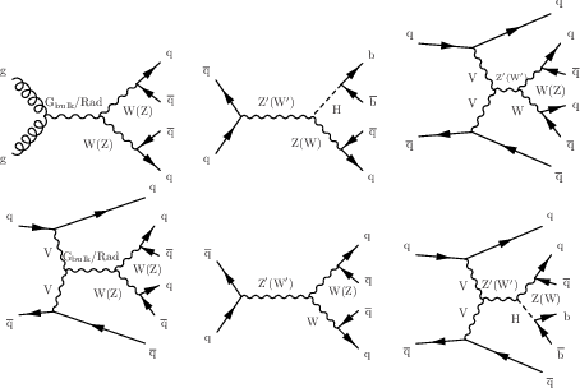
png pdf	Additional Figure 1: Example Feynman diagrams of signal processes: (top left) $ \mathrm{g} \mathrm{g} $ produced graviton or radion decaying to WW or ZZ; (top center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively; (top right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom left) VBF produced graviton or radion decaying to WW or ZZ; (bottom center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively. The diagrams on the top are shown in the paper as well, and are included here for convenience.
png pdf	Additional Figure 1-a: Example Feynman diagrams of signal processes: (top left) $ \mathrm{g} \mathrm{g} $ produced graviton or radion decaying to WW or ZZ; (top center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively; (top right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom left) VBF produced graviton or radion decaying to WW or ZZ; (bottom center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively. The diagrams on the top are shown in the paper as well, and are included here for convenience.
png pdf	Additional Figure 1-b: Example Feynman diagrams of signal processes: (top left) $ \mathrm{g} \mathrm{g} $ produced graviton or radion decaying to WW or ZZ; (top center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively; (top right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom left) VBF produced graviton or radion decaying to WW or ZZ; (bottom center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively. The diagrams on the top are shown in the paper as well, and are included here for convenience.
png pdf	Additional Figure 1-c: Example Feynman diagrams of signal processes: (top left) $ \mathrm{g} \mathrm{g} $ produced graviton or radion decaying to WW or ZZ; (top center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively; (top right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom left) VBF produced graviton or radion decaying to WW or ZZ; (bottom center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively. The diagrams on the top are shown in the paper as well, and are included here for convenience.
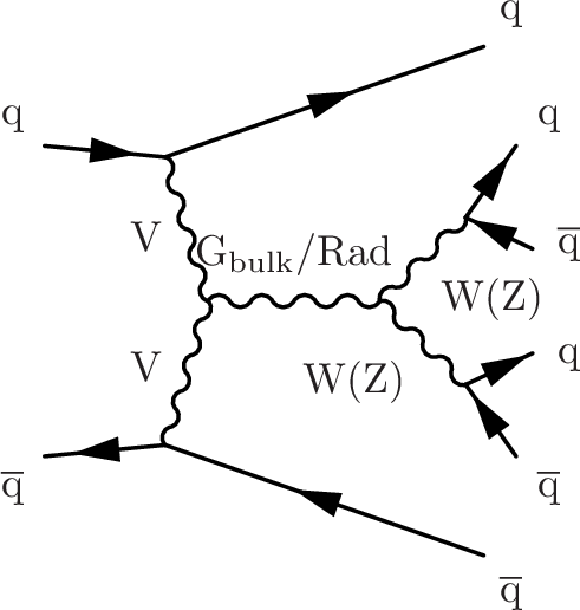
png pdf	Additional Figure 1-d: Example Feynman diagrams of signal processes: (top left) $ \mathrm{g} \mathrm{g} $ produced graviton or radion decaying to WW or ZZ; (top center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively; (top right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom left) VBF produced graviton or radion decaying to WW or ZZ; (bottom center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively. The diagrams on the top are shown in the paper as well, and are included here for convenience.
png pdf	Additional Figure 1-e: Example Feynman diagrams of signal processes: (top left) $ \mathrm{g} \mathrm{g} $ produced graviton or radion decaying to WW or ZZ; (top center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively; (top right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom left) VBF produced graviton or radion decaying to WW or ZZ; (bottom center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively. The diagrams on the top are shown in the paper as well, and are included here for convenience.
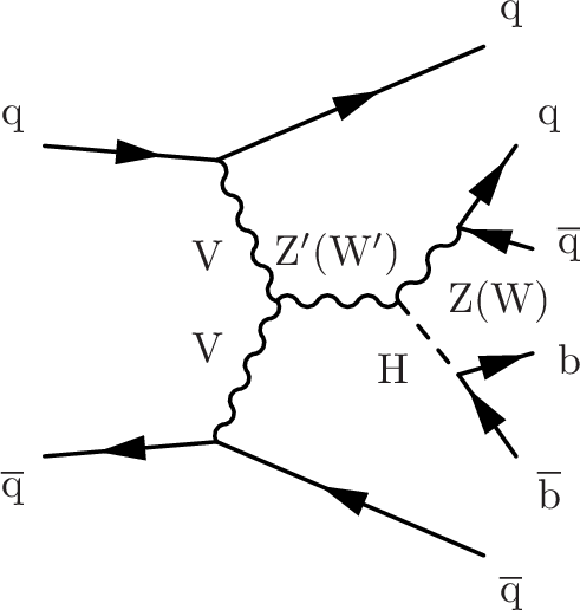
png pdf	Additional Figure 1-f: Example Feynman diagrams of signal processes: (top left) $ \mathrm{g} \mathrm{g} $ produced graviton or radion decaying to WW or ZZ; (top center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively; (top right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom left) VBF produced graviton or radion decaying to WW or ZZ; (bottom center) DY produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to WW and WZ, respectively; (bottom right) VBF produced $ \mathrm{Z}^{'} $ and $ \mathrm{W^{'}} $ decaying to ZH and WH, respectively. The diagrams on the top are shown in the paper as well, and are included here for convenience.
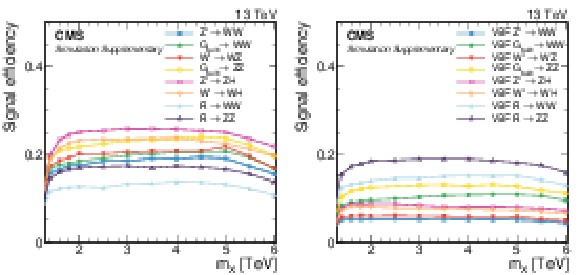
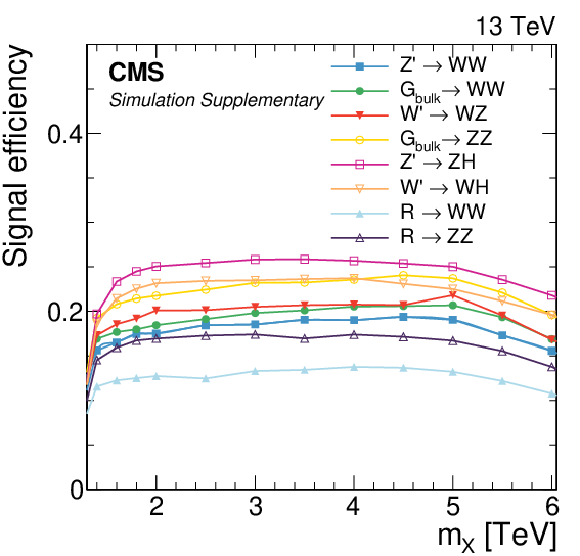
png pdf	Additional Figure 2: Total signal efficiency including all event categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF (left) and VBF (right) signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 2-a: Total signal efficiency including all event categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF (left) and VBF (right) signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 2-b: Total signal efficiency including all event categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF (left) and VBF (right) signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
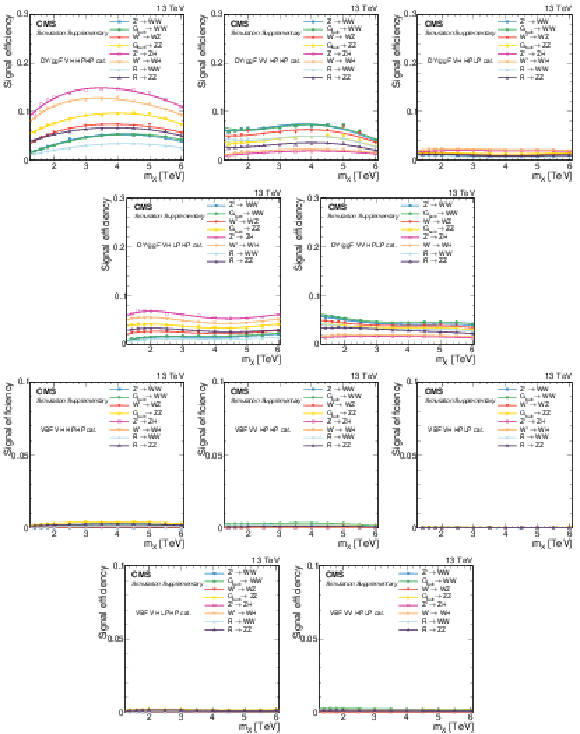
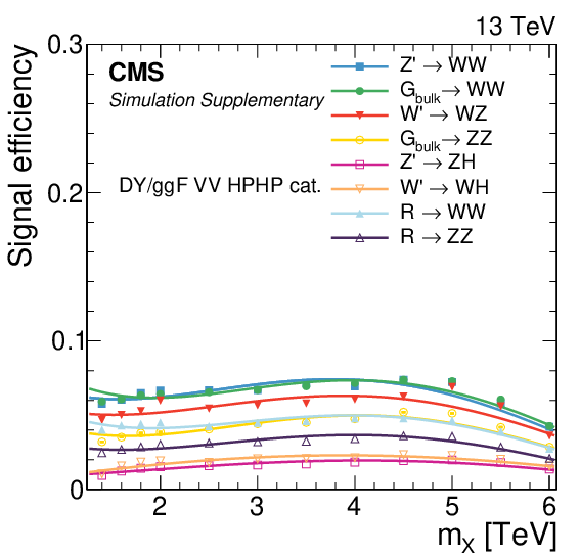
png pdf	Additional Figure 3: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 3-a: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 3-b: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 3-c: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
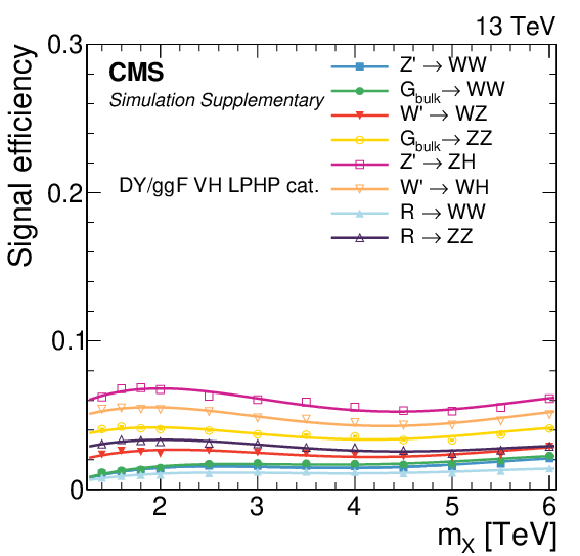
png pdf	Additional Figure 3-d: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
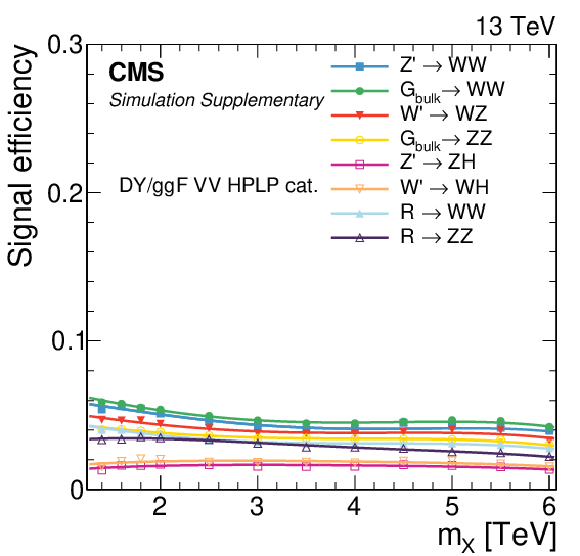
png pdf	Additional Figure 3-e: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 3-f: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
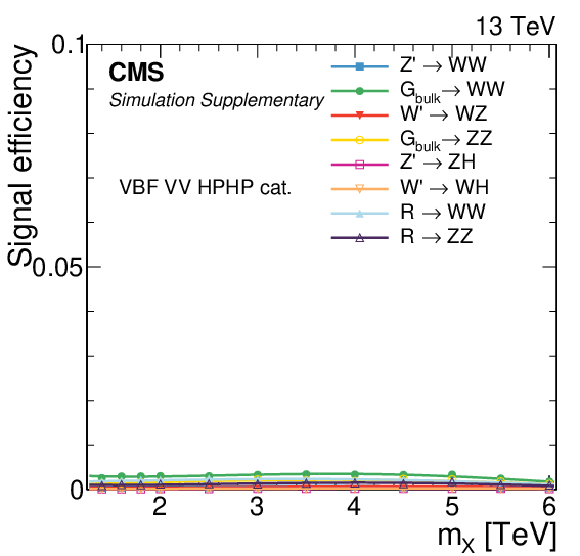
png pdf	Additional Figure 3-g: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
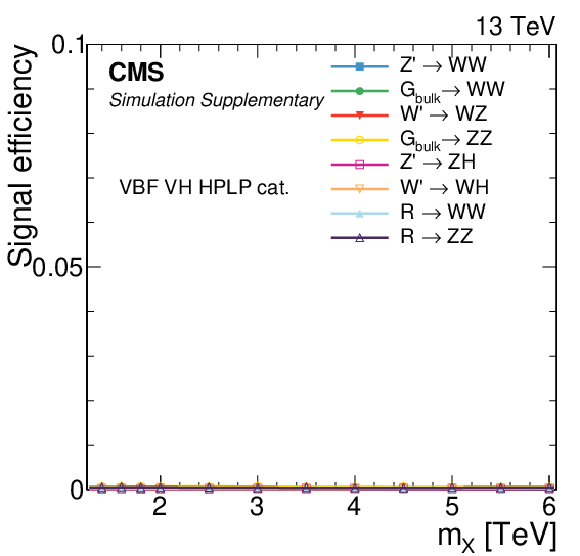
png pdf	Additional Figure 3-h: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
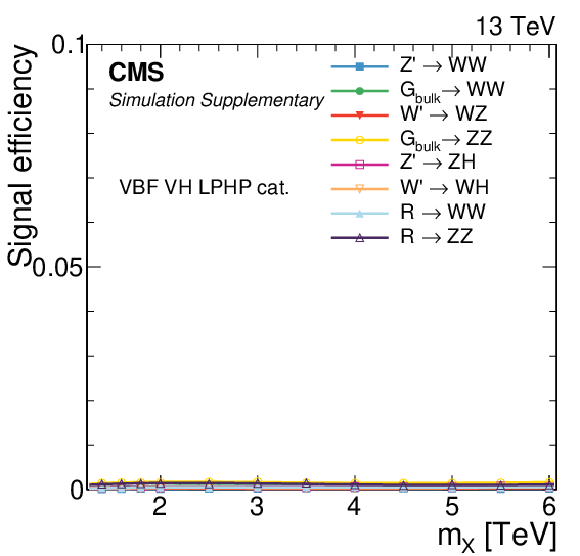
png pdf	Additional Figure 3-i: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
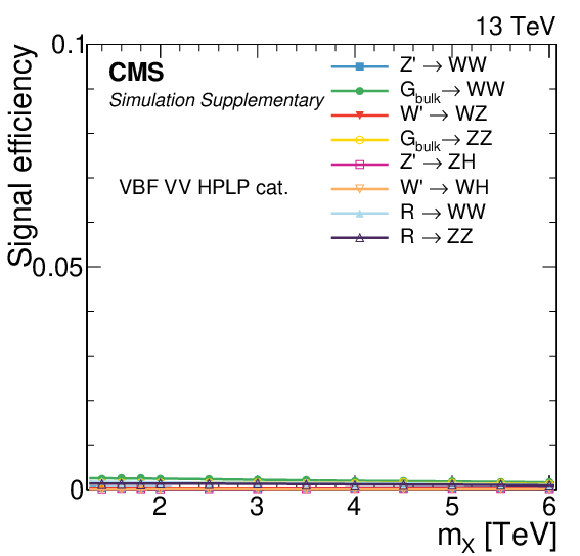
png pdf	Additional Figure 3-j: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all DY/ggF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 4: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
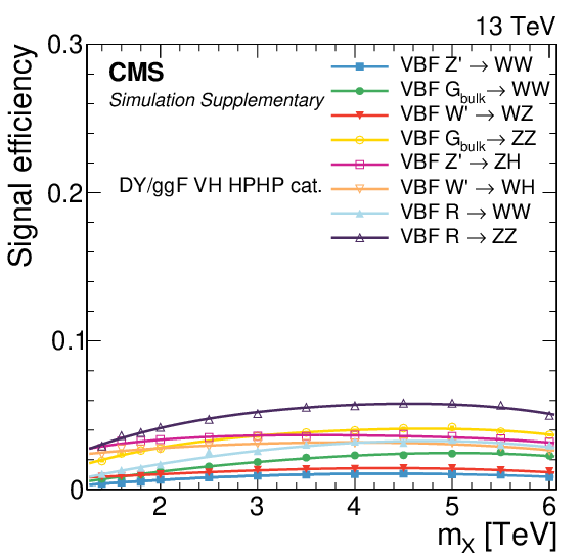
png pdf	Additional Figure 4-a: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 4-b: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
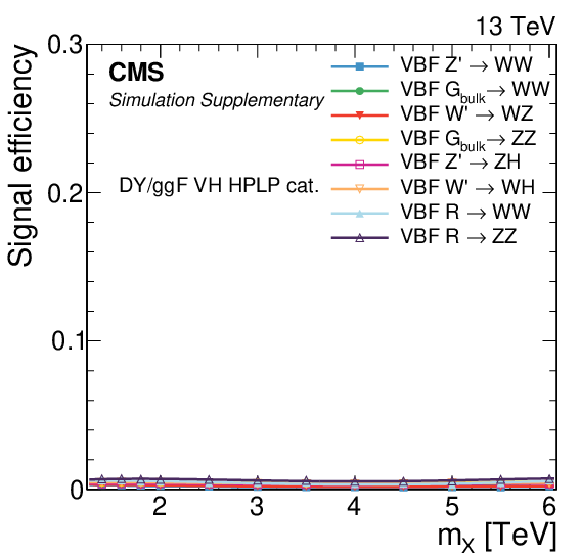
png pdf	Additional Figure 4-c: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
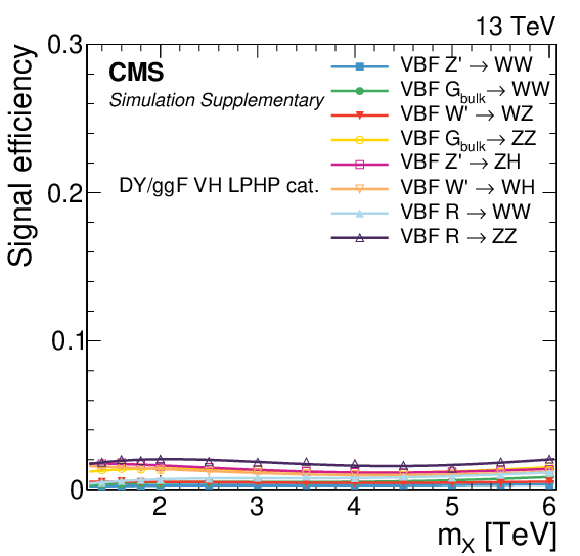
png pdf	Additional Figure 4-d: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 4-e: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
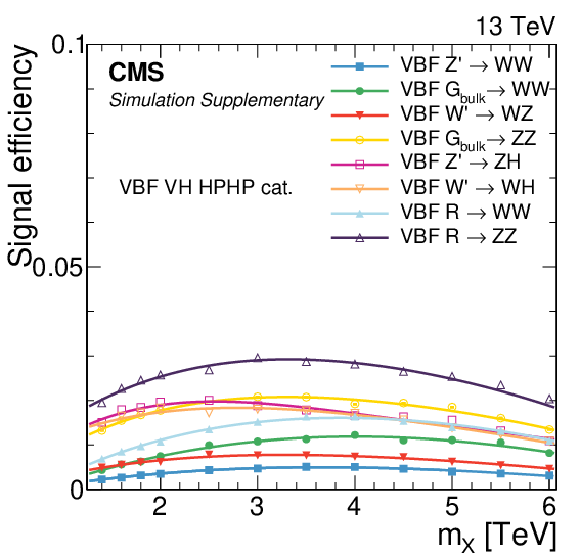
png pdf	Additional Figure 4-f: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 4-g: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
png pdf	Additional Figure 4-h: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
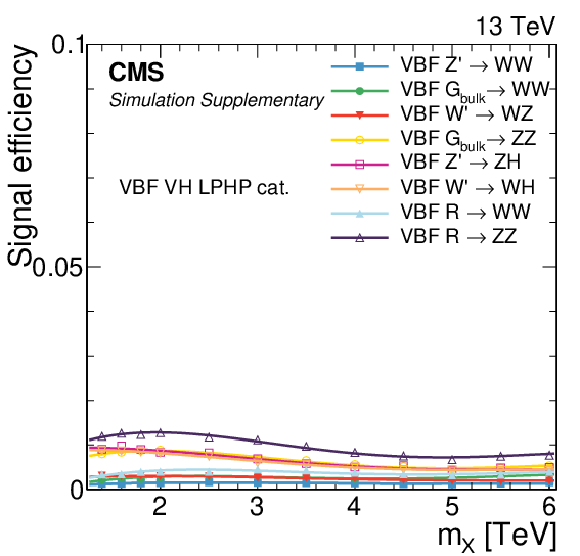
png pdf	Additional Figure 4-i: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
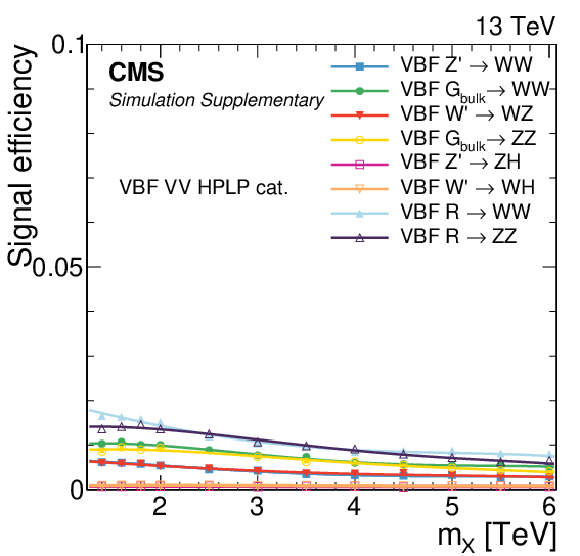
png pdf	Additional Figure 4-j: Signal efficiency in each of the categories as a function of the resonance mass $M_{\mathrm{X}}$ for all VBF signal models under consideration. The estimates from MC simulation (markers) are interpolated with a functional form (lines).
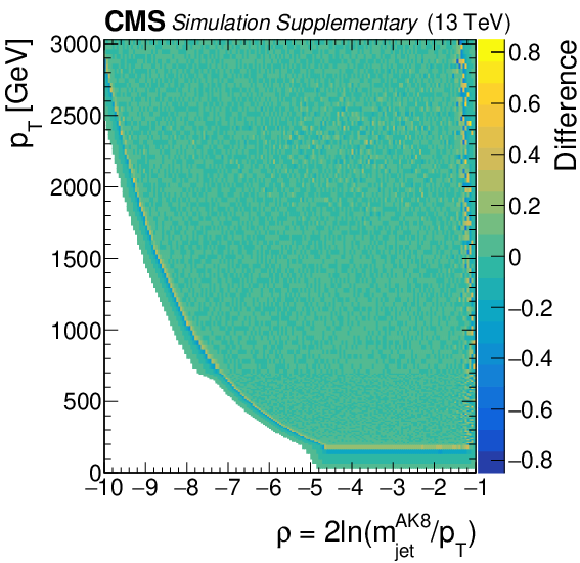
png pdf	Additional Figure 5: Left: Selection requirement on the $ \mathrm{q}\overline{\mathrm{q}} $ discriminator to obtain a 5% misidentification rate in QCD multijet simulation as a function of jet $ p_{\mathrm{T}} $ and $ \rho=2\ln(m_\text{jet}^{\mathrm{AK8}}/p_{\mathrm{T}}) $. Right: Difference in the requirement to be applied on the $ \mathrm{q}\overline{\mathrm{q}} $ tagger to obtain a 5% background misidentification rate between the nominal and a smoothed version of this histogram.
png pdf	Additional Figure 5-a: Left: Selection requirement on the $ \mathrm{q}\overline{\mathrm{q}} $ discriminator to obtain a 5% misidentification rate in QCD multijet simulation as a function of jet $ p_{\mathrm{T}} $ and $ \rho=2\ln(m_\text{jet}^{\mathrm{AK8}}/p_{\mathrm{T}}) $. Right: Difference in the requirement to be applied on the $ \mathrm{q}\overline{\mathrm{q}} $ tagger to obtain a 5% background misidentification rate between the nominal and a smoothed version of this histogram.
png pdf	Additional Figure 5-b: Left: Selection requirement on the $ \mathrm{q}\overline{\mathrm{q}} $ discriminator to obtain a 5% misidentification rate in QCD multijet simulation as a function of jet $ p_{\mathrm{T}} $ and $ \rho=2\ln(m_\text{jet}^{\mathrm{AK8}}/p_{\mathrm{T}}) $. Right: Difference in the requirement to be applied on the $ \mathrm{q}\overline{\mathrm{q}} $ tagger to obtain a 5% background misidentification rate between the nominal and a smoothed version of this histogram.
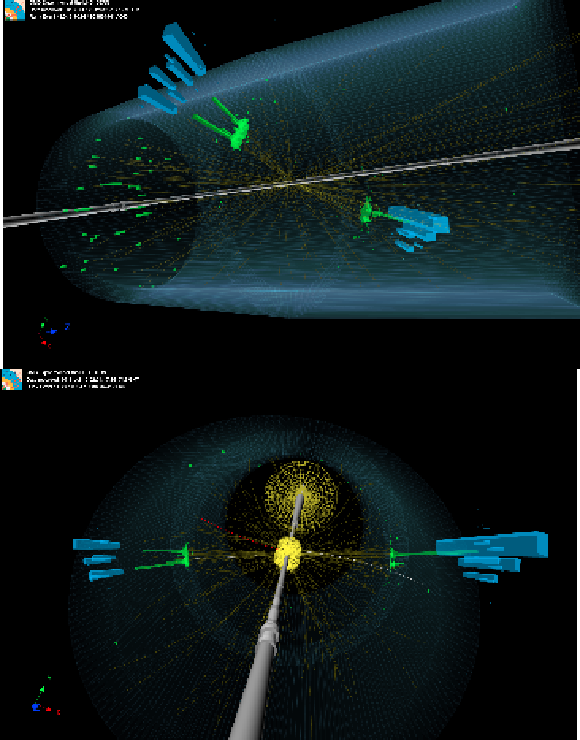
png pdf	Additional Figure 6: Displays of an event with a reconstructed dijet invariant mass $ m_\mathrm{jj}^{\mathrm{AK8}}= $ 2.94 TeV in the DY/ggF VV HPHP category, with $ m_\text{jet1}^{\mathrm{AK8}}= $ 82 GeV and $ m_\text{jet2}^{\mathrm{AK8}}= $ 86 GeV, consistent with a WW, WZ or ZZ signal hypothesis. Reconstructed tracks are indicated as lines. Energy deposits in the electromagnetic and hadronic calorimeter are indicated as green and blue bars, respectively. The two leading AK8 jets have $ p_{\mathrm{T}}= $ 1.47 TeV, $ \eta= $ 0.27 and $ p_{\mathrm{T}}= $ 1.45 TeV, $ \eta= $ 0.17.
png	Additional Figure 6-a: Displays of an event with a reconstructed dijet invariant mass $ m_\mathrm{jj}^{\mathrm{AK8}}= $ 2.94 TeV in the DY/ggF VV HPHP category, with $ m_\text{jet1}^{\mathrm{AK8}}= $ 82 GeV and $ m_\text{jet2}^{\mathrm{AK8}}= $ 86 GeV, consistent with a WW, WZ or ZZ signal hypothesis. Reconstructed tracks are indicated as lines. Energy deposits in the electromagnetic and hadronic calorimeter are indicated as green and blue bars, respectively. The two leading AK8 jets have $ p_{\mathrm{T}}= $ 1.47 TeV, $ \eta= $ 0.27 and $ p_{\mathrm{T}}= $ 1.45 TeV, $ \eta= $ 0.17.
png	Additional Figure 6-b: Displays of an event with a reconstructed dijet invariant mass $ m_\mathrm{jj}^{\mathrm{AK8}}= $ 2.94 TeV in the DY/ggF VV HPHP category, with $ m_\text{jet1}^{\mathrm{AK8}}= $ 82 GeV and $ m_\text{jet2}^{\mathrm{AK8}}= $ 86 GeV, consistent with a WW, WZ or ZZ signal hypothesis. Reconstructed tracks are indicated as lines. Energy deposits in the electromagnetic and hadronic calorimeter are indicated as green and blue bars, respectively. The two leading AK8 jets have $ p_{\mathrm{T}}= $ 1.47 TeV, $ \eta= $ 0.27 and $ p_{\mathrm{T}}= $ 1.45 TeV, $ \eta= $ 0.17.
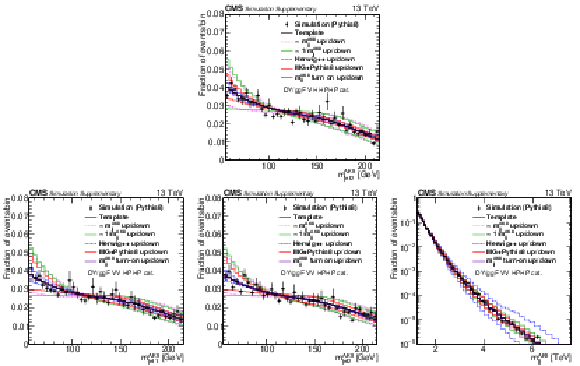
png pdf	Additional Figure 7: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH HPHP (upper) and VV HPHP (lower) categories.
png pdf	Additional Figure 7-a: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH HPHP (upper) and VV HPHP (lower) categories.
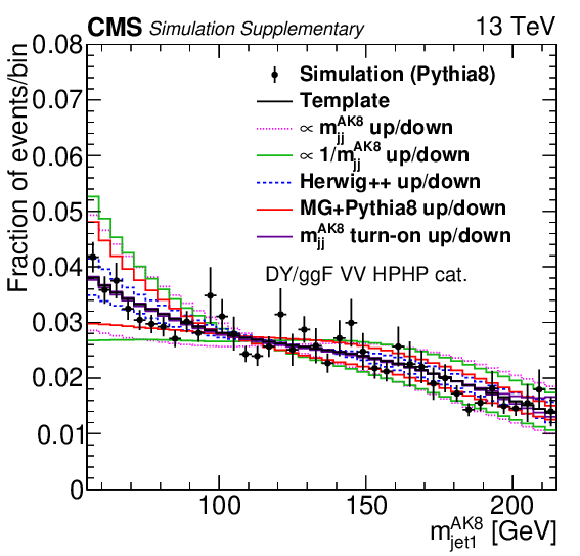
png pdf	Additional Figure 7-b: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH HPHP (upper) and VV HPHP (lower) categories.
png pdf	Additional Figure 7-c: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH HPHP (upper) and VV HPHP (lower) categories.
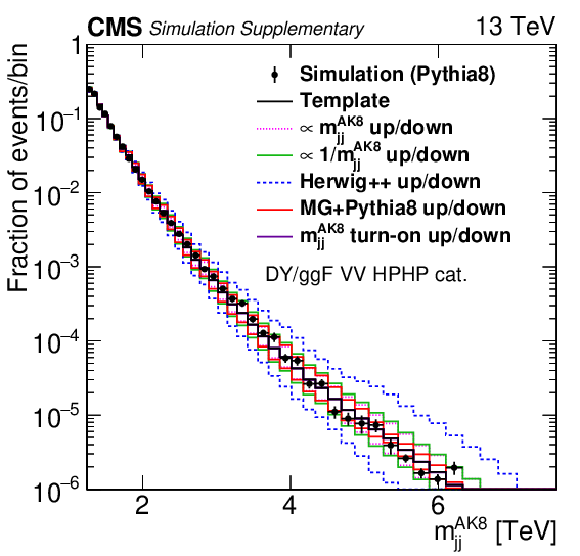
png pdf	Additional Figure 7-d: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH HPHP (upper) and VV HPHP (lower) categories.
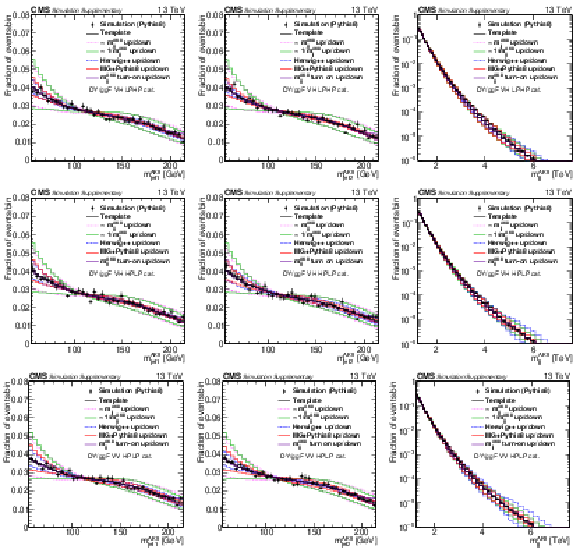
png pdf	Additional Figure 8: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
png pdf	Additional Figure 8-a: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
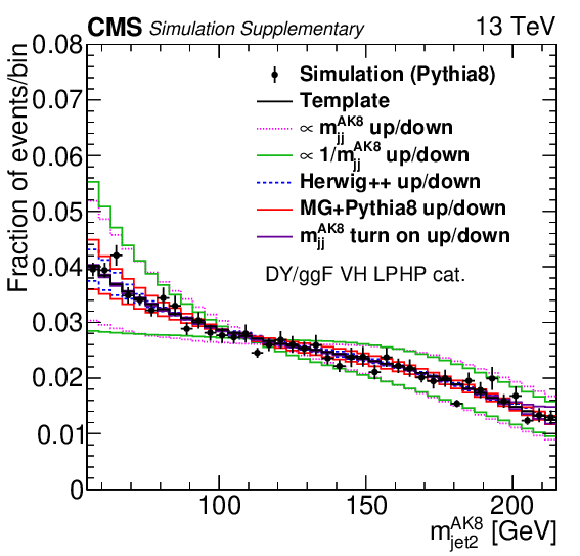
png pdf	Additional Figure 8-b: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
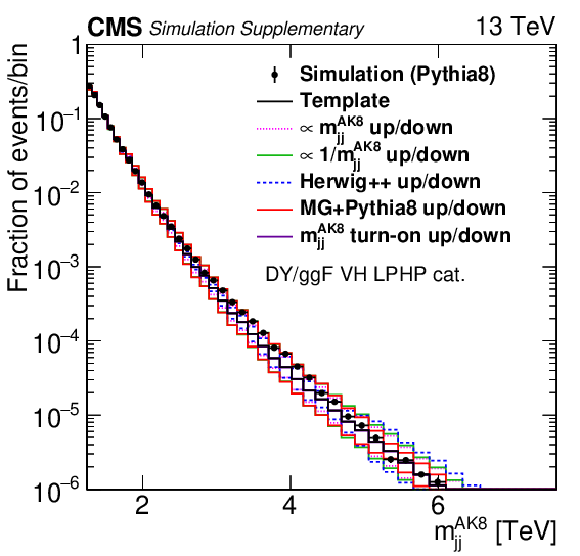
png pdf	Additional Figure 8-c: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
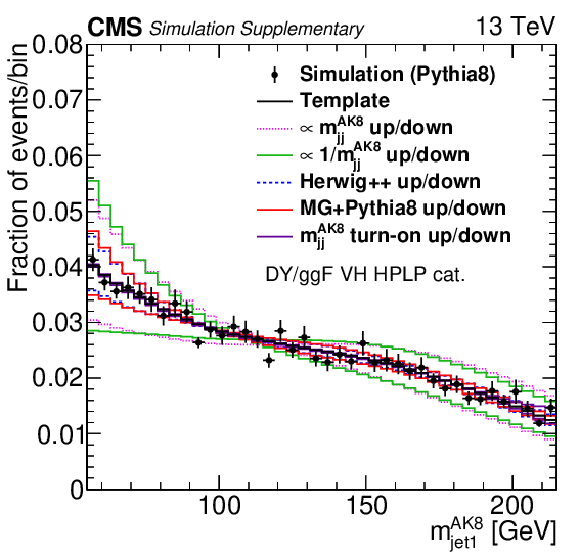
png pdf	Additional Figure 8-d: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
png pdf	Additional Figure 8-e: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
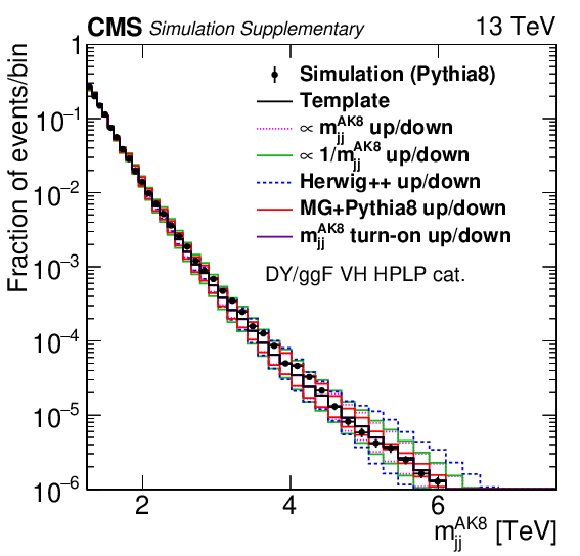
png pdf	Additional Figure 8-f: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
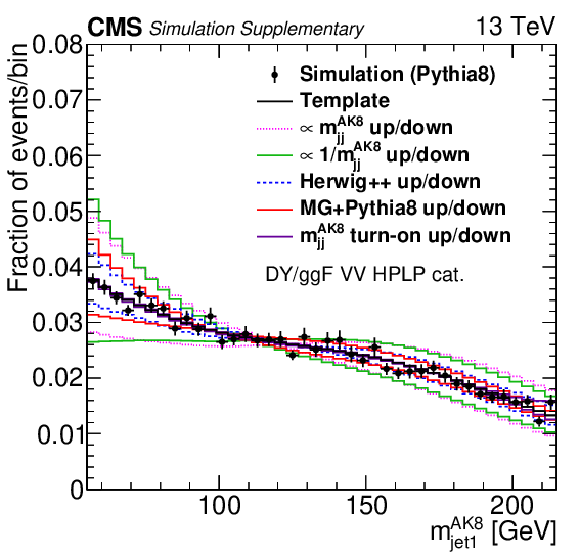
png pdf	Additional Figure 8-g: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
png pdf	Additional Figure 8-h: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
png pdf	Additional Figure 8-i: Projections of PYTHIA8 MC simulation of the QCD multijet background distribution onto the $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle), and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) dimensions are compared to the nominal QCD background template and the five alternate shapes added to the fit as shape nuisance parameters for the VH LPHP (upper), VH HPLP (middle), and VV HPLP (lower) categories.
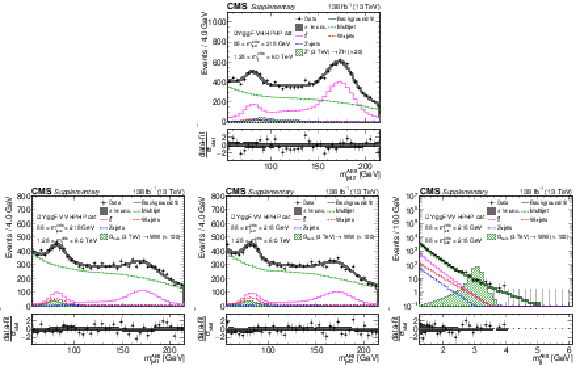
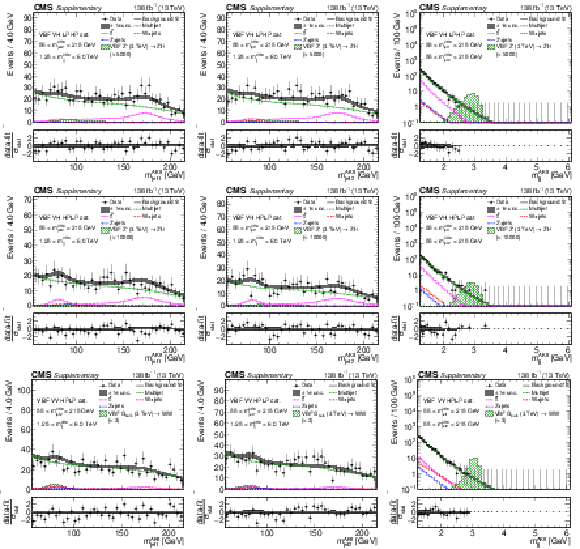
png pdf	Additional Figure 9: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH HPHP (upper) and VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty of the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty on the background estimate fitted to the data divided by the statistical uncertainty of the data is shown as a band.
png pdf	Additional Figure 9-a: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH HPHP (upper) and VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty of the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty on the background estimate fitted to the data divided by the statistical uncertainty of the data is shown as a band.
png pdf	Additional Figure 9-b: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH HPHP (upper) and VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty of the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty on the background estimate fitted to the data divided by the statistical uncertainty of the data is shown as a band.
png pdf	Additional Figure 9-c: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH HPHP (upper) and VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty of the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty on the background estimate fitted to the data divided by the statistical uncertainty of the data is shown as a band.
png pdf	Additional Figure 9-d: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH HPHP (upper) and VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty of the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty on the background estimate fitted to the data divided by the statistical uncertainty of the data is shown as a band.
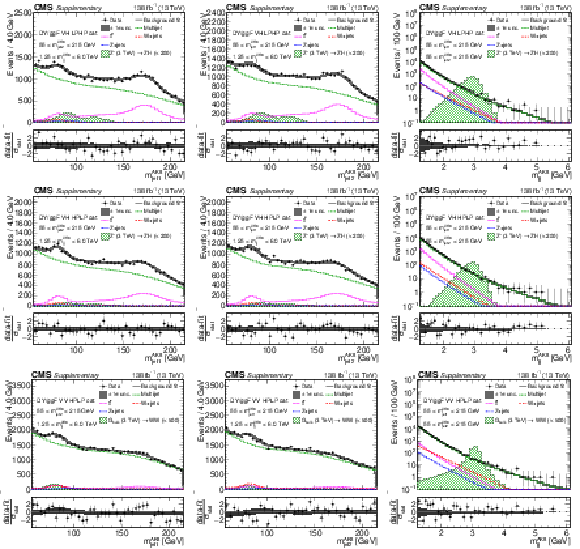
png pdf	Additional Figure 10: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 10-a: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
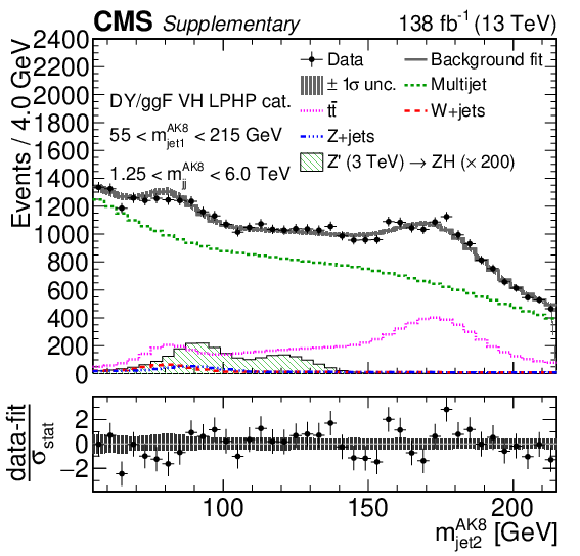
png pdf	Additional Figure 10-b: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 10-c: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
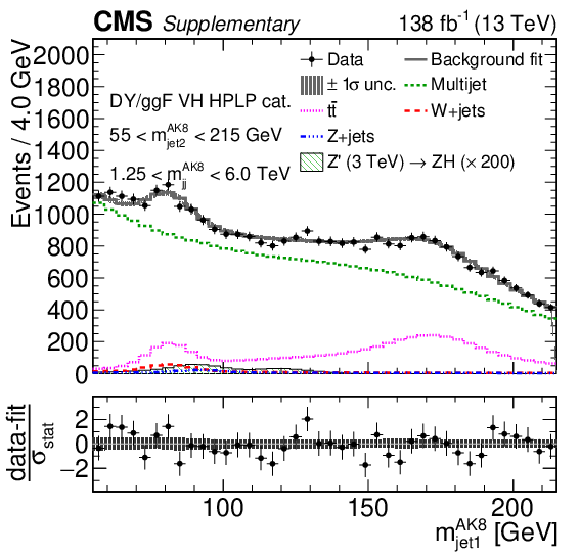
png pdf	Additional Figure 10-d: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 10-e: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
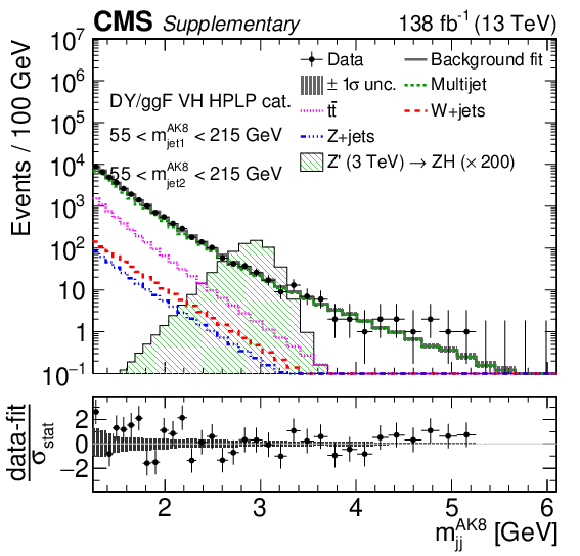
png pdf	Additional Figure 10-f: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
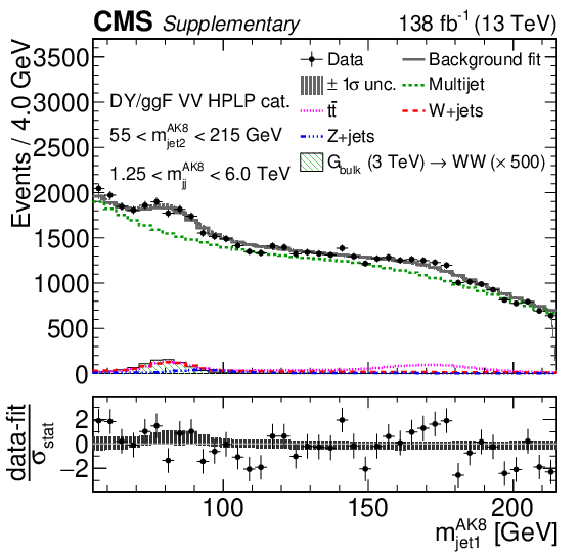
png pdf	Additional Figure 10-g: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
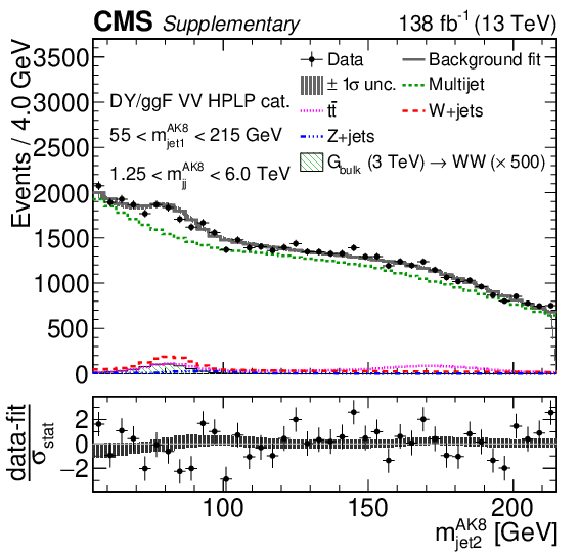
png pdf	Additional Figure 10-h: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 10-i: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the DY/ggF VH LPHP (upper), DY/ggF VH HPLP (middle), and DY/ggF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
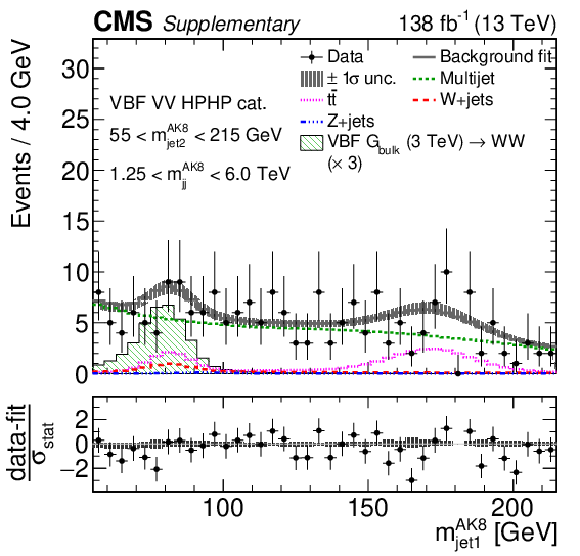
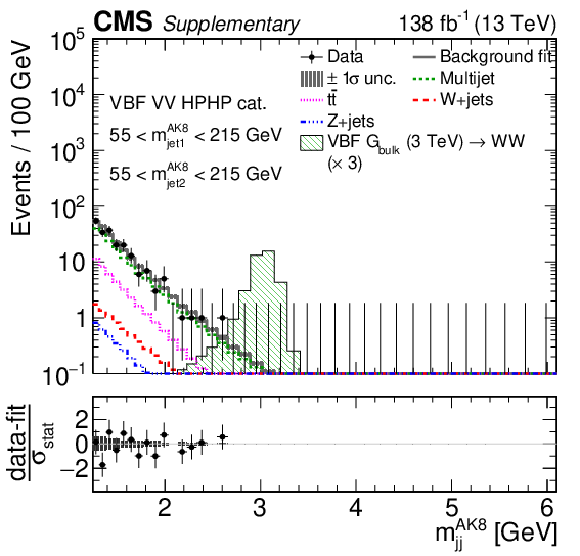
png pdf	Additional Figure 11: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH HPHP (upper) and VBF VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
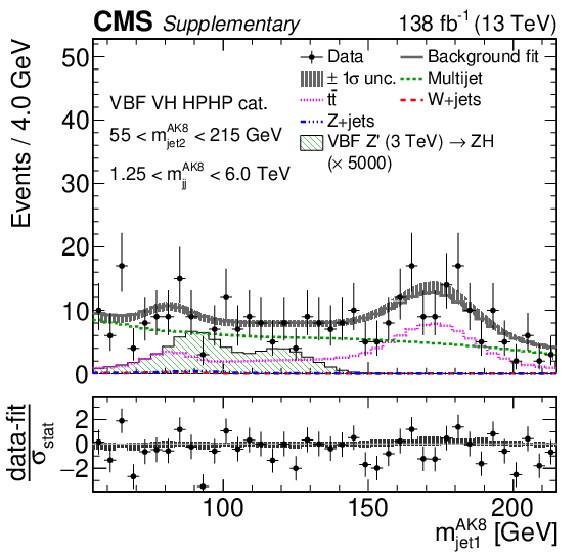
png pdf	Additional Figure 11-a: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH HPHP (upper) and VBF VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
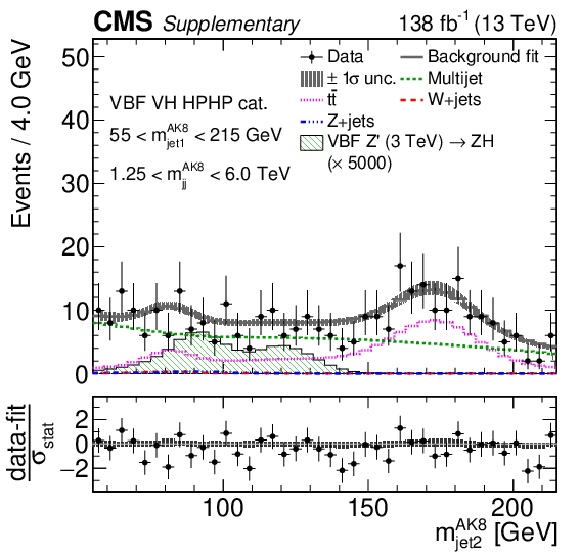
png pdf	Additional Figure 11-b: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH HPHP (upper) and VBF VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
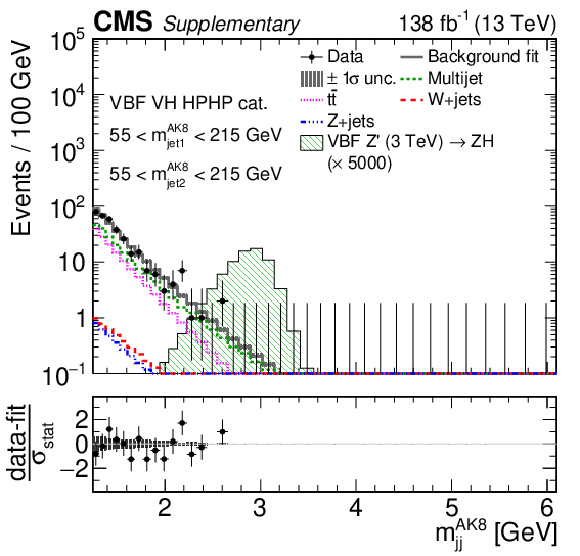
png pdf	Additional Figure 11-c: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH HPHP (upper) and VBF VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 11-d: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH HPHP (upper) and VBF VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
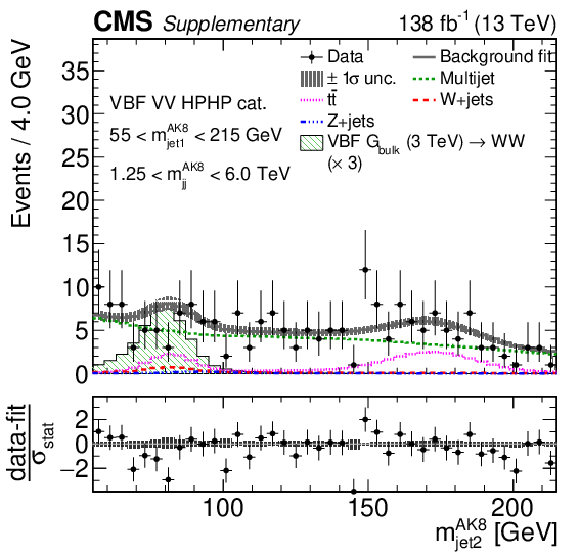
png pdf	Additional Figure 11-e: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH HPHP (upper) and VBF VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 11-f: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH HPHP (upper) and VBF VV HPHP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
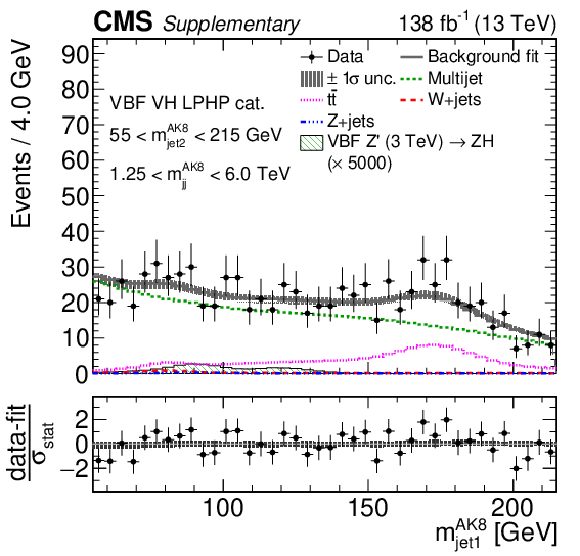
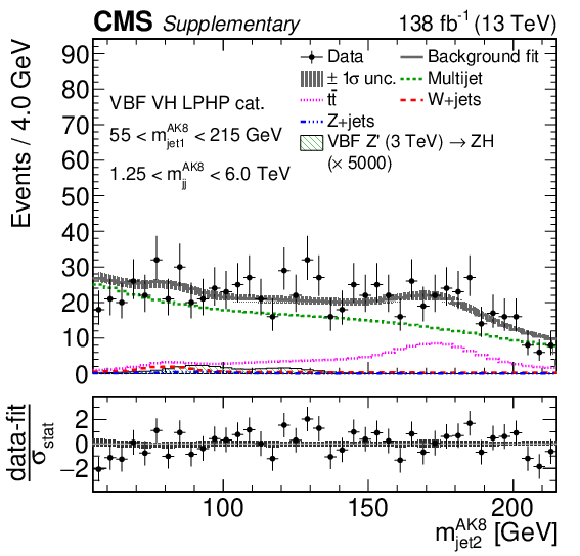
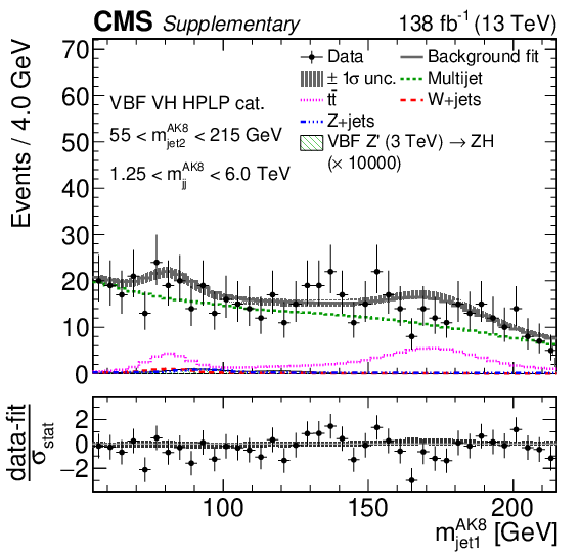
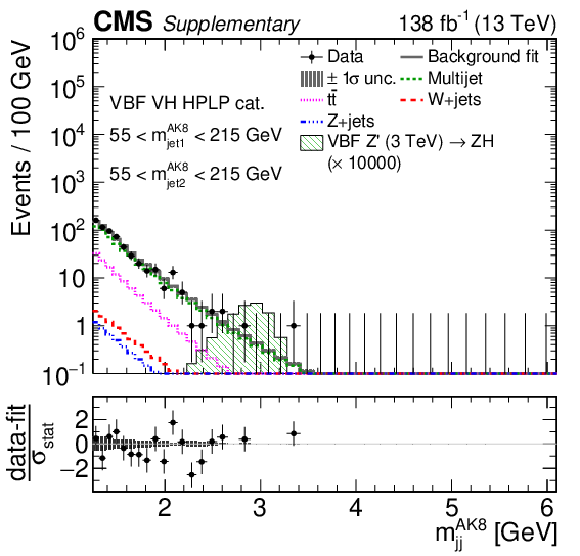
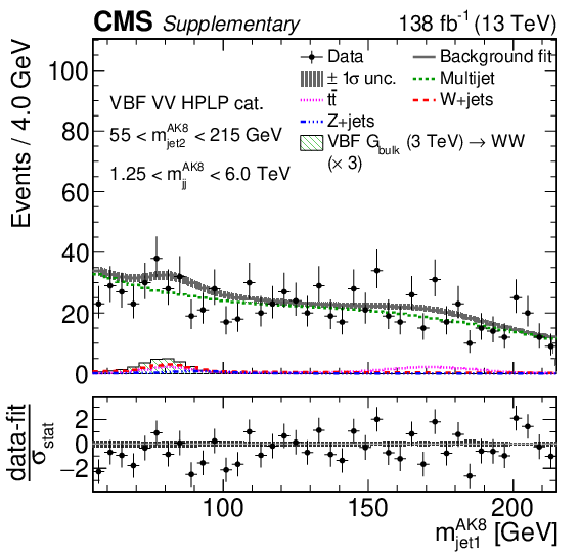
png pdf	Additional Figure 12: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 12-a: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 12-b: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 12-c: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 12-d: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 12-e: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 12-f: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 12-g: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 12-h: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
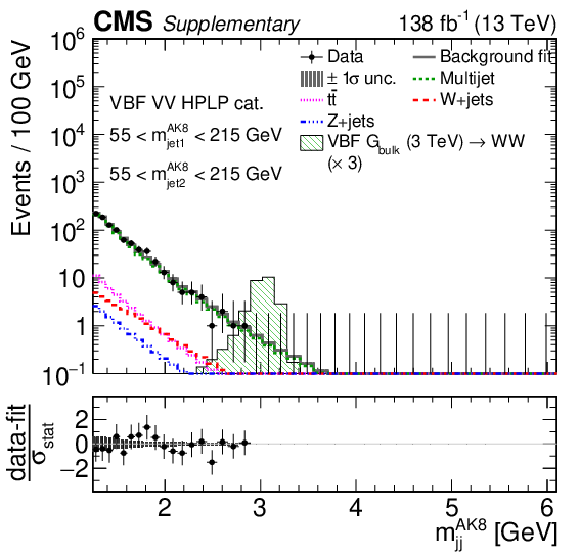
png pdf	Additional Figure 12-i: Comparison between the background post-fit and the data distributions of $ m_\text{jet1}^{\mathrm{AK8}} $ (left), $ m_\text{jet2}^{\mathrm{AK8}} $ (middle) and $ m_\mathrm{jj}^{\mathrm{AK8}} $ (right) in the VBF VH LPHP (upper), VBF VH HPLP (middle), and VBF VV HPLP (lower) categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. An example of a signal distribution is overlaid, where the number of expected events is scaled by an arbitrary normalization factor. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 13: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VV (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV) for the VH LPHP (left), VH HPLP (middle), and VV HPLP DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
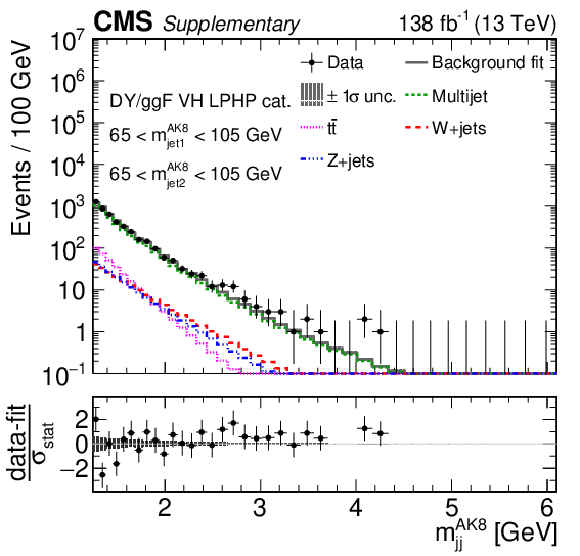
png pdf	Additional Figure 13-a: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VV (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV) for the VH LPHP (left), VH HPLP (middle), and VV HPLP DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
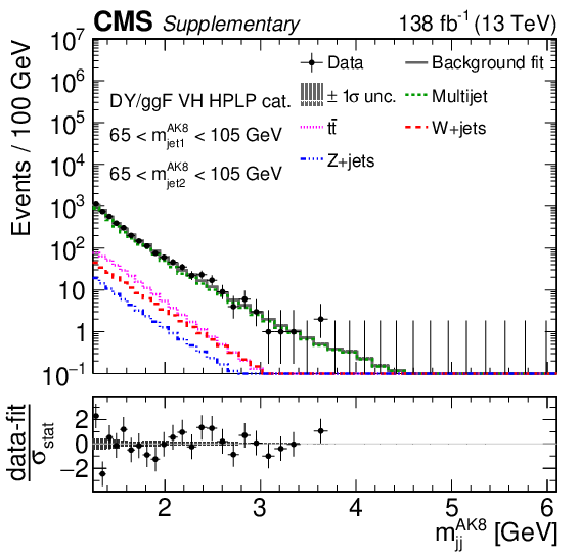
png pdf	Additional Figure 13-b: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VV (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV) for the VH LPHP (left), VH HPLP (middle), and VV HPLP DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
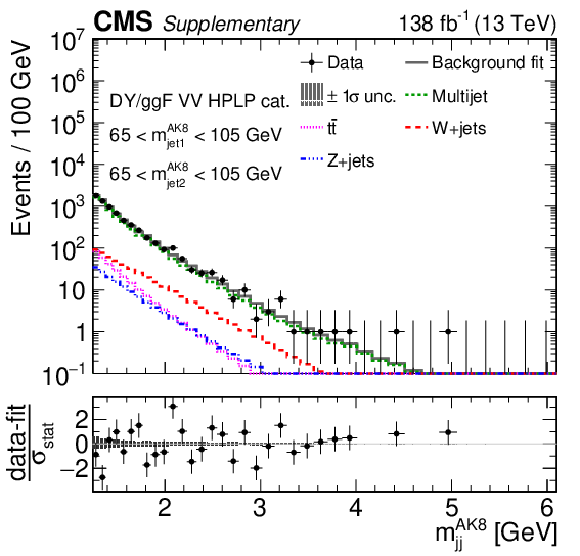
png pdf	Additional Figure 13-c: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VV (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 105 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 105 GeV) for the VH LPHP (left), VH HPLP (middle), and VV HPLP DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 14: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VH (65 $ < m_\text{jet1/2}^{\mathrm{AK8}} < $ 105 GeV, 110 $ < m_\text{jet2/1}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
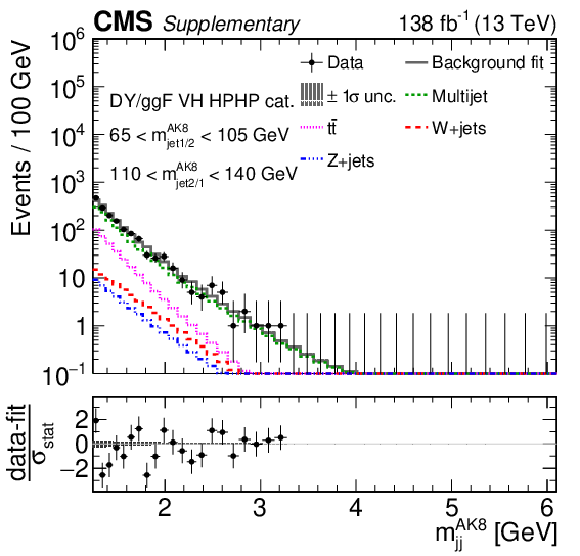
png pdf	Additional Figure 14-a: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VH (65 $ < m_\text{jet1/2}^{\mathrm{AK8}} < $ 105 GeV, 110 $ < m_\text{jet2/1}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 14-b: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VH (65 $ < m_\text{jet1/2}^{\mathrm{AK8}} < $ 105 GeV, 110 $ < m_\text{jet2/1}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
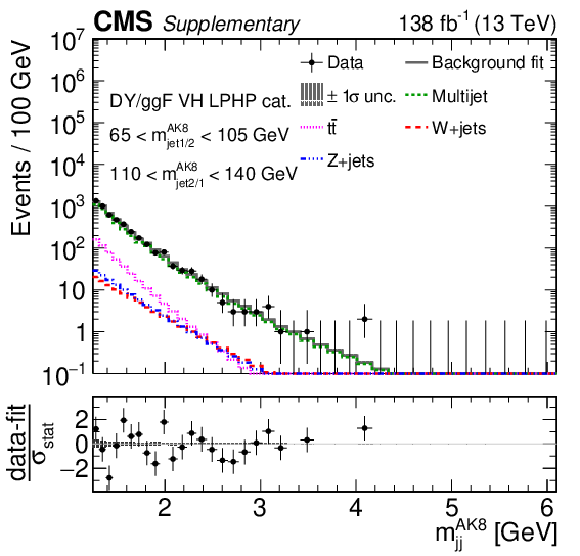
png pdf	Additional Figure 14-c: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VH (65 $ < m_\text{jet1/2}^{\mathrm{AK8}} < $ 105 GeV, 110 $ < m_\text{jet2/1}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
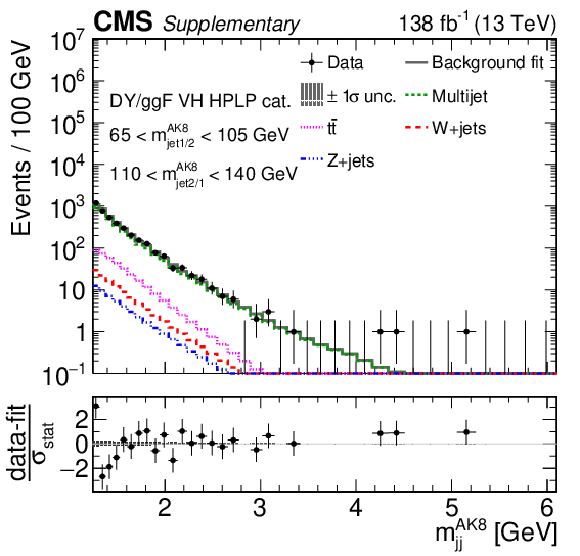
png pdf	Additional Figure 14-d: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VH (65 $ < m_\text{jet1/2}^{\mathrm{AK8}} < $ 105 GeV, 110 $ < m_\text{jet2/1}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 14-e: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from DY/ggF VH (65 $ < m_\text{jet1/2}^{\mathrm{AK8}} < $ 105 GeV, 110 $ < m_\text{jet2/1}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) DY/ggF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
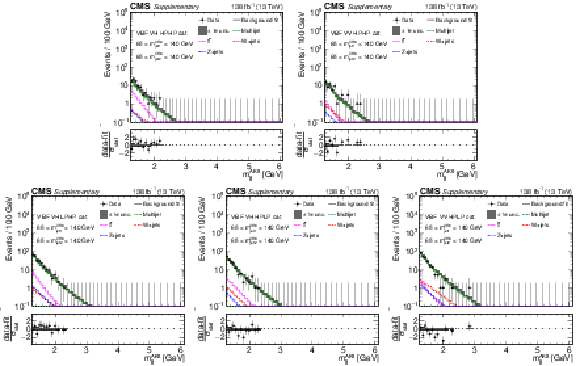
png pdf	Additional Figure 15: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from VBF VV/VH (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 140 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) VBF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
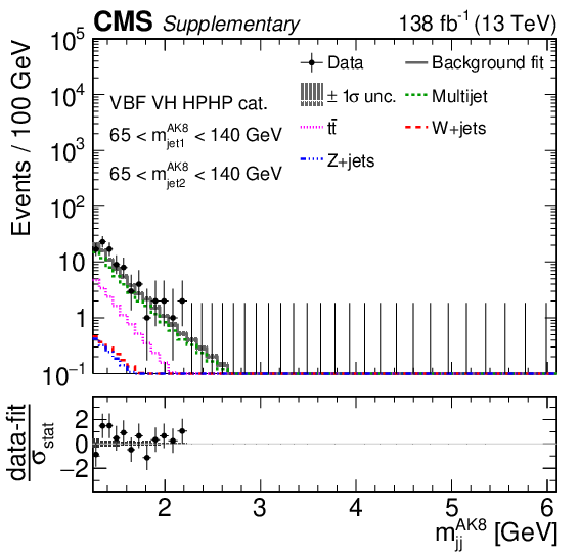
png pdf	Additional Figure 15-a: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from VBF VV/VH (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 140 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) VBF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
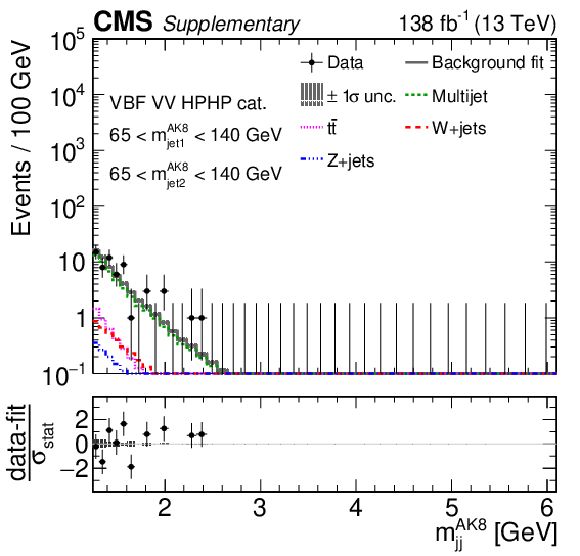
png pdf	Additional Figure 15-b: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from VBF VV/VH (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 140 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) VBF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
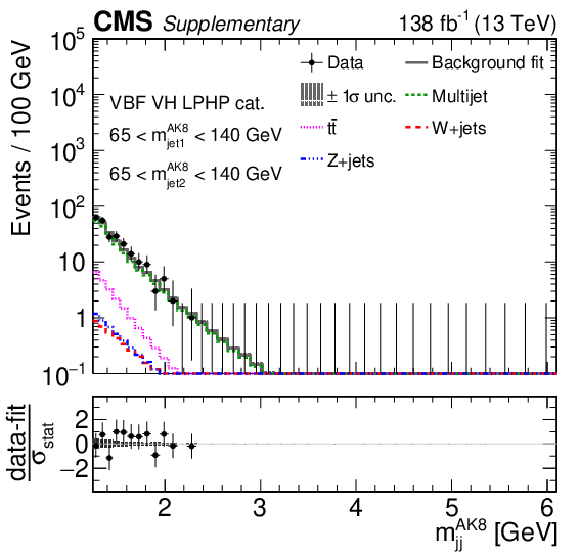
png pdf	Additional Figure 15-c: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from VBF VV/VH (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 140 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) VBF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
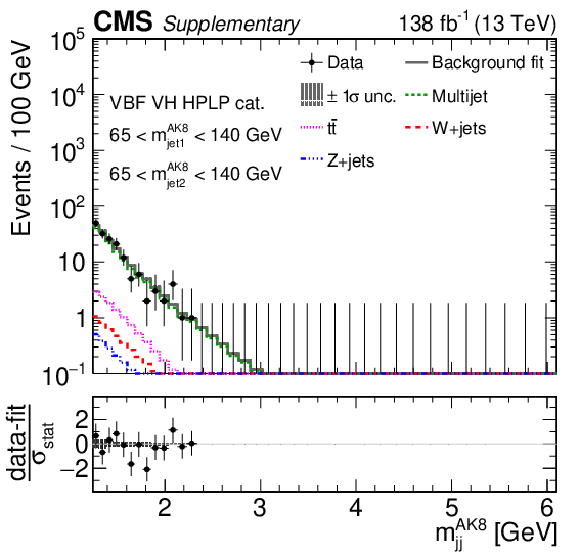
png pdf	Additional Figure 15-d: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from VBF VV/VH (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 140 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) VBF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
png pdf	Additional Figure 15-e: Projections of data and background post-fit distributions onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $ dimension in regions enriched in signal from VBF VV/VH (65 $ < m_\text{jet1}^{\mathrm{AK8}} < $ 140 GeV, 65 $ < m_\text{jet2}^{\mathrm{AK8}} < $ 140 GeV) for the HPHP (upper) and HPLP/LPHP (lower) VBF categories. The background shape uncertainty is shown as a gray shaded band around the result of the maximum likelihood fit to the data under the background-only assumption (gray solid line), and the statistical uncertainties in the data are shown as vertical bars. The various background components contributing to the total background fit are also shown with different line colors. Shown below each mass plot is the difference between the data and the fit divided by the statistical uncertainty in the data; the uncertainty bar represents the statistical uncertainty only. The total uncertainty in the background estimate fitted to the data divided by the statistical uncertainty in the data is shown as a band.
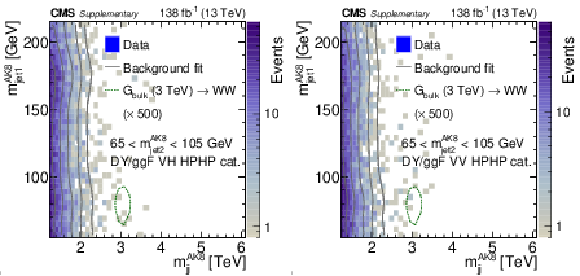
png pdf	Additional Figure 16: Projection of the 3D phase space of the data onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $--$ m_\text{jet1}^{\mathrm{AK8}} $ plane for a selected region in $ m_\text{jet2}^{\mathrm{AK8}} $ enriched in signal from DY/ggF VV. Contours of the signal and background distributions after the background post-fit are overlaid. The projections are shown for the HPHP VH (VV) DY/ggF category on the left (right).
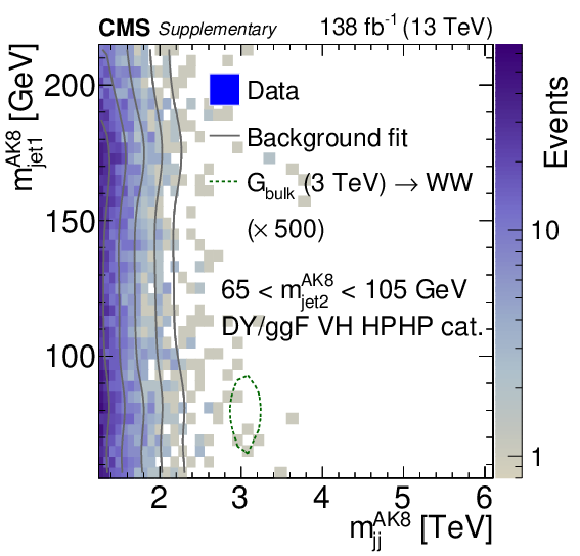
png pdf	Additional Figure 16-a: Projection of the 3D phase space of the data onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $--$ m_\text{jet1}^{\mathrm{AK8}} $ plane for a selected region in $ m_\text{jet2}^{\mathrm{AK8}} $ enriched in signal from DY/ggF VV. Contours of the signal and background distributions after the background post-fit are overlaid. The projections are shown for the HPHP VH (VV) DY/ggF category on the left (right).
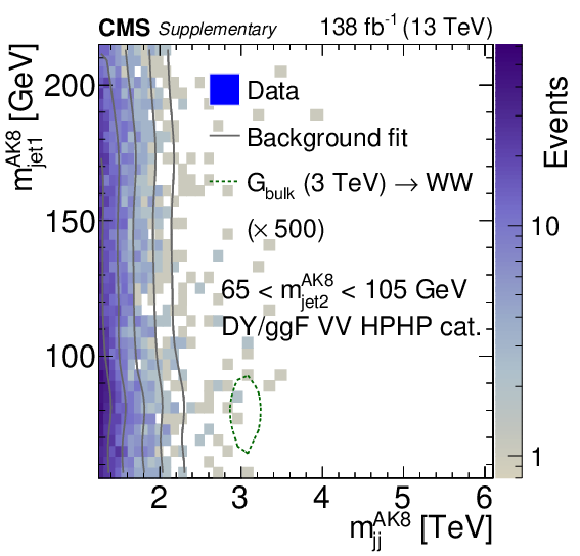
png pdf	Additional Figure 16-b: Projection of the 3D phase space of the data onto the $ m_\mathrm{jj}^{\mathrm{AK8}} $--$ m_\text{jet1}^{\mathrm{AK8}} $ plane for a selected region in $ m_\text{jet2}^{\mathrm{AK8}} $ enriched in signal from DY/ggF VV. Contours of the signal and background distributions after the background post-fit are overlaid. The projections are shown for the HPHP VH (VV) DY/ggF category on the left (right).
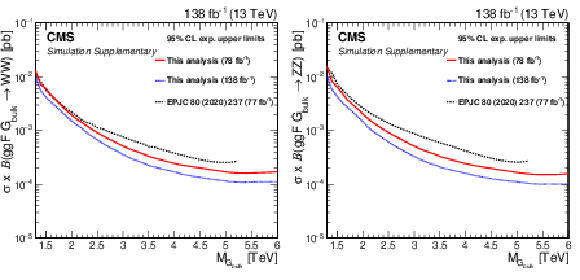
png pdf	Additional Figure 17: Expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction for a $ \mathrm{G}_{\text{bulk}}\to\mathrm{W}\mathrm{W} $ (left) and a $ \mathrm{G}_{\text{bulk}}\to\mathrm{Z}\mathrm{Z} $ (right) signal using 77.3 fb$ ^{-1} $ of data collected in 2016+2017 obtained using the methods presented here (red solid line), compared to the result obtained with previous methods (black dash-dotted line), published in EPJC 80 (2020) 237. The limit obtained combining data collected in 2016--2018 in this paper is also shown (blue dashed line).
png pdf	Additional Figure 17-a: Expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction for a $ \mathrm{G}_{\text{bulk}}\to\mathrm{W}\mathrm{W} $ (left) and a $ \mathrm{G}_{\text{bulk}}\to\mathrm{Z}\mathrm{Z} $ (right) signal using 77.3 fb$ ^{-1} $ of data collected in 2016+2017 obtained using the methods presented here (red solid line), compared to the result obtained with previous methods (black dash-dotted line), published in EPJC 80 (2020) 237. The limit obtained combining data collected in 2016--2018 in this paper is also shown (blue dashed line).
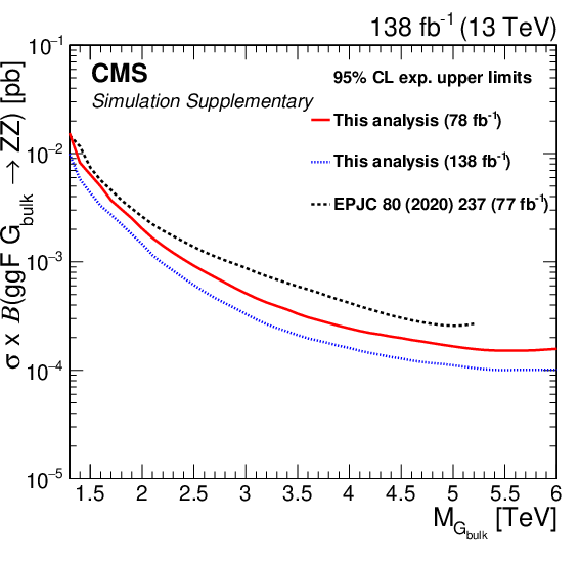
png pdf	Additional Figure 17-b: Expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction for a $ \mathrm{G}_{\text{bulk}}\to\mathrm{W}\mathrm{W} $ (left) and a $ \mathrm{G}_{\text{bulk}}\to\mathrm{Z}\mathrm{Z} $ (right) signal using 77.3 fb$ ^{-1} $ of data collected in 2016+2017 obtained using the methods presented here (red solid line), compared to the result obtained with previous methods (black dash-dotted line), published in EPJC 80 (2020) 237. The limit obtained combining data collected in 2016--2018 in this paper is also shown (blue dashed line).
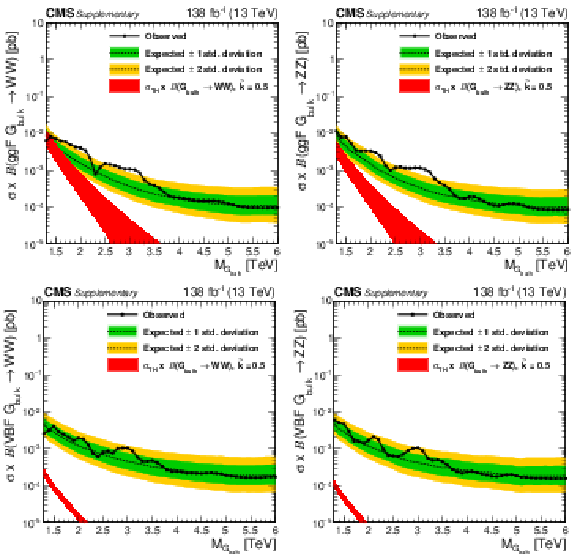
png pdf	Additional Figure 18: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{G}_{\text{bulk}}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{G}_{\text{bulk}}\to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
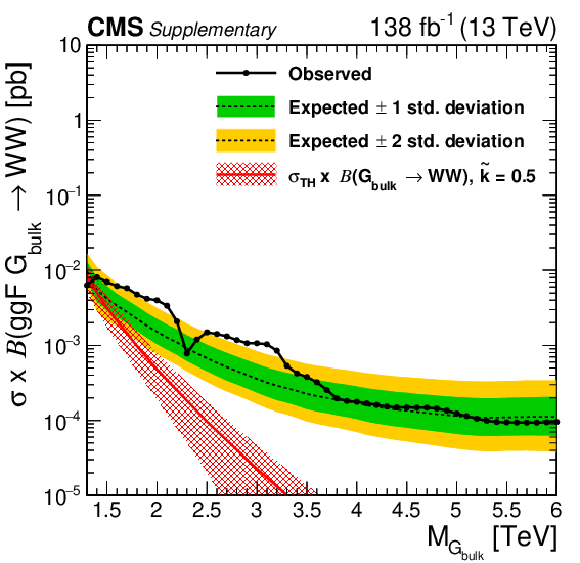
png pdf	Additional Figure 18-a: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{G}_{\text{bulk}}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{G}_{\text{bulk}}\to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
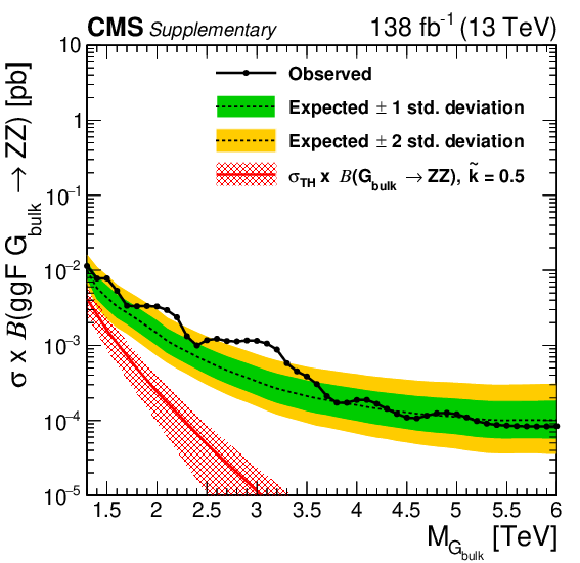
png pdf	Additional Figure 18-b: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{G}_{\text{bulk}}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{G}_{\text{bulk}}\to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
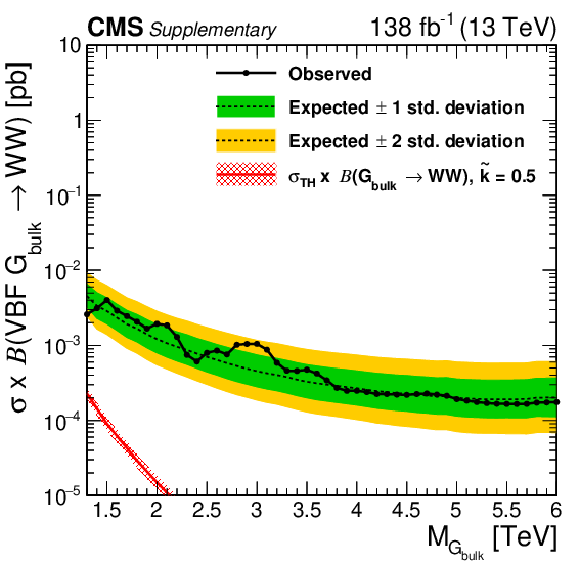
png pdf	Additional Figure 18-c: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{G}_{\text{bulk}}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{G}_{\text{bulk}}\to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
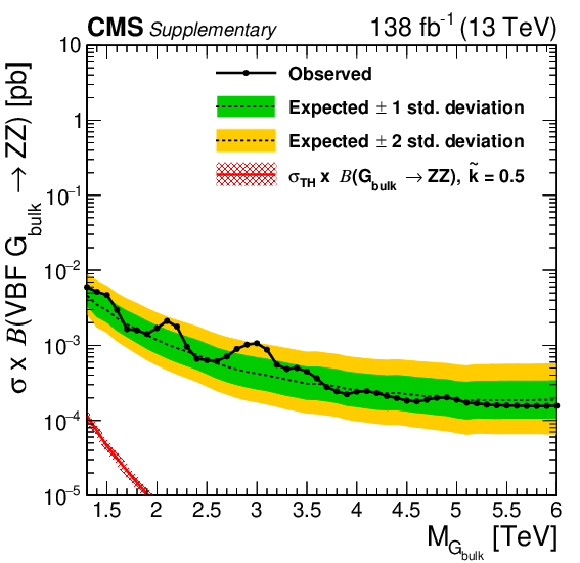
png pdf	Additional Figure 18-d: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{G}_{\text{bulk}}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{G}_{\text{bulk}}\to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
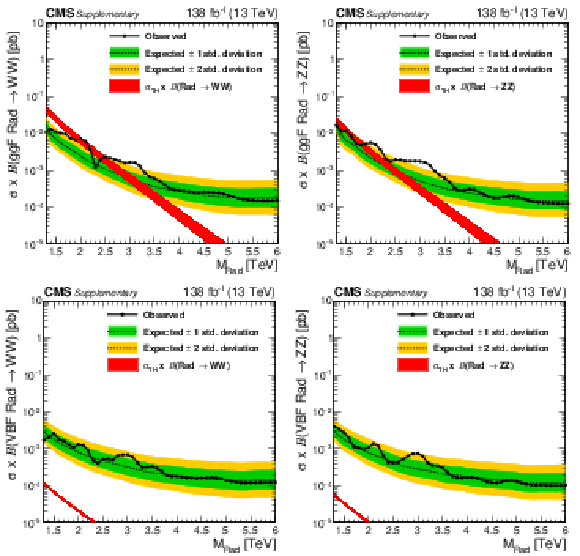
png pdf	Additional Figure 19: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \text{Rad} \to\mathrm{W}\mathrm{W} $ (left) and $ \text{Rad} \to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
png pdf	Additional Figure 19-a: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \text{Rad} \to\mathrm{W}\mathrm{W} $ (left) and $ \text{Rad} \to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
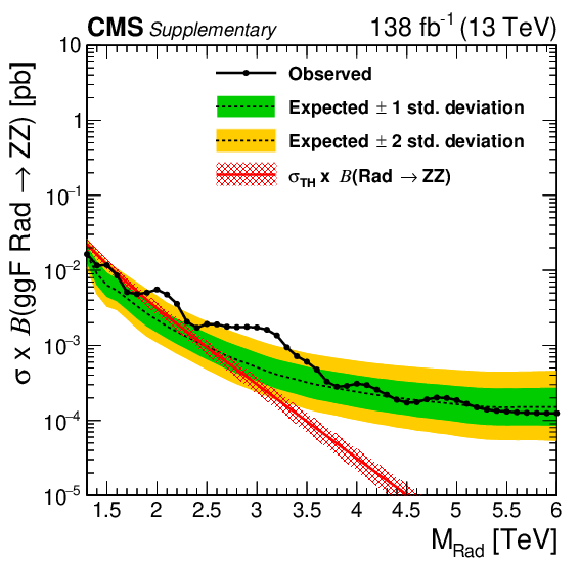
png pdf	Additional Figure 19-b: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \text{Rad} \to\mathrm{W}\mathrm{W} $ (left) and $ \text{Rad} \to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
png pdf	Additional Figure 19-c: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \text{Rad} \to\mathrm{W}\mathrm{W} $ (left) and $ \text{Rad} \to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
png pdf	Additional Figure 19-d: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \text{Rad} \to\mathrm{W}\mathrm{W} $ (left) and $ \text{Rad} \to\mathrm{Z}\mathrm{Z} $ (right) signals. In the upper panel the ggF production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
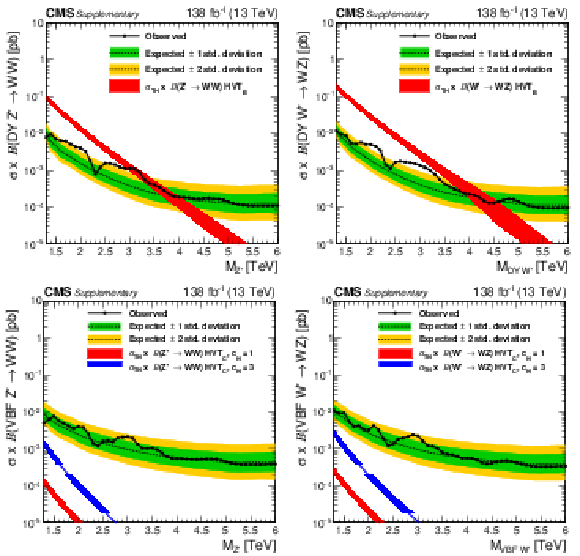
png pdf	Additional Figure 20: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{Z} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
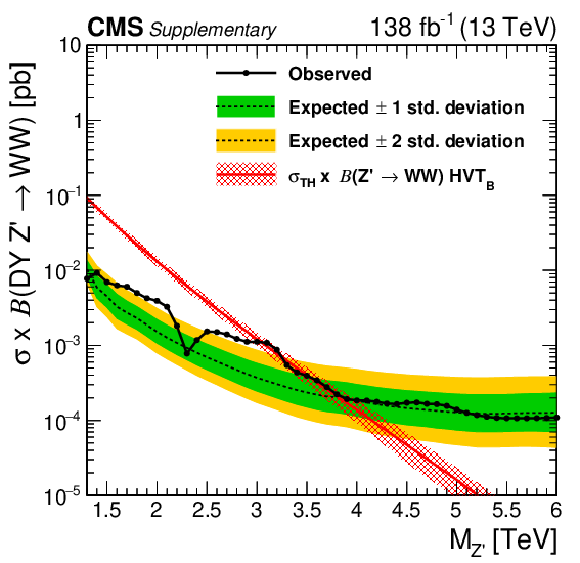
png pdf	Additional Figure 20-a: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{Z} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
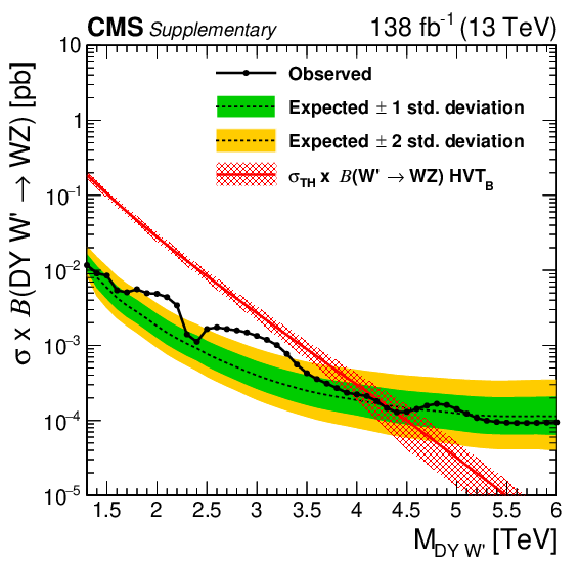
png pdf	Additional Figure 20-b: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{Z} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
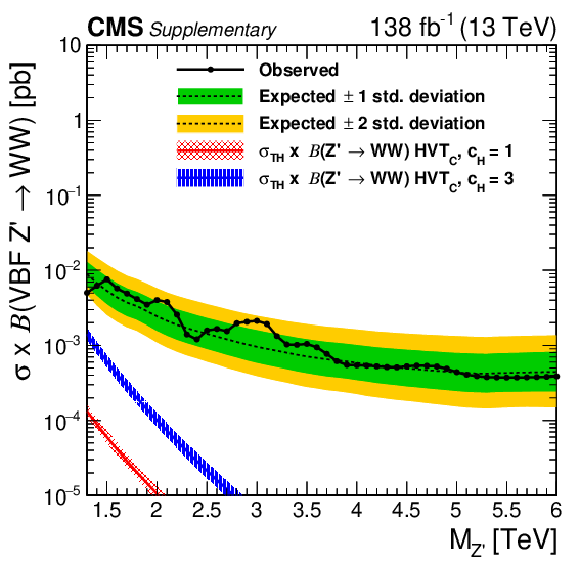
png pdf	Additional Figure 20-c: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{Z} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
png pdf	Additional Figure 20-d: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{W}\mathrm{W} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{Z} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
png pdf	Additional Figure 21: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{Z}\mathrm{H} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{H} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
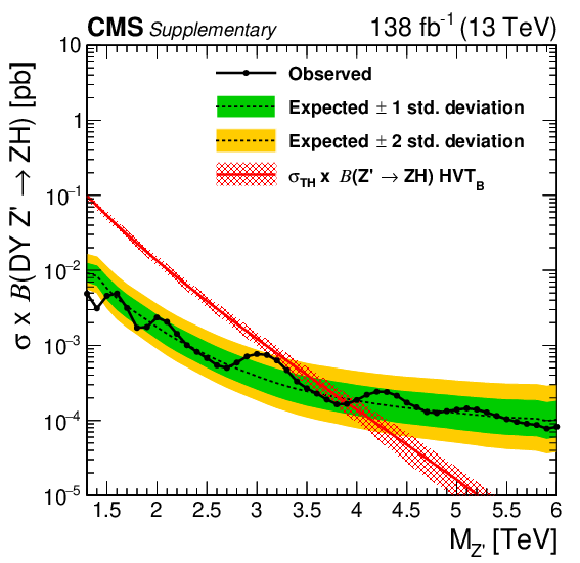
png pdf	Additional Figure 21-a: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{Z}\mathrm{H} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{H} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
png pdf	Additional Figure 21-b: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{Z}\mathrm{H} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{H} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
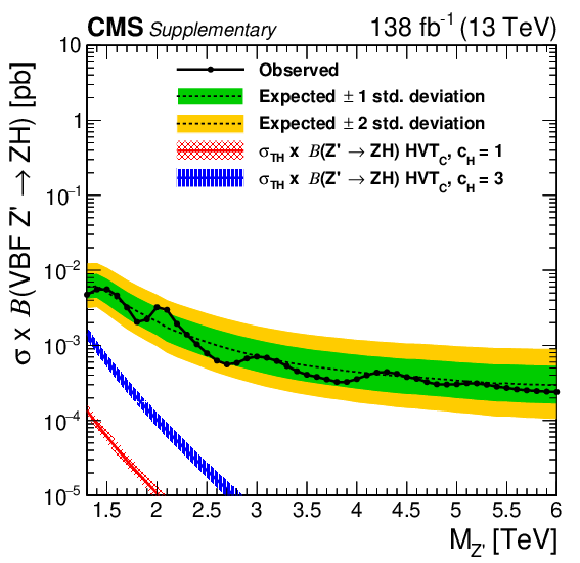
png pdf	Additional Figure 21-c: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{Z}\mathrm{H} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{H} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
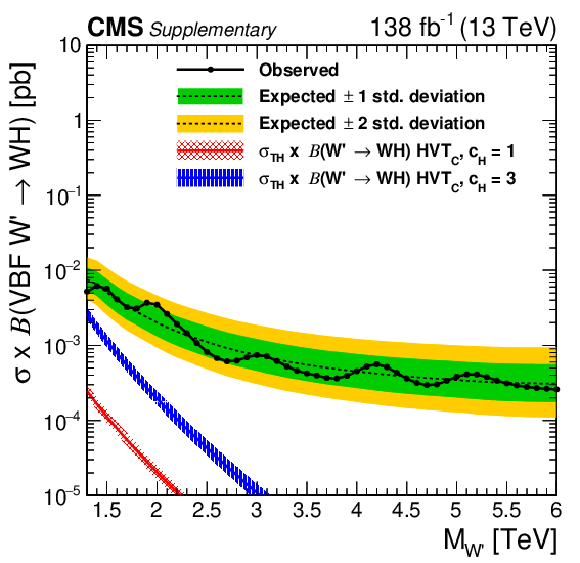
png pdf	Additional Figure 21-d: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{Z}^{'}\to\mathrm{Z}\mathrm{H} $ (left) and $ \mathrm{W^{'}}\to\mathrm{W}\mathrm{H} $ (right) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
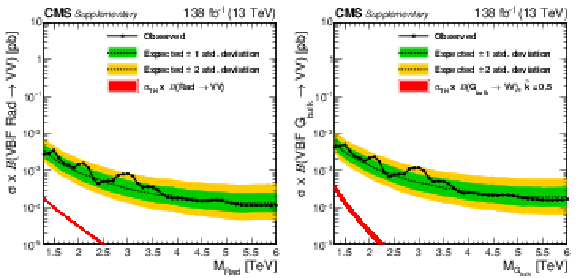
png pdf	Additional Figure 22: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for VBF produced $ \text{Rad} \to\mathrm{V}\mathrm{V} $ (left) and $ \mathrm{G}_{\text{bulk}}\to\mathrm{V}\mathrm{V} $ (right) signals. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
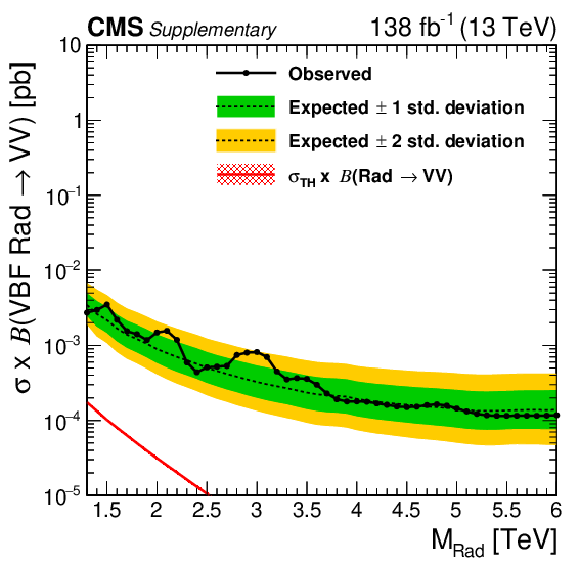
png pdf	Additional Figure 22-a: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for VBF produced $ \text{Rad} \to\mathrm{V}\mathrm{V} $ (left) and $ \mathrm{G}_{\text{bulk}}\to\mathrm{V}\mathrm{V} $ (right) signals. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
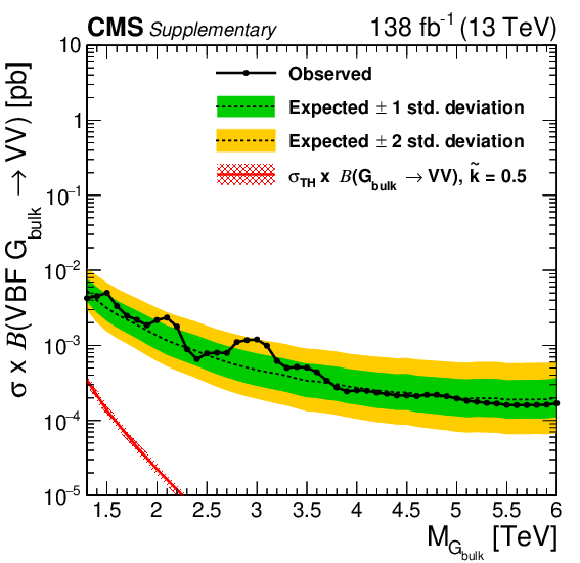
png pdf	Additional Figure 22-b: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for VBF produced $ \text{Rad} \to\mathrm{V}\mathrm{V} $ (left) and $ \mathrm{G}_{\text{bulk}}\to\mathrm{V}\mathrm{V} $ (right) signals. For each signal scenario the theoretical prediction (red line) and its uncertainty associated with the choice of PDF set (red hashed band) is shown.
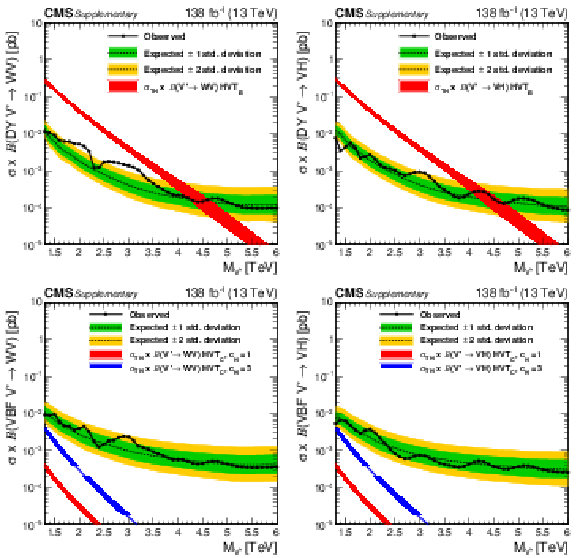
png pdf	Additional Figure 23: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{V}^\prime\to\mathrm{W}\mathrm{V} $ (upper) and $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{H} $ (lower) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
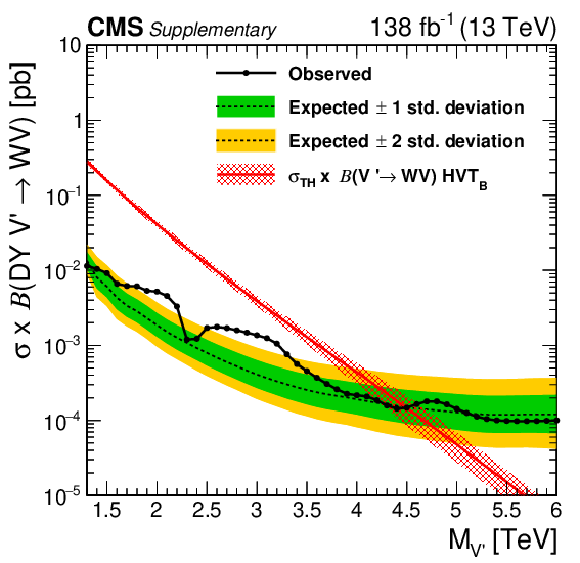
png pdf	Additional Figure 23-a: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{V}^\prime\to\mathrm{W}\mathrm{V} $ (upper) and $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{H} $ (lower) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
png pdf	Additional Figure 23-b: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{V}^\prime\to\mathrm{W}\mathrm{V} $ (upper) and $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{H} $ (lower) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
png pdf	Additional Figure 23-c: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{V}^\prime\to\mathrm{W}\mathrm{V} $ (upper) and $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{H} $ (lower) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.
png pdf	Additional Figure 23-d: Observed and expected 95% CL\ upper limits on the product of the production cross section ($ \sigma $) and the branching fraction, obtained after combining all categories with 138 fb$^{-1}$ fb$ ^{-1} $ of data at $ \sqrt{s}= $ 13 TeV, for $ \mathrm{V}^\prime\to\mathrm{W}\mathrm{V} $ (upper) and $ \mathrm{V}^\prime\to\mathrm{V}\mathrm{H} $ (lower) signals. In the upper panel the DY production mode is shown while in the lower panel the VBF mode is presented. For each signal scenario the theoretical prediction (red line for $ c_{\mathrm{H}} = $ 1, blue line for $ c_{\mathrm{H}} = $ 3) and its uncertainty associated with the choice of PDF set (red and blue hashed bands) is shown.

References
1	L. Randall and R. Sundrum	A large mass hierarchy from a small extra dimension	PRL 83 (1999) 3370	hep-ph/9905221
2	L. Randall and R. Sundrum	An alternative to compactification	PRL 83 (1999) 4690	hep-th/9906064
3	W. D. Goldberger and M. B. Wise	Phenomenology of a stabilized modulus	PLB 475 (2000) 275	hep-ph/9911457
4	W. D. Goldberger and M. B. Wise	Modulus stabilization with bulk fields	PRL 83 (1999) 4922	hep-ph/9907447
5	K. Agashe, H. Davoudiasl, G. Perez, and A. Soni	Warped gravitons at the LHC and beyond	PRD 76 (2007) 036006	hep-ph/0701186
6	A. L. Fitzpatrick, J. Kaplan, L. Randall, and L.-T. Wang	Searching for the Kaluza--Klein graviton in bulk RS models	JHEP 09 (2007) 013	hep-ph/0701150
7	O. Antipin, D. Atwood, and A. Soni	Search for RS gravitons via $ {\mathrm{W}}_\mathrm{L}{\mathrm{W}}_\mathrm{L} $ decays	PLB 666 (2008) 155	0711.3175
8	C. Grojean, E. Salvioni, and R. Torre	A weakly constrained W' at the early LHC	JHEP 07 (2011) 002	1103.2761
9	E. Salvioni, G. Villadoro, and F. Zwirner	Minimal Z' models: present bounds and early LHC reach	JHEP 11 (2009) 068	0909.1320
10	B. Bellazzini, C. Csaki, and J. Serra	Composite Higgses	EPJC 74 (2014) 2766	1401.2457
11	R. Contino, D. Marzocca, D. Pappadopulo, and R. Rattazzi	On the effect of resonances in composite Higgs phenomenology	JHEP 10 (2011) 081	1109.1570
12	D. Marzocca, M. Serone, and J. Shu	General composite Higgs models	JHEP 08 (2012) 013	1205.0770
13	D. Greco and D. Liu	Hunting composite vector resonances at the LHC: naturalness facing data	JHEP 12 (2014) 126	1410.2883
14	K. Lane and L. Pritchett	The light composite Higgs boson in strong extended technicolor	JHEP 06 (2017) 140	1604.07085
15	M. Schmaltz and D. Tucker-Smith	Little Higgs review	Ann. Rev. Nucl. Part. Sci. 55 (2005) 229	hep-ph/0502182
16	N. Arkani-Hamed, A. G. Cohen, E. Katz, and A. E. Nelson	The littlest Higgs	JHEP 07 (2002) 034	hep-ph/0206021
17	D. Pappadopulo, A. Thamm, R. Torre, and A. Wulzer	Heavy vector triplets: Bridging theory and data	JHEP 09 (2014) 060	1402.4431
18	CMS Collaboration	Search for heavy resonances decaying to WW, WZ, or WH boson pairs in the lepton plus merged jet final state in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	PRD 105 (2022) 032008	2109.06055
19	CMS Collaboration	A multi-dimensional search for new heavy resonances decaying to boosted WW, WZ, or ZZ boson pairs in the dijet final state at 13 TeV	EPJC 80 (2020) 237	1906.05977
20	CMS Collaboration	Combination of CMS searches for heavy resonances decaying to pairs of bosons or leptons	PLB 798 (2019) 134952	1906.00057
21	CMS Collaboration	Search for a heavy resonance decaying to a pair of vector bosons in the lepton plus merged jet final state at $ \sqrt{s}= $ 13 TeV	JHEP 05 (2018) 088	1802.09407
22	CMS Collaboration	Search for a heavy resonance decaying into a Z boson and a Z or W boson in $ {2\ell2\mathrm{q}} $ final states at $ \sqrt{s}= $ 13 TeV	JHEP 09 (2018) 101	1803.10093
23	CMS Collaboration	Search for a heavy resonance decaying into a Z boson and a vector boson in the $ {\nu\overline{\nu}\mathrm{q}\overline{\mathrm{q}}} $ final state	JHEP 07 (2018) 075	1803.03838
24	CMS Collaboration	Search for ZZ resonances in the $ {2\ell2\nu} $ final state in proton-proton collisions at 13 TeV	JHEP 03 (2018) 003	1711.04370
25	CMS Collaboration	Search for massive resonances decaying into WW, WZ, ZZ, qW, and qZ with dijet final states at $ \sqrt{s}= $ 13 TeV	PRD 97 (2018) 072006	1708.05379
26	CMS Collaboration	Search for massive resonances decaying into WW, WZ or ZZ bosons in proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JHEP 03 (2017) 162	1612.09159
27	CMS Collaboration	Search for new resonances decaying via WZ to leptons in proton-proton collisions at $ \sqrt{s}= $ 8 TeV	PLB 740 (2015) 83	CMS-EXO-12-025 1407.3476
28	CMS Collaboration	Search for massive resonances in dijet systems containing jets tagged as W or Z boson decays in pp collisions at $ \sqrt{s}= $ 8 TeV	JHEP 08 (2014) 173	CMS-EXO-12-024 1405.1994
29	CMS Collaboration	Search for massive resonances decaying into pairs of boosted bosons in semi-leptonic final states at $ \sqrt{s}= $ 8 TeV	JHEP 08 (2014) 174	CMS-EXO-13-009 1405.3447
30	CMS Collaboration	Search for heavy resonances decaying into two Higgs bosons or into a Higgs boson and a W or Z boson in proton-proton collisions at 13 TeV	JHEP 01 (2019) 051	1808.01365
31	CMS Collaboration	Search for heavy resonances decaying into a vector boson and a Higgs boson in final states with charged leptons, neutrinos and b quarks at $ \sqrt{s}= $ 13 TeV	JHEP 11 (2018) 172	1807.02826
32	CMS Collaboration	Search for heavy resonances that decay into a vector boson and a Higgs boson in hadronic final states at $ \sqrt{s}= $ 13 TeV	EPJC 77 (2017) 636	1707.01303
33	CMS Collaboration	Search for heavy resonances decaying into a vector boson and a Higgs boson in final states with charged leptons, neutrinos, and b quarks	PLB 768 (2017) 137	1610.08066
34	CMS Collaboration	Search for massive WH resonances decaying into the $ {\ell\nu\mathrm{b}\overline{\mathrm{b}}} $ final state at $ \sqrt{s}= $ 8 TeV	EPJC 76 (2016) 237	CMS-EXO-14-010 1601.06431
35	CMS Collaboration	Search for a massive resonance decaying into a Higgs boson and a W or Z boson in hadronic final states in proton-proton collisions at $ \sqrt{s}= $ 8 TeV	JHEP 02 (2016) 145	CMS-EXO-14-009 1506.01443
36	CMS Collaboration	Search for narrow high-mass resonances in proton-proton collisions at $ \sqrt{s}= $ 8 TeV decaying to a Z and a Higgs boson	PLB 748 (2015) 255	CMS-EXO-13-007 1502.04994
37	ATLAS Collaboration	Search for heavy diboson resonances in semileptonic final states in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	EPJC 80 (2020) 1165	2004.14636
38	ATLAS Collaboration	Search for diboson resonances in hadronic final states in 139 fb $^{-1}$ of pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	JHEP 09 (2019) 091	1906.08589
39	ATLAS Collaboration	Combination of searches for heavy resonances decaying into bosonic and leptonic final states using 36 fb $^{-1}$ of proton-proton collision data at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	Phys. Rev. D ) 0, 2018 link	1808.02380
40	ATLAS Collaboration	Search for heavy resonances decaying to a W or Z boson and a Higgs boson in the $ {\mathrm{q}\overline{\mathrm{q}}^{(\prime)}\mathrm{b}\overline{\mathrm{b}}} $ final state in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	PLB 774 (2017) 494	1707.06958
41	ATLAS Collaboration	Search for diboson resonances with boson-tagged jets in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	PLB 777 (2018) 91	1708.04445
42	ATLAS Collaboration	Searches for heavy diboson resonances in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	JHEP 09 (2016) 173	1606.04833
43	ATLAS Collaboration	Search for production of $ {\mathrm{W}\mathrm{W}/\mathrm{W}\mathrm{Z}} $ resonances decaying to a lepton, neutrino and jets in pp collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector	EPJC 75 (2015) 209	1503.04677
44	ATLAS Collaboration	Search for resonant diboson production in the $ {\ell\ell\mathrm{q}\overline{\mathrm{q}}} $ final state in pp collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector	EPJC 75 (2015) 69	1409.6190
45	ATLAS Collaboration	Search for WZ resonances in the fully leptonic channel using pp collisions at $ \sqrt{s}= $ 8 TeV collisions with the ATLAS detector	PLB 737 (2014) 223	1406.4456
46	ATLAS Collaboration	Search for resonances decaying into a weak vector boson and a Higgs boson in the fully hadronic final state produced in proton-proton collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	PRD 102 (2020) 112008	2007.05293
47	ATLAS Collaboration	Search for a new resonance decaying to a W or Z boson and a Higgs boson in the $ {\ell\ell/\ell\nu/\nu\nu}+\mathrm{b}\overline{\mathrm{b}} $ final states with the ATLAS detector	EPJC 75 (2015) 263	1503.08089
48	ATLAS Collaboration	Search for new resonances decaying to a W or Z boson and a Higgs boson in the $ {\ell^+\ell^-\mathrm{b}\overline{\mathrm{b}}} $, $ {\ell\nu\mathrm{b}\overline{\mathrm{b}}} $, and $ {\nu\overline{\nu}\mathrm{b}\overline{\mathrm{b}}} $ channels with pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector	PLB 765 (2017) 32	1607.05621
49	ATLAS Collaboration	Search for high-mass diboson resonances with boson-tagged jets in proton-proton collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector	JHEP 12 (2015) 055	1506.00962
50	CMS Collaboration	Identification of heavy, energetic, hadronically decaying particles using machine-learning techniques	JINST 15 (2020) P06005	CMS-JME-18-002 2004.08262
51	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004
52	CMS Collaboration	Particle-flow reconstruction and global event description with the CMS detector	JINST 12 (2017) P10003	CMS-PRF-14-001 1706.04965
53	M. Cacciari, G. P. Salam, and G. Soyez	The anti-$ k_{T} $ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
54	M. Cacciari, G. P. Salam, and G. Soyez	FastJet user manual	EPJC 72 (2012) 1896	1111.6097
55	CMS Collaboration	Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV	JINST 12 (2017) P02014	CMS-JME-13-004 1607.03663
56	CMS Collaboration	Jet algorithms performance in 13 TeV data	CMS Physics Analysis Summary, 2016 CMS-PAS-JME-16-003	CMS-PAS-JME-16-003
57	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
58	D. Krohn, J. Thaler, and L.-T. Wang	Jet trimming	JHEP 02 (2010) 084	0912.1342
59	A. Oliveira	Gravity particles from warped extra dimensions, predictions for LHC		1404.0102
60	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
61	T. Sjöstrand et al.	An introduction to PYTHIA 8.2	Comput. Phys. Commun. 191 (2015) 159	1410.3012
62	NNPDF Collaboration	Parton distributions for the LHC Run II	JHEP 04 (2015) 040	1410.8849
63	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2016) 155	CMS-GEN-14-001 1512.00815
64	CMS Collaboration	Extraction and validation of a new set of CMS PYTHIA 8 tunes from underlying-event measurements	EPJC 80 (2020) 4	CMS-GEN-17-001 1903.12179
65	J. Butterworth et al.	PDF4LHC recommendations for LHC Run II	JPG 43 (2016) 023001	1510.03865
66	S. Dulat et al.	New parton distribution functions from a global analysis of quantum chromodynamics	PRD 93 (2016) 033006	1506.07443
67	L. A. Harland-Lang, A. D. Martin, P. Motylinski, and R. S. Thorne	Parton distributions in the LHC era: MMHT 2014 PDFs	EPJC 75 (2015) 204	1412.3989
68	J. Gao and P. Nadolsky	A meta-analysis of parton distribution functions	JHEP 07 (2014) 035	1401.0013
69	S. Carrazza et al.	An unbiased Hessian representation for Monte Carlo PDFs	EPJC 75 (2015) 369	1505.06736
70	J. Alwall et al.	Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions	EPJC 53 (2008) 473	0706.2569
71	M. B ä hr et al.	HERWIG++ physics and manual	EPJC 58 (2008) 639	0803.0883
72	S. Alioli, S.-O. Moch, and P. Uwer	Hadronic top-quark pair-production with one jet and parton showering	JHEP 01 (2012) 137	1110.5251
73	S. Kallweit et al.	NLO electroweak automation and precise predictions for W+multijet production at the LHC	JHEP 04 (2015) 012	1412.5157
74	S. Kallweit et al.	NLO QCD+EW predictions for V+jets including off-shell vector-boson decays and multijet merging	JHEP 04 (2016) 021	1511.08692
75	NNPDF Collaboration	Parton distributions from high-precision collider data	EPJC 77 (2017) 663	1706.00428
76	GEANT4 Collaboration	GEANT 4---a simulation toolkit	NIM A 506 (2003) 250
77	CMS Collaboration	Jet energy scale and resolution performance with 13 TeV data collected by CMS in 2016-2018	CMS Detector Performance Note CMS-DP-2020-019, 2020 CDS
78	CMS Collaboration	Jet energy scale and resolution measurement with Run 2 Legacy Data Collected by CMS at 13 TeV	Technical Report CMS-DP-2021-033, 2021 CDS
79	CMS Collaboration	Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2015 and 2016 at CMS	EPJC 81 (2021) 800	CMS-LUM-17-003 2104.01927
80	CMS Collaboration	CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s}= $ 13 TeV	CMS Physics Analysis Summary, 2018 CMS-PAS-LUM-17-004	CMS-PAS-LUM-17-004
81	CMS Collaboration	CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s}= $ 13 TeV	CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002	CMS-PAS-LUM-18-002
82	CMS Collaboration	Description and performance of track and primary-vertex reconstruction with the CMS tracker	JINST 9 (2014) P10009	CMS-TRK-11-001 1405.6569
83	CMS Collaboration	Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid	CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS
84	CMS Collaboration	Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV	JINST 13 (2018) P06015	CMS-MUO-16-001 1804.04528
85	CMS Collaboration	Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s}= $ 8 TeV	JINST 10 (2015) P06005	CMS-EGM-13-001 1502.02701
86	CMS Collaboration	Pileup mitigation at CMS in 13 TeV data	JINST 15 (2020) P09018	CMS-JME-18-001 2003.00503
87	D. Bertolini, P. Harris, M. Low, and N. Tran	Pileup per particle identification	JHEP 10 (2014) 59	1407.6013
88	A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler	Soft drop	JHEP 05 (2014) 146	1402.2657
89	Y. L. Dokshitzer, G. D. Leder, S. Moretti, and B. R. Webber	Better jet clustering algorithms	JHEP 08 (1997) 001	hep-ph/9707323
90	M. Wobisch and T. Wengler	Hadronization corrections to jet cross-sections in deep inelastic scattering	in Monte Carlo generators for HERA physics, 1998	hep-ph/9907280
91	J. Dolen et al.	Thinking outside the ROCs: Designing decorrelated taggers (DDT) for jet substructure	JHEP 05 (2016) 156	1603.00027
92	CMS Collaboration	Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV	JINST 13 (2018) P05011	CMS-BTV-16-002 1712.07158
93	CMS Collaboration	Measurements of $ \mathrm{t}\overline{\mathrm{t}} $ differential cross sections in proton-proton collisions at $ \sqrt{s}= $ 13 TeV using events containing two leptons	JHEP 02 (2018) 149	CMS-TOP-17-014 1811.06625
94	CMS Collaboration	Measurement of differential cross sections for top quark pair production using the lepton+jets final state in proton-proton collisions at 13 TeV	PRD 95 (2016) 092001	CMS-TOP-16-008 1610.04191
95	L. Demortier and L. Lyons	Everything you always wanted to know about pulls	Technical Report CDF/ANAL/PUBLIC/5776, CDF, 2002 link
96	T. Junk	Confidence level computation for combining searches with small statistics	NIM A 434 (1999) 435	hep-ex/9902006
97	A. L. Read	Presentation of search results: the CL$ _\text{s} $ technique	JPG 28 (2002) 2693
98	G. Cowan, K. Cranmer, E. Gross, and O. Vitells	Asymptotic formulae for likelihood-based tests of new physics	EPJC 71 (2011) 1554	1007.1727
99	CMS Collaboration	HEPData record for this analysis	link