Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-HIG-16-043 | ||
| Observation of the SM scalar boson decaying to a pair of $\tau$ leptons with the CMS experiment at the LHC | ||
| CMS Collaboration | ||
| May 2017 | ||
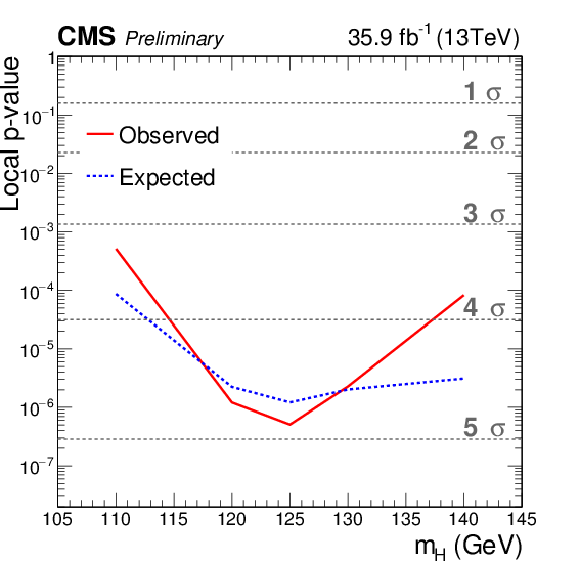
| Abstract: A search for a standard model scalar boson decaying into a pair of $\tau$ leptons is performed using events recorded in proton-proton collisions by the CMS experiment at the LHC in 2016. The dataset corresponds to an integrated luminosity of 35.9 fb$^{-1}$ at a center-of-mass energy of $\sqrt{s}= $ 13 TeV. The $\tau$ leptons decay semi-hadronically, or leptonically to an electron or a muon, and the four final states with the largest branching fractions are considered. An excess of events is observed over the expected background prediction with a significance of 4.9 standard deviations for the scalar boson mass $m_{H} = $ 125 GeV, to be compared to an expected significance of 4.7 standard deviations. The best fit of the observed $H \to \tau \tau$ signal cross section times branching fraction for $m_{H}= $ 125 GeV is 1.06$^{+0.25}_{-0.24}$ times the standard model expectation. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, PLB 779 (2018) 283. The superseded preliminary plots can be found here. |
||
| Figures | Summary | Additional Figures | References | CMS Publications |
|---|
| Figures | |
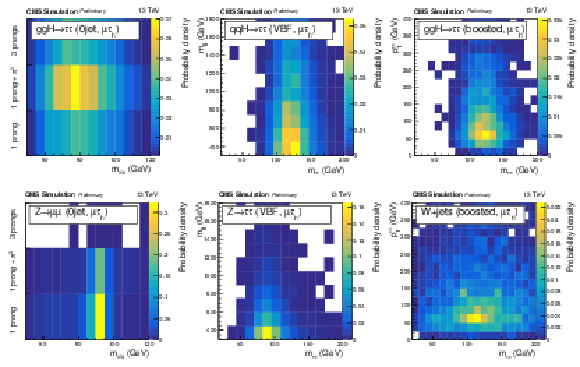
png pdf |
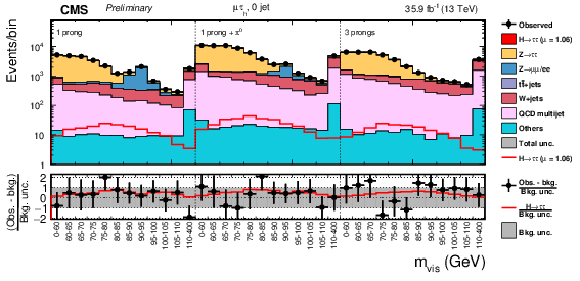
Figure 1:
Distributions for the signal (top) and typical background processes (bottom) of the two observables chosen in the 0 jet (left), VBF (center), and boosted (right) categories in the $\mu {\tau _{\rm h}} $ final state. The $Z\rightarrow \mu \mu $ background in the 0 jet category is concentrated in the regions where the visible mass is close to 90 GeV and is negligible when the reconstructed $ {\tau _{\rm h}} $ decay mode is 3-prongs. The $Z\rightarrow \tau \tau $ background in the VBF category mostly lies at low $m_{jj}$ values whereas the distribution of VBF signal events extends to high $m_{jj}$ values. In the boosted category, the W+jets background, which behaves similarly as the QCD background, is rather flat with respect to $ {m_{\tau \tau }} $, and is concentrated at low $ { {p_{\mathrm {T}}} ^{\tau \tau }} $ values. |
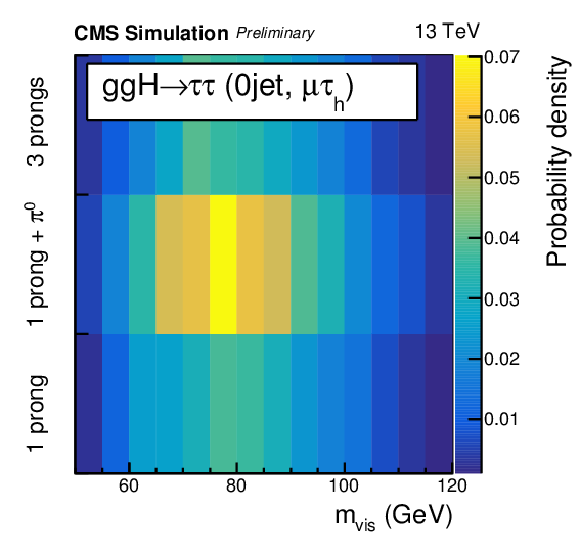
png pdf |
Figure 1-a:
Distribution for the signal of the $m_{\text{vis}}$ variable in the 0 jet category in the $\mu {\tau _{\rm h}} $ final state. |
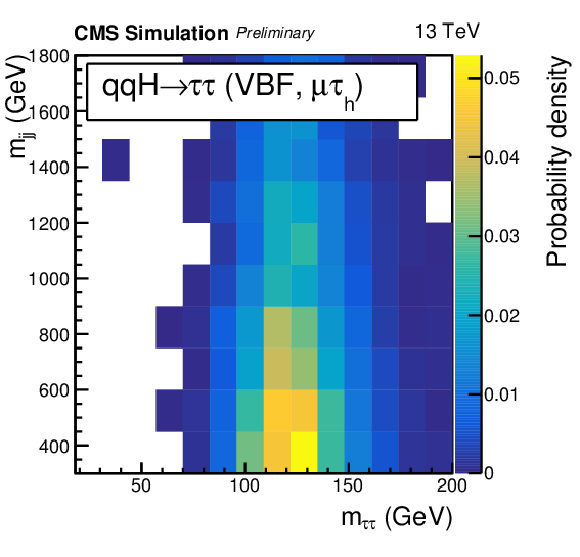
png pdf |
Figure 1-b:
Distribution for the signal of the $m_{\tau \tau}$ variable in the VBF category in the $\mu {\tau _{\rm h}} $ final state. |
png pdf |
Figure 1-c:
Distribution for the signal of the $m_{\tau \tau}$ variable in the boosted category in the $\mu {\tau _{\rm h}} $ final state. |
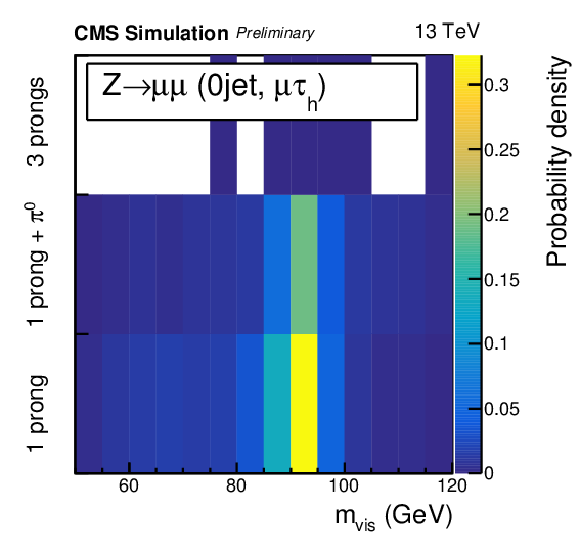
png pdf |
Figure 1-d:
Distribution for the $Z\rightarrow \mu \mu $ background process of the $m_{\text{vis}}$ variable in the 0 jet category in the $\mu {\tau _{\rm h}} $ final state. The $Z\rightarrow \mu \mu $ background in the 0 jet category is concentrated in the regions where the visible mass is close to 90 GeV and is negligible when the reconstructed $ {\tau _{\rm h}} $ decay mode is 3-prongs. |
png pdf |
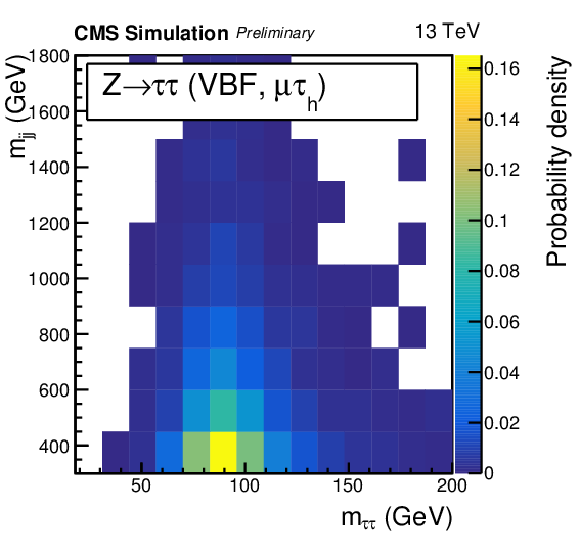
Figure 1-e:
Distribution for the $Z\rightarrow \tau \tau $ background process of the $m_{\tau \tau}$ variable in the VBF category in the $\mu {\tau _{\rm h}} $ final state. The $Z\rightarrow \tau \tau $ background in the VBF category mostly lies at low $m_{jj}$ values whereas the distribution of VBF signal events extends to high $m_{jj}$ values. |
png pdf |
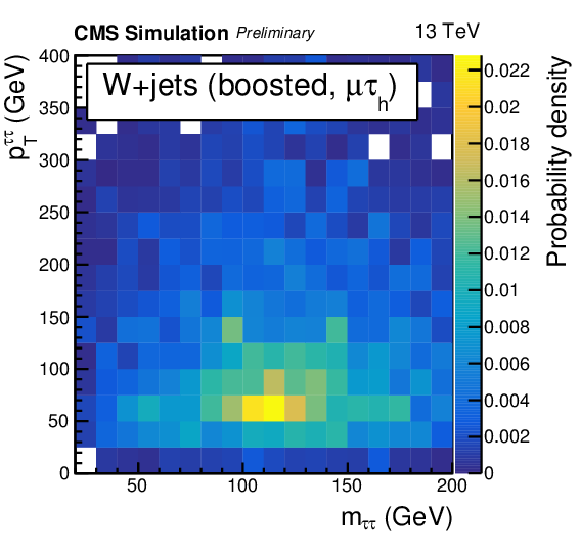
Figure 1-f:
Distribution for the W+jets background process of the $m_{\tau \tau}$ variable in the boosted category in the $\mu {\tau _{\rm h}} $ final state. In the boosted category, the W+jets background, which behaves similarly as the QCD background, is rather flat with respect to $ {m_{\tau \tau }} $, and is concentrated at low $ { {p_{\mathrm {T}}} ^{\tau \tau }} $ values. |
png pdf |
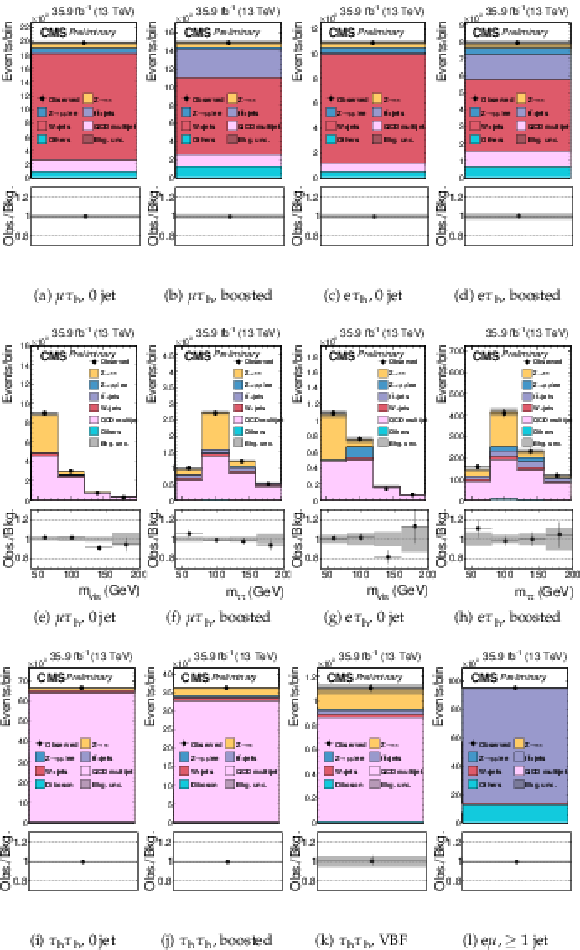
Figure 2:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
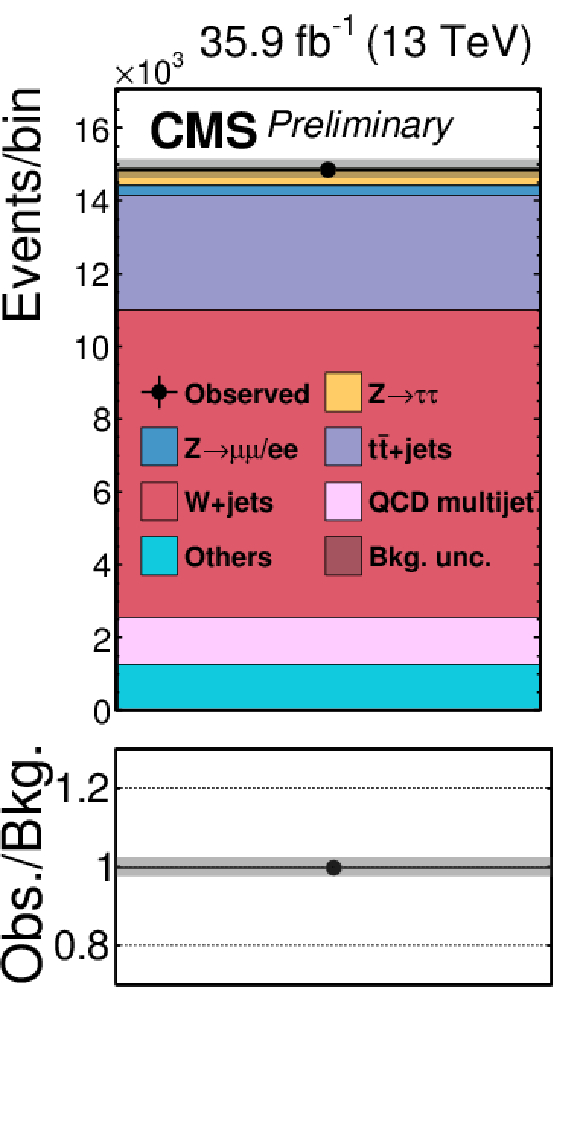
Figure 2-a:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
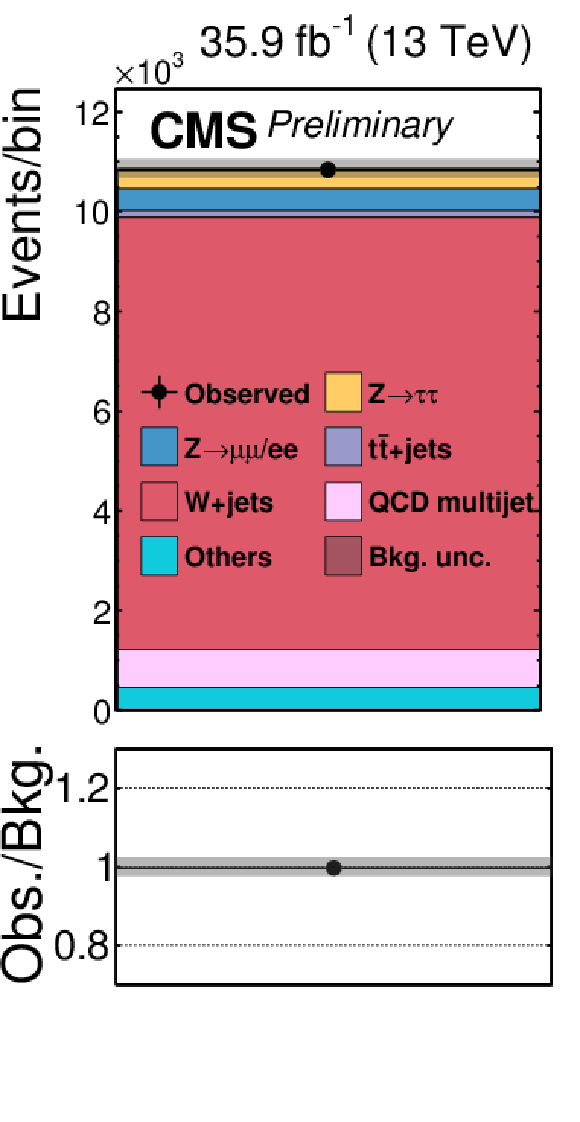
Figure 2-b:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
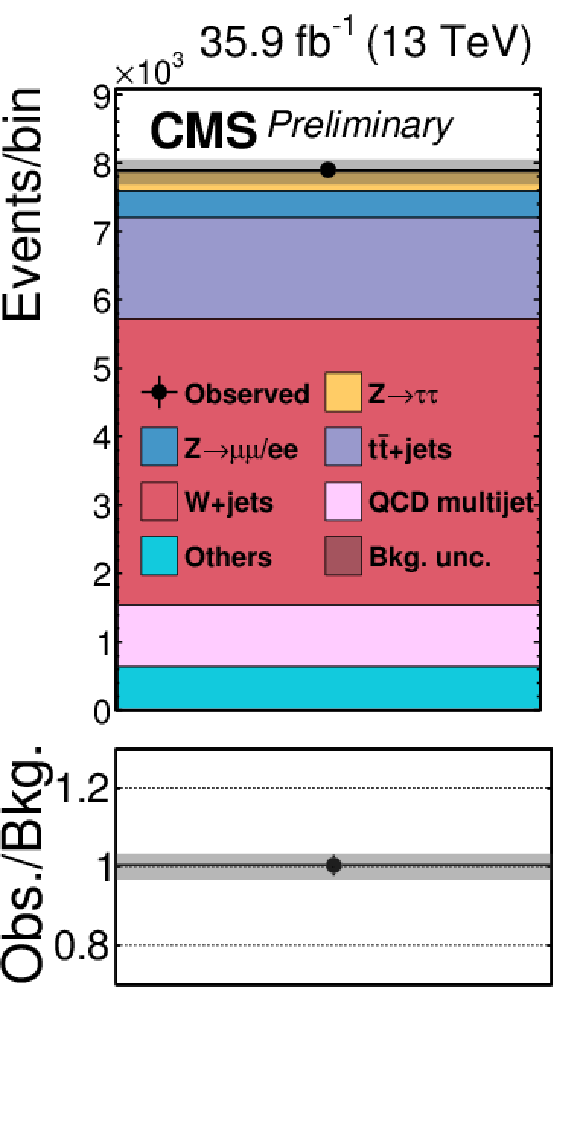
Figure 2-c:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
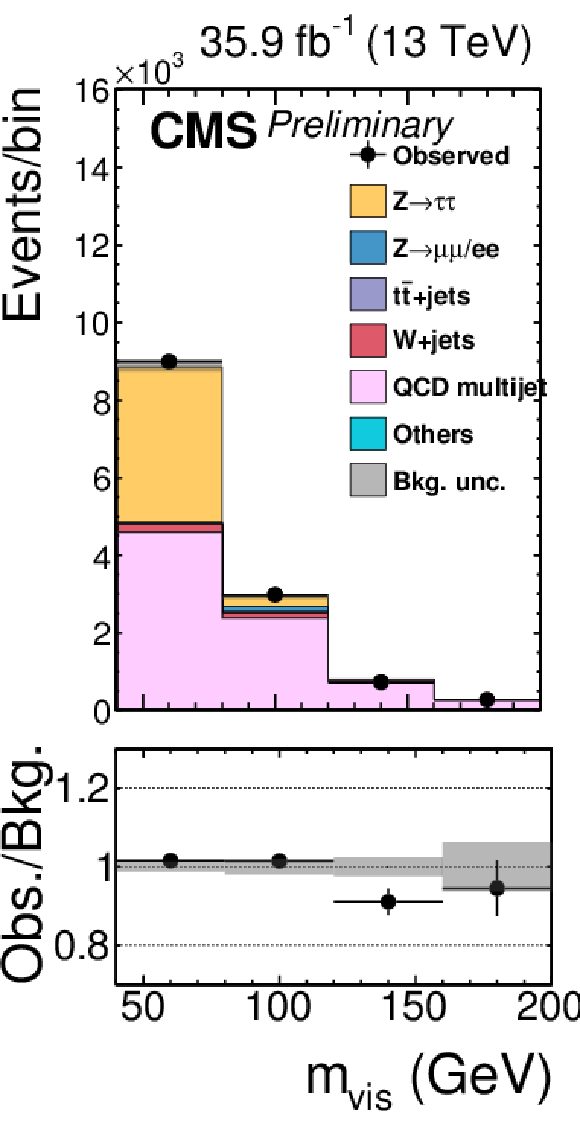
Figure 2-d:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
Figure 2-e:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
Figure 2-f:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
Figure 2-g:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
Figure 2-h:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
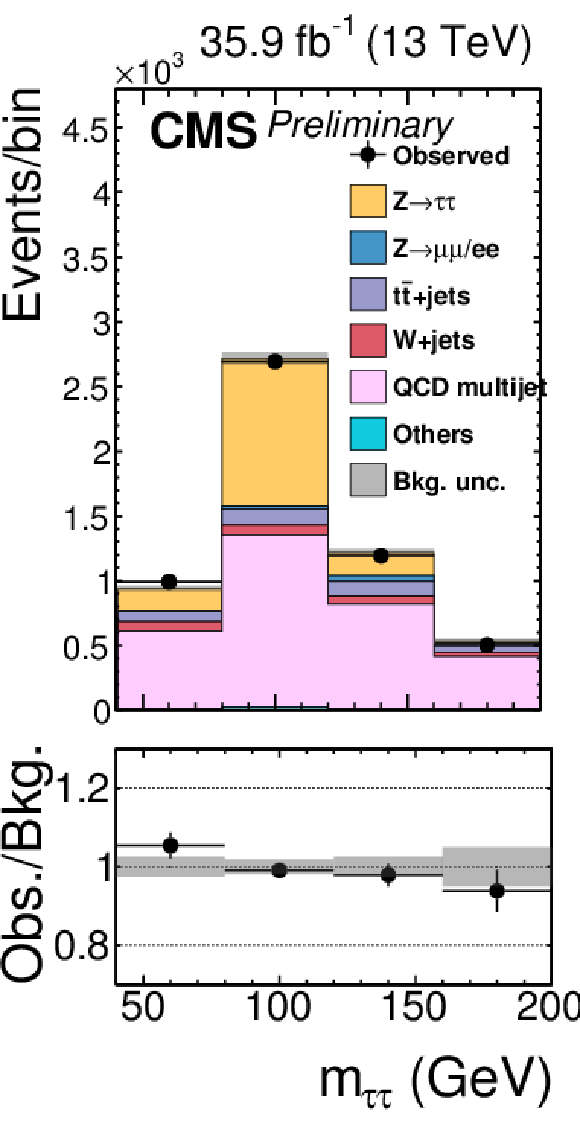
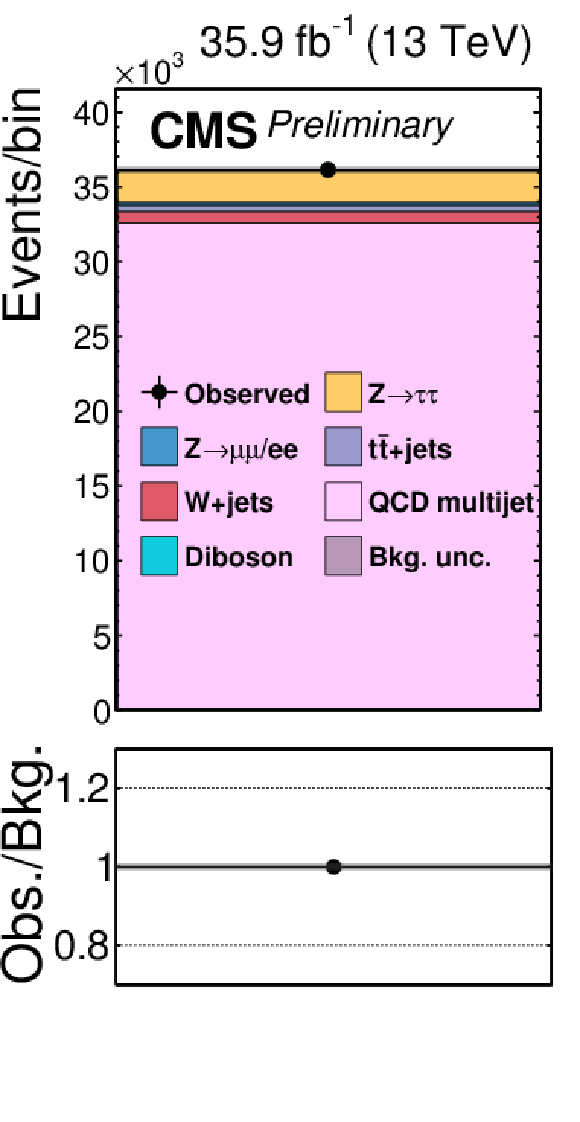
Figure 2-i:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
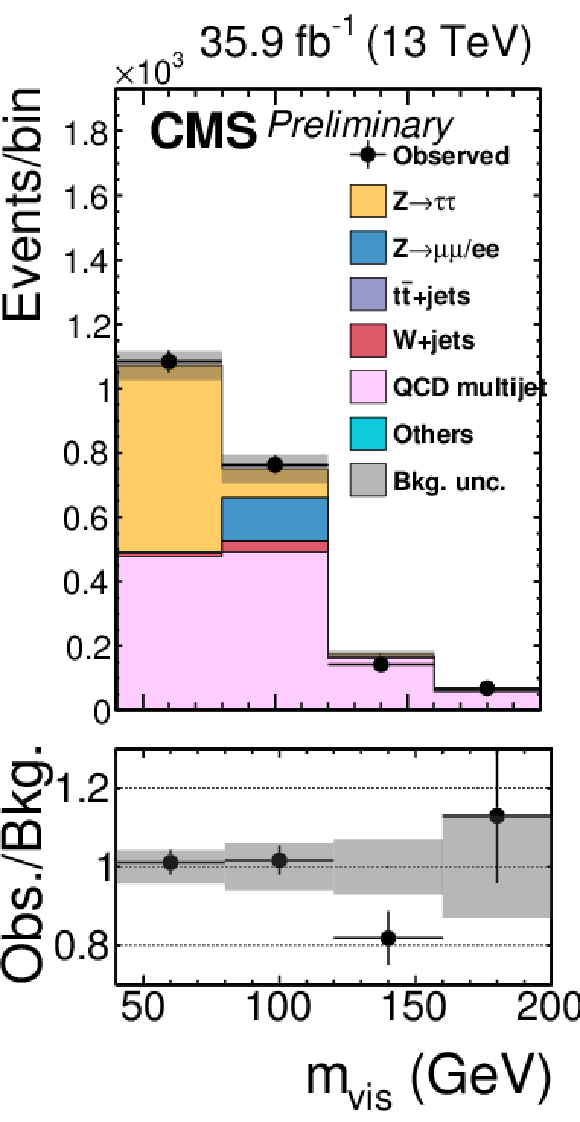
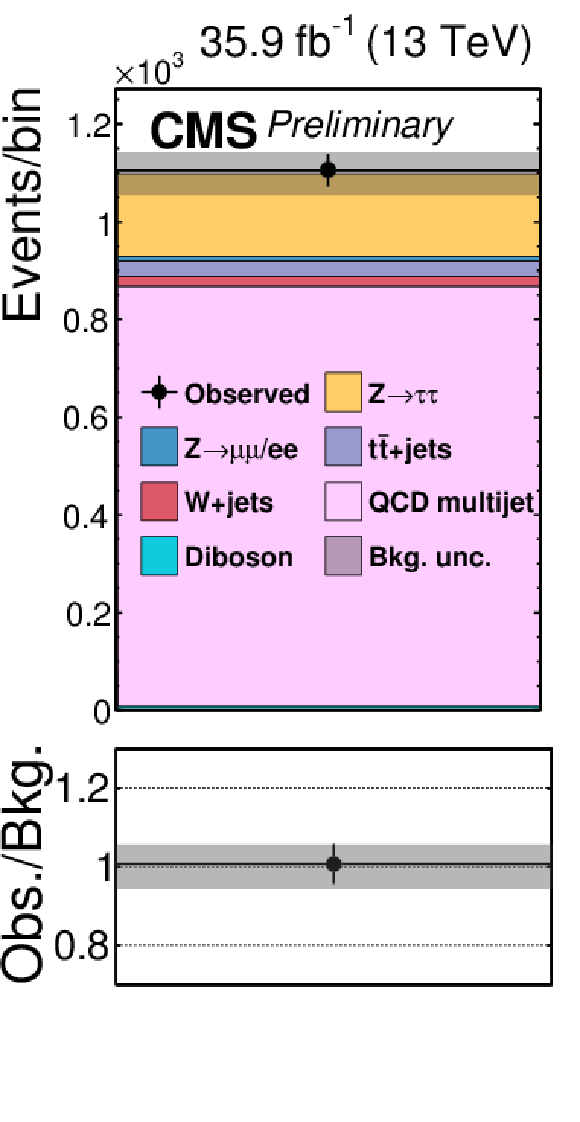
Figure 2-j:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
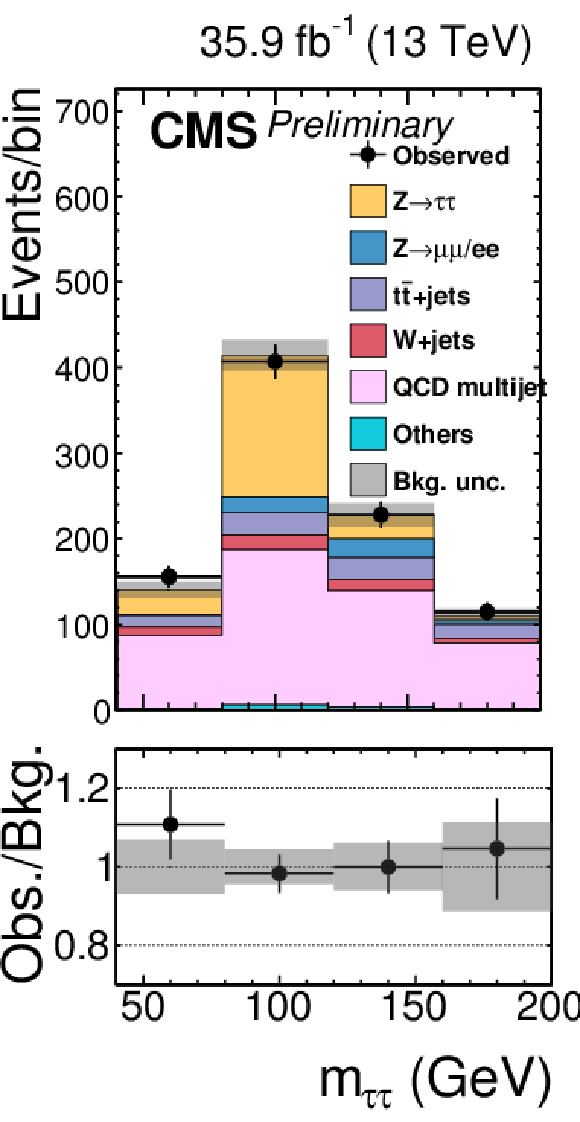
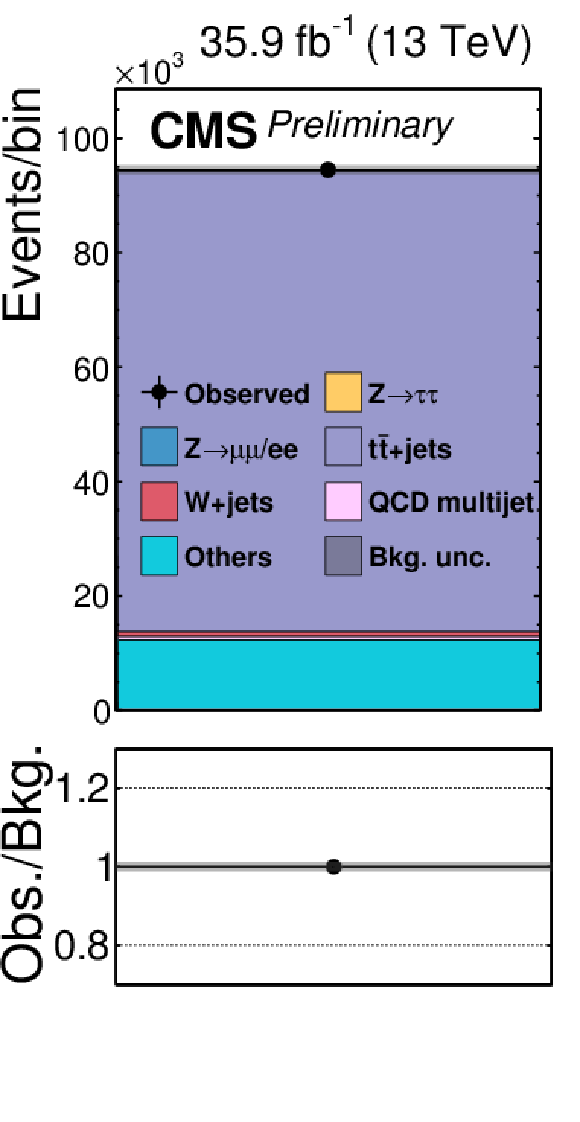
Figure 2-k:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
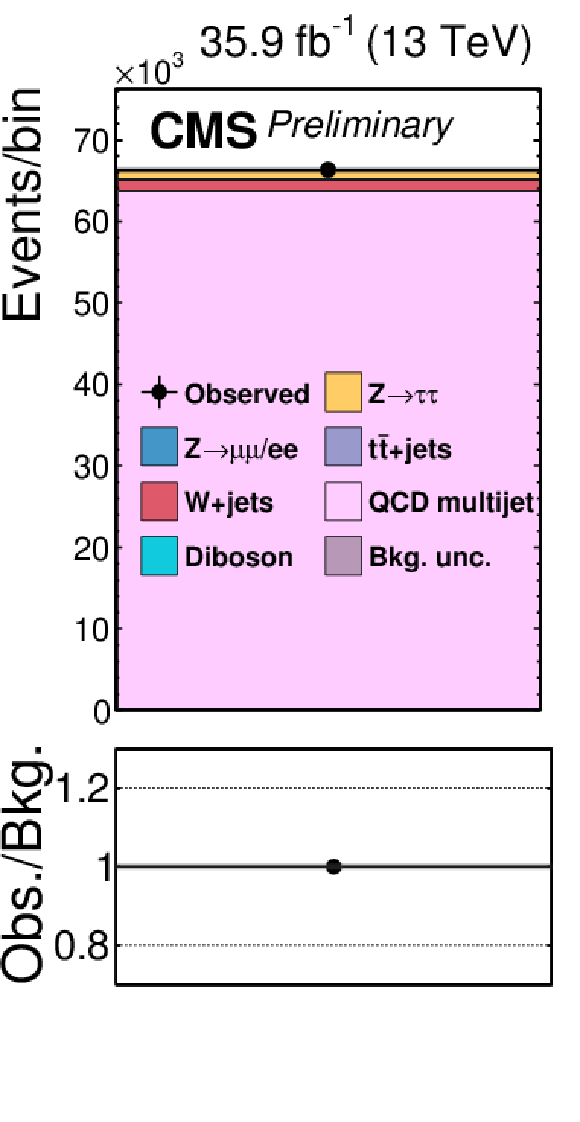
Figure 2-l:
Signal-free control regions used in the maximum likelihood fit, together with the signal regions, to extract the results. These regions control the yields of the W+jets (a,b,c,d), QCD multijet (e,f,g,h,i,j,k), and ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ (l) backgrounds, in the $\mu {\tau _{\rm h}} $ (a,b,e,f), $\mathrm{ e } {\tau _{\rm h}} $ (c,d,g,h), $ {\tau _{\rm h}} {\tau _{\rm h}} $ (i,j,k) or $\mathrm{ e } \mu $ (l) final states. The constraint on the ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ background is obtained in the $\mathrm{ e } \mu $ final state, but propagated to all final states. The constraints on the W+jets and QCD multijet backgrounds obtained in the boosted categories of the $\mu {\tau _{\rm h}} $ and $\mathrm{ e } {\tau _{\rm h}} $ final states are propagated to the VBF categories of these final states. |
png pdf |
Figure 3:
Observed and predicted 2D distributions in the 0-jet category of the $\mathrm{ e } \mu $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
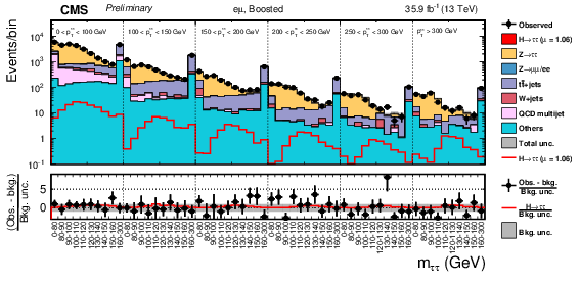
Figure 4:
Observed and predicted 2D distributions in the VBF category of the $\mathrm{ e } \mu $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
Figure 5:
Observed and predicted 2D distributions in the boosted category of the $\mathrm{ e } \mu $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
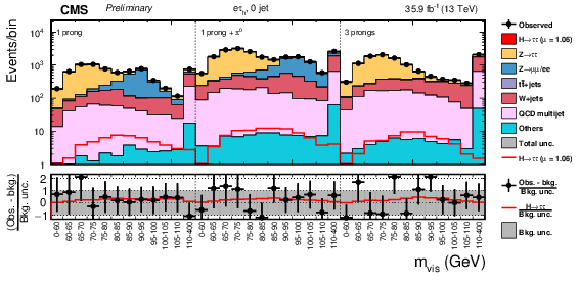
Figure 6:
Observed and predicted 2D distributions in the 0-jet category of the $\mathrm{ e } {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
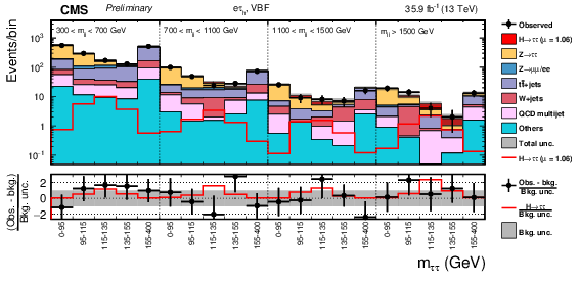
Figure 7:
Observed and predicted 2D distributions in the VBF category of the $\mathrm{ e } {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
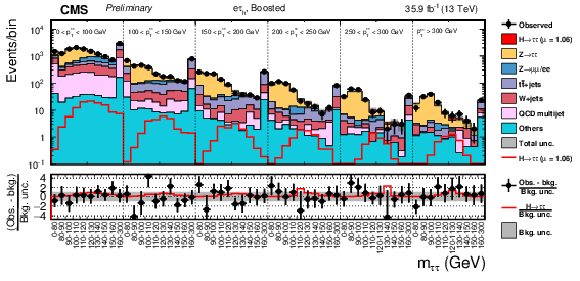
Figure 8:
Observed and predicted 2D distributions in the boosted category of the $\mathrm{ e } {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
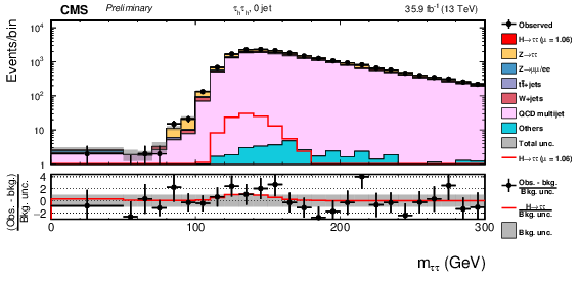
Figure 9:
Observed and predicted 2D distributions in the 0-jet category of the $\mu {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
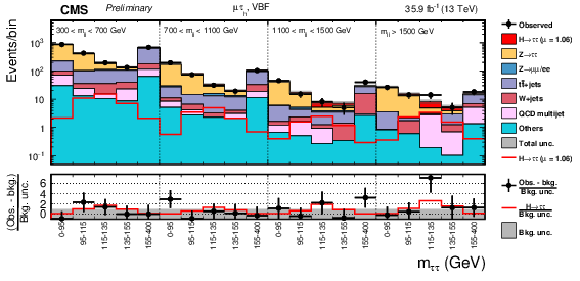
Figure 10:
Observed and predicted 2D distributions in the VBF category of the $\mu {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
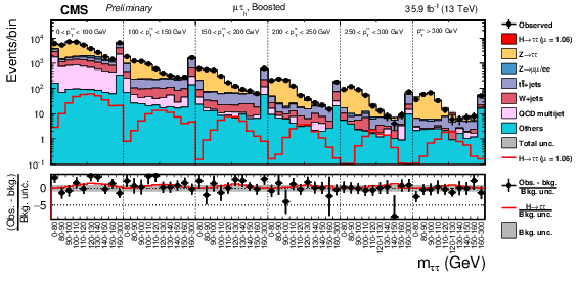
Figure 11:
Observed and predicted 2D distributions in the boosted category of the $\mu {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
Figure 12:
Observed and predicted 2D distributions in the 0-jet category of the $ {\tau _{\rm h}} {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
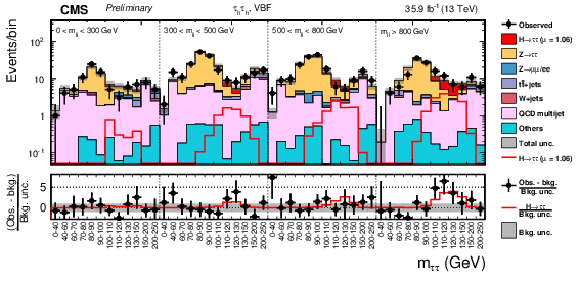
Figure 13:
Observed and predicted 2D distributions in the VBF category of the $ {\tau _{\rm h}} {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
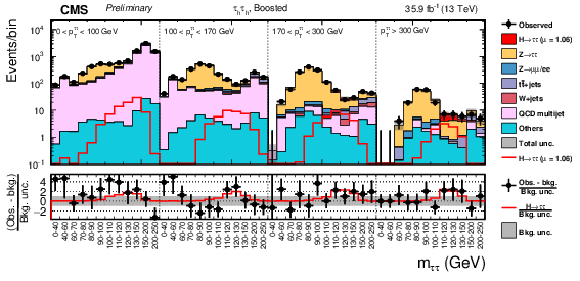
Figure 14:
Observed and predicted 2D distributions in the boosted category of the $ {\tau _{\rm h}} {\tau _{\rm h}} $ final state. The normalization of the predicted background distributions corresponds to the result of the global fit. The signal distribution is normalized to its best-fit signal strength. The background histograms are stacked. The "others" background contribution includes events from diboson and single-top-quark production, as well as scalar boson decays to a pair of W bosons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. |
png pdf |
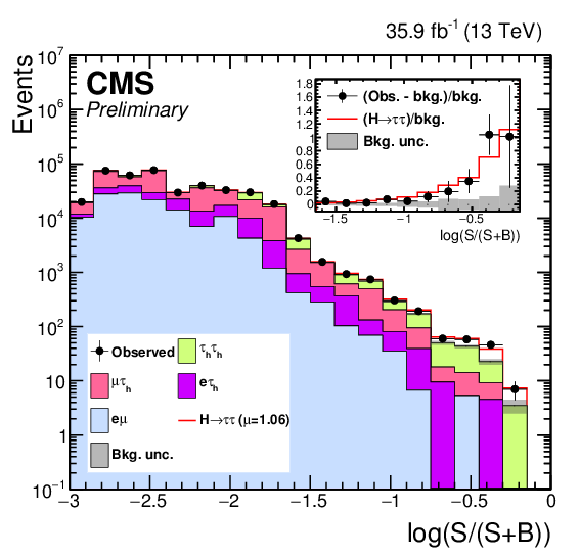
Figure 15:
Distribution of the decimal logarithm of the ratio between the expected signal and the sum of expected signal and expected background in each bin of the mass distributions used to extract the results, in all signal regions. The background contributions are separated by decay channel. The inset shows the corresponding difference between the observed data and expected background distributions divided by the background expectation, as well as the signal expectation divided by the background expectation. |
png pdf |
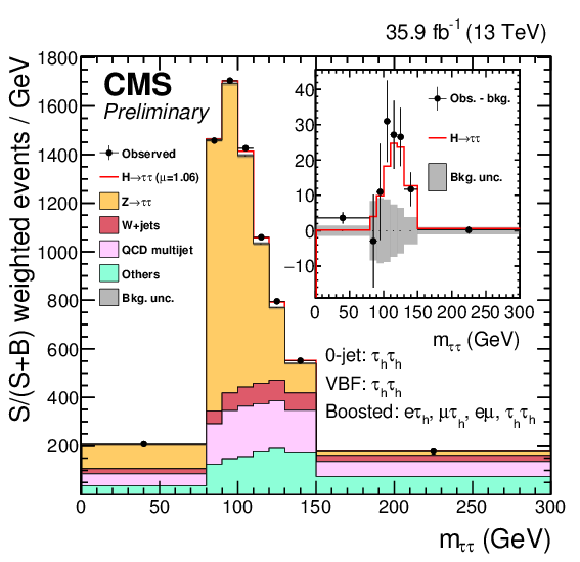
Figure 16:
Combined observed and predicted $ {m_{\tau \tau }} $ distributions. The right figure includes the VBF category of the $\mathrm{ e } \mu $, $\mathrm{ e } {\tau _{\rm h}} $ and $\mu {\tau _{\rm h}} $ channels, and the left figure includes all other channels that make use of $ {m_{\tau \tau }} $ and not $ {m_\text {vis}} $. The normalization of the predicted background distributions corresponds to the result of the global fit, while the signal is normalized to its best-fit signal strength. The mass distribution for a constant range of the second dimension of the signal distributions are weighted according to $S/(S+B)$, where $S$ and $B$ are computed, respectively, as the signal or background contribution in the mass distribution excluding the first and last bins. The "others" background contribution includes events from diboson, $t\bar{t}$, and single-top-quark production, as well as scalar boson decays to a pair of W bosons and Z bosons decaying to a pair of light leptons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. The inset shows the corresponding difference between the observed data and expected background distributions, together with the signal expectation. The signal normalization is equal to its normalization before reweighting. |
png pdf |
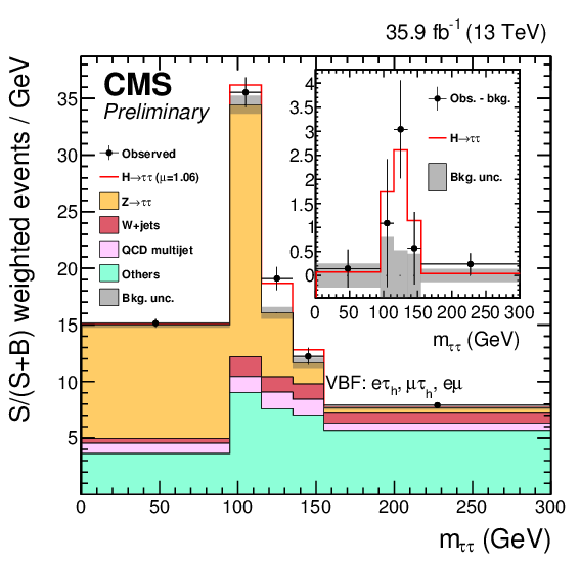
Figure 16-a:
Combined observed and predicted $ {m_{\tau \tau }} $ distribution. The figure includes all channels that make use of $ {m_{\tau \tau }} $ and not $ {m_\text {vis}} $ other than the VBF category of the $\mathrm{ e } \mu $, $\mathrm{ e } {\tau _{\rm h}} $ and $\mu {\tau _{\rm h}} $ channels. The normalization of the predicted background distributions corresponds to the result of the global fit, while the signal is normalized to its best-fit signal strength. The mass distribution for a constant range of the second dimension of the signal distributions are weighted according to $S/(S+B)$, where $S$ and $B$ are computed, respectively, as the signal or background contribution in the mass distribution excluding the first and last bins. The "others" background contribution includes events from diboson, $t\bar{t}$, and single-top-quark production, as well as scalar boson decays to a pair of W bosons and Z bosons decaying to a pair of light leptons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. The inset shows the corresponding difference between the observed data and expected background distributions, together with the signal expectation. The signal normalization is equal to its normalization before reweighting. |
png pdf |
Figure 16-b:
Combined observed and predicted $ {m_{\tau \tau }} $ distribution. The figure includes the VBF category of the $\mathrm{ e } \mu $, $\mathrm{ e } {\tau _{\rm h}} $ and $\mu {\tau _{\rm h}} $ channels. The normalization of the predicted background distributions corresponds to the result of the global fit, while the signal is normalized to its best-fit signal strength. The mass distribution for a constant range of the second dimension of the signal distributions are weighted according to $S/(S+B)$, where $S$ and $B$ are computed, respectively, as the signal or background contribution in the mass distribution excluding the first and last bins. The "others" background contribution includes events from diboson, $t\bar{t}$, and single-top-quark production, as well as scalar boson decays to a pair of W bosons and Z bosons decaying to a pair of light leptons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. The inset shows the corresponding difference between the observed data and expected background distributions, together with the signal expectation. The signal normalization is equal to its normalization before reweighting. |
png pdf |
Figure 17:
Local p-value and significance as a function of the SM scalar boson mass hypothesis. The observation (black) is compared to the expectation (blue) for a scalar boson with a mass $ {m_{\mathrm{ H } }} = $ 125 GeV. The background includes scalar boson decays to a pair of W bosons, with $ {m_{\mathrm{ H } }} = $ 125 GeV. |
png pdf |
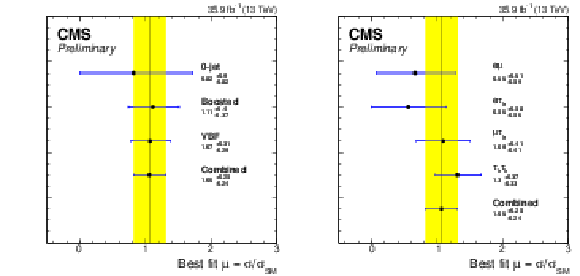
Figure 18:
Best-fit signal strength per category (left) and channel (right), for $ {m_{\mathrm{ H } }} = $ 125 GeV. The constraints from the global fit are used to extract each of the individual best-fit signal strengths. The combined best-fit signal strength is $\hat\mu = $ 1.06 $\pm$ 0.25. |
png pdf |
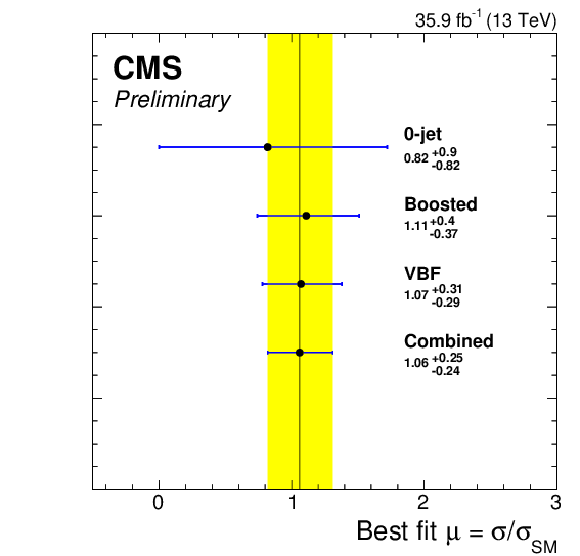
Figure 18-a:
Best-fit signal strength per category, for $ {m_{\mathrm{ H } }} = $ 125 GeV. The constraints from the global fit are used to extract each of the individual best-fit signal strengths. The combined best-fit signal strength is $\hat\mu = $ 1.06 $\pm$ 0.25. |
png pdf |
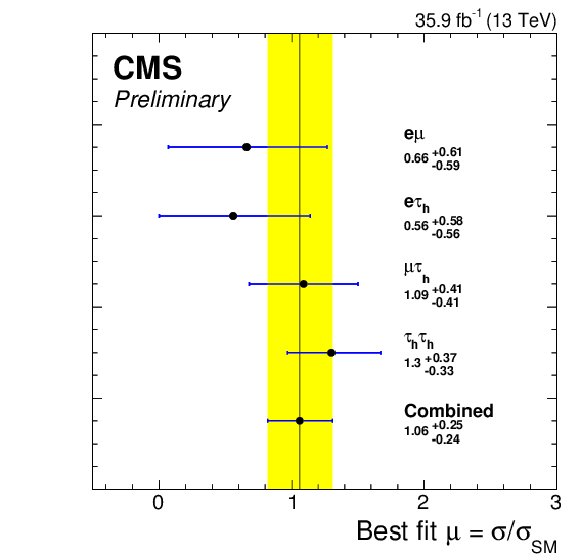
Figure 18-b:
Best-fit signal strength per channel, for $ {m_{\mathrm{ H } }} = $ 125 GeV. The constraints from the global fit are used to extract each of the individual best-fit signal strengths. The combined best-fit signal strength is $\hat\mu = $ 1.06 $\pm$ 0.25. |
png pdf |
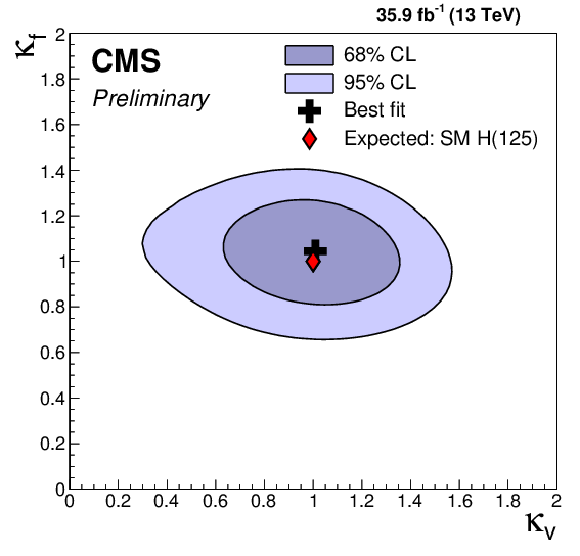
Figure 19:
Scan of the negative log-likelihood difference as a function of $\kappa _V$ and $\kappa _f$, for $ {m_{\mathrm{ H } }} = $ 125 GeV. All nuisance parameters are profiled for each point. For this scan, the $pp\rightarrow H$(125 GeV)$\rightarrow WW$ contribution is treated as a signal process. |
| Summary |
| A search for the SM scalar boson based on data collected in pp collisions by the CMS detector in 2016 at a center-of-mass energy of 13 TeV, has been presented. The four di-$\tau$ final states with the largest branching fraction have been studied, in event categories targeting Higgs boson signal events produced via gluon-gluon fusion and vector boson fusion. The results are extracted via two-dimensional maximum likelihood fits in the planes defined by the full or visible di-$\tau$ mass, and the lepton transverse momentum or $\tau_{\mathrm{h}}$ reconstructed decay mode in the 0-jet category, the invariant mass of the di-jets in the VBF category, and the scalar boson candidate transverse momentum in the boosted category. This leads to the observation of decays of the SM scalar boson to pairs of $\tau$ leptons, with an observed significance of 4.9 standard deviations for a mass of 125 GeV. This is to be compared with an expected significance of 4.7 standard deviations. |
| Additional Figures | |
png pdf |
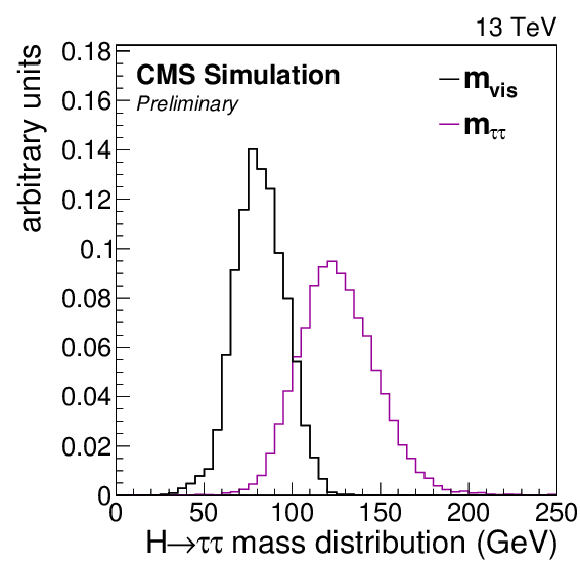
Additional Figure 1:
Normalized distributions of the visible mass, $ {m_\text {vis}} $, and of the SVfit mass, $ {m_{\tau \tau }} $, for a signal sample with a SM scalar boson of mass $ {m_{\mathrm{ H } }} = $ 125 GeV decaying to a pair of $\tau $ leptons in the $\mu {\tau _{\rm h}} $ final state. |
png pdf |
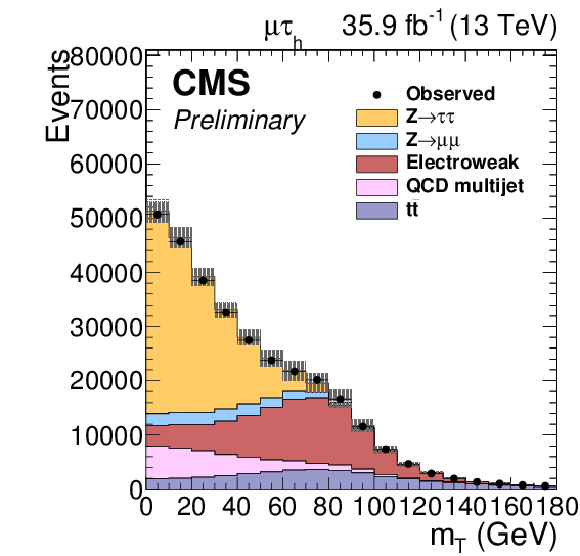
Additional Figure 2:
Observed and expected distributions of the transverse mass between the muon and $ {E_{\mathrm {T}}^{\text {miss}}} $, in the $\mu {\tau _{\rm h}} $ final state. The selection is inclusive in the number of jets. The background distributions have not been fitted to the data. The electroweak component of the background includes W+jets, single top quark, and diboson production events. |
png pdf |
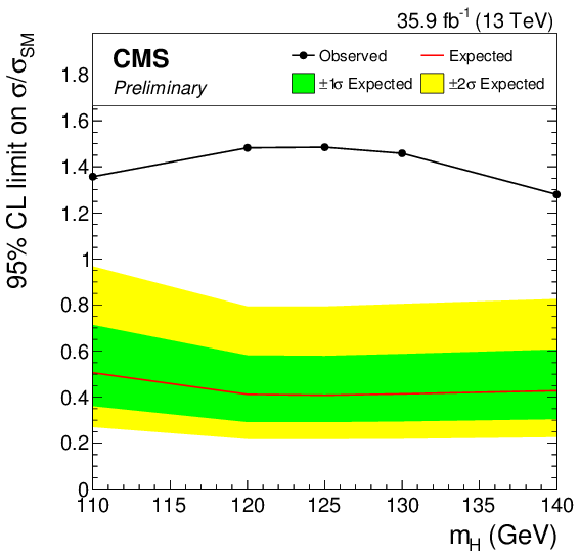
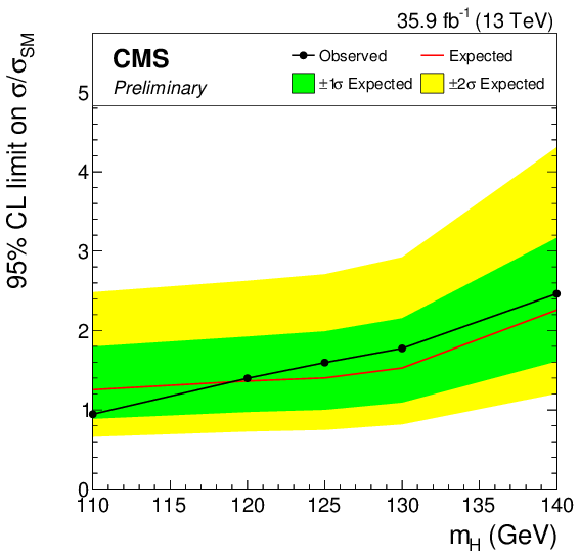
Additional Figure 3:
Combined observed 95% CL upper limit on the signal strength parameter $\mu $, together with the expected limit obtained in the background-only hypothesis. The uncertainty bands show the expected one- and two-standard-deviation probability intervals around the expected limit. Scalar boson decays to pairs of W bosons are considered as a background. |
png pdf |
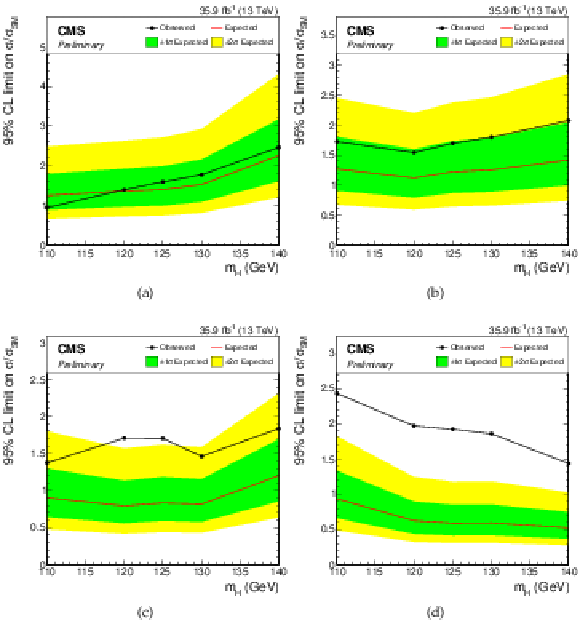
Additional Figure 4:
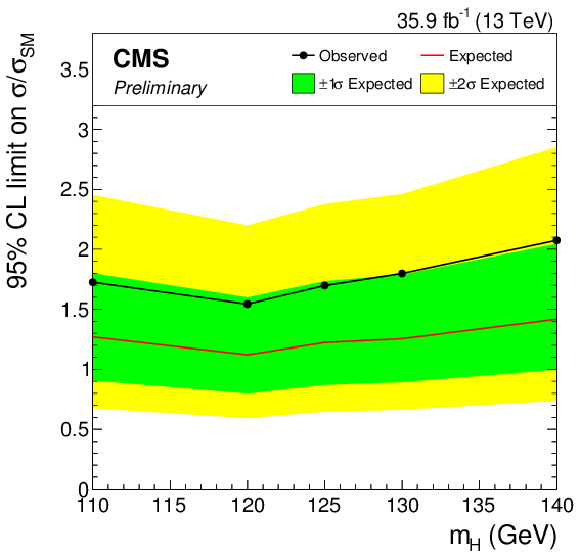
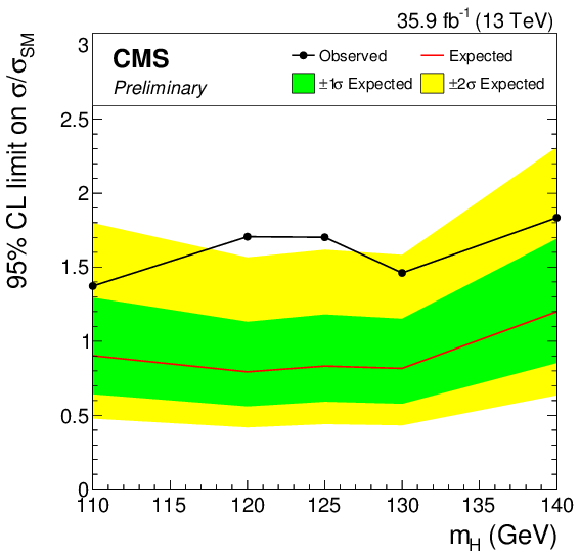
Observed 95% CL upper limit on the signal strength parameter $\mu $, in the $\mathrm{ e } \mu $ (a), $\mathrm{ e } {\tau _{\rm h}} $ (b), $\mu {\tau _{\rm h}} $ (c), and $ {\tau _{\rm h}} {\tau _{\rm h}} $ (d) final states, together with the expected limit obtained in the background-only hypothesis. The uncertainty bands show the expected one- and two-standard-deviation probability intervals around the expected limit. Scalar boson decays to pairs of W bosons are considered as a background. |
png pdf |
Additional Figure 4-a:
Observed 95% CL upper limit on the signal strength parameter $\mu $, in the $\mathrm{ e } \mu $ final state, together with the expected limit obtained in the background-only hypothesis. The uncertainty bands show the expected one- and two-standard-deviation probability intervals around the expected limit. Scalar boson decays to pairs of W bosons are considered as a background. |
png pdf |
Additional Figure 4-b:
Observed 95% CL upper limit on the signal strength parameter $\mu $, in the $\mathrm{ e } {\tau _{\rm h}} $ final state, together with the expected limit obtained in the background-only hypothesis. The uncertainty bands show the expected one- and two-standard-deviation probability intervals around the expected limit. Scalar boson decays to pairs of W bosons are considered as a background. |
png pdf |
Additional Figure 4-c:
Observed 95% CL upper limit on the signal strength parameter $\mu $, in the $\mu {\tau _{\rm h}} $ final state, together with the expected limit obtained in the background-only hypothesis. The uncertainty bands show the expected one- and two-standard-deviation probability intervals around the expected limit. Scalar boson decays to pairs of W bosons are considered as a background. |
png pdf |
Additional Figure 4-d:
Observed 95% CL upper limit on the signal strength parameter $\mu $, in the $ {\tau _{\rm h}} {\tau _{\rm h}} $ final state, together with the expected limit obtained in the background-only hypothesis. The uncertainty bands show the expected one- and two-standard-deviation probability intervals around the expected limit. Scalar boson decays to pairs of W bosons are considered as a background. |
png pdf |
Additional Figure 5:
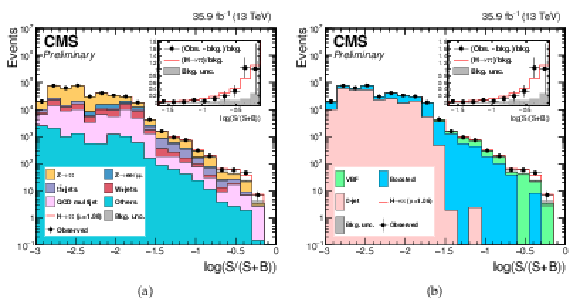
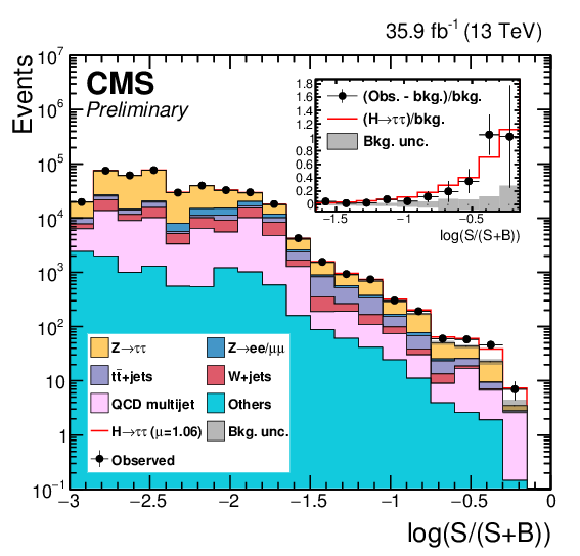
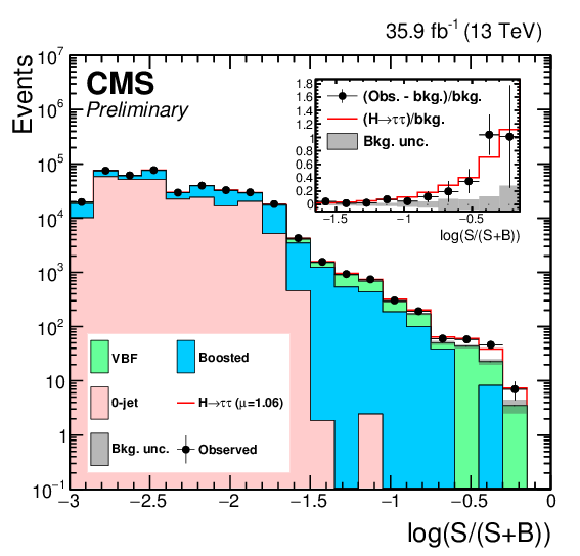
Distribution of the decimal logarithm of the ratio between the expected signal and the sum of expected signal and expected background in each bin of the mass distributions used to extract the results, in all signal regions. The background contributions are separated by process (a) or by category (b). The inset shows the corresponding difference between the observed data and expected background distributions divided by the background expectation, as well as the signal expectation divided by the background expectation. |
png pdf |
Additional Figure 5-a:
Distribution of the decimal logarithm of the ratio between the expected signal and the sum of expected signal and expected background in each bin of the mass distributions used to extract the results, in all signal regions. The background contributions are separated by process. The inset shows the corresponding difference between the observed data and expected background distributions divided by the background expectation, as well as the signal expectation divided by the background expectation. |
png pdf |
Additional Figure 5-b:
Distribution of the decimal logarithm of the ratio between the expected signal and the sum of expected signal and expected background in each bin of the mass distributions used to extract the results, in all signal regions. The background contributions are separated by category. The inset shows the corresponding difference between the observed data and expected background distributions divided by the background expectation, as well as the signal expectation divided by the background expectation. |
png pdf |
Additional Figure 6:
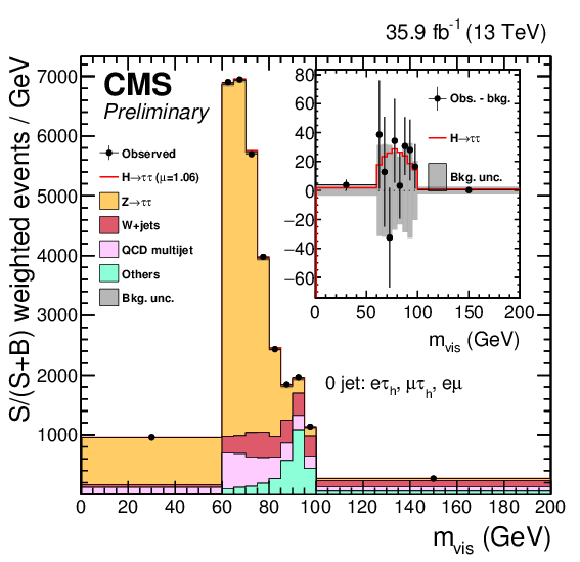
Combined observed and predicted $ {m_\text {vis}} $ distributions, in the 0-jet category of the $\mathrm{ e } \mu $, $\mathrm{ e } {\tau _{\rm h}} $, and $\mu {\tau _{\rm h}} $ channels. The normalization of the predicted background distributions corresponds to the result of the global fit, while the signal is normalized to its best-fit signal strength. The mass distributions for a constant range of the second dimension of the signal distributions are weighted according to $S/(S+B)$, where $S$ and $B$ are computed, respectively, as the signal or background contribution in the mass distribution excluding the first and last bins. The "others" background contribution includes events from diboson, $\mathrm{ t \bar{t} }$, and single-top-quark production, as well as scalar boson decays to a pair of W bosons and Z bosons decaying to a pair of light leptons. The background uncertainty band accounts for all sources of background uncertainties, systematic as well as statistical, after the global fit. The inset shows the corresponding difference between the observed data and expected background distributions, together with the signal expectation. The signal normalization after reweighting is equal to its normalization before reweighting, by construction. |
png pdf |
Additional Figure 7:
Profile likelihood ratio as a function of the signal strength parameter. The solid curve represents the observed profile likelihood ration. The green line is obtained by removing the theory-related uncertainties, the blue line by further removing the bin-by-bin background statistical uncertainties, and the red one by keeping only the statistical uncertainties. |
png pdf |
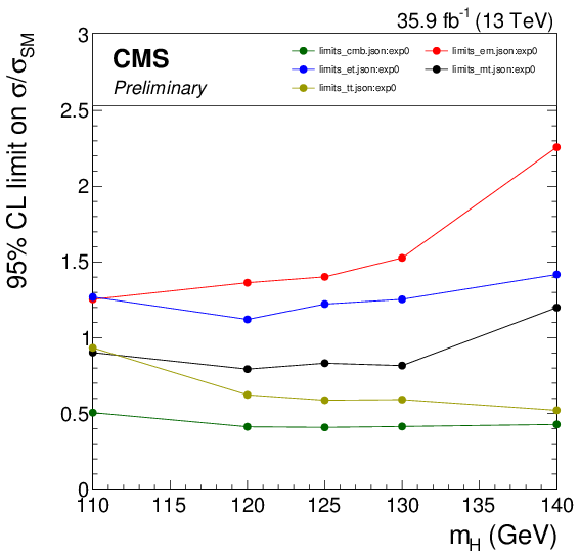
Additional Figure 8:
Expected 95% CL upper limits on the signal strength parameter for the $\mathrm{ e } \mu $, $\mathrm{ e } {\tau _{\rm h}} $, $\mu {\tau _{\rm h}} $, and $ {\tau _{\rm h}} {\tau _{\rm h}} $ channels, together with the expected combined upper limit. |
png pdf |
Additional Figure 9:
Best-fit signal strength for the ggH production, and for the other production modes, for $ {m_{\mathrm{ H } }} = 125$ GeV. The constraints from the global fit are used to extract each of the individual best-fit signal strengths. The combined best-fit signal strength is $\hat\mu = $ 1.06 $\pm$ 0.25. |
| References | ||||
| 1 | S. Weinberg | A Model of Leptons | PRL 19 (1967) 1264 | |
| 2 | A. Salam | Weak and electromagnetic interactions | in Elementary particle physics: relativistic groups and analyticity, 1968, Proceedings of the eighth Nobel symposium | |
| 3 | F. Englert and R. Brout | Broken Symmetry and the Mass of Gauge Vector Mesons | PRL 13 (1964) 321 | |
| 4 | P. W. Higgs | Broken symmetries, massless particles and gauge fields | PL12 (1964) 132 | |
| 5 | P. W. Higgs | Broken Symmetries and the Masses of Gauge Bosons | PRL 13 (1964) 508 | |
| 6 | G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble | Global Conservation Laws and Massless Particles | PRL 13 (1964) 585 | |
| 7 | P. W. Higgs | Spontaneous Symmetry Breakdown without Massless Bosons | PR145 (1966) 1156 | |
| 8 | T. W. B. Kibble | Symmetry Breaking in Non-Abelian Gauge Theories | PR155 (1967) 1554 | |
| 9 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 10 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 11 | CMS Collaboration | Observation of a new boson with mass near 125 GeV in pp collisions at $ \sqrt{s} $ = 7 and 8 TeV | JHEP 06 (2013) 081 | CMS-HIG-12-036 1303.4571 |
| 12 | ATLAS Collaboration | Measurements of the Higgs boson production and decay rates and coupling strengths using pp collision data at $ \sqrt{s}=$ 7 and 8 TeV in the ATLAS experiment | EPJC 76 (2016) 6 | 1507.04548 |
| 13 | CMS Collaboration | Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV | EPJC 75 (2015), no. 5, 212 | CMS-HIG-14-009 1412.8662 |
| 14 | CMS Collaboration | Study of the Mass and Spin-Parity of the Higgs Boson Candidate Via Its Decays to Z Boson Pairs | PRL 110 (2013), no. 8, 081803 | CMS-HIG-12-041 1212.6639 |
| 15 | ATLAS Collaboration | Evidence for the spin-0 nature of the Higgs boson using ATLAS data | PLB 726 (2013) 120 | 1307.1432 |
| 16 | CMS Collaboration | Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV | PRD 92 (2015) 012004 | CMS-HIG-14-018 1411.3441 |
| 17 | ATLAS, CMS Collaboration | Combined Measurement of the Higgs Boson Mass in $ pp $ Collisions at $ \sqrt{s}=$ 7 and 8 TeV with the ATLAS and CMS Experiments | PRL 114 (2015) 191803 | 1503.07589 |
| 18 | ALEPH Collaboration | Observation of an excess in the search for the Standard Model Higgs boson at ALEPH | PLB 495 (2000) 1 | hep-ex/0011045 |
| 19 | DELPHI Collaboration | Final results from DELPHI on the searches for SM and MSSM neutral Higgs bosons | EPJC 32 (2004) 145 | hep-ex/0303013 |
| 20 | L3 Collaboration | Standard model Higgs boson with the L3 experiment at LEP | PLB 517 (2001) 319 | hep-ex/0107054 |
| 21 | OPAL Collaboration | Search for the Standard Model Higgs boson in e$ ^+ $e$ ^- $ collisions at $ \sqrt{s} $ = 192--209 GeV | PLB 499 (2001) 38 | hep-ex/0101014 |
| 22 | CDF Collaboration | Search for a Low-Mass Standard Model Higgs Boson in the $ \tau $$ \tau $ Decay Channel in $ \text{p}\bar{\text{p}} $ Collisions at $ \sqrt{s} $ = 1.96 TeV | PRL 108 (2012) 181804 | 1201.4880 |
| 23 | D0 Collaboration | Search for the standard model Higgs boson in tau lepton final states | PLB 714 (2012) 237 | 1203.4443 |
| 24 | ATLAS Collaboration | Evidence for the Higgs-boson Yukawa coupling to tau leptons with the ATLAS detector | JHEP 04 (2015) 117 | 1501.04943 |
| 25 | CMS Collaboration | Evidence for the 125 GeV Higgs boson decaying to a pair of $ \tau $ leptons | JHEP 05 (2014) 104 | CMS-HIG-13-004 1401.5041 |
| 26 | ATLAS, CMS Collaboration | Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $ \sqrt{s}=$ 7 and 8 TeV | JHEP 08 (2016) 045 | 1606.02266 |
| 27 | CMS Collaboration | The CMS trigger system | CMS-TRG-12-001 1609.02366 |
|
| 28 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 29 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 30 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 31 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 32 | S. Alioli et al. | Jet pair production in POWHEG | JHEP 04 (2011) 081 | 1012.3380 |
| 33 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO Higgs boson production via gluon fusion matched with shower in POWHEG | JHEP 04 (2009) 002 | 0812.0578 |
| 34 | J. Alwall et al. | MadGraph 5: going beyond | JHEP 06 (2011) 128 | 1106.0522 |
| 35 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 36 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016), no. 3, 155 | CMS-GEN-14-001 1512.00815 |
| 37 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs cross sections: 1. Inclusive observables | CERN Report CERN-2011-002 | 1101.0593 |
| 38 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs cross sections: 2. Differential Distributions | CERN Report CERN-2012-002 | 1201.3084 |
| 39 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs cross sections: 3. Higgs Properties | CERN Report CERN-2013-004 | 1307.1347 |
| 40 | A. Djouadi, M. Spira, and P. M. Zerwas | Production of Higgs bosons in proton colliders. QCD corrections | PLB 264 (1991) 440 | |
| 41 | S. Dawson | Radiative corrections to Higgs boson production | Nucl. Phys. B 359 (1991) 283 | |
| 42 | M. Spira, A. Djouadi, D. Graudenz, and P. M. Zerwas | Higgs boson production at the LHC | Nucl. Phys. B 453 (1995) 17 | hep-ph/9504378 |
| 43 | R. V. Harlander and W. B. Kilgore | Next-to-Next-to-Leading Order Higgs Production at Hadron Colliders | PRL 88 (2002) 201801 | hep-ph/0201206 |
| 44 | C. Anastasiou and K. Melnikov | Higgs boson production at hadron colliders in NNLO QCD | Nucl. Phys. B 646 (2002) 220 | hep-ph/0207004 |
| 45 | V. Ravindran, J. Smith, and W. L. van Neerven | NNLO corrections to the total cross section for Higgs boson production in hadron-hadron collisions | Nucl. Phys. B 665 (2003) 325 | hep-ph/0302135 |
| 46 | S. Catani, D. de Florian, M. Grazzini, and P. Nason | Soft-gluon resummation for Higgs boson production at hadron colliders | JHEP 07 (2003) 028 | |
| 47 | U. Aglietti, R. Bonciani, G. Degrassi, and A. Vicini | Two-loop light fermion contribution to Higgs production and decays | PLB 595 (2004) 432 | hep-ph/0404071 |
| 48 | G. Degrassi and F. Maltoni | Two-loop electroweak corrections to Higgs production at hadron colliders | PLB 600 (2004) 255 | hep-ph/0407249 |
| 49 | S. Actis, G. Passarino, C. Sturm, and S. Uccirati | NLO electroweak corrections to Higgs boson production at hadron colliders | PLB 670 (2008) 12 | 0809.1301 |
| 50 | C. Anastasiou, R. Boughezal, and F. Petriello | Mixed QCD-electroweak corrections to Higgs boson production in gluon fusion | JHEP 04 (2009) 003 | 0811.3458 |
| 51 | D. de Florian and M. Grazzini | Higgs production through gluon fusion: Updated cross sections at the Tevatron and the LHC | PLB 674 (2009) 291 | 0901.2427 |
| 52 | J. Baglio and A. Djouadi | Higgs production at the LHC | JHEP 03 (2011) 055 | 1012.0530 |
| 53 | M. Ciccolini, A. Denner, and S. Dittmaier | Strong and Electroweak Corrections to the Production of a Higgs Boson + 2 Jets via Weak Interactions at the Large Hadron Collider | PRL 99 (2007) 161803 | 0707.0381 |
| 54 | M. Ciccolini, A. Denner, and S. Dittmaier | Electroweak and QCD corrections to Higgs production via vector-boson fusion at the CERN LHC | PRD 77 (2008) 013002 | 0710.4749 |
| 55 | K. Arnold et al. | VBFNLO: A parton level Monte Carlo for processes with electroweak bosons | CPC 180 (2009) 1661 | 0811.4559 |
| 56 | O. Brein, A. Djouadi, and R. Harlander | NNLO QCD corrections to the Higgs-strahlung processes at hadron colliders | PLB 579 (2004) 149 | hep-ph/0307206 |
| 57 | M. L. Ciccolini, S. Dittmaier, and M. Kramer | Electroweak radiative corrections to associated $ \mathrm{ W }\mathrm{ H } $ and $ \mathrm{ Z }\mathrm{ H } $ production at hadron colliders | PRD 68 (2003) 073003 | hep-ph/0306234 |
| 58 | A. Djouadi, J. Kalinowski, M. Muhlleitner, and M. Spira | An update of the program HDECAY | in The Les Houches 2009 workshop on TeV colliders: The tools and Monte Carlo working group summary report 2010 | 1003.1643 |
| 59 | A. Denner et al. | Standard model Higgs-boson branching ratios with uncertainties | EPJC 71 (2011) 1753 | 1107.5909 |
| 60 | S. Alekhin et al. | The PDF4LHC Working Group Interim Report | 1101.0536 | |
| 61 | M. Botje et al. | The PDF4LHC Working Group Interim Recommendations | 1101.0538 | |
| 62 | H.-L. Lai et al. | New parton distributions for collider physics | PRD 82 (2010) 074024 | 1007.2241 |
| 63 | NNPDF Collaboration | Impact of heavy quark masses on parton distributions and LHC phenomenology | Nucl. Phys. B 849 (2011) 296 | 1101.1300 |
| 64 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector | 1610.07922 | |
| 65 | GEANT4 Collaboration | GEANT4 --- a simulation toolkit | NIMA 506 (2003) 250 | |
| 66 | CMS Collaboration | Particle--Flow Event Reconstruction in CMS and Performance for Jets, Taus, and $ E_{\mathrm{T}}^{\text{miss}} $ | CDS | |
| 67 | CMS Collaboration | Commissioning of the Particle-Flow Reconstruction in Minimum-Bias and Jet Events from $ \mathrm{ p }\mathrm{ p } $ Collisions at 7 TeV | CDS | |
| 68 | CMS Collaboration | Commissioning of the particle-flow event reconstruction with leptons from J/$ \psi $ and W decays at 7 TeV | CDS | |
| 69 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s}=$ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 70 | CMS Collaboration | Electron Reconstruction and Identification at $ \sqrt{s} = $ 7 TeV | CDS | |
| 71 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 72 | M. Cacciari and G. P. Salam | Dispelling the $ N^{3} $ myth for the $ k_t $ jet-finder | PLB 641 (2006) 57 | hep-ph/0512210 |
| 73 | CMS Collaboration | Determination of jet energy calibration and transverse momentum resolution in CMS | JINST 6 (2011) 11002 | CMS-JME-10-011 1107.4277 |
| 74 | CMS Collaboration | Reconstruction and identification of $ \tau $ lepton decays to hadrons and $ \nu_\tau $ at CMS | JINST 11 (2016) P01019 | CMS-TAU-14-001 1510.07488 |
| 75 | CMS Collaboration | Performance of reconstruction and identification of tau leptons in their decays to hadrons and tau neutrino in LHC Run-2 | CMS-PAS-TAU-16-002 | CMS-PAS-TAU-16-002 |
| 76 | H. Voss, A. Hocker, J. Stelzer, and F. Tegenfeldt | TMVA, the Toolkit for Multivariate Data Analysis with ROOT | in XI Int. Workshop on Advanced Computing and Analysis Techniques in Physics Research 2007 PoS ACAT:040 | physics/0703039 |
| 77 | CMS Collaboration | Performance of Missing Transverse Momentum Reconstruction Algorithms in Proton-Proton Collisions at $ \sqrt{s}= $ 8 TeV with the CMS Detector | CMS-PAS-JME-12-002 | CMS-PAS-JME-12-002 |
| 78 | L. Bianchini, J. Conway, E. K. Friis, and C. Veelken | Reconstruction of the Higgs mass in $ H \to \tau\tau $ Events by Dynamical Likelihood techniques | J. Phys. Conf. Ser. 513 (2014) 022035 | |
| 79 | D. de Florian, G. Ferrera, M. Grazzini, and D. Tommasini | Higgs boson production at the LHC: transverse momentum resummation effects in the $ \mathrm{H}\rightarrow \gamma\gamma $, $ \mathrm{H}\rightarrow WW \rightarrow l\nu l\nu $ and $ \mathrm{H}\rightarrow ZZ\rightarrow 4l $ decay modes | JHEP 06 (2012) 132 | 1203.6321 |
| 80 | M. Grazzini and H. Sargsyan | Heavy-quark mass effects in Higgs boson production at the LHC | JHEP 09 (2013) 129 | 1306.4581 |
| 81 | J. S. Conway | Incorporating Nuisance Parameters in Likelihoods for Multisource Spectra | in Proceedings of PHYSTAT 2011 Workshop on Statistical Issues Related to Discovery Claims in Search Experiments and Unfolding, p. 115 CERN-2011-006 | |
| 82 | ATLAS and CMS Collaborations, LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | Technical Report ATL-PHYS-PUB 2011-11, CMS NOTE 2011/005, CERN | |
| 83 | CMS Collaboration | Combined results of searches for the standard model Higgs boson in pp collisions at $ \sqrt{s}=$ 7 TeV | PLB 710 (2012) 26 | CMS-HIG-11-032 1202.1488 |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|