

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-16-040 | ||
| Measurements of properties of the Higgs boson in the diphoton decay channel with the full 2016 data set | ||
| CMS Collaboration | ||
| May 2017 | ||
| Abstract: Measurements of properties of the Higgs boson SM(125) in the $\mathrm{H}\rightarrow\gamma\gamma$ decay channel are reported. The analysis uses the data collected by the CMS experiment in proton-proton collisions during the 2016 LHC running period. The data sample corresponds to an integrated luminosity of 35.9 fb$^{-1}$. The measured signal strength relative to the standard model prediction is 1.16 $^{+0.15}_{-0.14} $ =1.16 $^{+0.11}_{-0.10}$ (stat.) $^{+0.09}_{-0.08}$ (syst.) $^{+0.06}_{-0.05}$ (theo.). Signal strengths associated with the different Higgs boson production mechanisms, coupling modifiers to bosons and fermions, and effective couplings to photons and gluons are also measured. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JHEP 11 (2018) 185. The superseded preliminary plots can be found here. |
||
| Figures & Tables | Summary | Additional Figures | References | CMS Publications |
|---|
| Figures | |

png pdf |
Figure 1 :
Comparison of the dielectron invariant mass distributions in data and simulation (after energy smearing) for ${\mathrm{ Z } } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ events where electrons are reconstructed as photons. The comparison is shown requiring $ {R_\mathrm {9}}> $ 0.94 for both photons and for (left) events with both showers in the barrel, and (right) the remaining events. The simulated distribution is normalized to the integral of the data distribution in the range 87 $ < m_{e^{+}e^{-}} < $ 93 GeV. |
png pdf |
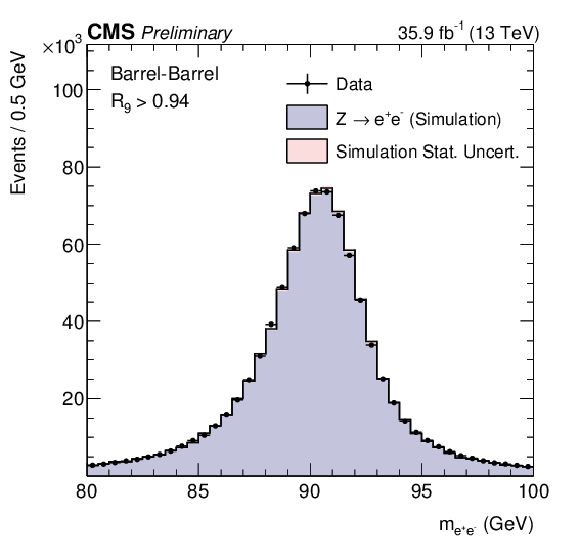
Figure 1-a:
Comparison of the dielectron invariant mass distributions in data and simulation (after energy smearing) for ${\mathrm{ Z } } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ events where electrons are reconstructed as photons. The comparison is shown requiring $ {R_\mathrm {9}}> $ 0.94 for both photons and for events with both showers in the barrel. The simulated distribution is normalized to the integral of the data distribution in the range 87 $ < m_{e^{+}e^{-}} < $ 93 GeV. |
png pdf |
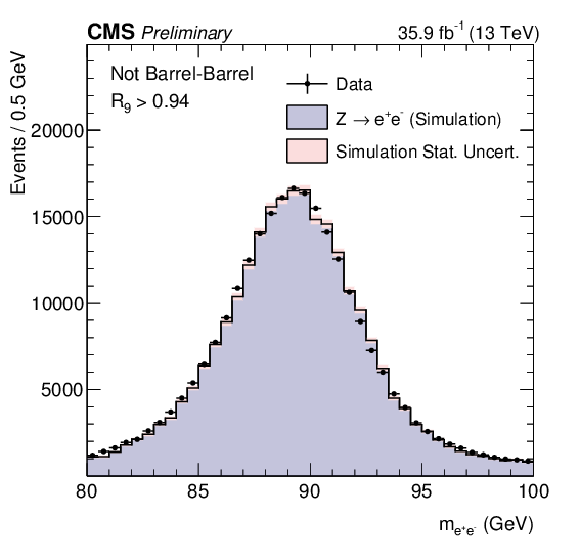
Figure 1-b:
Comparison of the dielectron invariant mass distributions in data and simulation (after energy smearing) for ${\mathrm{ Z } } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ events where electrons are reconstructed as photons. The comparison is shown requiring $ {R_\mathrm {9}}> $ 0.94 for both photons and for events with at least one shower in the endcap region. The simulated distribution is normalized to the integral of the data distribution in the range 87 $ < m_{e^{+}e^{-}} < $ 93 GeV. |

png pdf |
Figure 2:
(Left) Photon identification BDT score of the lower-scoring photon of diphoton pairs with an invariant mass in the range 100 $ < m_{\gamma \gamma } < $ 180 GeV, for events passing the preselection in the 13 TeV data set (points), and for simulated background events (blue histogram). Histograms are also shown for different components of the simulated background. The sum of all background distributions is scaled up to data. The red histogram corresponds to simulated Higgs boson signal events. (Right) Photon identification BDT score for ${\mathrm{ Z } } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ events in data and simulation, where the electrons are reconstructed as photons. The systematic uncertainty applied to the shape from simulation (hashed region) is also shown. |
png pdf |
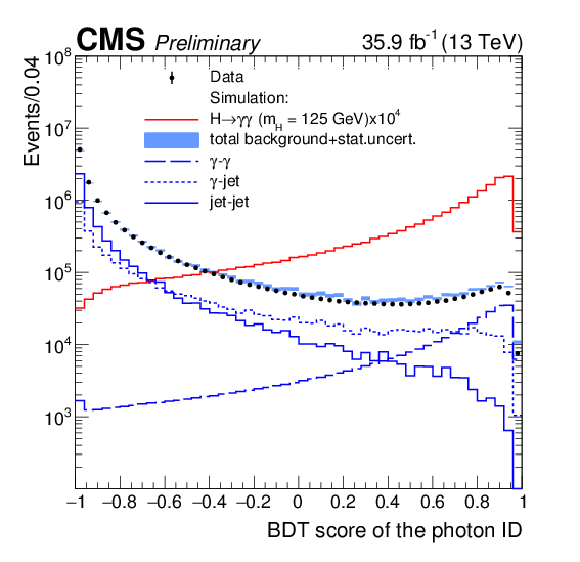
Figure 2-a:
Photon identification BDT score of the lower-scoring photon of diphoton pairs with an invariant mass in the range 100 $ < m_{\gamma \gamma } < $ 180 GeV, for events passing the preselection in the 13 TeV data set (points), and for simulated background events (blue histogram). Histograms are also shown for different components of the simulated background. The sum of all background distributions is scaled up to data. The red histogram corresponds to simulated Higgs boson signal events. |

png pdf |
Figure 2-b:
Photon identification BDT score for ${\mathrm{ Z } } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ events in data and simulation, where the electrons are reconstructed as photons. The systematic uncertainty applied to the shape from simulation (hashed region) is also shown. |
png pdf |
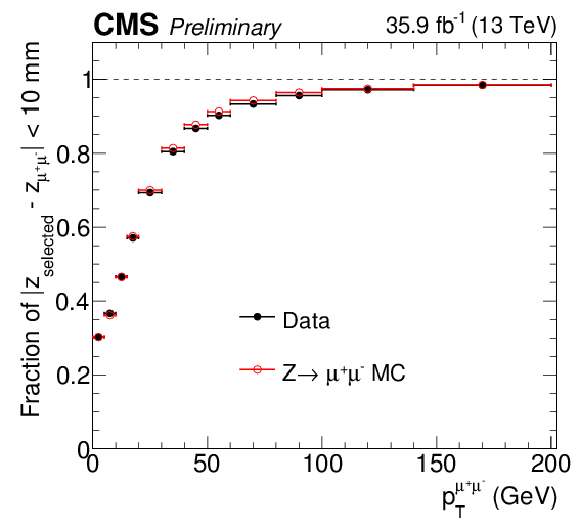
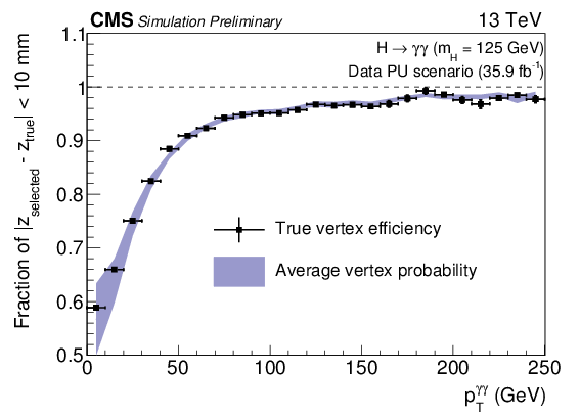
Figure 3:
Validation of the $ {\mathrm{ H } \to \gamma \gamma }$ vertex identification algorithm on $\mathrm{ Z } \to {\mu^{+} \mu^{-} } $ events omitting the muon tracks. Simulated events are weighted to match the distributions of pileup and location of primary vertices in data. |
png pdf |
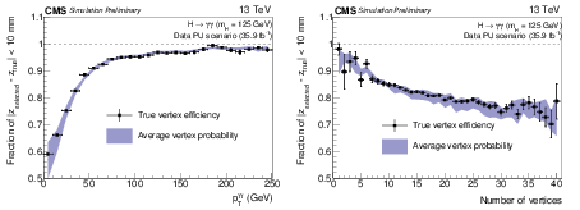
Figure 4:
Comparison of the true vertex identification efficiency and the average estimated vertex probability as a function of the reconstructed diphoton ${p_{\mathrm {T}}}$ (left) and of the number of primary vertices (right) in simulated $ {\mathrm{ H } \to \gamma \gamma }$ events with $m_{\mathrm{ H } } = $ 125 GeV. Events are weighted according to the cross sections of the different production modes and to match the distributions of pileup and location of primary vertices in data. |
png pdf |
Figure 4-a:
Comparison of the true vertex identification efficiency and the average estimated vertex probability as a function of the reconstructed diphoton ${p_{\mathrm {T}}}$ in simulated $ {\mathrm{ H } \to \gamma \gamma }$ events with $m_{\mathrm{ H } } = $ 125 GeV. Events are weighted according to the cross sections of the different production modes and to match the distributions of pileup and location of primary vertices in data. |

png pdf |
Figure 4-b:
Comparison of the true vertex identification efficiency and the average estimated vertex probability as a function of the number of primary vertices in simulated $ {\mathrm{ H } \to \gamma \gamma }$ events with $m_{\mathrm{ H } } = $ 125 GeV. Events are weighted according to the cross sections of the different production modes and to match the distributions of pileup and location of primary vertices in data. |
png pdf |
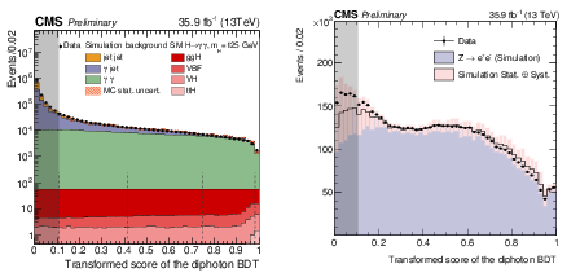
Figure 5:
(Left) Transformed score of the diphoton multivariate classifier for events with two photons satisfying the preselection requirements in data (points), simulated signal (red shades), and simulated background (coloured histograms). Both signal and background are stacked together. The vertical dashed lines show the boundaries of the untagged categories, the grey shade indicates events discarded from the analysis. (Right) Score of the diphoton multivariate classifier in $\mathrm{ Z } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ events where the electrons are reconstructed as photons. The points show the score for data, the histogram shows the score for simulated Drell-Yan events. The pink band indicates the statistical and systematic uncertainties on the simulation. |

png pdf |
Figure 5-a:
Transformed score of the diphoton multivariate classifier for events with two photons satisfying the preselection requirements in data (points), simulated signal (red shades), and simulated background (coloured histograms). Both signal and background are stacked together. The vertical dashed lines show the boundaries of the untagged categories, the grey shade indicates events discarded from the analysis. |

png pdf |
Figure 5-b:
Score of the diphoton multivariate classifier in $\mathrm{ Z } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ events where the electrons are reconstructed as photons. The points show the score for data, the histogram shows the score for simulated Drell-Yan events. The pink band indicates the statistical and systematic uncertainties on the simulation. |
png pdf |
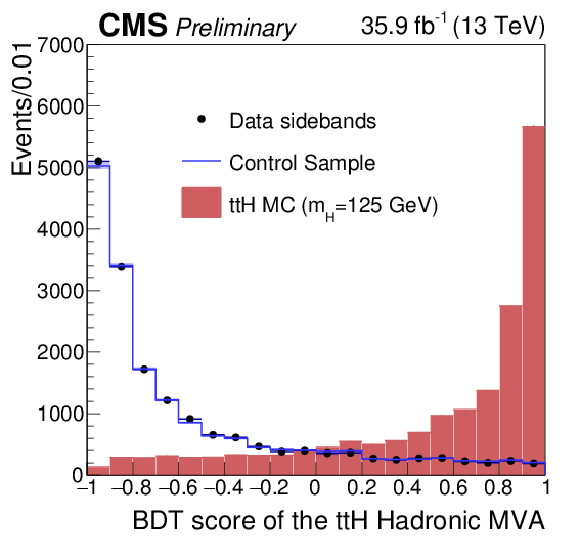
Figure 6:
Score of the jet multivariate discriminant used to enhance jet tagging in the ttHHadronic category. The points show the score for data in the signal region side-bands, $\text {m}_{\gamma \gamma } < $ 115 GeV or $\text {m}_{\gamma \gamma } > $ 135 GeV; the histogram shows the score for events in the data control sample; the filled histogram shows the score for simulated signal events. The distributions in the simulated and control samples are scaled as to match the integral of that from the data side-bands. |

png pdf |
Figure 7:
Score of the combined VBF multivariate classifier in (left) ggH and VBF signal distributions, compared to background taken from data in the mass side-band region, and (right) $\mathrm{ Z } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ + jets events. At left, the signal region selection is applied to the expected simulated ggH and VBF events; these are compared to points representing the background, as determined from data using the signal region selection in mass side-bands. At right, the signal selection is applied with electrons reconstructed as photons, with points showing the score for data and the histogram showing the score for simulated Drell-Yan events, including statistical and systematic uncertainties (pink band). Dotted lines indicate the three VBF categories, while the grey region is discarded from the analysis. |
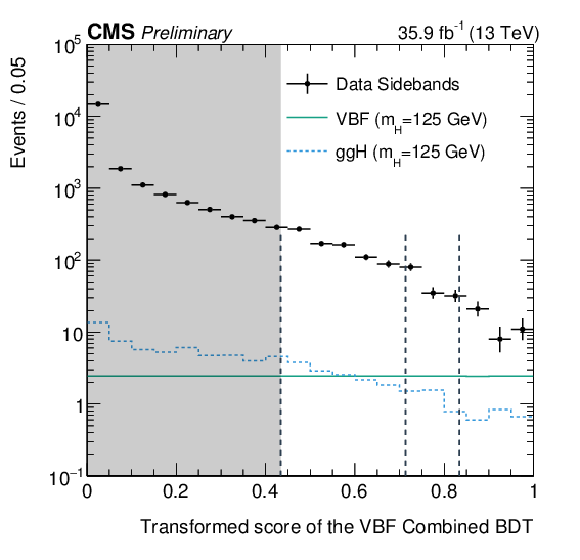
png pdf |
Figure 7-a:
Score of the combined VBF multivariate classifier in ggH and VBF signal distributions, compared to background taken from data in the mass side-band region. The signal region selection is applied to the expected simulated ggH and VBF events; these are compared to points representing the background, as determined from data using the signal region selection in mass side-bands. Dotted lines indicate the three VBF categories, while the grey region is discarded from the analysis. |

png pdf |
Figure 7-b:
Score of the combined VBF multivariate classifier in $\mathrm{ Z } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ + jets events. The signal selection is applied with electrons reconstructed as photons, with points showing the score for data and the histogram showing the score for simulated Drell-Yan events, including statistical and systematic uncertainties (pink band). Dotted lines indicate the three VBF categories, while the grey region is discarded from the analysis. |
png pdf |
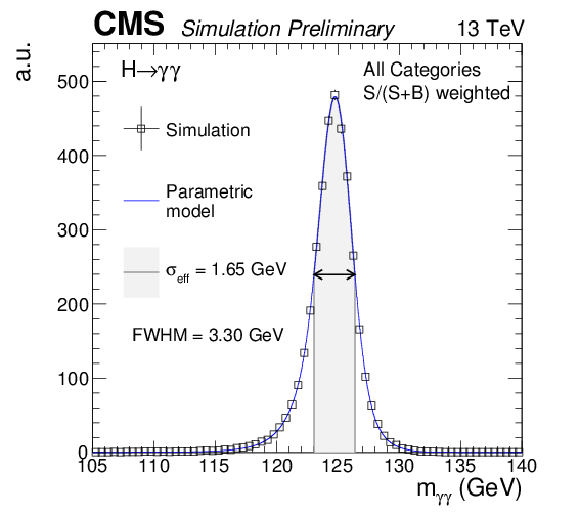
Figure 8:
Parametrized signal shape for the best resolution category (left) and for all categories combined together and weighted by the ratio $S/(S+B)$ (right) for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $\text {m}_{\mathrm{ H } } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
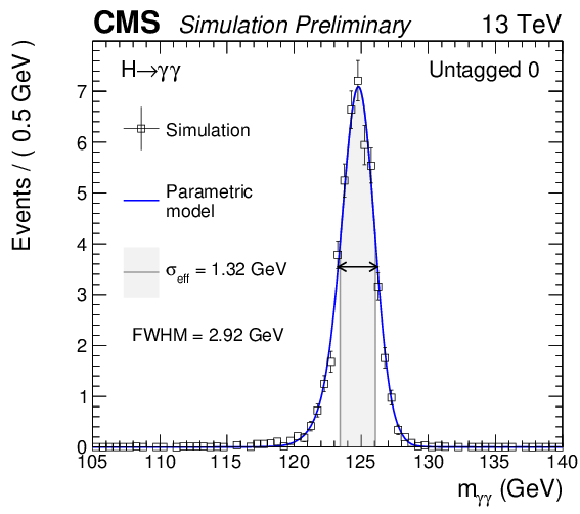
png pdf |
Figure 8-a:
Parametrized signal shape for the best resolution category for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $\text {m}_{\mathrm{ H } } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
Figure 8-b:
Parametrized signal shape for for all categories combined together and weighted by the ratio $S/(S+B)$ for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $\text {m}_{\mathrm{ H } } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
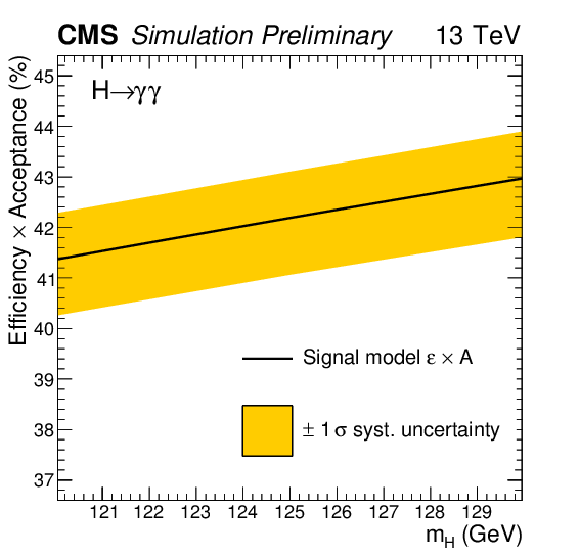
Figure 9:
The efficiency$\times $acceptance of the signal model as a function of $\text {m}_{\mathrm{ H } } $ for all categories combined. The black line represents the yields from the signal model. The yellow band indicates the effect of the systematic uncertainties for trigger, photon identification and selection, photon energy scale and modelling of the photon energy resolution, vertex identification (see Section 9). |
png pdf |
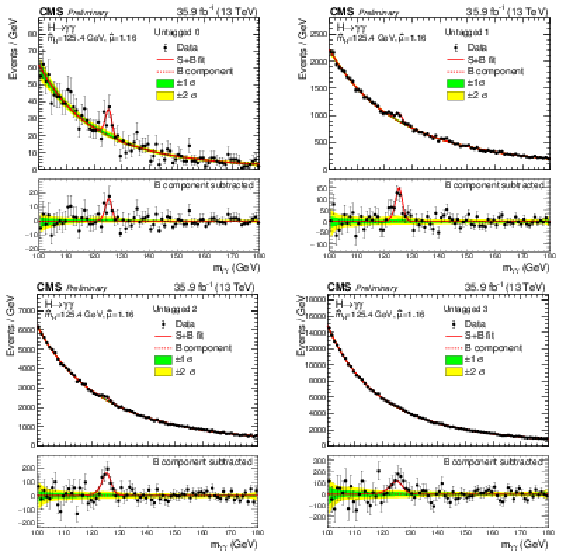
Figure 10:
Data points (black) and signal plus background model fits in the four untagged categories are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
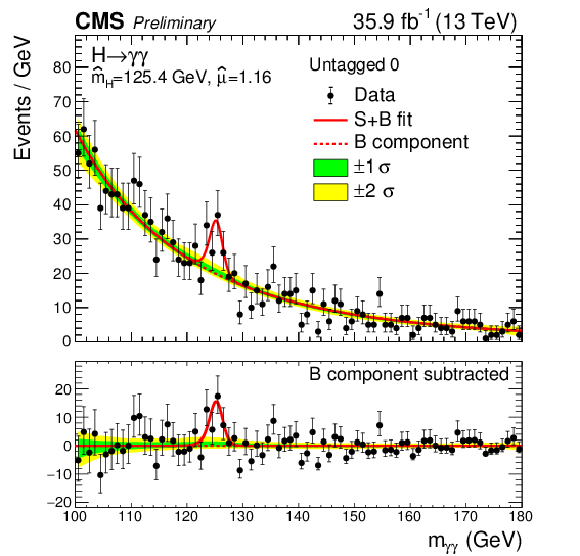
Figure 10-a:
Data points (black) and signal plus background model fits in the untagged 0 category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |

png pdf |
Figure 10-b:
Data points (black) and signal plus background model fits in the untagged 1 category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
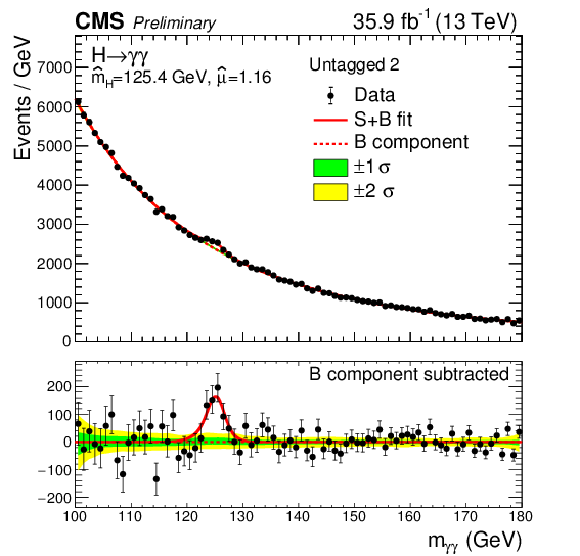
Figure 10-c:
Data points (black) and signal plus background model fits in the untagged 2 category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
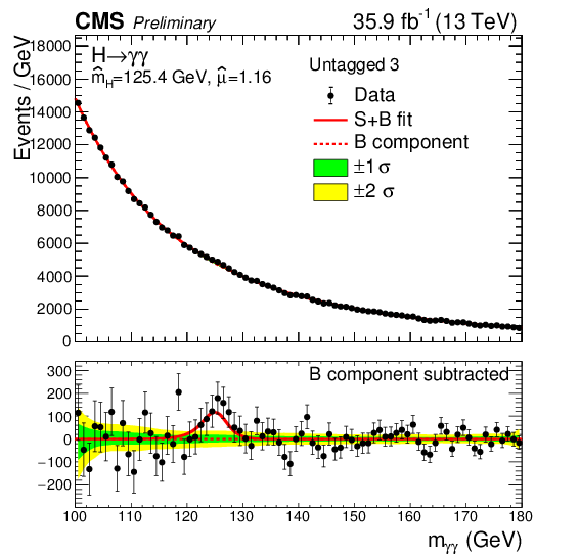
Figure 10-d:
Data points (black) and signal plus background model fits in the untagged 3 category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |

png pdf |
Figure 11:
Data points (black) and signal plus background model fits in VBF and $\mathrm {t\bar{t}H}$ categories are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
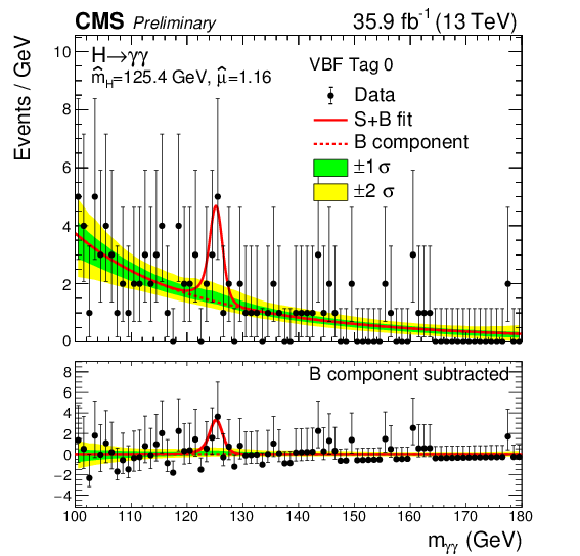
Figure 11-a:
Data points (black) and signal plus background model fits in the VBF 0 category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
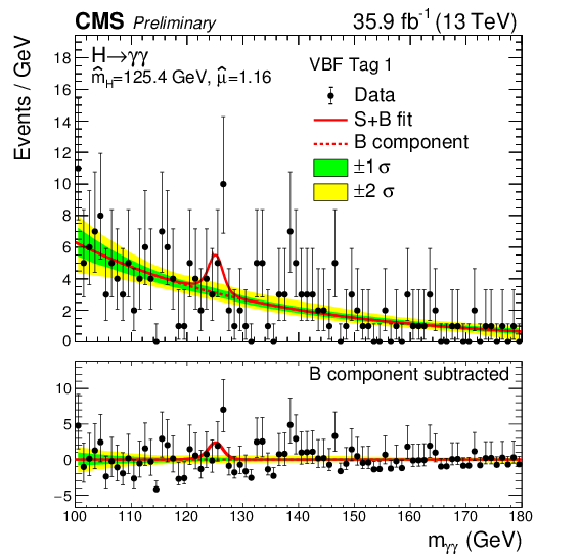
Figure 11-b:
Data points (black) and signal plus background model fits in the VBF 1 category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
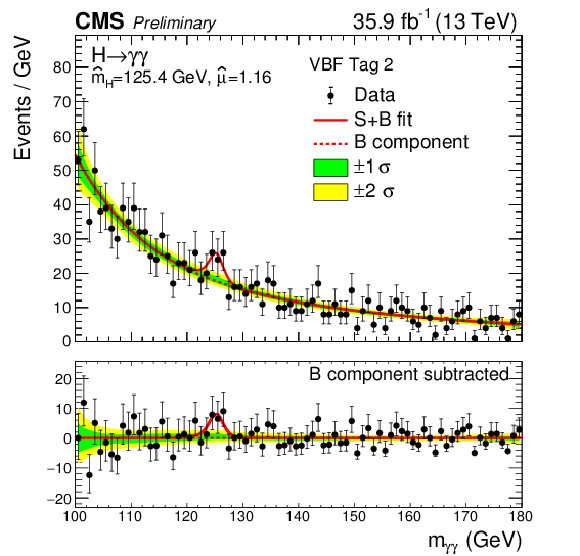
Figure 11-c:
Data points (black) and signal plus background model fits in the VBF 2 category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
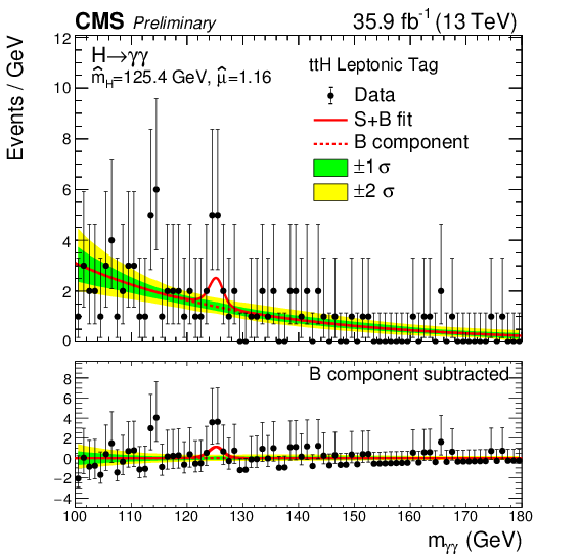
Figure 11-d:
Data points (black) and signal plus background model fits in the $\mathrm {t\bar{t}H}$ Leptonic category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |

png pdf |
Figure 11-e:
Data points (black) and signal plus background model fits in the $\mathrm {t\bar{t}H}$ Hadronic category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
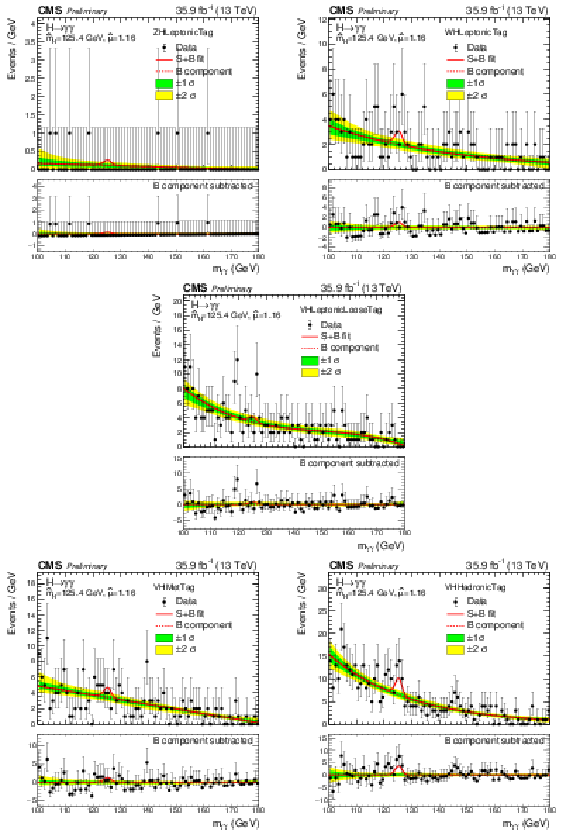
Figure 12:
Data points (black) and signal plus background model fits in VH categories are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
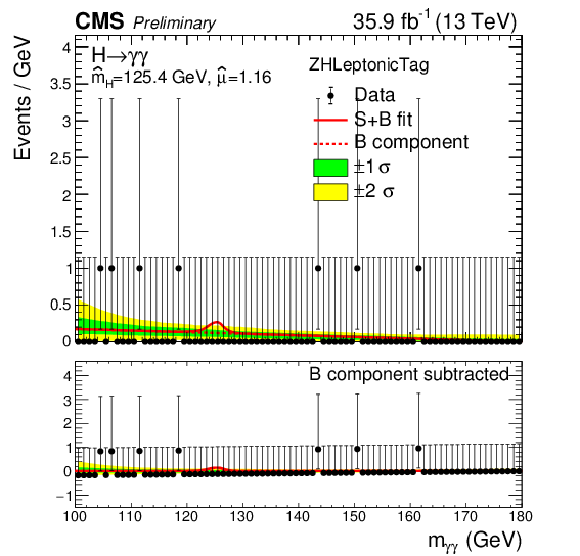
Figure 12-a:
Data points (black) and signal plus background model fits in ZH Leptonic category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |

png pdf |
Figure 12-b:
Data points (black) and signal plus background model fits in WH Leptonic category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
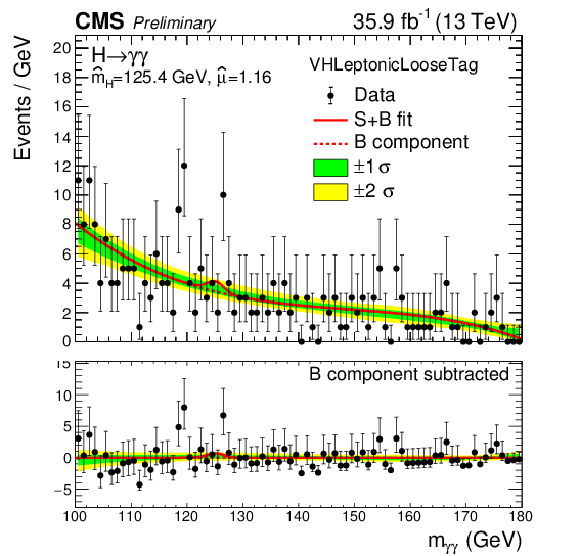
Figure 12-c:
Data points (black) and signal plus background model fits in VH Leptonic Loose category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
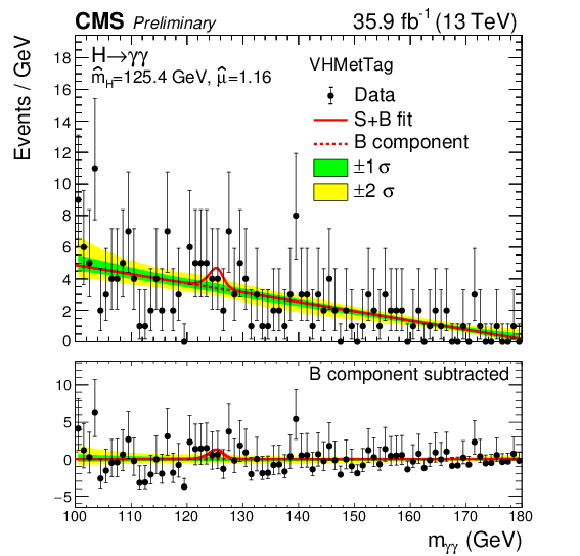
Figure 12-d:
Data points (black) and signal plus background model fits in VH Met category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |

png pdf |
Figure 12-e:
Data points (black) and signal plus background model fits in VH Hadronic category are shown. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |

png pdf |
Figure 13:
Data points (black) and signal plus background model fits for all categories summed (left) and where the categories are summed weighted by their sensitivity (right). The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |

png pdf |
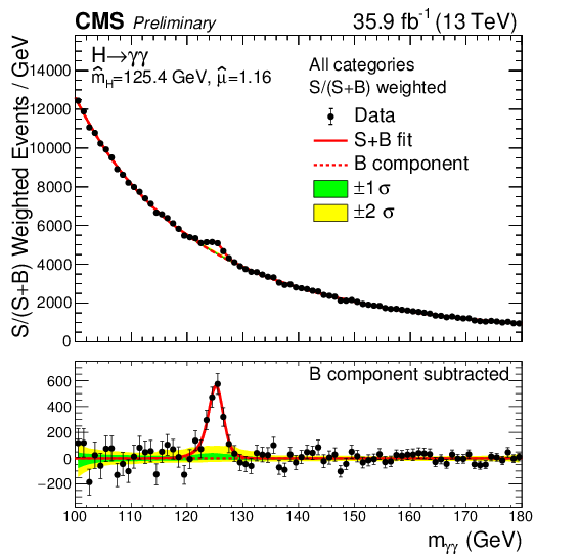
Figure 13-a:
Data points (black) and signal plus background model fits for all categories summed. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
Figure 13-b:
Data points (black) and signal plus background model fits where the categories are summed weighted by their sensitivity. The one standard deviation (green) and two standard deviation bands (yellow) include the uncertainties in the background component of the fit. The bottom plot shows the residuals after background subtraction. |
png pdf |
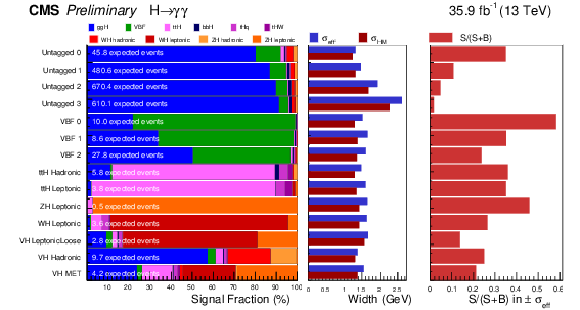
Figure 14:
Expected fraction of signal events per production mode in the different categories. For each category, the $\sigma _{eff}$ and $\sigma _{HM}$ of the signal model are given, as described in the text. The ratio of the number of signal events (S) to the number of signal plus background events (S+B) is shown on the right hand side. |
png pdf |
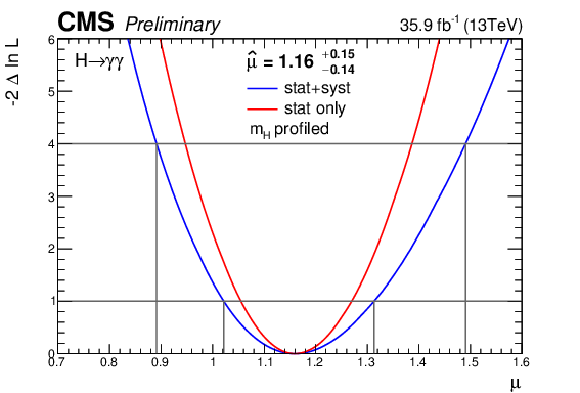
Figure 15:
The likelihood scan for the signal strength where the value of the standard model Higgs boson mass is profiled in the fit. |
png pdf |
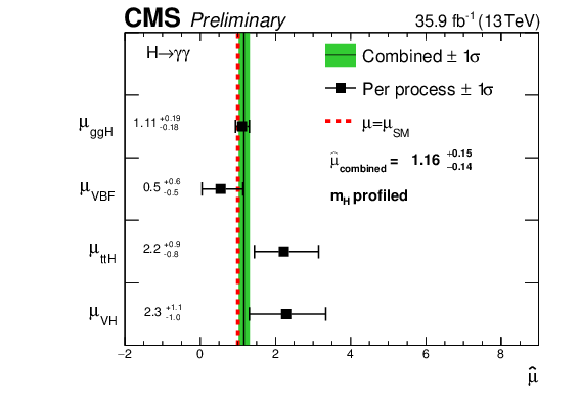
Figure 16:
Signal strength modifiers measured for each process (black points) for profiled $m_{H}$, compared to the overall signal strength (green band) and to the SM expectation (dashed red line). |
png pdf |
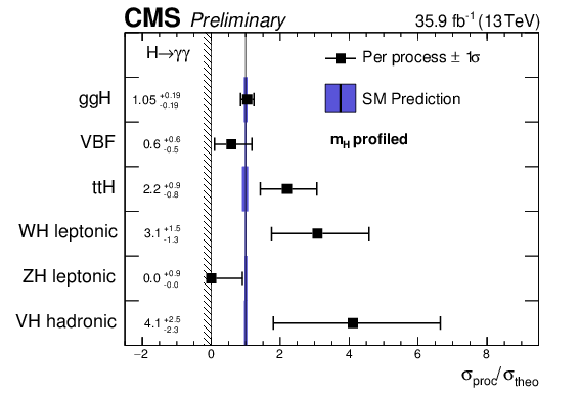
Figure 17:
Cross section ratios measured for each process (black points) in the Higgs Simplified Template Cross Section framework, for profiled $m_{H}$, compared to the SM expectation and its uncertainties (green band). The signal strength modifiers are constrained to be non-negative, as indicated by the vertical line and hashed pattern at zero. |

png pdf |
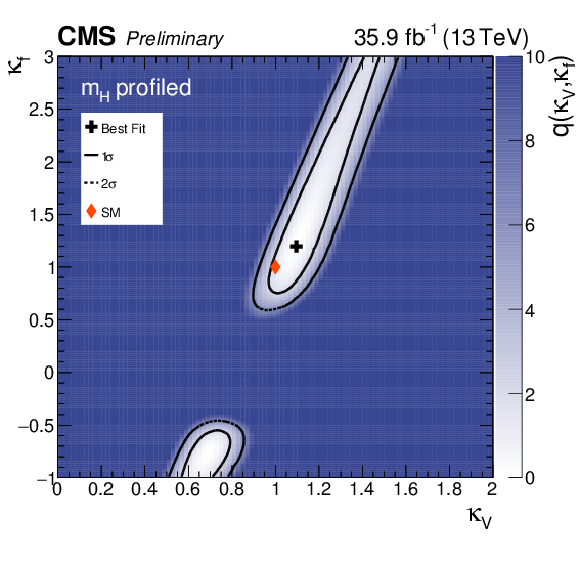
Figure 18:
The two-dimensional best-fit (black cross) of the signal strengths for fermionic (ggH, $\mathrm {t\bar{t}H}$) and bosonic (VBF, ZH, WH) production modes compared to the SM expectations (red diamond). The Higgs boson mass is profiled in the fit. The solid (dashed) line represents the 1 (2) standard deviation confidence region. |
png pdf |
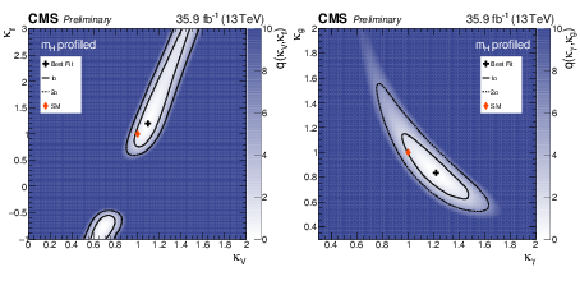
Figure 19:
Two-dimensional likelihood scans of $\kappa _{f}$ versus $\kappa _{V}$ (left) and $\kappa _{g}$ versus $\kappa _{\gamma }$ (right). All four variables are expressed relative to the SM expectations. The mass of the Higgs boson is profiled in the fits. The crosses indicate the best-fit values, the diamonds indicate the Standard Model expectations. The color maps indicate the value of the test statistic q as described in the text. |
png pdf |
Figure 19-a:
Two-dimensional likelihood scans of $\kappa _{f}$ versus $\kappa _{V}$. All four variables are expressed relative to the SM expectations. The mass of the Higgs boson is profiled in the fits. The crosses indicate the best-fit values, the diamonds indicate the Standard Model expectations. The color maps indicate the value of the test statistic q as described in the text. |

png pdf |
Figure 19-b:
Two-dimensional likelihood scans of $\kappa _{g}$ versus $\kappa _{\gamma }$. All four variables are expressed relative to the SM expectations. The mass of the Higgs boson is profiled in the fits. The crosses indicate the best-fit values, the diamonds indicate the Standard Model expectations. The color maps indicate the value of the test statistic q as described in the text. |
| Tables | |

png pdf |
Table 1:
Schema of the photon preselection requirements. |
png pdf |
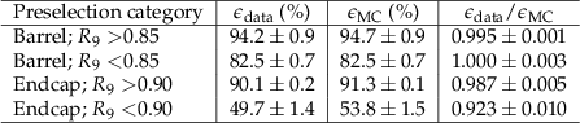
Table 2:
Photon preselection efficiencies as measured in four photon categories, obtained with tag and probe techniques using $\mathrm{ Z } \to {\mathrm{ e }^{+} \mathrm{ e }^{-} } $ and $\mathrm{ Z } \to {\mu^{+} \mu^{-} } \gamma $. The quoted uncertainties include statistical and systematic terms. |
png pdf |
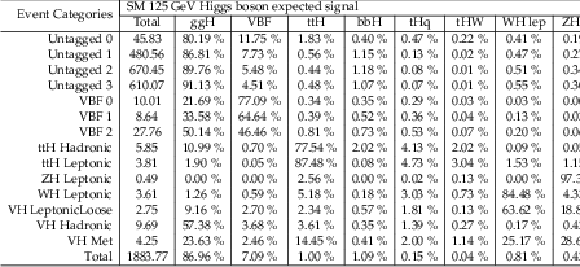
Table 3:
The expected number of signal events per category and the percentage breakdown per production mode in that category. The $\sigma _{eff}$, computed as the smallest interval containing 68.3% of the invariant mass distribution, and $\sigma _{HM}$, computed as the width of the distribution at half of its highest point divided by 2.35 are also shown as an estimate of the $\text {m}_{\gamma \gamma } $ resolution in that category. The expected number of background events per GeV around 125 GeV is also listed. |
| Summary |
| We report the measurements of several of the properties of the standard model Higgs boson using its diphoton decay: the overall signal strength, the signal strength for each production mode separately, the rates for signal strengths $\mu_{\text{VBF, VH}}$ and $\mu_{\text{ggH, ttH}}$ for the model with these two parameters allowed to vary, cross section ratios for the Stage 0 STXS process definitions, and the best-fit coupling modifiers in the $\kappa_{f}$-$\kappa_{V}$ and $\kappa_{\gamma}$-$\kappa_{g}$ planes. The analysis uses 35.9 fb$^{-1}$ of proton-proton collision data collected at $ \sqrt{s} = $ 13 TeV by the CMS experiment at the LHC in 2016. The best fit signal strength obtained profiling $m_{\mathrm{H}}$ is reported to be $\hat{\mu} = $ 1.16 $^{+0.15}_{-0.14} $ =1.16 $^{+0.11}_{-0.10}$ (stat.) $^{+0.09}_{-0.08}$ (syst.) $^{+0.06}_{-0.05}$ (theo.). The best-fit values for the signal strength modifiers associated with the ggH and ttH production mechanisms, and with the VBF and VH production processes are measured; the best fit values for each modifier are $\mu_{\text{ggH, ttH}} = $ 1.19 $^{+0.20}_{-0.18}$ and $\mu_{\text{VBF, VH}}= $ 1.01 $^{+0.57}_{-0.51}$. When $\mu_{\text{ttH}}$ is considered separately, the best-fit value is $\mu_{\text{ttH}} = $ 2.2 $^{+0.9}_{-0.8}$, corresponding to a 3.3$\sigma$ excess with respect to the absence of $\mu_{\text{ttH}}$ production, and compatible within 1.6$\sigma$ with the SM $\mu_{\text{ttH}}$ prediction. |
| Additional Figures | |

png pdf |
Additional Figure 1:
Signal strength modifiers measured for each analysis category (black points) for profiled $m_\mathrm{ H } $, compared to the overall signal strength (green band) and to the SM expectation (dashed red line). The signal strength modifiers are constrained to be non-negative, as indicated by the vertical line and hashed pattern at zero. |
png pdf |
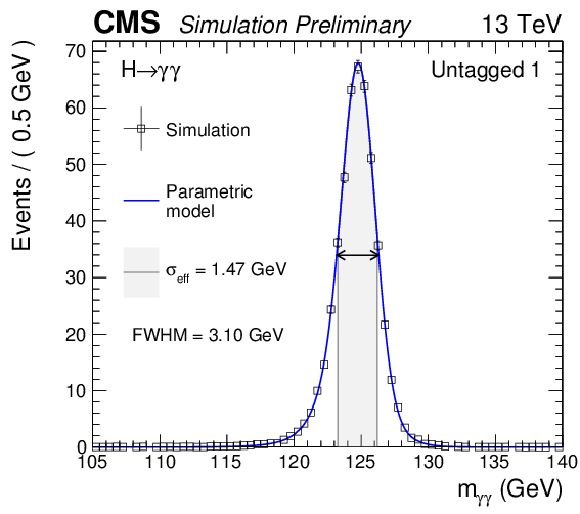
Additional Figure 2:
Parametrized signal shape for the untagged category with second-highest signal-to-background for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
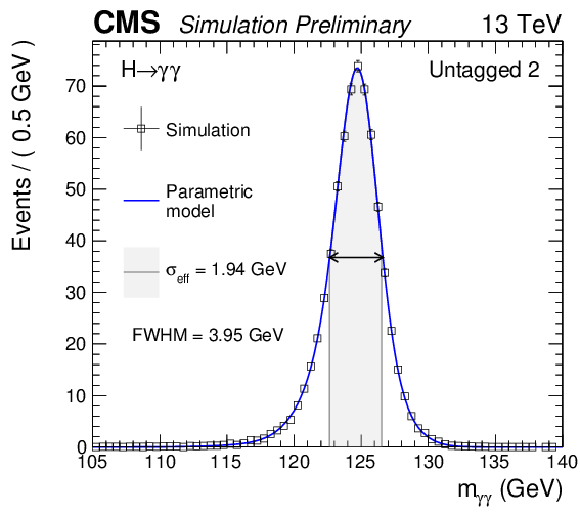
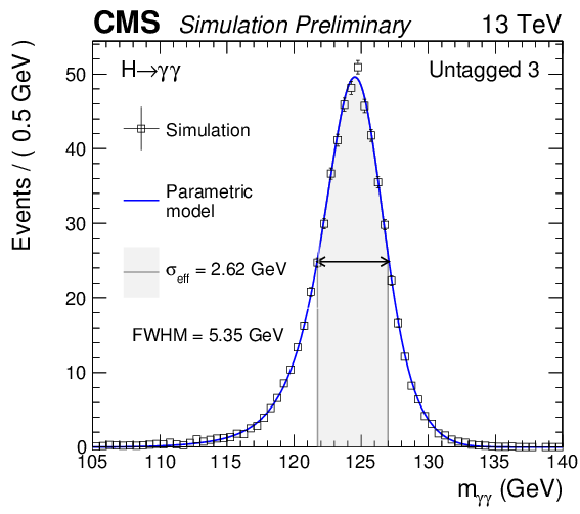
Additional Figure 3:
Parametrized signal shape for the untagged category with third-highest signal-to-background for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
Additional Figure 4:
Parametrized signal shape for the untagged category with lowest signal-to-background for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |

png pdf |
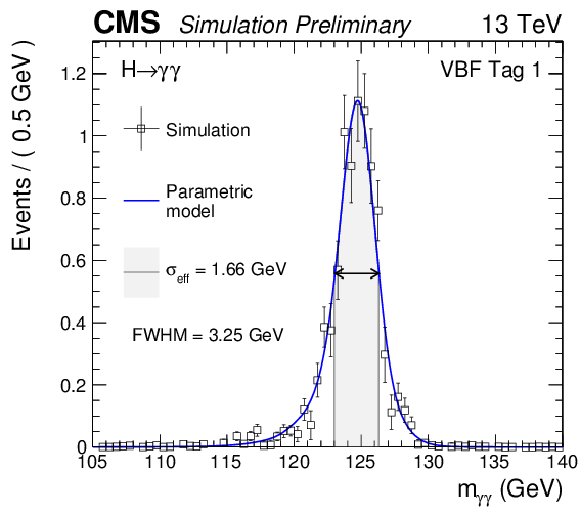
Additional Figure 5:
Parametrized signal shape for the VBF category with highest signal-to-background for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
Additional Figure 6:
Parametrized signal shape for the VBF category with second-highest signal-to-background for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |

png pdf |
Additional Figure 7:
Parametrized signal shape for the VBF category with lowest signal-to-background for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
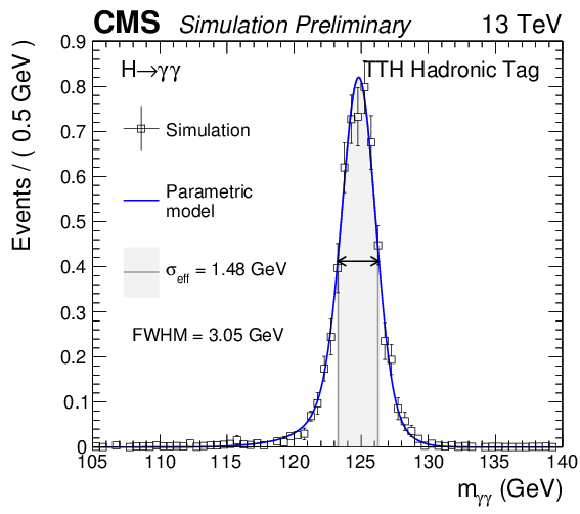
Additional Figure 8:
Parametrized signal shape for the hadronic $\mathrm {t\bar{t}}$H category for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
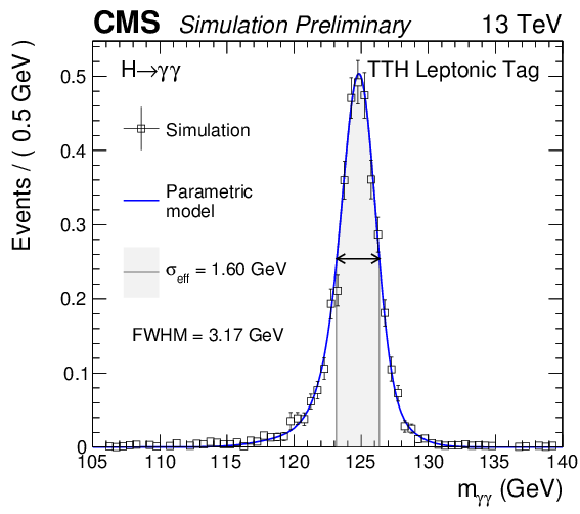
Additional Figure 9:
Parametrized signal shape for the leptonic $\mathrm {t\bar{t}}$H category for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
Additional Figure 10:
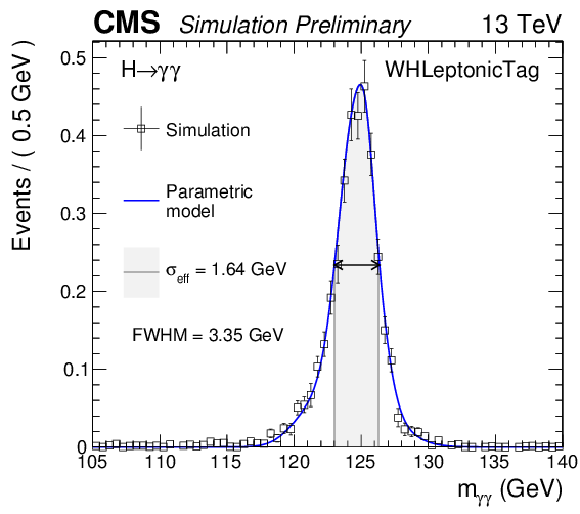
Parametrized signal shape for the leptonic WH category for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
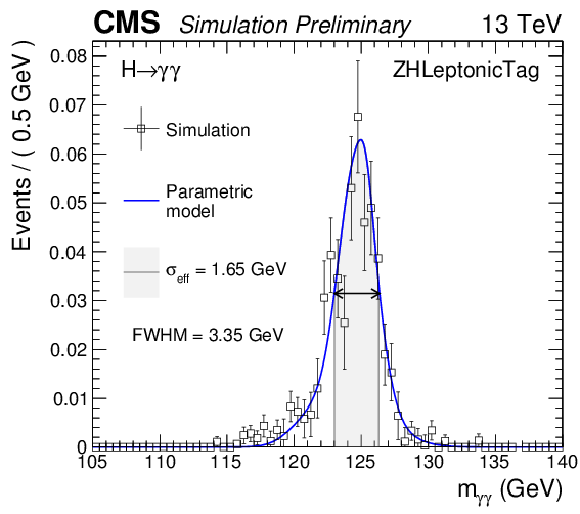
Additional Figure 11:
Parametrized signal shape for the leptonic ZH category for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |

png pdf |
Additional Figure 12:
Parametrized signal shape for the loose leptonic VH category for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
Additional Figure 13:
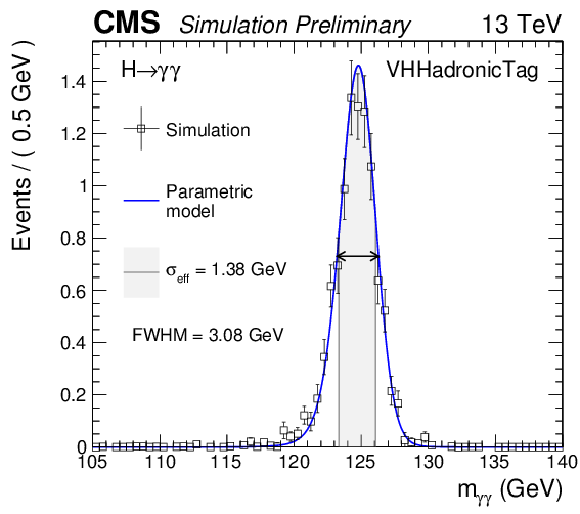
Parametrized signal shape for the hadronic VH category for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
png pdf |
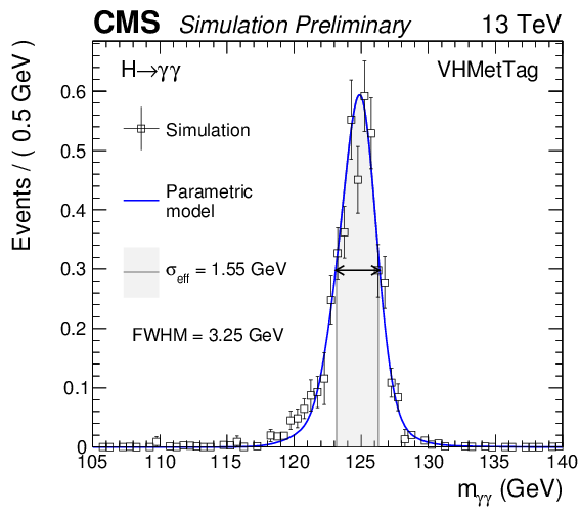
Additional Figure 14:
Parametrized signal shape for the VH missing transverse momentum (MET) category for a simulated $\mathrm{ H } \to \gamma \gamma $ signal sample with $m_\mathrm{ H } = $ 125 GeV. The black points represent weighted simulation events and the blue lines are the corresponding models. Also shown are the $\sigma _{\text {eff}}$ value (half the width of the narrowest interval containing 68.3% of the invariant mass distribution), FWHM and the corresponding interval. |
| References | ||||
| 1 | S. L. Glashow | Partial-symmetries of weak interactions | Nucl. Phys. 22 (1961) 579 | |
| 2 | S. Weinberg | A model of leptons | PRL 19 (1967) 1264 | |
| 3 | A. Salam | Weak and electromagnetic interactions | in Elementary particle physics: relativistic groups and analyticity, N. Svartholm, ed., p. 367 Almquvist \& Wiskell, 1968 Proceedings of the eighth Nobel symposium | |
| 4 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | PLB716 (2012) 1--29 | 1207.7214 |
| 5 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB716 (2012) 30--61 | CMS-HIG-12-028 1207.7235 |
| 6 | F. Englert and R. Brout | Broken symmetries and the masses of gauge bosons | PRL 13 (1964) 321 | |
| 7 | P. W. Higgs | Broken symmetry and the mass of gauge vector mesons | PRL 13 (1964) 508 | |
| 8 | G. Guralnik, C. Hagen, and T. Kibble | Global Conservation Laws and Massless Particles | Phys.Rev.Lett. 13 (1964) 585 | |
| 9 | ATLAS, CMS Collaboration | Combined Measurement of the Higgs Boson Mass in pp Collisions at $ \sqrt{s}= $ 7 and 8 TeV with the ATLAS and CMS Experiments | PRL 114 (2015) 191803 | 1503.07589 |
| 10 | ATLAS, CMS Collaboration | Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $ \sqrt{s}= $ 7 and 8 TeV | JHEP 08 (2016) 045 | 1606.02266 |
| 11 | CMS Collaboration | First results on $ \mathrm{ H }\rightarrow\gamma\gamma $ measurements at $ \sqrt{s} =$ 13 TeV | CMS-PAS-HIG-15-005 | CMS-PAS-HIG-15-005 |
| 12 | CMS Collaboration | Particle-Flow Event Reconstruction in CMS and Performance for Jets, Taus, and MET | CDS | |
| 13 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 14 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 15 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 16 | CMS Collaboration | Measurement of the inclusive W and Z production cross sections in pp collisions at $ \sqrt{s} =$ 7 TeV with the CMS experiment | JHEP 2011 (2011) 1 | |
| 17 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 18 | T. Sjostrand, S. Mrenna, and P. Z. Skands | A Brief Introduction to PYTHIA 8.1 | CPC 178 (2008) 852--867 | 0710.3820 |
| 19 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | CMS-GEN-14-001 1512.00815 |
|
| 20 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector | technical report | 1610.07922 |
| 21 | T. Gleisberg et al. | Event generation with SHERPA 1.1 | JHEP 02 (2009) 007 | 0811.4622 |
| 22 | GEANT4 Collaboration | GEANT4: A Simulation toolkit | NIMA 506 (2003) 250 | |
| 23 | CMS Collaboration | Energy calibration and resolution of the CMS electromagnetic calorimeter in pp collisions at$ \sqrt{s} =$ 7 TeV | JINST 8 (2013) 09009 | CMS-EGM-11-001 1306.2016 |
| 24 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet User Manual | EPJC72 (2012) 1896 | 1111.6097 |
| 25 | CMS Collaboration | Electron and Photon performance using data collected by CMS at $ \sqrt{s} =$ 13 TeV and 25ns | CDS | |
| 26 | P. D. Dauncey, M. Kenzie, N. Wardle, and G. J. Davies | Handling uncertainties in background shapes: the discrete profiling method | JINST 10 (2015), no. 04, P04015 | 1408.6865 |
| 27 | R. A. Fisher | On the interpretation of $ \chi^{2} $ from contingency tables, and the calculation of p | Journal of the Royal Statistical Society 85 (1922) | |
| 28 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG43 (2016) 023001 | 1510.03865 |
| 29 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 30 | S. Carrazza et al. | An Unbiased Hessian Representation for Monte Carlo PDFs | EPJC75 (2015), no. 8, 369 | 1505.06736 |
| 31 | CMS Collaboration | Measurement of the differential cross section for $ \mathrm{ t \bar{t} } $ production in the dilepton final state at $ \sqrt{s}=13 $~TeV | Technical Report CMS-PAS-TOP-16-011, CERN, 2016 | |
| 32 | CMS Collaboration | Measurement of the cross section ratio $ \sigma_{\rm t\bar{t}b\bar{b}} $ / $ \sigma_{\rm t\bar{t}jj} $ using dilepton final states in pp collisions at $ \sqrt{s} = $ 13 TeV | Technical Report CMS-PAS-TOP-16-010, CERN, 2016 | |
| 33 | CMS Collaboration | Performance of missing energy reconstruction in 13 TeV pp collision data using the CMS detector | CMS-PAS-JME-16-004 | CMS-PAS-JME-16-004 |
| 34 | CMS Collaboration | CMS Luminosity Measurements for the 2016 Data Taking Period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 35 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 3. Higgs Properties | 1307.1347 | |
| 36 | G. Cowan et al. | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1 | 1007.1727 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|