Compact Muon Solenoid
LHC, CERN

Visit us: CMS Public Website, CMS Physics ; Contact us: CMS Publications Committee

CMS-PAS-HIG-16-029

Search for resonant Higgs boson pair production in the $\mathrm{b\overline{b}}\tau^+\tau^-$ final state using 2016 data

CMS Collaboration

August 2016

Abstract: A search for resonant Higgs boson pair production in proton-proton collisions in the $\mathrm{b\overline{b}}\tau^+\tau^-$ final state is presented. The existence of a new heavy scalar boson H, which decays into a pair of the known h boson, is assumed. The search for ${\mathrm{pp} \to \mathrm{H} \to \mathrm{hh} \to \mathrm{b\overline{b}}\tau^+\tau^-}$ is performed using three $\tau\tau$ final states, $e\tau_{h}$, $\mu\tau_{h}$, and $\tau_{h}\tau_{h}$, where $\tau_{h}$ indicates a $\tau$ lepton decay involving hadrons. The analysis uses proton-proton collision data collected with the CMS detector at the LHC in 2016 at a centre-of-mass energy of 13 TeV and corresponding to an integrated luminosity of 12.9 fb$^{-1}$.

Links: CDS record (PDF) ; inSPIRE record ; CADI line (restricted) ;

Figures
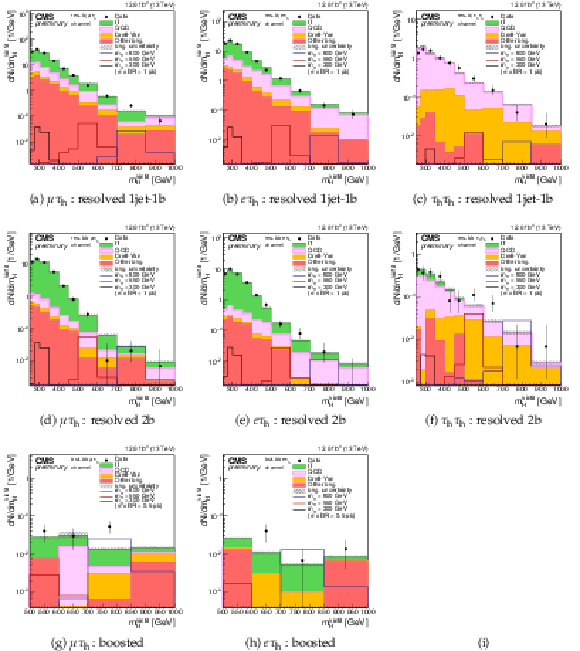
png pdf	Figure 1: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plots are shown for (a)-(d)-(g) $\mu \tau _{\rm h}$, (b)-(e)-(h) $e\tau _{\rm h}$, and (c)-(f) $\tau _{\rm h}\tau _{\rm h}$ final states and for the three categories: resolved 1jet-1b (first row), resolved 2b (second row), and boosted (third row). In the boosted $\tau _{\rm h}\tau _{\rm h}$ category a counting experiment is performed and the plot is not shown. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
png pdf	Figure 1-a: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plot is shown for the $ \mu \tau _{\rm h} $ and for the resolved 1jet-1b category. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
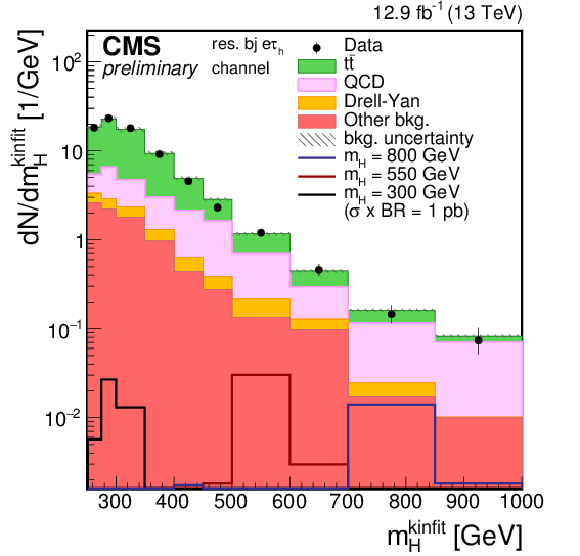
png pdf	Figure 1-b: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plot is shown for the $e\tau _{\rm h}$ final state and for the resolved 1jet-1b category. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
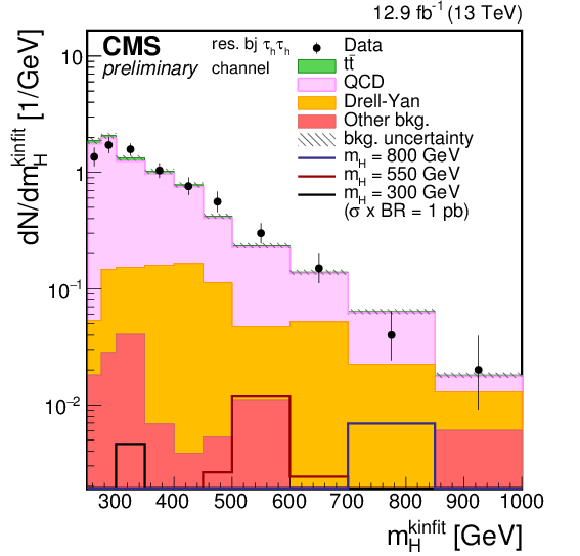
png pdf	Figure 1-c: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plot is shown for the $\tau _{\rm h}\tau _{\rm h}$ final state and for the resolved 1jet-1b category. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
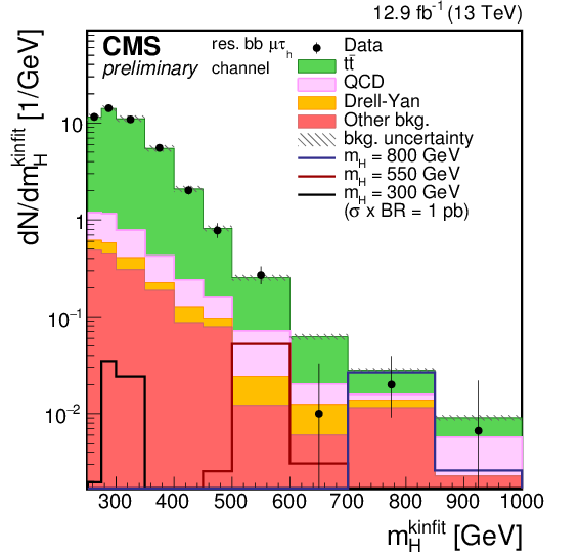
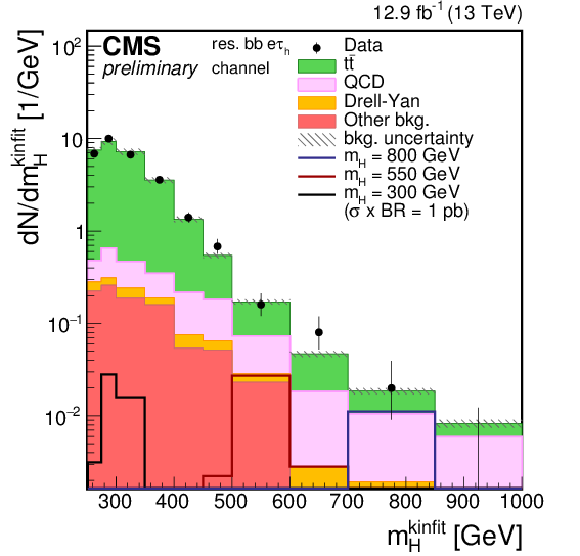
png pdf	Figure 1-d: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plot is shown for the $\mu \tau _{\rm h}$ and for the resolved 2b category. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
png pdf	Figure 1-e: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plot is shown for the $e\tau _{\rm h}$ final state and for the resolved 2b category. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
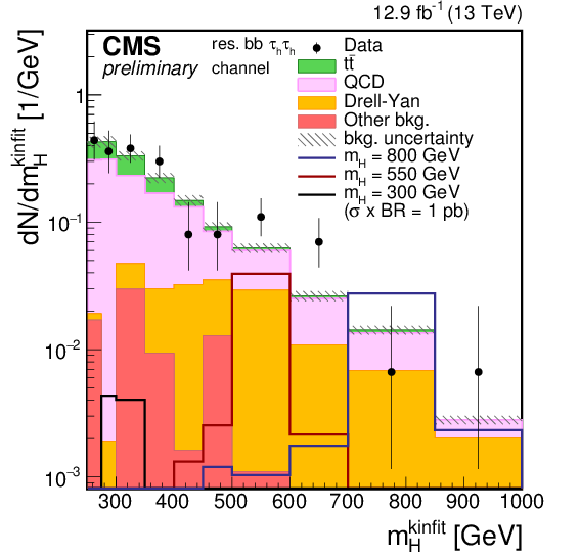
png pdf	Figure 1-f: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plot is shown for the $\tau _{\rm h}\tau _{\rm h}$ final state and for the resolved 2b category. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
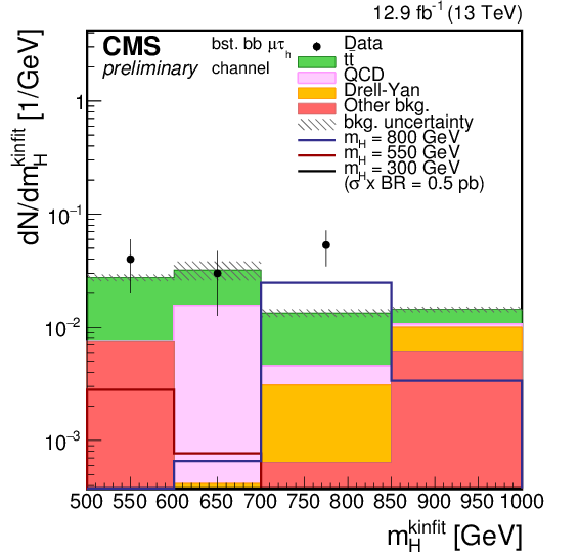
png pdf	Figure 1-g: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plot is shown for the $\mu \tau _{\rm h}$ final state and for the boosted category. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
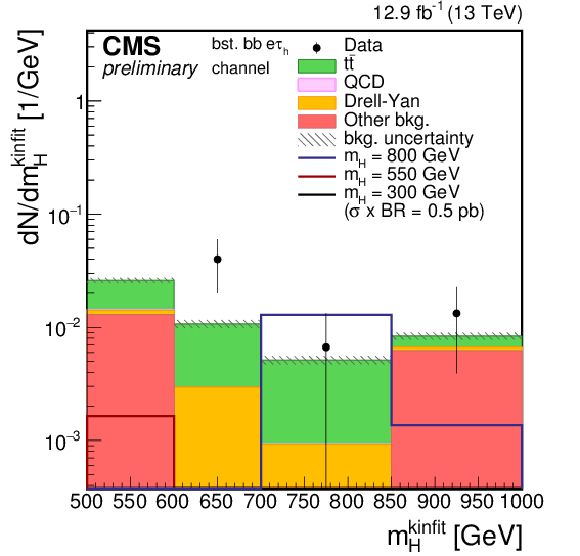
png pdf	Figure 1-h: Distributions of the four-body mass reconstructed with the kinematic fit after applying the event selections. The plot is shown for the $e \tau _{\rm h}$ and for the boosted category. Points with error bars represent the data and shaded histograms represent the backgrounds. The black, red, and blue unshaded histograms are the signal expectations for $m_{\rm H}= $ 300 GeV, $m_{\rm H}= $ 550 GeV, and $m_{\rm H}= $ 800 GeV. The signal expectations are plotted for a value of $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} )$ of 1pb in the resolved categories and 0.5 pb in the boosted categories. Event yields in each bin are divided by the bin width. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked.
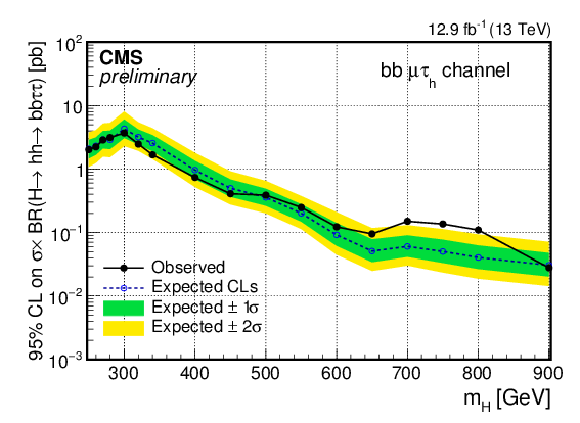
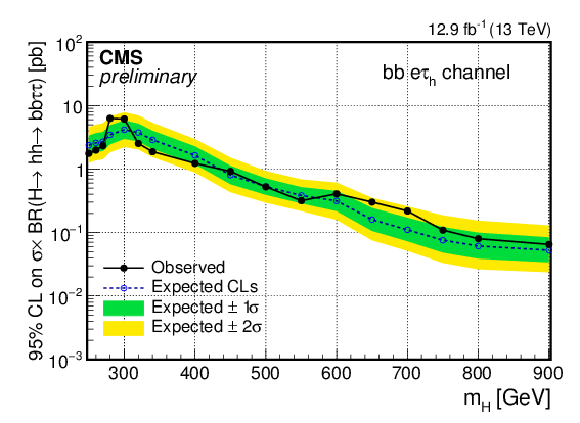
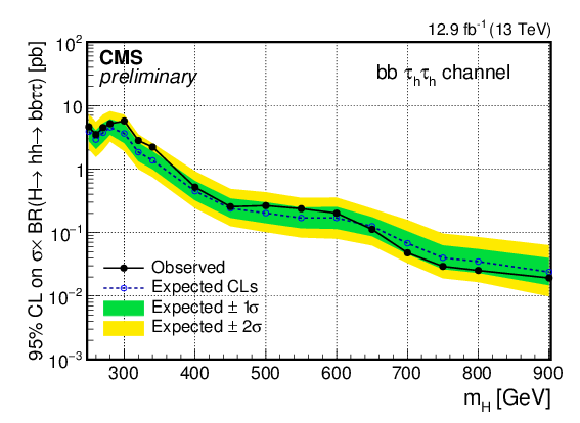
png pdf	Figure 2: Observed and expected 95% CL upper limits on ${\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} \to {\rm bb} \tau \tau )}$ as a function of the mass of the resonance $m_{\rm H}$ and combining the resolved and boosted categories. (a) bb $\mu \tau _{\rm h}$ (b) bb $e\tau _{\rm h}$ (c) bb $\tau _{\rm h}\tau _{\rm h}$.
png pdf	Figure 2-a: Observed and expected 95% CL upper limits on ${\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} \to {\rm bb} \tau \tau )}$ as a function of the mass of the resonance $m_{\rm H}$ and combining the resolved and boosted categories: bb $\mu \tau _{\rm h}$ channel.
png pdf	Figure 2-b: Observed and expected 95% CL upper limits on ${\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} \to {\rm bb} \tau \tau )}$ as a function of the mass of the resonance $m_{\rm H}$ and combining the resolved and boosted categories: bb $e\tau _{\rm h}$ channel.
png pdf	Figure 2-c: Observed and expected 95% CL upper limits on ${\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} \to {\rm bb} \tau \tau )}$ as a function of the mass of the resonance $m_{\rm H}$ and combining the resolved and boosted categories: $\tau _{\rm h}\tau _{\rm h}$ channel.
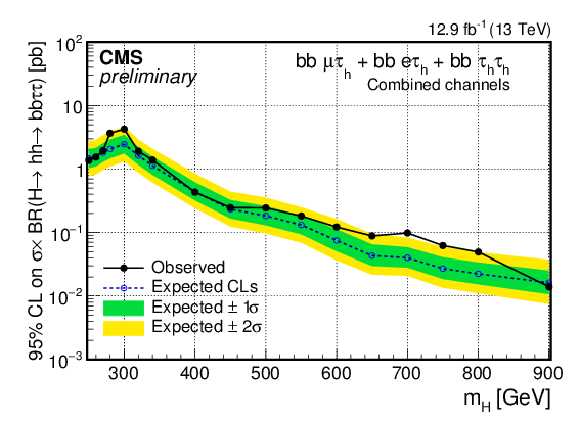
png pdf	Figure 3: Observed and expected 95% CL upper limits on ${\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} \to {\rm bb} \tau \tau )}$ from the combination of the three channels as a function of the mass of the resonance $m_{\rm H}$.

Tables
png pdf	Table 1: Lists of the systematic uncertainties affecting the normalization of the different processes.
png pdf	Table 2: Observed and expected event yields in different final states for the resolved 1jet-1b category. Quoted uncertainties represent the combination of statistical plus systematic uncertainties. The signal expected yields are for $\sigma ({\rm pp} \rightarrow {\rm H}) \times {\rm BR} ({\rm H} \rightarrow {\rm hh} \rightarrow {\rm bb}\tau \tau ) = $ 10 pb.
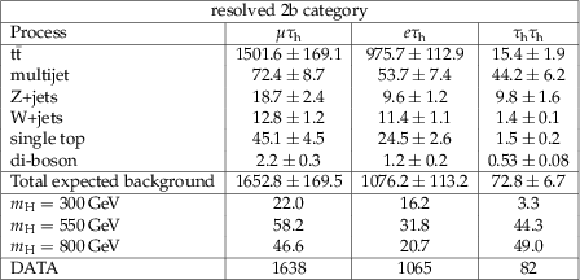
png pdf	Table 3: Observed and expected event yields in different final states for the resolved 2b category. Quoted uncertainties represent the combination of statistical plus systematic uncertainties. The signal expected yields are for $\sigma ({\rm pp} \rightarrow {\rm H}) \times {\rm BR} ({\rm H} \rightarrow {\rm hh} \rightarrow {\rm bb}\tau \tau ) = $ 10 pb.
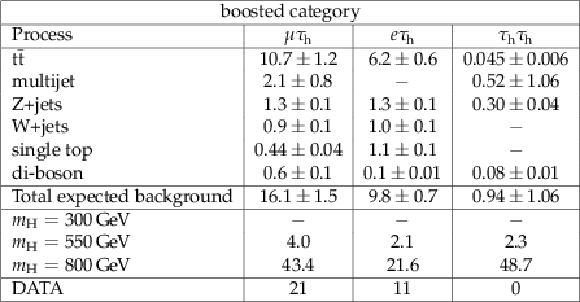
png pdf	Table 4: Observed and expected event yields in different final states for the boosted category. Quoted uncertainties represent the combination of statistical plus systematic uncertainties. The signal expected yields are for $\sigma ({\rm pp} \rightarrow {\rm H}) \times {\rm BR} ({\rm H} \rightarrow {\rm hh} \rightarrow {\rm bb}\tau \tau ) = $ 10 pb.
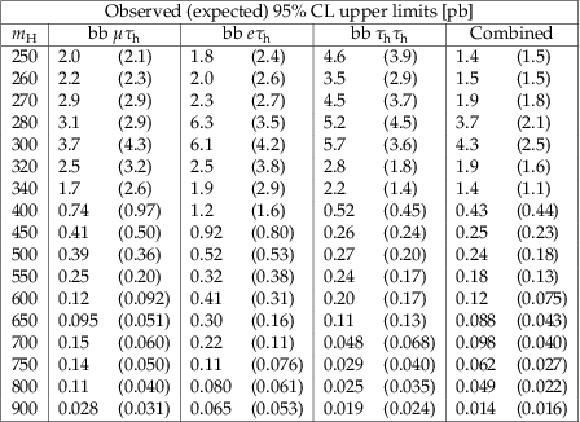
png pdf	Table 5: Observed and expected 95% CL upper limits on $\sigma ({\rm pp} \to {\rm H} ) \times {\rm BR} ({\rm H} \to {\rm hh} \to {\rm bb} \tau \tau )$ for the combination of the three b-jet categories for the $\mu \tau _{\rm h}$, $e\tau _{\rm h}$, and $\tau _{\rm h}\tau _{\rm h}$ final states and their combination.

Summary

A search for resonant Higgs boson pair production in the bb$\tau\tau$ final state with the data collected by the CMS experiment in 2016 at $\sqrt{s} =$ 13 TeV, and corresponding to an integrated luminosity of 12.9 fb$^{-1}$, is presented. The search is performed using the three most sensitive decay channels of the $\tau$ lepton pair, $e\tau_{\rm h}, \mu\tau_{\rm h}, \tau_{\rm h}\tau_{\rm h}$, where $\tau_{\rm h}$ indicates a tau decay involving hadrons. No excess over the SM background prediction is observed and model independent upper limits on the values of the cross section times branching ratio are derived for different signal mass hypotheses between 250 and 900 GeV. These are currently the best limits on Higgs boson pair production in the high mass range considered for this analysis and substantially improve the sensitivity with respect to the previous analysis.

Additional Figures
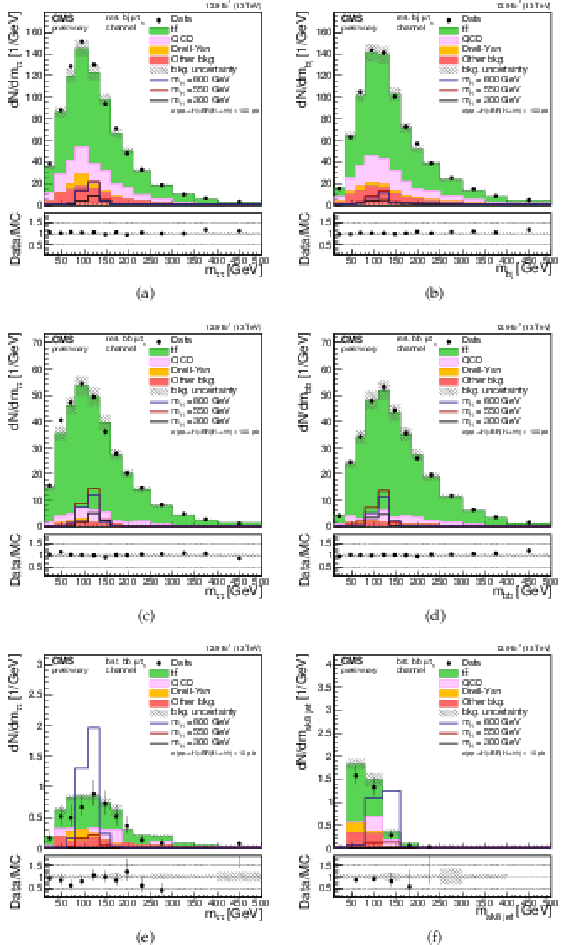
png pdf	Additional Figure 1: (a)-(c)-(e) distributions of the invariant mass of the $\tau \tau $ pair reconstructed using the SVfit algorithm, (b)-(d) distributions of the invariant mass of the bb pair, and (f) distribution of the invariant mass of the ak8 jet. $\tau \tau $ and bb candidates selections are applied but no selection on the invariant mass is requested. (a)-(b) resolved 1b-1jet $\mu \tau _{\rm h}$ category, (c)-(d) resolved 2b $\mu \tau _{\rm h}$ category, and (e)-(f) boosted $\mu \tau _{\rm h}$ category. Points with error bars represent the data and shaded histograms represent the backgrounds. The blue, black, and red lines denote respectively the signal hypothesis of 800, 550, and 300 GeV, and are scaled to a production cross section of the hh pair of 10 pb. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked. The bottom panel shows the ratio of the observed data to the simulation prediction.
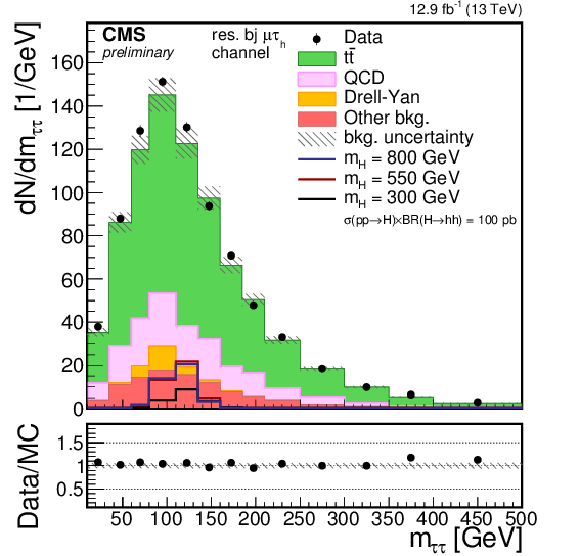
png pdf	Additional Figure 1-a: Distribution of the invariant mass of the $\tau \tau $ pair reconstructed using the SVfit algorithm for the resolved 1b-1jet $\mu \tau _{\rm h}$ category. Points with error bars represent the data and shaded histograms represent the backgrounds. $\tau \tau $ and bb candidates selections are applied but no selection on the invariant mass is requested. The blue, black, and red lines denote respectively the signal hypothesis of 800, 550, and 300 GeV, and are scaled to a production cross section of the hh pair of 10 pb. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked. The bottom panel shows the ratio of the observed data to the simulation prediction.
png pdf	Additional Figure 1-b: Distribution of the invariant mass of the bb pair for the resolved 1b-1jet $\mu \tau _{\rm h}$ category. Points with error bars represent the data and shaded histograms represent the backgrounds. $\tau \tau $ and bb candidates selections are applied but no selection on the invariant mass is requested. The blue, black, and red lines denote respectively the signal hypothesis of 800, 550, and 300 GeV, and are scaled to a production cross section of the hh pair of 10 pb. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked. The bottom panel shows the ratio of the observed data to the simulation prediction.
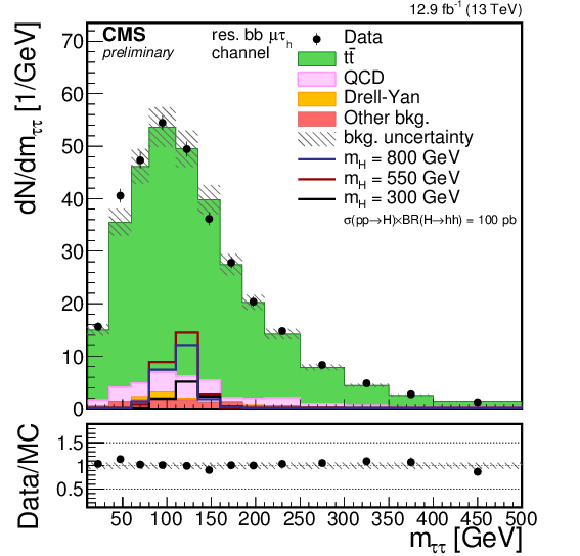
png pdf	Additional Figure 1-c: Distribution of the invariant mass of the $\tau \tau $ pair reconstructed using the SVfit algorithm for the resolved 2b $\mu \tau _{\rm h}$ category. Points with error bars represent the data and shaded histograms represent the backgrounds. $\tau \tau $ and bb candidates selections are applied but no selection on the invariant mass is requested. The blue, black, and red lines denote respectively the signal hypothesis of 800, 550, and 300 GeV, and are scaled to a production cross section of the hh pair of 10 pb. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked. The bottom panel shows the ratio of the observed data to the simulation prediction.
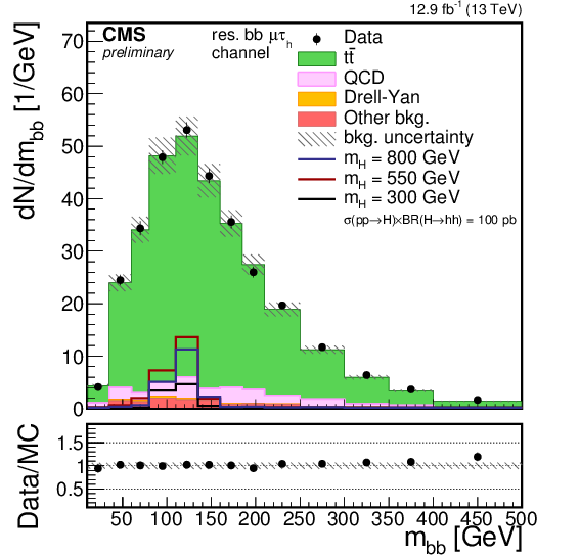
png pdf	Additional Figure 1-d: Distribution of the invariant mass of the bb pair for the resolved 2b $\mu \tau _{\rm h}$ category. Points with error bars represent the data and shaded histograms represent the backgrounds. $\tau \tau $ and bb candidates selections are applied but no selection on the invariant mass is requested. The blue, black, and red lines denote respectively the signal hypothesis of 800, 550, and 300 GeV, and are scaled to a production cross section of the hh pair of 10 pb. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked. The bottom panel shows the ratio of the observed data to the simulation prediction.
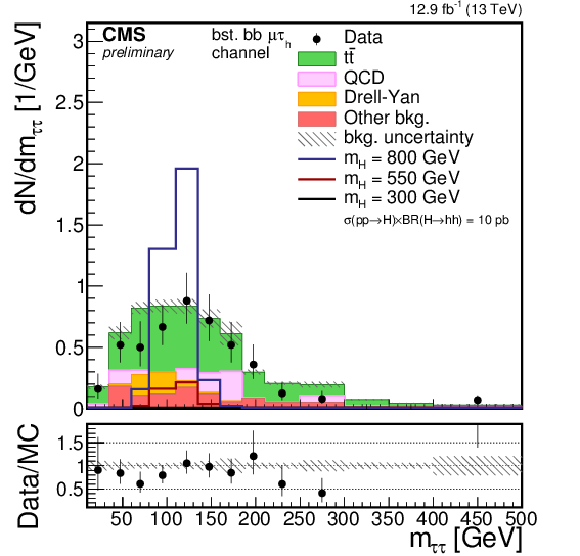
png pdf	Additional Figure 1-e: Distribution of the invariant mass of the $\tau \tau $ pair reconstructed using the SVfit algorithm for the boosted $\mu \tau _{\rm h}$ category. Points with error bars represent the data and shaded histograms represent the backgrounds. $\tau \tau $ and bb candidates selections are applied but no selection on the invariant mass is requested. The blue, black, and red lines denote respectively the signal hypothesis of 800, 550, and 300 GeV, and are scaled to a production cross section of the hh pair of 10 pb. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked. The bottom panel shows the ratio of the observed data to the simulation prediction.
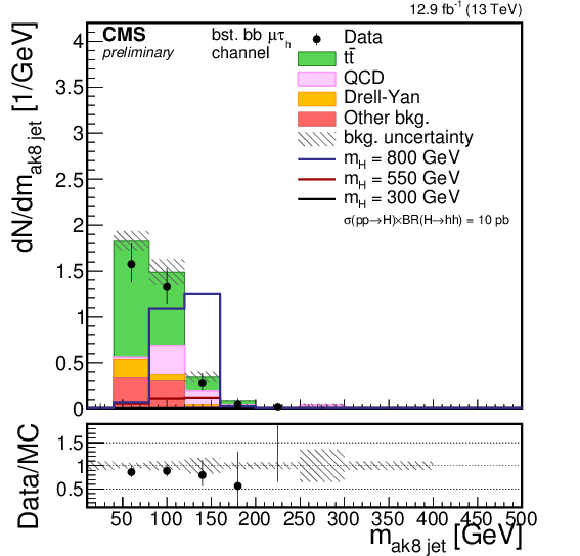
png pdf	Additional Figure 1-f: Distribution of the invariant mass of the ak8 jet for the boosted $\mu \tau _{\rm h}$ category. Points with error bars represent the data and shaded histograms represent the backgrounds. $\tau \tau $ and bb candidates selections are applied but no selection on the invariant mass is requested. The blue, black, and red lines denote respectively the signal hypothesis of 800, 550, and 300 GeV, and are scaled to a production cross section of the hh pair of 10 pb. Expected background contributions are shown for the values of nuisance parameters (systematic uncertainties) obtained after fitting the background-only hypothesis to the data. Signal and background histograms are not stacked. The bottom panel shows the ratio of the observed data to the simulation prediction.
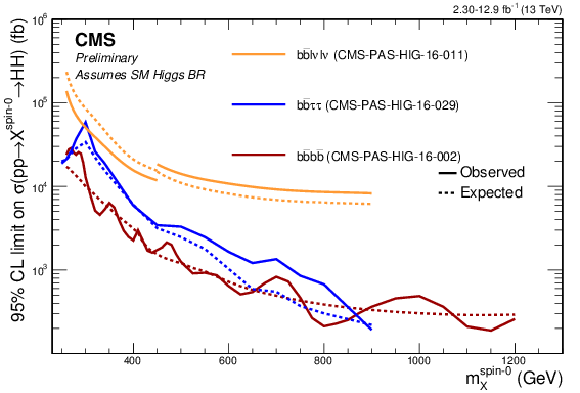
png pdf	Additional Figure 2: Comparison of the observed (solid lines) and expected (dashed lines) 95% CL upper limits on $\sigma ({\rm gg\rightarrow {\rm hh}})$ from the analyses currently performed by the CMS collaboration using the data collected ad $ \sqrt{s} = $ 13 TeV. Orange: ${\rm hh} \rightarrow {\rm bb}{\rm l}\nu _{\rm l} {\rm l}\nu _{\rm l}$ (CMS-PAS-HIG-16-011). Red: ${{\rm hh} \rightarrow {\rm bbbb}}$ (CMS-PAS-HIG-16-002). Blue: ${\rm hh} \rightarrow {\rm bb}\tau \tau $ (this analyis).

References
1	ATLAS Collaboration	Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC	Physics Letters B 716 (2012), no. 1, 1 -- 29
2	CMS Collaboration	Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC	Physics Letters B 716 (2012), no. 1, 30 -- 61
3	ATLAS, CMS Collaboration	Combined Measurement of the Higgs Boson Mass in $ pp $ Collisions at $ \sqrt{s}=7 $ and 8 TeV with the ATLAS and CMS Experiments	PRL 114 (2015) 191803	1503.07589
4	ATLAS and CMS Collaborations	Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $ \sqrt{s} $ = 7 and 8 TeV	CMS-PAS-HIG-15-002	CMS-PAS-HIG-15-002
5	T. Binoth and J. J. van der Bij	Influence of strongly coupled, hidden scalars on Higgs signals	Z. Phys. C75 (1997) 17--25	hep-ph/9608245
6	R. Schabinger and J. D. Wells	A Minimal spontaneously broken hidden sector and its impact on Higgs boson physics at the large hadron collider	PRD72 (2005) 093007	hep-ph/0509209
7	B. Patt and F. Wilczek	Higgs-field portal into hidden sectors		hep-ph/0605188
8	S. Y. Choi, C. Englert, and P. M. Zerwas	Multiple Higgs-Portal and Gauge-Kinetic Mixings	EPJC73 (2013) 2643	1308.5784
9	ATLAS Collaboration	Constraints on New Phenomena via Higgs Coupling Measurements with the ATLAS Detector	ATLAS-CONF-2014-010
10	T. Robens and T. Stefaniak	Status of the Higgs Singlet Extension of the Standard Model after LHC Run 1	EPJC75 (2015) 104	1501.02234
11	P. Fayet	Supergauge Invariant Extension of the Higgs Mechanism and a Model for the electron and Its Neutrino	Nucl. Phys. B90 (1975) 104--124
12	P. Fayet	Spontaneously Broken Supersymmetric Theories of Weak, Electromagnetic and Strong Interactions	PLB69 (1977) 489
13	A. Djouadi et al.	Fully covering the MSSM Higgs sector at the LHC	JHEP 06 (2015) 168	1502.05653
14	ATLAS Collaboration	Searches for Higgs boson pair production in the $ hh\to bb\tau\tau, \gamma\gamma WW^*, \gamma\gamma bb, bbbb $ channels with the ATLAS detector	PRD92 (2015) 092004	1509.04670
15	CMS Collaboration	Searches for a heavy scalar boson H decaying to a pair of 125 GeV Higgs bosons hh or for a heavy pseudoscalar boson A decaying to Zh, in the final states with $ h \to \tau \tau $	PLB755 (2016) 217--244	CMS-HIG-14-034 1510.01181
16	CMS Collaboration	Search for resonant Higgs boson pair production in the $ \mathrm{b\overline{b}}\tau^+\tau^- $ final state	CMS-PAS-HIG-16-013	CMS-PAS-HIG-16-013
17	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
18	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
19	S. Alioli, P. Nason, C. Oleari, and E. Re	NLO single-top production matched with shower in POWHEG: s- and t-channel contributions	JHEP 09 (2009) 111, , [Erratum: JHEP02,011(2010)]	0907.4076
20	J. M. Campbell, R. K. Ellis, P. Nason, and E. Re	Top-pair production and decay at NLO matched with parton showers	JHEP 04 (2015) 114	1412.1828
21	T. Sjostrand, S. Mrenna, and P. Z. Skands	A Brief Introduction to PYTHIA 8.1	CPC 178 (2008) 852--867	0710.3820
22	CMS Collaboration	Particle--flow event reconstruction in CMS and performance for jets, taus, and $ E_{\mathrm{T}}^{\text{miss}} $	CDS
23	CMS Collaboration	Commissioning of the particle-flow event reconstruction with the first LHC collisions recorded in the CMS detector	CDS
24	K. Rose	Deterministic annealing for clustering, compression, classification, regression and related optimisation problems	in Proceedings of the IEEE, volume 86, p. 86 1998
25	W. Waltenberger, R. Fr\"uhwirth, and P. Vanlaer	Adaptive vertex fitting	JPG 34 (2007) N343
26	CMS Collaboration	Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} $ = 8 TeV	JINST 10 (2015), no. 06, P06005	CMS-EGM-13-001 1502.02701
27	A. Hocker et al.	TMVA - Toolkit for Multivariate Data Analysis	PoS ACAT (2007) 040	physics/0703039
28	CMS Collaboration	Performance of CMS muon reconstruction in $ pp $ collision events at $ \sqrt{s}=7 $ TeV	JINST 7 (2012) P10002	CMS-MUO-10-004 1206.4071
29	M. Cacciari, G. P. Salam, and G. Soyez	The anti-$ k_t $ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
30	M. Cacciari, G. P. Salam, and G. Soyez	FastJet user manual	EPJC 72 (2012) 1896	1111.6097
31	A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler	Soft Drop	JHEP 05 (2014) 146	1402.2657
32	CMS Collaboration	Algorithms for b Jet identification in CMS	CDS
33	CMS Collaboration	Performance of tau-lepton reconstruction and identification in CMS	JINST 7 (2012) P01001	CMS-TAU-11-001 1109.6034
34	CMS Collaboration	Reconstruction and identification of $ \tau $ lepton decays to hadrons and $ \nu_\tau $ at CMS		CMS-TAU-14-001 1510.07488
35	CMS Collaboration	Performance of reconstruction and identification of tau leptons in their decays to hadrons and tau neutrino in LHC Run-2	CMS-PAS-TAU-16-002	CMS-PAS-TAU-16-002
36	L. Bianchini, J. Conway, E. K. Friis, and C. Veelken	Reconstruction of the Higgs mass in H to tautau Events by Dynamical Likelihood techniques	Journal of Physics: Conference Series 513 (2014), no. 2, 022035
37	CMS Collaboration	Measurement of the inclusive and differential tt production cross sections in lepton + jets final states at 13 TeV	CMS-PAS-TOP-15-005	CMS-PAS-TOP-15-005
38	M. Czakon and A. Mitov	Top++: A Program for the Calculation of the Top-Pair Cross-Section at Hadron Colliders	CPC 185 (2014) 2930	1112.5675
39	G. Cowan, K. Cranmer, E. Gross, and O. Vitells	Asymptotic formulae for likelihood-based tests of new physics	EPJC71 (2011) 1554, , [Erratum: Eur. Phys. J.C73,2501(2013)]	1007.1727

Compact Muon Solenoid LHC, CERN

© Copyright CERN 2018 for the benefit of the CMS Collaboration