

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-16-021 | ||
| Higgs to WW measurements with 15.2 fb$^{-1}$ of 13 TeV proton-proton collisions | ||
| CMS Collaboration | ||
| July 2017 | ||
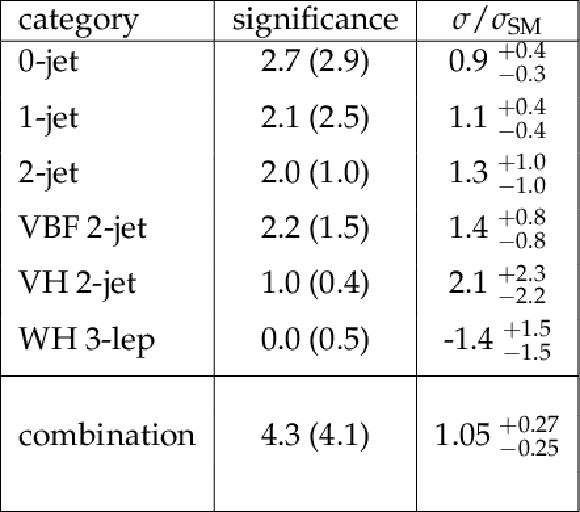
| Abstract: Results on the measurements of the standard model Higgs boson decaying to a W-boson pair at $\sqrt{s}= $ 13 TeV at the LHC with 2015 and early 2016 data are reported. The event sample corresponds to integrated luminosities of 2.3 fb$^{-1}$ and 12.9 fb$^{-1}$, collected by the CMS detector in 2015 and up to August 2016 respectively. The W$^+$W$^-$ candidates are selected in events with an oppositely charged e$\mu$ pair and large missing transverse momentum, and with different number of jets. Dedicated categories with two jets or three leptons, designed to select Higgs bosons produced via vector boson fusion or associated production with a W or Z boson, are also explored. Combining all the channels studied, the observed (expected) significance for the SM Higgs boson with a mass of 125 GeV is 4.3$\sigma$ (4.1$\sigma$), corresponding to an observed cross section times branching ratio of 1.05 $\pm$ 0.26 times the standard model prediction. | ||
| Links: CDS record (PDF) ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
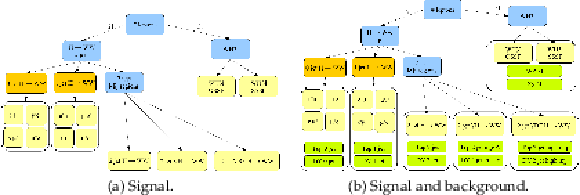
Figure 1:
The flowchart of the analysis is reported here. On the left without background control regions, on the right with the background control regions. The green boxes correspond to a separate cut based analyses used to control background normalization. The yellow boxes correspond to signal phase spaces for the analysis, and for each of them a template shape approach is followed. The orange boxes represent interesting combinations of categories, while blue boxes are the selections criteria. The WW normalization is part of the nominal signal phase space (yellow boxes), since it's difficult to define a complete orthogonal set of selections to disentangle from the Higgs. The normalization of WW is done independently in 0 jet, 1 jet, 2 jet, 2 jet close to W/Z mass, and high di-jet invariant mass. Every green box corresponds to a phase space used to regulate the normalization for the background normalization (WZ, Z$\gamma $, Top, DY$\tau \tau $). |
png |
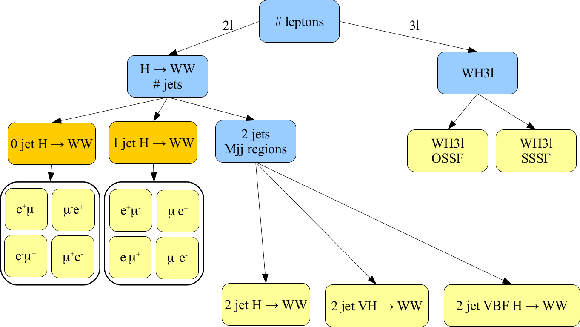
Figure 1-a:
The flowchart of the analysis is reported here, without background control regions. The green boxes correspond to a separate cut based analyses used to control background normalization. The yellow boxes correspond to signal phase spaces for the analysis, and for each of them a template shape approach is followed. The orange boxes represent interesting combinations of categories, while blue boxes are the selections criteria. The WW normalization is part of the nominal signal phase space (yellow boxes), since it's difficult to define a complete orthogonal set of selections to disentangle from the Higgs. The normalization of WW is done independently in 0 jet, 1 jet, 2 jet, 2 jet close to W/Z mass, and high di-jet invariant mass. |
png |
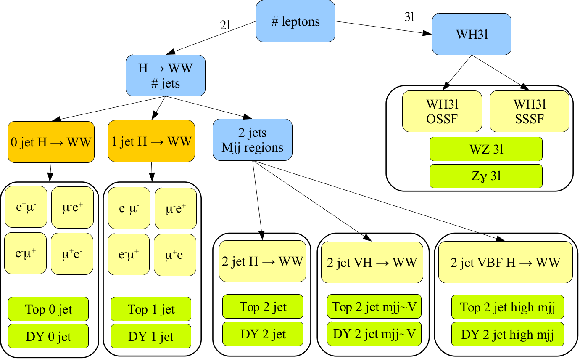
Figure 1-b:
The flowchart of the analysis is reported here, with the background control regions. The green boxes correspond to a separate cut based analyses used to control background normalization. The yellow boxes correspond to signal phase spaces for the analysis, and for each of them a template shape approach is followed. The orange boxes represent interesting combinations of categories, while blue boxes are the selections criteria. The WW normalization is part of the nominal signal phase space (yellow boxes), since it's difficult to define a complete orthogonal set of selections to disentangle from the Higgs. The normalization of WW is done independently in 0 jet, 1 jet, 2 jet, 2 jet close to W/Z mass, and high di-jet invariant mass. Every green box corresponds to a phase space used to regulate the normalization for the background normalization (WZ, Z$\gamma $, Top, DY$\tau \tau $). |
png pdf |
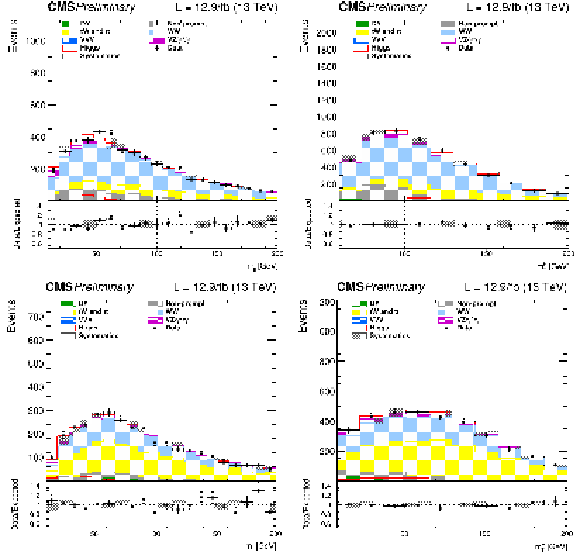
Figure 2:
Distributions of ${m_{\ell \ell }}$ (left) and ${m_\mathrm {T}^\mathrm {H}}$ (right) for events with 0 jet (upper row) and 1 jet (lower row) for the main backgrounds (stacked histograms), and for the expected SM Higgs boson signal with $m_H = $ 125 GeV (superimposed and stacked red histogram) after all selection criteria. The last bin of the histograms includes overflows. Scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
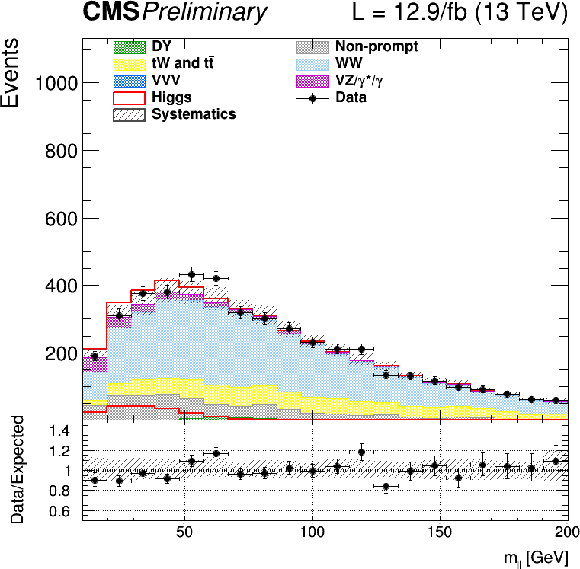
Figure 2-a:
Distributions of ${m_{\ell \ell }}$ for events with 0 jet for the main backgrounds (stacked histograms), and for the expected SM Higgs boson signal with $m_H = $ 125 GeV (superimposed and stacked red histogram) after all selection criteria. The last bin of the histogram includes overflows. Scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
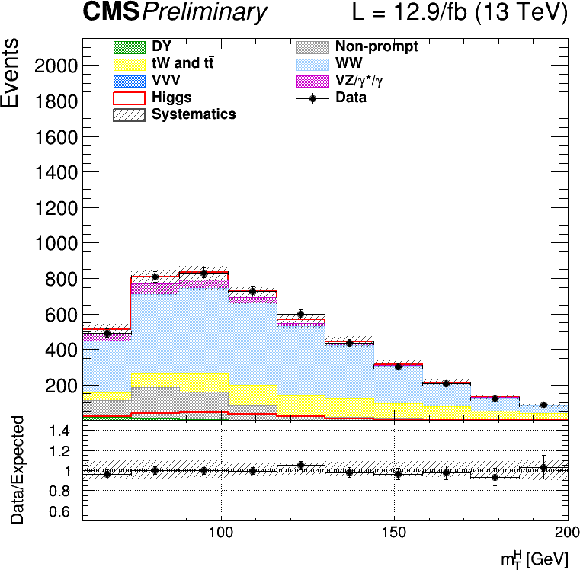
Figure 2-b:
Distributions of ${m_\mathrm {T}^\mathrm {H}}$ for events with 0 jet for the main backgrounds (stacked histograms), and for the expected SM Higgs boson signal with $m_H = $ 125 GeV (superimposed and stacked red histogram) after all selection criteria. The last bin of the histogram includes overflows. Scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
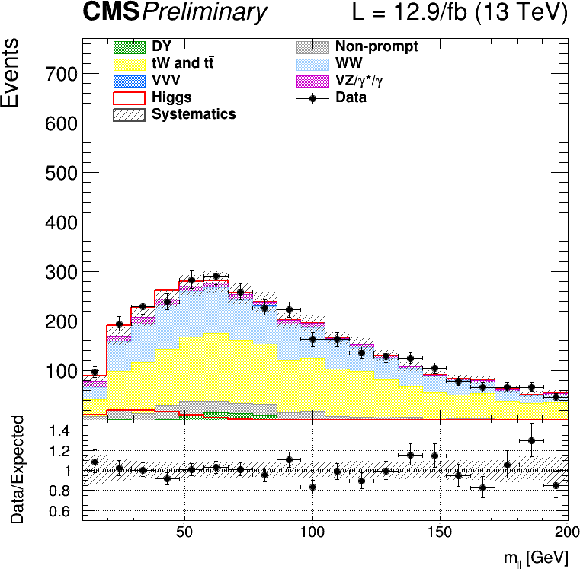
Figure 2-c:
Distributions of ${m_{\ell \ell }}$ for events with 1 jet for the main backgrounds (stacked histograms), and for the expected SM Higgs boson signal with $m_H = $ 125 GeV (superimposed and stacked red histogram) after all selection criteria. The last bin of the histogram includes overflows. Scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
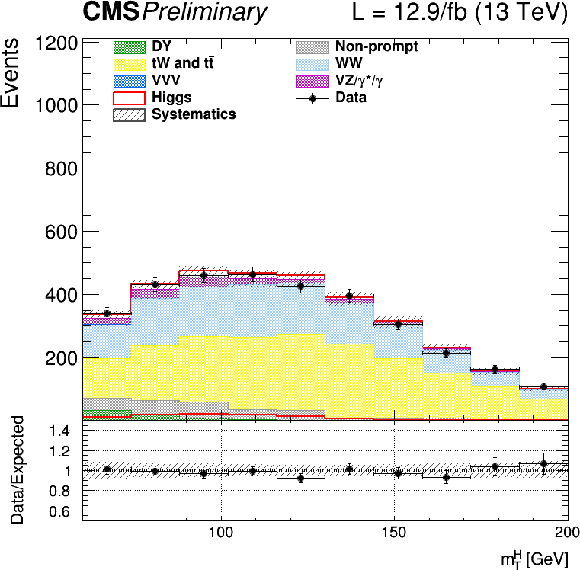
Figure 2-d:
Distributions of ${m_\mathrm {T}^\mathrm {H}}$ for events with 1 jet for the main backgrounds (stacked histograms), and for the expected SM Higgs boson signal with $m_H = $ 125 GeV (superimposed and stacked red histogram) after all selection criteria. The last bin of the histogram includes overflows. Scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
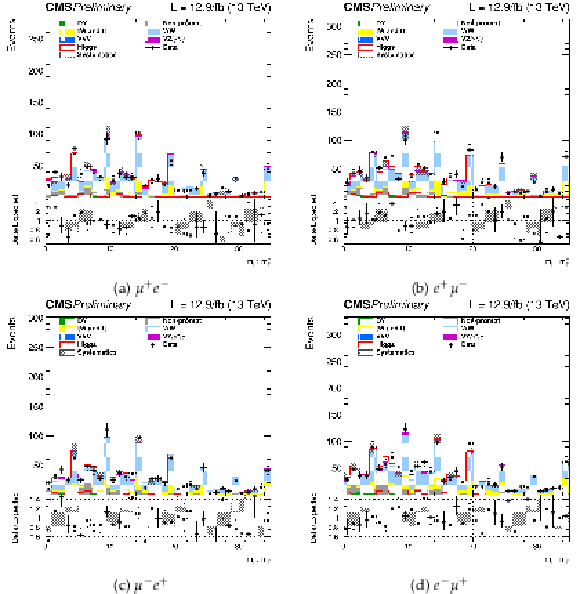
png pdf |
Figure 3:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 0 jet bin, $\mu $e and e$\mu $, +/- and -/+ categories. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
Figure 3-a:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 0 jet bin, $\mu^+ \mathrm{e}^- $ category. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
Figure 3-b:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 0 jet bin, $ \mathrm{e}^+ \mu^-$ category. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
Figure 3-c:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 0 jet bin, $\mu^- \mathrm{e}^+ $ category. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |

png |
Figure 3-d:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 0 jet bin, $ \mathrm{e}^- \mu^+$ category. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
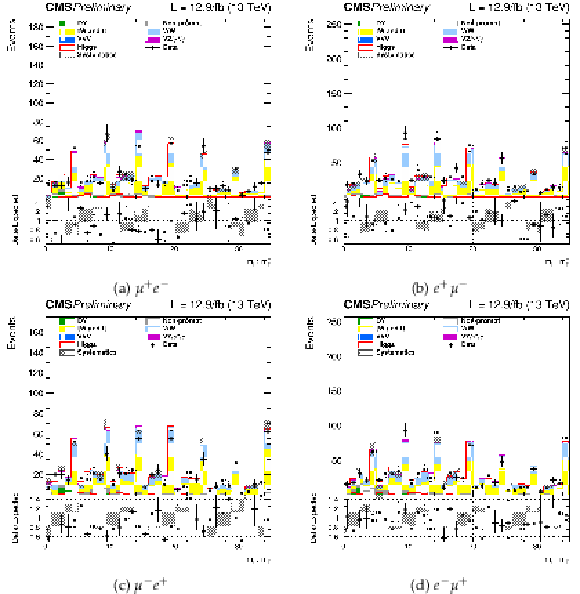
png pdf |
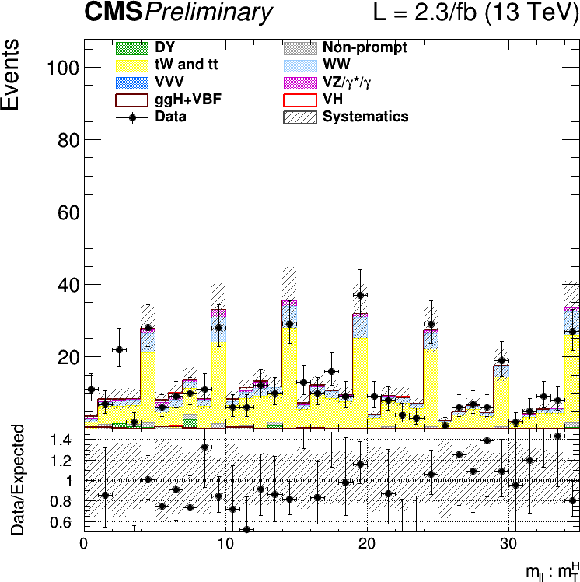
Figure 4:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 1 jet bin, $\mu $e and e$\mu $, +/- and -/+ categories. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
Figure 4-a:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 1 jet bin, $\mu^+ \mathrm{e}^- $ category. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |

png |
Figure 4-b:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 1 jet bin, $ \mathrm{e}^+ \mu^-$ category. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |

png |
Figure 4-c:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 1 jet bin, $\mu^- \mathrm{e}^+ $ category. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |

png |
Figure 4-d:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates in the 1 jet bin, $ \mathrm{e}^- \mu^+$ category. The distributions are unrolled to one dimensional histograms such that that identical values of ${m_\mathrm {T}^\mathrm {H}}$ are in adjacent bins. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png pdf |
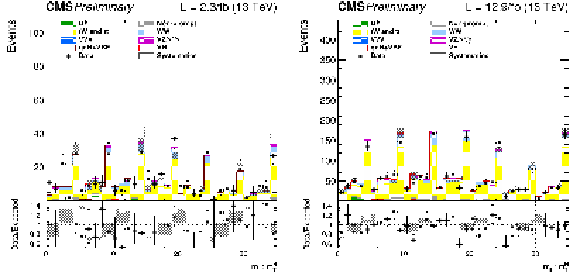
Figure 5:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates for the 2 jets category with 2015 (left) and 2016 (right) data. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
png |
Figure 5-a:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates for the 2 jets category with 2015 data. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |
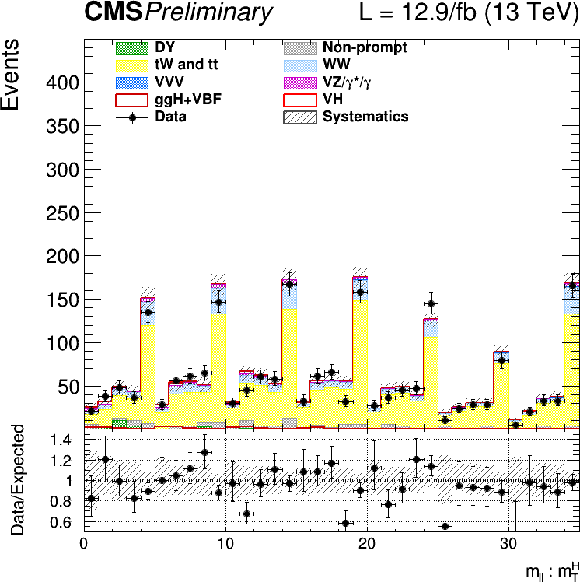
png |
Figure 5-b:
Bi-dimensional distributions of the ${m_{\ell \ell }}$ and ${m_\mathrm {T}^\mathrm {H}}$ templates for the 2 jets category with 2016 data. The background and signal contributions are normalized according to their pre-fit values except that scale factors estimated from data are applied to the jet induced, the Drell-Yan, and top backgrounds. |

png pdf |
Figure 6:
Distribution of ${m_{\ell \ell }}$ for the VBF analysis with 2015 (left) and 2016 (right) data. |
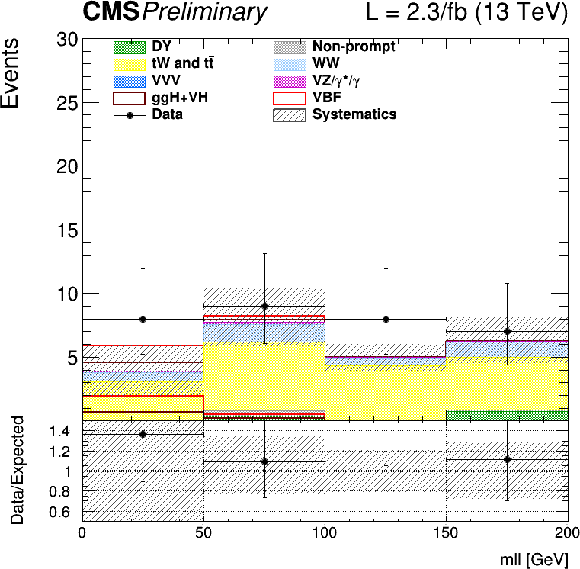
png |
Figure 6-a:
Distribution of ${m_{\ell \ell }}$ for the VBF analysis with 2015 data. |

png |
Figure 6-b:
Distribution of ${m_{\ell \ell }}$ for the VBF analysis with 2016 data. |

png pdf |
Figure 7:
Distribution of ${m_{\ell \ell }}$ for the VH 2-jets analysis with 2015 (left) and 2016 (right) data. |
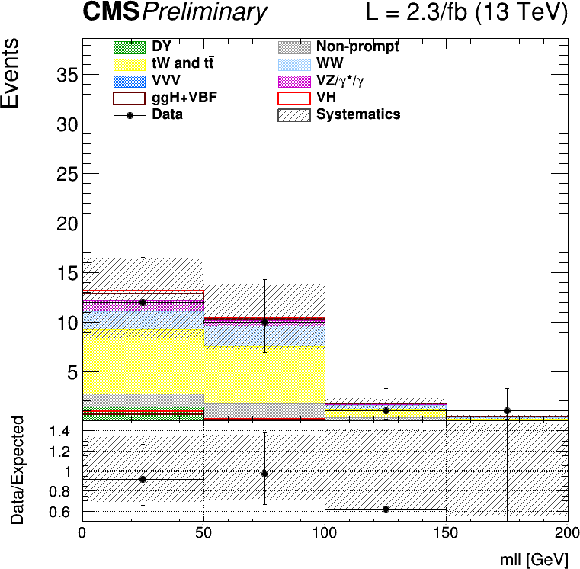
png |
Figure 7-a:
Distribution of ${m_{\ell \ell }}$ for the VH 2-jets analysis with 2015 data. |
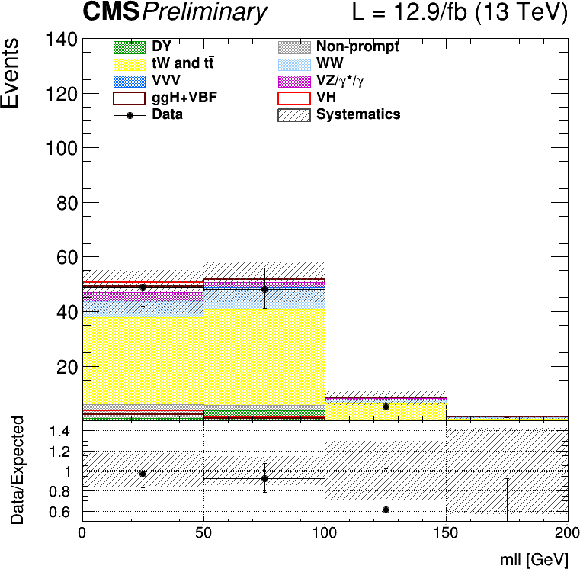
png |
Figure 7-b:
Distribution of ${m_{\ell \ell }}$ for the VH 2-jets analysis with 2016 data. |
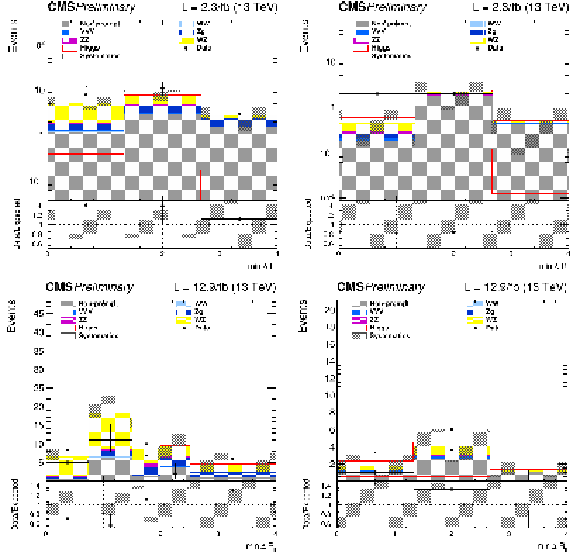
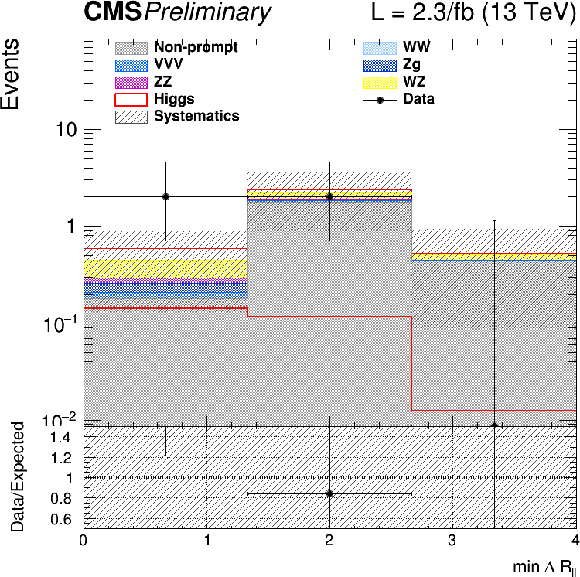
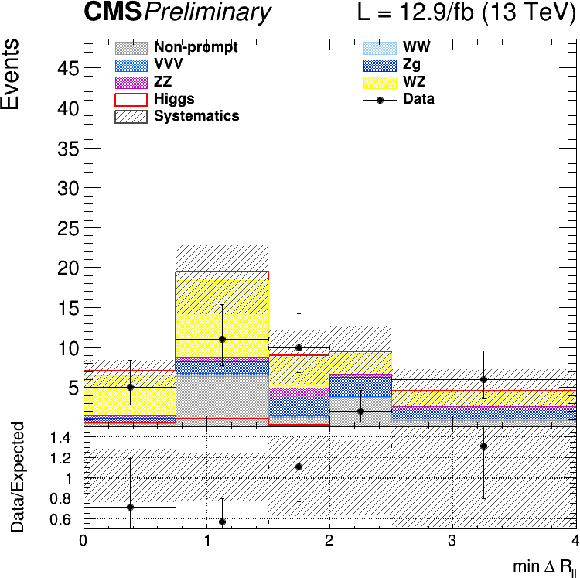
png pdf |
Figure 8:
$\Delta R$ template for OSSF (left) and SSSF (right) event categories for 2015 (upper row) and 2016 (lower row) data. |

png |
Figure 8-a:
$\Delta R$ template for OSSF event categories for 2015 data. |
png |
Figure 8-b:
$\Delta R$ template for SSSF event categories for 2015 data. |
png |
Figure 8-c:
$\Delta R$ template for OSSF event categories for 2016 data. |

png |
Figure 8-d:
$\Delta R$ template for SSSF event categories for 2016 data. |

png pdf |
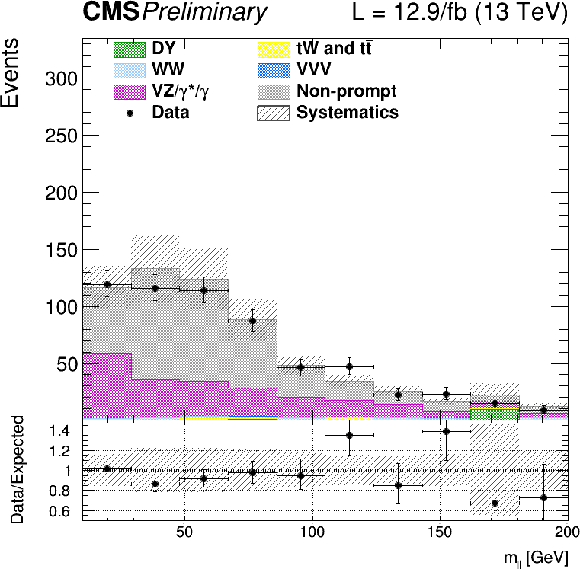
Figure 9:
Distributions of ${m_{\ell \ell }}$ for events with 0 jet, 1 jet, and 2 jets in the same-charge di-lepton control region. The last bin of the histograms includes overflows. |
png |
Figure 9-a:
Distribution of ${m_{\ell \ell }}$ for events with 0 jet in the same-charge di-lepton control region. The last bin of the histogram includes overflows. |
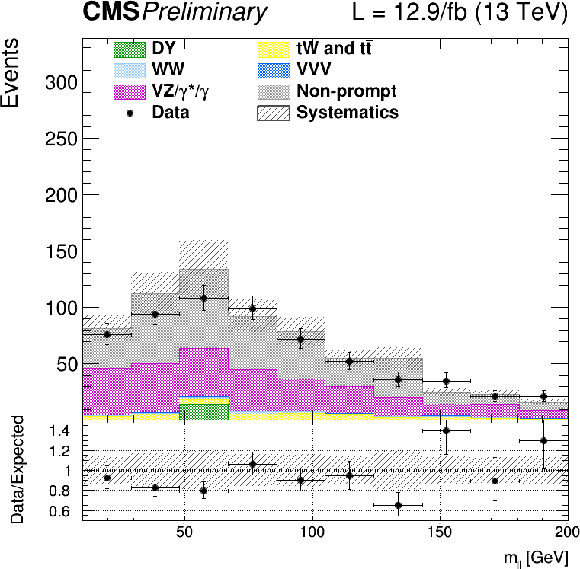
png |
Figure 9-b:
Distribution of ${m_{\ell \ell }}$ for events with 1 jet in the same-charge di-lepton control region. The last bin of the histogram includes overflows. |

png |
Figure 9-c:
Distribution of ${m_{\ell \ell }}$ for events with 2 jets in the same-charge di-lepton control region. The last bin of the histogram includes overflows. |
png pdf |
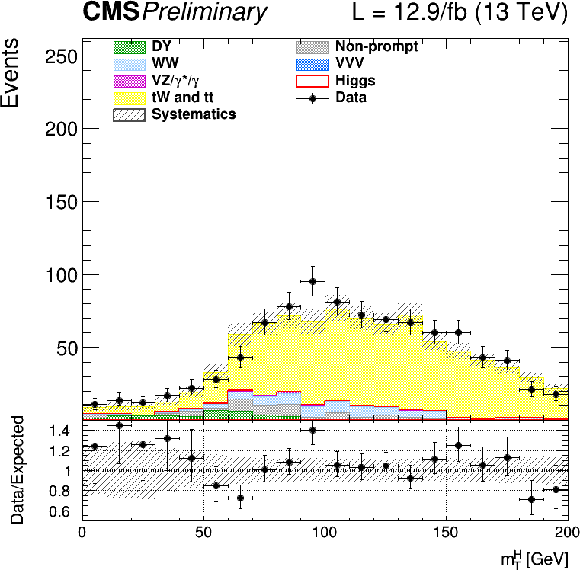
Figure 10:
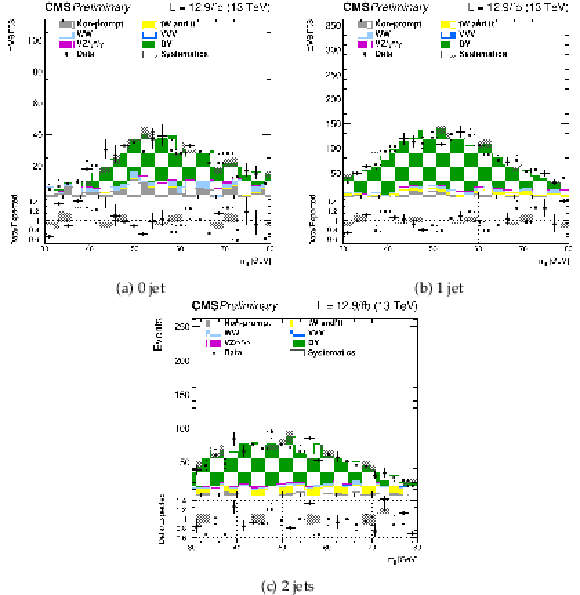
Distributions of ${m_{\ell \ell }}$ (left) and ${m_\mathrm {T}^\mathrm {H}}$ (right) for events with 0 jet (top row), 1 jet (middle row), and 2 jets (lower row) in top enriched phase space. Scale factors estimated from data are applied (see text). |
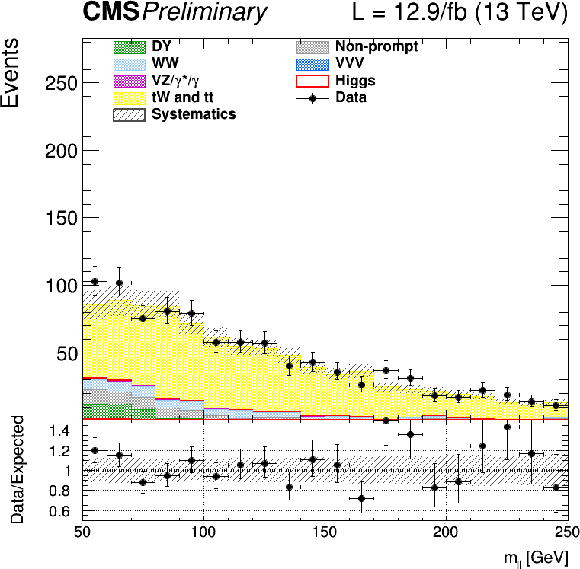
png |
Figure 10-a:
Distributions of ${m_{\ell \ell }}$ for events with 0 jet in top enriched phase space. Scale factors estimated from data are applied (see text). |
png |
Figure 10-b:
Distributions of ${m_\mathrm {T}^\mathrm {H}}$ for events with 0 jet in top enriched phase space. Scale factors estimated from data are applied (see text). |
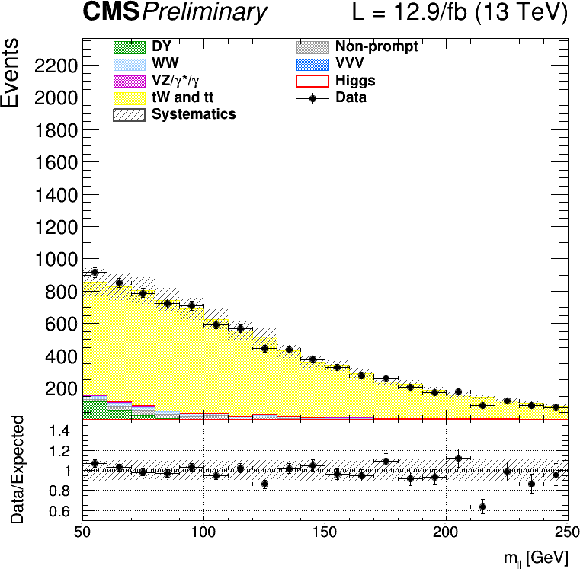
png |
Figure 10-c:
Distributions of ${m_{\ell \ell }}$ for events with 1 jet in top enriched phase space. Scale factors estimated from data are applied (see text). |
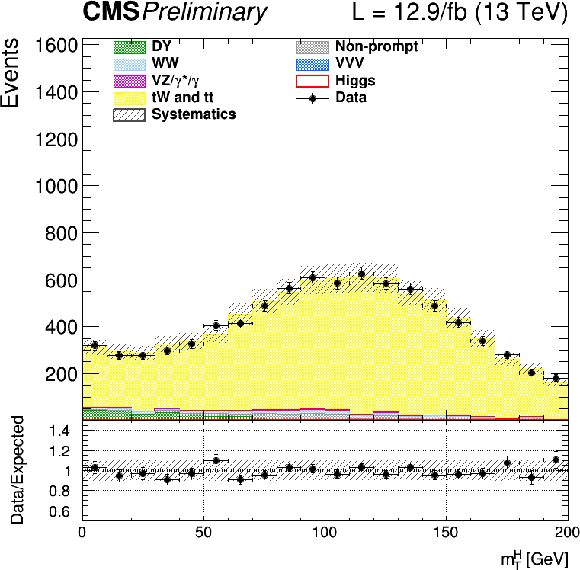
png |
Figure 10-d:
Distributions of ${m_\mathrm {T}^\mathrm {H}}$ for events with 1 jet in top enriched phase space. Scale factors estimated from data are applied (see text). |
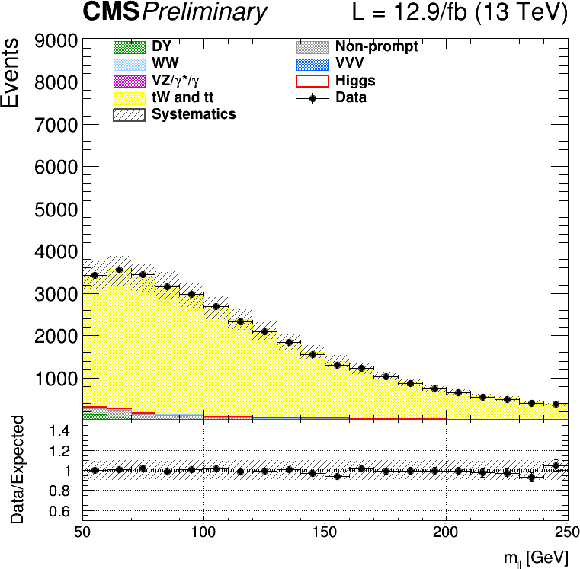
png |
Figure 10-e:
Distributions of ${m_{\ell \ell }}$ for events with 2 jets in top enriched phase space. Scale factors estimated from data are applied (see text). |
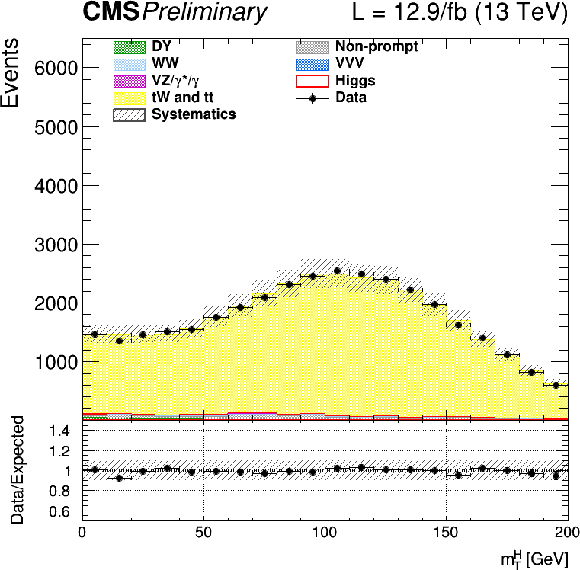
png |
Figure 10-f:
Distributions of ${m_\mathrm {T}^\mathrm {H}}$ for events with 2 jets in top enriched phase space. Scale factors estimated from data are applied (see text). |
png pdf |
Figure 11:
Distributions of ${m_{\ell \ell }}$ for events with 0 jet, 1 jet, and 2 jets in the DY$\rightarrow \tau \tau {m_\mathrm {T}^\mathrm {H}} <$ 60 GeV and 30 GeV $< {m_{\ell \ell }} <$ 80 GeV control region. Scale factors estimated from the normalization difference to the data are applied (see text). |
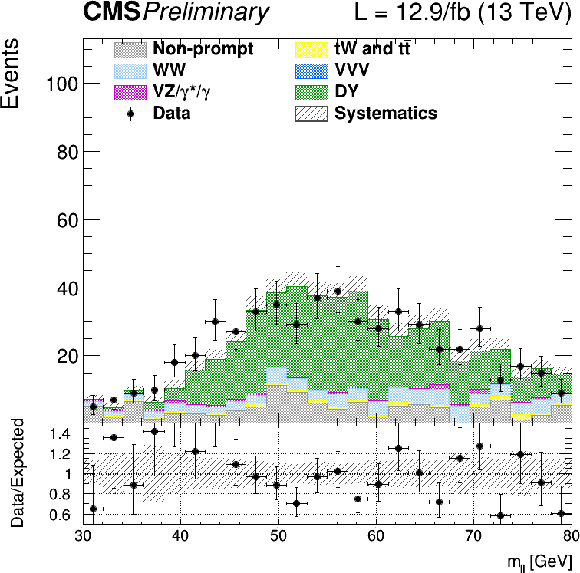
png |
Figure 11-a:
Distribution of ${m_{\ell \ell }}$ for events with 0 jet in the DY$\rightarrow \tau \tau {m_\mathrm {T}^\mathrm {H}} <$ 60 GeV and 30 GeV $< {m_{\ell \ell }} <$ 80 GeV control region. Scale factors estimated from the normalization difference to the data are applied (see text). |

png |
Figure 11-b:
Distribution of ${m_{\ell \ell }}$ for events with 1 jet in the DY$\rightarrow \tau \tau {m_\mathrm {T}^\mathrm {H}} <$ 60 GeV and 30 GeV $< {m_{\ell \ell }} <$ 80 GeV control region. Scale factors estimated from the normalization difference to the data are applied (see text). |

png |
Figure 11-c:
Distribution of ${m_{\ell \ell }}$ for events with 2 jets in the DY$\rightarrow \tau \tau {m_\mathrm {T}^\mathrm {H}} <$ 60 GeV and 30 GeV $< {m_{\ell \ell }} <$ 80 GeV control region. Scale factors estimated from the normalization difference to the data are applied (see text). |

png pdf |
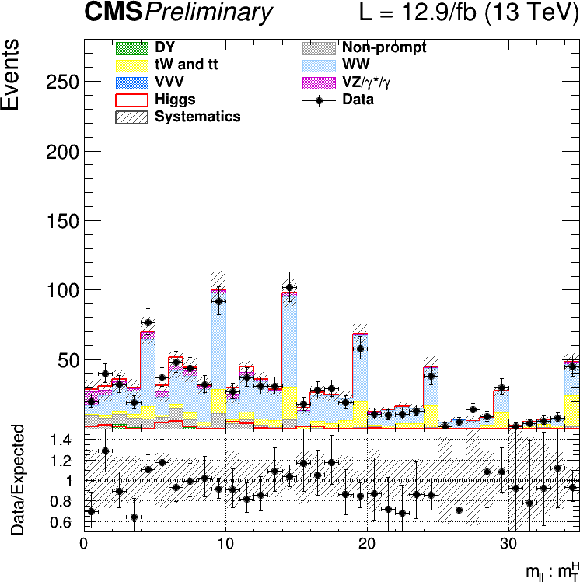
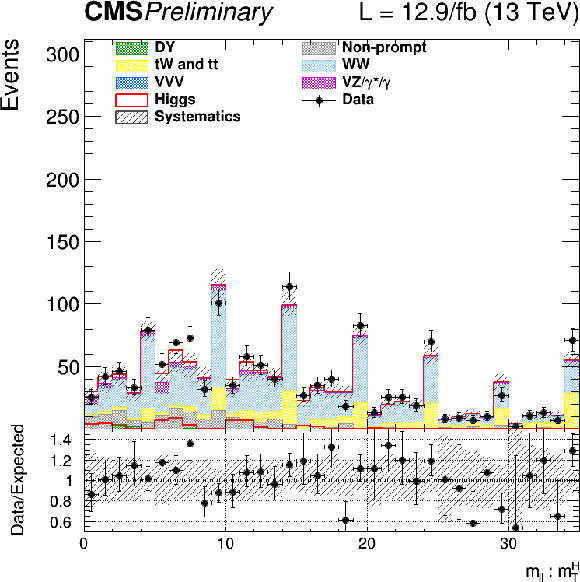
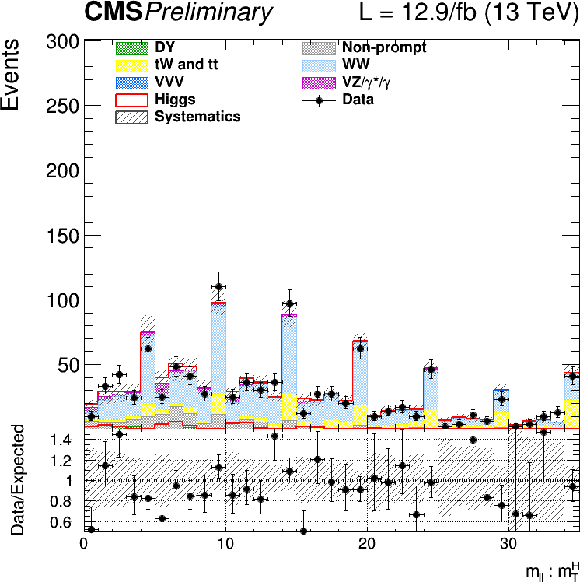
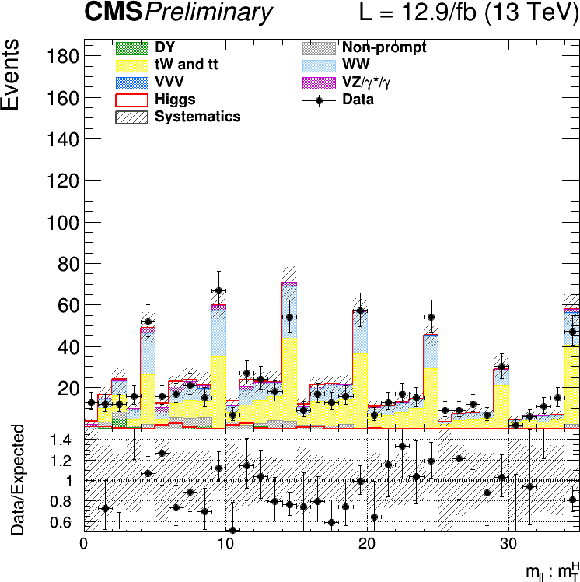
Figure 12:
The $ {m_{\ell \ell }} $ distribution for the 0, 1 and 2 jets categories weighted and combined. For each window in $ {m_\mathrm {T}^\mathrm {H}} $, and for each category and data taking period, a weight is calculated as the ratio of the expected signal to the sum of background events. The different $ {m_{\ell \ell }} $ distributions in windows in $ {m_\mathrm {T}^\mathrm {H}} $, and for each category, are then summed and normalized to the expected total signal yield. The weighted distribution is shown on the left, and the background subtracted distribution on the right: the red line is the expected signal distribution, while the black points represent the data subtracted distribution. The shaded grey area is the uncertainty on the expected background. |

png |
Figure 12-a:
The $ {m_{\ell \ell }} $ distribution for the 0, 1 and 2 jets categories weighted and combined. For each window in $ {m_\mathrm {T}^\mathrm {H}} $, and for each category and data taking period, a weight is calculated as the ratio of the expected signal to the sum of background events. The different $ {m_{\ell \ell }} $ distributions in windows in $ {m_\mathrm {T}^\mathrm {H}} $, and for each category, are then summed and normalized to the expected total signal yield. The weighted distribution is shown. The shaded grey area is the uncertainty on the expected background. |
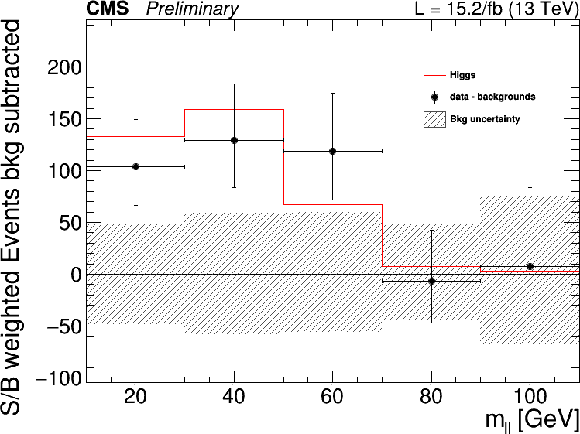
png |
Figure 12-b:
The $ {m_{\ell \ell }} $ distribution for the 0, 1 and 2 jets categories weighted and combined. For each window in $ {m_\mathrm {T}^\mathrm {H}} $, and for each category and data taking period, a weight is calculated as the ratio of the expected signal to the sum of background events. The different $ {m_{\ell \ell }} $ distributions in windows in $ {m_\mathrm {T}^\mathrm {H}} $, and for each category, are then summed and normalized to the expected total signal yield. The background subtracted distribution is shown: the red line is the expected signal distribution, while the black points represent the data subtracted distribution. The shaded grey area is the uncertainty on the expected background. |

png pdf |
Figure 13:
Likelihood scan on the signal strength for gluon fusion and VBF/VH, including one and two $\sigma $ contours. The red circle represents the minimum of the likelihood scan, while the black triangle is the [1,1] coordinate, corresponding to the SM prediction. |
| Tables | |
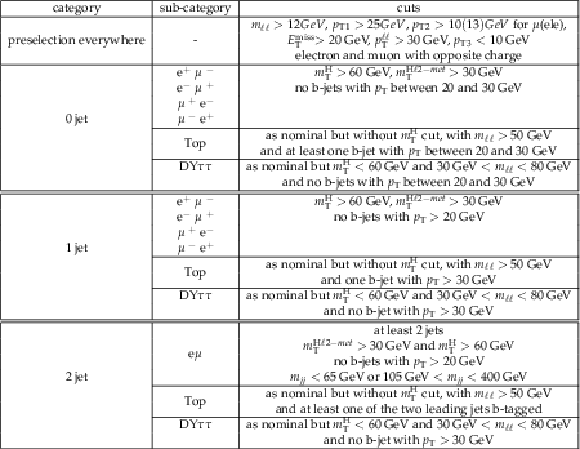
png pdf |
Table 1:
Analysis strategy and selections for the 0, 1, and 2 jet bins in the 2 leptons final state. |
png pdf |
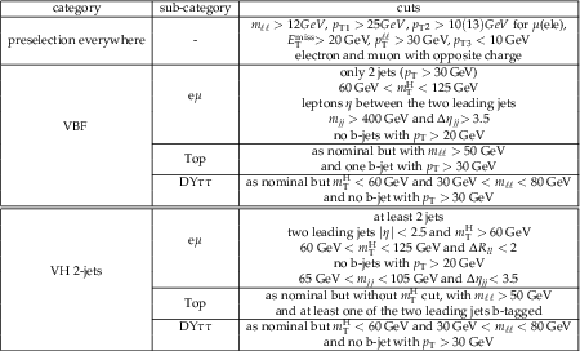
Table 2:
Analysis strategy and selections for VBF and VH, in the 2 jets category, in the 2 leptons final state. |

png pdf |
Table 3:
Analysis strategy and selections for WH 3-lep, in the 3 leptons final state. ${\text{min}(m_{\ell ^+\ell ^-})}$ is the minimum ${m_{\ell \ell }}$ between the opposite charge leptons, ${m_{\ell \ell \ell }}$ is the 3-lepton invariant mass. For the Z-tag/veto the ${m_{\ell \ell }}$ closer to Z mass is considered. |
png pdf |
Table 4:
Observed (and expected) significance and signal strength for the SM Higgs boson with a mass of 125 GeV , for the 0-jet, 1-jet, 2-jet, VBF, VH 2-jets, WH 3-lep categories. |
| Summary |
|
A measurement of the SM Higgs boson decaying to WW in pp collisions at $ \sqrt{s} = $ 13 TeV is performed by the CMS experiment using a data sample corresponding to an integrated luminosity of 2.3 fb$^{-1}$ from 2015 collisions and 12.9 fb$^{-1}$ from 2016 ones. The W$^+$W$^-$ candidates are selected in events with an oppositely charged e$\mu$ pair and large missing transverse momentum. The analysis has specific categories for gluon fusion production, which is the dominant production mode, vector boson fusion, and vector boson associated production with up to two jets, and two or three leptons in the final state. When all the channels are combined together, including the previous result using 2015 data [16], the observed (expected) significance is 4.3$\sigma$ (4.1$\sigma$), corresponding to an observed cross section times branching ratio of 1.05 $\pm$ 0.26 times the standard model prediction. |
| References | ||||
| 1 | F. Englert and R. Brout | Broken symmetry and the mass of gauge vector mesons | PRL 13 (1964) 321 | |
| 2 | P. W. Higgs | Broken symmetries, massless particles and gauge fields | PL12 (1964) 132 | |
| 3 | P. W. Higgs | Broken symmetries and the masses of gauge bosons | PRL 13 (1964) 508 | |
| 4 | G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble | Global conservation laws and massless particles | PRL 13 (1964) 585 | |
| 5 | P. W. Higgs | Spontaneous symmetry breakdown without massless bosons | PR145 (1966) 1156 | |
| 6 | T. W. B. Kibble | Symmetry breaking in non-Abelian gauge theories | PR155 (1967) 1554 | |
| 7 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 8 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 9 | ATLAS Collaboration | Measurements of the Higgs boson production and decay rates and coupling strengths using pp collision data at $ \sqrt{s}=$ 7 and 8 TeV in the ATLAS experiment | EPJC76 (2016), no. 1, 6 | 1507.04548 |
| 10 | ATLAS Collaboration | Evidence for the spin-0 nature of the Higgs boson using ATLAS data | PLB 726 (2013) 120--144 | 1307.1432 |
| 11 | CMS Collaboration | Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV | EPJC 75 (2015), no. 5, 212 | CMS-HIG-14-009 1412.8662 |
| 12 | CMS Collaboration | Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV | PRD 92 (2015), no. 1, 012004 | CMS-HIG-14-018 1411.3441 |
| 13 | ATLAS and C. Collaborations | Combined Measurement of the Higgs Boson Mass in $ pp $ Collisions at $ \sqrt{s}=$ 7 and 8 TeV with the ATLAS and CMS Experiments | PRL 114 (2015) 191803 | 1503.07589 |
| 14 | ATLAS and C. Collaborations | Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $ \sqrt{s} = $ 7 and 8 TeV | Technical Report CMS-PAS-HIG-15-002, CERN, Geneva | |
| 15 | CMS Collaboration | Measurement of Higgs boson production and properties in the WW decay channel with leptonic final states | JHEP 01 (2014) 096 | CMS-HIG-13-023 1312.1129 |
| 16 | CMS Collaboration | First results on Higgs to WW at $ \sqrt{s}= $ 13 TeV | CMS-PAS-HIG-15-003 | CMS-PAS-HIG-15-003 |
| 17 | P. Nason | A New method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 18 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 19 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 20 | G. Luisoni, P. Nason, C. Oleari, and F. Tramontano | $ HW^{\pm} $/HZ + 0 and 1 jet at NLO with the POWHEG BOX interfaced to GoSam and their merging within MiNLO | JHEP 10 (2013) 083 | 1306.2542 |
| 21 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO Higgs boson production via gluon fusion matched with shower in POWHEG | JHEP 04 (2009) 002 | 0812.0578 |
| 22 | P. Nason and C. Oleari | NLO Higgs boson production via vector-boson fusion matched with shower in POWHEG | JHEP 02 (2010) 037 | 0911.5299 |
| 23 | S. Bolognesi, Y. Gao, A. Gritsan et al. | JHU Generator | link | |
| 24 | T. Sjostrand, S. Mrenna, and P. Z. Skands | A Brief Introduction to PYTHIA 8.1 | CPC 178 (2008) 852--867 | 0710.3820 |
| 25 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector | 1610.07922 | |
| 26 | LHC Higgs Cross Section Working Group | Higgs Cross Sections | link | |
| 27 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 3. Higgs Properties | 1307.1347 | |
| 28 | T. Melia, P. Nason, R. Rontsch, and G. Zanderighi | W+W-, WZ and ZZ production in the POWHEG BOX | JHEP 11 (2011) 078 | 1107.5051 |
| 29 | J. M. Campbell, R. K. Ellis, and C. Williams | Bounding the Higgs width at the LHC: Complementary results from $ H \to WW $ | PRD 89 (2014), no. 5, 053011 | 1312.1628 |
| 30 | P. Meade, H. Ramani, and M. Zeng | Transverse momentum resummation effects in $ W^+W^- $ measurements | PRD 90 (2014), no. 11, 114006 | 1407.4481 |
| 31 | P. Jaiswal and T. Okui | Explanation of the $ WW $ excess at the LHC by jet-veto resummation | PRD 90 (2014), no. 7, 073009 | 1407.4537 |
| 32 | F. Caola, K. Melnikov, R. Ršntsch, and L. Tancredi | QCD corrections to $ W^+W^- $ production through gluon fusion | PLB 754 (2016) 275--280 | 1511.08617 |
| 33 | LHC Top Working Group Collaboration | Single Top | link | |
| 34 | LHC Top Working Group Collaboration | Top Cross Section | link | |
| 35 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 36 | NNPDF Collaboration | Parton distributions with QED corrections | Nucl. Phys. B 877 (2013) 290--320 | 1308.0598 |
| 37 | NNPDF Collaboration | Unbiased global determination of parton distributions and their uncertainties at NNLO and at LO | Nucl. Phys. B 855 (2012) 153--221 | 1107.2652 |
| 38 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016), no. 3, 155 | CMS-GEN-14-001 1512.00815 |
| 39 | P. Richardson and A. Wilcock | Monte Carlo Simulation of Hard Radiation in Decays in Beyond the Standard Model Physics in Herwig++ | EPJC 74 (2014) 2713 | 1303.4563 |
| 40 | J. Bellm et al. | Herwig++ 2.7 Release Note | 1310.6877 | |
| 41 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 42 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | Submitted to JINST | CMS-PRF-14-001 1706.04965 |
| 43 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119--126 | 0707.1378 |
| 44 | M. Cacciari, G. P. Salam, and G. Soyez | The Anti-k(t) jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 45 | CMS Collaboration | Determination of Jet Energy Calibration and Transverse Momentum Resolution in CMS | JINST 6 (2011) P11002 | CMS-JME-10-011 1107.4277 |
| 46 | CMS Collaboration | Measurements of inclusive and differential $ \mathrm{Z} $ boson production cross sections in $ \mathrm{p}\mathrm{p} $ collisions at $ \sqrt{s}= $ 13 TeV | CMS-PAS-SMP-15-011 | CMS-PAS-SMP-15-011 |
| 47 | ATLAS and C. Collaborations | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS Note ATL-PHYS-PUB 2011-11, CMS-NOTE 2011-005, CERN | |
| 48 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 49 | R. Boughezal et al. | Combining Resummed Higgs Predictions Across Jet Bins | PRD 89 (2014), no. 7, 074044 | 1312.4535 |
| 50 | G. Passarino | Higgs CAT | EPJC 74 (2014) 2866 | 1312.2397 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|