

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-TOP-18-006 | ||
| Measurement of the top quark polarization and tˉt spin correlations in dilepton final states at √s= 13 TeV | ||
| CMS Collaboration | ||
| December 2018 | ||
| Abstract: Measurements of the top quark polarization and top quark pair (tˉt) spin correlations are presented using events containing two leptons produced in proton-proton collisions at a center-of-mass energy of √s= 13 TeV. The data were recorded by the CMS experiment at the CERN LHC in 2016 and correspond to an integrated luminosity of 35.9 fb−1. A set of parton-level normalized differential cross sections, sensitive to each of the independent coefficients of the spin-dependent parts of the tˉt production density matrix, is measured for the first time at √s= 13 TeV. The measured distributions and extracted coefficients are compared with standard model predictions from Monte Carlo simulations with next-to-leading-order (NLO) accuracy in quantum chromodynamics (QCD) and from NLO QCD calculations including weak and mixed QCD-weak corrections. All measurements are found to be consistent with the expectations of the standard model, and are used in a simultaneous fit to constrain the anomalous chromomagnetic dipole moment of the top quark to −0.07<CtG/Λ2<0.16 TeV−2 at 95% confidence level. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, PRD 100 (2019) 072002. The superseded preliminary plots can be found here. |
||
| Figures | |

png pdf |
Figure 1:
Reconstructed distributions of cosθi for top quarks (antiquarks) in the first and third (second and fourth) rows. From left to right the top quark polarization is measured with respect to the ˆk, ˆr, and ˆn (upper rows), and ^k∗ and ^r∗ reference axes (lower rows). The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |

png pdf |
Figure 1-a:
Reconstructed distribution of cosθi for top quarks. The top quark polarization is measured with respect to the ˆk reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |

png pdf |
Figure 1-b:
Reconstructed distribution of cosθi for top quarks. The top quark polarization is measured with respect to the ˆr reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |

png pdf |
Figure 1-c:
Reconstructed distribution of cosθi for top quarks. The top quark polarization is measured with respect to the ˆn reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |

png pdf |
Figure 1-d:
Reconstructed distribution of cosθi for top antiquarks. The top quark polarization is measured with respect to the ˆk reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |

png pdf |
Figure 1-e:
Reconstructed distribution of cosθi for top antiquarks. The top quark polarization is measured with respect to the ˆr reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |

png pdf |
Figure 1-f:
Reconstructed distribution of cosθi for top antiquarks. The top quark polarization is measured with respect to the ˆn reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |

png pdf |
Figure 1-g:
Reconstructed distribution of cosθi for top quarks. The top quark polarization is measured with respect to the ^k∗ reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |

png pdf |
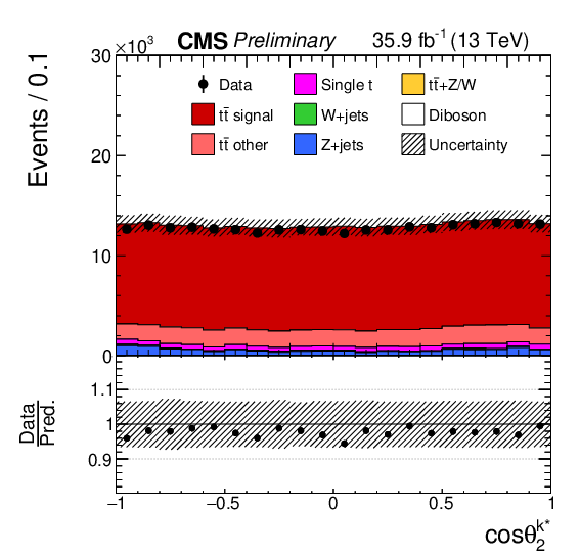
Figure 1-h:
Reconstructed distribution of cosθi for top quarks. The top quark polarization is measured with respect to the ^r∗ reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |
png pdf |
Figure 1-i:
Reconstructed distribution of cosθi for top antiquarks. The top quark polarization is measured with respect to the ^k∗ reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |

png pdf |
Figure 1-j:
Reconstructed distribution of cosθi for top antiquarks. The top quark polarization is measured with respect to the ^r∗ reference axis. The data (points) are compared to the simulated predictions (histograms). The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panel. |
png pdf |
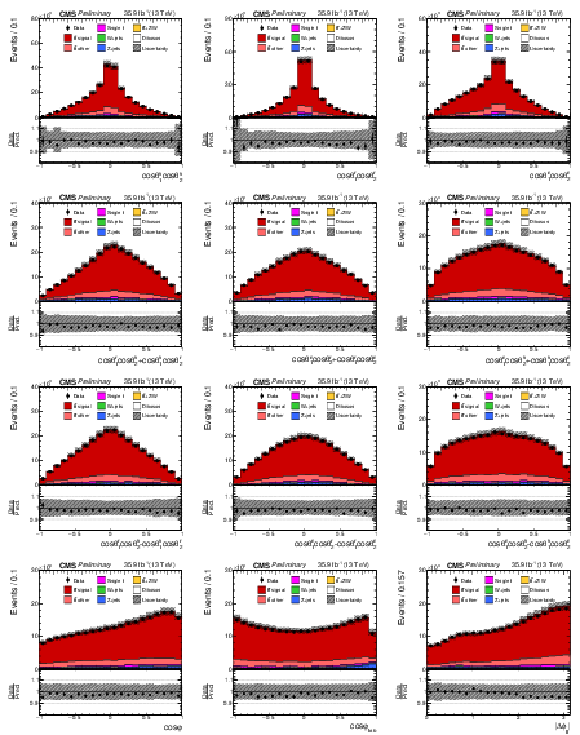
Figure 2:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |

png pdf |
Figure 2-a:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |
png pdf |
Figure 2-b:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |

png pdf |
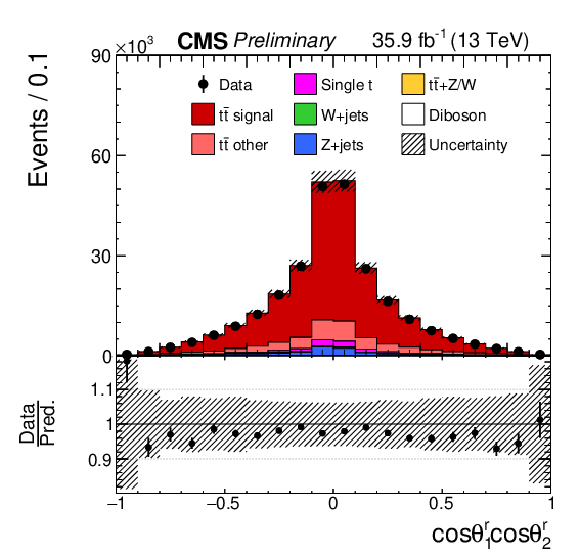
Figure 2-c:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |
png pdf |
Figure 2-d:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |
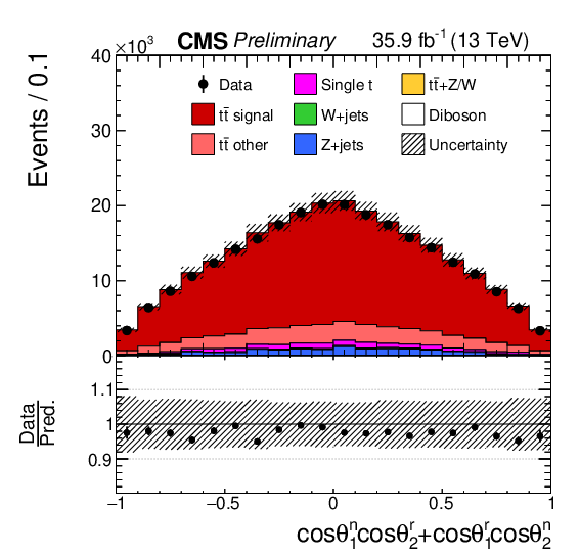
png pdf |
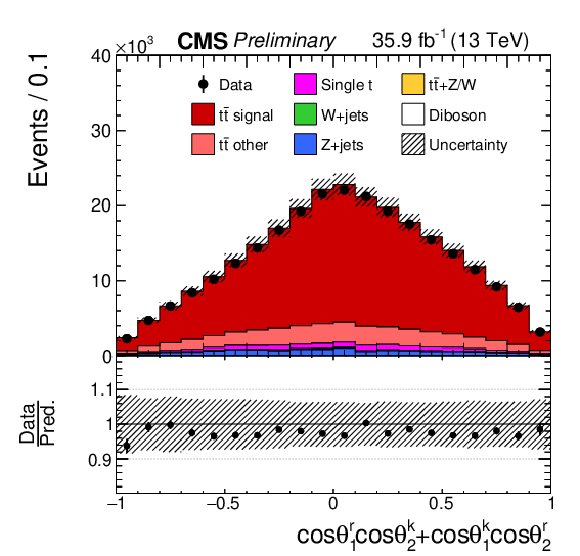
Figure 2-e:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |

png pdf |
Figure 2-f:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |
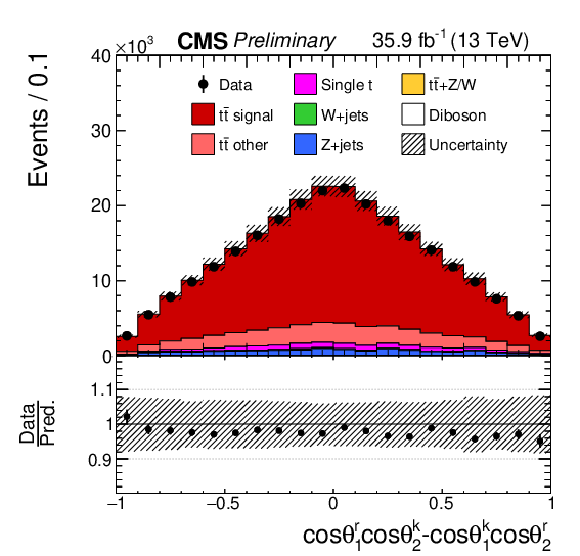
png pdf |
Figure 2-g:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |

png pdf |
Figure 2-h:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |

png pdf |
Figure 2-i:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |

png pdf |
Figure 2-j:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |

png pdf |
Figure 2-k:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |
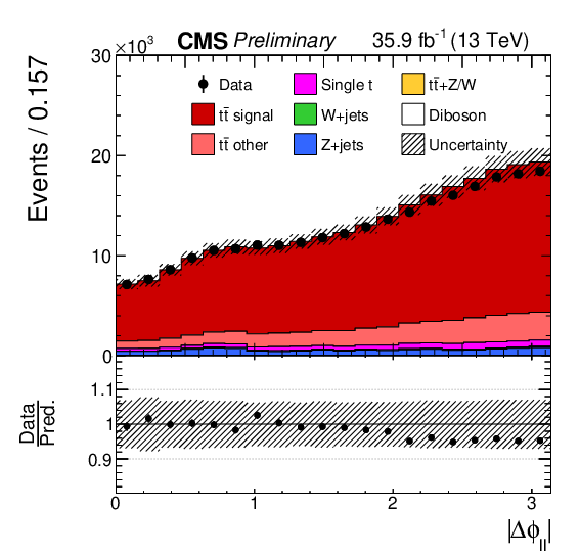
png pdf |
Figure 2-l:
Reconstructed distributions for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The vertical bars on the data points represent statistical uncertainties, and the estimated systematic uncertainties in the simulated histograms (considered in Section 6) are indicated by hatched bands. The ratio of the prediction to the data is shown in the lower panels. |
png pdf |
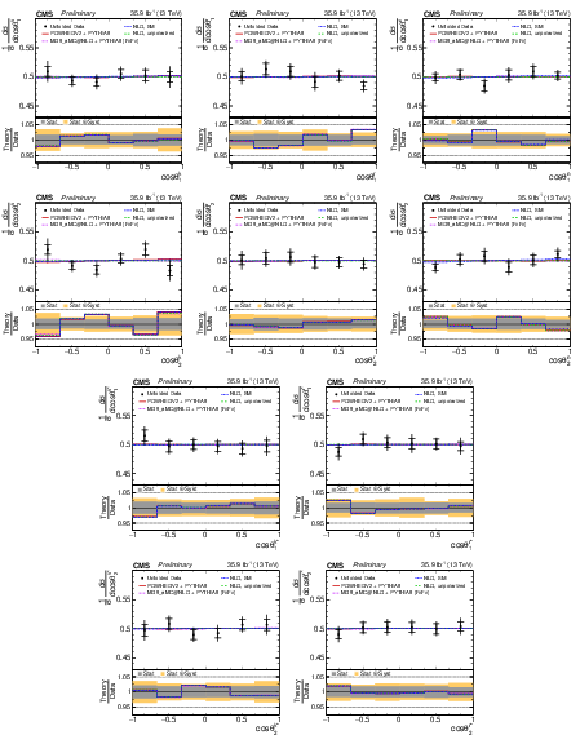
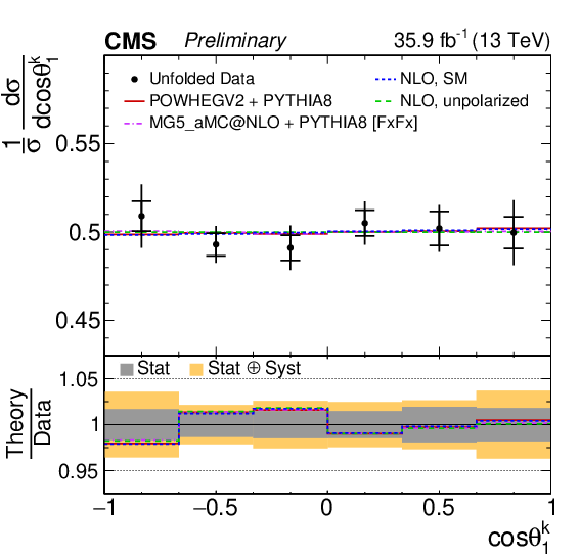
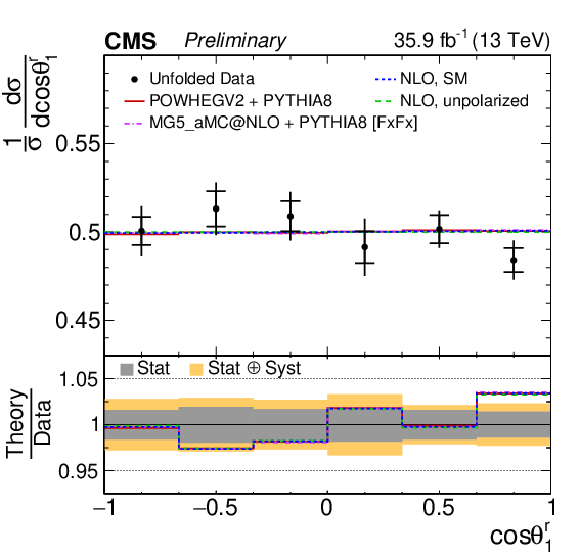
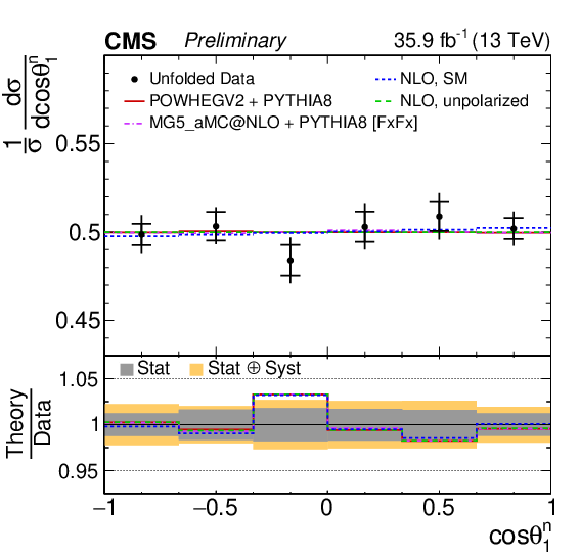
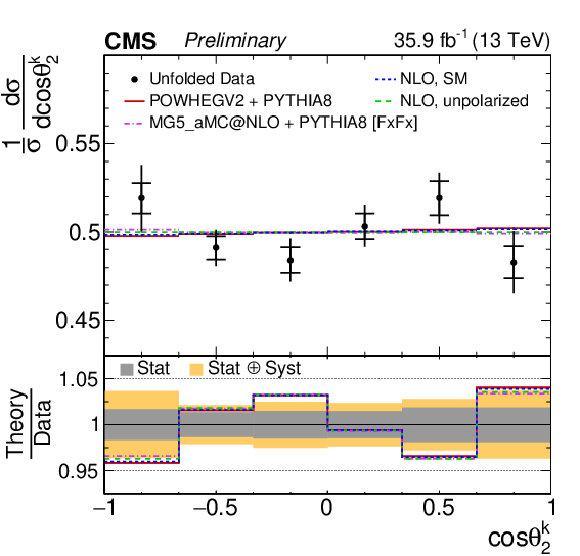
Figure 3:
Unfolded normalized differential cross sections with respect to cosθi for top quarks (antiquarks) in the first and third (second and fourth) rows, corresponding to the polarization coefficients Bi1 (Bi2). From left to right the top quark polarization is measured with respect to the ˆk, ˆr, and ˆn (upper rows), and ^k∗ and ^r∗ reference axes (lower rows). The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |
png pdf |
Figure 3-a:
Unfolded normalized differential cross sections with respect to cosθi for top quarks, corresponding to the polarization coefficients Bi1 (Bi2). The top quark polarization is measured with respect to the ˆk reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |
png pdf |
Figure 3-b:
Unfolded normalized differential cross sections with respect to cosθi for top quarks, corresponding to the polarization coefficients Bi1 (Bi2). The top quark polarization is measured with respect to the ˆk reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |
png pdf |
Figure 3-c:
Unfolded normalized differential cross sections with respect to cosθi for top quarks, corresponding to the polarization coefficients Bi1 (Bi2). The top quark polarization is measured with respect to the ˆn reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |
png pdf |
Figure 3-d:
Unfolded normalized differential cross sections with respect to cosθi for top antiquarks, corresponding to the polarization coefficients Bi1 (Bi2). The top antiquark polarization is measured with respect to the ˆk reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |

png pdf |
Figure 3-e:
Unfolded normalized differential cross sections with respect to cosθi for top antiquarks, corresponding to the polarization coefficients Bi1 (Bi2). The top antiquark polarization is measured with respect to the ˆr reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |

png pdf |
Figure 3-f:
Unfolded normalized differential cross sections with respect to cosθi for top antiquarks, corresponding to the polarization coefficients Bi1 (Bi2). The top antiquark polarization is measured with respect to the ˆn reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |
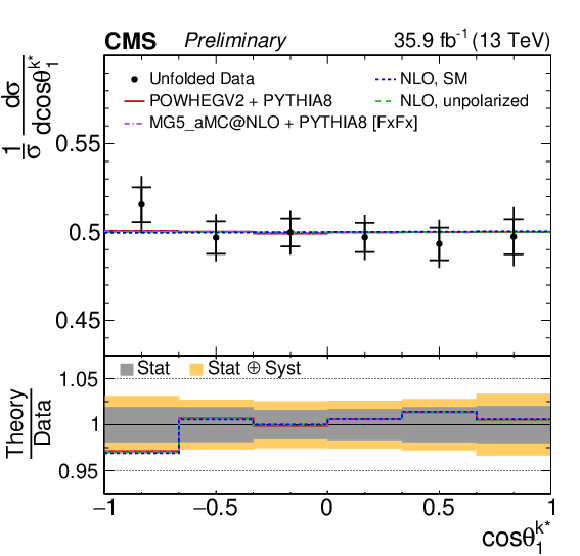
png pdf |
Figure 3-g:
Unfolded normalized differential cross sections with respect to cosθi for top quarks, corresponding to the polarization coefficients Bi1 (Bi2). The top quark polarization is measured with respect to the ^k∗ reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |
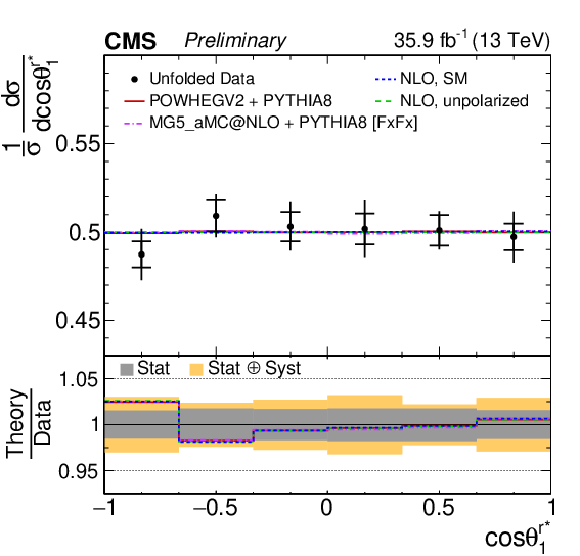
png pdf |
Figure 3-h:
Unfolded normalized differential cross sections with respect to cosθi for top quarks, corresponding to the polarization coefficients Bi1 (Bi2). The top quark polarization is measured with respect to the ^r∗ reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |

png pdf |
Figure 3-i:
Unfolded normalized differential cross sections with respect to cosθi for top antiquarks, corresponding to the polarization coefficients Bi1 (Bi2). The top antiquark polarization is measured with respect to the ^k∗ reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |

png pdf |
Figure 3-j:
Unfolded normalized differential cross sections with respect to cosθi for top antiquarks, corresponding to the polarization coefficients Bi1 (Bi2). The top antiquark polarization is measured with respect to the ^r∗ reference axis. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panel. |

png pdf |
Figure 4:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-a:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |
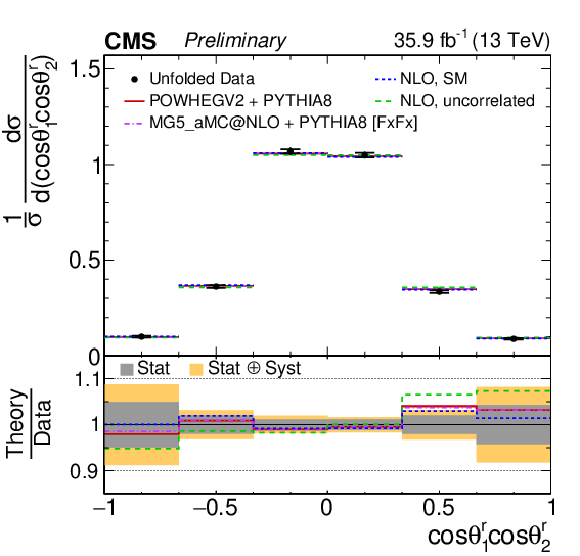
png pdf |
Figure 4-b:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |
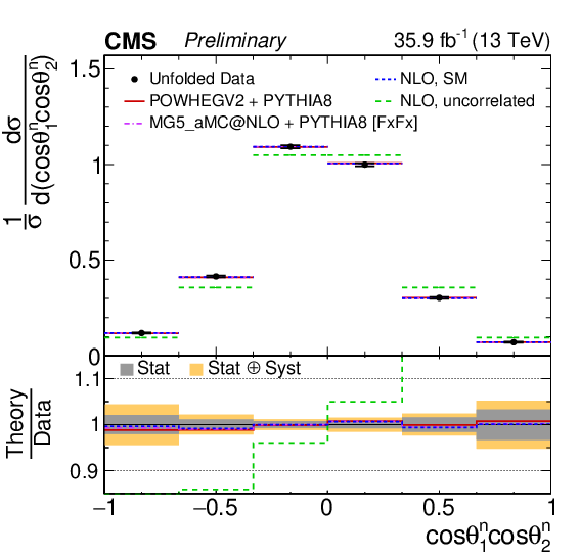
png pdf |
Figure 4-c:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-d:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |
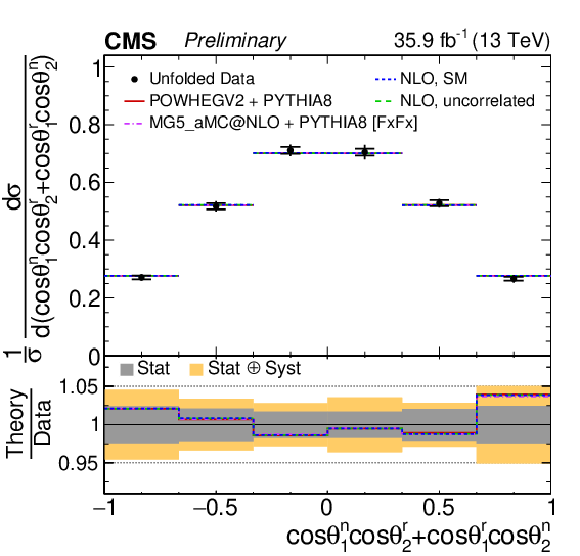
png pdf |
Figure 4-e:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-f:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-g:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-h:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-i:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-j:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-k:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |

png pdf |
Figure 4-l:
Unfolded normalized differential cross sections for the t¯t spin correlation observables. The vertical bars on the data points represent the total uncertainties, with the statistical component indicated by a horizontal bar. The ratios of various predictions to the data are shown in the lower panels. |
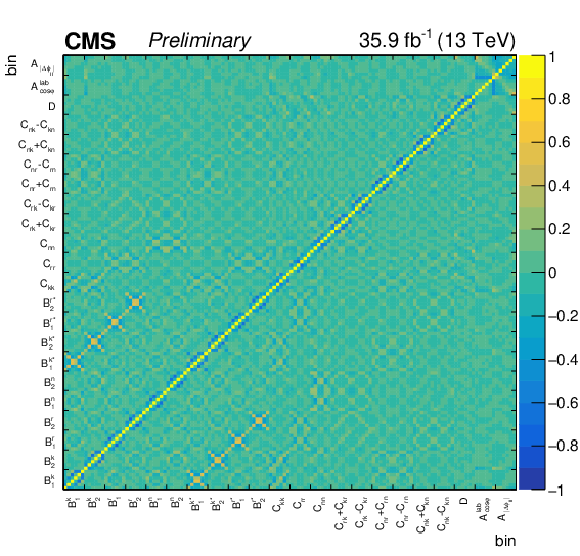
png pdf |
Figure 5:
Total statistical correlation matrix for all measured bins of the normalized differential cross sections (6 bins for each variable). |

png pdf |
Figure 6:
Total systematic correlation matrix for all measured bins of the normalized differential cross sections (6 bins for each variable). |

png pdf |
Figure 7:
Measured polarization coefficients and their total uncertainties. Coefficients from the POWHEG.V2 simulation are quoted with a combination of statistical and scale uncertainties, while the uncertainties for the MadGraph.5\_aMC@NLO simulation are statistical only. The calculated coefficients are quoted with scale uncertainties [3]. |
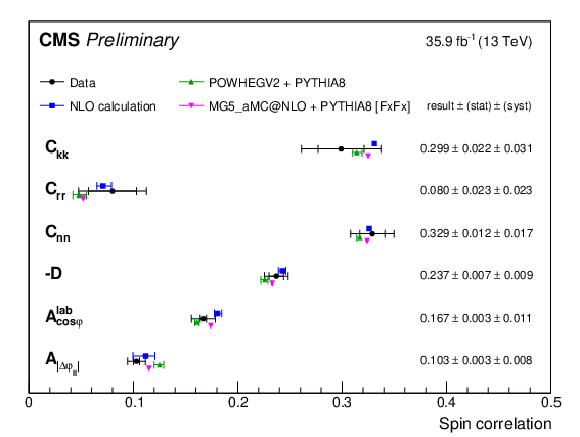
png pdf |
Figure 8:
Measured spin correlation coefficients and asymmetries and their total uncertainties. Coefficients from the POWHEG.V2 simulation are quoted with a combination of statistical and scale uncertainties, while the uncertainties for the MadGraph.5\_aMC@NLO simulation are statistical only. The calculated coefficients are quoted with scale uncertainties [3]. |

png pdf |
Figure 9:
Measured cross spin correlation coefficients and their total uncertainties. Coefficients from the POWHEG.V2 simulation are quoted with a combination of statistical and scale uncertainties, while the uncertainties for the MadGraph.5\_aMC@NLO simulation are statistical only. The calculated coefficients are quoted with scale uncertainties [3]. |
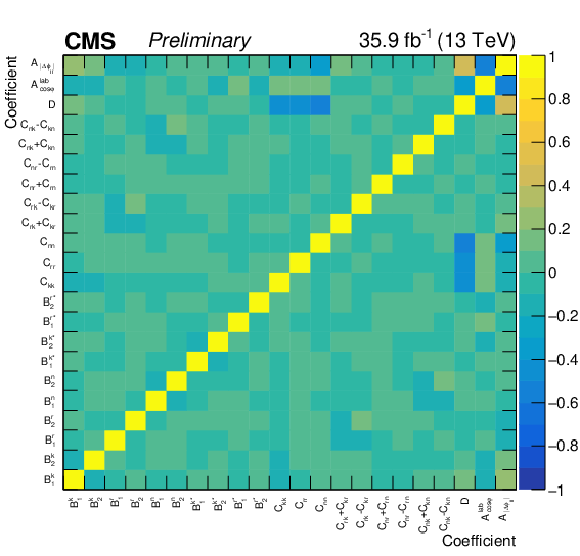
png pdf |
Figure 10:
Total statistical correlation matrix for all measured coefficients and the laboratory frame asymmetries. |
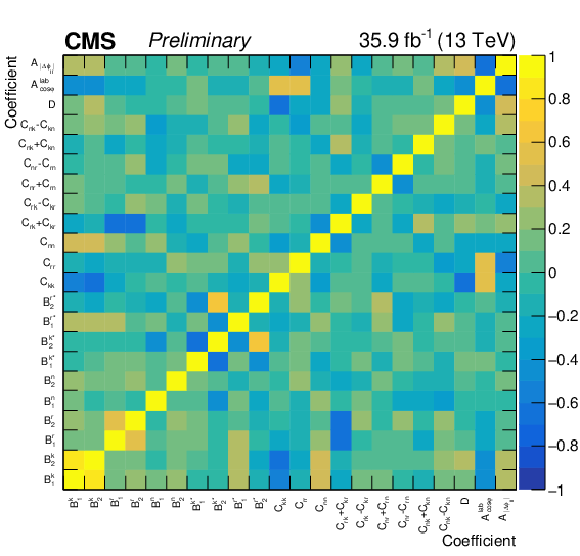
png pdf |
Figure 11:
Total systematic correlation matrix for all measured coefficients and the laboratory frame asymmetries. |

png pdf |
Figure 12:
Measured values of fSM, the strength of the measured spin correlations relative to the SM prediction. The uncertainties shown are a combination of those from experimental (statistical and systematic) and theoretical sources. |

png pdf |
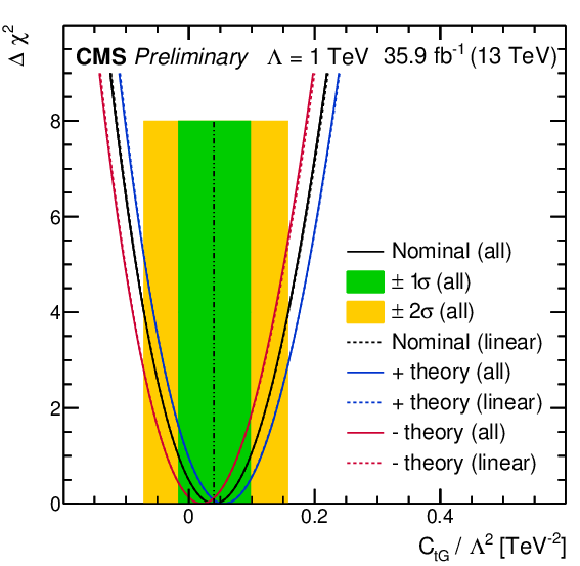
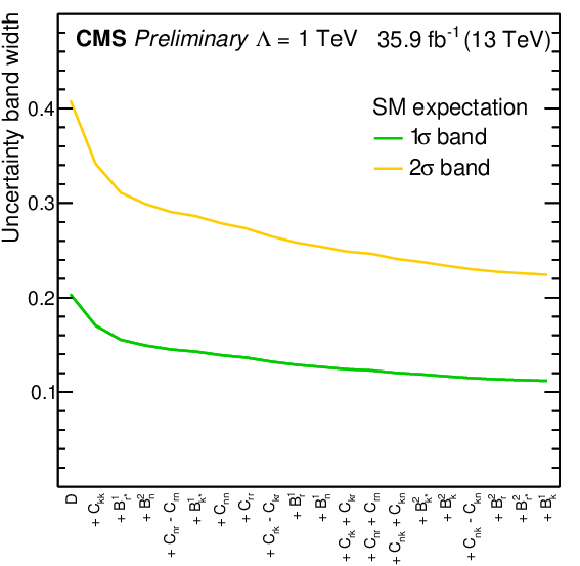
Figure 13:
Left: Δχ2 values from the fit to the data are shown in the left plot as a function of CtG/Λ2. The green area indicates 1σ CL, the orange the 2σ CL. Right: Decrease in total uncertainty on CtG/Λ2 for the case of adding one distribution at a time to the χ2 minimization. |
png pdf |
Figure 13-a:
Δχ2 values from the fit to the data are shown in the left plot as a function of CtG/Λ2. The green area indicates 1σ CL, the orange the 2σ CL. |
png pdf |
Figure 13-b:
Decrease in total uncertainty on CtG/Λ2 for the case of adding one distribution at a time to the χ2 minimization. |
| Tables | |
png pdf |
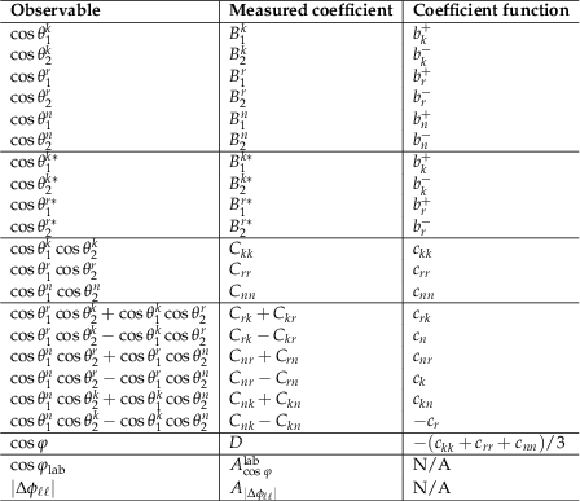
Table 1:
Observables and corresponding measured coefficients and production spin density matrix coefficient functions. For the laboratory-frame observables, there is no direct correspondence with the coefficient functions. |

png pdf |
Table 2:
Measured coefficients and their total uncertainties. Coefficients from the POWHEG.V2 simulation are quoted with a combination of statistical and scale uncertainties, while the uncertainties for the MadGraph.5\_aMC@NLO simulation are statistical only. The calculated coefficients are quoted with scale uncertainties [3]. |
png pdf |
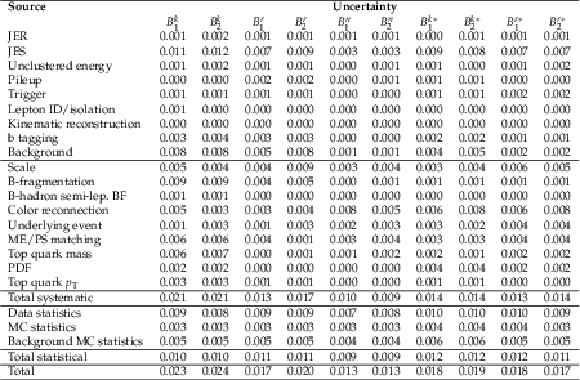
Table 3:
Summary of the systematic uncertainties in the extracted top quark polarization coefficients. |

png pdf |
Table 4:
Summary of the systematic uncertainties in the extracted t¯t spin correlation coefficients. |

png pdf |
Table 5:
Measured sums and differences of the B coefficients and their statistical and systematic uncertainties. The calculated coefficients are quoted with scale uncertainties. |

png pdf |
Table 6:
Values of fSM, the strength of the measured spin correlations relative to the SM prediction for the given observable, derived from the numbers in Table 2. The uncertainties shown are statistical, systematic, and theoretical, respectively. The total uncertainty in each result, found by adding the individual uncertainties in quadrature, is shown in the last column. |
| Summary |
| We present measurements of the top quark polarization and tˉt spin correlations, probing all the independent coefficients of the top quark spin-dependent parts of the tˉt production density matrix for the first time at √s= 13 TeV. Each coefficient is extracted from a normalized differential cross section, unfolded to the parton level and extrapolated to the full phase space. The measurements are made using a data sample of pp collision events containing two leptons, recorded by the CMS experiment in 2016 and corresponding to an integrated luminosity of 35.9 fb−1. The measured distributions and extracted coefficients are compared with standard model predictions from Monte Carlo simulations with NLO accuracy in QCD and from NLO QCD calculations including weak and mixed QCD-weak corrections. All measurements are found to be consistent with the expectations of the standard model. Statistical and systematic covariance matrices are provided for the set of all measured bins, and are used in a simultaneous fit to constrain the anomalous chromomagnetic dipole moment of the top quark. A constraint of −0.07<CtG/Λ2 <0.16 TeV−2 at 95% CL is obtained, with the impact from neglecting contributions quadratic in CtG/Λ2 found to be small. |
| References | ||||
| 1 | Particle Data Group, C. Patrignani et al. | Review of particle physics | CPC 40 (2016) 100001 | |
| 2 | G. Mahlon and S. J. Parke | Spin correlation effects in top quark pair production at the LHC | PRD 81 (2010) 074024 | 1001.3422 |
| 3 | W. Bernreuther, D. Heisler, and Z.-G. Si | A set of top quark spin correlation and polarization observables for the LHC: Standard model predictions and new physics contributions | JHEP 12 (2015) 026 | 1508.05271 |
| 4 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 5 | ATLAS Collaboration | Measurements of top quark spin observables in tˉt events using dilepton final states in √s= 8 TeV pp collisions with the ATLAS detector | JHEP 03 (2017) 113 | 1612.07004 |
| 6 | CMS Collaboration | Measurements of tˉt spin correlations and top-quark polarization using dilepton final states in pp collisions at √s= 7 TeV | PRL 112 (2014) 182001 | CMS-TOP-13-003 1311.3924 |
| 7 | ATLAS Collaboration | Measurements of spin correlation in top-antitop quark events from proton-proton collisions at √s= 7 TeV using the ATLAS detector | PRD 90 (2014) 112016 | 1407.4314 |
| 8 | ATLAS Collaboration | Measurement of the correlation between the polar angles of leptons from top quark decays in the helicity basis at √s= 7 TeV using the ATLAS detector | PRD 93 (2016) 012002 | 1510.07478 |
| 9 | CMS Collaboration | Measurements of tˉt spin correlations and top quark polarization using dilepton final states in pp collisions at √s= 8 TeV | PRD 93 (2016) 052007 | CMS-TOP-14-023 1601.01107 |
| 10 | CMS Collaboration | Measurements of t¯t differential cross sections in proton-proton collisions at √s= 13 TeV using events containing two leptons | CMS-TOP-17-014 1811.06625 |
|
| 11 | D. Buarque Franzosi and C. Zhang | Probing the top-quark chromomagnetic dipole moment at next-to-leading order in QCD | PRD 91 (2015) 114010 | 1503.08841 |
| 12 | R. Martinez, M. A. Perez, and N. Poveda | Chromomagnetic dipole moment of the top quark revisited | EPJC 53 (2008) 221 | hep-ph/0701098 |
| 13 | M. Baumgart and B. Tweedie | A new twist on top quark spin correlations | JHEP 03 (2013) 117 | 1212.4888 |
| 14 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 15 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 16 | S. Alioli et al. | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 17 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 18 | CMS Collaboration | Investigations of the impact of the parton shower tuning in \Pythia in the modelling of t¯t at √s= 8 and 13 TeV | CMS-PAS-TOP-16-021 | CMS-PAS-TOP-16-021 |
| 19 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 20 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA 8.1: the Monash 2013 Tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 21 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 22 | P. Artoisenet et al. | Automatic spin-entangled decays of heavy resonances in Monte Carlo simulations | JHEP 03 (2013) 015 | 1212.3460 |
| 23 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 24 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 437 | 0706.2569 |
| 25 | S. Alioli et al. | NLO single-top production matched with shower in POWHEG: s- and t-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 26 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 27 | NNPDF Collaboration | Unbiased global determination of parton distributions and their uncertainties at NNLO and LO | NPB 855 (2012) 153 | 1107.2652 |
| 28 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 29 | N. Kidonakis | Two-loop soft anomalous dimensions for single top quark associated production with W− or H− | PRD 82 (2010) 054018 | hep-ph/1005.4451 |
| 30 | J. M. Campbell, R. K. Ellis, and C. Williams | Vector boson pair production at the LHC | JHEP 07 (2011) 018 | 1105.0020 |
| 31 | F. Maltoni, D. Pagani, and I. Tsinikos | Associated production of a top-quark pair with vector bosons at NLO in QCD: impact on t¯tH searches at the LHC | JHEP 02 (2016) 113 | 1507.05640 |
| 32 | M. Czakon and A. Mitov | Top++: a program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 33 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 34 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 35 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at √s= 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 36 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at √s= 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 37 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-kt jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 38 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 39 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 40 | CMS Collaboration | Measurement of the differential cross section for top quark pair production in pp collisions at √s= 8 TeV | EPJC 75 (2015) 542 | CMS-TOP-12-028 1505.04480 |
| 41 | CMS Collaboration | Measurement of the top quark pair production cross section in proton-proton collisions at √s= 13 TeV with the CMS detector | PRL 116 (2016) 052002 | CMS-TOP-15-003 1510.05302 |
| 42 | S. Schmitt | TUnfold, an algorithm for correcting migration effects in high energy physics | JINST 7 (2012) T10003 | 1205.6201 |
| 43 | F. James | Statistical methods in experimental physics | World Scientific, second edition | |
| 44 | CMS Collaboration | Measurement of the Drell--Yan cross sections in pp collisions at √s= 7 TeV with the CMS experiment | JHEP 10 (2011) 007 | CMS-EWK-10-007 1108.0566 |
| 45 | ATLAS Collaboration | Measurement of the inelastic proton-proton cross section at √s= 13 TeV with the ATLAS detector at the LHC | PRL 117 (2016) 182002 | 1606.02625 |
| 46 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 47 | CMS Collaboration | Measurement of differential top-quark pair production cross sections in pp collisions at √s= 7 TeV | EPJC 73 (2013) 2339 | CMS-TOP-11-013 1211.2220 |
| 48 | M. Guzzi, K. Lipka, and S.-O. Moch | Top-quark pair production at hadron colliders: differential cross section and phenomenological applications with difftop | JHEP 01 (2015) 082 | 1406.0386 |
| 49 | N. Kidonakis | NNNLO soft-gluon corrections for the top-quark pT and rapidity distributions | PRD 91 (2015) 031501 | 1411.2633 |
| 50 | M. Czakon et al. | Top-pair production at the LHC through NNLO QCD and NLO EW | JHEP 10 (2017) 186 | 1705.04105 |
| 51 | M. Czakon et al. | Resummation for (boosted) top-quark pair production at NNLO+NNLL' in QCD | JHEP 05 (2018) 149 | 1803.07623 |
| 52 | S. Argyropoulos and T. Sjostrand | Effects of color reconnection on tˉt final states at the LHC | JHEP 11 (2014) 043 | 1407.6653 |
| 53 | J. R. Christiansen and P. Z. Skands | String formation beyond leading colour | JHEP 08 (2015) 003 | 1505.01681 |
| 54 | M. G. Bowler | e+e− production of heavy quarks in the string model | Z. Phys. C 11 (1981) 169 | |
| 55 | C. Peterson, D. Schlatter, I. Schmitt, and P. M. Zerwas | Scaling violations in inclusive e+e− annihilation spectra | PRD 27 (1983) 105 | |
| 56 | W. Bernreuther and Z.-G. Si | Top quark spin correlations and polarization at the LHC: standard model predictions and effects of anomalous top chromo moments | PLB 725 (2013) 115 | 1305.2066 |
| 57 | W. Bernreuther, D. Heisler, and Z.-G. Si | A set of top quark spin correlation and polarization observables for the LHC: Standard Model predictions and new physics contributions | JHEP 12 (2015) 026 | 1508.05271 |
| 58 | W. Buchmuller and D. Wyler | Effective lagrangian analysis of new interactions and flavor conservation | NPB 268 (1986) 621 | |
| 59 | B. Grzadkowski, M. Iskrzynski, M. Misiak, and J. Rosiek | Dimension-six terms in the standard model lagrangian | JHEP 10 (2010) 085 | 1008.4884 |
| 60 | A. Buckley et al. | Rivet user manual | CPC 184 (2013) 2803 | 1003.0694 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|