

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-TOP-17-019 | ||
| Search for standard model production of four top quarks with the single-lepton and opposite-sign dilepton final states in proton-proton collisions at √s= 13 TeV | ||
| CMS Collaboration | ||
| March 2019 | ||
| Abstract: A search for the standard model production of four top quarks (pp→tˉttˉt) is reported using events with single-lepton (e, μ) + jets and opposite-sign dilepton (μ+μ−, μ±e∓, or e+e−) + jets signatures. The events are collected in proton-proton collisions recorded by the CMS detector at the LHC at √s= 13 TeV in a sample corresponding to an integrated luminosity of 35.8 fb−1. A multivariate analysis using global event and jet properties based on boosted decision trees is used to discriminate tˉttˉt from tˉt production. No significant deviation is observed from the predicted background. An upper limit is set on the cross section for tˉttˉt production in the standard model of 48 fb at 95 confidence level. When combined with the previous measurement of σtˉttˉt by the CMS experiment from an analysis of other final states, the observed signal significance is 1.4 standard deviations and the combined cross section measurement is σtˉttˉt= 13+11−9 fb. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JHEP 11 (2019) 082. The superseded preliminary plots can be found here. |
||
| Figures | |

png pdf |
Figure 1:
Representative diagrams for tˉttˉt production at the lowest order in the SM. |

png pdf |
Figure 2:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |
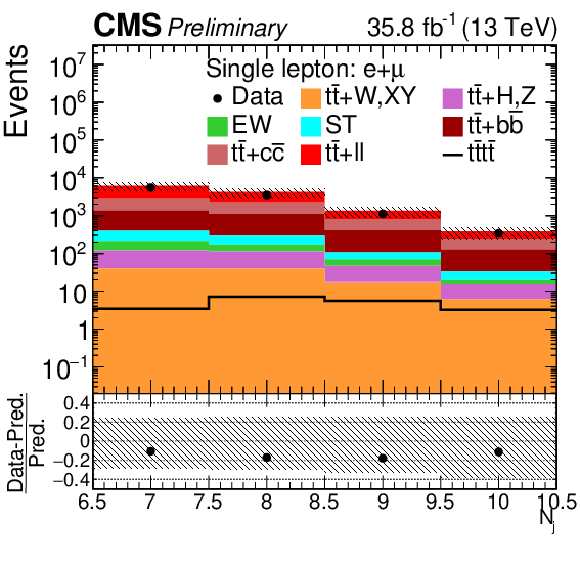
png pdf |
Figure 2-a:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |
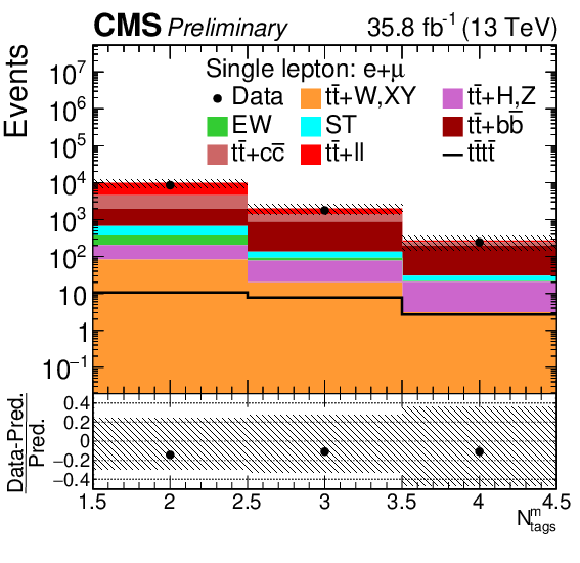
png pdf |
Figure 2-b:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |
png pdf |
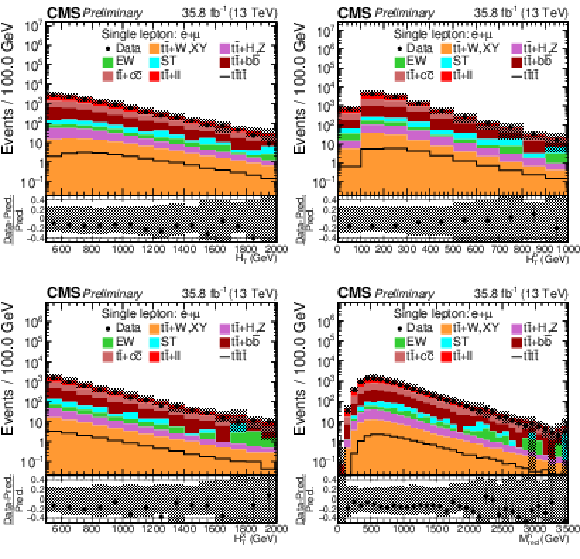
Figure 3:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |

png pdf |
Figure 3-a:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |
png pdf |
Figure 3-b:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |

png pdf |
Figure 3-c:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |
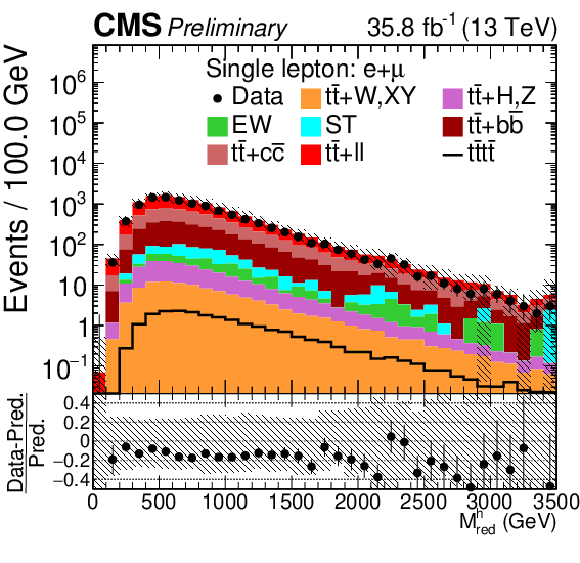
png pdf |
Figure 3-d:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |

png pdf |
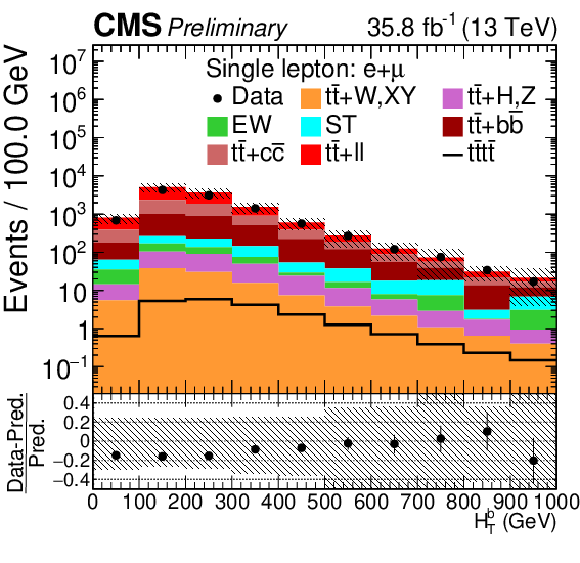
Figure 4:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |
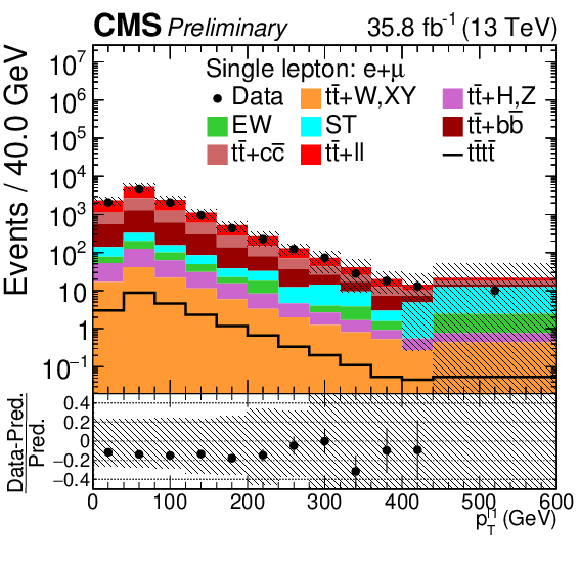
png pdf |
Figure 4-a:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |
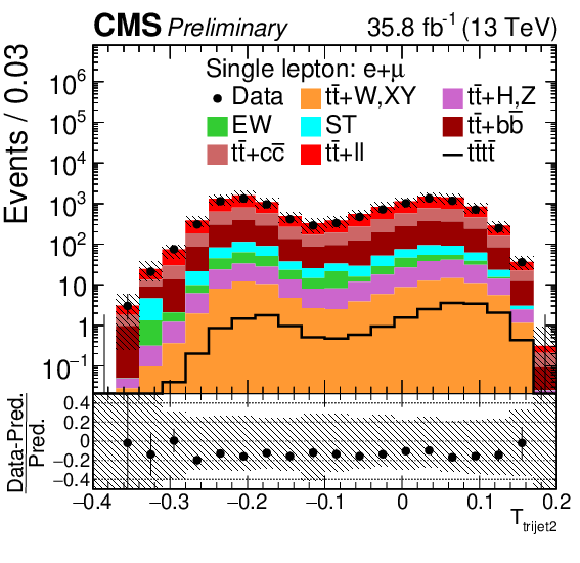
png pdf |
Figure 4-b:
Control distributions in the combined single-lepton channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total systematic and statistical uncertainty on the simulations added in quadrature. |
png pdf |
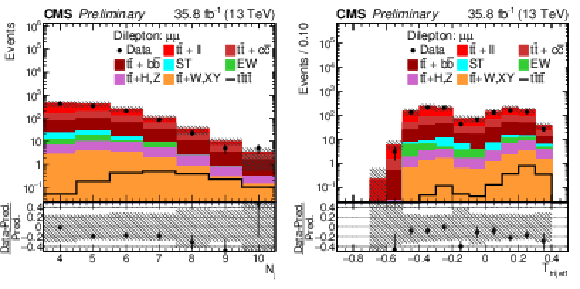
Figure 5:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton μ+μ− channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |
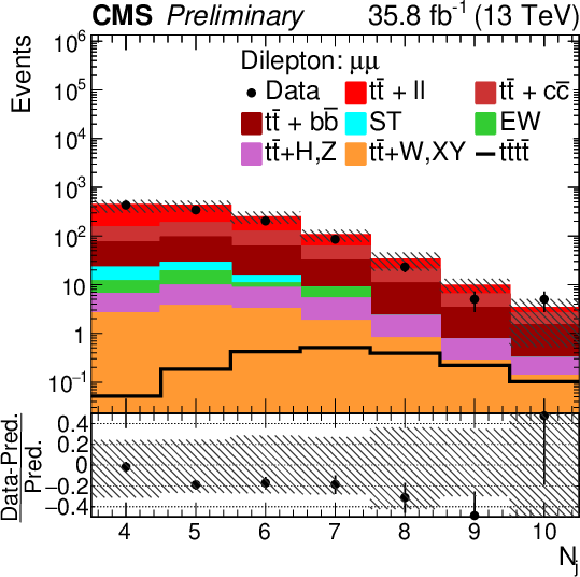
png pdf |
Figure 5-a:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton μ+μ− channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |
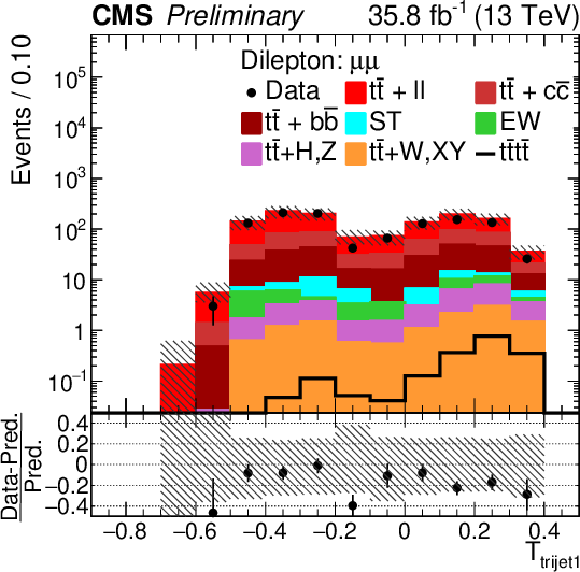
png pdf |
Figure 5-b:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton μ+μ− channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |
png pdf |
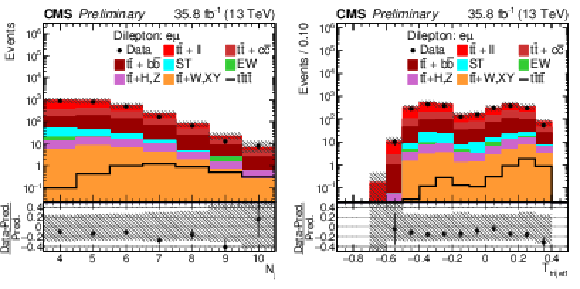
Figure 6:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton μ±e∓ channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |
png pdf |
Figure 6-a:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton μ±e∓ channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |

png pdf |
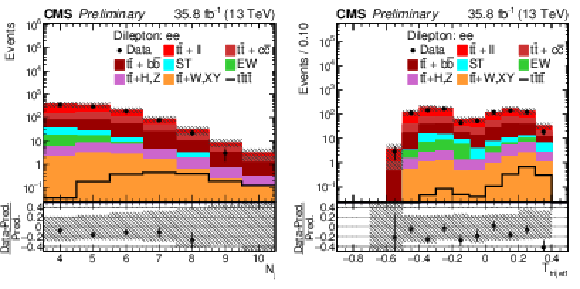
Figure 6-b:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton μ±e∓ channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |
png pdf |
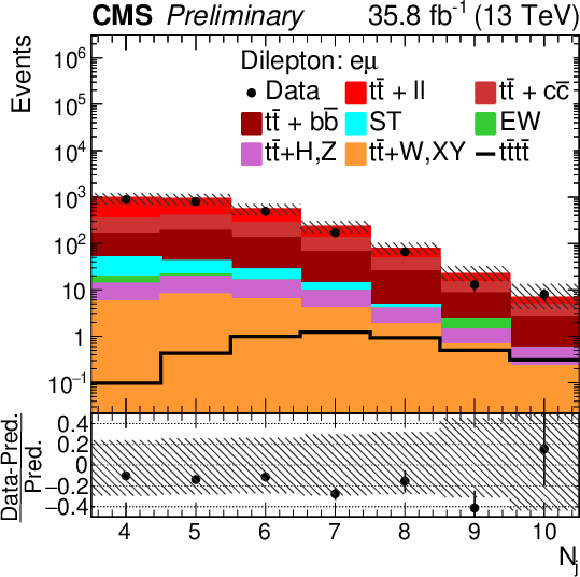
Figure 7:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton e+e− channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |

png pdf |
Figure 7-a:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton e+e− channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |
png pdf |
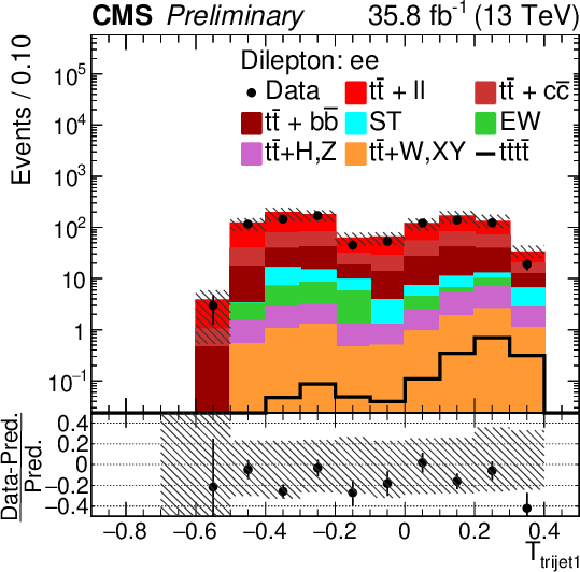
Figure 7-b:
Control distributions of Nj and Ttrijet1 in the combined OS dilepton e+e− channel. In the upper panel, the data are shown as dots with error bars representing statistical uncertainties, MC simulations are shown as a histogram. In the lower panel a relative difference with respect to MC prediction is also shown. The shaded band represents the total uncertainty on the main background |
png pdf |
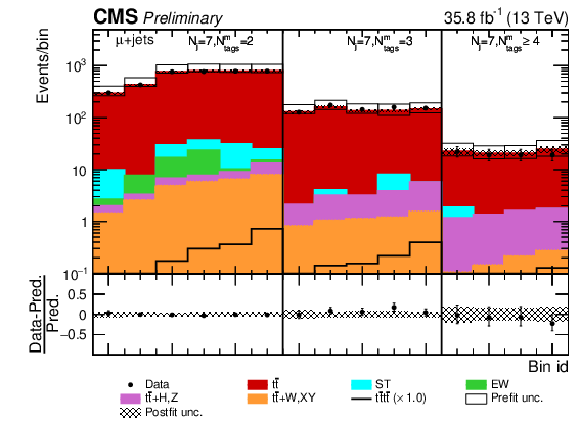
Figure 8:
Post-fit Dljtˉttˉt distribution in the single-muon channel for events satisfying baseline single-lepton selection and Nj= 7, Nmtags= 2, 3,≥ 4. Non-equidistant partitioning of the domain of the MVA discriminant was chosen to achieve approximately uniform distribution of the t¯t background. Dots represent data. Vertical error bars show the statistical uncertainties in the data. The post-fit background predictions are shown as shaded histograms. Open boxes demonstrate the size of the pre-fit uncertainty on the total background and are centered around the pre-fit expectation value of the prediction. The hatched area shows the size of the post-fit uncertainty on the background prediction. Signal histogram template is shown as a solid line. The lower panel shows the relative difference of the observed number of events over the post-fit background prediction. |
png pdf |
Figure 9:
Post-fit Dljtˉttˉt distribution in the single-muon (a) and single-electron (b) channel for events satisfying baseline single-lepton selection and Nj= 8, Nmtags= 2, 3,≥ 4. Other details as in Fig. 8. |
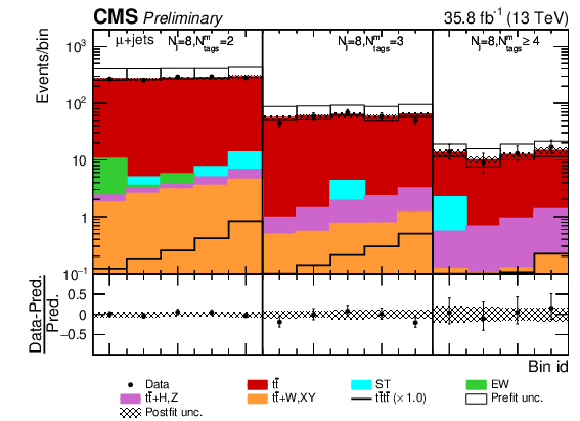
png pdf |
Figure 9-a:
Post-fit Dljtˉttˉt distribution in the single-muon (a) and single-electron (b) channel for events satisfying baseline single-lepton selection and Nj= 8, Nmtags= 2, 3,≥ 4. Other details as in Fig. 8. |
png pdf |
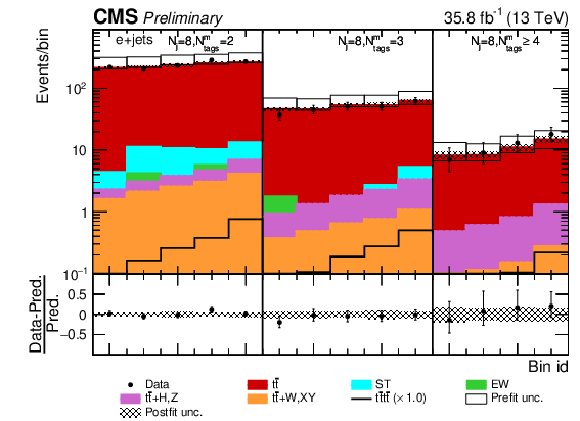
Figure 9-b:
Post-fit Dljtˉttˉt distribution in the single-muon (a) and single-electron (b) channel for events satisfying baseline single-lepton selection and Nj= 8, Nmtags= 2, 3,≥ 4. Other details as in Fig. 8. |
png pdf |
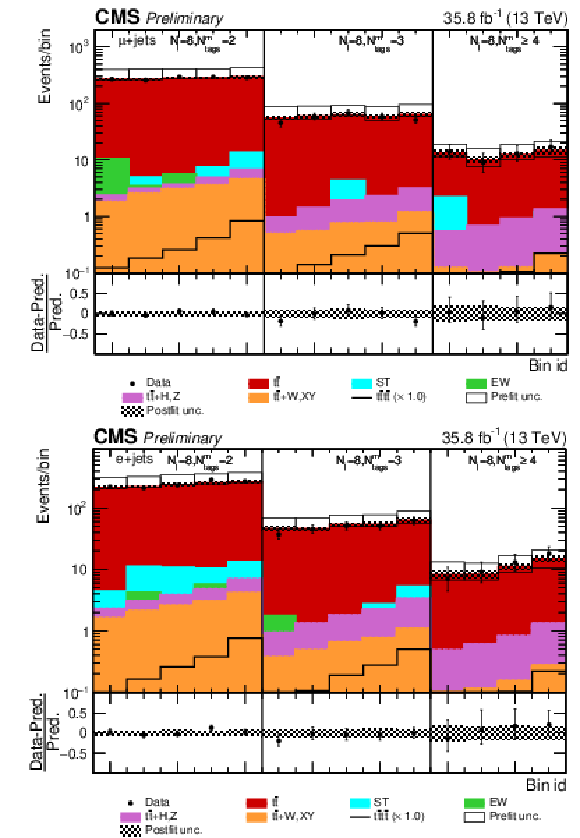
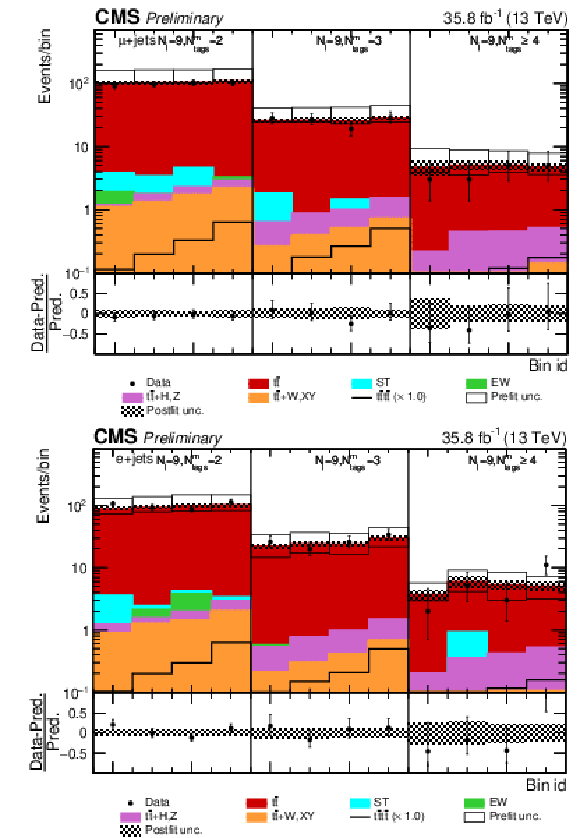
Figure 10:
Post-fit Dljtˉttˉt distribution in the single (a) muon, (b) electron channel for events satisfying baseline single-lepton selection and Nj= 9, Nmtags= 2, 3, ≥ 4. Other details as in Fig. 8. |

png pdf |
Figure 10-a:
Post-fit Dljtˉttˉt distribution in the single (a) muon, (b) electron channel for events satisfying baseline single-lepton selection and Nj= 9, Nmtags= 2, 3, ≥ 4. Other details as in Fig. 8. |
png pdf |
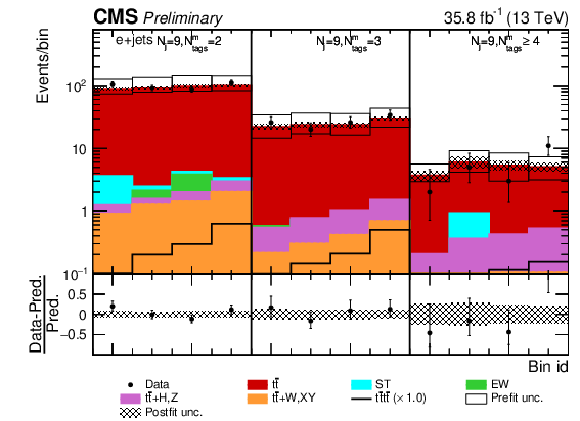
Figure 10-b:
Post-fit Dljtˉttˉt distribution in the single (a) muon, (b) electron channel for events satisfying baseline single-lepton selection and Nj= 9, Nmtags= 2, 3, ≥ 4. Other details as in Fig. 8. |

png pdf |
Figure 11:
Post-fit Dljtˉttˉt distribution in the single (a) muon, (b) electron channel for events satisfying baseline single-lepton selection and Nj≥ 10, Nmtags= 2, 3, ≥ 4. Other details as in Fig. 8. |
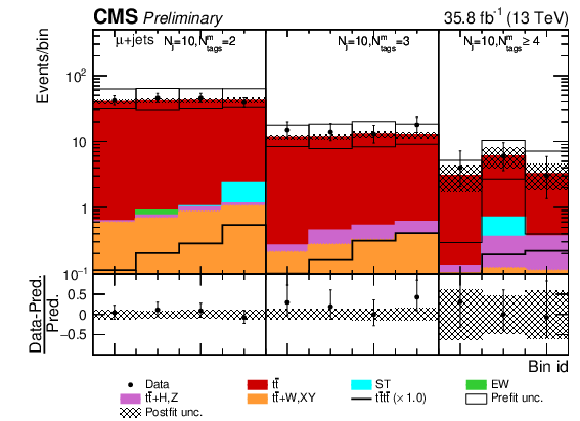
png pdf |
Figure 11-a:
Post-fit Dljtˉttˉt distribution in the single (a) muon, (b) electron channel for events satisfying baseline single-lepton selection and Nj≥ 10, Nmtags= 2, 3, ≥ 4. Other details as in Fig. 8. |

png pdf |
Figure 11-b:
Post-fit Dljtˉttˉt distribution in the single (a) muon, (b) electron channel for events satisfying baseline single-lepton selection and Nj≥ 10, Nmtags= 2, 3, ≥ 4. Other details as in Fig. 8. |
png pdf |
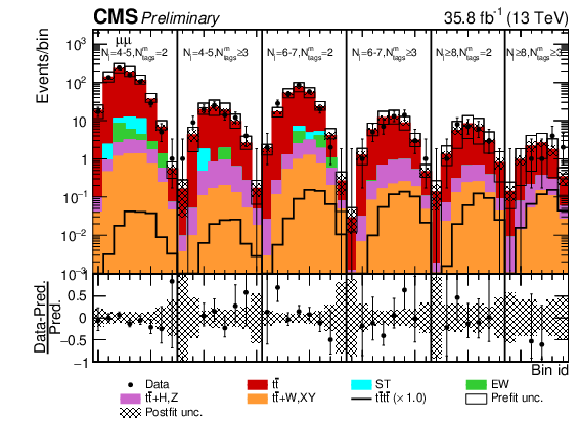
Figure 12:
Post-fit Ddiltˉttˉt distributions in the μ+μ− channel for events satisfying baseline opposite-sign dilepton selection. Dots represent data. Vertical error bars show the statistical uncertainties in the data. The post-fit background predictions are shown as shaded histograms. Open boxes demonstrate the size of the pre-fit uncertainty on the total background and are centered around the pre-fit expectation value of the prediction. The hatched area shows the size of the post-fit uncertainty on the background prediction. Signal histogram template is shown as a solid line. The lower panel shows the relative difference of the observed number of events over the post-fit background prediction. |
png pdf |
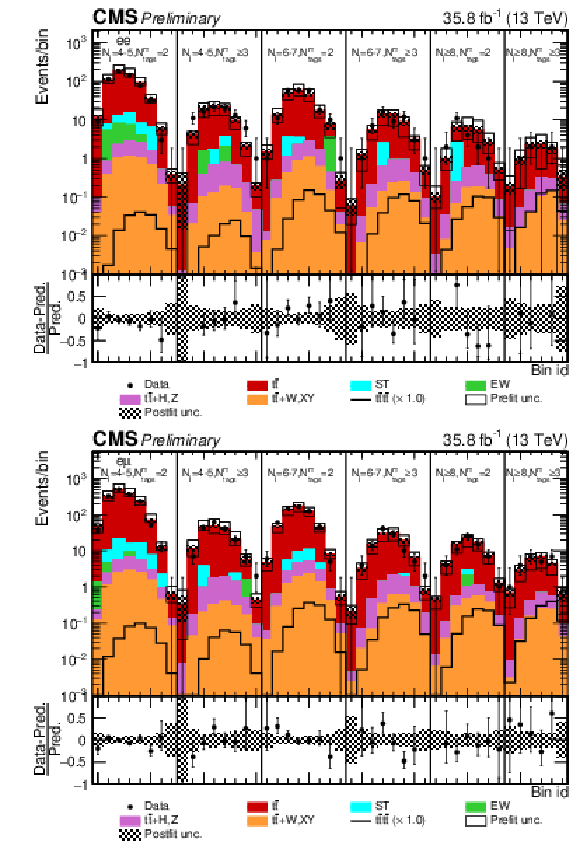
Figure 13:
Post-fit Ddiltˉttˉt distributions in the (a) e+e−, (b) μ±e∓ channel for events satisfying baseline opposite-sign dilepton selection. Other details as in Fig. 12. |
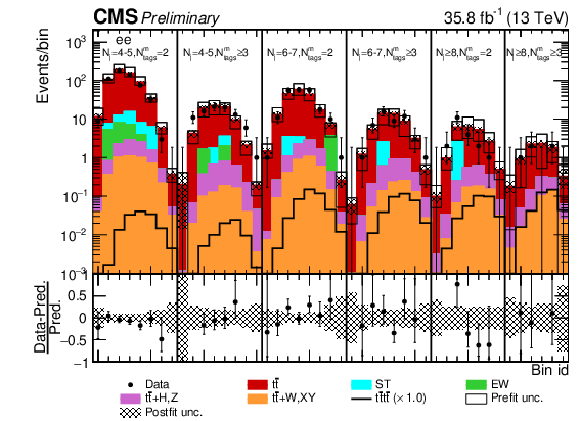
png pdf |
Figure 13-a:
Post-fit Ddiltˉttˉt distributions in the (a) e+e−, (b) μ±e∓ channel for events satisfying baseline opposite-sign dilepton selection. Other details as in Fig. 12. |
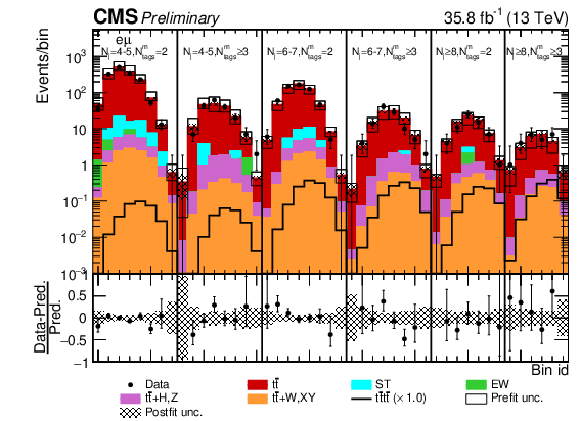
png pdf |
Figure 13-b:
Post-fit Ddiltˉttˉt distributions in the (a) e+e−, (b) μ±e∓ channel for events satisfying baseline opposite-sign dilepton selection. Other details as in Fig. 12. |
| Tables | |
png pdf |
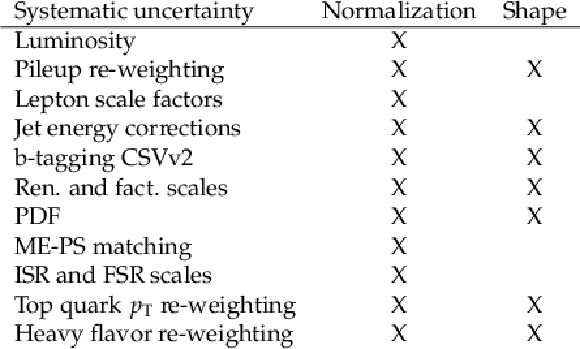
Table 1:
Uncertainties that affect the normalization of the data sets and shapes of the Dljtˉttˉt and Ddiltˉttˉt discriminants |

png pdf |
Table 2:
Maximum-likelihood signal-strength and cross section estimates, as well as the expected and observed significance of SM tˉttˉt production. The results for the two analyses from this note are shown separately and combined. The values quoted for the uncertainties on the signal-strengths and cross sections are the one standard deviation values and include all statistical and systematic uncertainties. |
png pdf |
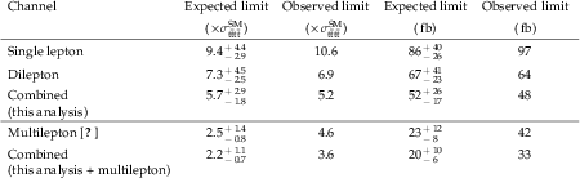
Table 3:
Expected and observed 95% CL upper limits on SM tˉttˉt production as a multiple of σSMtˉttˉt and in fb. The results for the two analyses from this note are shown separately and combined. The values quoted for the uncertainties on the expected limits are the one standard deviation values and include all statistical and systematic uncertainties. |

png pdf |
Table 4:
Linear parametrization coefficients, σ(1)k, of Eq. 6. The coefficients σ(1)k are in units (fb TeV2). |
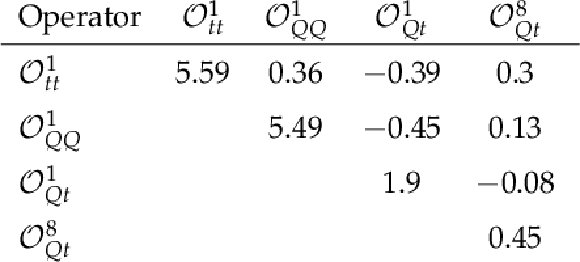
png pdf |
Table 5:
Quadratic parametrization coefficients, σ(2)j,k, of Eq. 6. The coefficients σ(2)j,k are in units (fb TeV4). |

png pdf |
Table 6:
Expected and observed 95% CL intervals for selected coupling parameters. The intervals are extracted from upper limit on the tˉttˉt production cross section in the EFT model, where only one selected operator has a non-vanishing contribution. |

png pdf |
Table 7:
Expected and observed 95% CL intervals for selected coupling parameters when contribution of other operators is marginalized. |
| Summary |
| A search for the standard model (SM) tˉttˉt production has been performed in final states with one or two oppositely charged electrons or muons. The observed yields attributed to tˉttˉt production are consistent with the SM predictions and a measured value for the tˉttˉt cross section of 0+20 fb has been obtained with an observed significance of 0.0 standard deviations. Combining this result with a previous same-sign dilepton and multilepton search [25] the resulting cross section is 13+11−9 fb with an observed significance of 1.4 standard deviations. The data were analysed in the effective field theory framework. The limits on dimension-6 four-fermion operators coupling to third generation quarks were obtained. These results constitute one of the most stringent constraints on the four top quarks production to date and can be used for phenomenological reinterpretation of a wide range of new physics models. |
| References | ||||
| 1 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 2 | Y. A. Gol'fand and E. P. Likhtman | Extension of the algebra of Poincar\'e group generators and violation of P invariance | JEPTL 13 (1971)323 | |
| 3 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | NPB 31 (1971) 86 | |
| 4 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JEPTL 16 (1972)438 | |
| 5 | J. Wess and B. Zumino | A lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 6 | J. Wess and B. Zumino | Supergauge transformations in four-dimensions | NPB 70 (1974) 39 | |
| 7 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 8 | H. P. Nilles | Supersymmetry, supergravity and particle physics | PR 110 (1984) 1 | |
| 9 | S. P. Martin | A supersymmetry primer | in Perspectives on Supersymmetry II, G. L. Kane, ed., p. 1 World Scientific, 2010 Adv. Ser. Direct. High Energy Phys., vol. 21 | |
| 10 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 11 | M. Toharia and J. D. Wells | Gluino decays with heavier scalar superpartners | JHEP 02 (2006) 015 | hep-ph/0503175 |
| 12 | S. Calvet, B. Fuks, P. Gris, and L. Valery | Searching for sgluons in multitop events at a center-of-mass energy of 8 TeV | JHEP 04 (2013) 043 | 1212.3360 |
| 13 | G. Cacciapaglia et al. | Composite scalars at the LHC: the Higgs, the Sextet and the Octet | JHEP 11 (2015) 201 | 1507.02283 |
| 14 | K. Kumar, T. M. P. Tait, and R. Vega-Morales | Manifestations of top compositeness at colliders | JHEP 05 (2009) 022 | 0901.3808 |
| 15 | G. Cacciapaglia, A. Deandrea, and J. Llodra-Perez | A Dark Matter candidate from Lorentz Invariance in 6D | JHEP 03 (2010) 083 | 0907.4993 |
| 16 | O. Ducu, L. Heurtier, and J. Maurer | LHC signatures of a Z′ mediator between dark matter and the SU(3) sector | JHEP 03 (2016) 006 | 1509.05615 |
| 17 | C. Degrande et al. | Non-resonant New Physics in Top Pair Production at Hadron Colliders | JHEP 03 (2011) 125 | 1010.6304 |
| 18 | G. Bevilacqua and M. Worek | Constraining BSM physics at the LHC: Four top final states with NLO accuracy in perturbative QCD | JHEP 07 (2012) 111 | 1206.3064 |
| 19 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 20 | R. Frederix, D. Pagani, and M. Zaro | Large NLO corrections in tˉtW± and tˉttˉt hadroproduction from supposedly subleading EW contributions | JHEP 02 (2018) 031 | 1711.02116 |
| 21 | CMS Collaboration | Search for Standard Model Production of Four Top Quarks in the Lepton + Jets Channel in pp Collisions at √s= 8 TeV | JHEP 11 (2014) 154 | CMS-TOP-13-012 1409.7339 |
| 22 | ATLAS Collaboration | Search for supersymmetry at √s= 8 TeV in final states with jets and two same-sign leptons or three leptons with the ATLAS detector | JHEP 06 (2014) 035 | 1404.2500 |
| 23 | CMS Collaboration | Search for standard model production of four top quarks in proton-proton collisions at √s= 13 TeV | PLB 772 (2017) 336 | CMS-TOP-16-016 1702.06164 |
| 24 | ATLAS Collaboration | Search for four-top-quark production in the single-lepton and opposite-sign dilepton final states in pp collisions at √s= 13 TeV with the ATLAS detector | Submitted to PRD | 1811.02305 |
| 25 | CMS Collaboration | Search for standard model production of four top quarks with same-sign and multilepton final states in proton-proton collisions at √s= 13 TeV | EPJC 78 (2017) 140 | CMS-TOP-17-009 1710.10614 |
| 26 | CMS Collaboration | Search for physics beyond the standard model in events with two leptons of same sign, missing transverse momentum, and jets in proton-proton collisions at √s= 13 TeV | EPJC77 (2017) 578 | CMS-SUS-16-035 1704.07323 |
| 27 | ATLAS Collaboration | Search for pair production of up-type vector-like quarks and for four-top-quark events in final states with multiple b-jets with the ATLAS detector | JHEP 07 (2018) 089 | 1803.09678 |
| 28 | M. L. Mangano, M. Moretti, F. Piccinini, and M. Treccani | Matching matrix elements and shower evolution for top-quark production in hadronic collisions | JHEP 01 (2007) 013 | hep-ph/0611129 |
| 29 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 30 | T. Sjostrand et al. | An Introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 31 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 32 | CMS Collaboration | Investigations of the impact of the parton shower tuning in Pythia 8 in the modelling of tˉt at √s= 8 and 13 TeV | CMS-PAS-TOP-16-021 | |
| 33 | S. Frixione et al. | A Positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 34 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 35 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 36 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 37 | S. Alioli, S.-O. Moch, and P. Uwer | Hadronic top-quark pair-production with one jet and parton showering | JHEP 01 (2012) 137 | 1110.5251 |
| 38 | M. Czakon and A. Mitov | Top++: A program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 39 | M. Beneke, P. Falgari, S. Klein, and C. Schwinn | Hadronic top-quark pair production with NNLL threshold resummation | NPB 855 (2012) 695 | 1109.1536 |
| 40 | M. Cacciari et al. | Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation | PLB 710 (2012) 612 | 1111.5869 |
| 41 | P. Barnreuther, M. Czakon, and A. Mitov | Percent Level Precision Physics at the Tevatron: First Genuine NNLO QCD Corrections to qˉq→tˉt+X | PRL 109 (2012) 132001 | 1204.5201 |
| 42 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels | JHEP 12 (2012) 054 | 1207.0236 |
| 43 | M. Czakon and A. Mitov | NNLO corrections to top pair production at hadron colliders: the quark-gluon reaction | JHEP 01 (2013) 080 | 1210.6832 |
| 44 | M. Czakon, P. Fiedler, and A. Mitov | Total Top-Quark Pair-Production Cross Section at Hadron Colliders Through O(α4S) | PRL 110 (2013) 252004 | 1303.6254 |
| 45 | CMS Collaboration | Measurements of t¯t differential cross sections in proton-proton collisions at √s= 13 TeV using events containing two leptons | Submitted to JHEP | CMS-TOP-17-014 1811.06625 |
| 46 | CMS Collaboration | Measurement of differential cross sections for the production of top quark pairs and of additional jets in lepton+jets events from pp collisions at √s= 13 TeV | PRD 97 (2018) 112003 | CMS-TOP-17-002 1803.08856 |
| 47 | M. Czakon, D. Heymes, and A. Mitov | High-precision differential predictions for top-quark pairs at the LHC | PRL 116 (2016) 082003 | 1511.00549 |
| 48 | N. Kidonakis | NNLL threshold resummation for top-pair and single-top production | Phys. Part. Nucl. 45 (2014) 714 | 1210.7813 |
| 49 | M. Aliev et al. | HATHOR: HAdronic Top and Heavy quarks crOss section calculatoR | CPC 182 (2011) 1034 | 1007.1327 |
| 50 | P. Kant et al. | HatHor for single top-quark production: Updated predictions and uncertainty estimates for single top-quark production in hadronic collisions | CPC 191 (2015) 74 | 1406.4403 |
| 51 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 52 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector | 1610.07922 | |
| 53 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 54 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 55 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at √s= 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 56 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at √s= 13 TeV | JINST 13 (2018), no. 06, P06015 | CMS-MUO-16-001 1804.04528 |
| 57 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-kt jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 58 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 59 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 60 | CMS Collaboration | Performance of missing transverse momentum in pp collisions at √s= 13 TeV using the CMS detector | CMS-PAS-JME-17-001 | CMS-PAS-JME-17-001 |
| 61 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 62 | L. Breiman, J. Friedman, R. A. Olshen, and C. J. Stone | Classification and Regression Trees | Chapman and Hall/CRC, 1984ISBN 9780412048418 | |
| 63 | J. H. Friedman | Recent Advances in Predictive (Machine) Learning | J. Classif. 23 (2006) 175 | |
| 64 | Y. Freund and R. E. Schapire | A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting | J. Comput. Syst. Sci. 55 (1997), no. 1, 119 | |
| 65 | H. Voss, A. Hocker, J. Stelzer, and F. Tegenfeldt | TMVA, the Toolkit for Multivariate Data Analysis with ROOT | in XIth International Workshop on Advanced Computing and Analysis Techniques in Physics Research (ACAT2007) 2007 | physics/0703039 |
| 66 | F. Pedregosa et al. | Scikit-learn: Machine learning in Python | Journal of Machine Learning Research 12 (2011) 2825 | 1201.0490 |
| 67 | J. D. Bjorken and S. J. Brodsky | Statistical model for electron-positron annihilation into hadrons | PRD 1 (1970) 1416 | |
| 68 | CMS Collaboration | CMS Luminosity Measurements for the 2016 Data Taking Period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 69 | CMS Collaboration | Measurement of the inelastic proton-proton cross section at √s= 13 TeV | JHEP 07 (2018) 161 | CMS-FSQ-15-005 1802.02613 |
| 70 | CMS Collaboration | Measurements of tˉt cross sections in association with b jets and inclusive jets and their ratio using dilepton final states in pp collisions at √s= 13 TeV | PLB 776 (2018) 355 | CMS-TOP-16-010 1705.10141 |
| 71 | L. Moneta et al. | The RooStats Project | in 13th International Workshop on Advanced Computing and Analysis Techniques in Physics Research (ACAT2010) 2010 | 1009.1003 |
| 72 | A. L. Read | Presentation of search results: the CLs technique | JPG 28 (2002) 2693 | |
| 73 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 74 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC. 71 (2011) 1554 | 1007.1727 |
| 75 | The ATLAS and CMS Collaborations and the LHC Higgs Combination Group | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 76 | W. Buchmuller and D. Wyler | Effective Lagrangian Analysis of New Interactions and Flavor Conservation | NPB268 (1986) 621 | |
| 77 | B. Grzadkowski et al. | Dimension-Six Terms in the Standard Model Lagrangian | JHEP 10 (2010) 085 | 1008.4884 |
| 78 | N. P. Hartland et al. | A Monte Carlo global analysis of the Standard Model Effective Field Theory: the top quark sector | 1901.05965 | |
| 79 | S. Weinberg | Baryon and lepton nonconserving processes | PRL 43 (1979) 1566 | |
| 80 | J. Aguilar-Saavedra et al. | Interpreting top-quark LHC measurements in the standard-model effective field theory | 1802.07237 | |
| 81 | A. Alloul et al. | FeynRules 2.0 - A complete toolbox for tree-level phenomenology | CPC 185 (2014) 2250 | 1310.1921 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|