Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-TAU-18-001 | ||
| An embedding technique to determine genuine $\tau\tau$ backgrounds from CMS data | ||
| CMS Collaboration | ||
| November 2018 | ||
| Abstract: The embedding technique allows an estimation of the genuine $\tau\tau$ standard model backgrounds from data, with minimal simulation input. In the data, the muons are removed from reconstructed $\mu\mu$ events and replaced with simulated tau leptons with the same kinematic properties. In that way a set of hybrid events is obtained that relies on simulation only for the decay of the tau leptons. Challenges in describing the underlying event or the production of associated jets in the simulation are avoided. In this note the technique developed for the CMS experiment is described, and its validation and relevant uncertainties are discussed. The description is based on the experimental setup of the year 2017. The data sample of proton-proton collisions at $\sqrt{s}= $ 13 TeV collected by the CMS experiment is used to demonstrate the performance of the method. It corresponds to an integrated luminosity of 41.5 fb$^{-1}$. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JINST 14 (2019) P06032. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
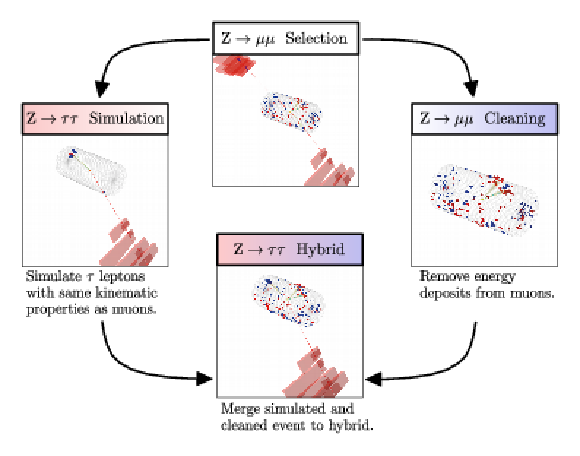
Figure 1:
Schematic view of the four main steps of the $ {\tau}$-embedding technique, as described in Section 5. A $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ candidate event is selected in data ("$ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ Selection''), all energy deposits associated to the muons are removed from the event record ("$ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ Cleaning''), and two tau lepton decays are simulated in an otherwise empty detector ("$ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ Simulation''). Finally all energy deposits of the simulated tau lepton decays are combined with the original reconstructed event record ("$ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ Hybrid''). In the example one of the simulated tau leptons decays into a muon and the other one into hadrons. |
png pdf |
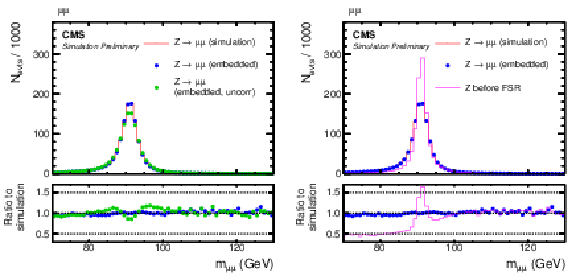
Figure 2:
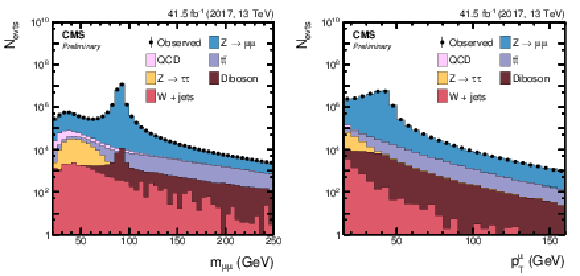
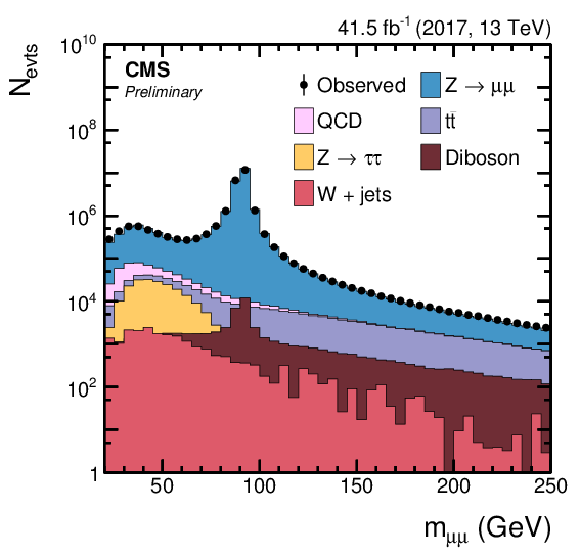
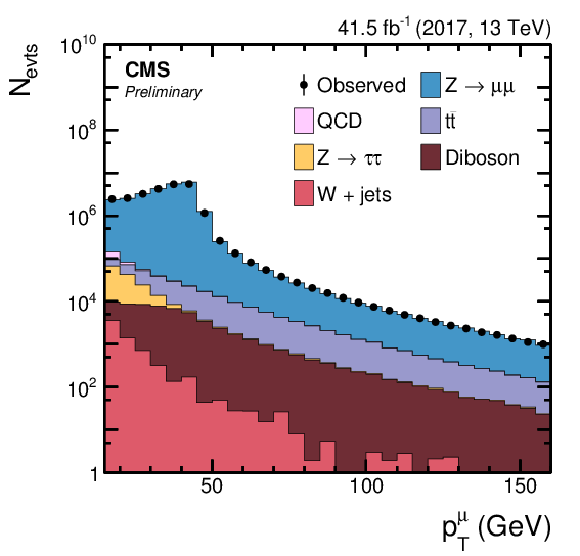
(Left) Invariant mass, $ {m_{\mu \mu}} $, of the selected dimuon Z boson candidate and (right) $ {p_{\mathrm {T}}} $ of the trailing muon after the event selection, as described in Section 5.2. |
png pdf |
Figure 2-a:
(Left) Invariant mass, $ {m_{\mu \mu}} $, of the selected dimuon Z boson candidate and (right) $ {p_{\mathrm {T}}} $ of the trailing muon after the event selection, as described in Section 5.2. |
png pdf |
Figure 2-b:
(Left) Invariant mass, $ {m_{\mu \mu}} $, of the selected dimuon Z boson candidate and (right) $ {p_{\mathrm {T}}} $ of the trailing muon after the event selection, as described in Section 5.2. |
png pdf |
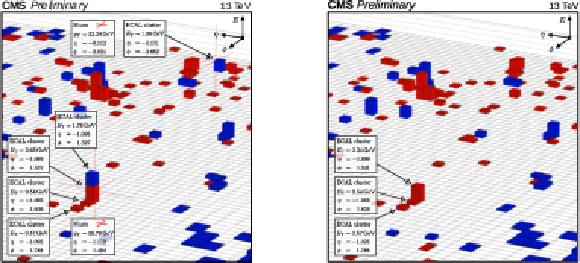
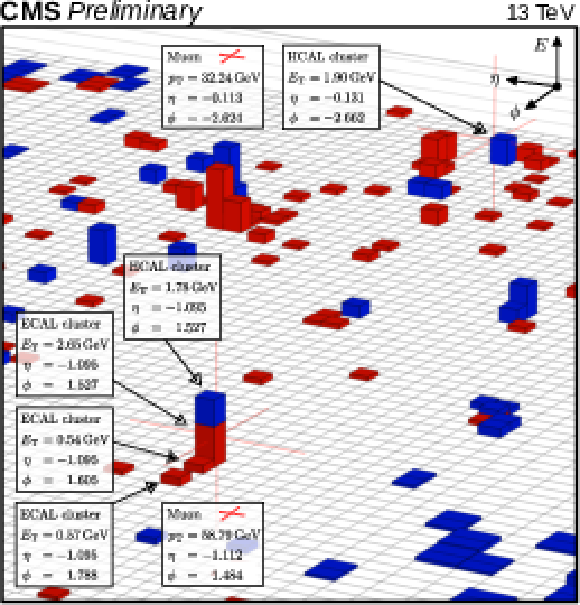
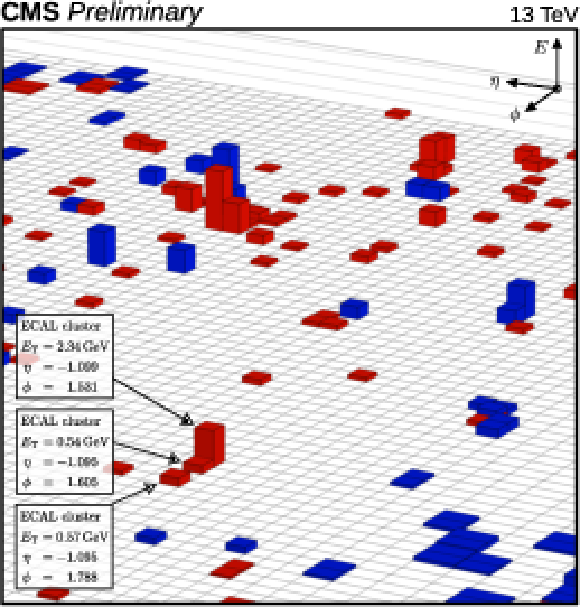
Figure 3:
Display of a $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ candidate event in the 2017 dataset, in the $\eta $-$\phi $ plane at the surface of the calorimeters, (left) before and (right) after the hits and energy deposits associated to the muons have been removed from the reconstructed event record. The red crosses indicate the intercepts of the reconstructed muon trajectories with the calorimeter surface. The red (blue) boxes correspond to clusters in the ECAL (HCAL). |
png pdf |
Figure 3-a:
Display of a $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ candidate event in the 2017 dataset, in the $\eta $-$\phi $ plane at the surface of the calorimeters, (left) before and (right) after the hits and energy deposits associated to the muons have been removed from the reconstructed event record. The red crosses indicate the intercepts of the reconstructed muon trajectories with the calorimeter surface. The red (blue) boxes correspond to clusters in the ECAL (HCAL). |
png pdf |
Figure 3-b:
Display of a $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ candidate event in the 2017 dataset, in the $\eta $-$\phi $ plane at the surface of the calorimeters, (left) before and (right) after the hits and energy deposits associated to the muons have been removed from the reconstructed event record. The red crosses indicate the intercepts of the reconstructed muon trajectories with the calorimeter surface. The red (blue) boxes correspond to clusters in the ECAL (HCAL). |
png pdf |
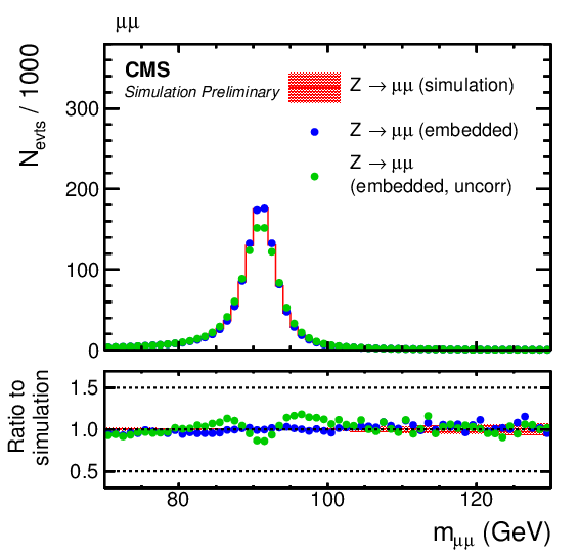
Figure 4:
Comparison of the reconstructed invariant mass, $ {m_{\mu \mu}} $, of the selected muons from a simulated validation sample with the corresponding $ {{\mu}}$-embedded event sample. On the left the (red histogram) validation sample and the $ {{\mu}}$-embedded event sample (blue dots) with and (green dots) without the correction for the effects of the finite detector resolution, as described in the text are shown. On the right (magenta histogram) $ {m_{\mu \mu}} $ from the validation sample before FSR is shown in addition, to illustrate the effect. |
png pdf |
Figure 4-a:
Comparison of the reconstructed invariant mass, $ {m_{\mu \mu}} $, of the selected muons from a simulated validation sample with the corresponding $ {{\mu}}$-embedded event sample. On the left the (red histogram) validation sample and the $ {{\mu}}$-embedded event sample (blue dots) with and (green dots) without the correction for the effects of the finite detector resolution, as described in the text are shown. On the right (magenta histogram) $ {m_{\mu \mu}} $ from the validation sample before FSR is shown in addition, to illustrate the effect. |
png pdf |
Figure 4-b:
Comparison of the reconstructed invariant mass, $ {m_{\mu \mu}} $, of the selected muons from a simulated validation sample with the corresponding $ {{\mu}}$-embedded event sample. On the left the (red histogram) validation sample and the $ {{\mu}}$-embedded event sample (blue dots) with and (green dots) without the correction for the effects of the finite detector resolution, as described in the text are shown. On the right (magenta histogram) $ {m_{\mu \mu}} $ from the validation sample before FSR is shown in addition, to illustrate the effect. |
png pdf |
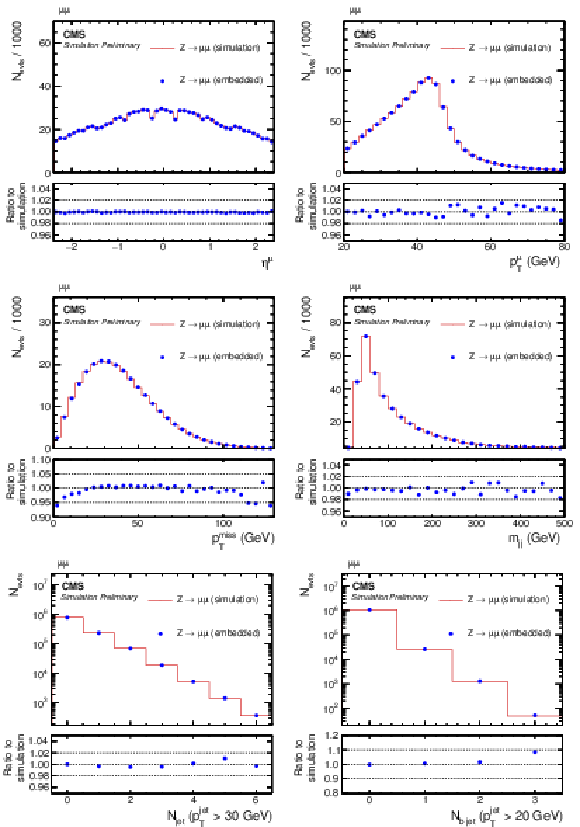
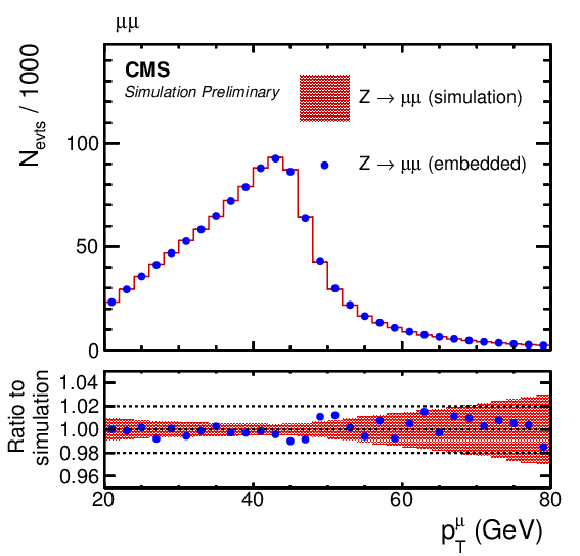
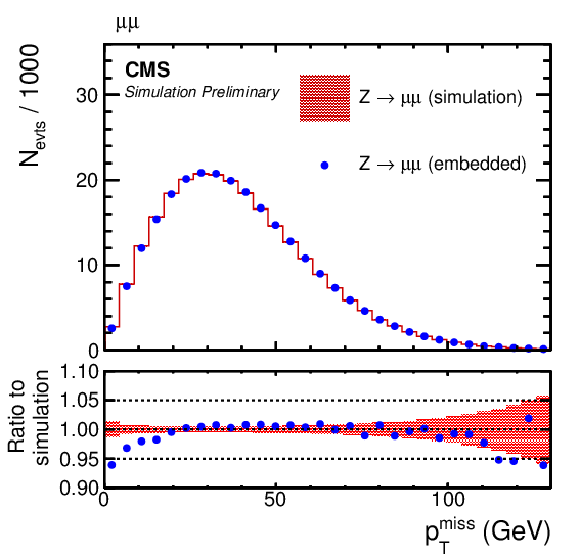
Figure 5:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown are the (upper left) $\eta $ and (upper right) $ {p_{\mathrm {T}}} $ distributions of the leading muon in $ {p_{\mathrm {T}}} $, (middle left) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) jet and (lower right) b jet multiplicities, as described in the text. |
png pdf |
Figure 5-a:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown are the (upper left) $\eta $ and (upper right) $ {p_{\mathrm {T}}} $ distributions of the leading muon in $ {p_{\mathrm {T}}} $, (middle left) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) jet and (lower right) b jet multiplicities, as described in the text. |
png pdf |
Figure 5-b:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown are the (upper left) $\eta $ and (upper right) $ {p_{\mathrm {T}}} $ distributions of the leading muon in $ {p_{\mathrm {T}}} $, (middle left) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) jet and (lower right) b jet multiplicities, as described in the text. |
png pdf |
Figure 5-c:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown are the (upper left) $\eta $ and (upper right) $ {p_{\mathrm {T}}} $ distributions of the leading muon in $ {p_{\mathrm {T}}} $, (middle left) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) jet and (lower right) b jet multiplicities, as described in the text. |
png pdf |
Figure 5-d:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown are the (upper left) $\eta $ and (upper right) $ {p_{\mathrm {T}}} $ distributions of the leading muon in $ {p_{\mathrm {T}}} $, (middle left) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) jet and (lower right) b jet multiplicities, as described in the text. |
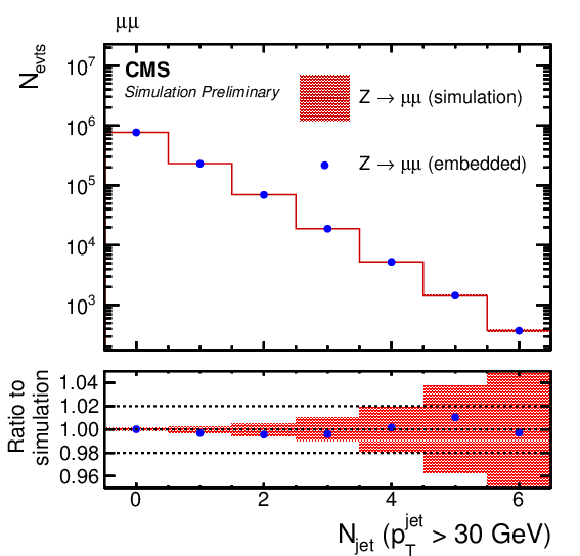
png pdf |
Figure 5-e:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown are the (upper left) $\eta $ and (upper right) $ {p_{\mathrm {T}}} $ distributions of the leading muon in $ {p_{\mathrm {T}}} $, (middle left) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) jet and (lower right) b jet multiplicities, as described in the text. |
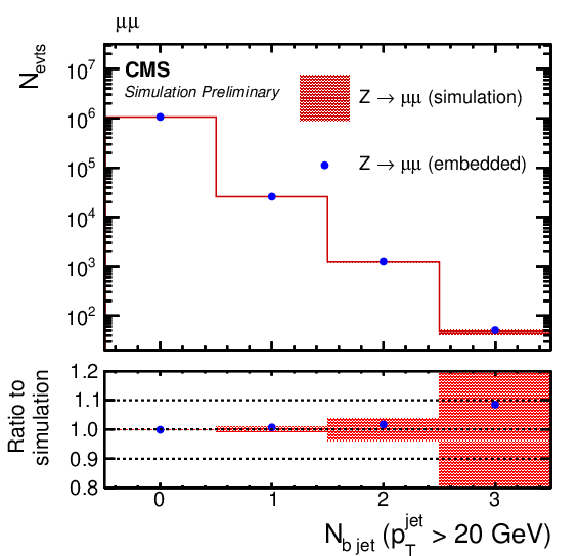
png pdf |
Figure 5-f:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown are the (upper left) $\eta $ and (upper right) $ {p_{\mathrm {T}}} $ distributions of the leading muon in $ {p_{\mathrm {T}}} $, (middle left) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) jet and (lower right) b jet multiplicities, as described in the text. |
png pdf |
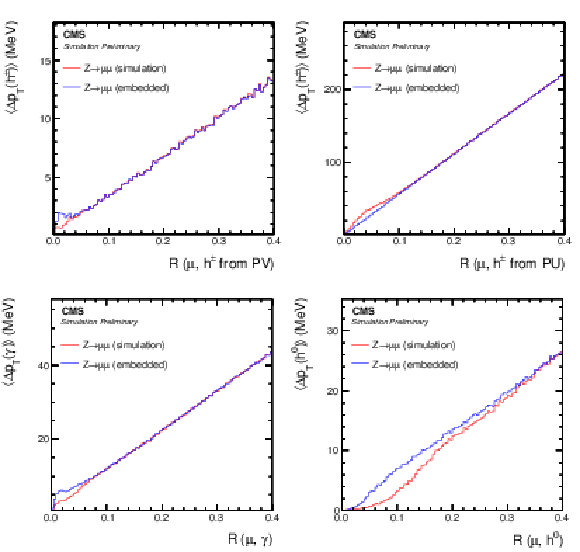
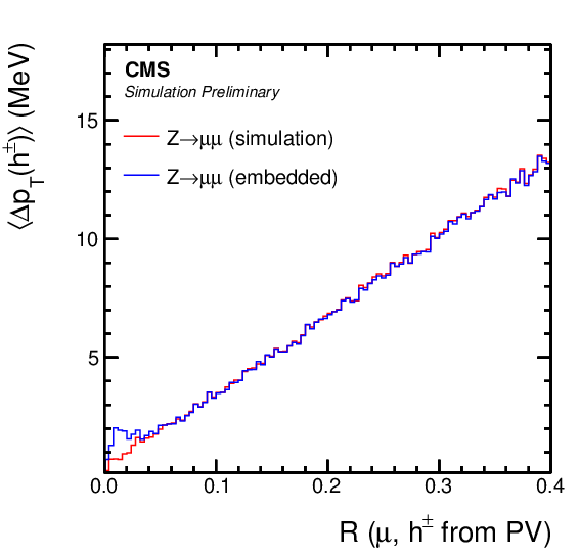
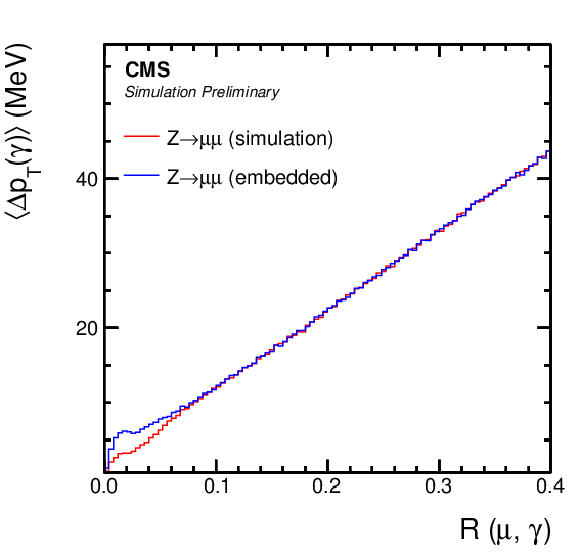
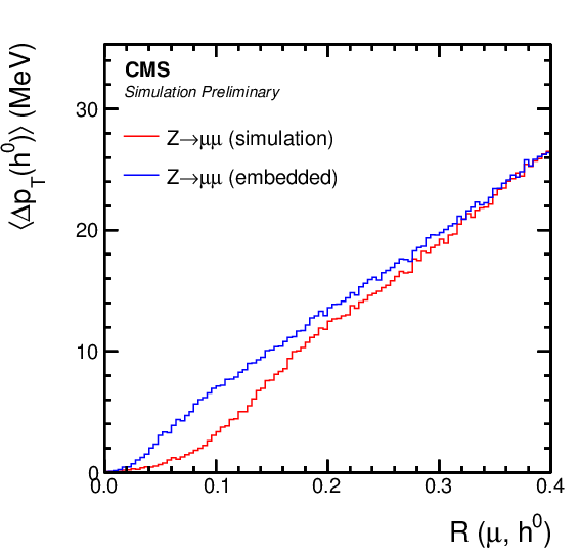
Figure 6:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown is the mean transverse momentum (energy) flux per muon, from all reconstructed particles in the distance $R$ to the muon, split by (upper left) charged hadrons from the PV and (upper right) PU vertices, (lower left) photons, and (lower right) neutral hadrons. The distributions are shown for the $ {{\mu}}^{-}$ and for events with $ {m_{\mu \mu}} $ close to the nominal Z boson mass. |
png pdf |
Figure 6-a:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown is the mean transverse momentum (energy) flux per muon, from all reconstructed particles in the distance $R$ to the muon, split by (upper left) charged hadrons from the PV and (upper right) PU vertices, (lower left) photons, and (lower right) neutral hadrons. The distributions are shown for the $ {{\mu}}^{-}$ and for events with $ {m_{\mu \mu}} $ close to the nominal Z boson mass. |
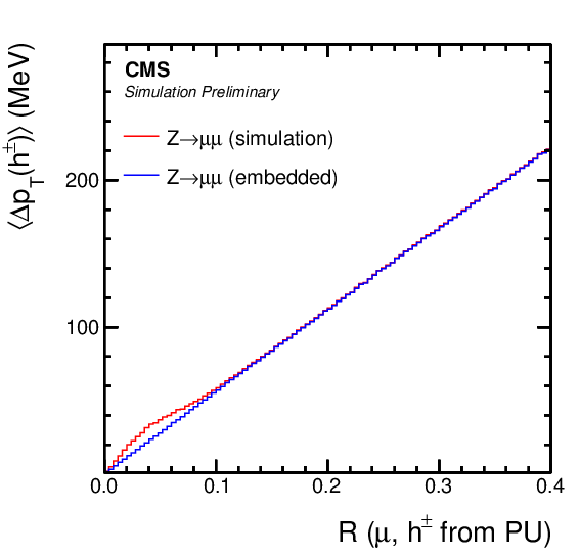
png pdf |
Figure 6-b:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown is the mean transverse momentum (energy) flux per muon, from all reconstructed particles in the distance $R$ to the muon, split by (upper left) charged hadrons from the PV and (upper right) PU vertices, (lower left) photons, and (lower right) neutral hadrons. The distributions are shown for the $ {{\mu}}^{-}$ and for events with $ {m_{\mu \mu}} $ close to the nominal Z boson mass. |
png pdf |
Figure 6-c:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown is the mean transverse momentum (energy) flux per muon, from all reconstructed particles in the distance $R$ to the muon, split by (upper left) charged hadrons from the PV and (upper right) PU vertices, (lower left) photons, and (lower right) neutral hadrons. The distributions are shown for the $ {{\mu}}^{-}$ and for events with $ {m_{\mu \mu}} $ close to the nominal Z boson mass. |
png pdf |
Figure 6-d:
Comparison of $ {{\mu}}$-embedded events with exactly the same $ {{{\mathrm {Z}} \to {{\mu}} {{\mu}}}}$ events from simulation. Shown is the mean transverse momentum (energy) flux per muon, from all reconstructed particles in the distance $R$ to the muon, split by (upper left) charged hadrons from the PV and (upper right) PU vertices, (lower left) photons, and (lower right) neutral hadrons. The distributions are shown for the $ {{\mu}}^{-}$ and for events with $ {m_{\mu \mu}} $ close to the nominal Z boson mass. |
png pdf |
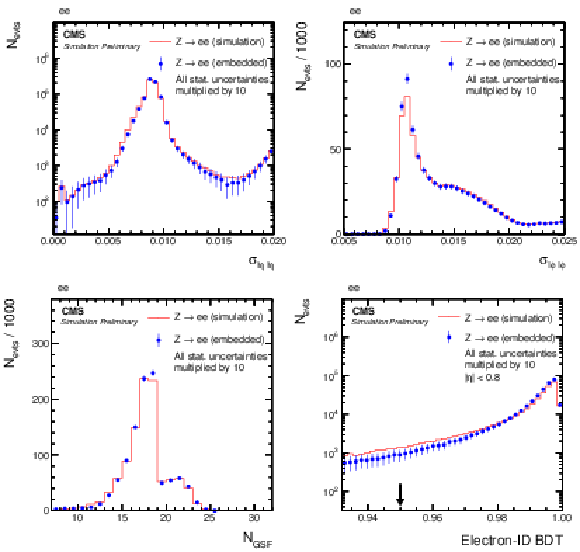
Figure 7:
Comparison of e-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\mathrm {e}} {\mathrm {e}}}}$ events. Shown are distributions of the energy-weighted standard deviations of a $5\times 5$ crystal array in (upper left) $\eta $, $\sigma _{i\eta i\eta}$, and (upper right) $\phi $, $\sigma _{i\phi i\phi}$, as described in the text, (lower left) the number $N_{\text {GSF}}$ of detector hits, used for the Gaussian Sum Filter algorithm [23] as described in Section 3, and (lower right) the multivariate discriminator for the identification of electrons (electron-ID BDT). The black arrow, shown in addition to the electron-ID BDT distribution, indicates the working point with 80% efficiency in the displayed electron $\eta $ region. For better visibility, the statistical uncertainties of both samples have been multiplied by 10 for the figures. |
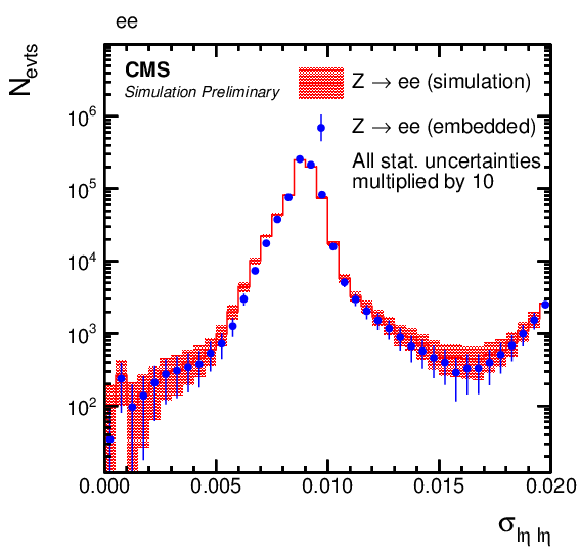
png pdf |
Figure 7-a:
Comparison of e-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\mathrm {e}} {\mathrm {e}}}}$ events. Shown are distributions of the energy-weighted standard deviations of a $5\times 5$ crystal array in (upper left) $\eta $, $\sigma _{i\eta i\eta}$, and (upper right) $\phi $, $\sigma _{i\phi i\phi}$, as described in the text, (lower left) the number $N_{\text {GSF}}$ of detector hits, used for the Gaussian Sum Filter algorithm [23] as described in Section 3, and (lower right) the multivariate discriminator for the identification of electrons (electron-ID BDT). The black arrow, shown in addition to the electron-ID BDT distribution, indicates the working point with 80% efficiency in the displayed electron $\eta $ region. For better visibility, the statistical uncertainties of both samples have been multiplied by 10 for the figures. |
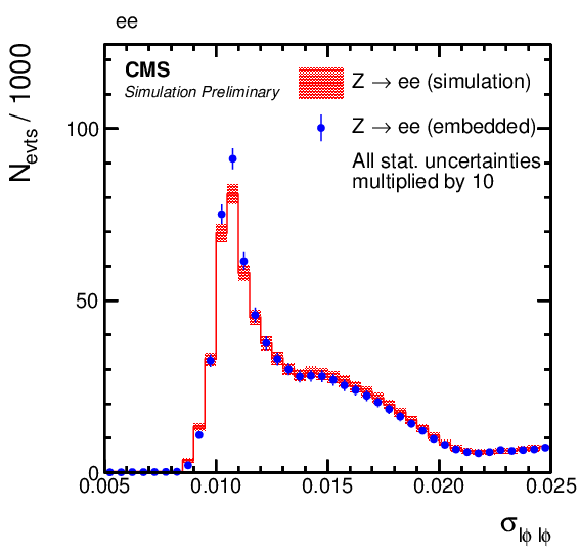
png pdf |
Figure 7-b:
Comparison of e-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\mathrm {e}} {\mathrm {e}}}}$ events. Shown are distributions of the energy-weighted standard deviations of a $5\times 5$ crystal array in (upper left) $\eta $, $\sigma _{i\eta i\eta}$, and (upper right) $\phi $, $\sigma _{i\phi i\phi}$, as described in the text, (lower left) the number $N_{\text {GSF}}$ of detector hits, used for the Gaussian Sum Filter algorithm [23] as described in Section 3, and (lower right) the multivariate discriminator for the identification of electrons (electron-ID BDT). The black arrow, shown in addition to the electron-ID BDT distribution, indicates the working point with 80% efficiency in the displayed electron $\eta $ region. For better visibility, the statistical uncertainties of both samples have been multiplied by 10 for the figures. |
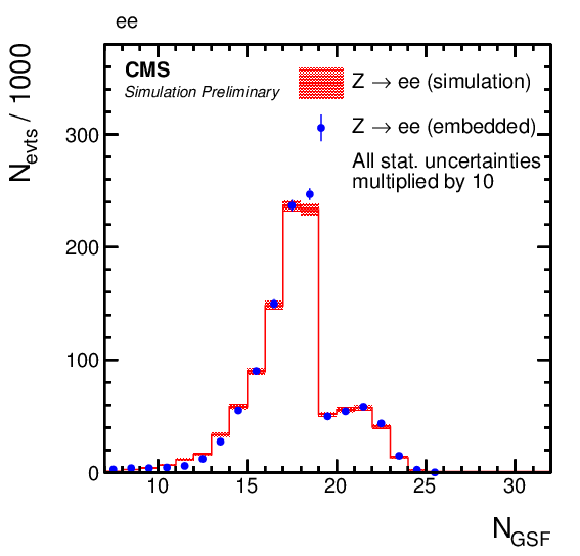
png pdf |
Figure 7-c:
Comparison of e-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\mathrm {e}} {\mathrm {e}}}}$ events. Shown are distributions of the energy-weighted standard deviations of a $5\times 5$ crystal array in (upper left) $\eta $, $\sigma _{i\eta i\eta}$, and (upper right) $\phi $, $\sigma _{i\phi i\phi}$, as described in the text, (lower left) the number $N_{\text {GSF}}$ of detector hits, used for the Gaussian Sum Filter algorithm [23] as described in Section 3, and (lower right) the multivariate discriminator for the identification of electrons (electron-ID BDT). The black arrow, shown in addition to the electron-ID BDT distribution, indicates the working point with 80% efficiency in the displayed electron $\eta $ region. For better visibility, the statistical uncertainties of both samples have been multiplied by 10 for the figures. |
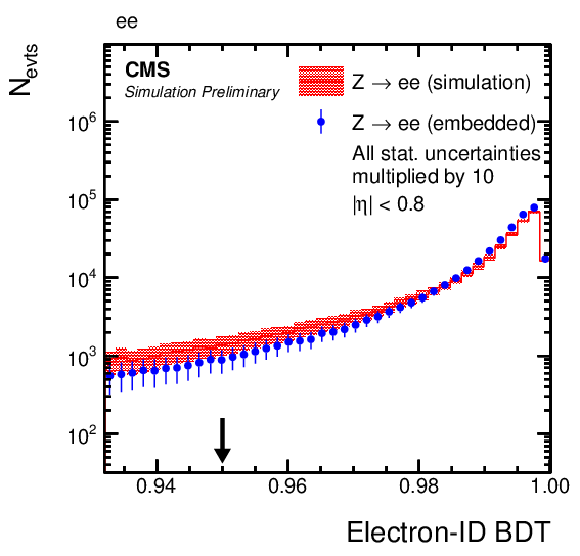
png pdf |
Figure 7-d:
Comparison of e-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\mathrm {e}} {\mathrm {e}}}}$ events. Shown are distributions of the energy-weighted standard deviations of a $5\times 5$ crystal array in (upper left) $\eta $, $\sigma _{i\eta i\eta}$, and (upper right) $\phi $, $\sigma _{i\phi i\phi}$, as described in the text, (lower left) the number $N_{\text {GSF}}$ of detector hits, used for the Gaussian Sum Filter algorithm [23] as described in Section 3, and (lower right) the multivariate discriminator for the identification of electrons (electron-ID BDT). The black arrow, shown in addition to the electron-ID BDT distribution, indicates the working point with 80% efficiency in the displayed electron $\eta $ region. For better visibility, the statistical uncertainties of both samples have been multiplied by 10 for the figures. |
png pdf |
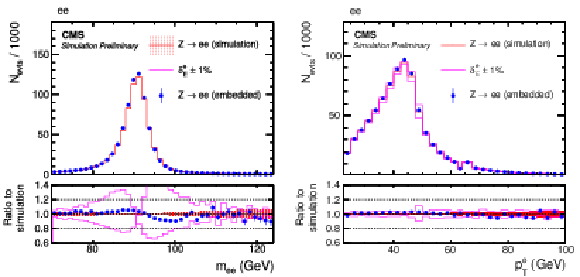
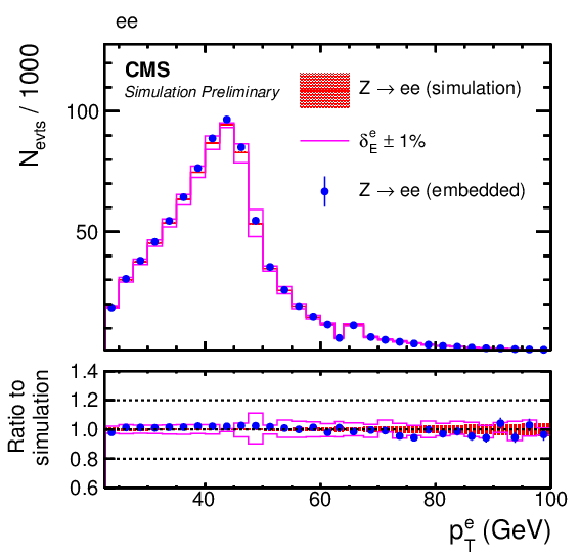
Figure 8:
Comparison of e-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\mathrm {e}} {\mathrm {e}}}}$ events. Shown are the distributions of (left) $m_{\text {ee}}$ and (right) $ {p_{\mathrm {T}}} $ of the leading electron on $ {p_{\mathrm {T}}} $. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. The effect of a variation of the electron energy scale of $ \pm $1% is also shown, by the magenta lines. |
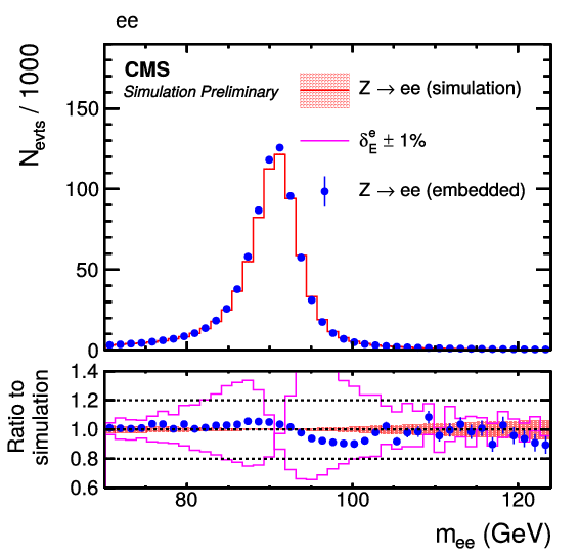
png pdf |
Figure 8-a:
Comparison of e-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\mathrm {e}} {\mathrm {e}}}}$ events. Shown are the distributions of (left) $m_{\text {ee}}$ and (right) $ {p_{\mathrm {T}}} $ of the leading electron on $ {p_{\mathrm {T}}} $. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. The effect of a variation of the electron energy scale of $ \pm $1% is also shown, by the magenta lines. |
png pdf |
Figure 8-b:
Comparison of e-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\mathrm {e}} {\mathrm {e}}}}$ events. Shown are the distributions of (left) $m_{\text {ee}}$ and (right) $ {p_{\mathrm {T}}} $ of the leading electron on $ {p_{\mathrm {T}}} $. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. The effect of a variation of the electron energy scale of $ \pm $1% is also shown, by the magenta lines. |
png pdf |
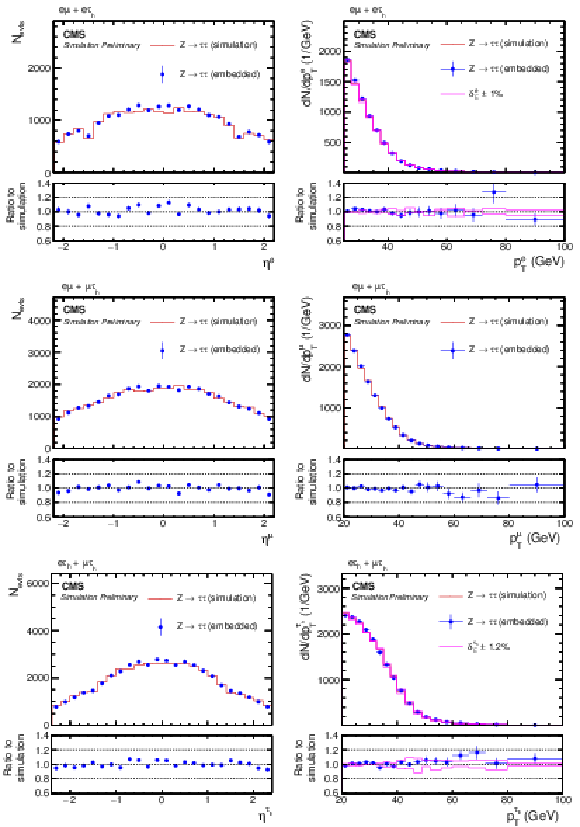
Figure 9:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are the (left) $\eta $ and (right) $ {p_{\mathrm {T}}} $ distributions of the (upper row) electron in the $ {\mathrm {e}} {{\mu}}+ {\mathrm {e}} {\tau}_{\text {h}} $ final state, (middle row) muon in $ {\mathrm {e}} {{\mu}}+ {{\mu}} {\tau}_{\text {h}} $ final state, and (lower row) $ {\tau}_{\text {h}} $ candidate in the $ {\mathrm {e}} {\tau}_{\text {h}} + {{\mu}} {\tau}_{\text {h}} $ final state. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
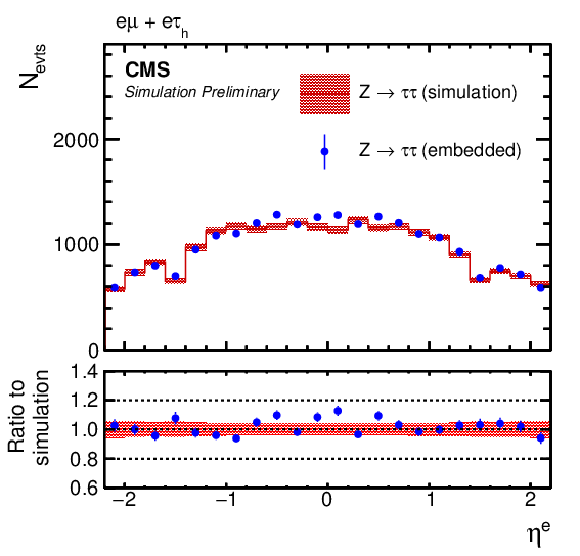
png pdf |
Figure 9-a:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are the (left) $\eta $ and (right) $ {p_{\mathrm {T}}} $ distributions of the (upper row) electron in the $ {\mathrm {e}} {{\mu}}+ {\mathrm {e}} {\tau}_{\text {h}} $ final state, (middle row) muon in $ {\mathrm {e}} {{\mu}}+ {{\mu}} {\tau}_{\text {h}} $ final state, and (lower row) $ {\tau}_{\text {h}} $ candidate in the $ {\mathrm {e}} {\tau}_{\text {h}} + {{\mu}} {\tau}_{\text {h}} $ final state. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
png pdf |
Figure 9-b:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are the (left) $\eta $ and (right) $ {p_{\mathrm {T}}} $ distributions of the (upper row) electron in the $ {\mathrm {e}} {{\mu}}+ {\mathrm {e}} {\tau}_{\text {h}} $ final state, (middle row) muon in $ {\mathrm {e}} {{\mu}}+ {{\mu}} {\tau}_{\text {h}} $ final state, and (lower row) $ {\tau}_{\text {h}} $ candidate in the $ {\mathrm {e}} {\tau}_{\text {h}} + {{\mu}} {\tau}_{\text {h}} $ final state. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
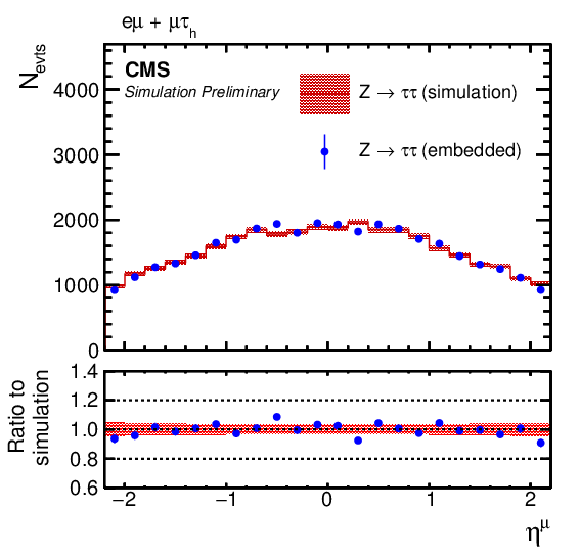
png pdf |
Figure 9-c:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are the (left) $\eta $ and (right) $ {p_{\mathrm {T}}} $ distributions of the (upper row) electron in the $ {\mathrm {e}} {{\mu}}+ {\mathrm {e}} {\tau}_{\text {h}} $ final state, (middle row) muon in $ {\mathrm {e}} {{\mu}}+ {{\mu}} {\tau}_{\text {h}} $ final state, and (lower row) $ {\tau}_{\text {h}} $ candidate in the $ {\mathrm {e}} {\tau}_{\text {h}} + {{\mu}} {\tau}_{\text {h}} $ final state. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
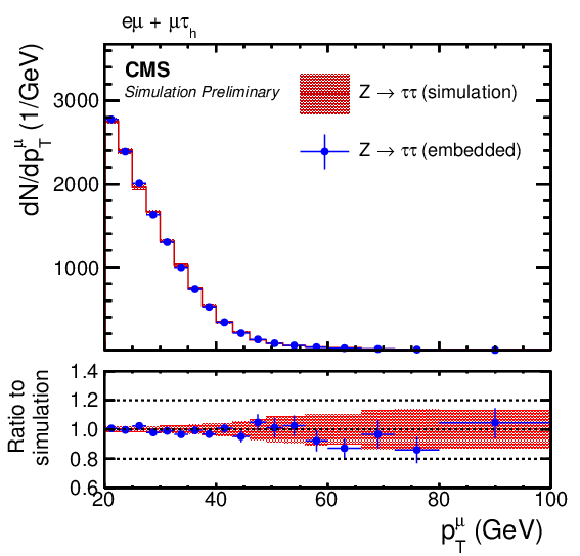
png pdf |
Figure 9-d:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are the (left) $\eta $ and (right) $ {p_{\mathrm {T}}} $ distributions of the (upper row) electron in the $ {\mathrm {e}} {{\mu}}+ {\mathrm {e}} {\tau}_{\text {h}} $ final state, (middle row) muon in $ {\mathrm {e}} {{\mu}}+ {{\mu}} {\tau}_{\text {h}} $ final state, and (lower row) $ {\tau}_{\text {h}} $ candidate in the $ {\mathrm {e}} {\tau}_{\text {h}} + {{\mu}} {\tau}_{\text {h}} $ final state. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
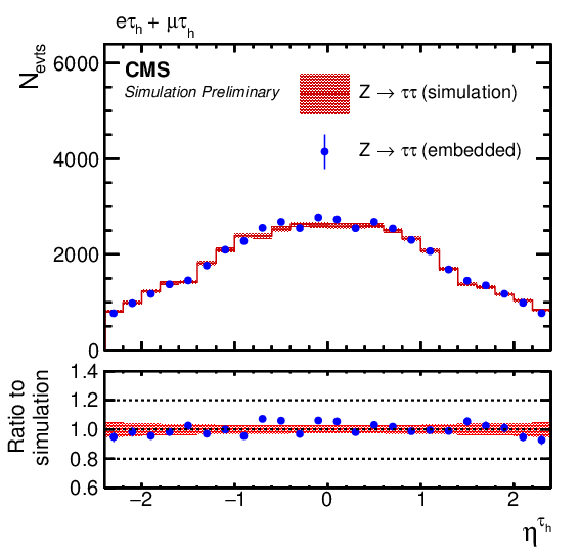
png pdf |
Figure 9-e:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are the (left) $\eta $ and (right) $ {p_{\mathrm {T}}} $ distributions of the (upper row) electron in the $ {\mathrm {e}} {{\mu}}+ {\mathrm {e}} {\tau}_{\text {h}} $ final state, (middle row) muon in $ {\mathrm {e}} {{\mu}}+ {{\mu}} {\tau}_{\text {h}} $ final state, and (lower row) $ {\tau}_{\text {h}} $ candidate in the $ {\mathrm {e}} {\tau}_{\text {h}} + {{\mu}} {\tau}_{\text {h}} $ final state. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
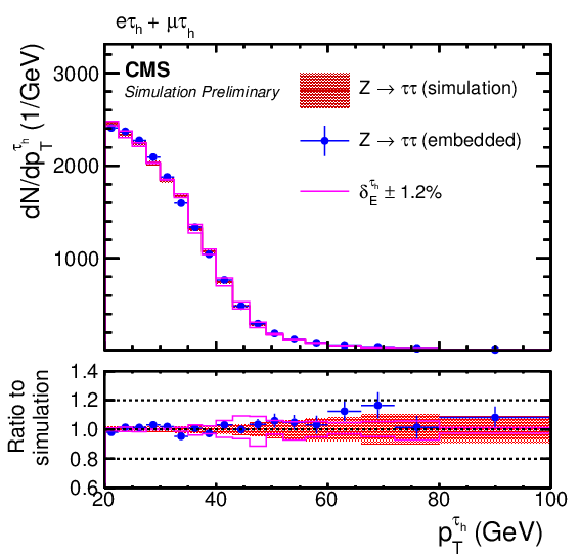
png pdf |
Figure 9-f:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are the (left) $\eta $ and (right) $ {p_{\mathrm {T}}} $ distributions of the (upper row) electron in the $ {\mathrm {e}} {{\mu}}+ {\mathrm {e}} {\tau}_{\text {h}} $ final state, (middle row) muon in $ {\mathrm {e}} {{\mu}}+ {{\mu}} {\tau}_{\text {h}} $ final state, and (lower row) $ {\tau}_{\text {h}} $ candidate in the $ {\mathrm {e}} {\tau}_{\text {h}} + {{\mu}} {\tau}_{\text {h}} $ final state. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
png pdf |
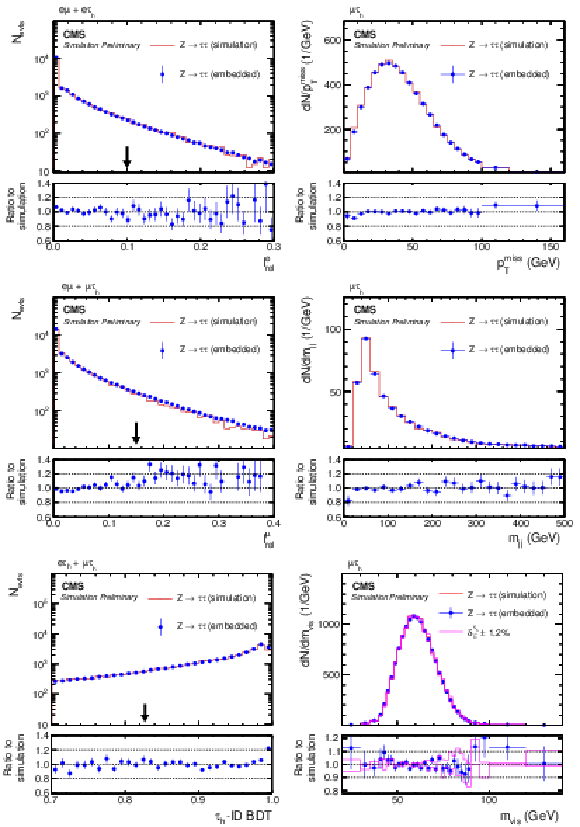
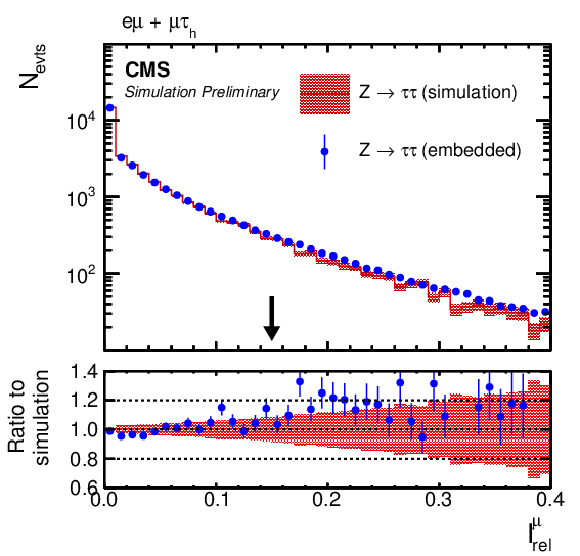
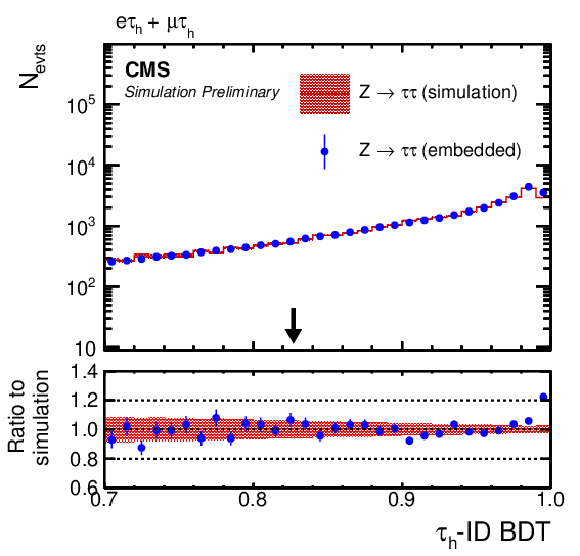
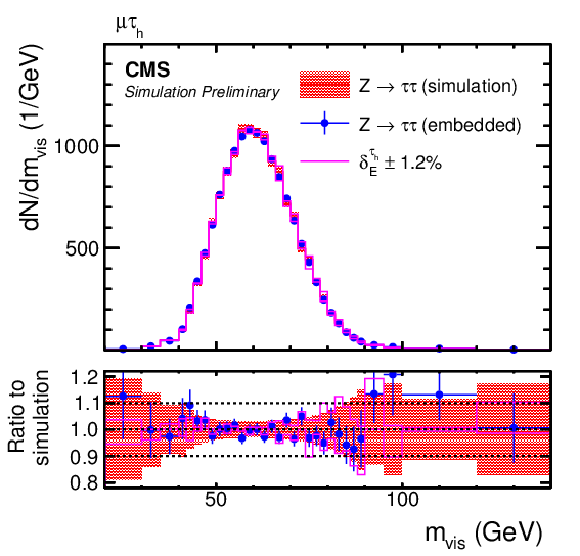
Figure 10:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are distributions of (upper left) $ {I_{\text {rel}}^{\text {e}}} $, (upper right) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle left) $ {I_{\text {rel}}^{\mu}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) $ {\tau}_{\text {h}} $-ID BDT, and $ {m_{\text {vis}}} $ as discussed in the text. The black arrows indicate the working points used in the target analysis. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
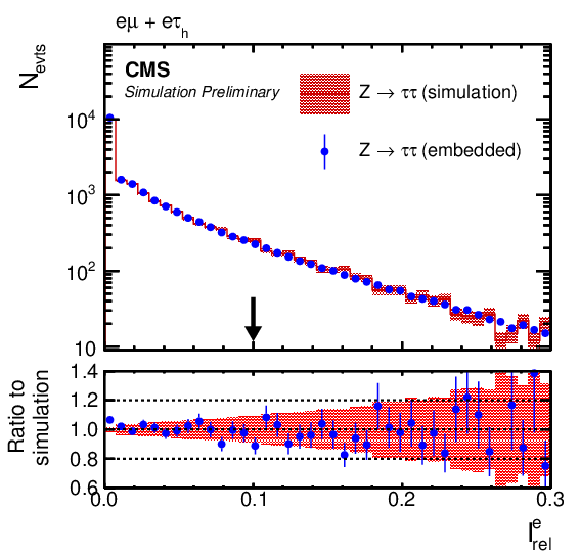
png pdf |
Figure 10-a:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are distributions of (upper left) $ {I_{\text {rel}}^{\text {e}}} $, (upper right) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle left) $ {I_{\text {rel}}^{\mu}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) $ {\tau}_{\text {h}} $-ID BDT, and $ {m_{\text {vis}}} $ as discussed in the text. The black arrows indicate the working points used in the target analysis. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
png pdf |
Figure 10-b:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are distributions of (upper left) $ {I_{\text {rel}}^{\text {e}}} $, (upper right) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle left) $ {I_{\text {rel}}^{\mu}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) $ {\tau}_{\text {h}} $-ID BDT, and $ {m_{\text {vis}}} $ as discussed in the text. The black arrows indicate the working points used in the target analysis. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
png pdf |
Figure 10-c:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are distributions of (upper left) $ {I_{\text {rel}}^{\text {e}}} $, (upper right) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle left) $ {I_{\text {rel}}^{\mu}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) $ {\tau}_{\text {h}} $-ID BDT, and $ {m_{\text {vis}}} $ as discussed in the text. The black arrows indicate the working points used in the target analysis. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
png pdf |
Figure 10-d:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are distributions of (upper left) $ {I_{\text {rel}}^{\text {e}}} $, (upper right) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle left) $ {I_{\text {rel}}^{\mu}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) $ {\tau}_{\text {h}} $-ID BDT, and $ {m_{\text {vis}}} $ as discussed in the text. The black arrows indicate the working points used in the target analysis. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
png pdf |
Figure 10-e:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are distributions of (upper left) $ {I_{\text {rel}}^{\text {e}}} $, (upper right) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle left) $ {I_{\text {rel}}^{\mu}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) $ {\tau}_{\text {h}} $-ID BDT, and $ {m_{\text {vis}}} $ as discussed in the text. The black arrows indicate the working points used in the target analysis. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
png pdf |
Figure 10-f:
Comparison of $ {\tau}$-embedded events with a statistically independent sample of simulated $ {{{\mathrm {Z}} \to {\tau} {\tau}}}$ events. Shown are distributions of (upper left) $ {I_{\text {rel}}^{\text {e}}} $, (upper right) $ {{p_{\mathrm {T}}} ^\text {miss}} $, (middle left) $ {I_{\text {rel}}^{\mu}} $, (middle right) $ {m_{\text {jj}}} $, (lower left) $ {\tau}_{\text {h}} $-ID BDT, and $ {m_{\text {vis}}} $ as discussed in the text. The black arrows indicate the working points used in the target analysis. The blue error bars and red shaded bands correspond to the statistical uncertainty of each sample. |
png pdf |
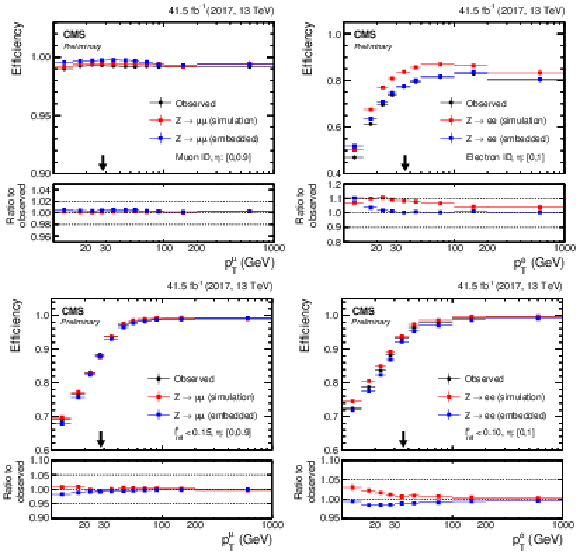
Figure 11:
(Left column) Muon and (right column) electron (upper row) identification and (lower row) isolation efficiencies as a function of the $ {p_{\mathrm {T}}} $ of the corresponding lepton in the central region of the detector. The black arrows indicate typical trigger thresholds of the target analyses. |
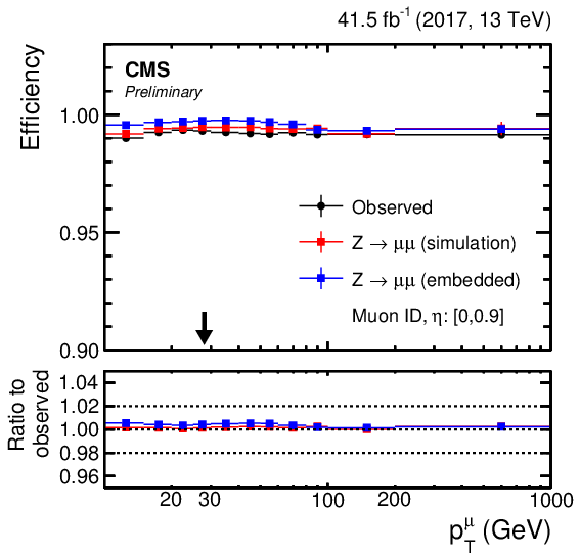
png pdf |
Figure 11-a:
(Left column) Muon and (right column) electron (upper row) identification and (lower row) isolation efficiencies as a function of the $ {p_{\mathrm {T}}} $ of the corresponding lepton in the central region of the detector. The black arrows indicate typical trigger thresholds of the target analyses. |
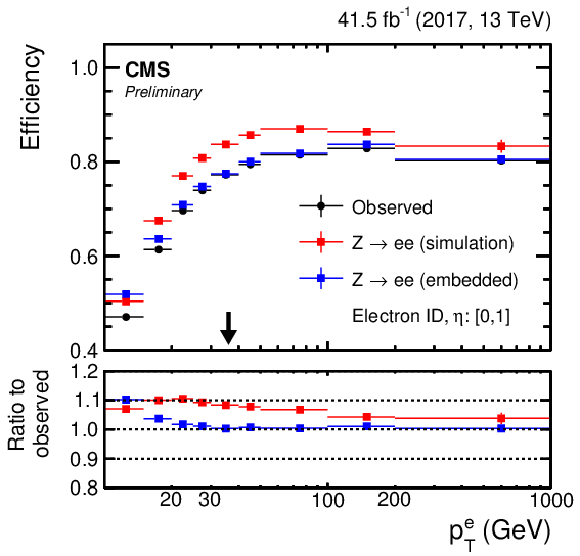
png pdf |
Figure 11-b:
(Left column) Muon and (right column) electron (upper row) identification and (lower row) isolation efficiencies as a function of the $ {p_{\mathrm {T}}} $ of the corresponding lepton in the central region of the detector. The black arrows indicate typical trigger thresholds of the target analyses. |
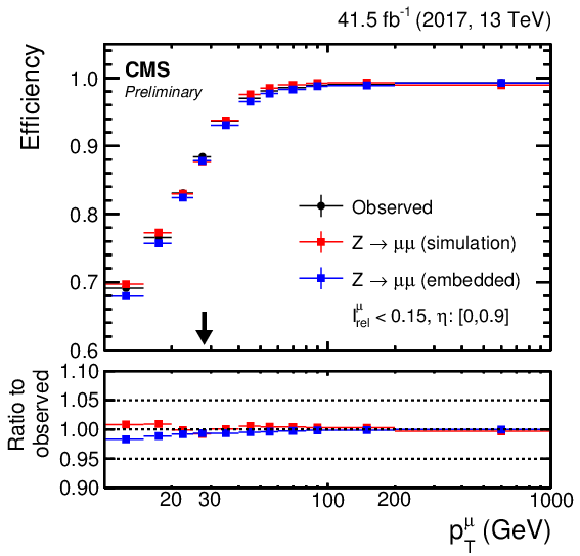
png pdf |
Figure 11-c:
(Left column) Muon and (right column) electron (upper row) identification and (lower row) isolation efficiencies as a function of the $ {p_{\mathrm {T}}} $ of the corresponding lepton in the central region of the detector. The black arrows indicate typical trigger thresholds of the target analyses. |
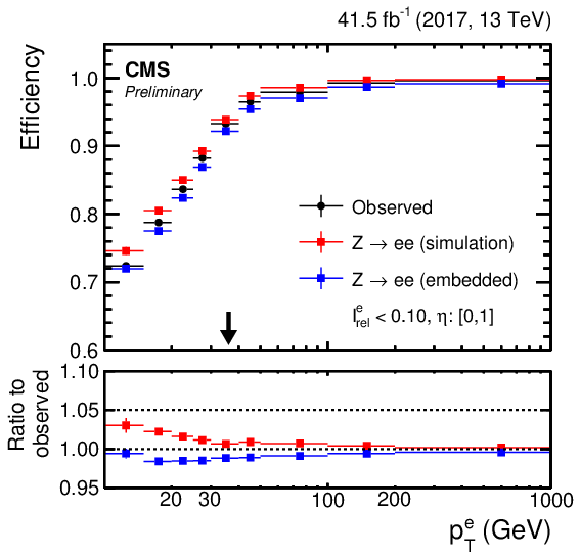
png pdf |
Figure 11-d:
(Left column) Muon and (right column) electron (upper row) identification and (lower row) isolation efficiencies as a function of the $ {p_{\mathrm {T}}} $ of the corresponding lepton in the central region of the detector. The black arrows indicate typical trigger thresholds of the target analyses. |
png pdf |
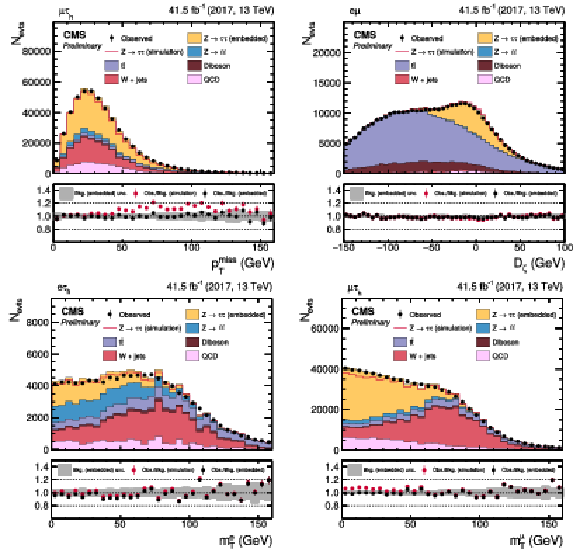
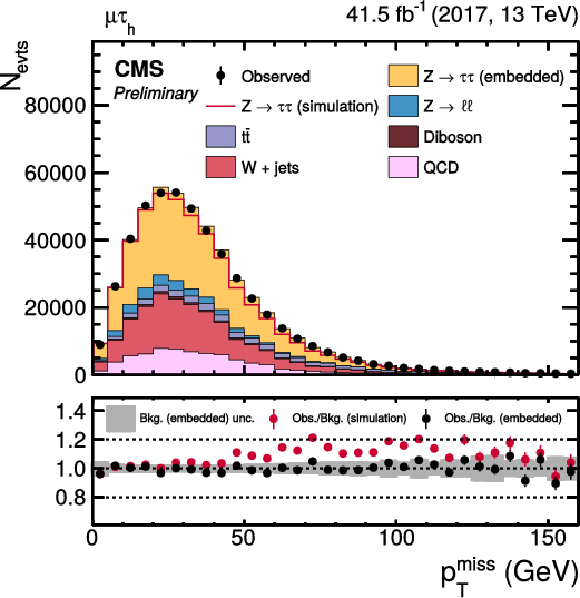
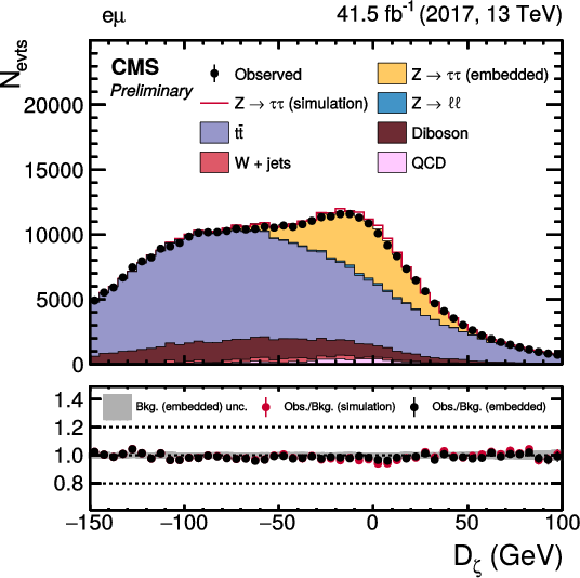
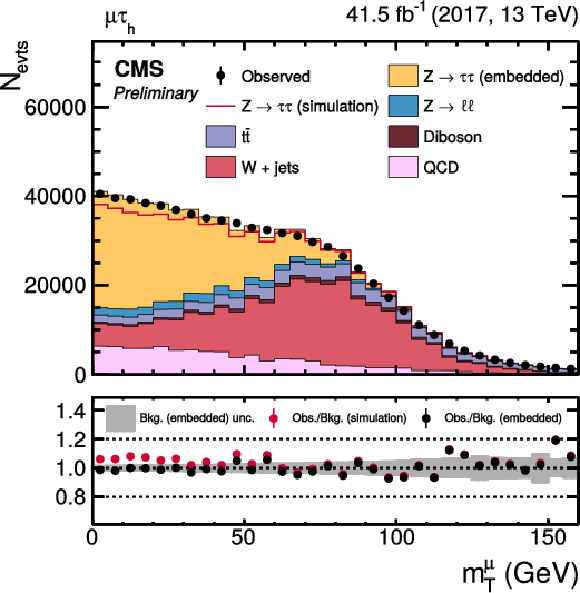
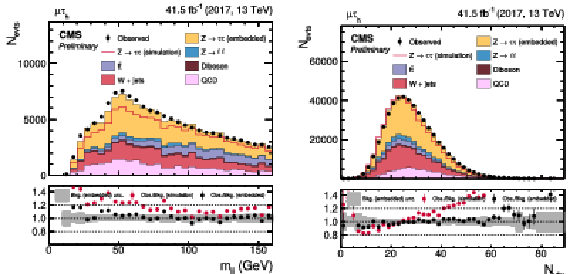
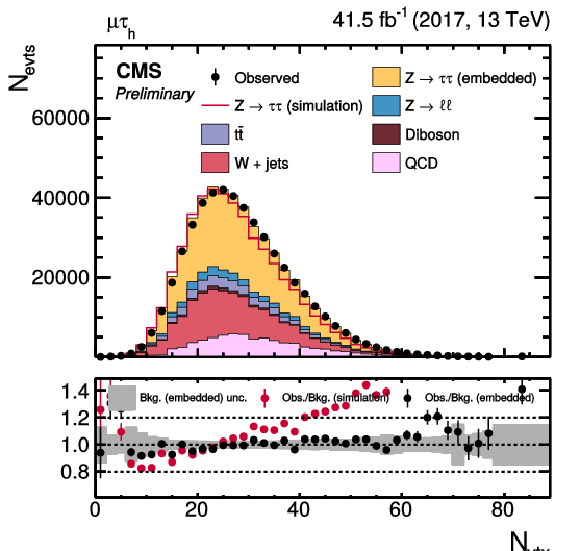
Figure 12:
Distributions of (upper left) $ {{p_{\mathrm {T}}} ^\text {miss}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state, (upper right) $ {D_{\zeta}} $ in the $ {\mathrm {e}} {{\mu}}$ final state, (lower left) $ {m_{\text {T}}^{{\mathrm {e}}}} $ in the $ {\mathrm {e}} {\tau}_{\text {h}} $ final state, and (lower right) $ {m_{\text {T}}^{{{\mu}}}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state. The distributions are shown prior to the maximum likelihood fit described in the text. For these figures no uncertainties that affect the shape of the distributions have been included in the uncertainty bel. The background estimation purely by the CMS simulation is shown as an additional red line. |
png pdf |
Figure 12-a:
Distributions of (upper left) $ {{p_{\mathrm {T}}} ^\text {miss}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state, (upper right) $ {D_{\zeta}} $ in the $ {\mathrm {e}} {{\mu}}$ final state, (lower left) $ {m_{\text {T}}^{{\mathrm {e}}}} $ in the $ {\mathrm {e}} {\tau}_{\text {h}} $ final state, and (lower right) $ {m_{\text {T}}^{{{\mu}}}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state. The distributions are shown prior to the maximum likelihood fit described in the text. For these figures no uncertainties that affect the shape of the distributions have been included in the uncertainty bel. The background estimation purely by the CMS simulation is shown as an additional red line. |
png pdf |
Figure 12-b:
Distributions of (upper left) $ {{p_{\mathrm {T}}} ^\text {miss}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state, (upper right) $ {D_{\zeta}} $ in the $ {\mathrm {e}} {{\mu}}$ final state, (lower left) $ {m_{\text {T}}^{{\mathrm {e}}}} $ in the $ {\mathrm {e}} {\tau}_{\text {h}} $ final state, and (lower right) $ {m_{\text {T}}^{{{\mu}}}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state. The distributions are shown prior to the maximum likelihood fit described in the text. For these figures no uncertainties that affect the shape of the distributions have been included in the uncertainty bel. The background estimation purely by the CMS simulation is shown as an additional red line. |
png pdf |
Figure 12-c:
Distributions of (upper left) $ {{p_{\mathrm {T}}} ^\text {miss}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state, (upper right) $ {D_{\zeta}} $ in the $ {\mathrm {e}} {{\mu}}$ final state, (lower left) $ {m_{\text {T}}^{{\mathrm {e}}}} $ in the $ {\mathrm {e}} {\tau}_{\text {h}} $ final state, and (lower right) $ {m_{\text {T}}^{{{\mu}}}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state. The distributions are shown prior to the maximum likelihood fit described in the text. For these figures no uncertainties that affect the shape of the distributions have been included in the uncertainty bel. The background estimation purely by the CMS simulation is shown as an additional red line. |
png pdf |
Figure 12-d:
Distributions of (upper left) $ {{p_{\mathrm {T}}} ^\text {miss}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state, (upper right) $ {D_{\zeta}} $ in the $ {\mathrm {e}} {{\mu}}$ final state, (lower left) $ {m_{\text {T}}^{{\mathrm {e}}}} $ in the $ {\mathrm {e}} {\tau}_{\text {h}} $ final state, and (lower right) $ {m_{\text {T}}^{{{\mu}}}} $ in the $ {{\mu}} {\tau}_{\text {h}} $ final state. The distributions are shown prior to the maximum likelihood fit described in the text. For these figures no uncertainties that affect the shape of the distributions have been included in the uncertainty bel. The background estimation purely by the CMS simulation is shown as an additional red line. |
png pdf |
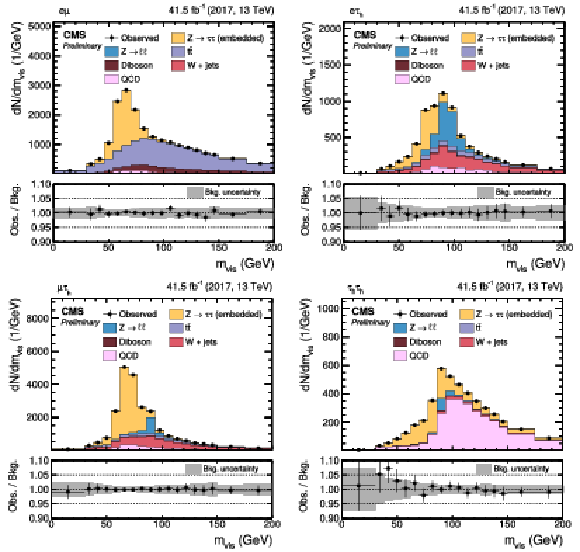
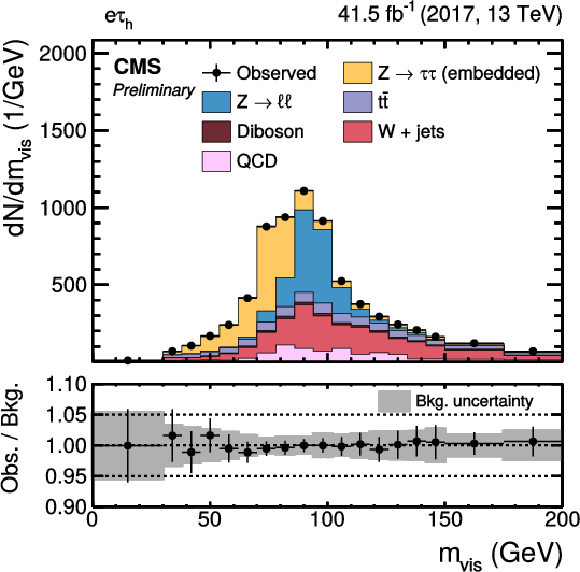
Figure 13:
Invariant mass distribution of the visible $ {\tau} {\tau}$ decay products, $ {m_{\text {vis}}} $, in the (upper left) $ {\mathrm {e}} {{\mu}}$, (upper right) $ {\mathrm {e}} {\tau}_{\text {h}} $, (lower left) $ {{\mu}} {\tau}_{\text {h}} $, and (lower right) $ {\tau}_{\text {h}} {\tau}_{\text {h}} $ final states, after a fit to the data exploiting a typical uncertainty model as, e.g., discussed in Ref. [39]. |
png pdf |
Figure 13-a:
Invariant mass distribution of the visible $ {\tau} {\tau}$ decay products, $ {m_{\text {vis}}} $, in the (upper left) $ {\mathrm {e}} {{\mu}}$, (upper right) $ {\mathrm {e}} {\tau}_{\text {h}} $, (lower left) $ {{\mu}} {\tau}_{\text {h}} $, and (lower right) $ {\tau}_{\text {h}} {\tau}_{\text {h}} $ final states, after a fit to the data exploiting a typical uncertainty model as, e.g., discussed in Ref. [39]. |
png pdf |
Figure 13-b:
Invariant mass distribution of the visible $ {\tau} {\tau}$ decay products, $ {m_{\text {vis}}} $, in the (upper left) $ {\mathrm {e}} {{\mu}}$, (upper right) $ {\mathrm {e}} {\tau}_{\text {h}} $, (lower left) $ {{\mu}} {\tau}_{\text {h}} $, and (lower right) $ {\tau}_{\text {h}} {\tau}_{\text {h}} $ final states, after a fit to the data exploiting a typical uncertainty model as, e.g., discussed in Ref. [39]. |
png pdf |
Figure 13-c:
Invariant mass distribution of the visible $ {\tau} {\tau}$ decay products, $ {m_{\text {vis}}} $, in the (upper left) $ {\mathrm {e}} {{\mu}}$, (upper right) $ {\mathrm {e}} {\tau}_{\text {h}} $, (lower left) $ {{\mu}} {\tau}_{\text {h}} $, and (lower right) $ {\tau}_{\text {h}} {\tau}_{\text {h}} $ final states, after a fit to the data exploiting a typical uncertainty model as, e.g., discussed in Ref. [39]. |
png pdf |
Figure 13-d:
Invariant mass distribution of the visible $ {\tau} {\tau}$ decay products, $ {m_{\text {vis}}} $, in the (upper left) $ {\mathrm {e}} {{\mu}}$, (upper right) $ {\mathrm {e}} {\tau}_{\text {h}} $, (lower left) $ {{\mu}} {\tau}_{\text {h}} $, and (lower right) $ {\tau}_{\text {h}} {\tau}_{\text {h}} $ final states, after a fit to the data exploiting a typical uncertainty model as, e.g., discussed in Ref. [39]. |
png pdf |
Figure 14:
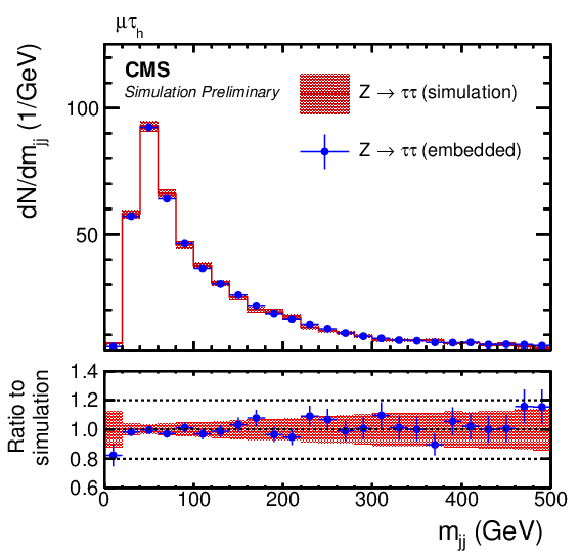
Distributions of (left) $ {m_{\text {jj}}} $ and (right) the number of reconstructed primary vertices $N_{\text {vtx}}$ in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
png pdf |
Figure 14-a:
Distributions of (left) $ {m_{\text {jj}}} $ and (right) the number of reconstructed primary vertices $N_{\text {vtx}}$ in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
png pdf |
Figure 14-b:
Distributions of (left) $ {m_{\text {jj}}} $ and (right) the number of reconstructed primary vertices $N_{\text {vtx}}$ in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
png pdf |
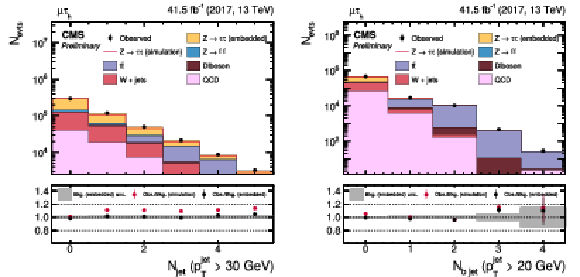
Figure 15:
Distributions of the (left) jet and (right) b jet multiplicity, as described in the text, in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
png pdf |
Figure 15-a:
Distributions of the (left) jet and (right) b jet multiplicity, as described in the text, in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
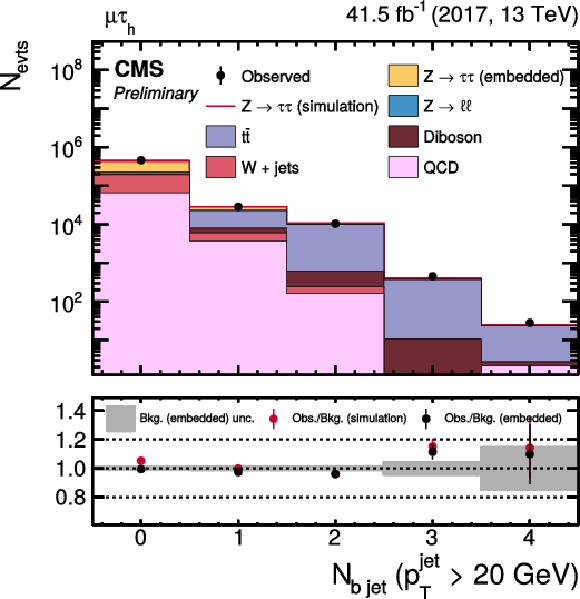
png pdf |
Figure 15-b:
Distributions of the (left) jet and (right) b jet multiplicity, as described in the text, in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
png pdf |
Figure 16:
Distributions of the $ {p_{\mathrm {T}}} $ of the (left) leading and (right) trailing jet for events with more than one jet in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
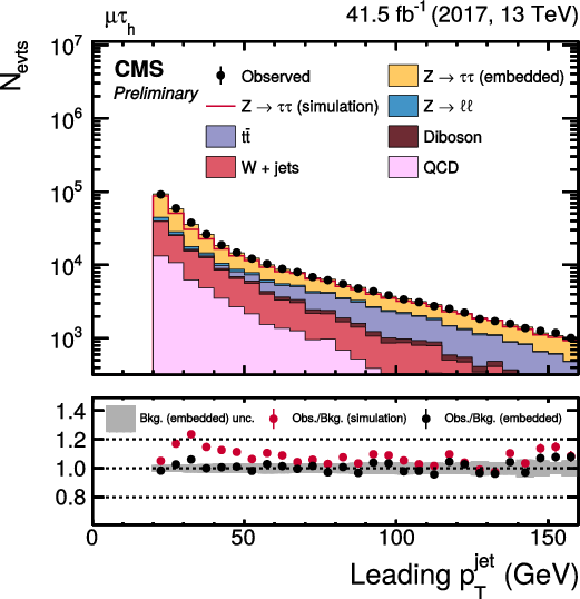
png pdf |
Figure 16-a:
Distributions of the $ {p_{\mathrm {T}}} $ of the (left) leading and (right) trailing jet for events with more than one jet in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
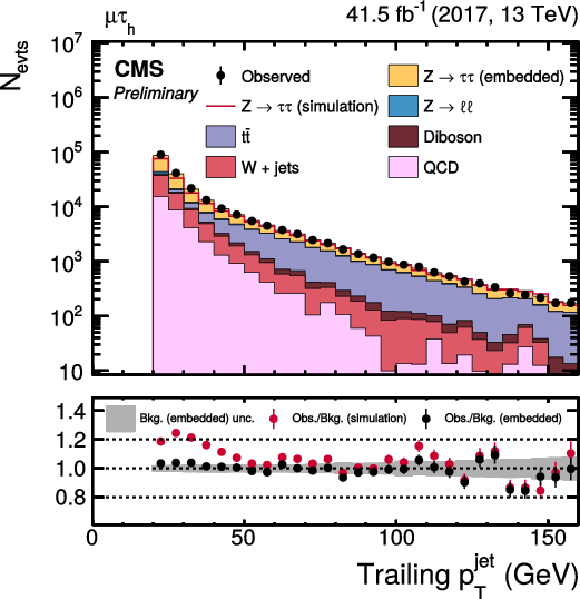
png pdf |
Figure 16-b:
Distributions of the $ {p_{\mathrm {T}}} $ of the (left) leading and (right) trailing jet for events with more than one jet in the $ {{\mu}} {\tau}_{\text {h}} $ final state. |
| Tables | |
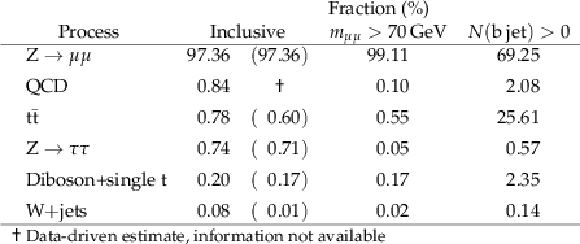
png pdf |
Table 1:
Expected event composition after the selection of two muons, as described in Section 5.2. The composition with an additional requirement of $ {m_{\mu \mu}} > $ 70 GeV and with an additional requirement of at least one b jet with $ {p_{\mathrm {T}}} > $ 20 GeV are given in the third and fourth column respectively. In the second column the fraction of events where the corresponding process has two genuine muons in the final state is given in parentheses. |
png pdf |
Table 2:
Kinematic range of eligibility for each $ {\tau}$-embedded event sample in the $ {\mathrm {e}} {{\mu}}$, $ {\mathrm {e}} {\tau}_{\text {h}} $, $ {{\mu}} {\tau}_{\text {h}} $, and $ {\tau}_{\text {h}} {\tau}_{\text {h}} $ final states. The expression "First/Second object'' refers to the final state label used in the first column. Also given are the probability of the simulated tau lepton pair to pass the kinematic filtering ($\epsilon _{\text {kin}}$), described in the text, and the equivalent of the integrated luminosity $\mathcal {L}_{\text {int}}$, of the corresponding $ {\tau}$-embedded event sample, in multiples of the dataset, from which the embedded event sample has been created. |
png pdf |
Table 3:
Normalization of the $ {\tau}$-embedded event samples and p-values of the saturated model (SAT), Kolmogorov-Smirnov (KS) and Anderson-Darling (AD) test, as discussed in the text, separated by $ {\tau} {\tau}$ final state, as introduced in Section 5 and (where applicable) for all channels combined. The p-values have a statistical precision better than 0.5%. |
| Summary |
| The CMS $\tau$-embedding technique to estimate genuine $\tau\tau$ standard model backgrounds in various $\tau\tau$ final states has been presented. The main target of the procedure is to estimate the background from $\mathrm{Z}\to\tau^{+}\tau^{-}$ events using observed $\mathrm{Z}\to\mu^{+}\mu^{-}$ events. The estimate also includes events from $\mathrm{t\bar{t}}$ production with two genuine tau leptons in the final state. Recorded $\mu^{+}\mu^{-}$ events are selected, the muons removed from the reconstructed event record, and replaced with simulated tau leptons with the same kinematic properties as the removed muons. In that way a hybrid event is obtained, which relies on the simulation only for the decay of the tau leptons. Challenges in describing the underlying event or the production of associated jets in the simulation are avoided. The technique developed for the CMS experiment has been described, and its validation and relevant uncertainties discussed. The description is based on the experimental setup of the year 2017. The data used to demonstrate the performance of the method correspond to an integrated luminosity of 41.5 fb$^{-1}$. |
| References | ||||
| 1 | CMS Collaboration | Measurements of inclusive $ \mathrm{W} $ and $ \mathrm{Z} $ cross sections in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 7 TeV | JHEP 01 (2011) 080 | CMS-EWK-10-002 1012.2466 |
| 2 | CMS Collaboration | Search for neutral Higgs bosons decaying to tau pairs in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 7 TeV | PLB 713 (2012) 68 | CMS-HIG-11-029 1202.4083 |
| 3 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 4 | CMS Collaboration | Observation of a new boson with mass near 125 GeV in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 7 and 8 TeV | JHEP 06 (2013) 081 | CMS-HIG-12-036 1303.4571 |
| 5 | CMS Collaboration | Evidence for the 125 GeV Higgs boson decaying to a pair of $ \tau $ leptons | JHEP 05 (2014) 104 | CMS-HIG-13-004 1401.5041 |
| 6 | CMS Collaboration | Search for neutral minimal supersymmetric standard model Higgs bosons decaying to tau pairs in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 7 TeV | PRL 106 (2011) 231801 | CMS-HIG-10-002 1104.1619 |
| 7 | CMS Collaboration | Search for neutral MSSM Higgs bosons decaying to a pair of tau leptons in pp collisions | JHEP 10 (2014) 160 | CMS-HIG-13-021 1408.3316 |
| 8 | CMS Collaboration | Search for additional neutral MSSM Higgs bosons in the $ \tau\tau $ final state in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 09 (2018) 007 | CMS-HIG-17-020 1803.06553 |
| 9 | ATLAS Collaboration | Search for the Standard Model Higgs boson in the $ H $ to $ \tau^{+} \tau^{-} $ decay mode in $ \sqrt{s}=7 TeV pp $ collisions with ATLAS | JHEP 09 (2012) 070 | 1206.5971 |
| 10 | ATLAS Collaboration | Evidence for the Higgs-boson Yukawa coupling to tau leptons with the ATLAS detector | JHEP 04 (2015) 117 | 1501.04943 |
| 11 | ATLAS Collaboration | Search for the neutral Higgs bosons of the minimal supersymmetric standard model in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 7 TeV with the ATLAS detector | JHEP 02 (2013) 095 | 1211.6956 |
| 12 | ATLAS Collaboration | Modelling $ \mathrm{Z}\rightarrow\tau\tau $ processes in ATLAS with $ \tau $-embedded $ \mathrm{Z}\rightarrow\mu\mu $ data | JINST 10 (2015) P09018 | 1506.05623 |
| 13 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 14 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 15 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 16 | CMS Collaboration | Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P08010 | CMS-EGM-14-001 1502.02702 |
| 17 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 18 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 19 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 20 | K. Rose | Deterministic annealing for clustering, compression, classification, regression, and related optimization problems | Proceedings of the IEEE 86 (1998) 2210 | |
| 21 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 22 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 23 | W. Adam, R. Fruhwirth, A. Strandlie, and T. Todorov | Reconstruction of electrons with the Gaussian-sum filter in the CMS tracker at the lhc | JPG 31 (2005) N9 | |
| 24 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 25 | CMS Collaboration | Reconstruction and identification of $ \tau lepton $ decays to hadrons and $ \mathrm{g}n_\tau $ at CMS | JINST 11 (2016) P01019 | CMS-TAU-14-001 1510.07488 |
| 26 | CMS Collaboration | Performance of reconstruction and identification of $ \tau $ leptons in their decays to hadrons and $ \nu_{\tau} $ in LHC Run-2 | CMS-PAS-TAU-16-002 | CMS-PAS-TAU-16-002 |
| 27 | J. Alwall et al. | MadGraph 5: going beyond | JHEP 06 (2011) 128 | 1106.0522 |
| 28 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 29 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 30 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 31 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO Higgs boson production via gluon fusion matched with shower in POWHEG | JHEP 04 (2009) 002 | 0812.0578 |
| 32 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 33 | S. Alioli et al. | Jet pair production in POWHEG | JHEP 04 (2011) 081 | 1012.3380 |
| 34 | E. Bagnaschi, G. Degrassi, P. Slavich, and A. Vicini | Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM | JHEP 02 (2012) 088 | 1111.2854 |
| 35 | NNPDF Collaboration | Parton distributions for the LHC run II | JHEP 04 (2015) 040 | 1410.8849 |
| 36 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 37 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 38 | S. Agostinelli et al. | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 39 | CMS Collaboration | Measurement of the $ \mathrm{Z}\gamma^{*} \to \tau\tau $ cross section in pp collisions at $ \sqrt{s} = $ 13 TeV and validation of $ \tau $ lepton analysis techniques | EPJC 78 (2018) 708 | CMS-HIG-15-007 1801.03535 |
| 40 | CDF Collaboration | Search for neutral Higgs bosons of the minimal supersymmetric standard model decaying to $ \tau $ pairs in $ {\mathrm{p}}\bar{{\mathrm{p}}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PRL 96 (2006) 011802 | hep-ex/0508051 |
| 41 | S. Baker and R. D. Cousins | Clarification of the use of chi square and likelihood functions in fits to histograms | NIM221 (1984) 437 | |
| 42 | A. N. Kolmogorov | Sulla determinazione empirica di una legge di distribuzione | Giornale dell'Istituto Italiano degli Attuari 4 (1933) 83 | |
| 43 | N. Smirnov | Table for estimating the goodness of fit of empirical distributions | Ann. Math. Statist. 19 (1948) 279 | |
| 44 | T. W. Anderson and D. A. Darling | A test of goodness of fit | Journal of the American Statistical Association 49 (1954) 765 | |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|