CMS-HIN-21-011

CMS-HIN-21-011 ; CERN-EP-2023-094
Two-particle Bose-Einstein correlations and their Lévy parameters in PbPb collisions at $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 5.02 TeV
CMS Collaboration
20 June 2023
Phys. Rev. C 109 (2024) 024914
Abstract: Two-particle Bose-Einstein momentum correlation functions are studied for charged-hadron pairs in lead-lead collisions at a center-of-mass energy per nucleon pair of $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 5.02 TeV. The data sample, containing 4.27 10 $^{9}$ minimum bias events corresponding to an integrated luminosity of 0.607 nb $^{-1}$ , was collected by the CMS experiment in 2018. The experimental results are discussed in terms of a Lévy-type source distribution. The parameters of this distribution are extracted as functions of particle pair average transverse mass and collision centrality. These parameters include the Lévy index or shape parameter ( $\alpha$ ), the Lévy scale parameter ( $R$ ), and the correlation strength parameter ( $\lambda$ ). The source shape, characterized by $\alpha$ , is found to be neither Cauchy nor Gaussian, implying the need for a full Lévy analysis. Similarly to what was previously found for systems characterized by Gaussian source radii, a hydrodynamical scaling is observed for the Lévy $R$ parameter. The $\lambda$ parameter is studied in terms of the core-halo model.
Links: e-print arXiv:2306.11574 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ;

Figures & Tables	Summary	References	CMS Publications

Figures
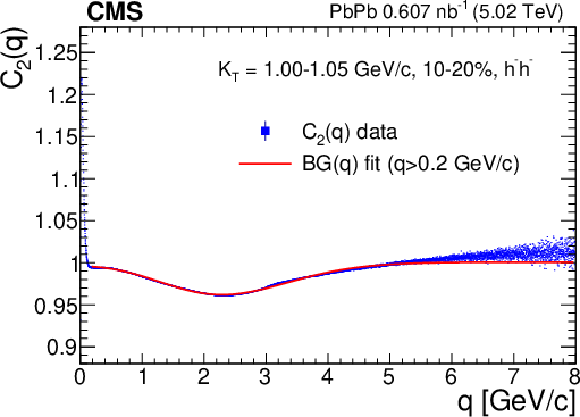
png pdf	Figure 1: An example of a long range background fit to the correlation function $C_2(q)$ of negatively charged hadron pairs with 1.00 $< K_{\mathrm{T}} <$ 1.05 GeV/ $c$ in the 10-20% centrality bin. The Bose-Einstein peak is below $q=$ 0.2 GeV/ $c$ , therefore the 0.2 $< q <$ 8.0 GeV/ $c$ region was used for the long range background fit.
png pdf	Figure 2: An example fit to the double-ratio correlation function $DR(q)$ of negatively charged hadron pairs with 1.30 $< K_{\mathrm{T}} <$ 1.35 GeV/ $c$ in the 20-30% centrality bin. The error bars show the statistical uncertainties. The fitted function is shown in blue, while the red overlay indicates the range used for the fit. The size of the Coulomb correction is indicated in magenta. The lower panel shows the deviation of the fit from the data in each bin in units of the standard deviation in that bin.
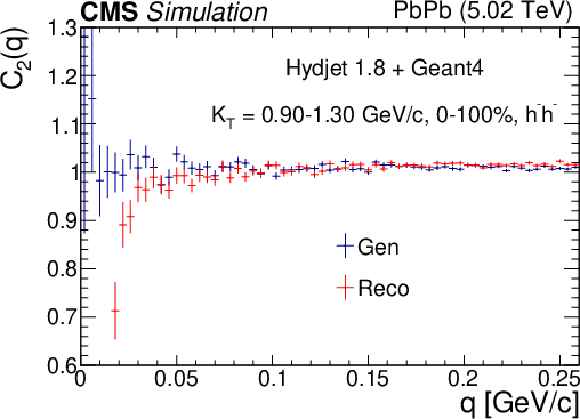
png pdf	Figure 3: The two-particle correlation function of negatively charged hadron pairs with 0.9 $< K_{\mathrm{T}} <$ 1.3 GeV/ $c$ in the 0-100% centrality range, calculated using Monte Carlo events with (Reco) and without (Gen) detector reconstruction effects. The error bars show the statistical uncertainties. The detector effects are most significant below approximately 50 MeVc. The quantum-statistical effects are not present in the simulations, hence there is no Bose-Einstein peak.
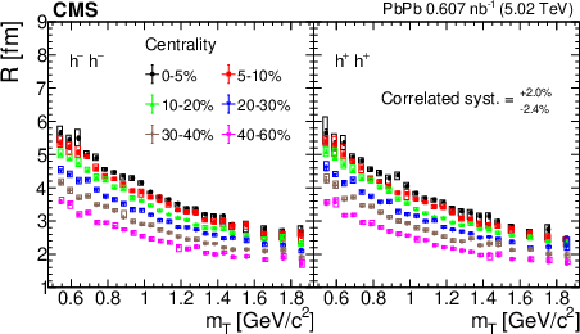
png pdf	Figure 4: The Lévy scale parameter $R$ versus the transverse mass $m_{\mathrm{T}}$ in different centrality classes, for negatively (left) and positively (right) charged hadron pairs. The error bars show the statistical uncertainties, while the boxes indicate the point-to-point systematic uncertainties. These boxes are slightly shifted along the horizontal axes for better visibility. The correlated systematic uncertainty is also indicated.
png pdf	Figure 5: The 1/ $R^2$ distribution vs. transverse mass $m_{\mathrm{T}}$ in different centrality classes, for negatively (left) and positively (right) charged hadron pairs. The error bars show the statistical uncertainties, while the boxes indicate the point-to-point systematic uncertainties. These boxes are slightly shifted along the horizontal axes for better visibility. The correlated systematic uncertainty is also indicated. A linear fit to the data is shown for each centrality bin. The fit parameters are tabulated in Table 3.
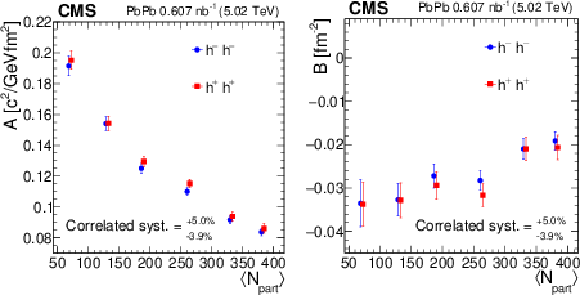
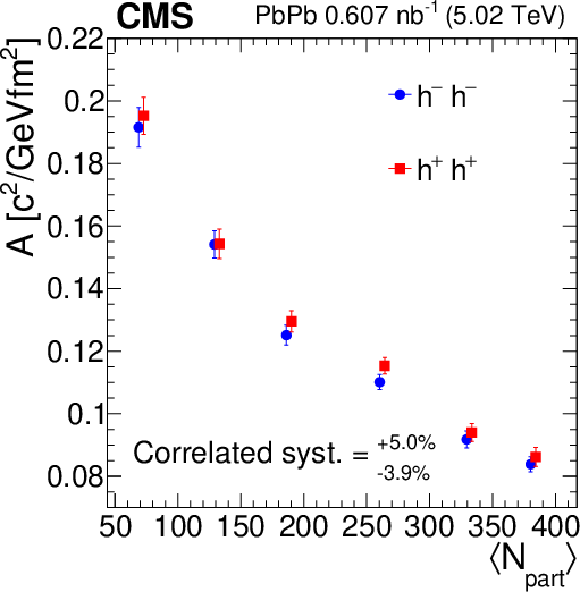
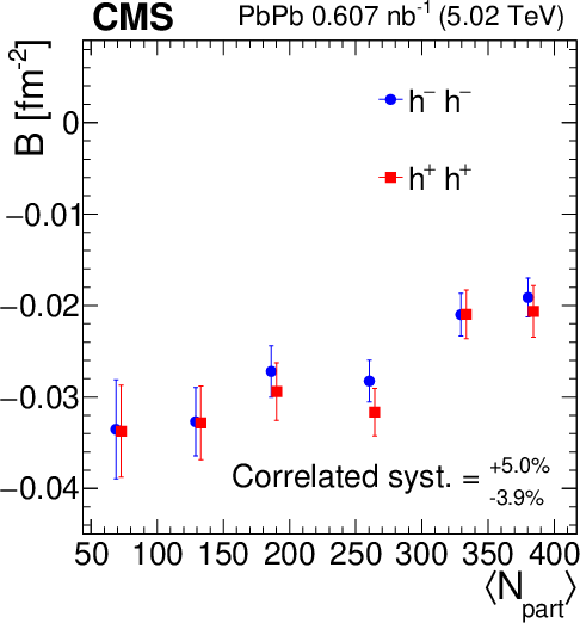
png pdf	Figure 6: The slope $A$ (left) and the intercept $B$ (right) linear-fit parameters versus $\langle N_{\text{part}}\rangle$ , for positively and negatively charged hadron pairs. The error bars show the statistical uncertainties. The correlated systematic uncertainty is also indicated. The points are slightly shifted along the horizontal axes for better visibility.
png pdf	Figure 6-a: The slope $A$ linear-fit parameter versus $\langle N_{\text{part}}\rangle$ , for positively and negatively charged hadron pairs. The error bars show the statistical uncertainties. The correlated systematic uncertainty is also indicated. The points are slightly shifted along the horizontal axes for better visibility.
png pdf	Figure 6-b: The intercept $B$ linear-fit parameter versus $\langle N_{\text{part}}\rangle$ , for positively and negatively charged hadron pairs. The error bars show the statistical uncertainties. The correlated systematic uncertainty is also indicated. The points are slightly shifted along the horizontal axes for better visibility.
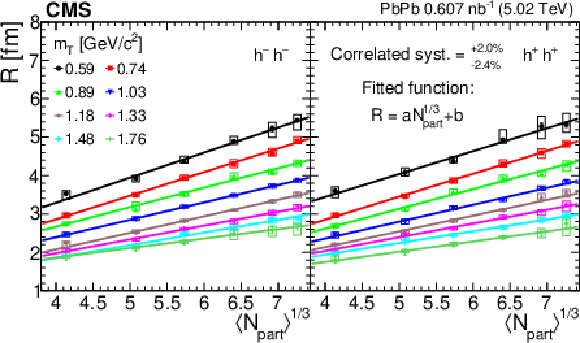
png pdf	Figure 7: The Lévy scale parameter $R$ versus $\langle N_{\text{part}}\rangle^{1/3}$ in different $m_{\mathrm{T}}$ classes, for negatively (left) and positively (right) charged hadron pairs. The error bars show the statistical uncertainties, while the boxes indicate the point-to-point systematic uncertainties. The correlated systematic uncertainty is also indicated. A linear fit to the data is shown for each $m_{\mathrm{T}}$ class. The fit parameters are tabulated in Table 4.
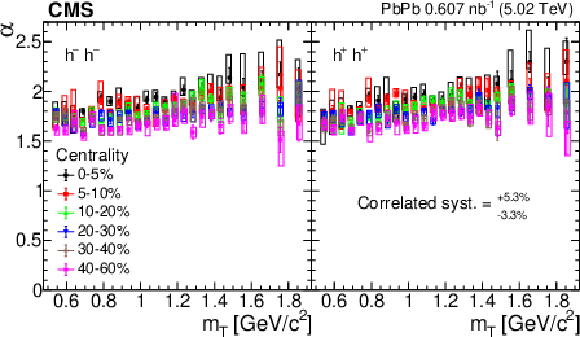
png pdf	Figure 8: The Lévy stability index $\alpha$ versus the transverse mass $m_{\mathrm{T}}$ in different centrality classes, for negatively (left) and positively (right) charged hadron pairs. The error bars show the statistical uncertainties, while the boxes indicate the point-to-point systematic uncertainties. These boxes are slightly shifted along the horizontal axes for better visibility. The correlated systematic uncertainty is also indicated.
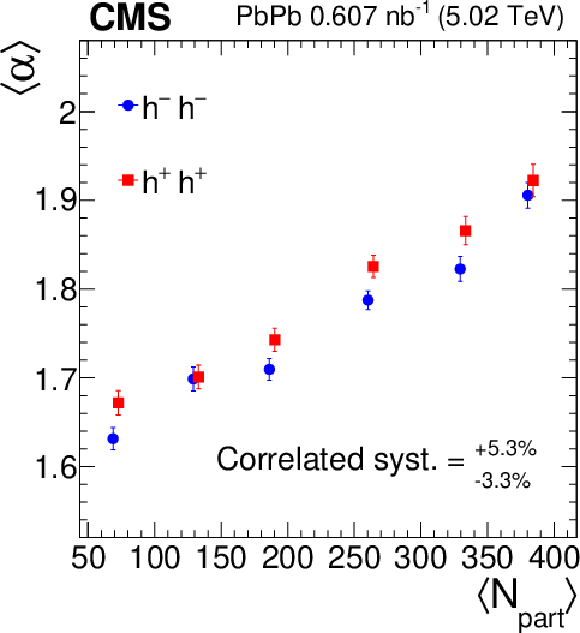
png pdf	Figure 9: The average Lévy stability index $\langle \alpha \rangle$ versus $\langle N_{\text{part}}\rangle$ , for both positively and negatively charged hadron pairs. The error bars show the statistical uncertainties. The correlated systematic uncertainty is also indicated. The points are slightly shifted along the horizontal axes for better visibility.
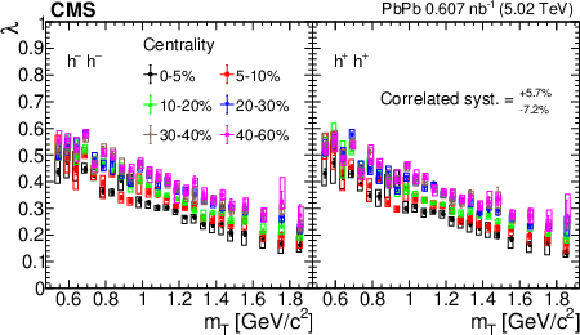
png pdf	Figure 10: The correlation strength $\lambda$ (upper panel) and $\lambda^*$ , which is re-scaled with the square of the pion fraction (lower panel), versus the transverse mass $m_{\mathrm{T}}$ in different centrality classes, for negatively (left) and positively (right) charged hadron pairs. The error bars show the statistical uncertainties, while the boxes indicate the point-to-point systematic uncertainties. These boxes are slightly shifted along the horizontal axes for better visibility. The correlated systematic uncertainty is also indicated.
png pdf	Figure 10-a: The correlation strength $\lambda$ versus the transverse mass $m_{\mathrm{T}}$ in different centrality classes, for negatively (left) and positively (right) charged hadron pairs. The error bars show the statistical uncertainties, while the boxes indicate the point-to-point systematic uncertainties. These boxes are slightly shifted along the horizontal axes for better visibility. The correlated systematic uncertainty is also indicated.
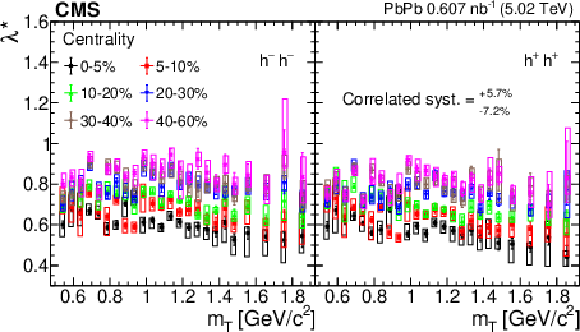
png pdf	Figure 10-b: $\lambda^*$ , which is re-scaled with the square of the pion fraction, versus the transverse mass $m_{\mathrm{T}}$ in different centrality classes, for negatively (left) and positively (right) charged hadron pairs. The error bars show the statistical uncertainties, while the boxes indicate the point-to-point systematic uncertainties. These boxes are slightly shifted along the horizontal axes for better visibility. The correlated systematic uncertainty is also indicated.

Tables
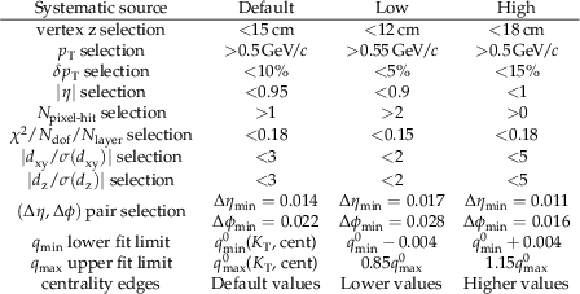
png pdf	Table 1: The sources of the systematic uncertainties with their values in the default and lower/upper settings. The meaning of the analysis parameters are given in Sections 4.1 and 4.2.
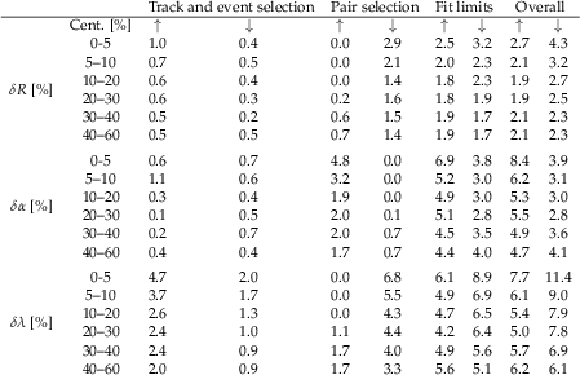
png pdf	Table 2: The relative effect of the different types of systematic sources in each centrality class for the $R$ (upper Table), $\alpha$ (middle Table) and $\lambda$ (lower Table) parameters (in percentage). The values were averaged over $K_{\mathrm{T}}$ and the two charge signs; the upwards (downwards) arrow, $\uparrow$ ( $\downarrow$ ) represents positive (negative) uncertainty in the value of the final fit parameters.
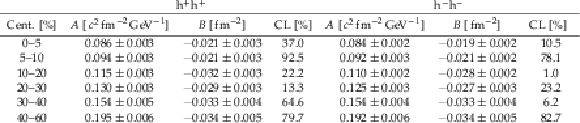
png pdf	Table 3: Fit parameters and the corresponding confidence levels (CL) of the linear fits to 1/ $R^2$ versus $m_{\mathrm{T}}$ , for positively (left) and negatively (right) charged hadron pairs.
png pdf	Table 4: Fit parameters and the corresponding confidence levels (CL) of the linear fits to $R$ versus $\langle N_{\text{part}}\rangle^{1/3}$ , for positively (left) and negatively (right) charged hadron pairs.

Summary

Two-particle Bose-Einstein momentum correlation function measurements are presented. The data sample consists of 4.27 10

$^{9}$ minimum bias lead-lead (PbPb) events, corresponding to an integrated luminosity of 0.607 nb

$^{-1}$ , at a center-of-mass energy per nucleon pair of

$\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 5.02 TeV, recorded by the CMS experiment at the LHC. The correlation functions found in different centrality and average transverse momentum classes are analyzed in terms of Lévy sources, including Coulomb effects. The values of the Lévy scale parameter

$R$ , the Lévy stability index

$\alpha$ , and the correlation strength

$\lambda$ are determined. A geometric interpretation of the

$R$ parameter is suggested by its dependence on the average number of participating nucleons in the collision. Assuming a pion mass for the charged particles, a linear dependence of 1/

$R^2$ on the transverse mass (

$m_{\mathrm{T}}$ ) is observed, consistent with a hydrodynamic scaling behavior, even for the case of Lévy sources. Based on the observed linear behavior, it is estimated that the Hubble constant of the quark-gluon plasma created in 5.02 TeV PbPb collisions increases from 0.11\ensuremath{\unit

$c$ /fm}} to 0.18\ensuremath{\unit

$c$ /fm}} when moving from most central to most peripheral collisions. The intercept of the 1/

$R^2$ versus

$m_{\mathrm{T}}$ linear fits is negative in all cases, requiring further studies for its interpretation. The

$\alpha$ parameter is found to have little, if any,

$m_{\mathrm{T}}$ dependence and to range between 1.6-2.0, increasing with centrality. The

$\alpha$ values found in this paper are approximately 45-60% larger than those reported for gold-gold collisions at

$\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 200 GeV at RHIC. This increase, while not fully understood, may result from the greater energy densities achieved at the LHC. As a function of

$m_{\mathrm{T}}$ , a strong and decreasing trend is observed for the

$\lambda$ parameter, which can be explained by the lack of particle identification. After rescaling the

$\lambda$ values to account for the fraction of pions among the charged hadrons, a nearly constant trend of the pion-fraction-corrected

$\lambda^*$ with

$m_{\mathrm{T}}$ is observed. The

$\lambda^*$ values are found to be smaller than unity, which can be interpreted on the basis of the core-halo model as a non-negligible halo contribution. Furthermore,

$\lambda^*$ is found to decrease as the collisions become more central. Altogether, these results imply that the hadron emitting source in

$\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 5.02 TeV PbPb collisions can be described by Lévy distributions. This allows for a new and precise characterization of this source in high-energy heavy ion collisions.

References
1	G. Goldhaber, W. B. Fowler, S. Goldhaber, and T. F. Hoang	Pion-pion correlations in antiproton annihilation events	PRL 3 (1959) 181
2	G. Goldhaber, S. Goldhaber, W.-Y. Lee, and A. Pais	Influence of Bose-Einstein statistics on the antiproton proton annihilation process	PR 120 (1960) 300
3	R. J. Glauber	Photon correlations	PRL 10 (1963) 84
4	R. J. Glauber	Nobel lecture: One hundred years of light quanta	Rev. Mod. Phys. 78 (2006) 1267
5	R. J. Glauber	Quantum optics and heavy ion physics	Nucl. Phys. A 774 (2006) 3	nucl-th/0604021
6	R. Hanbury Brown and R. Q. Twiss	A test of a new type of stellar interferometer on Sirius	Nature 178 (1956) 1046
7	R. Lednicky	Femtoscopy with unlike particles	in International Workshop on the Physics of the Quark Gluon Plasma, 2001	nucl-th/0112011
8	PHENIX Collaboration	Bose-Einstein correlations of charged pion pairs in Au+Au collisions at $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 200 GeV	PRL 93 (2004) 152302	nucl-ex/0401003
9	NA44 Collaboration	Two kaon correlations in central Pb+Pb collisions at 158A GeVc	PRL 87 (2001) 112301	nucl-ex/0107005
10	PHENIX Collaboration	Kaon interferometric probes of space-time evolution in Au+Au collisions at $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 200 GeV	PRL 103 (2009) 142301	0903.4863
11	A. N. Makhlin and Y. M. Sinyukov	Hydrodynamics of hadron matter under pion interferometric microscope	Z. Phys. C 39 (1988) 69
12	T. Csörgó and B. Lörstad	Bose-Einstein correlations for three-dimensionally expanding, cylindrically symmetric, finite systems	PRC 54 (1996) 1390	hep-ph/9509213
13	M. Csanád, T. Csörgó, B. Lörstad, and A. Ster	Indication of quark deconfinement and evidence for a Hubble flow in 130 GeV and 200 GeV Au+Au collisions	JPG 30 (2004) S1079	nucl-th/0403074
14	S. Pratt	Resolving the HBT puzzle in relativistic heavy ion collision	PRL 102 (2009) 232301	0811.3363
15	R. A. Lacey	Indications for a critical end point in the phase diagram for hot and dense nuclear matter	PRL 114 (2015) 142301	1411.7931
16	STAR Collaboration	Pion interferometry in Au+Au collisions at $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 200 GeV	PRC 71 (2005) 044906	nucl-ex/0411036
17	ALICE Collaboration	One-dimensional pion, kaon, and proton femtoscopy in Pb-Pb collisions at $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 2.76 TeV	PRC 92 (2015) 054908	1506.07884
18	CMS Collaboration	Bose-Einstein correlations in pp, pPb, and PbPb collisions at $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 0.9-7 TeV	PRC 97 (2018) 064912	CMS-FSQ-14-002 1712.07198
19	ATLAS Collaboration	Femtoscopy with identified charged pions in proton-lead collisions at $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 5.02 TeV with ATLAS	PRC 96 (2017) 064908	1704.01621
20	PHENIX Collaboration	Lévy-stable two-pion Bose-Einstein correlations in $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 200 GeV Au+Au collisions	PRC 97 (2018) 064911	1709.05649
21	NA61/SHINE Collaboration	Measurements of two-pion HBT correlations in Be+Be collisions at 150A GeV/c beam momentum, at the NA61/SHINE experiment at CERN		2302.04593
22	V. V. Uchaikin and V. M. Zolotarev	Chance and stability: stable distributions and their applications	De Gruyter, . , ISBN~978315974, 2011 link
23	T. Csörgó, S. Hegyi, T. Novák, and W. A. Zajc	Bose-Einstein or HBT correlations and the anomalous dimension of QCD	Acta Phys. Polon. B 36 (2005) 329	hep-ph/0412243
24	T. Csörgó, S. Hegyi, T. Novák, and W. A. Zajc	Bose-Einstein or HBT correlation signature of a second order QCD phase transition	AIP Conf. Proc. 828 (2006) 525	nucl-th/0512060
25	M. Csanád, T. Csörgó, and M. Nagy	Anomalous diffusion of pions at RHIC	Braz. J. Phys. 37 (2007) 1002	hep-ph/0702032
26	D. Kincses, M. Stefaniak, and M. Csanád	Event-by-event investigation of the two-particle source function in heavy-ion collisions with EPOS	Entropy 24 (2022) 308	2201.07962
27	B. Kórodi, D. Kincses, and M. Csanád	Event-by-event investigation of the two-particle source function in ${\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}}}=$ 2.76 TeV PbPb collisions with EPOS		2212.02980
28	CMS Collaboration	HEPData record for this analysis	link
29	T. Csörgó	Particle interferometry from 40 MeV to 40 TeV	Acta Phys. Hung. A 15 (2002) 1	hep-ph/0001233
30	U. A. Wiedemann and U. W. Heinz	Particle interferometry for relativistic heavy ion collisions	Phys. Rept. 319 (1999) 145	nucl-th/9901094
31	J. Bolz et al.	Resonance decays and partial coherence in Bose-Einstein correlations	PRD 47 (1993) 3860
32	T. Csörgó, B. Lörstad, and J. Zimányi	Bose-Einstein correlations for systems with large halo	Z. Phys. C 71 (1996) 491	hep-ph/9411307
33	R. Metzler, E. Barkai, and J. Klafter	Anomalous diffusion and relaxation close to thermal equilibrium: A fractional Fokker-Planck equation approach	PRL 82 (1999) 3563
34	T. Csörgó, S. Hegyi, and W. A. Zajc	Bose-Einstein correlations for Lévy stable source distributions	EPJC 36 (2004) 67	nucl-th/0310042
35	Y. Sinyukov et al.	Coulomb corrections for interferometry analysis of expanding hadron systems	PLB 432 (1998) 248
36	M. Csanád, S. Lökös, and M. Nagy	Expanded empirical formula for Coulomb final state interaction in the presence of Lévy sources	Phys. Part. Nucl. 51 (2020) 238	1910.02231
37	CMS Tracker Group Collaboration	The CMS phase-1 pixel detector upgrade	JINST 16 (2021) P02027	2012.14304
38	CMS Collaboration	Track impact parameter resolution for the full pseudo rapidity coverage in the 2017 dataset with the CMS phase-1 pixel detector	CMS Detector Performance Note CMS-DP-2020-049, 2020 CDS
39	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
40	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004
41	CMS Collaboration	Precision luminosity measurement in proton-proton collisions at $\sqrt{s}=$ 13 TeV in 2015 and 2016 at CMS	EPJC 81 (2021) 800	CMS-LUM-17-003 2104.01927
42	CMS Collaboration	CMS luminosity measurement using nucleus-nucleus collisions at ${\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}}}=$ 5.02 TeV in 2018	CMS Physics Analysis Summary, 2022 CMS-PAS-LUM-18-001	CMS-PAS-LUM-18-001
43	CMS Collaboration	Charged-particle nuclear modification factors in PbPb and pPb collisions at ${\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}}}=$ 5.02 TeV	JHEP 04 (2017) 039	CMS-HIN-15-015 1611.01664
44	CMS Collaboration	Observation and studies of jet quenching in PbPb collisions at ${\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}}}=$ 2.76 TeV	PRC 84 (2011) 024906	CMS-HIN-10-004 1102.1957
45	CMS Collaboration	Description and performance of track and primary-vertex reconstruction with the CMS tracker	JINST 9 (2014) P10009	CMS-TRK-11-001 1405.6569
46	M. Csanád, T. Csörgó, B. Lörstad, and A. Ster	Understanding the rapidity dependence of the elliptic flow and the HBT radii at RHIC	AIP Conf. Proc. 828 (2006) 479	nucl-th/0510027
47	ALICE Collaboration	Production of charged pions, kaons, and (anti-)protons in Pb-Pb and inelastic pp collisions at $\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}} =$ 5.02 TeV	PRC 101 (2020) 044907	1910.07678
48	L3 Collaboration	Test of the $\tau$ -model of Bose-Einstein correlations and reconstruction of the source function in hadronic Z-boson decay at LEP	EPJC 71 (2011) 1648	1105.4788
49	CMS Collaboration	Bose-Einstein correlations of charged hadrons in proton-proton collisions at $\sqrt{s} =$ 13 TeV	JHEP 03 (2020) 014	CMS-FSQ-15-009 1910.08815
50	B. Kurgyis, D. Kincses, M. Nagy, and M. Csanád	Coulomb interaction for Lévy sources		2007.10173
51	CMS Collaboration	$\mathrm{K}^0_\mathrm{S}$ and $\lambda(\overline\lambda)$ two-particle femtoscopic correlations in PbPb collisions at ${\sqrt{\smash[b]{s_{_{\mathrm{NN}}}}}}=$ 5.02 TeV		CMS-HIN-21-006 2301.05290
52	F. James and M. Roos	Minuit: A system for function minimization and analysis of the parameter errors and correlations	Comput. Phys. Commun. 10 (1975) 343
53	R. Brun and F. Rademakers	ROOT: An object oriented data analysis framework	NIM A 389 (1997) 81
54	I. P. Lokhtin and A. M. Snigirev	A model of jet quenching in ultrarelativistic heavy ion collisions and high- $p_{\text{T}}$ hadron spectra at RHIC	EPJC 45 (2006) 211	hep-ph/0506189
55	GEANT4 Collaboration	GEANT 4---a simulation toolkit	NIM A 506 (2003) 250
56	D. Kincses, M. I. Nagy, and M. Csanád	Coulomb and strong interactions in the final state of Hanbury-Brown-Twiss correlations for Lévy-type source functions	PRC 102 (2020) 064912	1912.01381
57	M. Chojnacki, W. Florkowski, and T. Csörgó	On the formation of Hubble flow in little bangs	PRC 71 (2005) 044902	nucl-th/0410036
58	C. Loizides, J. Kamin, and D. d'Enterria	Improved Monte Carlo Glauber predictions at present and future nuclear colliders	PRC 97 (2018) 054910	1710.07098
59	HotQCD Collaboration	The QCD crossover at zero and non-zero baryon densities from Lattice QCD	Nucl. Phys. A 982 (2019) 847	1807.05607
60	T. Csörgó	Simple analytic solution of fireball hydrodynamics	Central Eur. J. Phys. 2 (2004) 556	nucl-th/9809011