CMS-PAS-TOP-25-001

CMS-PAS-TOP-25-001
Observation of magic states of top quark pairs produced in proton-proton collisions at $\sqrt{s}=$ 13 TeV
CMS Collaboration
14 March 2025

Abstract: An observation of magic states of top quark-antiquark ( $\mathrm{t\bar{t}}$ ) systems produced in proton-proton collisions at the LHC at $\sqrt{s}=$ 13 TeV is presented. Magic, defined here using the second stabilizer Renyi entropy, is an important property used to characterize quantum states in quantum information science. Quantum states with high magic provide computational advantage over classical systems. This observation is based on measurements of the polarization and spin correlation coefficients in $\mathrm{t\bar{t}}$ systems using the final states with an electron or muon and jets. Magic is determined in various kinematic regions of the $\mathrm{t\bar{t}}$ system and is found to agree with the standard model predictions. This study represents the first experimental measurement of this quantity at the TeV energy scale.
Links: CDS record (PDF) ; CADI line (restricted) ;

Figures	Summary	References	CMS Publications

Figures
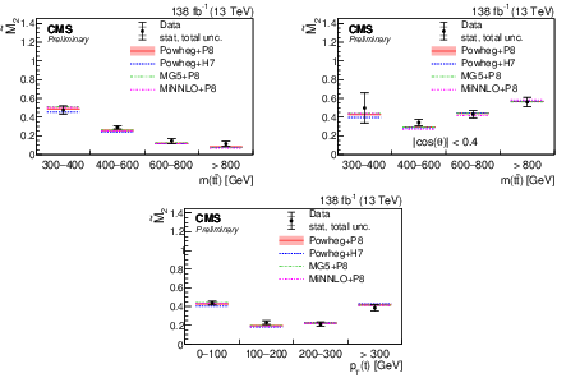
png pdf	Figure 1: Results of $\tilde{M}_\mathrm{2}$ measurements in bins of $m({\mathrm{t}\overline{\mathrm{t}}} )$ (upper left ), $m({\mathrm{t}\overline{\mathrm{t}}} )$ with $\|\cos(\theta)\| <$ 0.4 (upper right ), and $p_{\mathrm{T}}(\mathrm{t})$ (lower). The measurements (points) are shown with the statistical uncertainty (inner error bars) and total uncertainty (outer error bars) and compared to the predictions of POWHEG + PYTHIA, POWHEG + HERWIG, MADGRAPH5\_aMC@NLO+ PYTHIA, and MINNLO+ PYTHIA. The POWHEG + PYTHIA prediction is displayed with the matrix element scale and parton distribution function uncertainties, while for all other predictions only the central values are indicated.
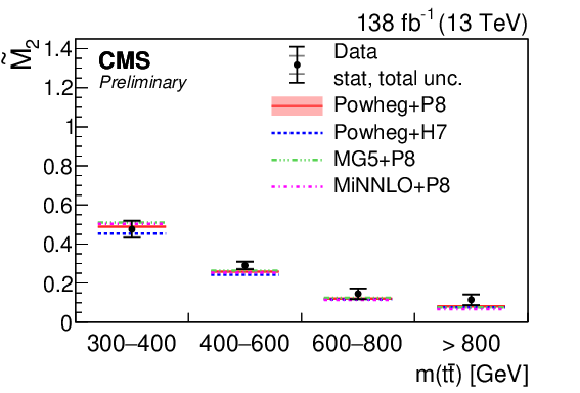
png pdf	Figure 1-a: Results of $\tilde{M}_\mathrm{2}$ measurements in bins of $m({\mathrm{t}\overline{\mathrm{t}}} )$ (upper left ), $m({\mathrm{t}\overline{\mathrm{t}}} )$ with $\|\cos(\theta)\| <$ 0.4 (upper right ), and $p_{\mathrm{T}}(\mathrm{t})$ (lower). The measurements (points) are shown with the statistical uncertainty (inner error bars) and total uncertainty (outer error bars) and compared to the predictions of POWHEG + PYTHIA, POWHEG + HERWIG, MADGRAPH5\_aMC@NLO+ PYTHIA, and MINNLO+ PYTHIA. The POWHEG + PYTHIA prediction is displayed with the matrix element scale and parton distribution function uncertainties, while for all other predictions only the central values are indicated.
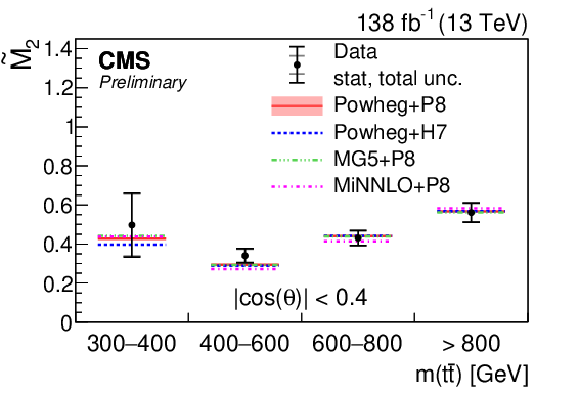
png pdf	Figure 1-b: Results of $\tilde{M}_\mathrm{2}$ measurements in bins of $m({\mathrm{t}\overline{\mathrm{t}}} )$ (upper left ), $m({\mathrm{t}\overline{\mathrm{t}}} )$ with $\|\cos(\theta)\| <$ 0.4 (upper right ), and $p_{\mathrm{T}}(\mathrm{t})$ (lower). The measurements (points) are shown with the statistical uncertainty (inner error bars) and total uncertainty (outer error bars) and compared to the predictions of POWHEG + PYTHIA, POWHEG + HERWIG, MADGRAPH5\_aMC@NLO+ PYTHIA, and MINNLO+ PYTHIA. The POWHEG + PYTHIA prediction is displayed with the matrix element scale and parton distribution function uncertainties, while for all other predictions only the central values are indicated.
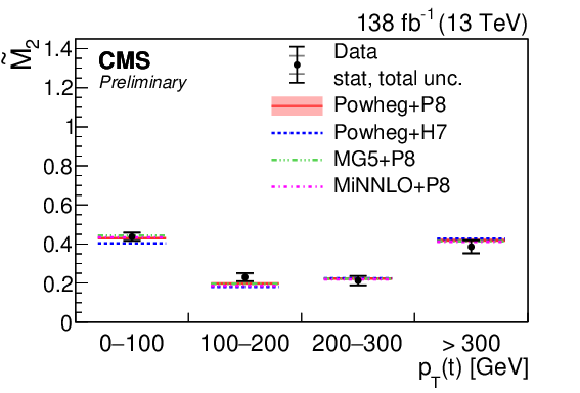
png pdf	Figure 1-c: Results of $\tilde{M}_\mathrm{2}$ measurements in bins of $m({\mathrm{t}\overline{\mathrm{t}}} )$ (upper left ), $m({\mathrm{t}\overline{\mathrm{t}}} )$ with $\|\cos(\theta)\| <$ 0.4 (upper right ), and $p_{\mathrm{T}}(\mathrm{t})$ (lower). The measurements (points) are shown with the statistical uncertainty (inner error bars) and total uncertainty (outer error bars) and compared to the predictions of POWHEG + PYTHIA, POWHEG + HERWIG, MADGRAPH5\_aMC@NLO+ PYTHIA, and MINNLO+ PYTHIA. The POWHEG + PYTHIA prediction is displayed with the matrix element scale and parton distribution function uncertainties, while for all other predictions only the central values are indicated.

Summary

In conclusion, we performed the first evaluation of the generalized magic

$\tilde{M}_\mathrm{2}$ in top quark-antiquark (

$\mathrm{t} \overline{\mathrm{t}}$ ) pairs, a property from quantum information science. Magic reflects how far a quantum state is from being efficiently simulated by classical systems, making it an important measure of a state's potential for quantum computational advantages. The observed magic values are in agreement with the standard model expectations. The results underscore the potential of collider experiments as a platform for exploring fundamental aspects of quantum mechanics, including properties like magic, which play a crucial role in quantum computation. Future studies could refine these measurements further and explore their implications for both quantum information science and high-energy physics.

References
1	ATLAS Collaboration	Observation of quantum entanglement with top quarks at the ATLAS detector	Nature 633 (2024) 542	2311.07288
2	CMS Collaboration	Observation of quantum entanglement in top quark pair production in proton-proton collisions at $\sqrt{s}=$ 13 TeV	Reports on Progress in Physics 87 (2024) 117801	CMS-TOP-23-001 2406.03976
3	CMS Collaboration	Measurements of polarization and spin correlation and observation of entanglement in top quark pairs using lepton $+$ jets events from proton-proton collisions at $\sqrt{s}=$ 13 TeV	PRD 110 (2024) 112016	CMS-TOP-23-007 2409.11067
4	M. A. Nielsen and I. L. Chuang	Quantum Computation and Quantum Information	Cambridge University Press, ISBN~978-0-521-63503-5, 2012 link
5	P. W. Shor	Polynomial time algorithms for prime factorization and discrete logarithms on a quantum computer	SIAM J. Sci. Statist. Comput. 26 (1997) 1484	quant-ph/9508027
6	P. W. Shor	Algorithms for quantum computation: discrete logarithms and factoring	in Proceedings 35th Annual Symposium on Foundations of Computer Science, 1994 link
7	L. K. Grover	A fast quantum mechanical algorithm for database search	in Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, STOC '96, 1996 link
8	L. K. Grover	Quantum mechanics helps in searching for a needle in a haystack	PRL 79 (1997) 325	quant-ph/9706033
9	D. Gottesman	The Heisenberg representation of quantum computers	in 22nd International Colloquium on Group Theoretical Methods in Physics, 1998	quant-ph/9807006
10	K. Goto, T. Nosaka, and M. Nozaki	Probing chaos by magic monotones	PRD 106 (2022) 126009	2112.14593
11	L. Leone, S. F. E. Oliviero, Y. Zhou, and A. Hamma	Quantum Chaos is Quantum	Quantum 5 453, 2021 link	2102.08406
12	C. D. White, C. Cao, and B. Swingle	Conformal field theories are magical	Phys. Rev. B 103 (2021) 075145	2007.01303
13	Z.-W. Liu and A. Winter	Many-Body Quantum Magic	PRX Quantum 3 (2022) 020333	2010.13817
14	A. Gu, S. F. E. Oliviero, and L. Leone	Doped stabilizer states in many-body physics and where to find them	Phys. Rev. A 110 (2024) 062427	2403.14912
15	S. F. E. Oliviero, L. Leone, and A. Hamma	Magic-state resource theory for the ground state of the transverse-field Ising model	Phys. Rev. A 106 (2022) 042426	2205.02247
16	D. Rattacaso, L. Leone, S. F. E. Oliviero, and A. Hamma	Stabilizer entropy dynamics after a quantum quench	Phys. Rev. A 108 (2023) 042407	2304.13768
17	P. S. Tarabunga, E. Tirrito, T. Chanda, and M. Dalmonte	Many-Body Magic Via Pauli-Markov Chains\textemdashFrom Criticality to Gauge Theories	PRX Quantum 4 (2023) 040317	2305.18541
18	S. Zhou, Z. Yang, A. Hamma, and C. Chamon	Single T gate in a Clifford circuit drives transition to universal entanglement spectrum statistics	SciPost Phys. 9 (2020) 087
19	A. Gu, S. F. E. Oliviero, and L. Leone	Magic-induced computational separation in entanglement theory		2403.19610
20	S. Cepollaro et al.	Stabilizer entropy of quantum tetrahedra	PRD 109 (2024) 126008	2402.07843
21	L. Leone, S. F. E. Oliviero, and A. Hamma	Stabilizer Rényi Entropy	PRL 128 (2022) 050402	2106.12587
22	C. D. White and M. J. White	Magic states of top quarks	PRD 110 (2024) 116016	2406.07321
23	P. Nason	A new method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
24	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with parton shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
25	S. Frixione, G. Ridolfi, and P. Nason	A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction	JHEP 09 (2007) 126	0707.3088
26	T. Sjöstrand et al.	An introduction to PYTHIA8.2	Comput. Phys. Commun. 191 (2015) 159	1410.3012
27	CMS Collaboration	Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements	EPJC 80 (2020) 4	CMS-GEN-17-001 1903.12179
28	M. Bähr et al.	HERWIG++ physics and manual	EPJC 58 (2008) 639	0803.0883
29	CMS Collaboration	Development and validation of HERWIG 7 tunes from CMS underlying-event measurements	EPJC 81 (2021) 312	CMS-GEN-19-001 2011.03422
30	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
31	R. Frederix and S. Frixione	Merging meets matching in MC@NLO	JHEP 12 (2012) 061	1209.6215
32	J. Mazzitelli et al.	Next-to-next-to-leading order event generation for top-quark pair production	PRL 127 (2021) 062001	2012.14267