

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-TOP-17-013 | ||
| Measurement of jet substructure observables in tˉt events from pp collisions at √s= 13 TeV | ||
| CMS Collaboration | ||
| March 2018 | ||
| Abstract: A measurement of differential jet substructure observables is presented using tˉt lepton+jets events from proton-proton collisions at √s= 13 TeV recorded by the CMS experiment at the LHC in 2016 corresponding to an integrated luminosity of 35.9 fb−1. Multiple jet substructure variables, such as the particle multiplicity, width, eccentricity, pT dispersion, N-subjettiness ratios, generalized angularities, and energy correlation functions, are measured for inclusive jets, as well as for identified bottom, light-quark, and gluon jets from the tˉt final state. The results are unfolded to the stable-particle level and compared to predictions from POWHEG interfaced with PYTHIA 8 and HERWIG 7.1, as well as from SHERPA 2 and DIRE. A reasonable agreement between the data and the Monte Carlo predictions is found. From a comparison of the jet width distribution to the prediction, it is shown that a lower value of the effective strong coupling in the PYTHIA 8 final-state parton shower is preferred. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, PRD 98 (2018) 092014. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
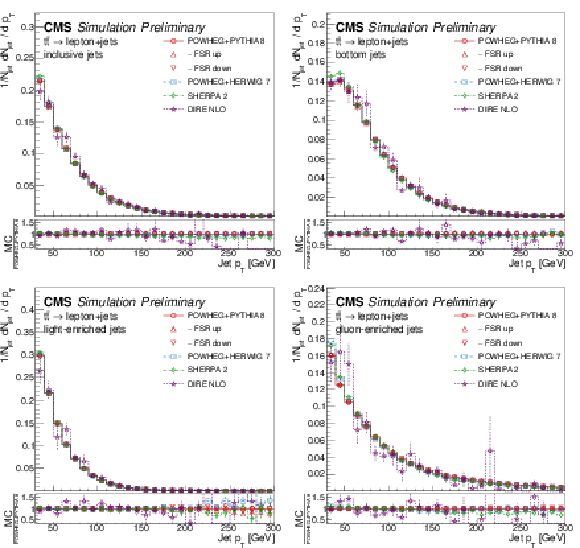
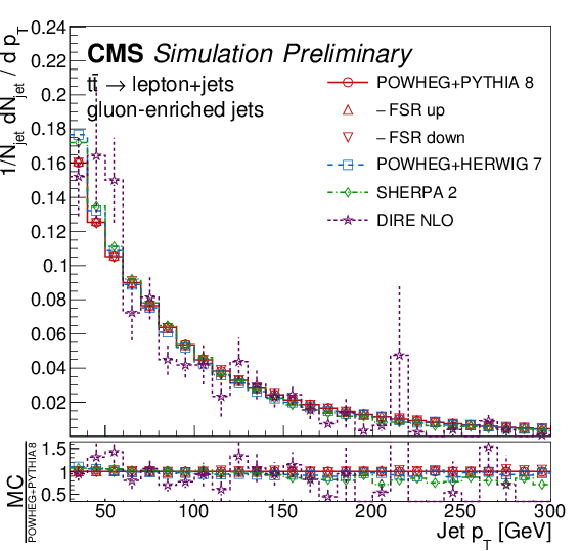
Figure 1:
Transverse momentum distribution at the particle level, for inclusive jets (upper left), bottom jets (upper right), light-quark enriched jets (lower left), and gluon-enriched jets (lower right). The bottom panels show the corresponding ratios of the different MC predictions over POWHEG+PYTHIA 8. |
png pdf |
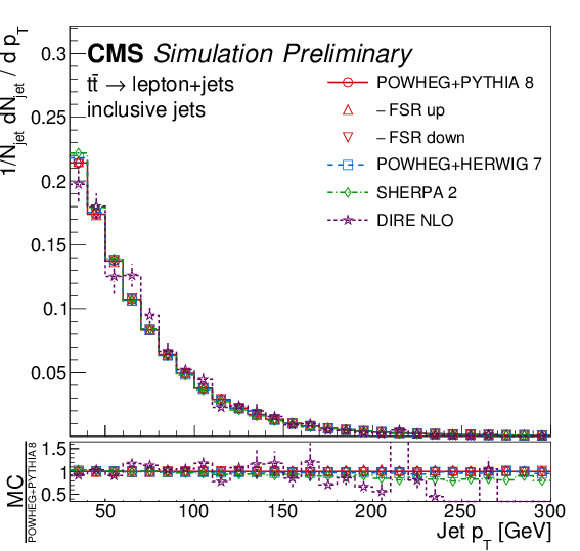
Figure 1-a:
Transverse momentum distribution at the particle level, for inclusive jets (upper left), bottom jets (upper right), light-quark enriched jets (lower left), and gluon-enriched jets (lower right). The bottom panels show the corresponding ratios of the different MC predictions over POWHEG+PYTHIA 8. |
png pdf |
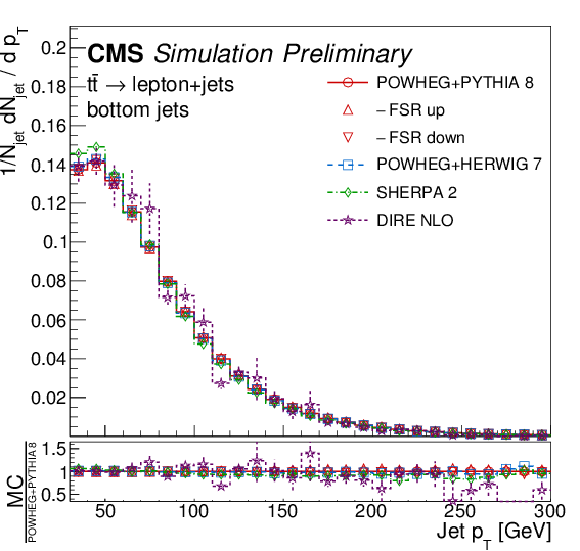
Figure 1-b:
Transverse momentum distribution at the particle level, for inclusive jets (upper left), bottom jets (upper right), light-quark enriched jets (lower left), and gluon-enriched jets (lower right). The bottom panels show the corresponding ratios of the different MC predictions over POWHEG+PYTHIA 8. |
png pdf |
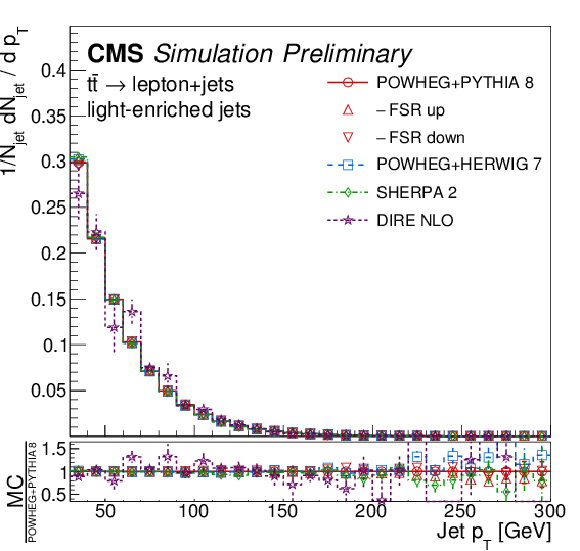
Figure 1-c:
Transverse momentum distribution at the particle level, for inclusive jets (upper left), bottom jets (upper right), light-quark enriched jets (lower left), and gluon-enriched jets (lower right). The bottom panels show the corresponding ratios of the different MC predictions over POWHEG+PYTHIA 8. |
png pdf |
Figure 1-d:
Transverse momentum distribution at the particle level, for inclusive jets (upper left), bottom jets (upper right), light-quark enriched jets (lower left), and gluon-enriched jets (lower right). The bottom panels show the corresponding ratios of the different MC predictions over POWHEG+PYTHIA 8. |

png pdf |
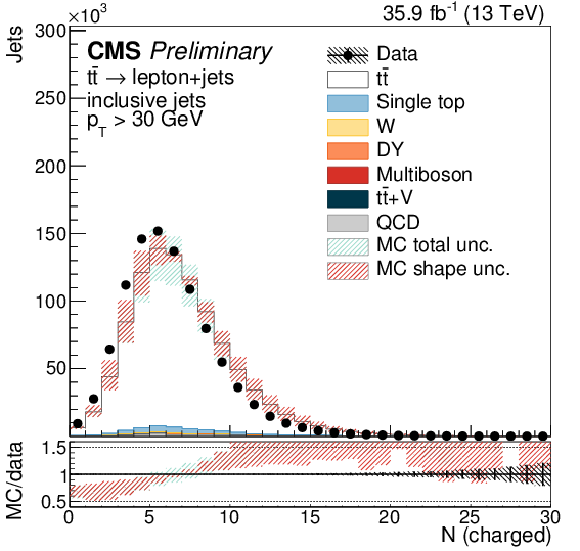
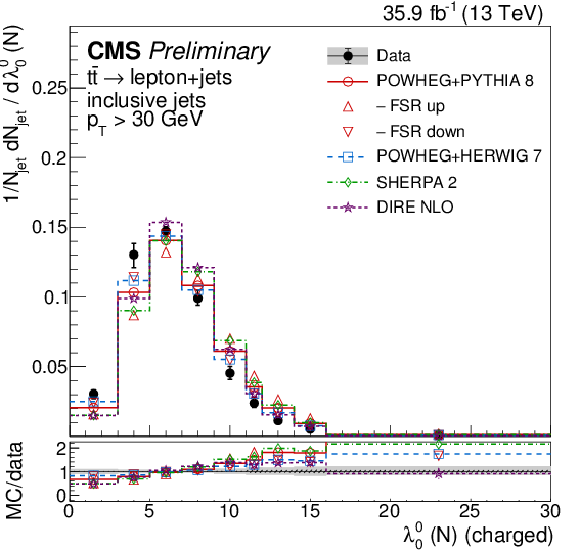
Figure 2:
Charged particle multiplicity at the reconstructed level (left) and normalized and unfolded to the particle level (right), in inclusive jets measured in t¯t events at √s= 13 TeV. The reconstruction-level plot shows the sum of the expected contributions from each process (stacked histograms) compared to the data points (upper panel), and the ratio of the MC prediction (POWHEG+PYTHIA 8) to the data (lower panel), where the dashed band represents the uncertainty on the prediction affecting either the shape or both the shape and normalization of the distribution. The particle-level plot shows the normalized differential cross section (upper panel), and the ratio of multiple MC predictions to data (lower panel) where the grey band indicates the total uncertainty and the hatched black area the statistical uncertainty. |
png pdf |
Figure 2-a:
Charged particle multiplicity at the reconstructed level (left) and normalized and unfolded to the particle level (right), in inclusive jets measured in t¯t events at √s= 13 TeV. The reconstruction-level plot shows the sum of the expected contributions from each process (stacked histograms) compared to the data points (upper panel), and the ratio of the MC prediction (POWHEG+PYTHIA 8) to the data (lower panel), where the dashed band represents the uncertainty on the prediction affecting either the shape or both the shape and normalization of the distribution. The particle-level plot shows the normalized differential cross section (upper panel), and the ratio of multiple MC predictions to data (lower panel) where the grey band indicates the total uncertainty and the hatched black area the statistical uncertainty. |
png pdf |
Figure 2-b:
Charged particle multiplicity at the reconstructed level (left) and normalized and unfolded to the particle level (right), in inclusive jets measured in t¯t events at √s= 13 TeV. The reconstruction-level plot shows the sum of the expected contributions from each process (stacked histograms) compared to the data points (upper panel), and the ratio of the MC prediction (POWHEG+PYTHIA 8) to the data (lower panel), where the dashed band represents the uncertainty on the prediction affecting either the shape or both the shape and normalization of the distribution. The particle-level plot shows the normalized differential cross section (upper panel), and the ratio of multiple MC predictions to data (lower panel) where the grey band indicates the total uncertainty and the hatched black area the statistical uncertainty. |
png pdf |
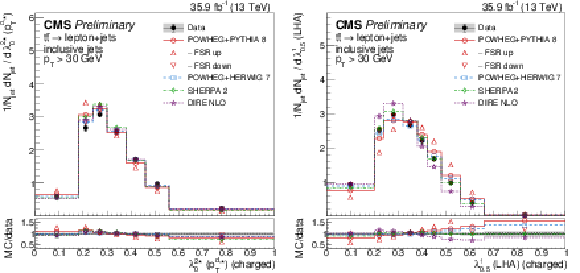
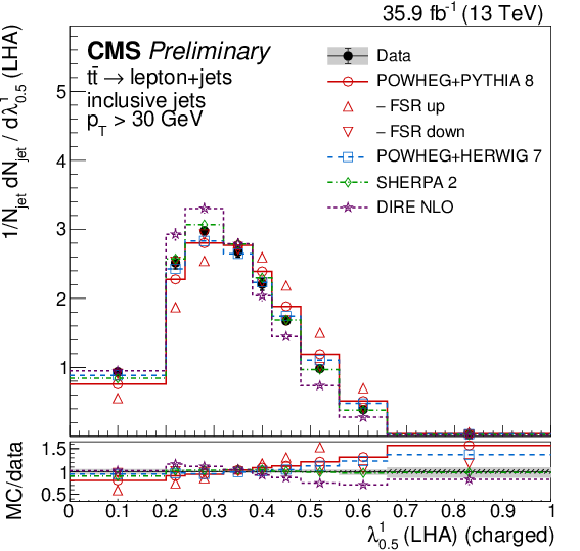
Figure 3:
Distributions of the scaled pT dispersion (λ2∗0, left) and Les Houches angularity (λ10.5, right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
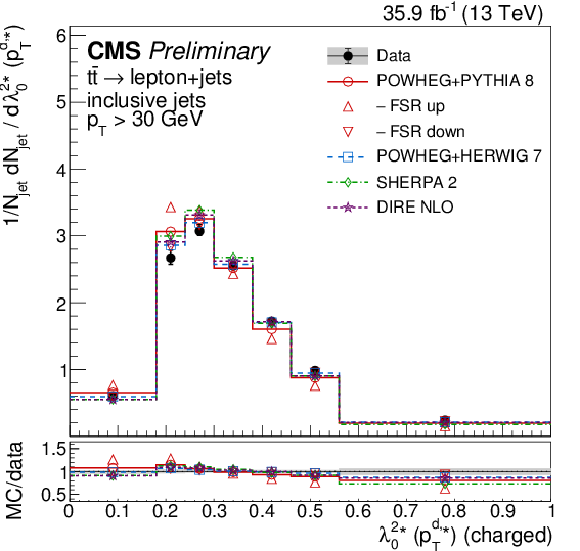
png pdf |
Figure 3-a:
Distributions of the scaled pT dispersion (λ2∗0, left) and Les Houches angularity (λ10.5, right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 3-b:
Distributions of the scaled pT dispersion (λ2∗0, left) and Les Houches angularity (λ10.5, right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
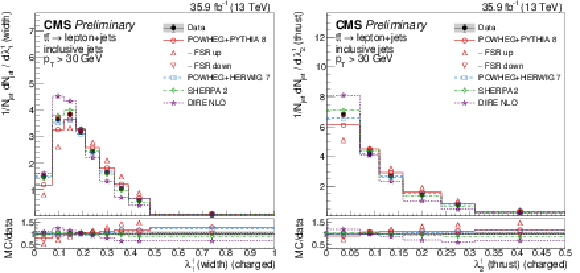
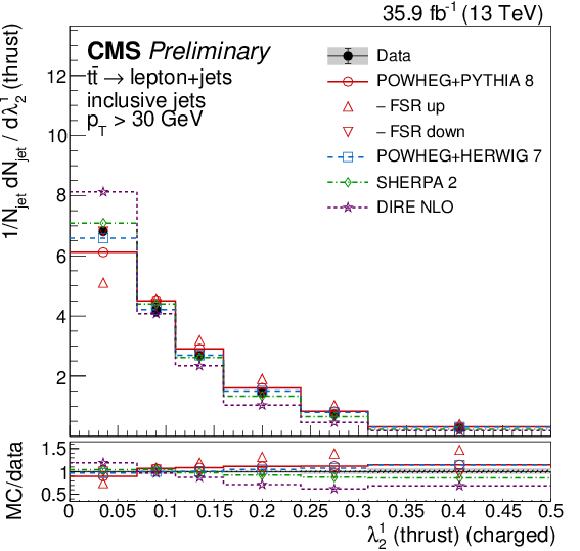
Figure 4:
Distributions of the jet width (λ11, left) and thrust (λ12, right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
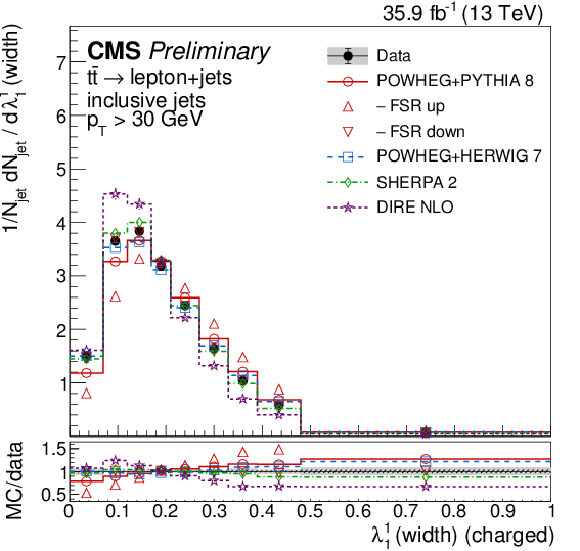
png pdf |
Figure 4-a:
Distributions of the jet width (λ11, left) and thrust (λ12, right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 4-b:
Distributions of the jet width (λ11, left) and thrust (λ12, right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |

png pdf |
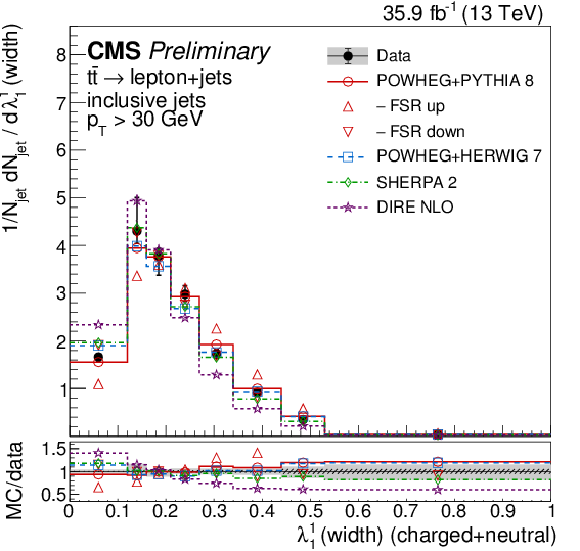
Figure 5:
Distributions of the Les Houches angularity (λ10.5, left) and jet width (λ11, right), unfolded to the particle level, for inclusive jets reconstructed with charged+neutral particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |

png pdf |
Figure 5-a:
Distributions of the Les Houches angularity (λ10.5, left) and jet width (λ11, right), unfolded to the particle level, for inclusive jets reconstructed with charged+neutral particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 5-b:
Distributions of the Les Houches angularity (λ10.5, left) and jet width (λ11, right), unfolded to the particle level, for inclusive jets reconstructed with charged+neutral particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
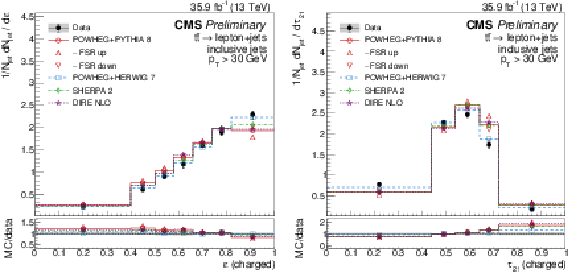
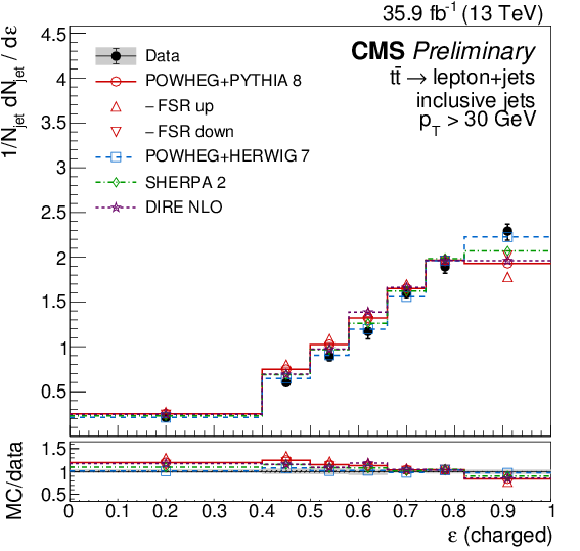
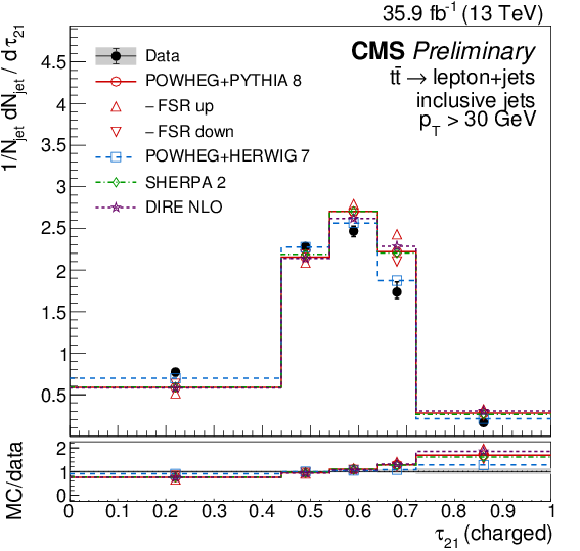
Figure 6:
Distributions of the eccentricity ε (left) and the N-subjettiness ratio τ21 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 6-a:
Distributions of the eccentricity ε (left) and the N-subjettiness ratio τ21 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 6-b:
Distributions of the eccentricity ε (left) and the N-subjettiness ratio τ21 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
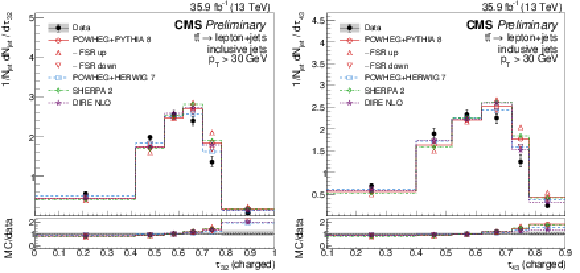
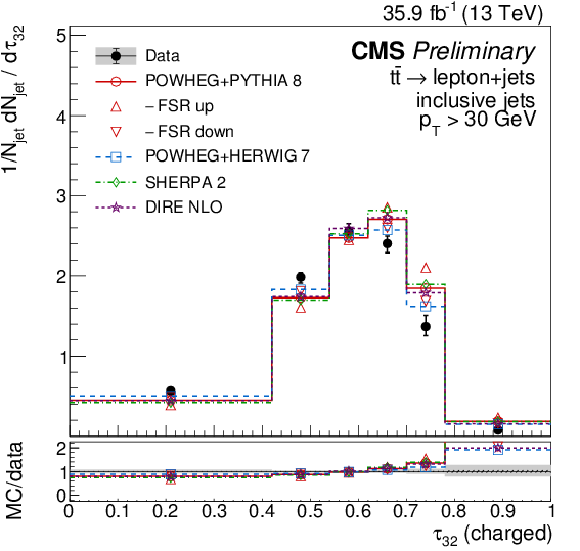
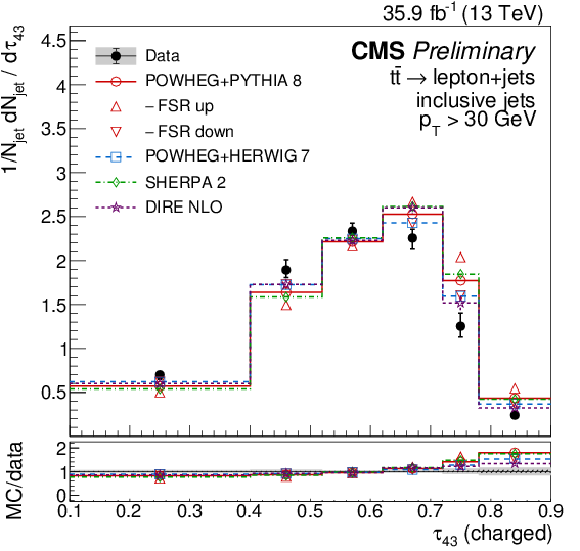
Figure 7:
Distributions of N-subjettiness ratios τ32 (left) and τ43 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 7-a:
Distributions of N-subjettiness ratios τ32 (left) and τ43 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 7-b:
Distributions of N-subjettiness ratios τ32 (left) and τ43 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
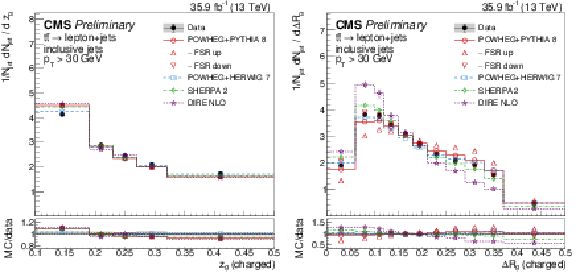
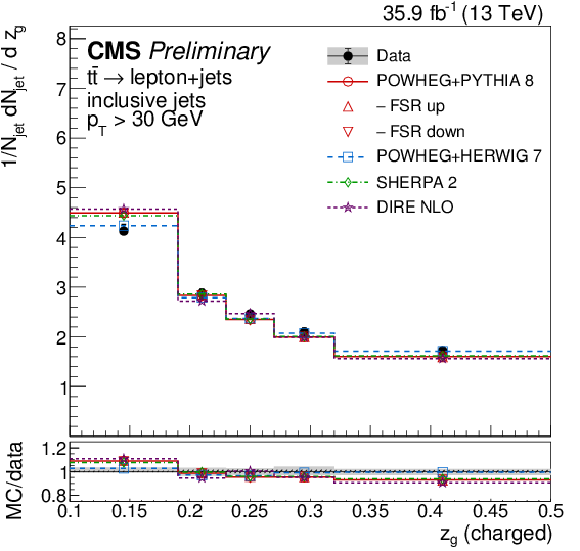
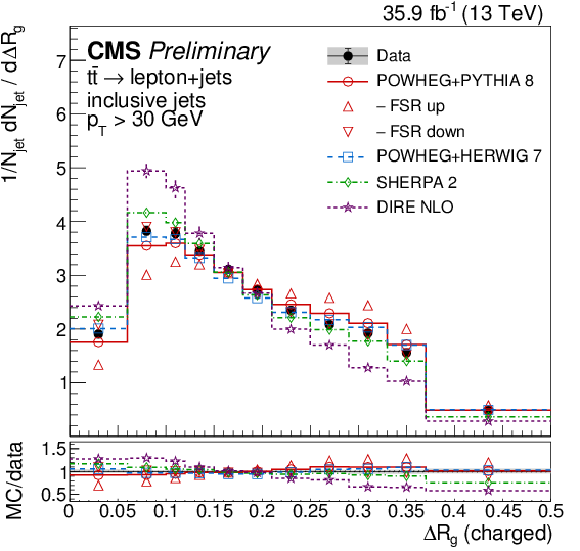
Figure 8:
Distributions of the groomed momentum fraction zg (left) and the angle between the groomed subjets ΔRg (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 8-a:
Distributions of the groomed momentum fraction zg (left) and the angle between the groomed subjets ΔRg (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 8-b:
Distributions of the groomed momentum fraction zg (left) and the angle between the groomed subjets ΔRg (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |

png pdf |
Figure 9:
Distribution of the soft drop multiplicity nSD, unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
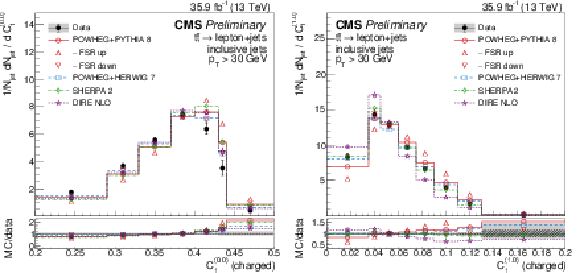
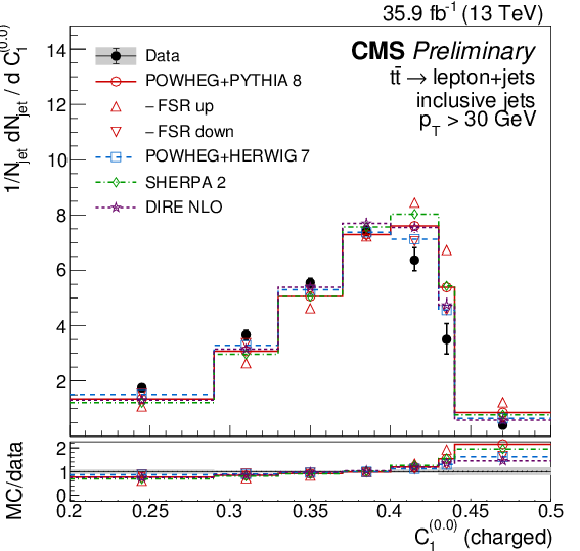
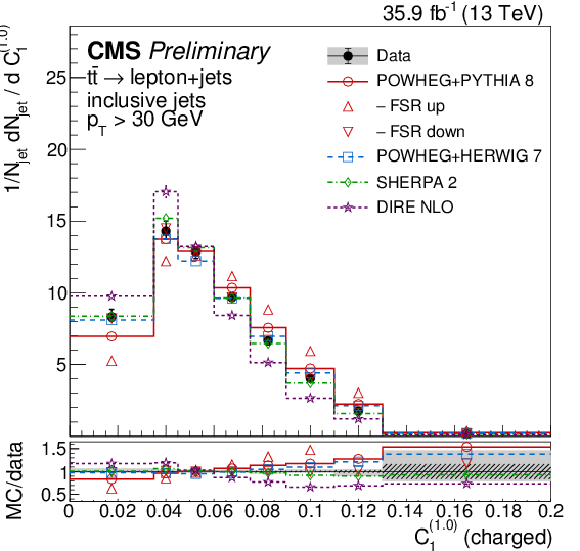
Figure 10:
Distributions of energy correlation ratios C(0.0)1 (left) and C(1.0)1 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 10-a:
Distributions of energy correlation ratios C(0.0)1 (left) and C(1.0)1 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 10-b:
Distributions of energy correlation ratios C(0.0)1 (left) and C(1.0)1 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
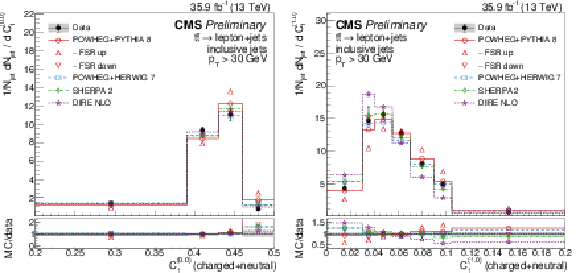
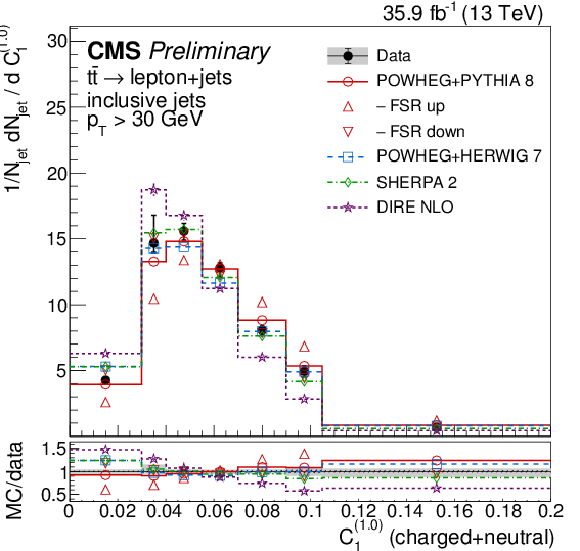
Figure 11:
Distributions of energy correlation ratios C(0.0)1 (left) and C(1.0)1 (right), unfolded to the particle level, for inclusive jets reconstructed with charged+neutral particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |

png pdf |
Figure 11-a:
Distributions of energy correlation ratios C(0.0)1 (left) and C(1.0)1 (right), unfolded to the particle level, for inclusive jets reconstructed with charged+neutral particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 11-b:
Distributions of energy correlation ratios C(0.0)1 (left) and C(1.0)1 (right), unfolded to the particle level, for inclusive jets reconstructed with charged+neutral particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
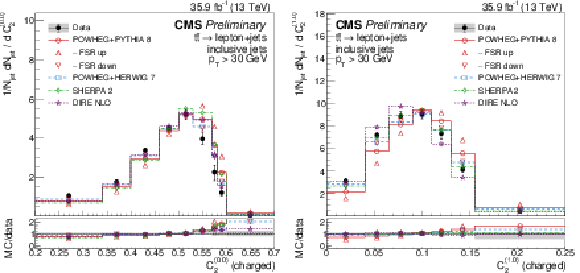
Figure 12:
Distributions of energy correlation ratios C(0.0)2 (left) and C(1.0)2 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
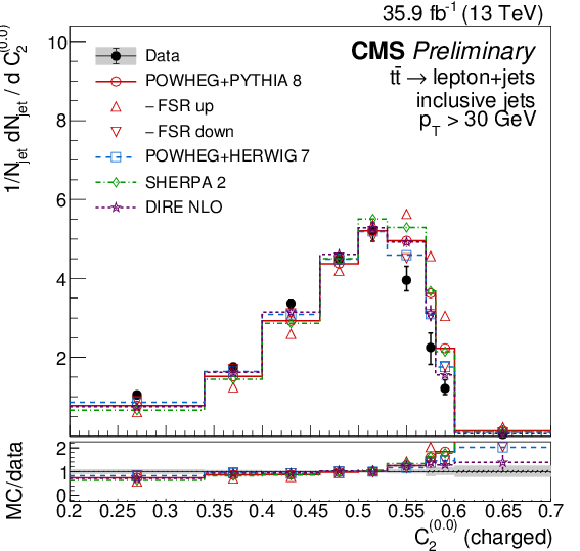
png pdf |
Figure 12-a:
Distributions of energy correlation ratios C(0.0)2 (left) and C(1.0)2 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |

png pdf |
Figure 12-b:
Distributions of energy correlation ratios C(0.0)2 (left) and C(1.0)2 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
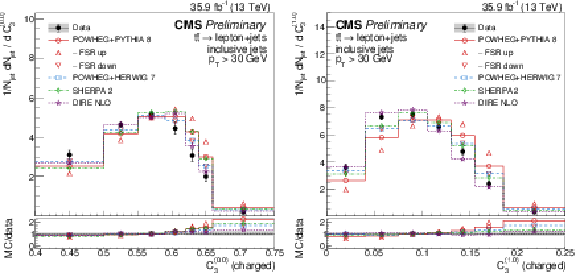
Figure 13:
Distributions of energy correlation ratios C(0.0)3 (left) and C(1.0)3 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
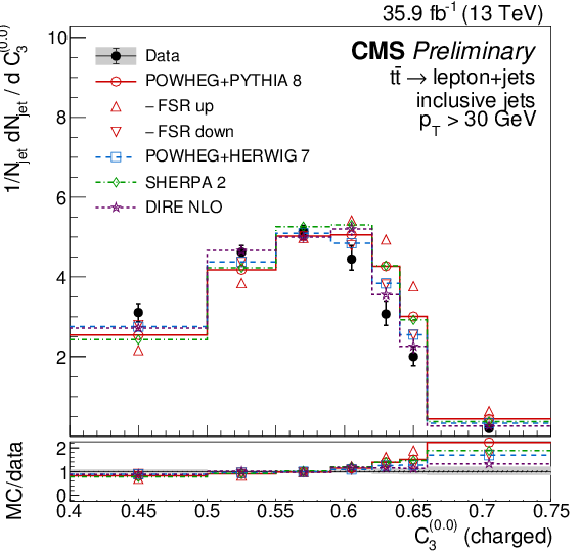
png pdf |
Figure 13-a:
Distributions of energy correlation ratios C(0.0)3 (left) and C(1.0)3 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
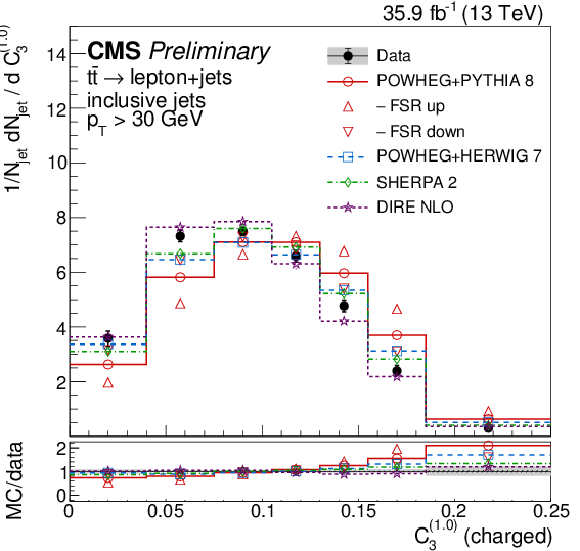
png pdf |
Figure 13-b:
Distributions of energy correlation ratios C(0.0)3 (left) and C(1.0)3 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
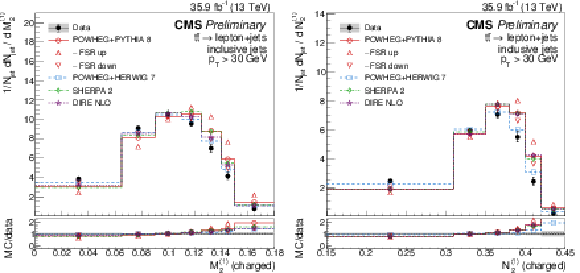
Figure 14:
Distributions of the energy correlation ratios M(1)2 (left) and N(1)2 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 14-a:
Distributions of the energy correlation ratios M(1)2 (left) and N(1)2 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
Figure 14-b:
Distributions of the energy correlation ratios M(1)2 (left) and N(1)2 (right), unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
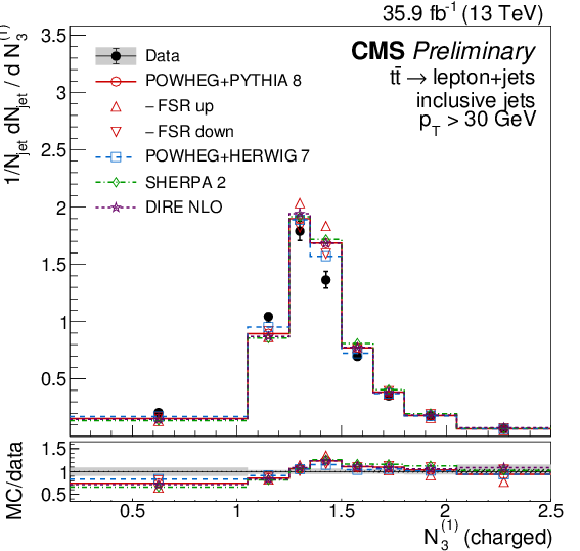
Figure 15:
Distribution of the energy correlation ratio N(1)3, unfolded to the particle level, for inclusive jets reconstructed with charged particles in t¯t events at √s= 13 TeV. Data (points) are compared to different MC predictions absolutely (upper), and as MC/data ratios (lower). |
png pdf |
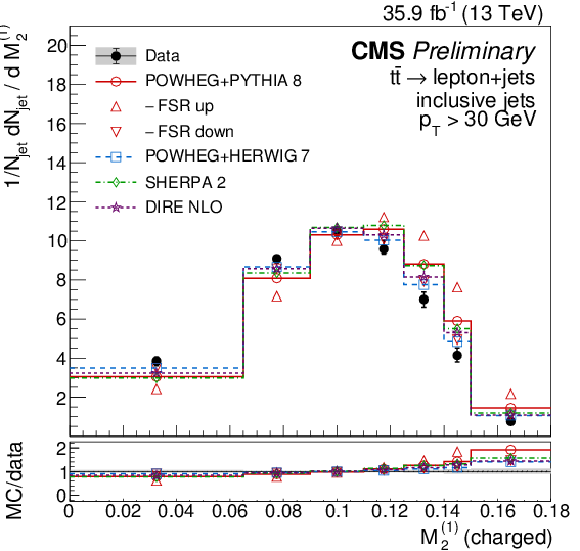
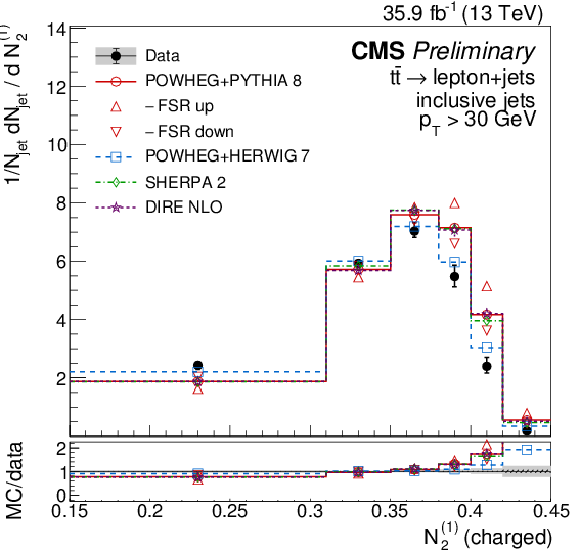
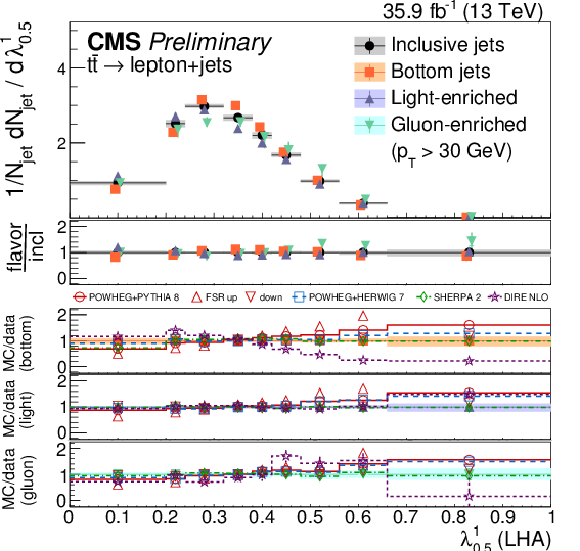
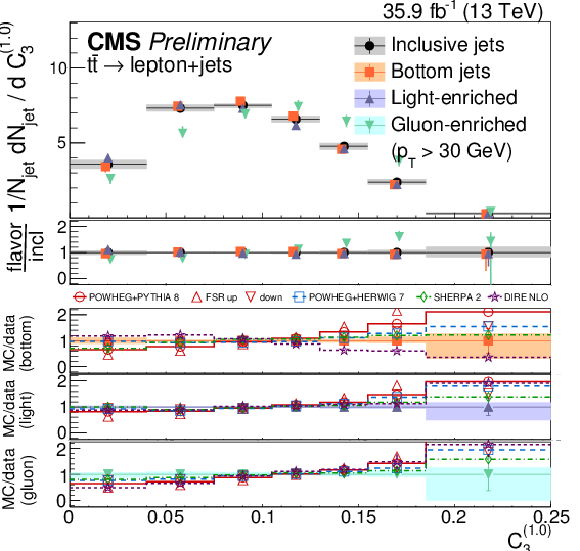
Figure 16:
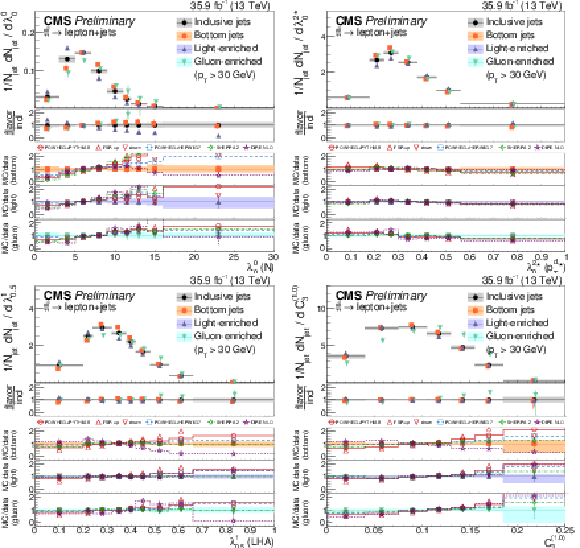
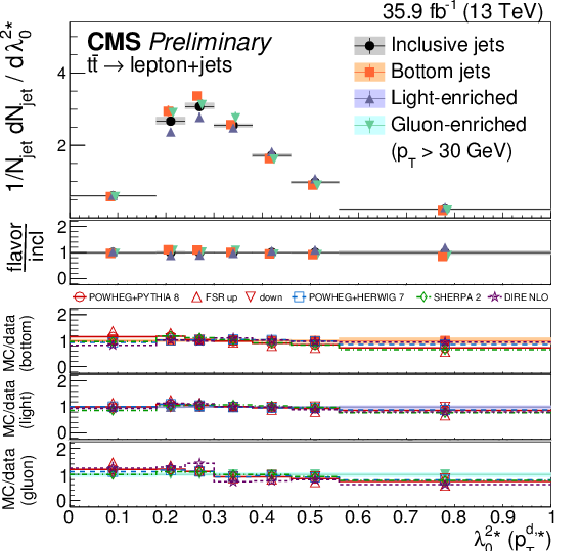
Distributions of the charged multiplicity (upper left), scaled pT dispersion (λ2∗0) (upper right), Les Houches angularity (λ10.5) (lower left), and the energy correlation ratio C(1.0)3 (lower right), unfolded to the particle level, for jets of different flavors measured in t¯t events at √s= 13 TeV. |
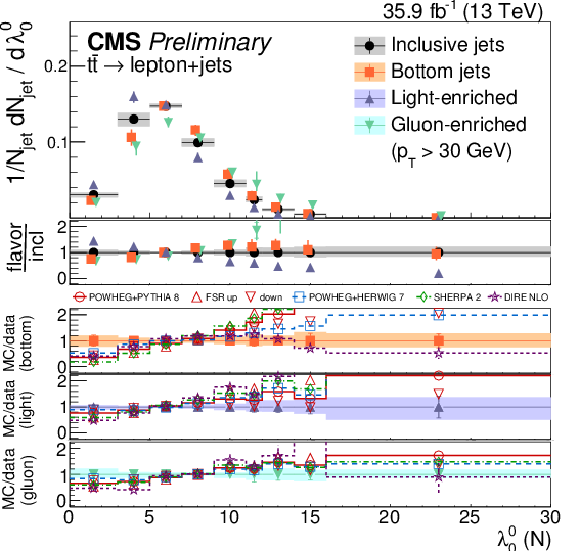
png pdf |
Figure 16-a:
Distributions of the charged multiplicity (upper left), scaled pT dispersion (λ2∗0) (upper right), Les Houches angularity (λ10.5) (lower left), and the energy correlation ratio C(1.0)3 (lower right), unfolded to the particle level, for jets of different flavors measured in t¯t events at √s= 13 TeV. |
png pdf |
Figure 16-b:
Distributions of the charged multiplicity (upper left), scaled pT dispersion (λ2∗0) (upper right), Les Houches angularity (λ10.5) (lower left), and the energy correlation ratio C(1.0)3 (lower right), unfolded to the particle level, for jets of different flavors measured in t¯t events at √s= 13 TeV. |
png pdf |
Figure 16-c:
Distributions of the charged multiplicity (upper left), scaled pT dispersion (λ2∗0) (upper right), Les Houches angularity (λ10.5) (lower left), and the energy correlation ratio C(1.0)3 (lower right), unfolded to the particle level, for jets of different flavors measured in t¯t events at √s= 13 TeV. |
png pdf |
Figure 16-d:
Distributions of the charged multiplicity (upper left), scaled pT dispersion (λ2∗0) (upper right), Les Houches angularity (λ10.5) (lower left), and the energy correlation ratio C(1.0)3 (lower right), unfolded to the particle level, for jets of different flavors measured in t¯t events at √s= 13 TeV. |
png pdf |
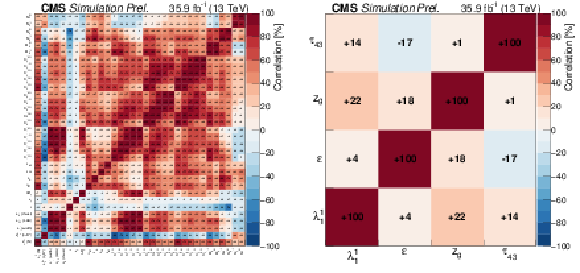
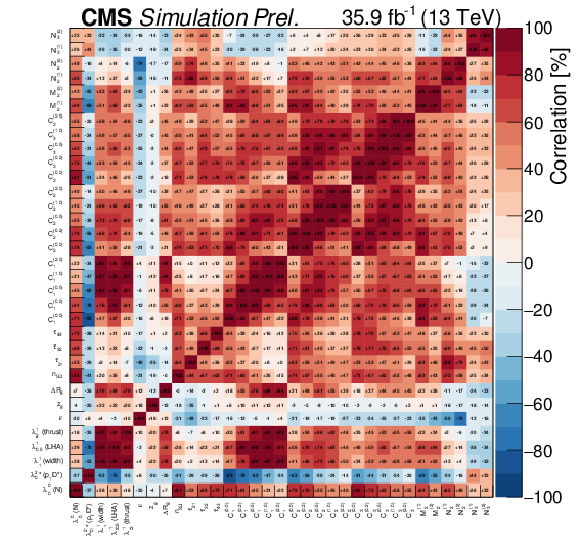
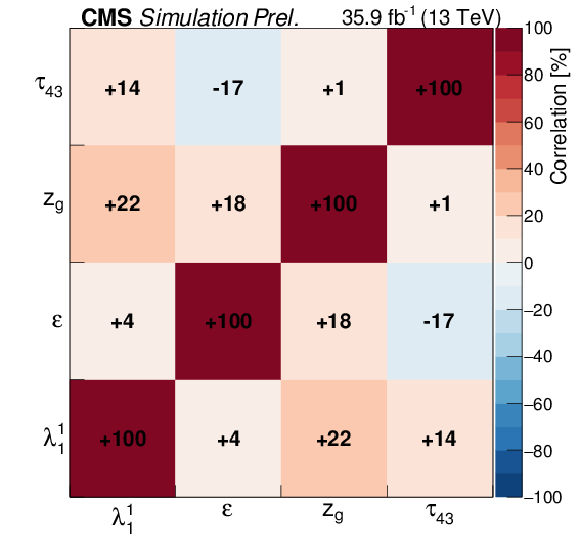
Figure 17:
Correlations of the jet-shapes observables used in this analysis obtained at particle level based on the full matrix (left), and of four (FSR-sensitive) observables with low correlation (right). |
png pdf |
Figure 17-a:
Correlations of the jet-shapes observables used in this analysis obtained at particle level based on the full matrix (left), and of four (FSR-sensitive) observables with low correlation (right). |
png pdf |
Figure 17-b:
Correlations of the jet-shapes observables used in this analysis obtained at particle level based on the full matrix (left), and of four (FSR-sensitive) observables with low correlation (right). |
png pdf |
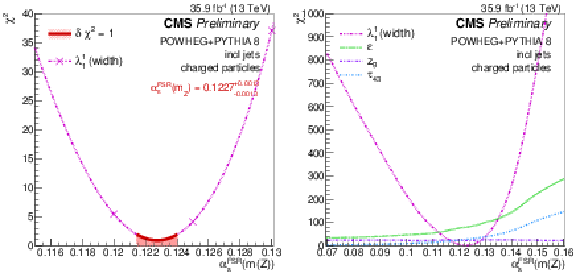
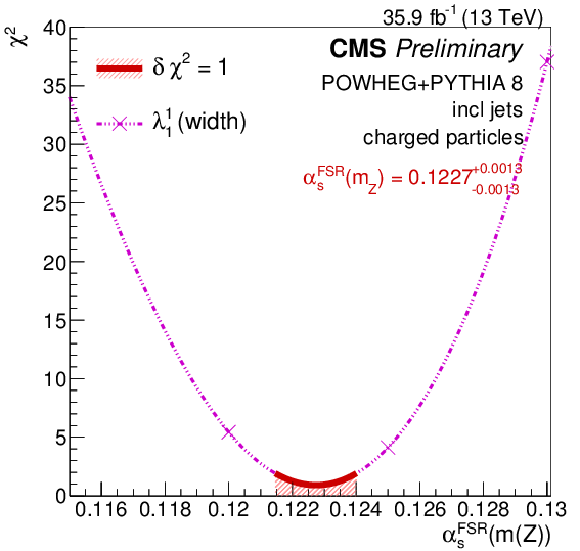
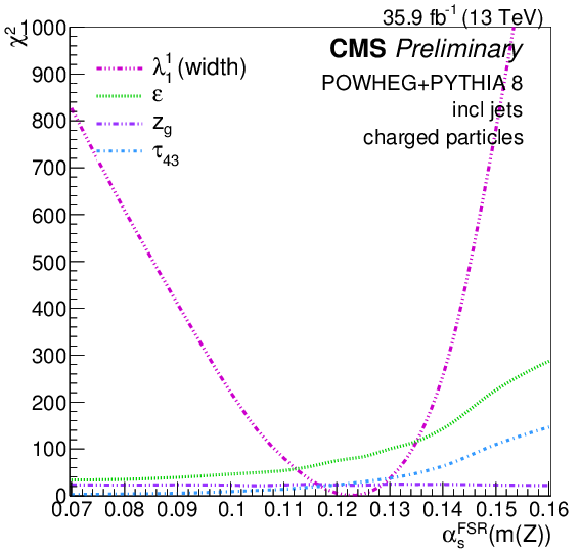
Figure 18:
Fit of αFSRs(mZ) using the jet width λ11 (left), and a scan adding three other observables (ε, zg, and τ43) lightly correlated with it and with each other (right). |
png pdf |
Figure 18-a:
Fit of αFSRs(mZ) using the jet width λ11 (left), and a scan adding three other observables (ε, zg, and τ43) lightly correlated with it and with each other (right). |
png pdf |
Figure 18-b:
Fit of αFSRs(mZ) using the jet width λ11 (left), and a scan adding three other observables (ε, zg, and τ43) lightly correlated with it and with each other (right). |
png pdf |
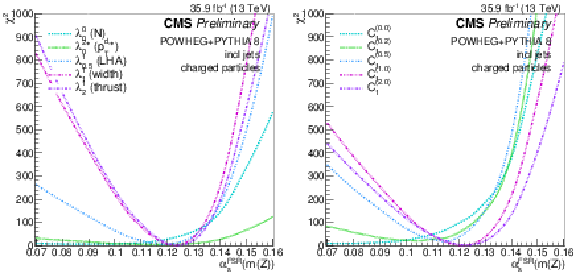
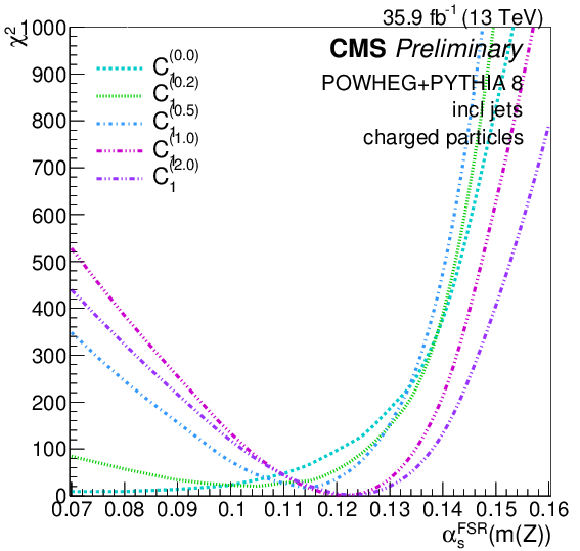
Figure 19:
Scans of αFSRs(mZ) using the λ and C1 families of jet substructure observables. |
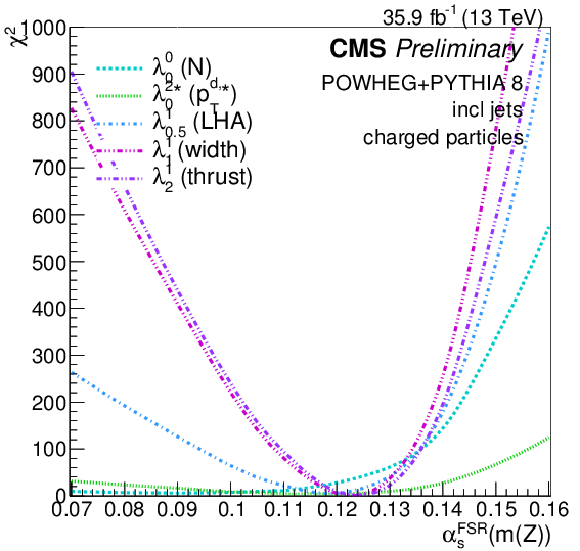
png pdf |
Figure 19-a:
Scans of αFSRs(mZ) using the λ and C1 families of jet substructure observables. |
png pdf |
Figure 19-b:
Scans of αFSRs(mZ) using the λ and C1 families of jet substructure observables. |
png pdf |
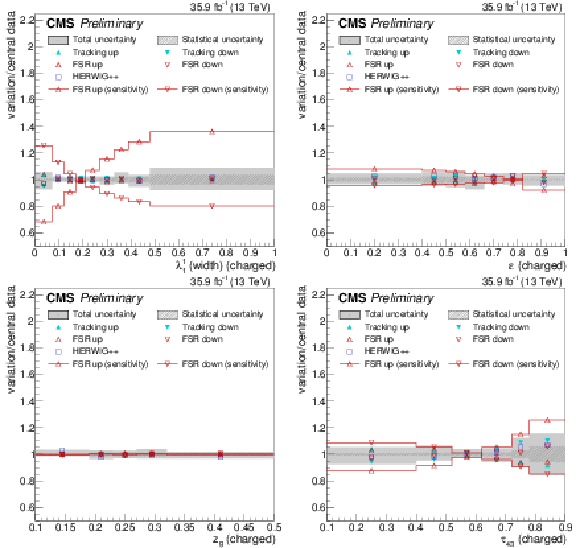
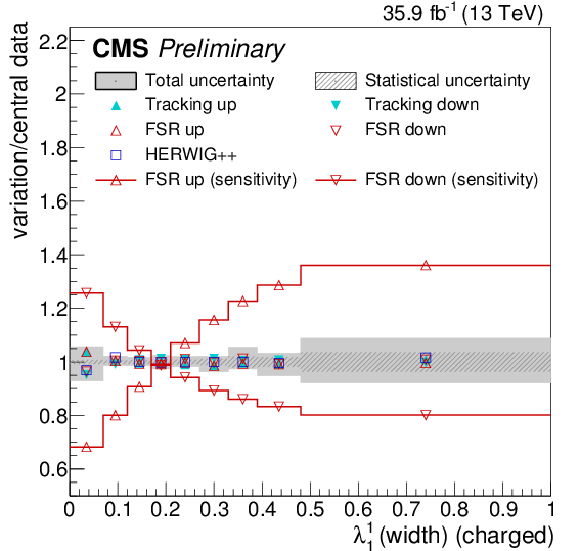
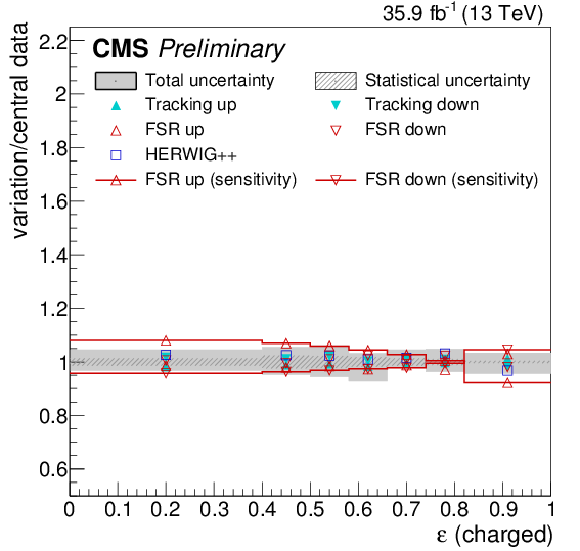
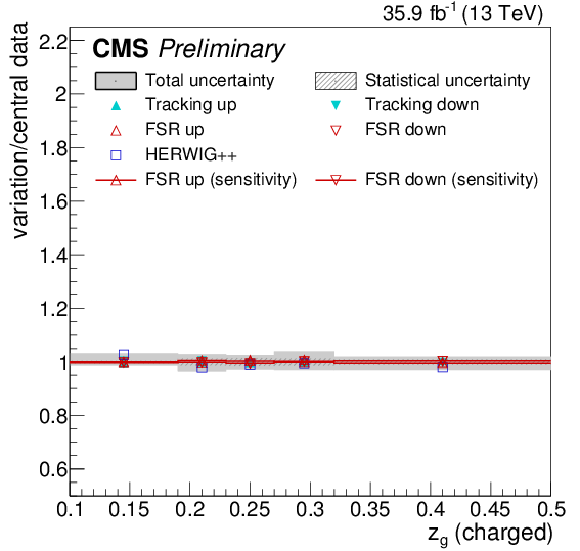
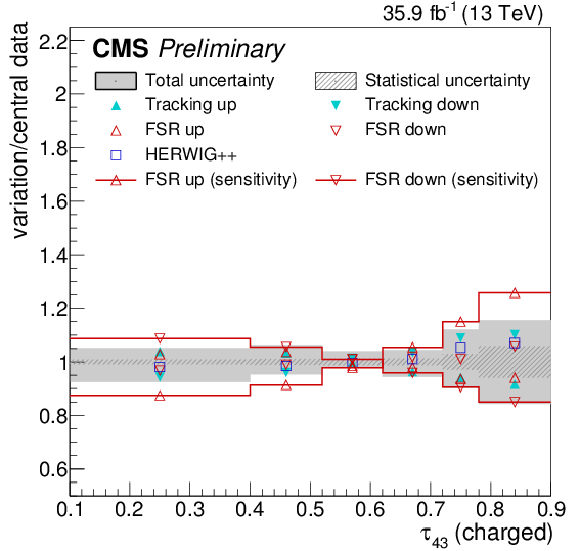
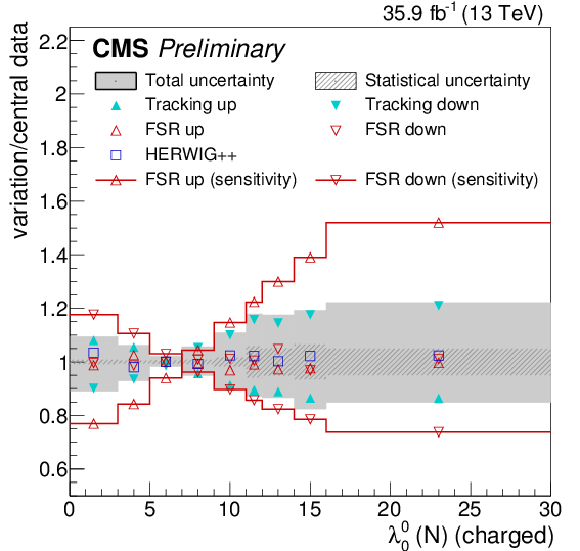
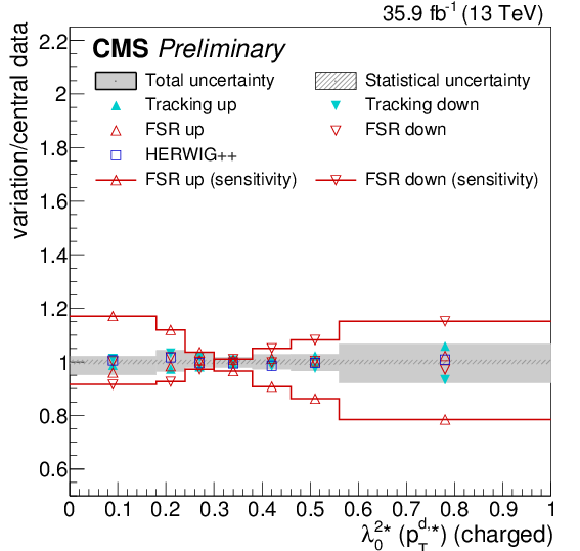
Figure 20:
Systematic uncertainties for the jet width λ11 (upper left), eccentricity ε (upper right), groomed momentum fraction zg (lower left), and N-subjettiness ratio τ43 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
png pdf |
Figure 20-a:
Systematic uncertainties for the jet width λ11 (upper left), eccentricity ε (upper right), groomed momentum fraction zg (lower left), and N-subjettiness ratio τ43 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
png pdf |
Figure 20-b:
Systematic uncertainties for the jet width λ11 (upper left), eccentricity ε (upper right), groomed momentum fraction zg (lower left), and N-subjettiness ratio τ43 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
png pdf |
Figure 20-c:
Systematic uncertainties for the jet width λ11 (upper left), eccentricity ε (upper right), groomed momentum fraction zg (lower left), and N-subjettiness ratio τ43 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
png pdf |
Figure 20-d:
Systematic uncertainties for the jet width λ11 (upper left), eccentricity ε (upper right), groomed momentum fraction zg (lower left), and N-subjettiness ratio τ43 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
png pdf |
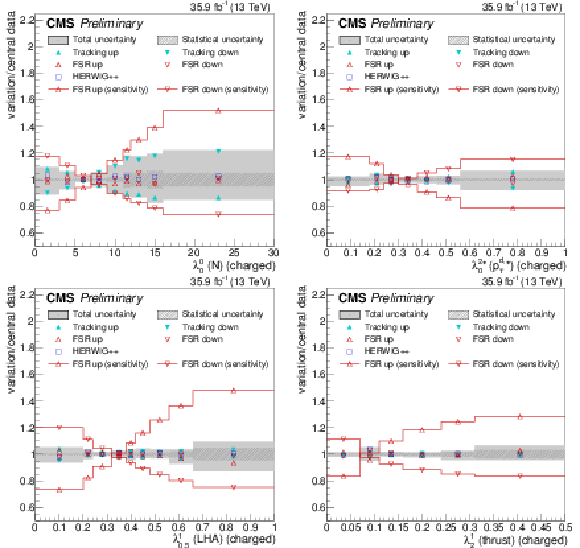
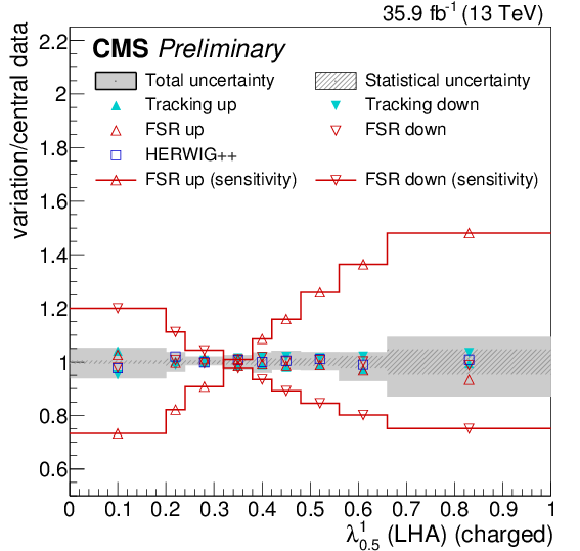
Figure 21:
Systematic uncertainties for charged multiplicity λ00 (upper left), scaled pT dispersion λ2∗0 (upper right), Les Houches angularity λ10.5 (lower left), and the jet thrust λ11 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
png pdf |
Figure 21-a:
Systematic uncertainties for charged multiplicity λ00 (upper left), scaled pT dispersion λ2∗0 (upper right), Les Houches angularity λ10.5 (lower left), and the jet thrust λ11 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
png pdf |
Figure 21-b:
Systematic uncertainties for charged multiplicity λ00 (upper left), scaled pT dispersion λ2∗0 (upper right), Les Houches angularity λ10.5 (lower left), and the jet thrust λ11 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
png pdf |
Figure 21-c:
Systematic uncertainties for charged multiplicity λ00 (upper left), scaled pT dispersion λ2∗0 (upper right), Les Houches angularity λ10.5 (lower left), and the jet thrust λ11 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
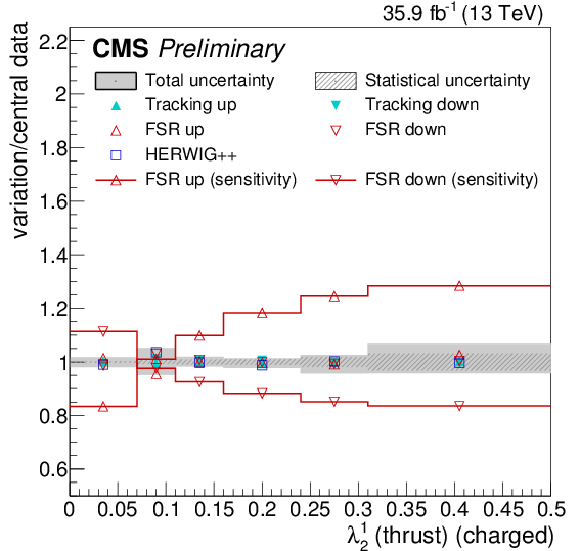
png pdf |
Figure 21-d:
Systematic uncertainties for charged multiplicity λ00 (upper left), scaled pT dispersion λ2∗0 (upper right), Les Houches angularity λ10.5 (lower left), and the jet thrust λ11 (lower right), compared to the full effect of FSR variations on the particle-level distributions. |
| Tables | |
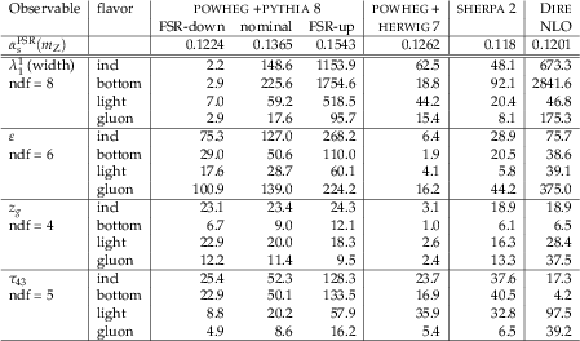
png pdf |
Table 1:
χ2 values for the data-MC comparison of the distributions of the four lightly-correlated jet substructure observables, λ11, ε, zg, and τ43. |
| Summary |
| A measurement of jet substructure observables in tˉt events from pp collisions at 13 TeV is presented, including several variables relevant for quark-gluon discrimination and heavy boosted object identification. The investigated observables are probes for the perturbative and non-perturbative phases of jet evolution, and their unfolded distributions have been derived for inclusive jets, as well as for samples enriched in jets originating from bottom quarks, light quarks, or gluons. The correlations between all jet substructure variables have been studied. Eliminating observables with a high level of correlation, a set of four variables is identified and used for quantifying the level of data-simulation agreement. Data are compared to theoretical predictions either based on NLO matrix-element calculations (POWHEG) interfaced with different generators for the parton shower and hadronization (either PYTHIA 8 or HERWIG 7), or based on SHERPA 2 with NLO corrections, as well as on the DIRE shower. Using the default tunes none of the predictions yields a good overall agreement. Thus, some further tuning of the models is required. For the POWHEG+PYTHIA 8 prediction, a better accord is achieved by lowering the default value of its (effective) strong coupling for final-state radiation, as confirmed by a one-parameter tuning to the jet width λ11 yielding a value αFSRs(mZ)= 0.1227 ± 0.0013. Besides tuning and improving final-state parton showers, the present data can also be compared against modern QCD analytical calculations for infrared and/or collinear-safe observables that include higher fixed-order corrections as well as logarithmic resummations. |
| References | ||||
| 1 | A. Buckley et al. | General-purpose event generators for LHC physics | Phys. Rep. 504 (2011) 145 | 1101.2599 |
| 2 | ALEPH Collaboration | Studies of QCD at e+e− centre-of-mass energies between 91 GeV and 209 GeV | EPJC 35 (2004) 457 | |
| 3 | DELPHI Collaboration | Tuning and test of fragmentation models based on identified particles and precision event shape data | Z. Phys. C 73 (1996) 11 | |
| 4 | DELPHI Collaboration | A study of the b-quark fragmentation function with the DELPHI detector at LEP I and an averaged distribution obtained at the Z pole | EPJC 71 (2011) 1557 | 1102.4748 |
| 5 | L3 Collaboration | Studies of hadronic event structure in e+e− annihilation from 30 GeV to 209 GeV with the L3 detector | Phys. Rep. 399 (2004) 71 | hep-ex/0406049 |
| 6 | OPAL Collaboration | Measurement of event shape distributions and moments in e+ e- → hadrons at 91 GeV - 209 GeV and a determination of αs | EPJC 40 (2005) 287 | hep-ex/0503051 |
| 7 | OPAL Collaboration | Measurements of flavor dependent fragmentation functions in Z0→qˉq events | EPJC 7 (1999) 369 | hep-ex/9807004 |
| 8 | SLD Collaboration | Production of π+,K+,K0,K∗0,ϕ,p and λbda0 in hadronic Z0 decays | PRD 59 (1999) 052001 | hep-ex/9805029 |
| 9 | SLD Collaboration | Measurement of the b quark fragmentation function in Z0 decays | PRD 65 (2002) 092006 | hep-ex/0202031 |
| 10 | C. Frye, A. J. Larkoski, J. Thaler, and K. Zhou | Casimir Meets Poisson: Improved Quark/Gluon Discrimination with Counting Observables | JHEP 09 (2017) 083 | 1704.06266 |
| 11 | S. D. Ellis, C. K. Vermilion, and J. R. Walsh | Techniques for improved heavy particle searches with jet substructure | PRD 80 (2009) 051501 | 0903.5081 |
| 12 | A. Altheimer et al. | Boosted objects and jet substructure at the LHC. Report of BOOST2012, held at IFIC Valencia, 23rd-27th of July 2012 | EPJC 74 (2014) 2792 | 1311.2708 |
| 13 | D. d'Enterria and P. Z. Skands, eds. | Parton Radiation and Fragmentation from LHC to FCC-ee | 1702.01329 | |
| 14 | A. J. Larkoski, I. Moult, and B. Nachman | Jet Substructure at the Large Hadron Collider: A Review of Recent Advances in Theory and Machine Learning | 1709.04464 | |
| 15 | S. Marzani, L. Schunk, and G. Soyez | A study of jet mass distributions with grooming | JHEP 07 (2017) 132 | 1704.02210 |
| 16 | C. Frye, A. J. Larkoski, M. D. Schwartz, and K. Yan | Factorization for groomed jet substructure beyond the next-to-leading logarithm | JHEP 07 (2016) 064 | 1603.09338 |
| 17 | ATLAS Collaboration | Study of Jet Shapes in Inclusive Jet Production in pp Collisions at √s= 7 TeV using the ATLAS Detector | PRD 83 (2011) 052003 | 1101.0070 |
| 18 | ATLAS Collaboration | ATLAS Measurements of the Properties of Jets for Boosted Particle Searches | PRD 86 (2012) 072006 | 1206.5369 |
| 19 | CMS Collaboration | Studies of jet mass in dijet and W/Z + jet events | JHEP 05 (2013) 090 | CMS-SMP-12-019 1303.4811 |
| 20 | ATLAS Collaboration | A measurement of the soft-drop jet mass in pp collisions at √s= 13 TeV with the ATLAS detector | Submitted to PRLett | 1711.08341 |
| 21 | ATLAS Collaboration | Measurement of jet shapes in top-quark pair events at √s= 7 TeV using the ATLAS detector | EPJC 73 (2013) 2676 | 1307.5749 |
| 22 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 23 | P. Nason | A New method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | 0409146 |
| 24 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 25 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 26 | S. Frixione, P. Nason, and G. Ridolfi | A Positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 27 | M. Czakon and A. Mitov | Top++: A program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | |
| 28 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 29 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 30 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 31 | T. Melia, P. Nason, R. Rontsch, and G. Zanderighi | W+W−, WZ and ZZ production in the POWHEG BOX | JHEP 11 (2011) 078 | 1107.5051 |
| 32 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 33 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: s- and t-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 34 | S. Frixione, E. Laenen, P. Motylinski, and B. R. Webber | Angular correlations of lepton pairs from vector boson and top quark decays in Monte Carlo simulations | JHEP 04 (2007) 081 | hep-ph/0702198 |
| 35 | P. Artoisenet, R. Frederix, O. Mattelaer, and R. Rietkerk | Automatic spin-entangled decays of heavy resonances in Monte Carlo simulations | JHEP 03 (2013) 015 | 1212.3460 |
| 36 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 37 | T. Sjostrand et al. | An Introduction to PYTHIA8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 38 | E. Norrbin and T. Sjostrand | QCD radiation off heavy particles | NPB 603 (2001) 297 | hep-ph/0010012 |
| 39 | B. Andersson, G. Gustafson, G. Ingelman, and T. Sjostrand | Parton Fragmentation and String Dynamics | Phys. Rep. 97 (1983) 31 | |
| 40 | T. Sjostrand | Jet Fragmentation of Nearby Partons | NPB 248 (1984) 469 | |
| 41 | M. G. Bowler | e+ e- Production of Heavy Quarks in the String Model | Z. Phys. C 11 (1981) 169 | |
| 42 | CMS Collaboration | Investigations of the impact of the parton shower tuning in PYTHIA8 in the modelling of t¯t at √s= 8 and 13 TeV | CMS-PAS-TOP-16-021 | CMS-PAS-TOP-16-021 |
| 43 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 44 | M. Bahr et al. | HERWIG++ Physics and Manual | EPJC 58 (2008) 639 | 0803.0883 |
| 45 | S. Gieseke, P. Stephens, and B. Webber | New formalism for QCD parton showers | JHEP 12 (2003) 045 | hep-ph/0310083 |
| 46 | B. R. Webber | A QCD Model for Jet Fragmentation Including Soft Gluon Interference | NPB 238 (1984) 492 | |
| 47 | GEANT4 Collaboration | GEANT4: A simulation toolkit | NIMA506 (2003) 250 | |
| 48 | J. Bellm et al. | HERWIG 7.0/HERWIG++ 3.0 release note | EPJC 76 (2016) 196 | 1512.01178 |
| 49 | T. Gleisberg et al. | Event generation with SHERPA 1.1 | JHEP 02 (2009) 007 | 0811.4622 |
| 50 | S. Frixione and B. R. Webber | Matching NLO QCD computations and parton shower simulations | JHEP 06 (2002) 029 | hep-ph/0204244 |
| 51 | S. Hoche and S. Prestel | The midpoint between dipole and parton showers | EPJC 75 (2015) 461 | 1506.05057 |
| 52 | S. Hoche and S. Prestel | Triple collinear emissions in parton showers | PRD 96 (2017) 074017 | 1705.00742 |
| 53 | S. Hoche, F. Krauss, and S. Prestel | Implementing NLO DGLAP evolution in Parton Showers | JHEP 10 (2017) 093 | 1705.00982 |
| 54 | S. Schumann and F. Krauss | A Parton shower algorithm based on Catani-Seymour dipole factorisation | JHEP 03 (2008) 038 | 0709.1027 |
| 55 | J.-C. Winter, F. Krauss, and G. Soff | A Modified cluster hadronization model | EPJC 36 (2004) 381 | hep-ph/0311085 |
| 56 | T. Sjostrand and M. van Zijl | A Multiple Interaction Model for the Event Structure in Hadron Collisions | PRD 36 (1987) 2019 | |
| 57 | J. M. Butterworth, J. R. Forshaw, and M. H. Seymour | Multiparton interactions in photoproduction at HERA | Z. Phys. C 72 (1996) 637 | hep-ph/9601371 |
| 58 | I. Borozan and M. H. Seymour | An Eikonal model for multiparticle production in hadron hadron interactions | JHEP 09 (2002) 015 | hep-ph/0207283 |
| 59 | M. Bahr, S. Gieseke, and M. H. Seymour | Simulation of multiple partonic interactions in HERWIG++ | JHEP 07 (2008) 076 | 0803.3633 |
| 60 | S. Gieseke, C. Rohr, and A. Siodmok | Colour reconnections in HERWIG++ | EPJC 72 (2012) 2225 | 1206.0041 |
| 61 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 62 | M. Cacciari, G. P. Salam, and G. Soyez | The Anti-kT jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 63 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 64 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 65 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 66 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | Submitted to JINST | CMS-BTV-16-002 1712.07158 |
| 67 | A. Buckley et al. | Rivet user manual | 1003.0694 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|