

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SUS-24-012 | ||
| Search for compressed electroweakinos with low-momentum isolated tracks | ||
| CMS Collaboration | ||
| 9 April 2025 | ||
| Abstract: A search is presented for higgsino dark matter (DM) in final states with a low momentum (soft), isolated track and large missing transverse momentum. In the minimal supersymmetric standard model (MSSM), charginos are most often produced in association with a nearly mass-degenerate neutralino or another chargino, and predominantly decay into the lightest neutralino (DM candidate) and a soft pion. For a mass difference $ \Delta m^{\pm} $ less than 1 GeV, a discernible displacement of the pion's track with respect to the primary vertex can arise, reaching up to about 1 cm for the smallest allowed $ \Delta m^{\pm} $. A parameterized multivariate classifier is employed to distinguish the signal track from background tracks, optimally targeting a range of $ \Delta m^{\pm} $ by exploiting the track transverse momentum, impact parameter, and event topology to varying degrees depending on the assumed $ \Delta m^{\pm} $. The analyzed data correspond to an integrated luminosity of 138 fb$^{-1} $ collected by the CMS experiment in proton-proton collisions at $ \sqrt{s}=$ 13 TeV. No evidence of new physics is observed, and limits are set at the 95% confidence level in the mass plane of the model. Assuming MSSM cross sections, values of $ \Delta m^{\pm} $ between 0.28 and 1.15 GeV are excluded for a 100 GeV mass chargino, and chargino masses up to 185 GeV are excluded for $ \Delta m^{\pm} $ of 0.55 GeV. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Feynman diagrams for electroweakino pair production. |

png pdf |
Figure 1-a:
Feynman diagrams for electroweakino pair production. |

png pdf |
Figure 1-b:
Feynman diagrams for electroweakino pair production. |

png pdf |
Figure 1-c:
Feynman diagrams for electroweakino pair production. |
png pdf |
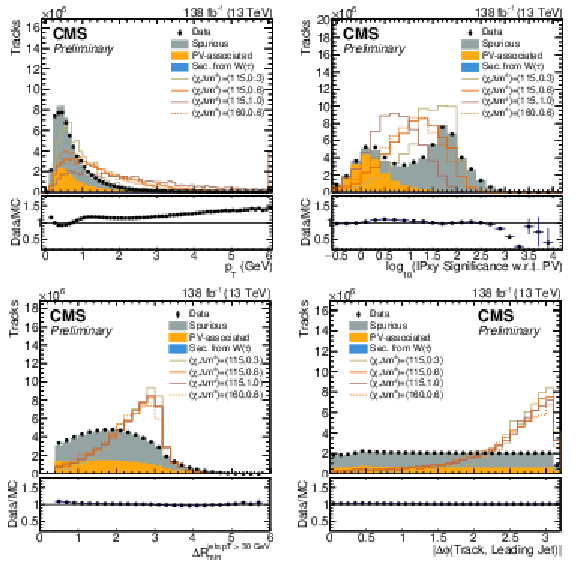
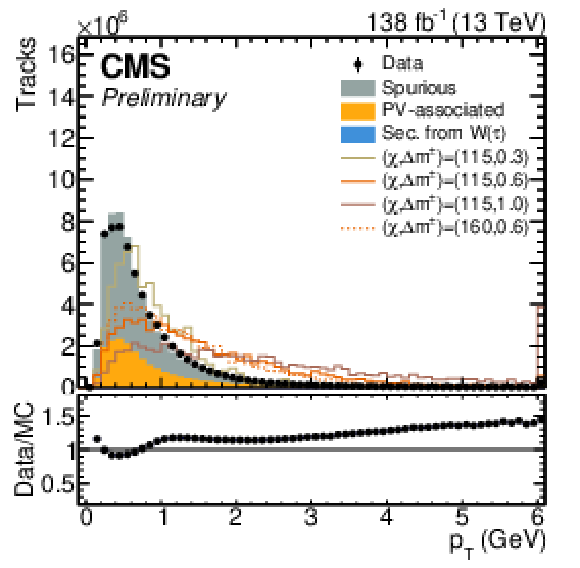
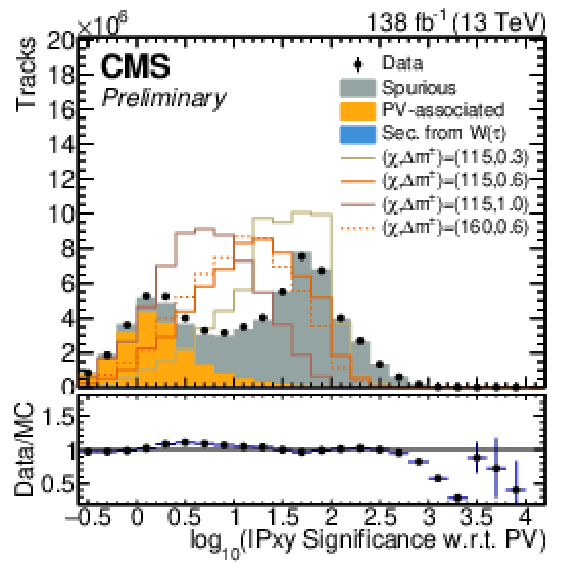
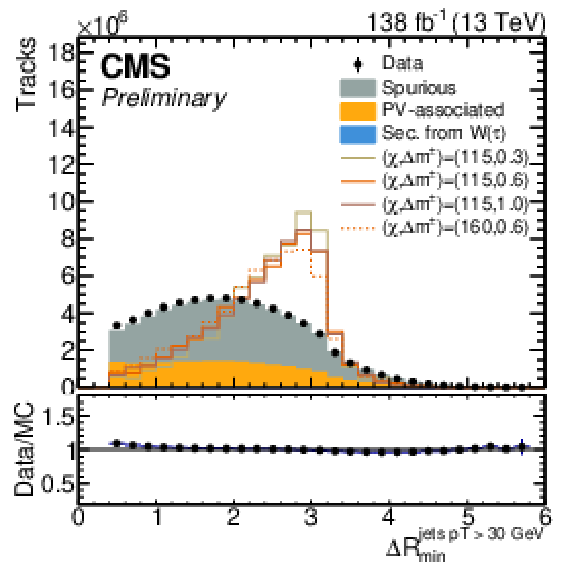
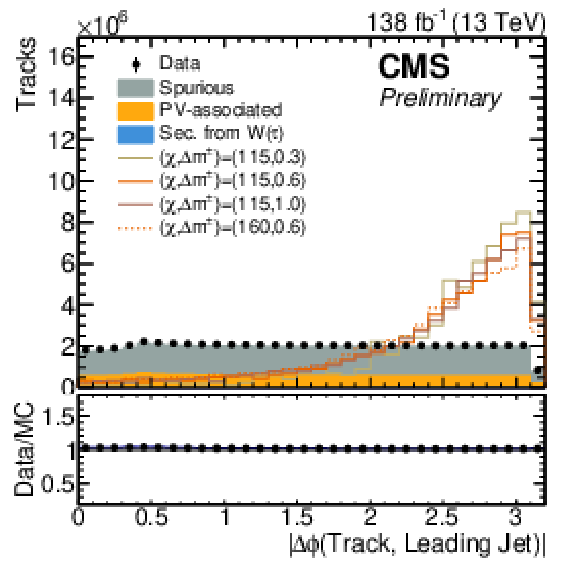
Figure 2:
Distributions of kinematic track observables for background tracks and signal tracks from four example signal model points. The filled histograms show distributions for background tracks in SM background events, normalized to the integral of the total background. Shown as lines are distributions of chargino-matched tracks in signal events for selected benchmark models. |
png pdf |
Figure 2-a:
Distributions of kinematic track observables for background tracks and signal tracks from four example signal model points. The filled histograms show distributions for background tracks in SM background events, normalized to the integral of the total background. Shown as lines are distributions of chargino-matched tracks in signal events for selected benchmark models. |
png pdf |
Figure 2-b:
Distributions of kinematic track observables for background tracks and signal tracks from four example signal model points. The filled histograms show distributions for background tracks in SM background events, normalized to the integral of the total background. Shown as lines are distributions of chargino-matched tracks in signal events for selected benchmark models. |
png pdf |
Figure 2-c:
Distributions of kinematic track observables for background tracks and signal tracks from four example signal model points. The filled histograms show distributions for background tracks in SM background events, normalized to the integral of the total background. Shown as lines are distributions of chargino-matched tracks in signal events for selected benchmark models. |
png pdf |
Figure 2-d:
Distributions of kinematic track observables for background tracks and signal tracks from four example signal model points. The filled histograms show distributions for background tracks in SM background events, normalized to the integral of the total background. Shown as lines are distributions of chargino-matched tracks in signal events for selected benchmark models. |

png pdf |
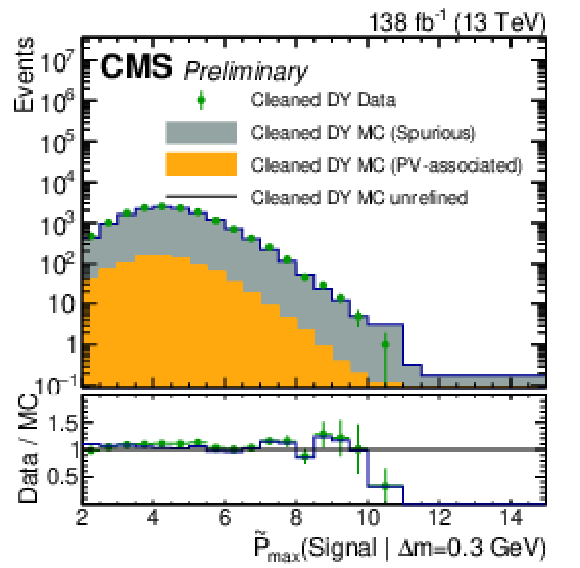
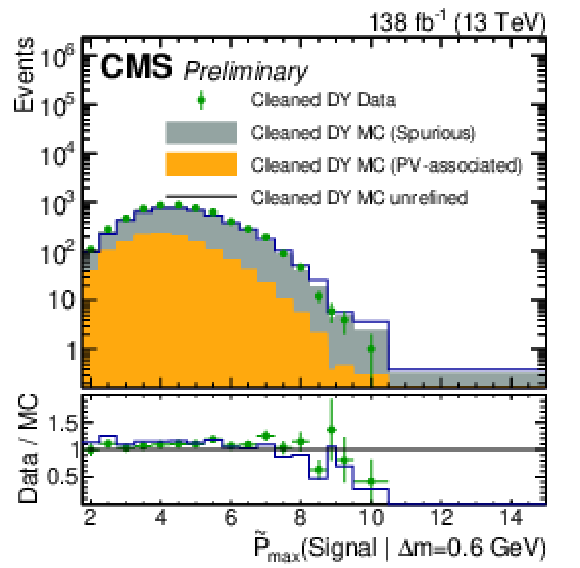
Figure 3:
Left: distributions of the three track variables subject to refinement. The distributions for data are shown alongside those for (unrefined) MC. Right: distributions of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) $, $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.6\ \text{GeV}) $, and $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 1.0\ \text{GeV}) $ for events in data as well as in MC with and without refinement applied to the input variables. |

png pdf |
Figure 3-a:
Left: distributions of the three track variables subject to refinement. The distributions for data are shown alongside those for (unrefined) MC. Right: distributions of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) $, $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.6\ \text{GeV}) $, and $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 1.0\ \text{GeV}) $ for events in data as well as in MC with and without refinement applied to the input variables. |
png pdf |
Figure 3-b:
Left: distributions of the three track variables subject to refinement. The distributions for data are shown alongside those for (unrefined) MC. Right: distributions of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) $, $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.6\ \text{GeV}) $, and $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 1.0\ \text{GeV}) $ for events in data as well as in MC with and without refinement applied to the input variables. |

png pdf |
Figure 3-c:
Left: distributions of the three track variables subject to refinement. The distributions for data are shown alongside those for (unrefined) MC. Right: distributions of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) $, $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.6\ \text{GeV}) $, and $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 1.0\ \text{GeV}) $ for events in data as well as in MC with and without refinement applied to the input variables. |
png pdf |
Figure 3-d:
Left: distributions of the three track variables subject to refinement. The distributions for data are shown alongside those for (unrefined) MC. Right: distributions of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) $, $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.6\ \text{GeV}) $, and $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 1.0\ \text{GeV}) $ for events in data as well as in MC with and without refinement applied to the input variables. |

png pdf |
Figure 3-e:
Left: distributions of the three track variables subject to refinement. The distributions for data are shown alongside those for (unrefined) MC. Right: distributions of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) $, $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.6\ \text{GeV}) $, and $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 1.0\ \text{GeV}) $ for events in data as well as in MC with and without refinement applied to the input variables. |

png pdf |
Figure 3-f:
Left: distributions of the three track variables subject to refinement. The distributions for data are shown alongside those for (unrefined) MC. Right: distributions of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) $, $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.6\ \text{GeV}) $, and $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 1.0\ \text{GeV}) $ for events in data as well as in MC with and without refinement applied to the input variables. |

png pdf |
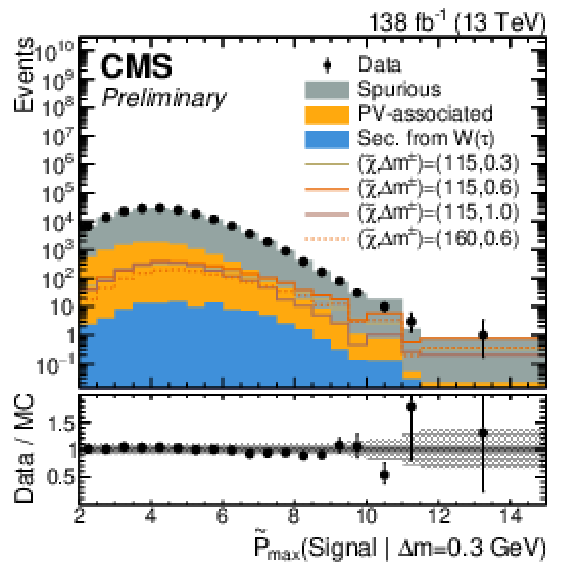
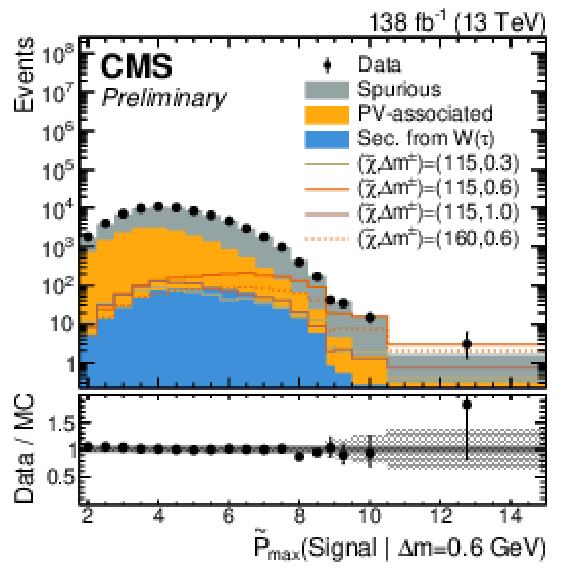
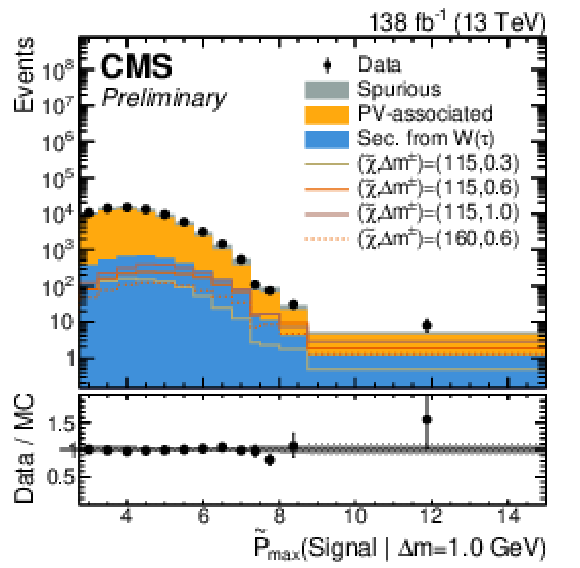
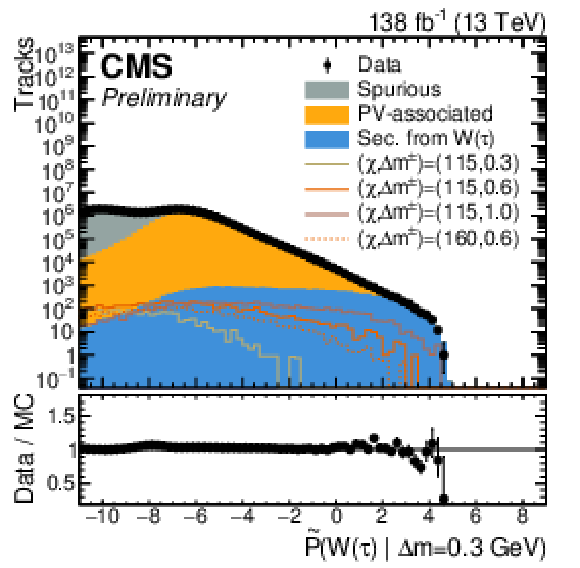
Figure 4:
The first three plots show the expected and observed data in the signal-sensitive observables $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3,\,0.6,\,1.0\ \text{GeV}) $. In the lower ratio panel, the gray shaded region shows the relative statistical uncertainty in the background estimate, while the black vertical error bars indicate the total uncertainty in each bin. The fourth plot shows the output of the $ \tau $ node of tracks with a loose selection of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) > - $2, indicating the $ \tau $-based signal proxy region. |
png pdf |
Figure 4-a:
The first three plots show the expected and observed data in the signal-sensitive observables $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3,\,0.6,\,1.0\ \text{GeV}) $. In the lower ratio panel, the gray shaded region shows the relative statistical uncertainty in the background estimate, while the black vertical error bars indicate the total uncertainty in each bin. The fourth plot shows the output of the $ \tau $ node of tracks with a loose selection of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) > - $2, indicating the $ \tau $-based signal proxy region. |
png pdf |
Figure 4-b:
The first three plots show the expected and observed data in the signal-sensitive observables $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3,\,0.6,\,1.0\ \text{GeV}) $. In the lower ratio panel, the gray shaded region shows the relative statistical uncertainty in the background estimate, while the black vertical error bars indicate the total uncertainty in each bin. The fourth plot shows the output of the $ \tau $ node of tracks with a loose selection of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) > - $2, indicating the $ \tau $-based signal proxy region. |
png pdf |
Figure 4-c:
The first three plots show the expected and observed data in the signal-sensitive observables $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3,\,0.6,\,1.0\ \text{GeV}) $. In the lower ratio panel, the gray shaded region shows the relative statistical uncertainty in the background estimate, while the black vertical error bars indicate the total uncertainty in each bin. The fourth plot shows the output of the $ \tau $ node of tracks with a loose selection of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) > - $2, indicating the $ \tau $-based signal proxy region. |
png pdf |
Figure 4-d:
The first three plots show the expected and observed data in the signal-sensitive observables $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3,\,0.6,\,1.0\ \text{GeV}) $. In the lower ratio panel, the gray shaded region shows the relative statistical uncertainty in the background estimate, while the black vertical error bars indicate the total uncertainty in each bin. The fourth plot shows the output of the $ \tau $ node of tracks with a loose selection of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3\ \text{GeV}) > - $2, indicating the $ \tau $-based signal proxy region. |
png pdf |
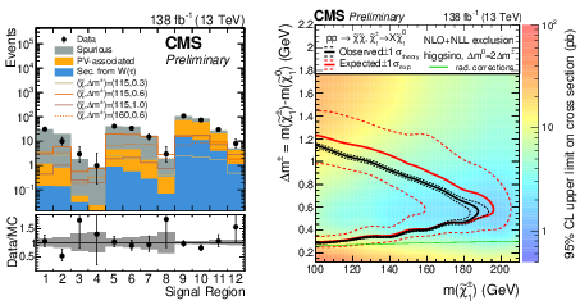
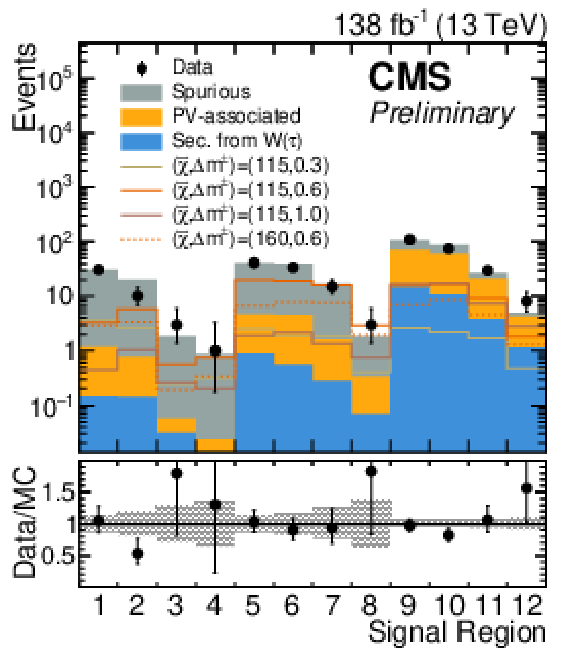
Figure 5:
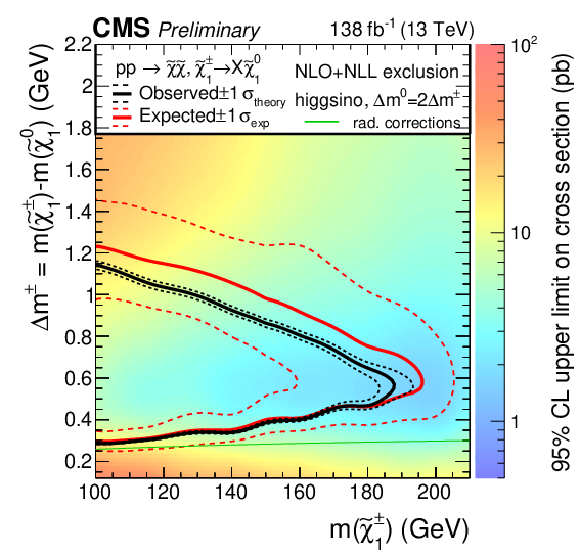
Left: Expected and observed counts in the 12 SRs. The black error bars and gray band in the lower panel show the relative statistical uncertainties in the data and prediction. Four signal benchmark models are shown, corresponding to the inclusive production of all possible pairs of higgsino-like electroweakinos. Right: The heat map shows the 95% CL upper limit on the cross section. The expected (red) and observed (black) bounds indicate the region to the left of which the model space is excluded, assuming theoretical cross sections calculated at NLO-NLL [56,57]. Red dashed lines show the expected limits varied by the experimental uncertainties while black dashed lines are the observed limits with theoretical cross sections varied by their uncertainty. Branching fractions of the chargino are taken from [58]. |
png pdf |
Figure 5-a:
Left: Expected and observed counts in the 12 SRs. The black error bars and gray band in the lower panel show the relative statistical uncertainties in the data and prediction. Four signal benchmark models are shown, corresponding to the inclusive production of all possible pairs of higgsino-like electroweakinos. Right: The heat map shows the 95% CL upper limit on the cross section. The expected (red) and observed (black) bounds indicate the region to the left of which the model space is excluded, assuming theoretical cross sections calculated at NLO-NLL [56,57]. Red dashed lines show the expected limits varied by the experimental uncertainties while black dashed lines are the observed limits with theoretical cross sections varied by their uncertainty. Branching fractions of the chargino are taken from [58]. |
png pdf |
Figure 5-b:
Left: Expected and observed counts in the 12 SRs. The black error bars and gray band in the lower panel show the relative statistical uncertainties in the data and prediction. Four signal benchmark models are shown, corresponding to the inclusive production of all possible pairs of higgsino-like electroweakinos. Right: The heat map shows the 95% CL upper limit on the cross section. The expected (red) and observed (black) bounds indicate the region to the left of which the model space is excluded, assuming theoretical cross sections calculated at NLO-NLL [56,57]. Red dashed lines show the expected limits varied by the experimental uncertainties while black dashed lines are the observed limits with theoretical cross sections varied by their uncertainty. Branching fractions of the chargino are taken from [58]. |
| Tables | |

png pdf |
Table 1:
The analysis baseline selection criteria. |

png pdf |
Table 2:
Expected and observed yields in the 12 SRs with a breakdown of the background components and three benchmark signal models, as well as the definitions of the SRs based on the bin boundaries in the range of $ \mathrm{ \tilde{P} }_{\text{max}}(\text{Signal} | \Delta m = 0.3,\,0.6,\,1.0\ \text{GeV}) $. Uncertainties are statistical only. |

png pdf |
Table 3:
Variables used by the NN soft track classifier. |

png pdf |
Table 4:
Custom track observables defined using the track helix extrapolation. All quantities are defined with respect to (a) the leading PV, (b) the closest PV from pileup interactions, (c) the PV associated to the track during reconstruction, and (d) the closest PV excluding the associated vertex. |
| Summary |
| A search for compressed higgsino and wino dark matter has been performed using events containing a soft, slightly displaced track and large $ p_{\mathrm{T}}^\text{miss} $. A parameterized NN was employed to optimize sensitivity across a wide range of models not previously probed, and no significant excess above the standard model prediction is observed. The resulting 95% confidence level limits exclude chargino masses up to 185 GeV for a mass splitting of 0.55 GeV, as well as mass splittings of 0.33-1.2 GeV for a 100 GeV higgsino -- currently the most stringent constraints in this model space -- thereby exerting additional pressure on natural SUSY dark matter scenarios. |
| References | ||||
| 1 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 2 | Y. A. Gol'fand and E. P. Likhtman | Extension of the algebra of Poincaré group generators and violation of P invariance | JETP Lett. 13 (1971) 323 | |
| 3 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | NPB 31 (1971) 86 | |
| 4 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JETP Lett. 16 (1972) 438 | |
| 5 | J. Wess and B. Zumino | A Lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 6 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | NPB 70 (1974) 39 | |
| 7 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | NPB 90 (1975) 104 | |
| 8 | P. Fayet and S. Ferrara | Supersymmetry | Phys. Rept. 32 (1977) 249 | |
| 9 | H. P. Nilles | Supersymmetry, supergravity and particle physics | Phys. Rep. 110 (1984) 1 | |
| 10 | F. Zwicky | On the masses of nebulae and of clusters of nebulae | Astrophys. J. 86 (1937) 217 | |
| 11 | V. C. Rubin and W. K. Ford, Jr. | Rotation of the Andromeda nebula from a spectroscopic survey of emission regions | Astrophys. J. 159 (1970) 379 | |
| 12 | R. Barbieri and G. F. Giudice | Upper bounds on supersymmetric particle masses | Nuclear Physics B 306 (1988) | |
| 13 | S. P. Martin | A supersymmetry primer | Adv. Ser. Direct. High Energy Phys. 18 (1998) 1 | hep-ph/9709356 |
| 14 | Planck Collaboration | Planck 2018 results. VI. Cosmological parameters | Astron. Astrophys. 641 (2020) A6 | 1807.06209 |
| 15 | ATLAS Collaboration | The ATLAS experiment at the CERN Large Hadron Collider | JINST 3 (2008) S08003 | |
| 16 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 17 | LZ Collaboration | First Dark Matter Search Results from the LUX-ZEPLIN (LZ) Experiment | PRL 131 (2023) | 2207.03764 |
| 18 | XENON100 Collaboration | XENON100 Dark Matter Results from a Combination of 477 Live Days | PRD 94 (2016) 122001 | 1609.06154 |
| 19 | PandaX Collaboration | First dark matter search results from the PandaX-I experiment | Sci. China Phys. Mech. Astron. 57 (2014) 2024 | 1408.5114 |
| 20 | CMS Collaboration | Phenomenological MSSM interpretation of CMS searches in pp collisions at 13 TeV | Technical Report, CERN, 2024 CDS |
|
| 21 | N. Nagata and S. Shirai | Higgsino Dark Matter in High-Scale Supersymmetry | JHEP 01 (2015) 029 | 1410.4549 |
| 22 | ATLAS Collaboration | Searches for electroweak production of supersymmetric particles with compressed mass spectra in $ \sqrt{s}= $ 13 TeV $ pp $ collisions with the ATLAS detector | PRD 101 (2020) | 1911.12606 |
| 23 | CMS Collaboration | Search for supersymmetry in final states with two or three soft leptons and missing transverse momentum in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JHEP 04 (2022) 091 | CMS-SUS-18-004 2111.06296 |
| 24 | CMS Collaboration | Search for disappearing tracks in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PLB 806 (2020) 135502 | CMS-EXO-19-010 2004.05153 |
| 25 | ATLAS Collaboration | Search for long-lived charginos based on a disappearing-track signature using 136 fb$ ^{-1} $ of $ pp $ collisions at $ \sqrt{s} $ = 13 TeV with the ATLAS detector | Technical Report, CERN, 2021 | |
| 26 | CMS Collaboration | Search for supersymmetry in final states with disappearing tracks in proton-proton collisions at $\sqrt{s} =$ 13 TeV | PRD 109 (2024) 072007 | CMS-SUS-21-006 2309.16823 |
| 27 | ATLAS Collaboration | Search for nearly mass-degenerate higgsinos using low-momentum mildly-displaced tracks in $ pp $ collisions at $ \sqrt{s} $ = 13 TeV with the ATLAS detector | PRL 132 (2024) 221801 | 2401.14046 |
| 28 | CMS Tracker Group Collaboration | The CMS phase-1 pixel detector upgrade | JINST 16 (2021) P02027 | 2012.14304 |
| 29 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 30 | CMS Collaboration | Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid | CMS Technical Proposal CERN-LHCC-2015-010, CMS-TDR-15-02, 2015 CDS |
|
| 31 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{\mathrm{T}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 32 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 33 | CMS Collaboration | Jet performance in pp collisions at $ \sqrt{s}= $ 7 TeV | CMS Physics Analysis Summary, 2010 link |
|
| 34 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS Physics Analysis Summary, 2017 CMS-PAS-JME-16-003 |
CMS-PAS-JME-16-003 |
| 35 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 36 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 37 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 38 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 39 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 40 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIM A 506 (2003) 250 | |
| 41 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 42 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 43 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 44 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 45 | T. Sjöstrand et al. | An Introduction to PYTHIA 8.2 | Comput. Phys. Commun. 191 (2015) 159 | 1410.3012 |
| 46 | S. Abdullin et al. | The fast simulation of the CMS detector at LHC | J. Phys. Conf. Ser. 331 (2011) 032049 | |
| 47 | A. Giammanco | The fast simulation of the CMS experiment | J. Phys. Conf. Ser. 513 (2014) 022012 | |
| 48 | R. Mahbubani, P. Schwaller, and J. Zurita | Closing the window for compressed Dark Sectors with disappearing charged tracks | JHEP 06 (2017) 119 | 1703.05327 |
| 49 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | Accepted by JINST, 2019 | CMS-JME-17-001 1903.06078 |
| 50 | A. Gretton et al. | A kernel two-sample test | Gretton Journal of Machine Learning Research 13 (2012) 723 | |
| 51 | M. Wolf et al. | Fast Perfekt: Regression-based refinement of fast simulation | SciPost Phys. Core 8 (2025) 021 | |
| 52 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 53 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2018 CMS-PAS-LUM-17-004 |
CMS-PAS-LUM-17-004 |
| 54 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s} = $ 13 TeV | CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 55 | A. Giraldi | Precision luminosity measurement with proton-proton collisions at the CMS experiment in Run 2 | in Proc. 41st Int. Conf. on High Energy Physics (ICHEP), 2022 link |
2208.08214 |
| 56 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Gaugino production in proton-proton collisions at a center-of-mass energy of 8 TeV | JHEP 10 (2012) 081 | 1207.2159 |
| 57 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Precision predictions for electroweak superpartner production at hadron colliders with Resummino | EPJC 73 (2013) 2480 | 1304.0790 |
| 58 | M. Ibe, Y. Nakayama, and S. Shirai | Precise estimate of charged Higgsino/Wino decay rate | JHEP 03 (2024) 012 | 2312.08087 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|