

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-17-005 | ||
| Search for production of a Higgs boson and a single top quark in multilepton final states in proton collisions at √s= 13 TeV | ||
| CMS Collaboration | ||
| May 2017 | ||
| Abstract: A search for the production of a Higgs boson in association with a single top quark is presented, focusing on leptonic signatures provided by the H→WW, H→ττ, and H→ZZ decay modes. Due to strong interference of the two main leading-order diagrams, the production cross section of this process is highly sensitive to the relative sign of the top-Higgs coupling modifier, κt, and the coupling modifier of vector bosons to the Higgs, κV. The analysis exploits signatures with two same-sign leptons or three leptons in the final state, and uses the 2016 data sample collected with the CMS detector at the LHC at a center of mass energy of 13 TeV, which corresponds to an integrated luminosity of 35.9 fb−1. Multivariate techniques are used to discriminate the signal from the dominant backgrounds. The analysis yields a 95% confidence level (C.L.) upper limit on the combined tH+t¯tH production cross section times branching ratio of 0.64 pb, with an expected limit of 0.32 pb, for a scenario with κt=−1.0 and κV=1.0. Values of κt outside the range of −1.25 to +1.60 are excluded at 95% C.L., assuming κV=1.0. | ||
| Links: CDS record (PDF) ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures & Tables | Summary | Additional Figures | References | CMS Publications |
|---|
| Figures | |
png pdf |
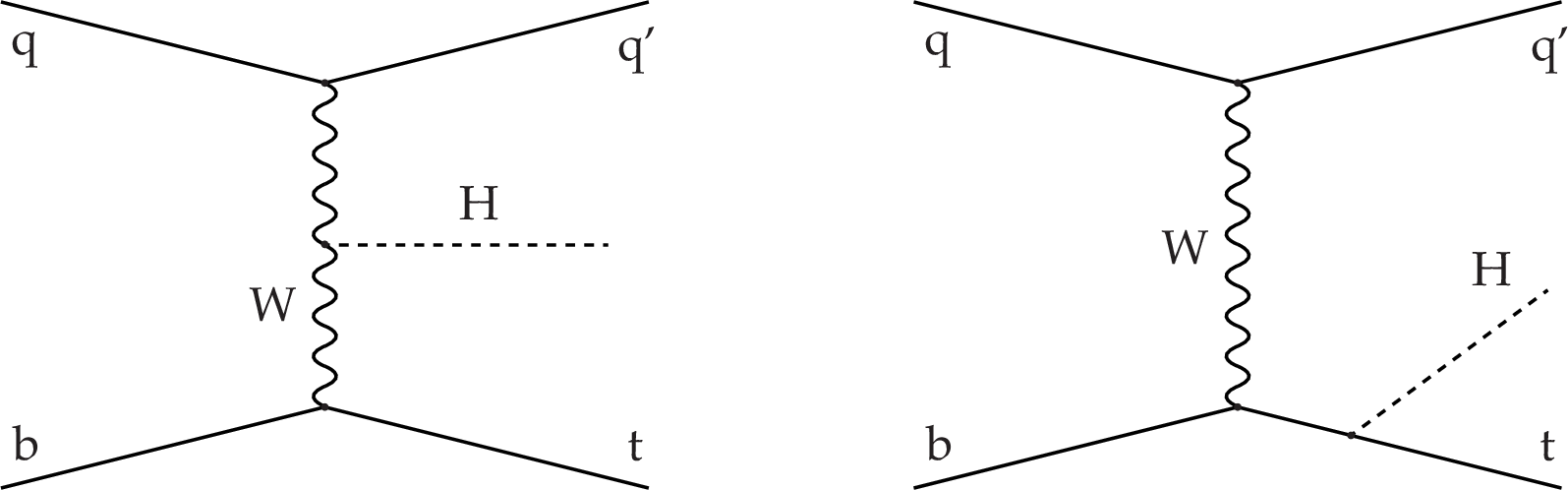
Figure 1:
Dominant leading order Feynman diagrams for the production of tHq events. The Higgs boson is either radiated from the W boson (left) or the top quark (right). |
png pdf |
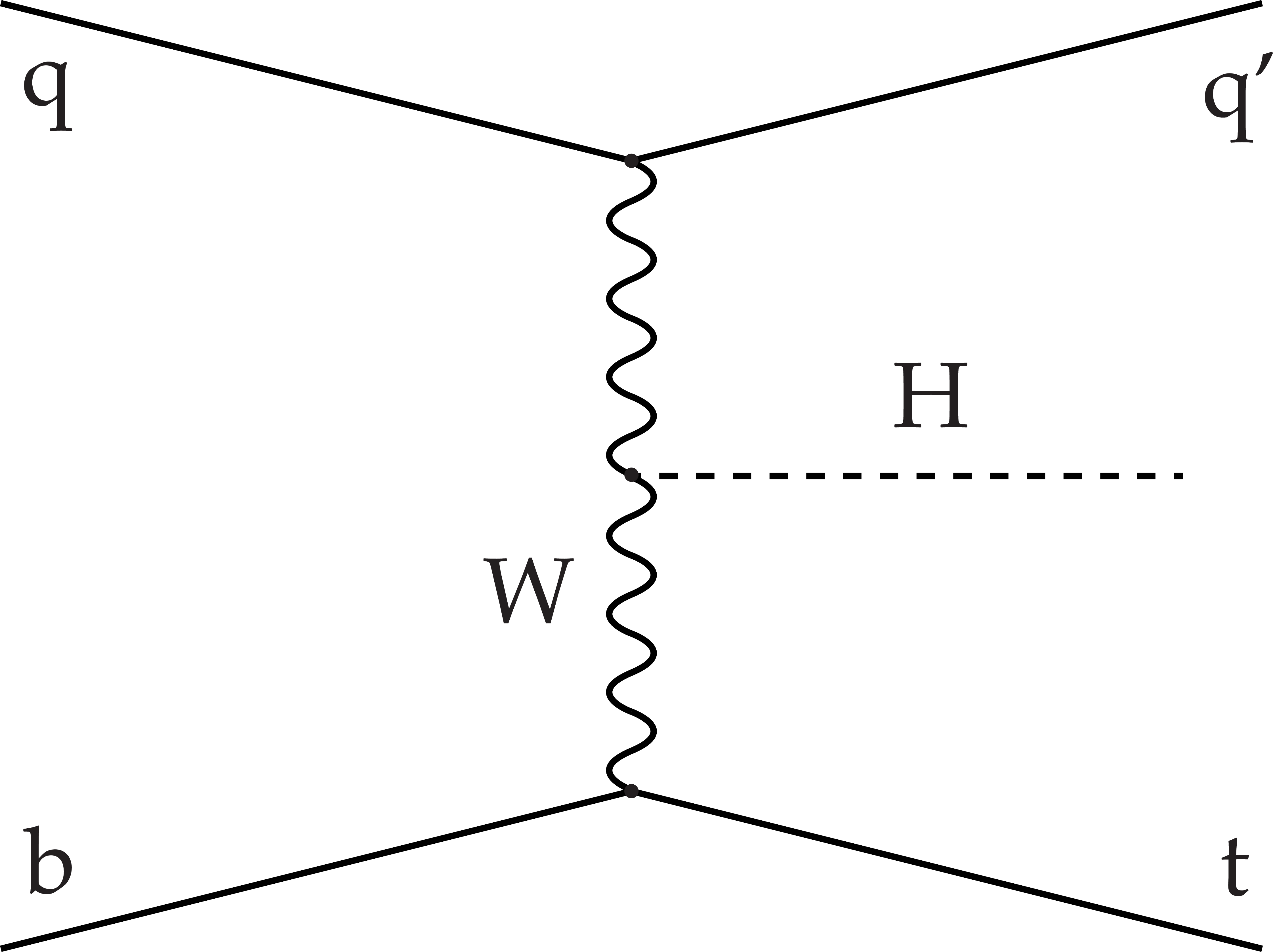
Figure 1-a:
Dominant leading order Feynman diagram for the production of tHq events. The Higgs boson is radiated from the W boson. |
png pdf |
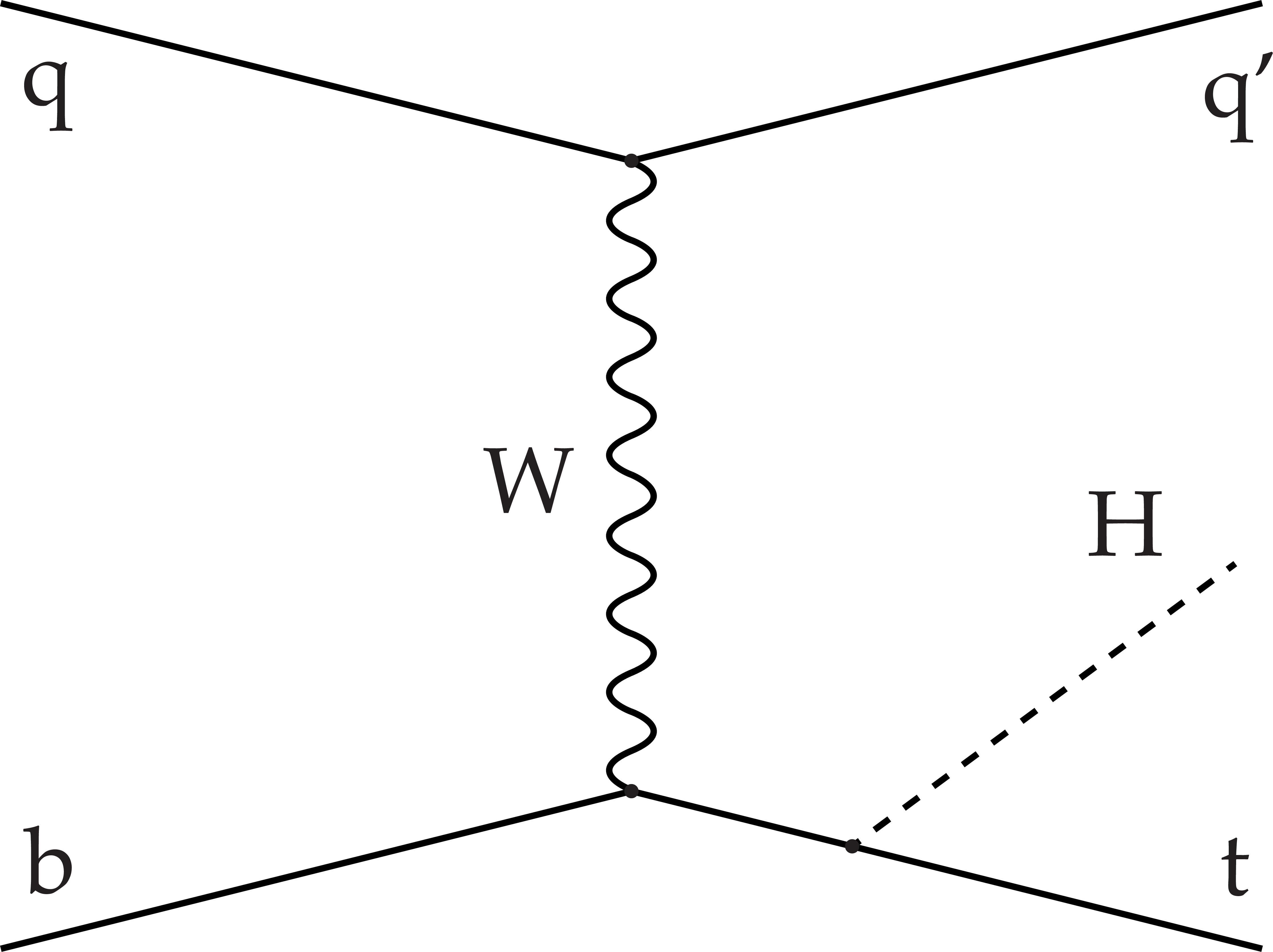
Figure 1-b:
Dominant leading order Feynman diagram for the production of tHq events. The Higgs boson is radiated from the top quark. |
png pdf |
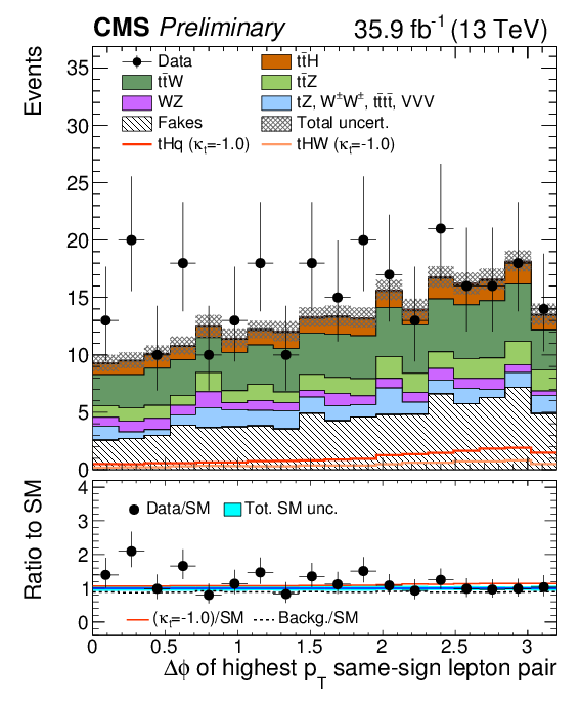
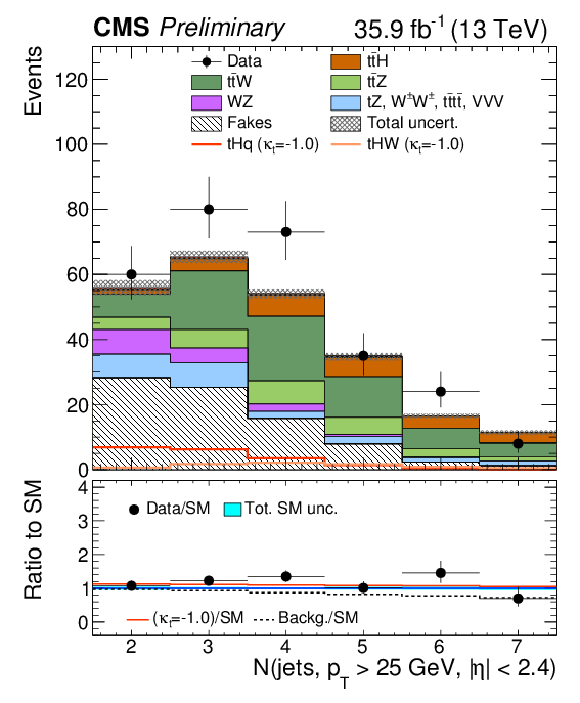
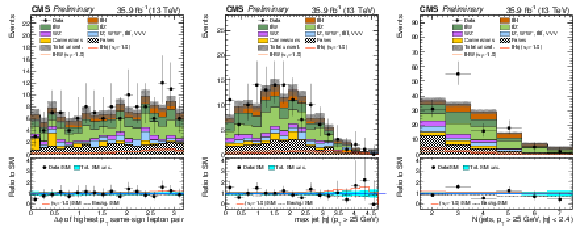
Figure 2:
Distributions of discriminating variables for the event pre-selection for the same-sign μμ channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
Figure 2-a:
Distribution for the event pre-selection for the same-sign μμ channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |

png pdf |
Figure 2-b:
Distribution for the event pre-selection for the same-sign μμ channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
Figure 2-c:
Distribution for the event pre-selection for the same-sign μμ channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |

png pdf |
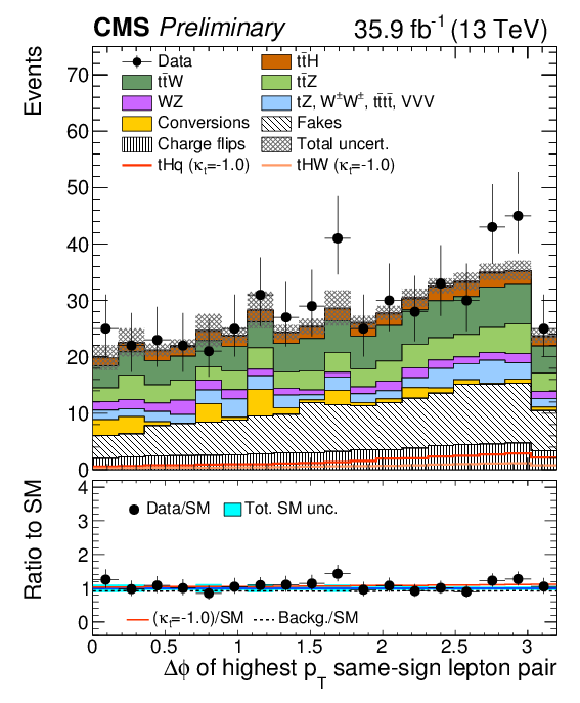
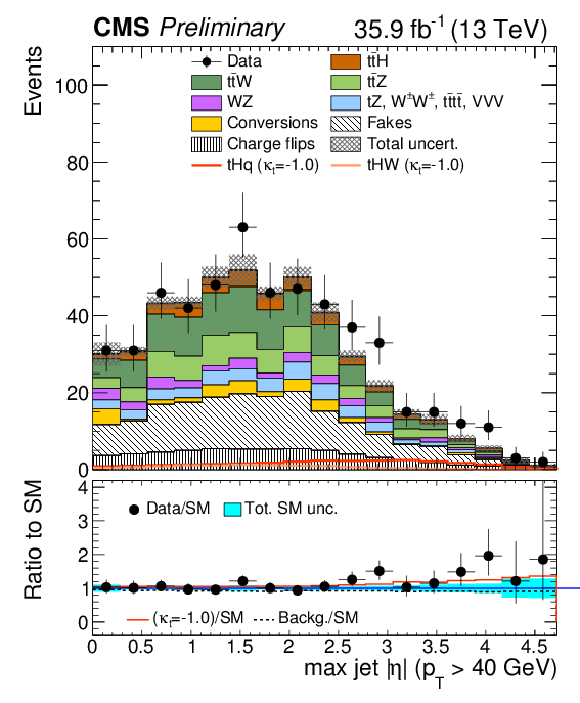
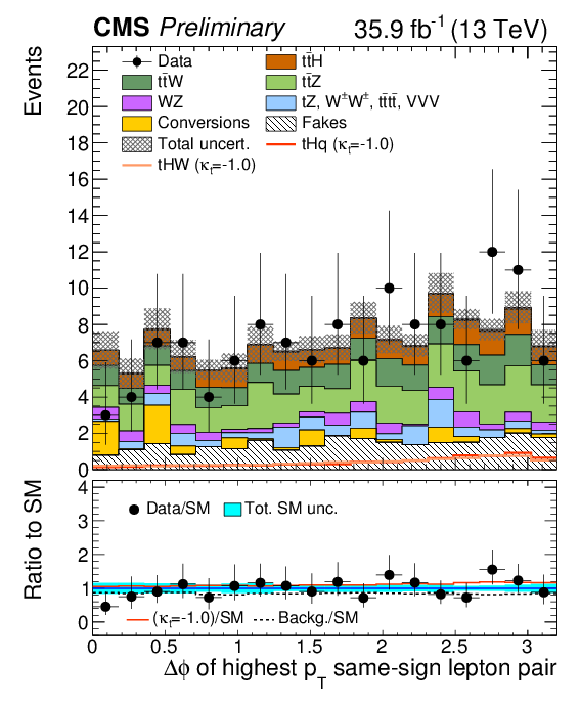
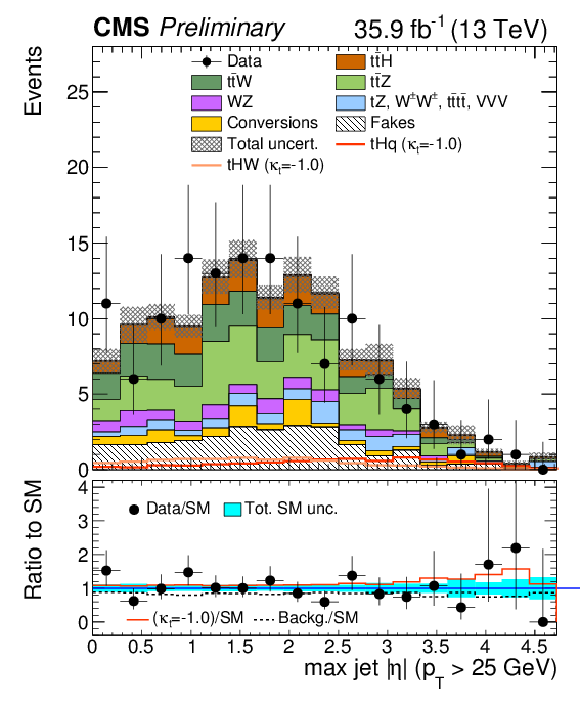
Figure 3:
Distributions of discriminating variables for the event pre-selection for the same-signeμ channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
Figure 3-a:
Distribution for the event pre-selection for the same-signeμ channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
Figure 3-b:
Distribution for the event pre-selection for the same-signeμ channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
Figure 3-c:
Distribution for the event pre-selection for the same-signeμ channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
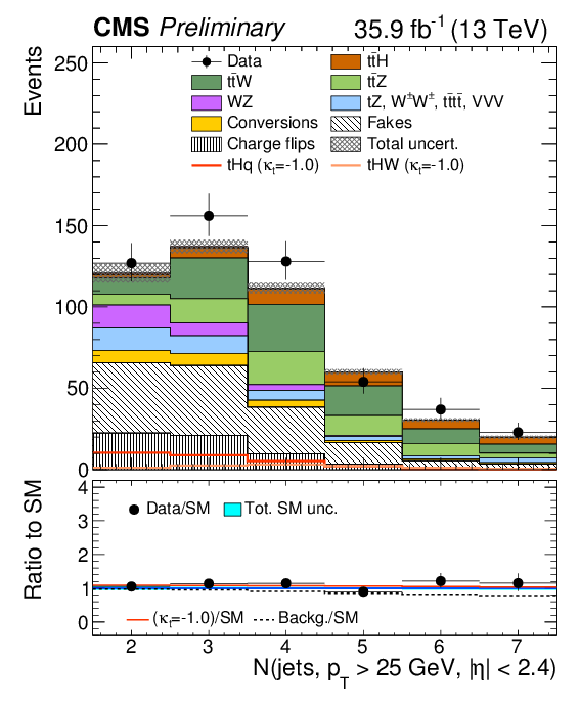
Figure 4:
Distributions of discriminating variables for the event pre-selection for the three lepton channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
Figure 4-a:
Distribution for the event pre-selection for the three lepton channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
Figure 4-b:
Distribution for the event pre-selection for the three lepton channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
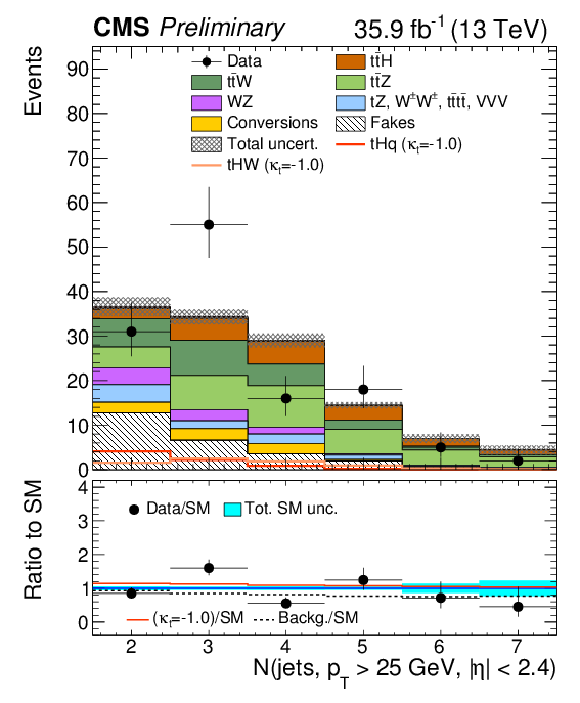
Figure 4-c:
Distribution for the event pre-selection for the three lepton channel, normalized to 35.9 fb−1, before fitting the signal discriminant to the observed data. Uncertainties are statistical and unconstrained (pre-fit) normalization systematics. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. |
png pdf |
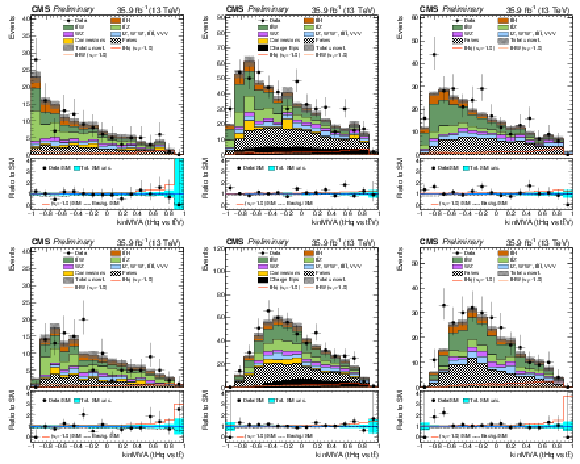
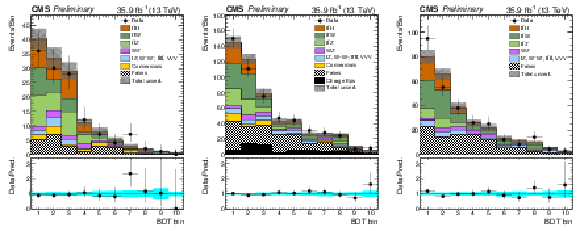
Figure 5:
Pre-fit BDT classifier outputs, for the three-lepton channel (left), eμ (center), and μμ (right), for 35.9 fb−1, for training against tˉtV (top row) and against tˉt (bottom row). In the box below each distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
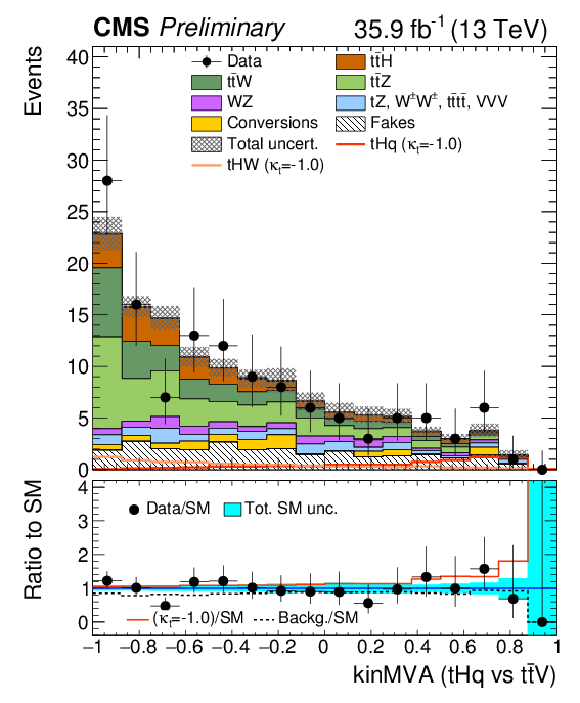
Figure 5-a:
Pre-fit BDT classifier output, for the three-lepton channel , for 35.9 fb−1, for training against tˉtV. In the box below the distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
Figure 5-b:
Pre-fit BDT classifier output, for eμ, for 35.9 fb−1, for training against tˉtV. In the box below the distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
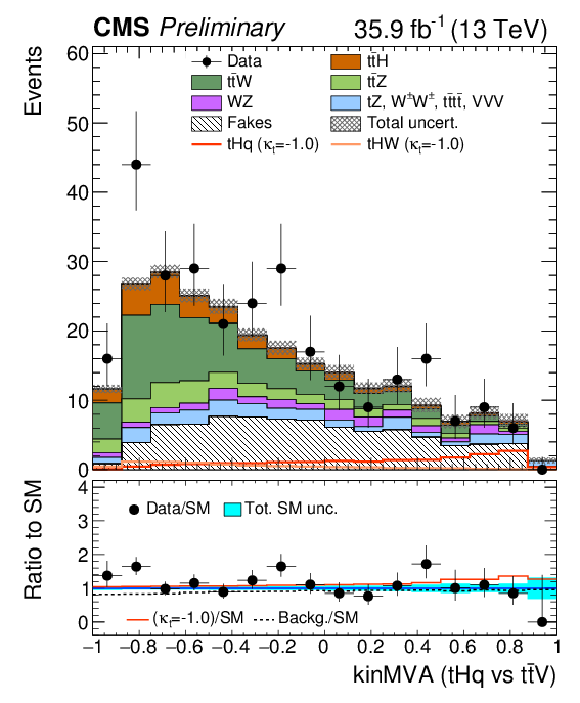
Figure 5-c:
Pre-fit BDT classifier output, for μμ, for 35.9 fb−1, for training against tˉtV. In the box below the distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
Figure 5-d:
Pre-fit BDT classifier output, for the three-lepton channel, for 35.9 fb−1, for training against tˉt. In the box below the distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |

png pdf |
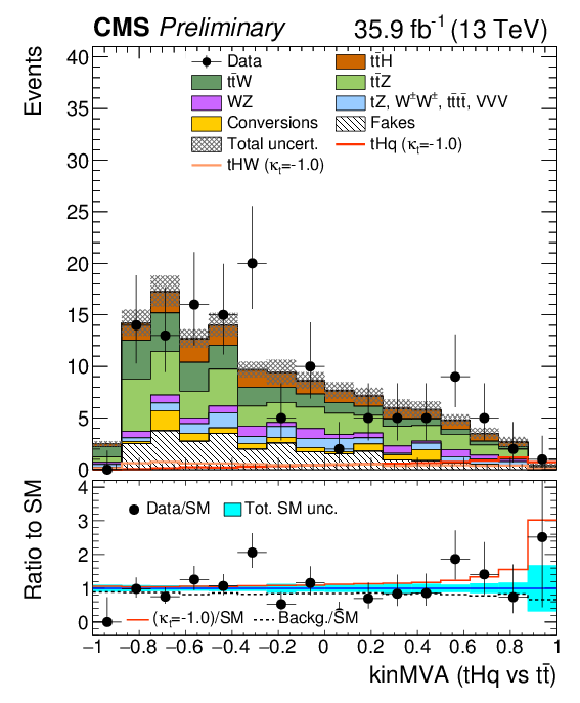
Figure 5-e:
Pre-fit BDT classifier output, for eμ, for 35.9 fb−1, for training against tˉt. In the box below the distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
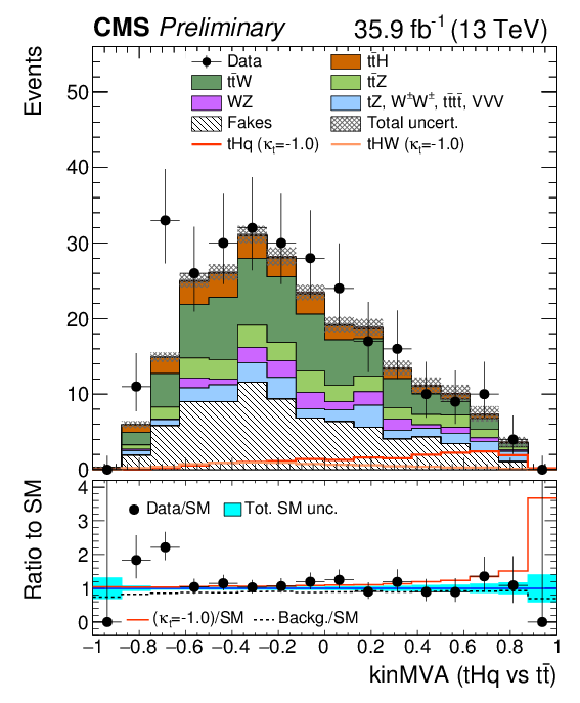
Figure 5-f:
Pre-fit BDT classifier output, for μμ, for 35.9 fb−1, for training against tˉt. In the box below the distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0,κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
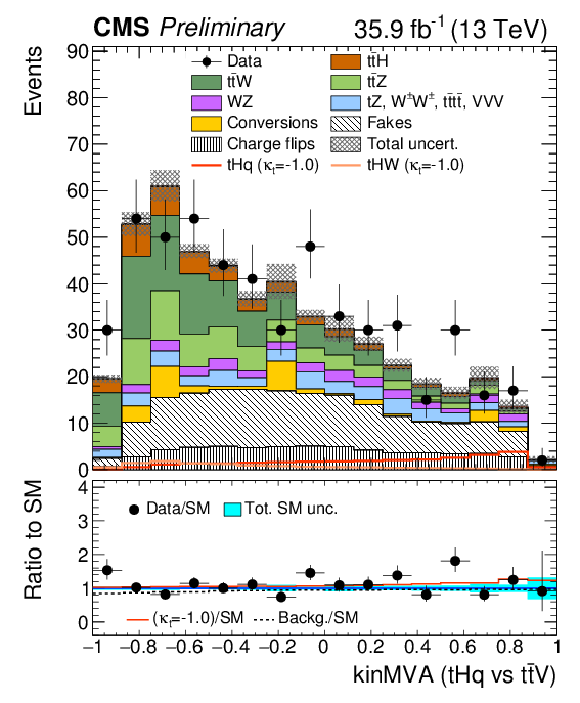
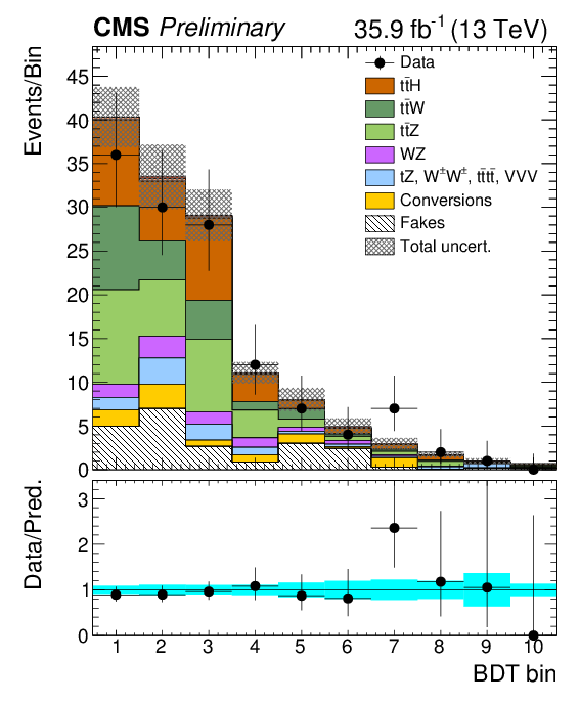
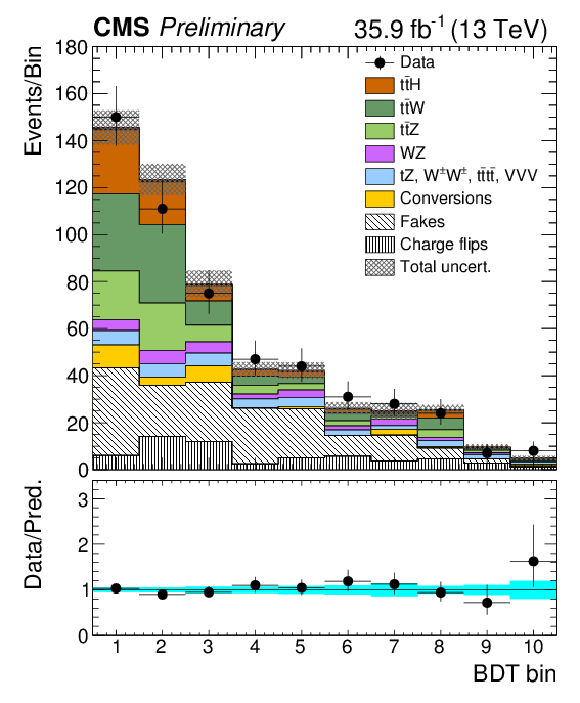
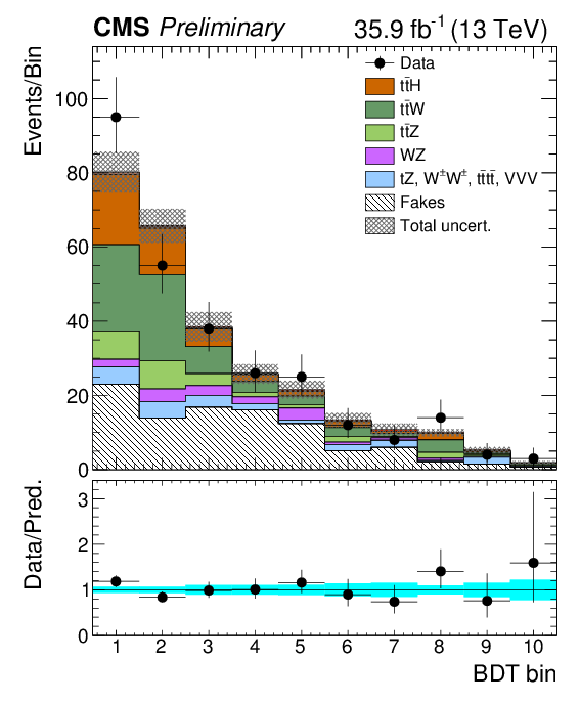
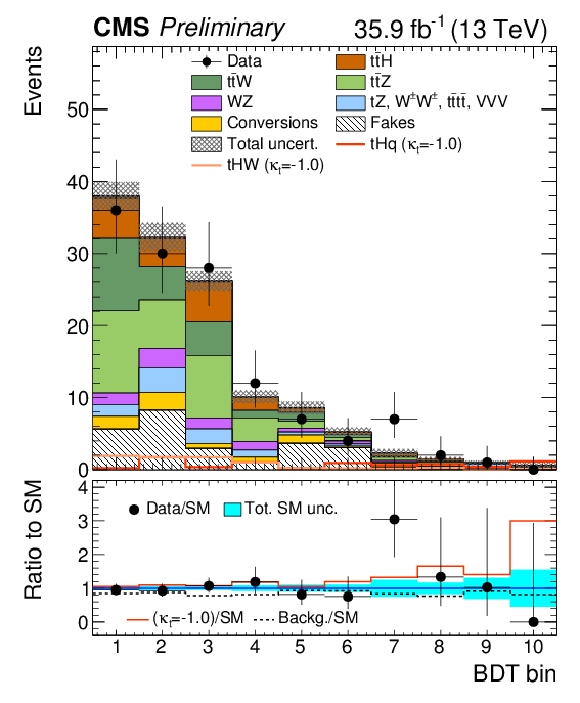
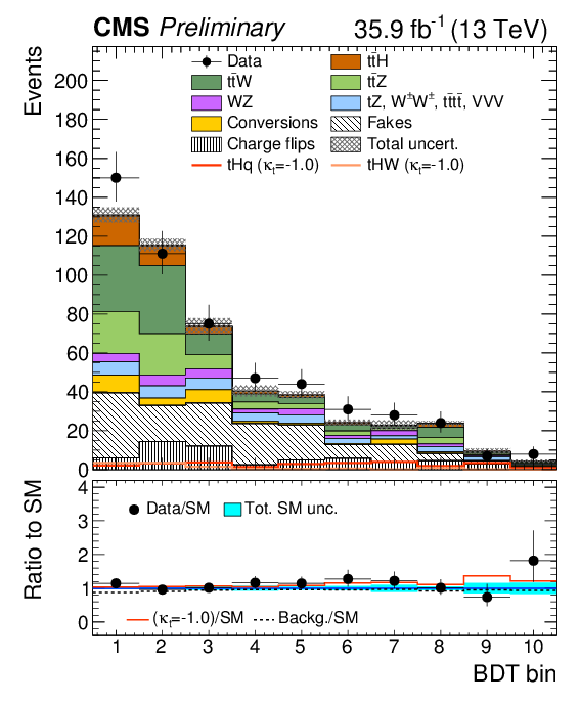
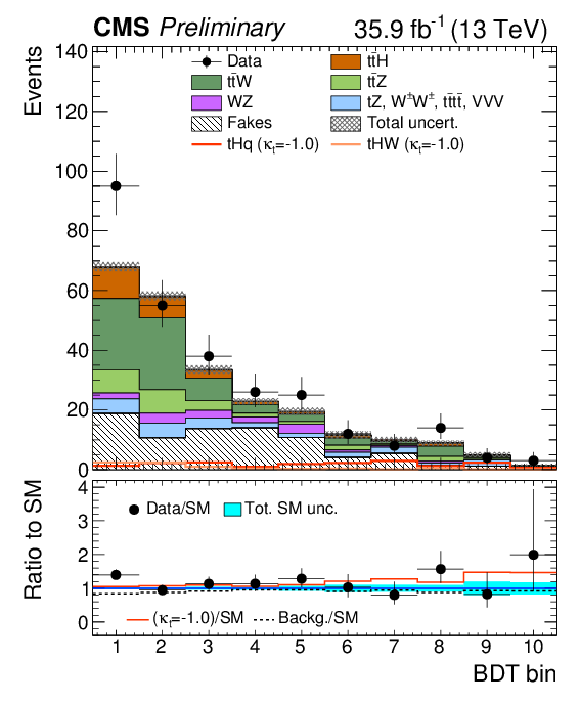
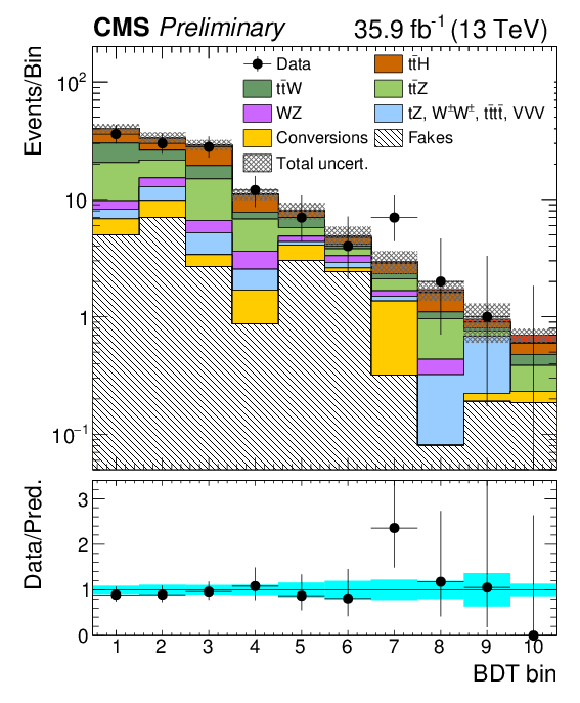
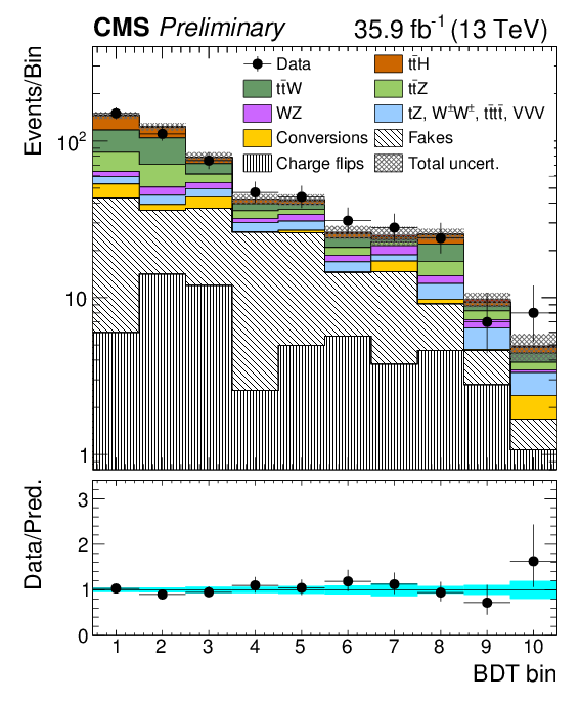
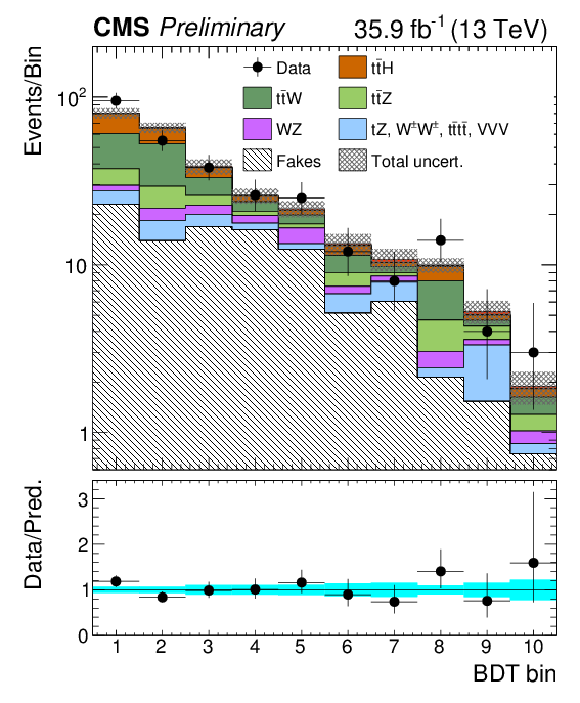
Figure 6:
Post-fit categorized BDT classifier outputs as used in the maximum likelihood fit for the three-lepton channel (left), eμ (center), and μμ (right), for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. |
png pdf |
Figure 6-a:
Post-fit categorized BDT classifier outputs as used in the maximum likelihood fit for the three-lepton channel, for 35.9 fb−1. In the box below the distribution, the ratio of the observed and predicted event yields is shown. |
png pdf |
Figure 6-b:
Post-fit categorized BDT classifier outputs as used in the maximum likelihood fit for eμ, for 35.9 fb−1. In the box below the distribution, the ratio of the observed and predicted event yields is shown. |
png pdf |
Figure 6-c:
Post-fit categorized BDT classifier outputs as used in the maximum likelihood fit for μμ, for 35.9 fb−1. In the box below the distribution, the ratio of the observed and predicted event yields is shown. |

png pdf |
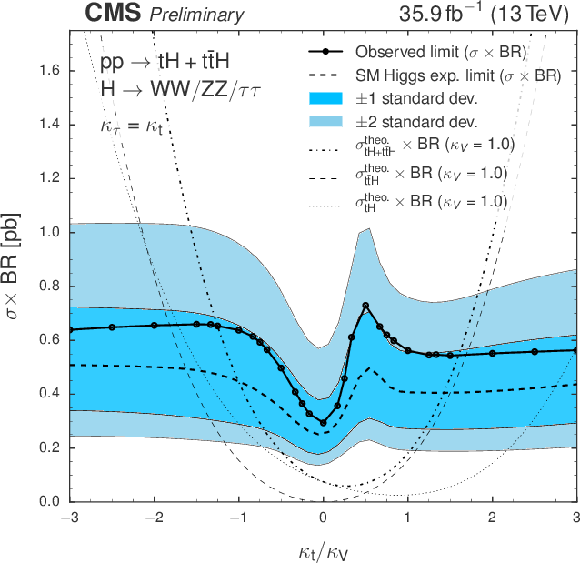
Figure 7:
Observed and expected 95% C.L. upper limit on the tH+tˉtH cross section times H→WW∗+ττ+ZZ∗ branching fraction for different values of the coupling ratio κt/κV. The expected limit is derived from a background-only MC dataset. |
| Tables | |

png pdf |
Table 1:
Summary of event selection. |
png pdf |
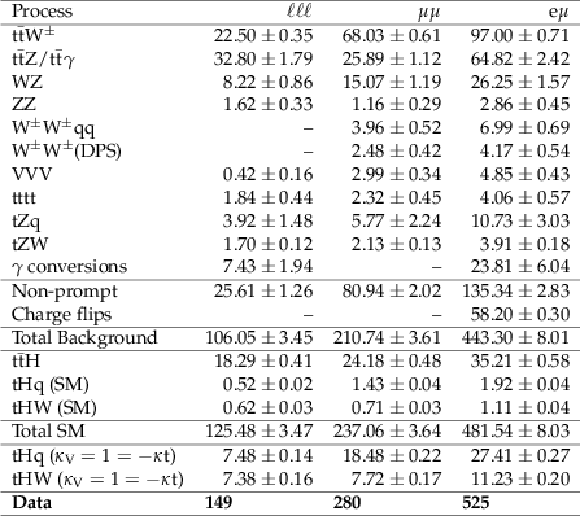
Table 2:
Data yields and expected backgrounds after the event pre-selection for the three channels in 35.9 fb−1 of integrated luminosity. Uncertainties are statistical only. |

png pdf |
Table 3:
Input variables to the signal discrimination classifier. |

png pdf |
Table 4:
Expected and observed 95% C.L. upper limits on the tH+tˉtH production cross section times H→WW∗+ττ+ZZ∗ branching ratio for a scenario of inverted couplings (κt/κV=−1.0, top rows) and for a standard-model-like signal (κt/κV=1.0, bottom rows), in pb. The expected limit is calculated on a background-only MC dataset. |
| Summary |
|
A search for the production of a Higgs boson in association with a single top quark has been presented, using the CMS detector and the full 2016 data sample of pp collisions at 13 TeV, corresponding to an integrated luminosity of 35.9 fb−1. Three channels have been analyzed, targeting the Higgs boson decaying to a pair of W or Z bosons, or two τ leptons and the leptonic decay of the top: two same-sign leptons (μμ, eμ) and three leptons. This process can benefit from a greatly enhanced production cross section in the case of anomalous top-Higgs couplings, and the results are used to constrain these couplings. Combining the results from all three channels yields a 95% confidence level (C.L.) upper limit on the production cross section times branching ratio of events containing a SM Higgs boson of 0.56 pb, with an expected limit of 0.24 pb. Values of the ratio of Higgs-top coupling modifier κt and Higgs-vector boson coupling modifier κV are outside the range −1.25 to +1.60 are excluded at 95% C.L. |
| Additional Figures | |
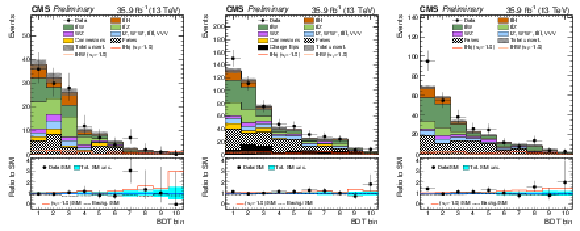
png pdf |
Additional Figure 1:
Pre-fit categorized BDT classifier outputs, for the three-lepton channel (left), eμ (center), and μμ (right), for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0, κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
Additional Figure 1-a:
Pre-fit categorized BDT classifier outputs, for the three-lepton channel, for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0, κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
Additional Figure 1-b:
Pre-fit categorized BDT classifier outputs, for eμ, for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0, κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
Additional Figure 1-c:
Pre-fit categorized BDT classifier outputs, for μμ, for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. The shape of the two tH signals for κt=−1.0 is shown, normalized to their respective cross sections for κt=−1.0, κV=1.0. The grey band represents the unconstrained (pre-fit) statistical and systematical uncertainties. |
png pdf |
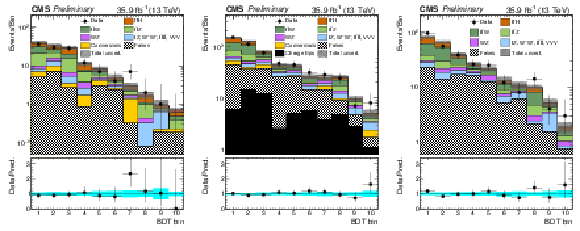
Additional Figure 2:
Post-fit categorized BDT classifier outputs (on logarithmic scale) as used in the maximum likelihood fit for the three-lepton channel (left), eμ (center), and μμ (right), for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. |
png pdf |
Additional Figure 2-a:
Post-fit categorized BDT classifier outputs (on logarithmic scale) as used in the maximum likelihood fit for the three-lepton channel, for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. |
png pdf |
Additional Figure 2-b:
Post-fit categorized BDT classifier outputs (on logarithmic scale) as used in the maximum likelihood fit for eμ, for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. |
png pdf |
Additional Figure 2-c:
Post-fit categorized BDT classifier outputs (on logarithmic scale) as used in the maximum likelihood fit for μμ, for 35.9 fb−1. In the box below each distribution, the ratio of the observed and predicted event yields is shown. |
png pdf |
Additional Figure 3:
Observed and expected 95% C.L. upper limit on the tH+tˉtH cross section times H→WW∗+ττ+ZZ∗ branching fraction for different values of the coupling ratio κt/κV. The expected limit is derived from a MC dataset of SM processes including the contributions from tˉtH and tH expected in the SM. |
| References | ||||
| 1 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | Phys.Lett. B716 (2012) 30--61 | CMS-HIG-12-028 1207.7235 |
| 2 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | Phys.Lett. B716 (2012) 1--29 | 1207.7214 |
| 3 | CMS Collaboration | Measurement of the top quark mass using proton-proton data at √s= 7 and 8 TeV | PRD93 (2016), no. 7, 072004 | CMS-TOP-14-022 1509.04044 |
| 4 | S. Biswas, E. Gabrielli, F. Margaroli, and B. Mele | Direct constraints on the top-Higgs coupling from the 8 TeV LHC data | JHEP 07 (2013) 73 | |
| 5 | B. Hespel, F. Maltoni, and E. Vryonidou | Higgs and Z boson associated production via gluon fusion in the SM and the 2HDM | JHEP 06 (2015) 065 | 1503.01656 |
| 6 | ATLAS Collaboration | Measurements of Higgs boson production and couplings in diboson final states with the ATLAS detector at the LHC | PLB726 (2013) 88--119 | 1307.1427 |
| 7 | CMS Collaboration | Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV | EPJC75 (2015) 212 | CMS-HIG-14-009 1412.8662 |
| 8 | ATLAS, CMS Collaboration | Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at √s= 7 and 8 TeV | Submitted to JHEP | 1606.02266 |
| 9 | J. Ellis and T. You | Updated Global Analysis of Higgs Couplings | JHEP 06 (2013) 103 | 1303.3879 |
| 10 | G. Bordes and B. van Eijk | On the associate production of a neutral intermediate mass Higgs boson with a single top quark at the LHC and SSC | PLB 299 (1993) 315 | |
| 11 | T. M. P. Tait and C. P. Yuan | Single top quark production as a window to physics beyond the standard model | PRD 63 (2000) 014018 | hep-ph/0007298 |
| 12 | M. Farina et al. | Lifting degeneracies in Higgs couplings using single top production in association with a Higgs boson | JHEP 1305 (2013) 022 | 1211.3736 |
| 13 | F. Demartin, F. Maltoni, K. Mawatari, and M. Zaro | Higgs production in association with a single top quark at the LHC | EPJC 75 (2015), no. 6, 267 | |
| 14 | F. Demartin et al. | tWH associated production at the LHC | EPJC77 (2017) 34 | 1607.05862 |
| 15 | CMS Collaboration | Search for the associated production of a Higgs boson with a single top quark in proton-proton collisions at √s= 8 TeV | JHEP 06 (2016) 177 | CMS-HIG-14-027 1509.08159 |
| 16 | CMS Collaboration | Search for H→bˉb in association with a single top quark as a test of Higgs boson couplings at √s= 13 TeV | CMS-PAS-HIG-16-019 | CMS-PAS-HIG-16-019 |
| 17 | CMS Collaboration | Search for Higgs boson production in association with top quarks in multilepton final states at √s= 13 TeV | ||
| 18 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 19 | CMS Collaboration | Particle-Flow Event Reconstruction in CMS and Performance for Jets, Taus, and EmissT | CDS | |
| 20 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet User Manual | EPJC72 (2012) 1896 | 1111.6097 |
| 21 | M. Cacciari and G. P. Salam | Dispelling the N3 myth for the kT jet-finder | PLB641 (2006) 57--61 | hep-ph/0512210 |
| 22 | CMS Collaboration | Determination of Jet Energy Calibration and Transverse Momentum Resolution in CMS | JINST 6 (2011) P11002 | CMS-JME-10-011 1107.4277 |
| 23 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 24 | CMS Collaboration | Identification of b quark jets at the CMS Experiment in the LHC Run 2 | CMS-PAS-BTV-15-001 | CMS-PAS-BTV-15-001 |
| 25 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at √s= 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 26 | CMS Collaboration | Performance of Electron Reconstruction and Selection with the CMS Detector in Proton-Proton Collisions at √s= 8 TeV | JINST 10 (2015), no. 06, P06005 | CMS-EGM-13-001 1502.02701 |
| 27 | K. Rehermann and B. Tweedie | Efficient Identification of Boosted Semileptonic Top Quarks at the LHC | JHEP 03 (2011) 059 | 1007.2221 |
| 28 | CMS Collaboration | Search for SUSY in same-sign dilepton events at √s= 13 TeV | EPJC76 (2016) 439 | CMS-SUS-15-008 1605.03171 |
| 29 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 30 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC53 (2008) 473--500 | 0706.2569 |
| 31 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 32 | R. Frederix and S. Frixione | Merging meets matching in MC@NLO | JHEP 12 (2012) 061 | 1209.6215 |
| 33 | P. Nason | A New method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 0411 (2004) 040 | hep-ph/0409146 |
| 34 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 35 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 36 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC71 (2011) 1547 | 1009.2450 |
| 37 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: s- and t-channel contributions | JHEP 0909 (2009) 111 | 0907.4076 |
| 38 | T. Melia, P. Nason, R. Rontsch, and G. Zanderighi | W+W−, WZ and ZZ production in the POWHEG BOX | JHEP 1111 (2011) 078 | 1107.5051 |
| 39 | T. Sjostrand et al. | An Introduction to PYTHIA 8.2 | CPC 191 (2015) 159--177 | 1410.3012 |
| 40 | J. Allison et al. | GEANT4 developments and applications | IEEE Trans. Nucl. Sci. 53 (2006) 270 | |
| 41 | LHC Higgs Cross Section Working Group | Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector | 1610.07922 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|