Compact Muon Solenoid
LHC, CERN
Visit us: CMS Public Website, CMS Physics ;
Contact us: CMS Publications Committee
| CMS-PAS-FTR-18-034 | ||
| Projection of the top quark spin correlation measurement and search for top squark pair production at the HL-LHC | ||
| CMS Collaboration | ||
| June 2022 | ||
| Abstract: The CMS prospects for the high-luminosity phase of the LHC on the measurement of the top quark spin correlation is presented, using events containing two oppositely charged lepton pairs (e$\mu$) produced in proton-proton collisions at a center-of-mass energy of 14 TeV assuming an integrated luminosity of 3 ab$^{-1}$. We investigate the normalised strength of the spin correlation in the sample and hence, provide a first performance study in future spin correlation measurements at 14 TeV. As an application, these observables are used in a Deep Neural Network to search for pair production of supersymmetric (anti-)top scalar quarks decaying into (anti-)top quarks and neutralinos, which escape the detector undetected. The observables sensitive to top quark spin correlation allow to study the corridor where the mass difference between the top scalar quark and the neutralino is about equal to the top quark mass. Compared to existing Run 2 results, this work will particularly push the discovery potential to the most natural top squark mass values below 300 GeV by one order of magnitude. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
Figure 1:
Feynman diagram for the production of (anti-)top squark pairs decaying into (anti-)top quarks and neutralinos. |
png pdf |
Figure 2:
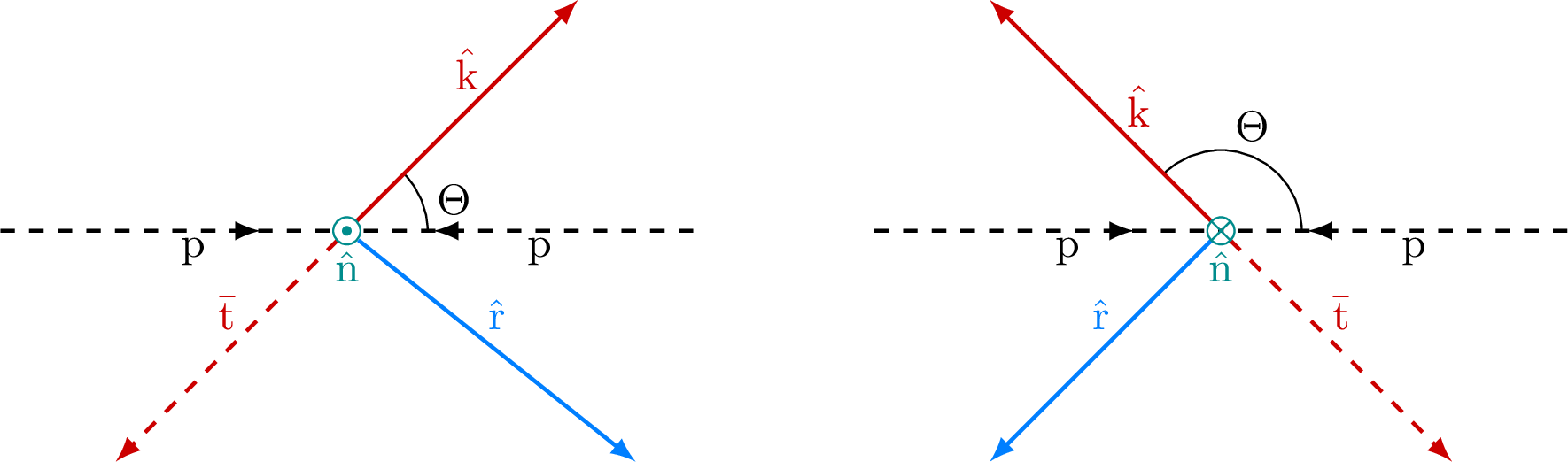
Coordinate system used for the spin measurements, illustrated in the scattering plane for $\Theta < \pi /2$ (left) and $\Theta > \pi /2$ (right), where the signs of $\hat{r}$ and $\hat{n}$ are flipped at $\Theta =\pi /2$ as shown in Eq. (4). The $\hat{k}$ axis is defined by the top quark direction, measured in the ${\mathrm{t} {}\mathrm{\bar{t}}}$ CM frame. For the basis used to define the coefficient functions in Eq. (3), the incoming particles p represent the incoming partons, while for the basis used to measure the coefficients in Eqs. (8)-(10) they represent the incoming protons. |
png pdf |
Figure 2-a:
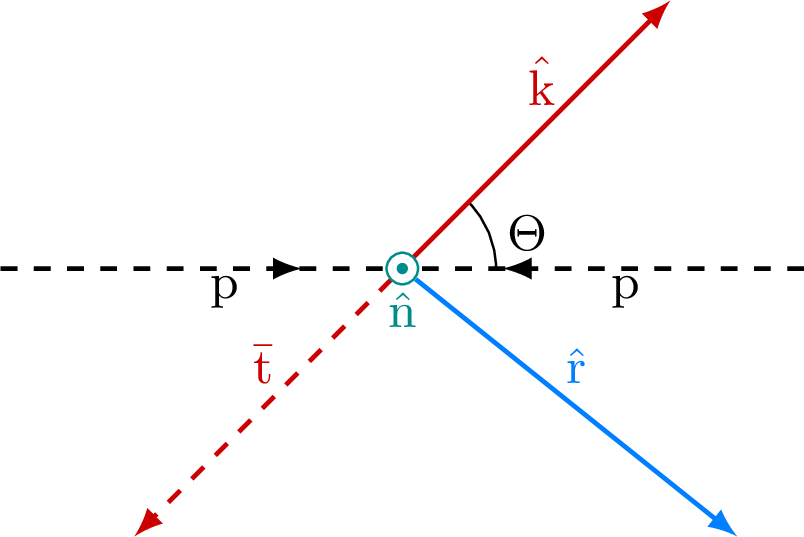
Coordinate system used for the spin measurements, illustrated in the scattering plane for $\Theta < \pi /2$ (left) and $\Theta > \pi /2$ (right), where the signs of $\hat{r}$ and $\hat{n}$ are flipped at $\Theta =\pi /2$ as shown in Eq. (4). The $\hat{k}$ axis is defined by the top quark direction, measured in the ${\mathrm{t} {}\mathrm{\bar{t}}}$ CM frame. For the basis used to define the coefficient functions in Eq. (3), the incoming particles p represent the incoming partons, while for the basis used to measure the coefficients in Eqs. (8)-(10) they represent the incoming protons. |
png pdf |
Figure 2-b:
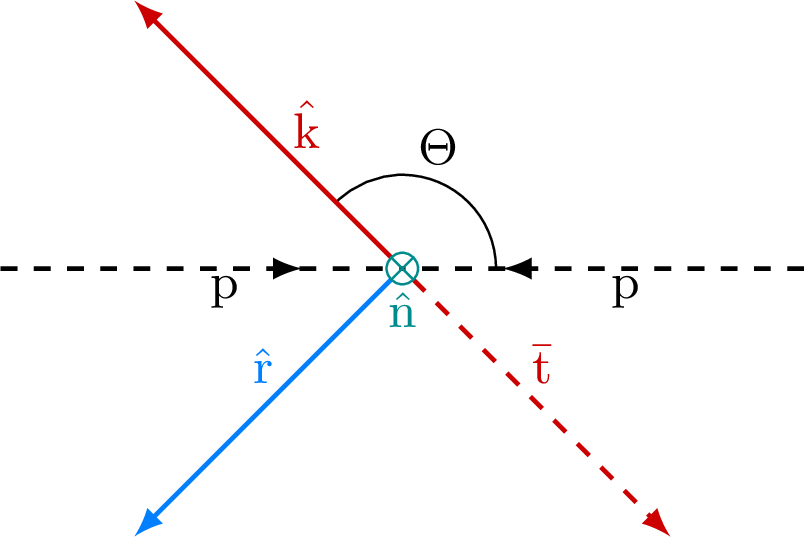
Coordinate system used for the spin measurements, illustrated in the scattering plane for $\Theta < \pi /2$ (left) and $\Theta > \pi /2$ (right), where the signs of $\hat{r}$ and $\hat{n}$ are flipped at $\Theta =\pi /2$ as shown in Eq. (4). The $\hat{k}$ axis is defined by the top quark direction, measured in the ${\mathrm{t} {}\mathrm{\bar{t}}}$ CM frame. For the basis used to define the coefficient functions in Eq. (3), the incoming particles p represent the incoming partons, while for the basis used to measure the coefficients in Eqs. (8)-(10) they represent the incoming protons. |
png pdf |
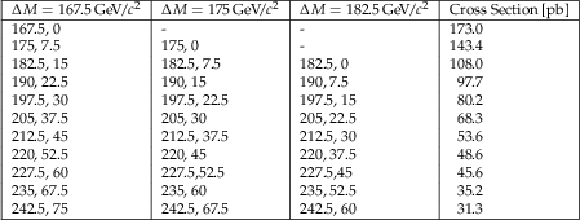
Figure 3:
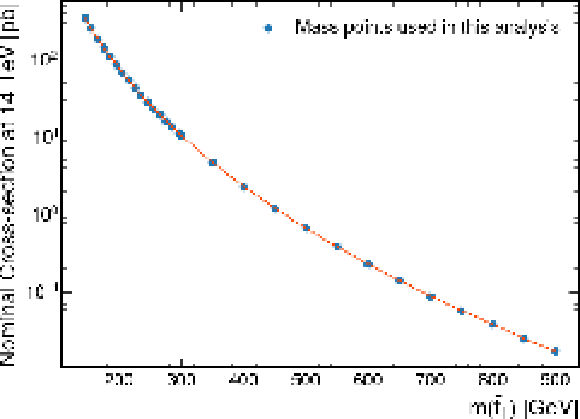
Signal cross sections for top squark pair production with top squark masses between 145 and 900 GeV from [24]. All signal mass points with the same top squark mass have the same cross section. An uncertainty of 14 $%$ is associated on the cross section for each mass point. |
png pdf |
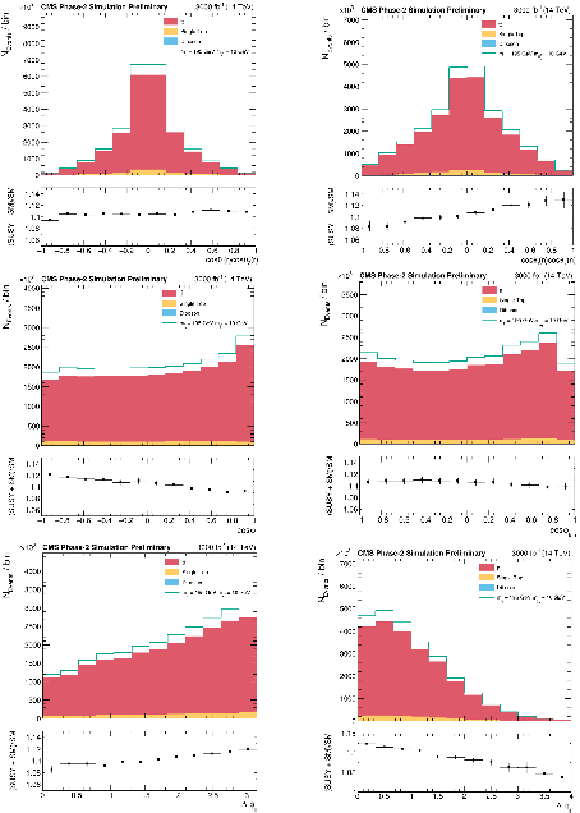
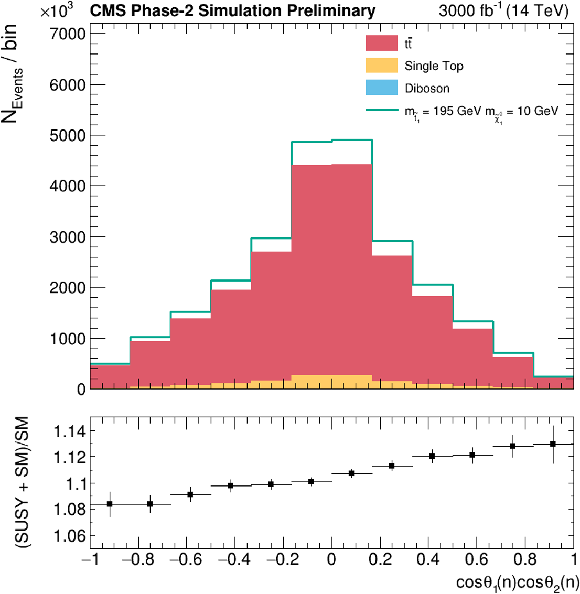
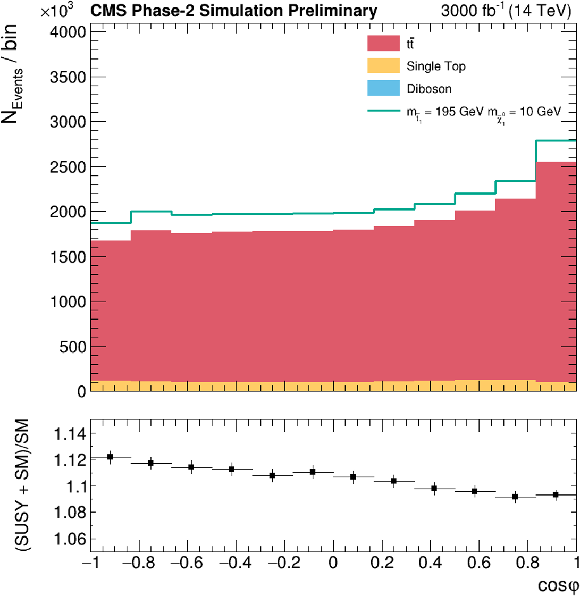
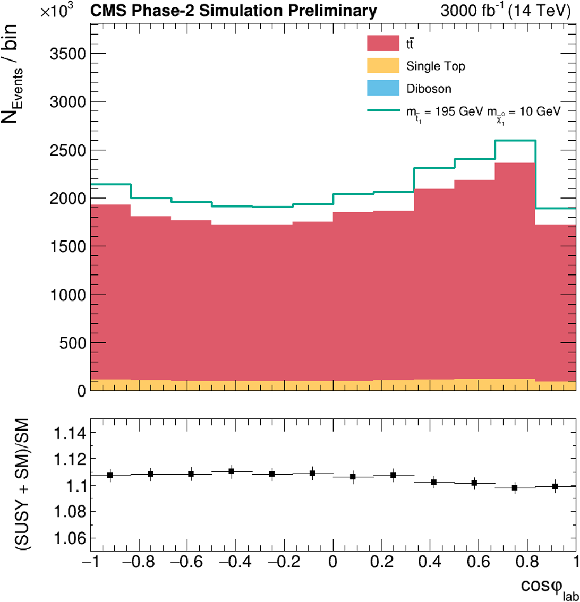
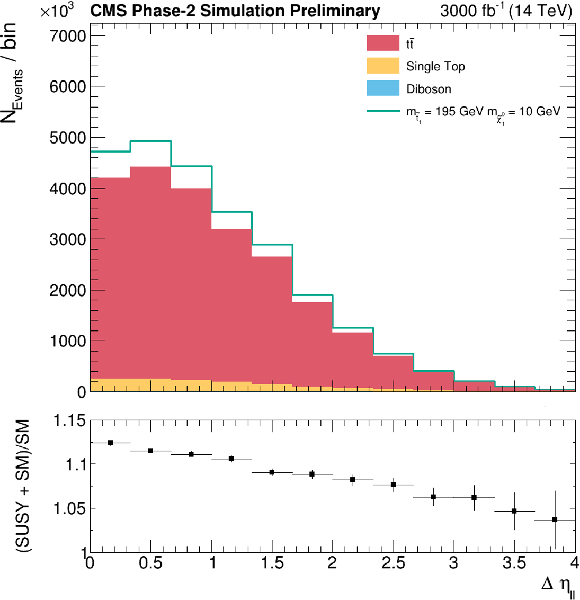
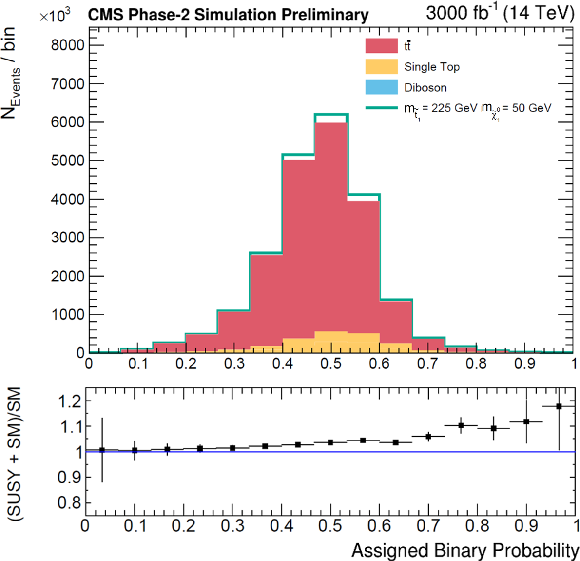
Figure 4:
From top to bottom and left to right: diagonal terms of the ${\mathrm{t} {}\mathrm{\bar{t}}}$ spin correlation matrix along the $r$ and $n$ axis; $\cos\varphi $ and $\cos\varphi _{\mathrm {lab}}$; $\Delta \phi $ and $\Delta \eta $ between the leptons. Lower pad shows a ratio of SUSY signal plus SM backgrounds over SM backgrounds, allowing to compare the shape of SUSY prediction versus the SM one. |
png |
Figure 4-a:
From top to bottom and left to right: diagonal terms of the ${\mathrm{t} {}\mathrm{\bar{t}}}$ spin correlation matrix along the $r$ and $n$ axis; $\cos\varphi $ and $\cos\varphi _{\mathrm {lab}}$; $\Delta \phi $ and $\Delta \eta $ between the leptons. Lower pad shows a ratio of SUSY signal plus SM backgrounds over SM backgrounds, allowing to compare the shape of SUSY prediction versus the SM one. |
png |
Figure 4-b:
From top to bottom and left to right: diagonal terms of the ${\mathrm{t} {}\mathrm{\bar{t}}}$ spin correlation matrix along the $r$ and $n$ axis; $\cos\varphi $ and $\cos\varphi _{\mathrm {lab}}$; $\Delta \phi $ and $\Delta \eta $ between the leptons. Lower pad shows a ratio of SUSY signal plus SM backgrounds over SM backgrounds, allowing to compare the shape of SUSY prediction versus the SM one. |
png |
Figure 4-c:
From top to bottom and left to right: diagonal terms of the ${\mathrm{t} {}\mathrm{\bar{t}}}$ spin correlation matrix along the $r$ and $n$ axis; $\cos\varphi $ and $\cos\varphi _{\mathrm {lab}}$; $\Delta \phi $ and $\Delta \eta $ between the leptons. Lower pad shows a ratio of SUSY signal plus SM backgrounds over SM backgrounds, allowing to compare the shape of SUSY prediction versus the SM one. |
png |
Figure 4-d:
From top to bottom and left to right: diagonal terms of the ${\mathrm{t} {}\mathrm{\bar{t}}}$ spin correlation matrix along the $r$ and $n$ axis; $\cos\varphi $ and $\cos\varphi _{\mathrm {lab}}$; $\Delta \phi $ and $\Delta \eta $ between the leptons. Lower pad shows a ratio of SUSY signal plus SM backgrounds over SM backgrounds, allowing to compare the shape of SUSY prediction versus the SM one. |
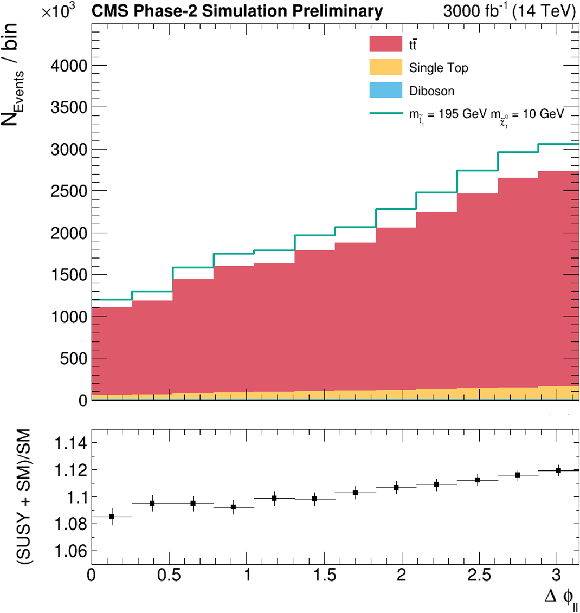
png |
Figure 4-e:
From top to bottom and left to right: diagonal terms of the ${\mathrm{t} {}\mathrm{\bar{t}}}$ spin correlation matrix along the $r$ and $n$ axis; $\cos\varphi $ and $\cos\varphi _{\mathrm {lab}}$; $\Delta \phi $ and $\Delta \eta $ between the leptons. Lower pad shows a ratio of SUSY signal plus SM backgrounds over SM backgrounds, allowing to compare the shape of SUSY prediction versus the SM one. |
png |
Figure 4-f:
From top to bottom and left to right: diagonal terms of the ${\mathrm{t} {}\mathrm{\bar{t}}}$ spin correlation matrix along the $r$ and $n$ axis; $\cos\varphi $ and $\cos\varphi _{\mathrm {lab}}$; $\Delta \phi $ and $\Delta \eta $ between the leptons. Lower pad shows a ratio of SUSY signal plus SM backgrounds over SM backgrounds, allowing to compare the shape of SUSY prediction versus the SM one. |
png pdf |
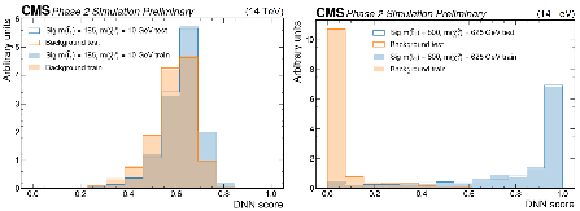
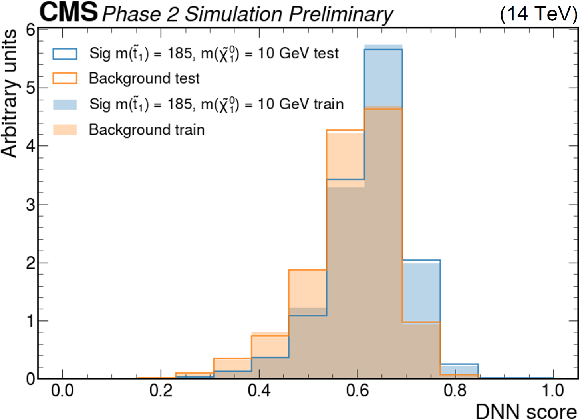
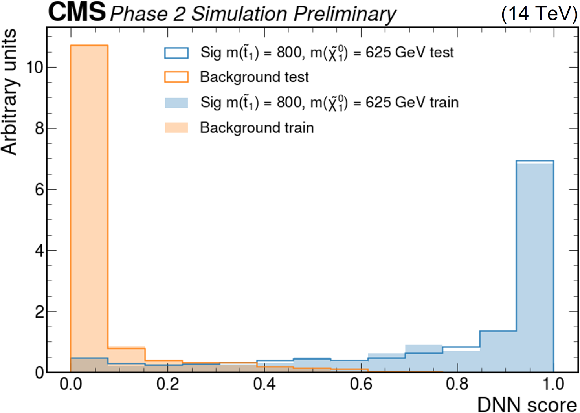
Figure 5:
Parametric DNN output for SM background ($\mathrm{t\bar{t}}$) and SUSY signal mass points with $m_{\tilde{t}_1} = $ 185 GeV and $m_{\tilde{\chi}_{1}^{0}} = $ 10 GeV, and with $m_{\tilde{t}_1} = $ 800 GeV and $m_{\tilde{\chi}_{1}^{0}} = $ 625 GeV, respectively. |
png |
Figure 5-a:
Parametric DNN output for SM background ($\mathrm{t\bar{t}}$) and SUSY signal mass points with $m_{\tilde{t}_1} = $ 185 GeV and $m_{\tilde{\chi}_{1}^{0}} = $ 10 GeV, and with $m_{\tilde{t}_1} = $ 800 GeV and $m_{\tilde{\chi}_{1}^{0}} = $ 625 GeV, respectively. |
png |
Figure 5-b:
Parametric DNN output for SM background ($\mathrm{t\bar{t}}$) and SUSY signal mass points with $m_{\tilde{t}_1} = $ 185 GeV and $m_{\tilde{\chi}_{1}^{0}} = $ 10 GeV, and with $m_{\tilde{t}_1} = $ 800 GeV and $m_{\tilde{\chi}_{1}^{0}} = $ 625 GeV, respectively. |
png pdf |
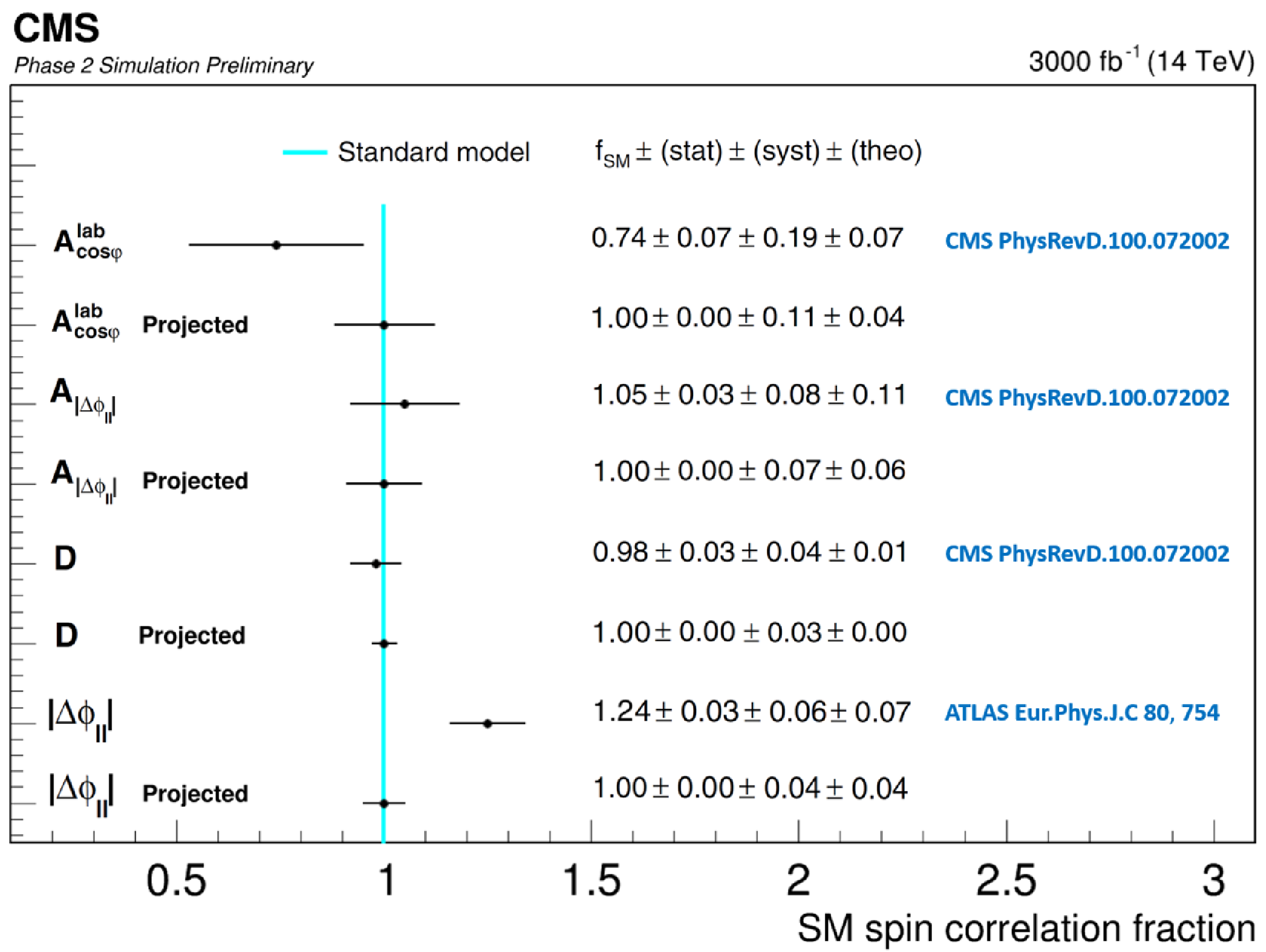
Figure 6:
Extracted values of $f_{SM}$ from laboratory-frame spin correlation variables by CMS [29] and ATLAS [30] at 13 TeV and projected values at 14 TeV. The measured and projected values with their statistical, systematic, and theoretical uncertainties are given on the right. Statistical uncertainties of the data on the projected values are smaller than 0.004 and hence, denoted with 0.00. As per Yellow Report recommendations theory uncertainties are reduced by 50% for projected values. |
png pdf |
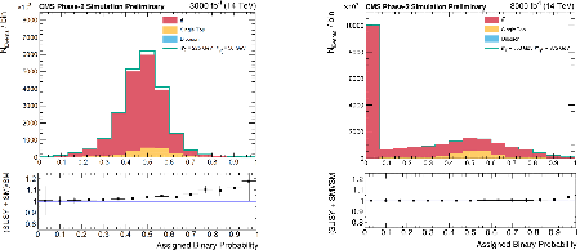
Figure 7:
DNN output on the test datasets for two different top squark masses : 225 and 550 GeV. |
png |
Figure 7-a:
DNN output on the test datasets for two different top squark masses : 225 and 550 GeV. |
png |
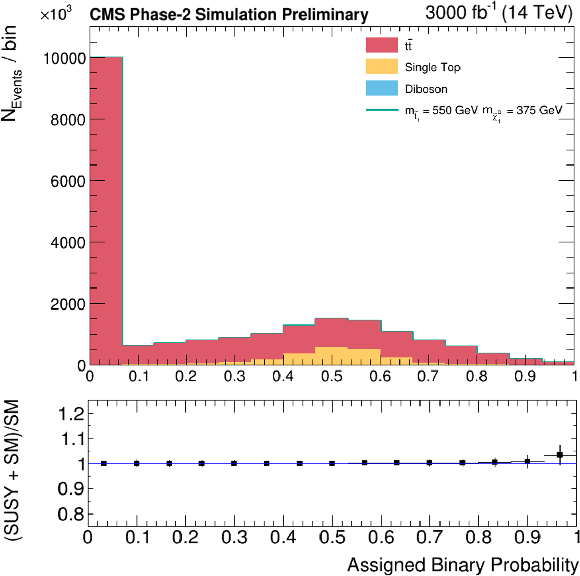
Figure 7-b:
DNN output on the test datasets for two different top squark masses : 225 and 550 GeV. |
png pdf |
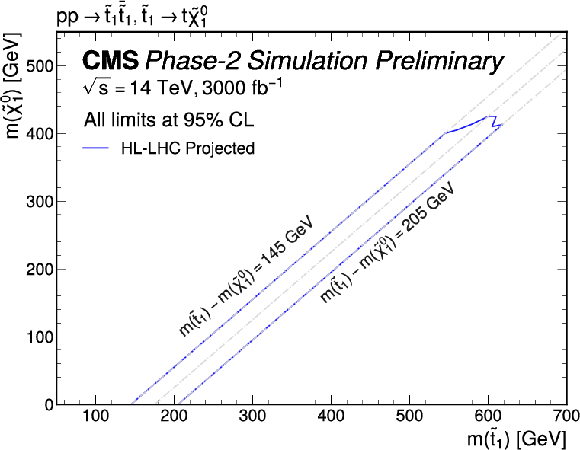
Figure 8:
Projected region of discovery potential in the top squark and neutralino mass plane. The center line corresponds to $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 175 GeV . |
png pdf |
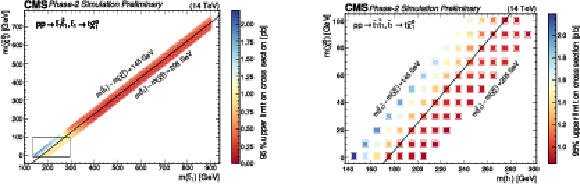
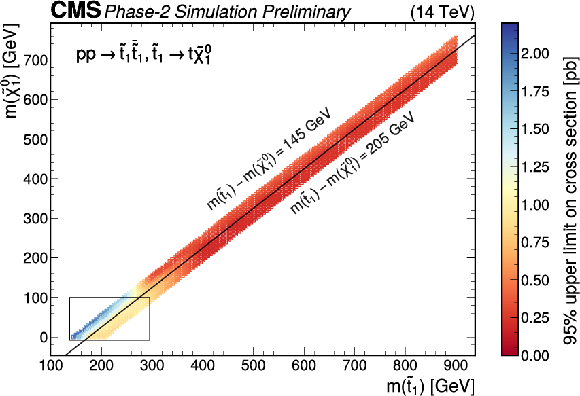
Figure 9:
Expected 95 $%$ CL upper limits on the SUSY cross section (in pb) as a function of the top squark and neutralino masses in the top quark corridor region (left). We highlight the limits (right) in the already excluded region in the low top squark-neutralino mass plane. In both plots we add a center line to guide the eye, which corresponds to $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 175 GeV . |
png pdf |
Figure 9-a:
Expected 95 $%$ CL upper limits on the SUSY cross section (in pb) as a function of the top squark and neutralino masses in the top quark corridor region (left). We highlight the limits (right) in the already excluded region in the low top squark-neutralino mass plane. In both plots we add a center line to guide the eye, which corresponds to $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 175 GeV . |
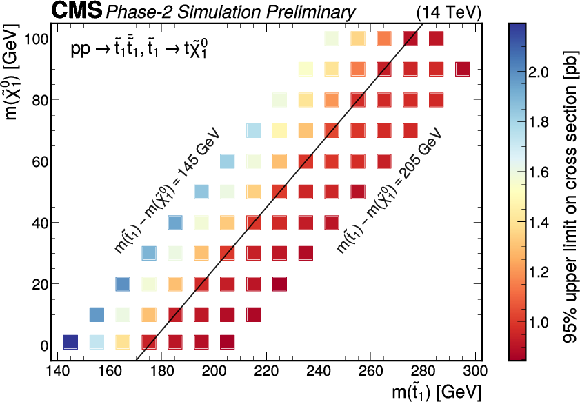
png pdf |
Figure 9-b:
Expected 95 $%$ CL upper limits on the SUSY cross section (in pb) as a function of the top squark and neutralino masses in the top quark corridor region (left). We highlight the limits (right) in the already excluded region in the low top squark-neutralino mass plane. In both plots we add a center line to guide the eye, which corresponds to $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 175 GeV . |
png pdf |
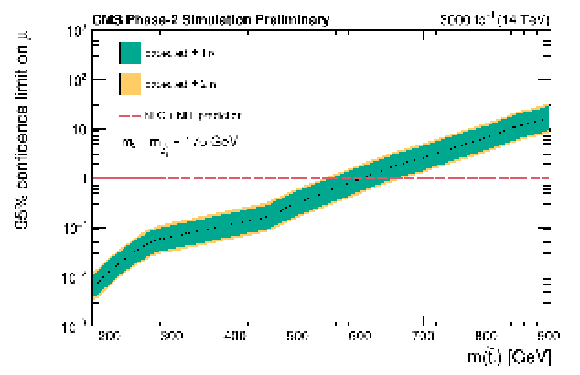
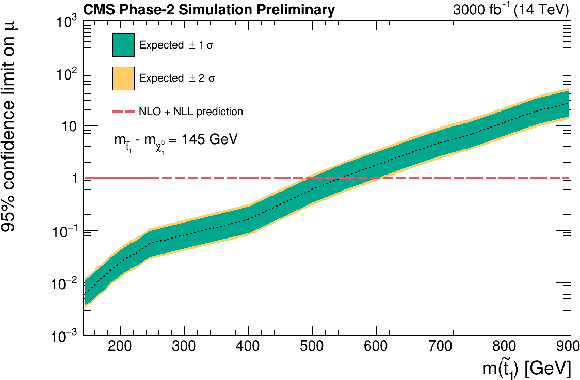
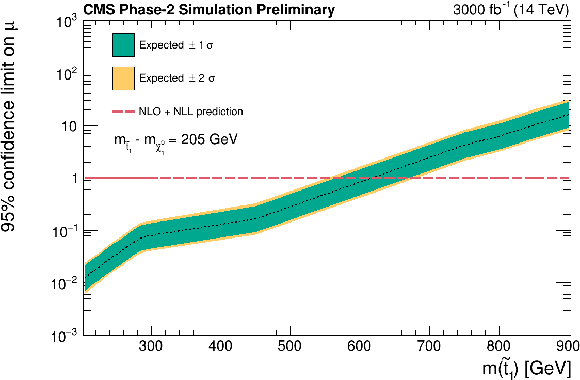
Figure 10:
Expected limits on signal strength calculated using asymptotic formulae. Corresponding to each top squark mass point there is a neutralino mass such that $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 175 GeV . The green and yellow bands represent the regions containing 68% and 95%, respectively, of the expected limits. The red dashed line indicates the approximate NLO+NLL prediction. |
png pdf |
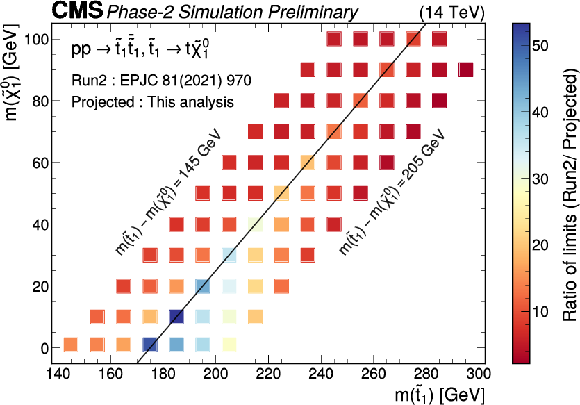
Figure 11:
Ratio of expected 95% CL upper limits of the combined search for top squarks from Ref. [31] to the ones derived in the context of this search for the low top squark-neutralino mass plane. The center line corresponds to $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 175 GeV . |
png pdf |
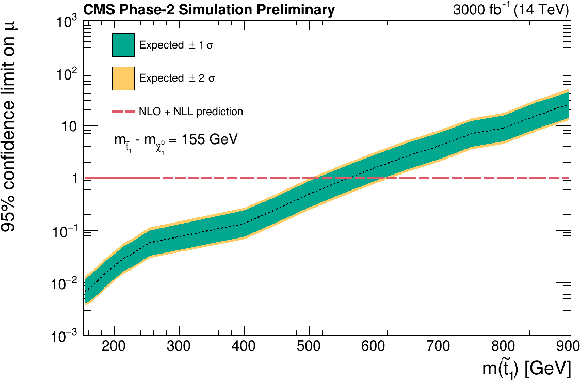
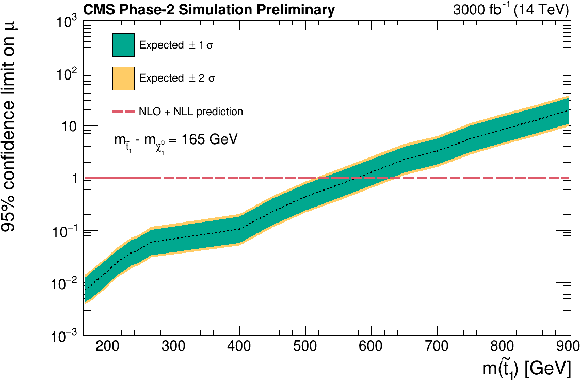
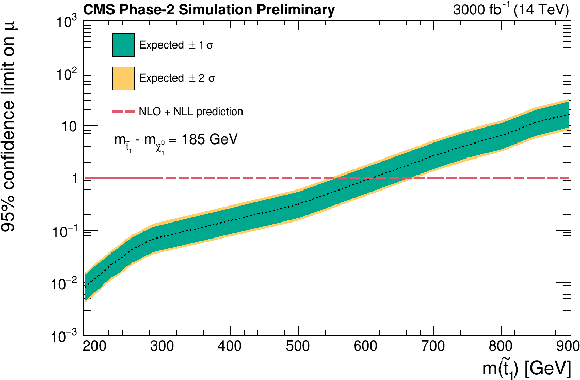
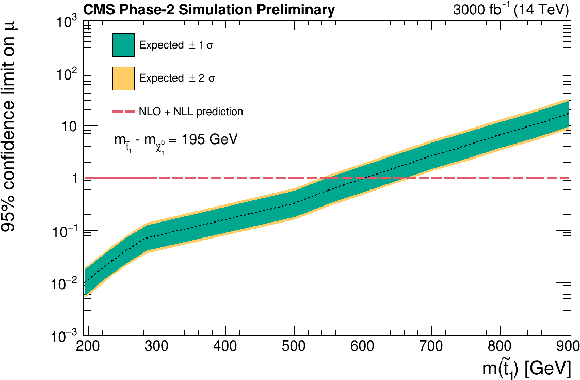
Figure 12:
Expected limits on signal strength calculated using asymptotic formulae. Corresponding to each top squark mass point there is a neutralino mass such that $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 145 GeV (top left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 155 GeV (top right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 165 GeV (middle left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 185 GeV (middle right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 195 GeV (bottom left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 205 GeV (bottom right). The green and yellow bands represent the regions containing 68% and 95%, respectively, of the expected limits. The red dashed line indicates the approximate NLO+NLL prediction. |
png |
Figure 12-a:
Expected limits on signal strength calculated using asymptotic formulae. Corresponding to each top squark mass point there is a neutralino mass such that $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 145 GeV (top left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 155 GeV (top right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 165 GeV (middle left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 185 GeV (middle right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 195 GeV (bottom left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 205 GeV (bottom right). The green and yellow bands represent the regions containing 68% and 95%, respectively, of the expected limits. The red dashed line indicates the approximate NLO+NLL prediction. |
png |
Figure 12-b:
Expected limits on signal strength calculated using asymptotic formulae. Corresponding to each top squark mass point there is a neutralino mass such that $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 145 GeV (top left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 155 GeV (top right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 165 GeV (middle left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 185 GeV (middle right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 195 GeV (bottom left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 205 GeV (bottom right). The green and yellow bands represent the regions containing 68% and 95%, respectively, of the expected limits. The red dashed line indicates the approximate NLO+NLL prediction. |
png |
Figure 12-c:
Expected limits on signal strength calculated using asymptotic formulae. Corresponding to each top squark mass point there is a neutralino mass such that $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 145 GeV (top left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 155 GeV (top right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 165 GeV (middle left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 185 GeV (middle right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 195 GeV (bottom left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 205 GeV (bottom right). The green and yellow bands represent the regions containing 68% and 95%, respectively, of the expected limits. The red dashed line indicates the approximate NLO+NLL prediction. |
png |
Figure 12-d:
Expected limits on signal strength calculated using asymptotic formulae. Corresponding to each top squark mass point there is a neutralino mass such that $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 145 GeV (top left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 155 GeV (top right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 165 GeV (middle left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 185 GeV (middle right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 195 GeV (bottom left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 205 GeV (bottom right). The green and yellow bands represent the regions containing 68% and 95%, respectively, of the expected limits. The red dashed line indicates the approximate NLO+NLL prediction. |
png |
Figure 12-e:
Expected limits on signal strength calculated using asymptotic formulae. Corresponding to each top squark mass point there is a neutralino mass such that $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 145 GeV (top left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 155 GeV (top right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 165 GeV (middle left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 185 GeV (middle right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 195 GeV (bottom left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 205 GeV (bottom right). The green and yellow bands represent the regions containing 68% and 95%, respectively, of the expected limits. The red dashed line indicates the approximate NLO+NLL prediction. |
png |
Figure 12-f:
Expected limits on signal strength calculated using asymptotic formulae. Corresponding to each top squark mass point there is a neutralino mass such that $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 145 GeV (top left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 155 GeV (top right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 165 GeV (middle left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 185 GeV (middle right), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 195 GeV (bottom left), $\Delta M(\tilde{t}_1, \tilde{\chi}_{1}^{0}) = $ 205 GeV (bottom right). The green and yellow bands represent the regions containing 68% and 95%, respectively, of the expected limits. The red dashed line indicates the approximate NLO+NLL prediction. |
| Tables | |
png pdf |
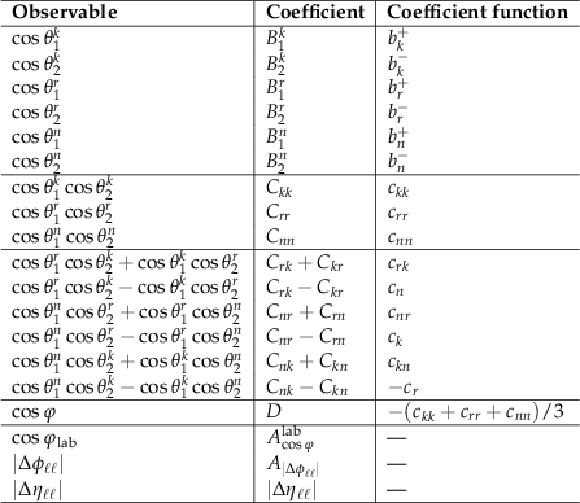
Table 1:
Observables and corresponding coefficients and production spin density matrix coefficient functions. For the laboratory-frame asymmetries shown in the last three rows, there is no direct correspondence with the coefficient functions. |
png pdf |
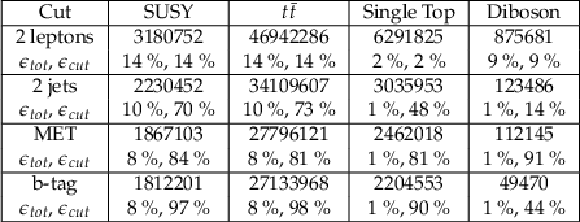
Table 2:
Event yields post cuts at 14 TeV and corresponding to 3000 fb$^{-1}$ of data. $\epsilon _{tot}$ is the fraction of events remaining after each cut relative to the original sample size, while $\epsilon _{cut}$ is the fraction of events remaining after the cut relative to the previous step. |
png pdf |
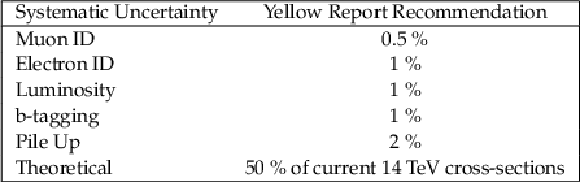
Table 3:
Summary of flat systematic uncertainties. |
png pdf |
Table 4:
Summary of shape-based systematic uncertainties. |
| Summary |
|
In this analysis we present a first study of the performance of the expected precision of a measurement of the strength of expected $\mathrm{t\bar{t}}$ spin correlation in 14 TeV proton-proton collisions. Unprecedented precision in measuring spin correlation variables is expected, with $D$ the most accurate variable with a 3% total uncertainty. We also presented a Deep Neural Network (DNN) based approach to searches for new physics in the low and high top quark mass corridor using top quark spin correlation. Using this method alone and extending the corridor up to masses in the 1 TeV range, we can significantly increase the ultimate reach of the LHC to discover top squarks in the degenerate mass corridor in the top squark-neutralino plane, or in the absence of a discovery exclude top squarks up to 600 GeV. In particular, in the top squark and neutralino mass corridor existing top squark pair production cross section limits can be improved by about one order of magnitude for top squark masses less than 300 GeV. Naturalness arguments still hint at the low top squark mass phase space region as a less fine-tuned implementation of SUSY, which so far might have escaped discovery given the abundance of top quarks in the same phase space folded with less favorable SUSY scenarios.\\ In principle, adding more kinematic variables to the DNN will improve the sensitivity further by an additional 5-10%. However, the purpose of this analysis is to show that $\mathrm{t\bar{t}}$ spin correlation variables will be an important asset for any type of searches for new physics involving top quark pairs. This is especially true for corners of the phase space that are difficult to access by classical searches using only kinematic variables in the low top quark mass corridor. This phase space represents less fine-tuned implementations of beyond the SM SUSY models. Given the model independent nature of this channel, other new physics signatures may be probed by this approach and make ample use of the ultimate 3 ab$^{-1}$ dataset. |
| References | ||||
| 1 | CMS Phase II Upgrade Performance Studies Group Collaboration | TWiki: Recommendations for Systematic Uncertainties HL-LHC (3 fb-1) | CMS twiki pages v1 | |
| 2 | M. Baumgart and B. Tweedie | A new twist on top quark spin correlations | link | 1212.4888 |
| 3 | C. Degrande et al. | Non-resonant new physics in top pair production at hadron colliders | JHEP 03 (2011) 125 | 1010.6304 |
| 4 | W. Bernreuther, D. Heisler, and Z.-G. Si | A set of top quark spin correlation and polarization observables for the LHC: Standard model predictions and new physics contributions | JHEP 12 (2015) 026 | 1508.05271 |
| 5 | G. Mahlon and S. J. Parke | Spin correlation effects in top quark pair production at the LHC | PRD 81 (2010) 074024 | 1001.3422 |
| 6 | A. Brandenburg, Z.-G. Si, and P. Uwer | QCD-corrected spin analysing power of jets in decays of polarized top quarks | PLB 539 (2002) 235 | hep-ph/0205023 |
| 7 | CMS Collaboration | The CMS Experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 8 | CMS Collaboration | Technical Proposal for the Phase-II Upgrade of the CMS Detector | CMS-PAS-TDR-15-002 | CMS-PAS-TDR-15-002 |
| 9 | CMS Collaboration | The Phase-2 Upgrade of the CMS Tracker | CMS-PAS-TDR-17-001 | CMS-PAS-TDR-17-001 |
| 10 | CMS Collaboration | The Phase-2 Upgrade of the CMS Barrel Calorimeters Technical Design Report | CMS-PAS-TDR-17-002 | CMS-PAS-TDR-17-002 |
| 11 | CMS Collaboration | The Phase-2 Upgrade of the CMS Endcap Calorimeter | CMS-PAS-TDR-17-007 | CMS-PAS-TDR-17-007 |
| 12 | CMS Collaboration | The Phase-2 Upgrade of the CMS Muon Detectors | CMS-PAS-TDR-17-003 | CMS-PAS-TDR-17-003 |
| 13 | C. CMS | A MIP Timing Detector for the CMS Phase-2 Upgrade | CERN-LHCC-2019-003 | |
| 14 | CMS Collaboration | The Phase-2 Upgrade of the CMS Level-1 Trigger | CMS-PAS-TDR-20-001 | CMS-PAS-TDR-20-001 |
| 15 | C. Collaboration | The Phase-2 Upgrade of the CMS Data Acquisition and High Level Trigger | CERN-LHCC-2021-007 | |
| 16 | CMS Collaboration | Expected performance of the physics objects with the upgraded CMS detector at the HL-LHC | CDS | |
| 17 | CMS Collaboration | Pileup mitigation at CMS in 13 TeV data | JINST 15 (2020) P09018 | CMS-JME-18-001 2003.00503 |
| 18 | B. A. Betchart, R. Demina, and A. Harel | Analytic solutions for neutrino momenta in decay of top quarks | NIM A 736 (2014) 169–178 | |
| 19 | Particle Data Group | Review of particle physics | PRD 98 (2018) 030001 | |
| 20 | CMS Collaboration | Measurements of $ \mathrm{t\overline{t}} $ differential cross sections in proton-proton collisions at $ \sqrt{s}= $ 13 TeV using events containing two leptons | JHEP 02 (2019) 149 | CMS-TOP-17-014 1811.06625 |
| 21 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 22 | DELPHES 3 Collaboration | DELPHES 3, A modular framework for fast simulation of a generic collider experiment | JHEP 02 (2014) 057 | 1307.6346 |
| 23 | LHC SUSY Cross Section Working Group Collaboration | TWiki: stop/sbottom cross section with squarks and gluinos decoupled | CMS twiki pages | |
| 24 | CMS Phase II Upgrade Performance Studies Group Collaboration | TWiki: SUSY Cross Sections at 14 TeV for stop/sbottom | CMS twiki pages v1 | |
| 25 | F. Chollet et al. | Keras | link | |
| 26 | Z. Han, A. Katz, D. Krohn, and M. Reece | (light) stop signs | Journal of High Energy Physics 2012 (Aug, 2012) | |
| 27 | CMS Phase II Upgrade Performance Studies Group Collaboration | TWiki: PDFs HL-LHC Summary Table | CMS twiki pages v1 | |
| 28 | S. P. Griso et al | Yellow Report Systematics | link | |
| 29 | CMS Collaboration | Measurement of the top quark polarization and $ \mathrm{t\bar{t}} $ spin correlations using dilepton final states in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRD 100 (2019), no. 7, 072002 | CMS-TOP-18-006 1907.03729 |
| 30 | ATLAS Collaboration | Measurements of top-quark pair spin correlations in the e$ \mu $ channel at $ \sqrt{s} = $ 13 TeV using pp collisions in the ATLAS detector | EPJC 80 (2020), no. 8, 754 | 1903.07570 |
| 31 | CMS Collaboration | Combined searches for the production of supersymmetric top quark partners in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | EPJC 81 (2021), no. 11, 970 | CMS-SUS-20-002 2107.10892 |
| 32 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 33 | A. L. Read | Presentation of search results: the CL$_s $ technique | JPG 28 (2002) 2693 | |
|
|
Compact Muon Solenoid LHC, CERN |
|
|
|
|
|
|