

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-EXO-17-024 | ||
| Search for low mass resonances decaying into bottom quark-antiquark pairs in pp collisions at $\sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| July 2018 | ||
| Abstract: A search for narrow scalar resonances decaying to bottom quark-antiquark pairs is presented. The search is based on events collected in $\sqrt{s}= $ 13 TeV proton-proton collisions with the CMS detector at the CERN LHC. The data sample, collected in 2016, corresponds to an integrated luminosity of 35.9 fb$^{-1}$. The resonance is produced with high transverse momentum due to initial state radiation, such that the decay products of the resonance are reconstructed as a single large-radius jet with high mass and two-pronged substructure. The signal is identified as a narrow excess in the jet invariant mass spectrum. No evidence for such a resonance is observed within the resonance mass range from 50 to 350 GeV. Upper limits at the 95% confidence level are set on the product of the cross section and branching fraction to a bottom quark-antiquark pair, constituting the first constraint from the LHC in this resonance mass range. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, PRD 99 (2019) 012005. The superseded preliminary plots can be found here. |
||
| Figures | |

png pdf |
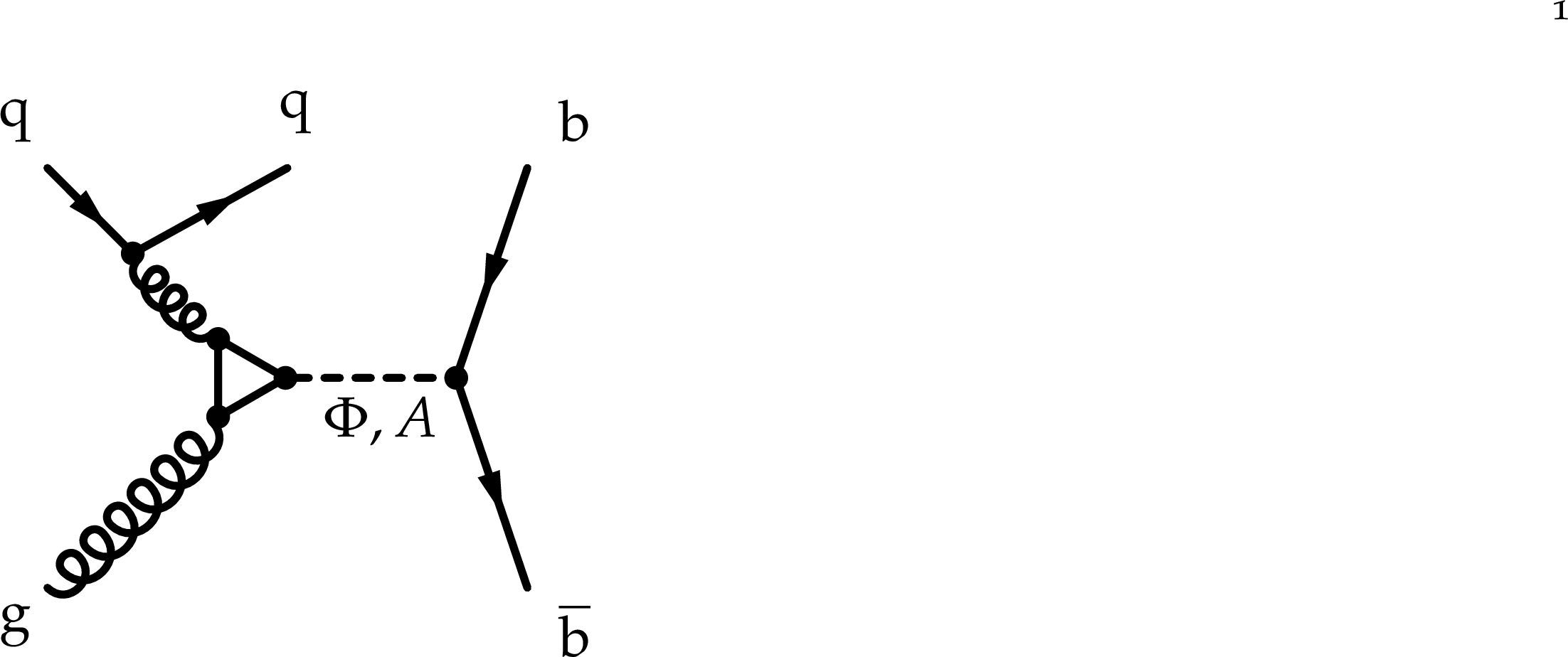
Figure 1:
One-loop diagrams of processes exchanging a scalar ($\mathrm{h}i $) or pseudoscalar ($A$) mediator, leading to a boosted double b-jet signature. |
png pdf |
Figure 1-a:
One-loop diagrams of processes exchanging a scalar ($\mathrm{h}i $) or pseudoscalar ($A$) mediator, leading to a boosted double b-jet signature. |

png pdf |
Figure 1-b:
One-loop diagrams of processes exchanging a scalar ($\mathrm{h}i $) or pseudoscalar ($A$) mediator, leading to a boosted double b-jet signature. |
png pdf |
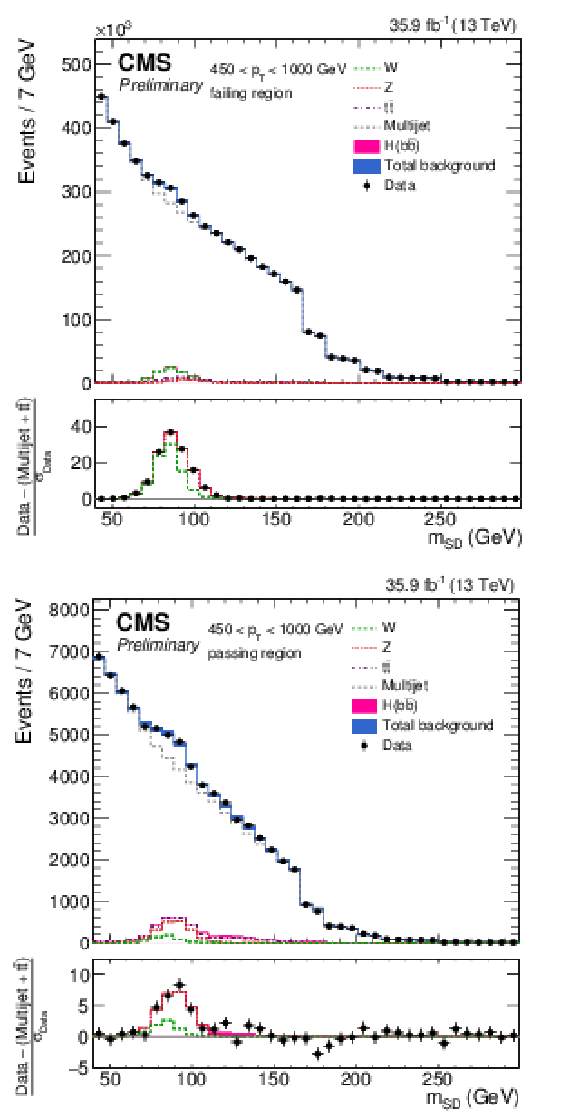
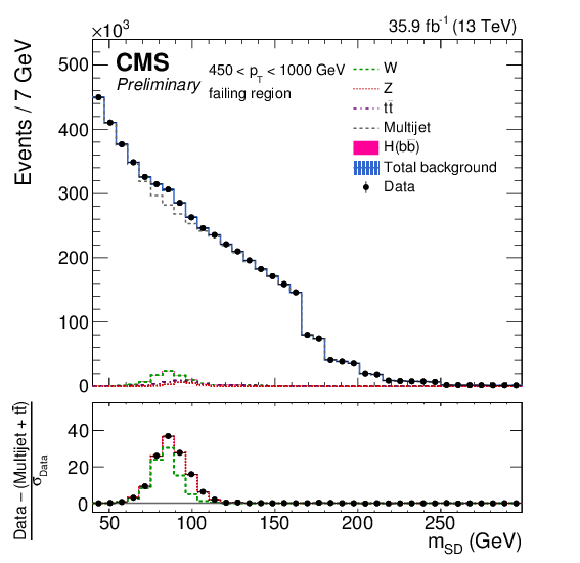
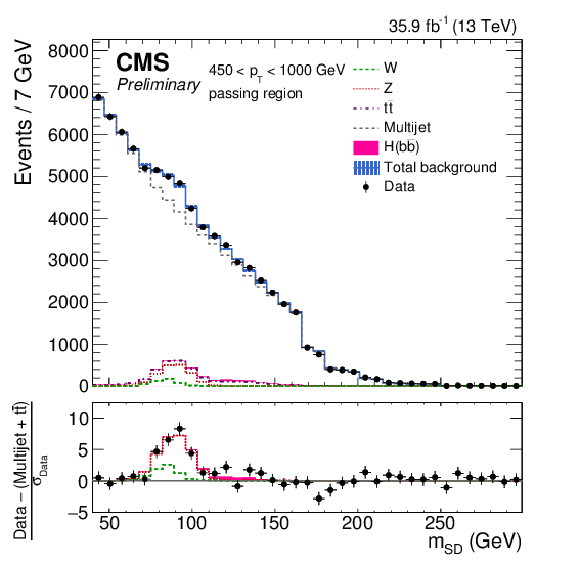
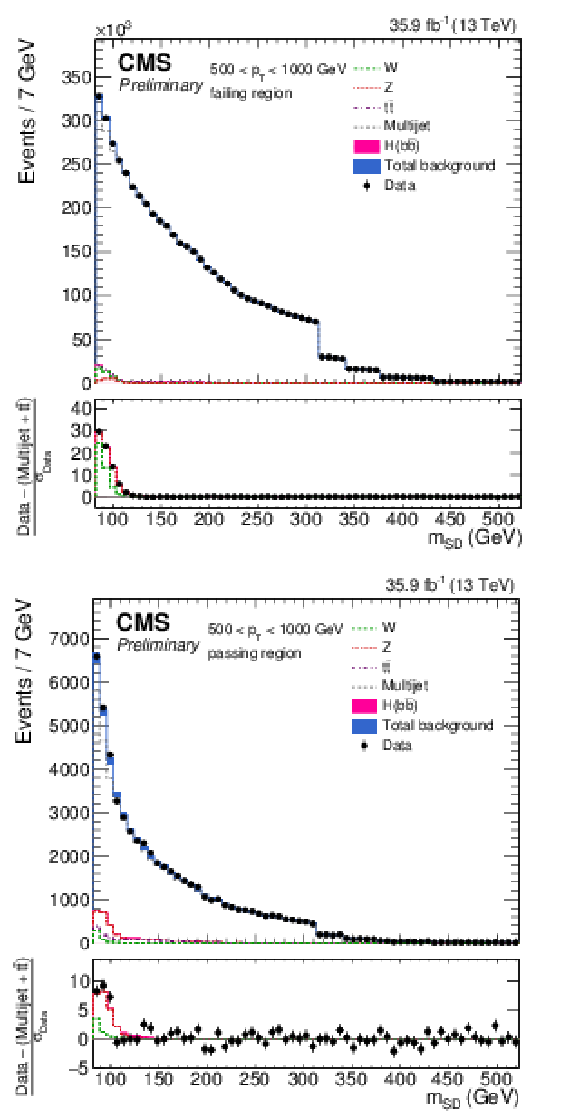
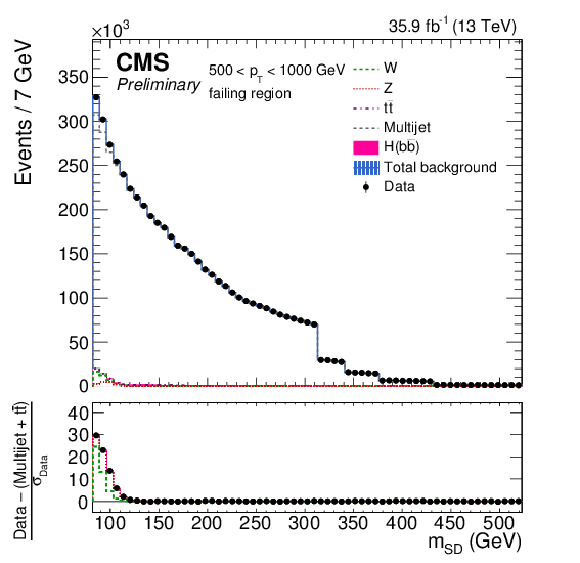
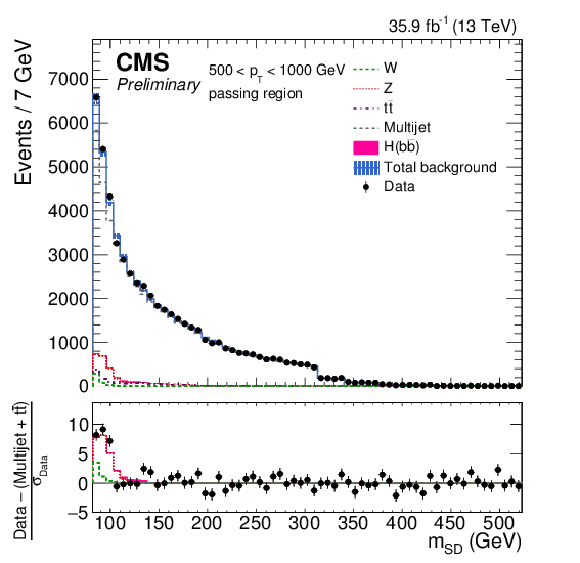
Figure 2:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions for the AK8 selection for the failing (top) and passing (bottom) regions, combining all the $ {p_{\mathrm {T}}} $ categories. The background fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The features at 166, 180, 201, 215, and 250 GeV in the $ {m_{\mathrm {SD}}} $ distribution are due to the $\rho $ boundaries, which define different $ {m_{\mathrm {SD}}} $ ranges for each $ {p_{\mathrm {T}}} $ category. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 2-a:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions for the AK8 selection for the failing (top) and passing (bottom) regions, combining all the $ {p_{\mathrm {T}}} $ categories. The background fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The features at 166, 180, 201, 215, and 250 GeV in the $ {m_{\mathrm {SD}}} $ distribution are due to the $\rho $ boundaries, which define different $ {m_{\mathrm {SD}}} $ ranges for each $ {p_{\mathrm {T}}} $ category. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 2-b:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions for the AK8 selection for the failing (top) and passing (bottom) regions, combining all the $ {p_{\mathrm {T}}} $ categories. The background fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The features at 166, 180, 201, 215, and 250 GeV in the $ {m_{\mathrm {SD}}} $ distribution are due to the $\rho $ boundaries, which define different $ {m_{\mathrm {SD}}} $ ranges for each $ {p_{\mathrm {T}}} $ category. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 3:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions for the CA15 selection for the failing (top) and passing (bottom) regions, combining all the $ {p_{\mathrm {T}}} $ categories. The background fit is performed under the background-only hypothesis. The features at 285, 313, 341, 376, and 432 GeV in the $ {m_{\mathrm {SD}}} $ distribution are due to the $\rho $ boundaries, which define different $ {m_{\mathrm {SD}}} $ ranges for each $ {p_{\mathrm {T}}} $ category. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 3-a:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions for the CA15 selection for the failing (top) and passing (bottom) regions, combining all the $ {p_{\mathrm {T}}} $ categories. The background fit is performed under the background-only hypothesis. The features at 285, 313, 341, 376, and 432 GeV in the $ {m_{\mathrm {SD}}} $ distribution are due to the $\rho $ boundaries, which define different $ {m_{\mathrm {SD}}} $ ranges for each $ {p_{\mathrm {T}}} $ category. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 3-b:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions for the CA15 selection for the failing (top) and passing (bottom) regions, combining all the $ {p_{\mathrm {T}}} $ categories. The background fit is performed under the background-only hypothesis. The features at 285, 313, 341, 376, and 432 GeV in the $ {m_{\mathrm {SD}}} $ distribution are due to the $\rho $ boundaries, which define different $ {m_{\mathrm {SD}}} $ ranges for each $ {p_{\mathrm {T}}} $ category. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
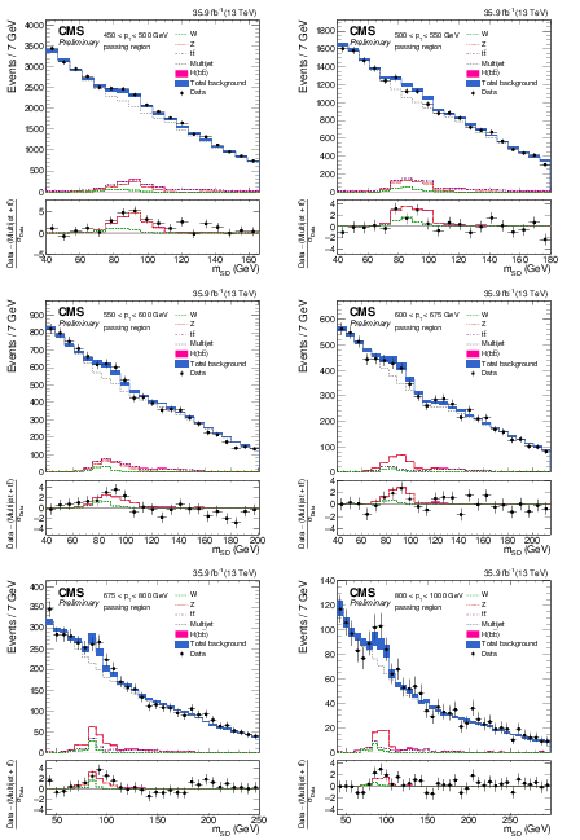
Figure 4:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the AK8 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
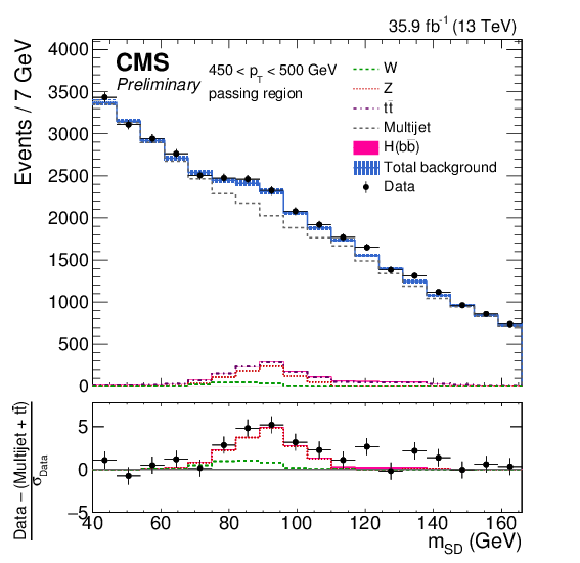
png pdf |
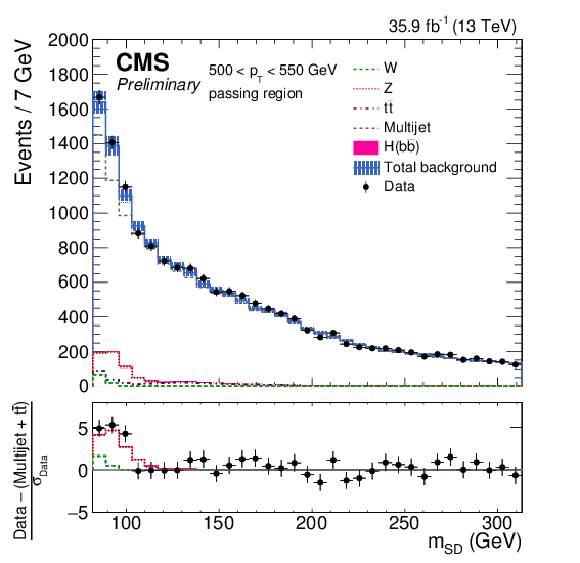
Figure 4-a:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the AK8 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
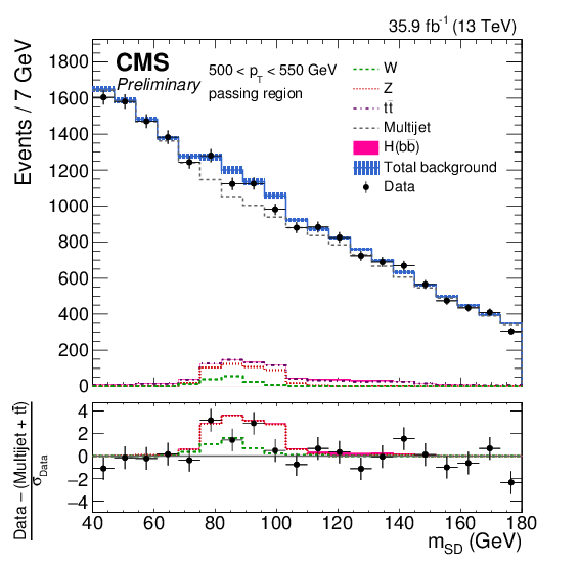
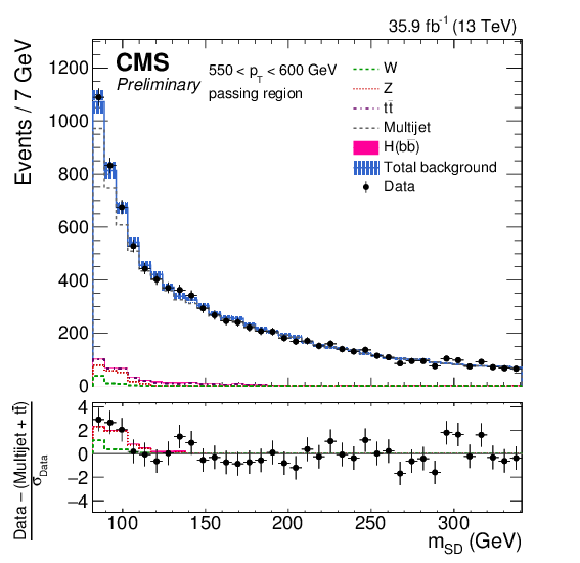
Figure 4-b:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the AK8 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
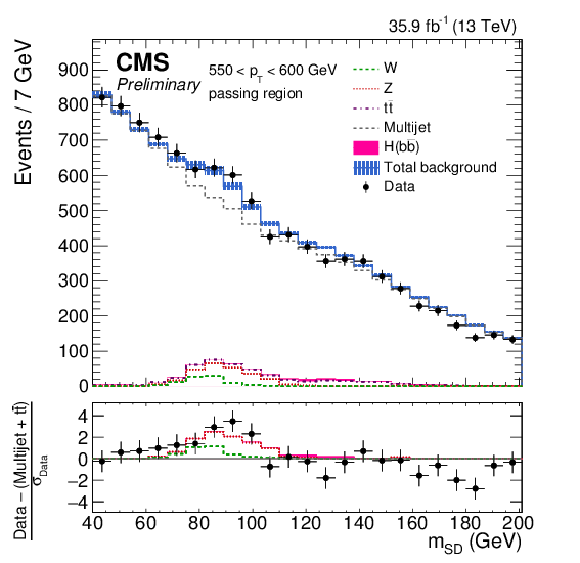
Figure 4-c:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the AK8 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
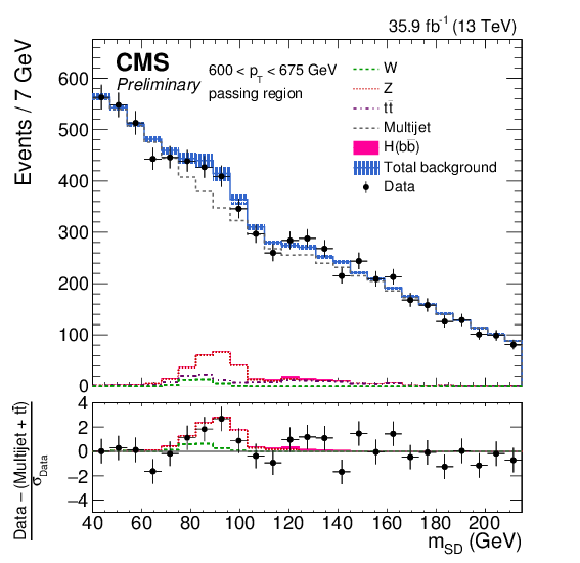
Figure 4-d:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the AK8 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
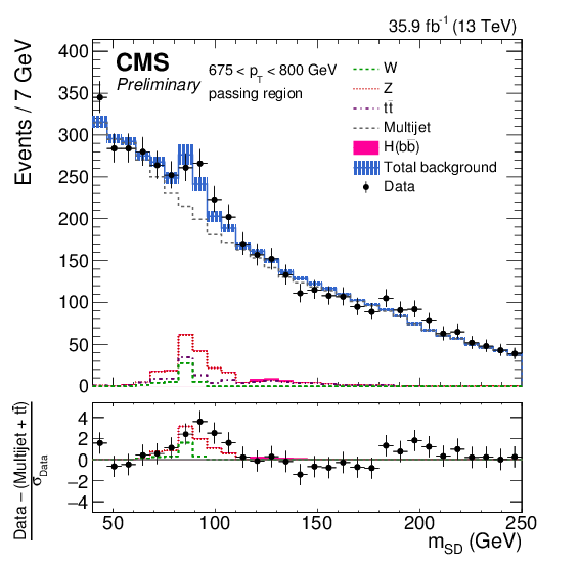
png pdf |
Figure 4-e:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the AK8 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |

png pdf |
Figure 4-f:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the AK8 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
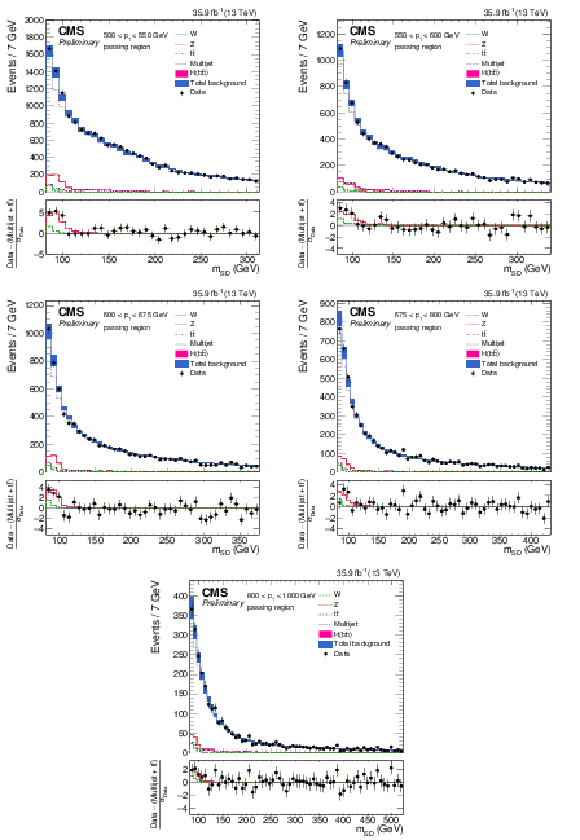
Figure 5:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the CA15 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 5-a:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the CA15 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 5-b:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the CA15 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 5-c:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the CA15 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
Figure 5-d:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the CA15 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
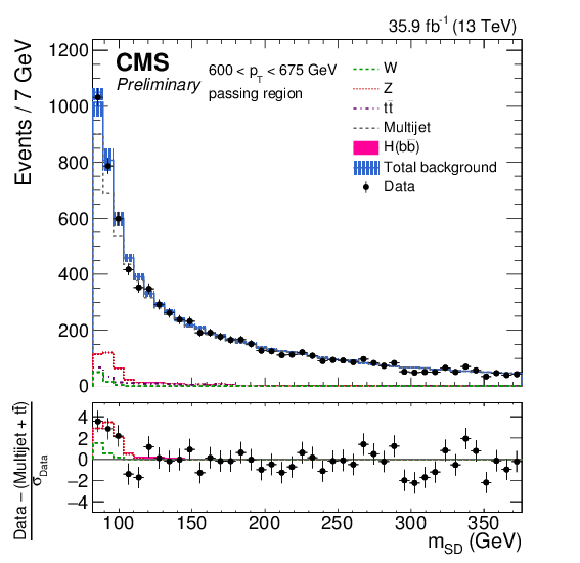
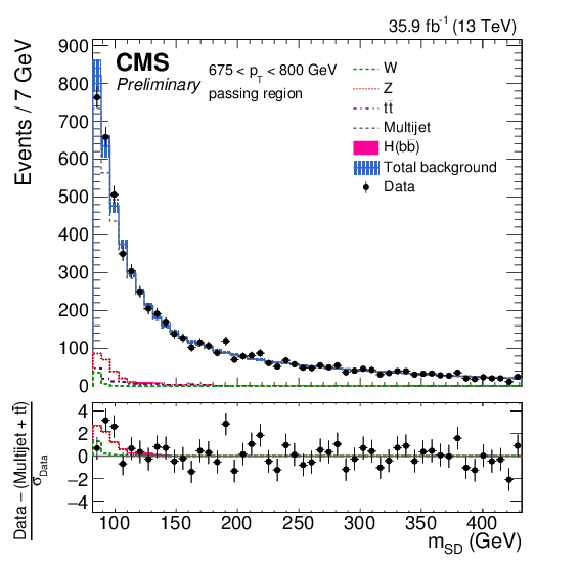
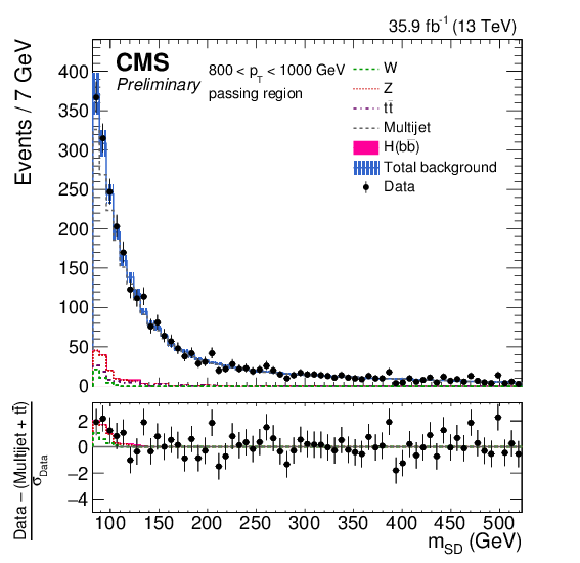
Figure 5-e:
The observed and fitted background $ {m_{\mathrm {SD}}} $ distributions in each $ {p_{\mathrm {T}}} $ category for the CA15 selection in the passing regions. The fit is performed under the background-only hypothesis. The QCD multijet background in the passing region is predicted using the failing region and the pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$. The bottom panel shows the difference between the data and the background prediction, divided by the statistical uncertainty on the data. |
png pdf |
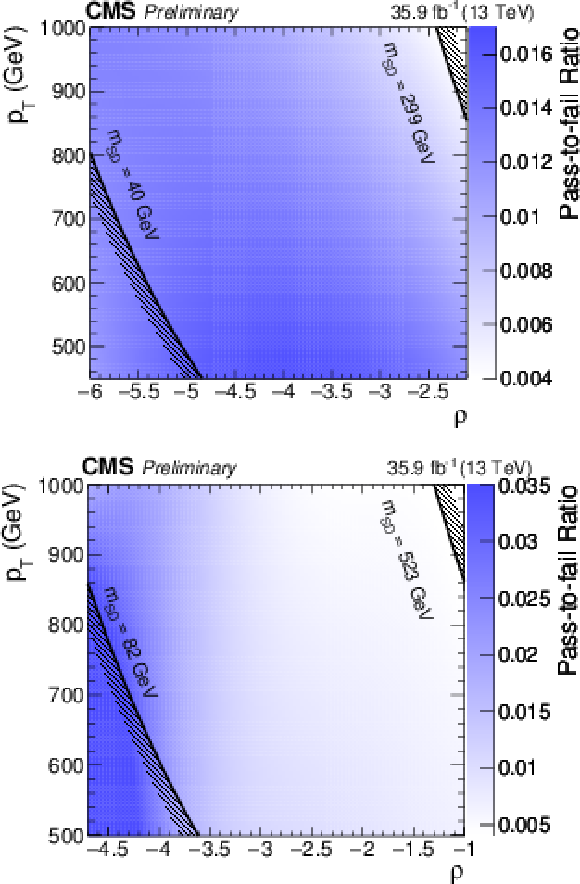
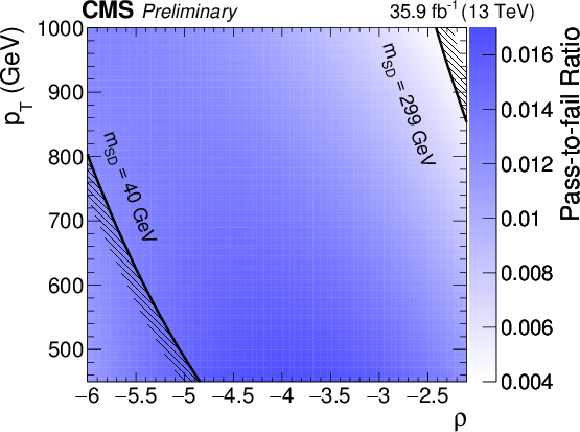
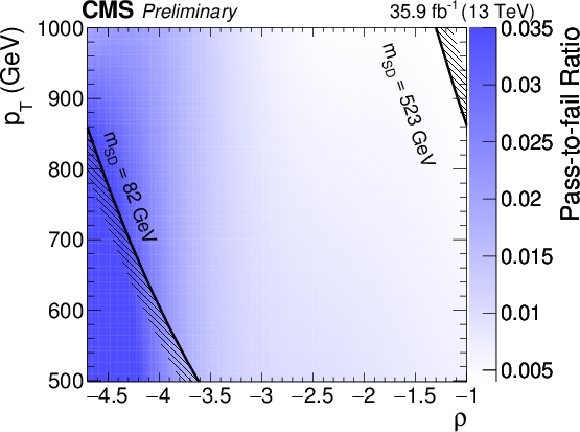
Figure 6:
The fitted pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$ as function of $ {p_{\mathrm {T}}} $ and $\rho $ for both the AK8 selection (top) and the CA15 selection (bottom). |
png pdf |
Figure 6-a:
The fitted pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$ as function of $ {p_{\mathrm {T}}} $ and $\rho $ for both the AK8 selection (top) and the CA15 selection (bottom). |
png pdf |
Figure 6-b:
The fitted pass-fail ratio $R_{\mathrm {p}/\mathrm {f}}$ as function of $ {p_{\mathrm {T}}} $ and $\rho $ for both the AK8 selection (top) and the CA15 selection (bottom). |
png pdf |
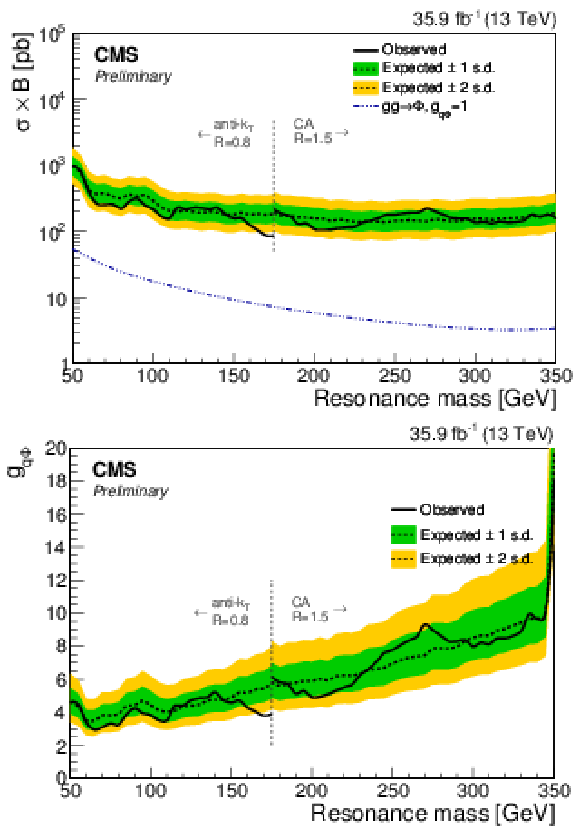
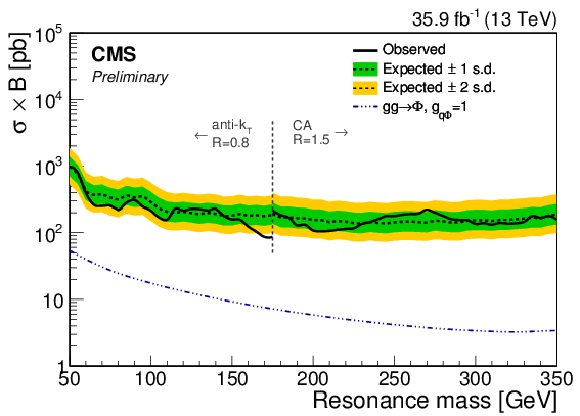
Figure 7:
95% CL upper limits on the $\mathrm{h}i ({{\mathrm {b}} {\overline {\mathrm {b}}}})$ production cross section times branching fraction (top) and on $ {g_{{\rm q}\mathrm{h}i}} $ (bottom) as a function of resonance mass. The blue dash-dotted line indicates the theoretical scalar production cross section assuming $ {g_{{\rm q}\mathrm{h}i}} =$ 1 as a chosen benchmark. The vertical line at 175 GeV corresponds to the transition between the AK8 and CA15 jet selections. |
png pdf |
Figure 7-a:
95% CL upper limits on the $\mathrm{h}i ({{\mathrm {b}} {\overline {\mathrm {b}}}})$ production cross section times branching fraction (top) and on $ {g_{{\rm q}\mathrm{h}i}} $ (bottom) as a function of resonance mass. The blue dash-dotted line indicates the theoretical scalar production cross section assuming $ {g_{{\rm q}\mathrm{h}i}} =$ 1 as a chosen benchmark. The vertical line at 175 GeV corresponds to the transition between the AK8 and CA15 jet selections. |
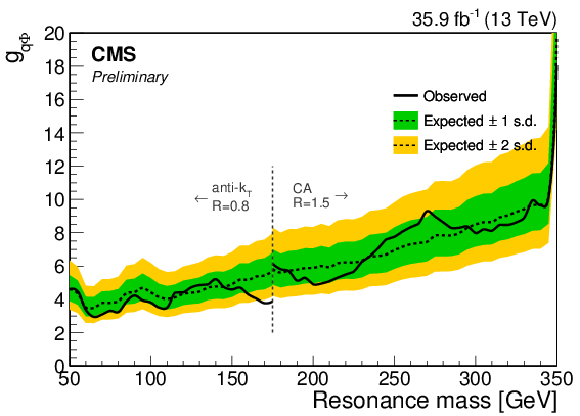
png pdf |
Figure 7-b:
95% CL upper limits on the $\mathrm{h}i ({{\mathrm {b}} {\overline {\mathrm {b}}}})$ production cross section times branching fraction (top) and on $ {g_{{\rm q}\mathrm{h}i}} $ (bottom) as a function of resonance mass. The blue dash-dotted line indicates the theoretical scalar production cross section assuming $ {g_{{\rm q}\mathrm{h}i}} =$ 1 as a chosen benchmark. The vertical line at 175 GeV corresponds to the transition between the AK8 and CA15 jet selections. |
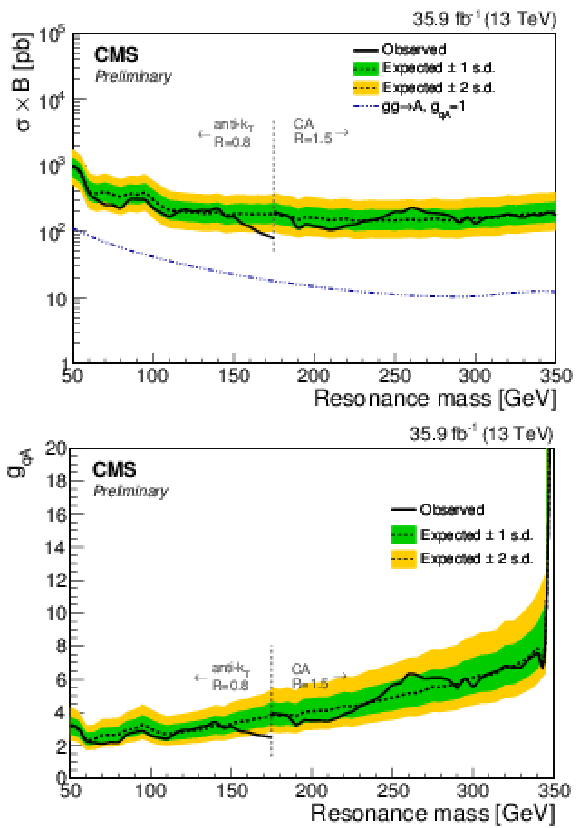
png pdf |
Figure 8:
95% CL upper limits on the $A({{\mathrm {b}} {\overline {\mathrm {b}}}})$ production cross section times branching fraction (top) and on $ {g_{{\rm q}A}} $ (bottom) as a function of resonance mass. The blue dash-dotted line indicates the theoretical pseudoscalar production cross section assuming $ {g_{{\rm q}A}} =$ 1 as a chosen benchmark. The vertical line at 175 GeV corresponds to the transition between the AK8 and CA15 jet selections. |
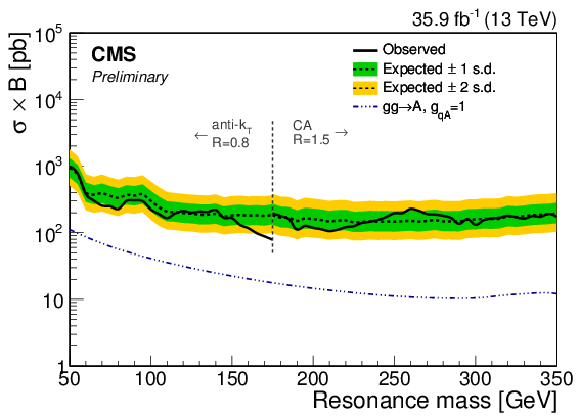
png pdf |
Figure 8-a:
95% CL upper limits on the $A({{\mathrm {b}} {\overline {\mathrm {b}}}})$ production cross section times branching fraction (top) and on $ {g_{{\rm q}A}} $ (bottom) as a function of resonance mass. The blue dash-dotted line indicates the theoretical pseudoscalar production cross section assuming $ {g_{{\rm q}A}} =$ 1 as a chosen benchmark. The vertical line at 175 GeV corresponds to the transition between the AK8 and CA15 jet selections. |
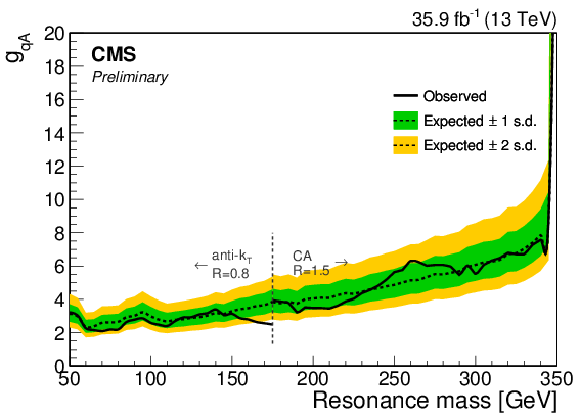
png pdf |
Figure 8-b:
95% CL upper limits on the $A({{\mathrm {b}} {\overline {\mathrm {b}}}})$ production cross section times branching fraction (top) and on $ {g_{{\rm q}A}} $ (bottom) as a function of resonance mass. The blue dash-dotted line indicates the theoretical pseudoscalar production cross section assuming $ {g_{{\rm q}A}} =$ 1 as a chosen benchmark. The vertical line at 175 GeV corresponds to the transition between the AK8 and CA15 jet selections. |
| Tables | |
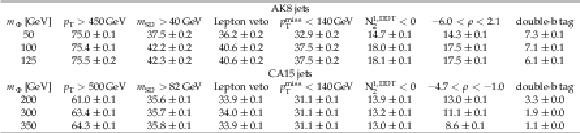
png pdf |
Table 1:
The selection efficiency in percentages for simulated $\mathrm{h}i ({{\mathrm {b}} {\overline {\mathrm {b}}}})$ signal events with parton-level $ {H_{\mathrm {T}}} > $ 400 GeV at different stages of the event selection, shown for each mass hypothesis and for AK8 and CA15 jets. The statistical uncertainties due to the MC sample size are also shown. |
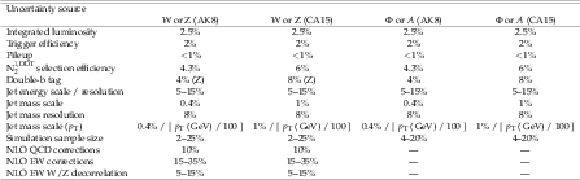
png pdf |
Table 2:
Summary of the systematic uncertainties affecting the signal, W and Z+jets processes. Instances where the uncertainty does not apply are indicated by "--". The reported percentages reflect a one standard deviation effect on the acceptance times efficiency of the different processes. For the uncertainties related to the jet mass scale and resolution, which affect the mass distribution shapes, the reported percentages reflect a one standard deviation effect on the nominal jet mass. |
| Summary |
| A search for a resonance decaying into a bottom quark-antiquark pair and reconstructed as a single wide jet has been presented, using a dataset of proton-proton collisions at $\sqrt{s} = $ 13 TeV corresponding to an integrated luminosity of 35.9 fb$^{-1}$. Novel substructure and double-b tagging techniques were employed to identify jets containing a resonance candidate over a smoothly falling soft-drop jet mass distribution in data. No significant excess above the standard model prediction was observed for signal masses between 50-350 GeV, and 95% confidence level upper limits are set on the resonance production cross section times branching fraction to bottom quark-antiquark pairs, as well as the coupling ${g_{{\rm q}\mathrm{h}i}} $ (${g_{{\rm q}A}} $) of a scalar (pseudoscalar) boson coupling to quarks. The search excludes the production through gluon fusion of a scalar (psuedoscalar) decaying to $\mathrm{b\bar{b}}$ with a cross section times branching ratio as low as 79 pb (86 pb) at a resonance mass of 175 GeV, corresponding to an upper limit on ${g_{{\rm q}\mathrm{h}i}} $ (${g_{{\rm q}A}} $) of 3.9 (2.5). This constitutes the first LHC constraint on such resonances in this mass range. |
| References | ||||
| 1 | CMS Collaboration | Search for narrow resonances in dijet final states at $ \sqrt{s}= $ 8 TeV with the novel CMS technique of data scouting | PRL 117 (2016) 031802 | CMS-EXO-14-005 1604.08907 |
| 2 | CMS Collaboration | Search for narrow resonances in the b-tagged dijet mass spectrum in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | PRL 120 (2018), no. 20, 201801 | CMS-EXO-16-057 1802.06149 |
| 3 | CMS Collaboration | Search for low mass vector resonances decaying to quark-antiquark pairs in proton-proton collisions at $ \sqrt{s}=13\text{}\text{}\mathrm{TeV} $ | PRL 119 (2017), no. 11, 111802 | CMS-EXO-16-030 1705.10532 |
| 4 | CMS Collaboration | Search for low mass vector resonances decaying into quark-antiquark pairs in proton-proton collisions at $ \sqrt{s}= 13 \mathrm$ TeV | JHEP 01 (2018) 097 | CMS-EXO-17-001 1710.00159 |
| 5 | ATLAS Collaboration | Search for light resonances decaying to boosted quark pairs and produced in association with a photon or a jet in proton-proton collisions at $ \sqrt{s}= $ 13 tev with the ATLAS detector | 1801.08769 | |
| 6 | CMS Collaboration | Inclusive search for a highly boosted Higgs boson decaying to a bottom quark-antiquark pair | PRL 120 (2018), no. 7, 071802 | CMS-HIG-17-010 1709.05543 |
| 7 | Abercrombie et al. | Dark matter benchmark models for early LHC Run-2 searches: Report of the ATLAS/CMS dark matter forum | 1507.00966 | |
| 8 | M. R. Buckley, D. Feld, and D. Goncalves | Scalar simplified models for dark matter | Phys.Rev. D91 (2015) 015017 | 1410.6497 |
| 9 | P. Harris, V. V. Khoze, M. Spannowsky, and C. Williams | Constraining dark sectors at colliders: Beyond the effective theory approach | Phys.Rev. D91 (2015) 055009 | 1411.0535 |
| 10 | U. Haisch and E. Re | Simplified dark matter top quark interactions at the LHC | JHEP 1506 (2015) 078 | 1503.00691 |
| 11 | D. Liu, J. Liu, C. E. M. Wagner, and X.-P. Wang | Bottom-quark Forward-Backward Asymmetry, Dark Matter and the LHC | PRD97 (2018), no. 5, 055021 | 1712.05802 |
| 12 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_{t} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 13 | Y. L. Dokshitzer, G. D. Leder, S. Moretti, and B. R. Webber | Better jet clustering algorithms | JHEP 08 (1997) 001 | hep-ph/9707323 |
| 14 | J. M. Butterworth, A. R. Davison, M. Rubin, and G. P. Salam | Jet substructure as a new Higgs search channel at the LHC | PRL 100 (2008) 242001 | 0802.2470 |
| 15 | I. Moult, L. Necib, and J. Thaler | New angles on energy correlation functions | JHEP 12 (2016) 153 | 1609.07483 |
| 16 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 tev | JINST 13 (2018), no. 05, P05011 | CMS-BTV-16-002 1712.07158 |
| 17 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 18 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 19 | GEANT4 Collaboration | $ GEANT4--a $ simulation toolkit | NIMA 506 (2003) 250 | |
| 20 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 21 | G. Busoni et al. | Recommendations on presenting LHC searches for missing transverse energy signals using simplified $ s $-channel models of dark matter | 1603.04156 | |
| 22 | S. P. Jones, M. Kerner, and G. Luisoni | Next-to-Leading-Order QCD Corrections to Higgs Boson Plus Jet Production with Full Top-Quark Mass Dependence | PRL 120 (2018), no. 16, 162001 | 1802.00349 |
| 23 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC53 (2008) 473--500 | 0706.2569 |
| 24 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 25 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 26 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower monte carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 27 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 28 | G. Luisoni, P. Nason, C. Oleari, and F. Tramontano | $ HW^{\pm} $/HZ + 0 and 1 jet at NLO with the POWHEG BOX interfaced to GoSam and their merging within MiNLO | JHEP 10 (2013) 083 | 1306.2542 |
| 29 | D. de Florian, G. Ferrera, M. Grazzini, and D. Tommasini | Higgs boson production at the LHC: transverse momentum resummation effects in the H$ \rightarrow 2\gamma $, H$ \rightarrow $WW$ \rightarrow \ell\nu\ell\nu $ and H$ \rightarrow $ZZ$ \rightarrow $4l decay modes | JHEP 06 (2012) 132 | 1203.6321 |
| 30 | M. Grazzini and H. Sargsyan | Heavy-quark mass effects in Higgs boson production at the LHC | JHEP 09 (2013) 129 | 1306.4581 |
| 31 | E. Bagnaschi, G. Degrassi, P. Slavich, and A. Vicini | Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM | JHEP 2012 (2012) 088 | 1111.2854 |
| 32 | E. Bagnaschi and A. Vicini | The Higgs transverse momentum distribution in gluon fusion as a multiscale problem | JHEP 01 (2016) 056 | 1505.00735 |
| 33 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159--177 | 1410.3012 |
| 34 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC76 (2016), no. 3, 155 | CMS-GEN-14-001 1512.00815 |
| 35 | J. M. Campbell and R. K. Ellis | MCFM for the Tevatron and the LHC | NPPS 205-206 (2010) 10 | 1007.3492 |
| 36 | M. Czakon, P. Fiedler, and A. Mitov | Total top quark pair-production cross section at hadron colliders through o($ \alpha_s^4 $) | PRL 110 (2013) 252004 | 1303.6254 |
| 37 | S. Kallweit et al. | NLO electroweak automation and precise predictions for w+multijet production at the LHC | JHEP 04 (2015) 012 | 1412.5157 |
| 38 | S. Kallweit et al. | NLO QCD+EW predictions for V + jets including off-shell vector-boson decays and multijet merging | JHEP 04 (2016) 021 | 1511.08692 |
| 39 | S. Kallweit et al. | NLO QCD+EW automation and precise predictions for V+multijet production | in Proceedings, 50th Rencontres de Moriond, QCD and high energy interactions, pp. 121--124 2015 | 1505.05704 |
| 40 | J. M. Lindert et al. | Precise predictions for $ v+ $ jets dark matter backgrounds | EPJC77 (2017), no. 12, 829 | 1705.04664 |
| 41 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 42 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017), no. 10, P10003 | CMS-PRF-14-001 1706.04965 |
| 43 | M. Cacciari, G. P. Salam, and G. Soyez | Fastjet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 44 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup Per Particle Identification | JHEP 10 (2014) 059 | 1407.6013 |
| 45 | D. Krohn, J. Thaler, and L.-T. Wang | Jet trimming | JHEP 02 (2010) 084 | 0912.1342 |
| 46 | M. Dasgupta, A. Fregoso, S. Marzani, and G. P. Salam | Towards an understanding of jet substructure | JHEP 09 (2013) 029 | 1307.0007 |
| 47 | A. J. Larkoski, S. Marzani, G. Soyez, and J. Thaler | Soft drop | JHEP 05 (2014) 146 | 1402.2657 |
| 48 | CMS Collaboration | Jet algorithms performance in 13 TeV data | CMS-PAS-JME-16-003 | |
| 49 | J. Dolen et al. | Thinking outside the ROCs: Designing decorrelated taggers (DDT) for jet substructure | JHEP 05 (2016) 156 | 1603.00027 |
| 50 | A. J. Larkoski, G. P. Salam, and J. Thaler | Energy correlation functions for jet substructure | JHEP 06 (2013) 108 | 1305.0007 |
| 51 | J. Thaler and K. Van Tilburg | Identifying boosted objects with N-subjettiness | JHEP 03 (2011) 015 | 1011.2268 |
| 52 | CMS Collaboration | Identification of b-quark jets at the CMS experiment in the LHC Run 2 startup | CMS-PAS-BTV-15-001 | CMS-PAS-BTV-15-001 |
| 53 | R. A. Fisher | On the interpretation of $ \chi^{2} $ from contingency tables, and the calculation of P | Journal of the Royal Statistical Society 85 (1922) 87 | |
| 54 | CMS Collaboration | Determination of jet energy calibration and transverse momentum resolution in CMS | JINST 6 (2011) 11002 | CMS-JME-10-011 1107.4277 |
| 55 | CMS Collaboration Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001, CERN, Geneva | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|