

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-EGM-24-002 | ||
| Highly boosted dielectron identification in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 2025-07-08 | ||
| Abstract: Searches for highly boosted new particles that decay to dielectron pairs can be challenging, as the relatively coarse granularity of many calorimeters and the size of their effective Molière radius can lead to their misidentification as single electrons. A new technique is developed to identify electron pairs in the range of Lorentz boost $ \gamma > $ 20 which produce one single merged cluster in the electromagnetic calorimeter of the CMS detector. The identification uses a multivariate technique based on compatibility between the calorimeter and tracking system information. The efficiency is determined using proton-proton collision data collected at a center-of-mass energy of 13 TeV containing boosted $ \mathrm{J}/\psi\rightarrow\mathrm{e^+e^-} $ decays or $ \mathrm{Z}\rightarrow\mu^+\mu^-\gamma $ events where the photon converts into a pair of collimated electrons. A dedicated energy correction for di-electron candidates is also developed using $ \mathrm{B^{\pm}}\rightarrow\mathrm{J}/\psi\mathrm{K^\pm}\rightarrow\mathrm{e^+e^-K^\pm} $ data. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
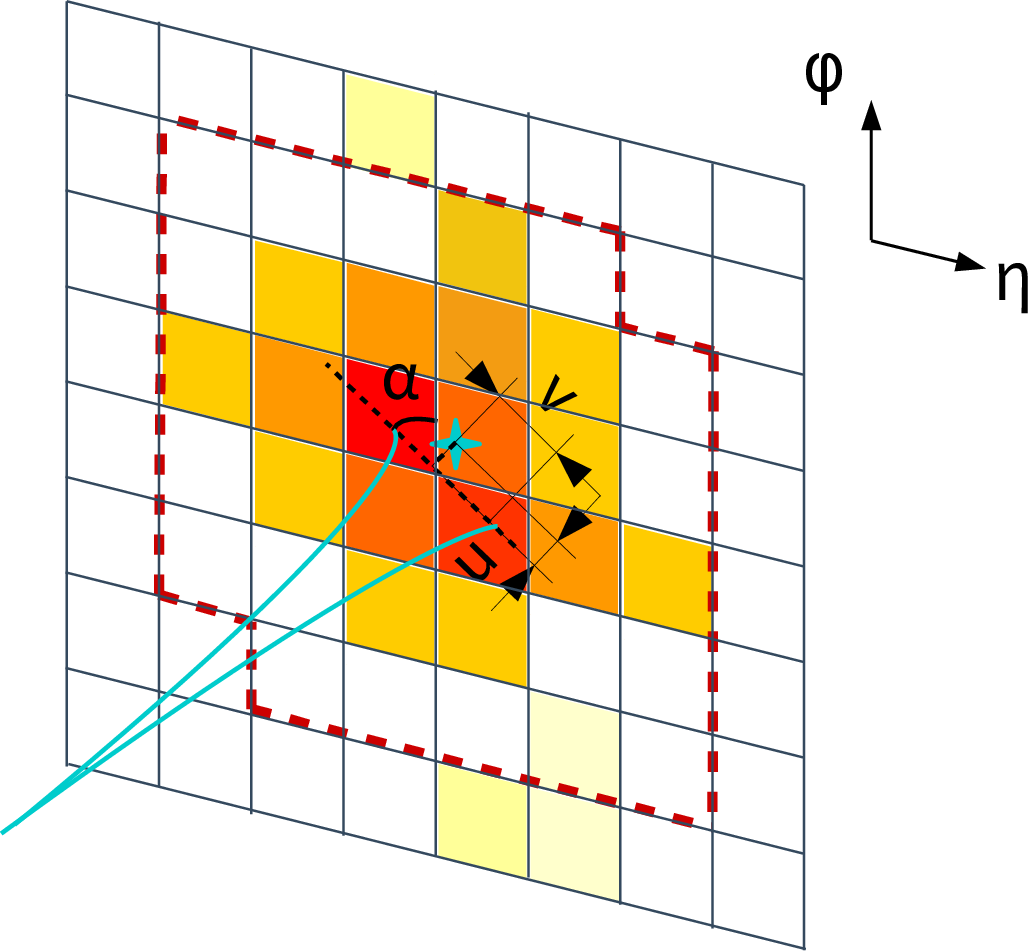
Figure 1:
Visual representations of the variable $ \alpha_{track} $, $ \Delta u_{in}^{5\times5} $ and $ \Delta v_{in}^{5\times5} $. Cyan-colored lines depict the incoming tracks of an electron pair. The Red dashed line represents the $ \textrm{U}_{5\times5} $ cluster around the closest crystal from the tracks. The cyan-colored star is the log-weighted CoG of the $ \textrm{U}_{5\times5} $ cluster. |
png pdf |
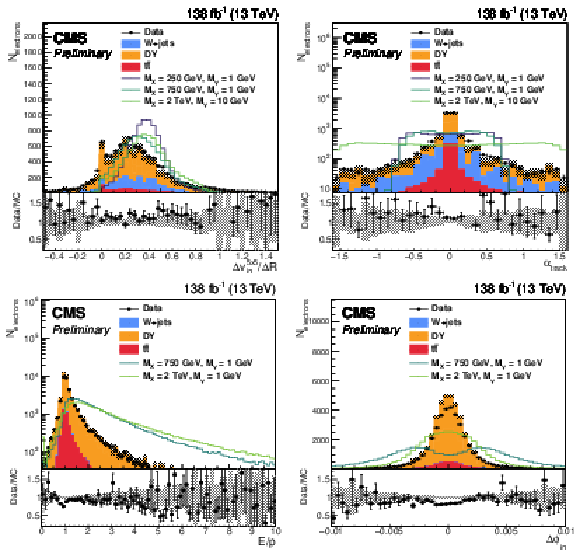
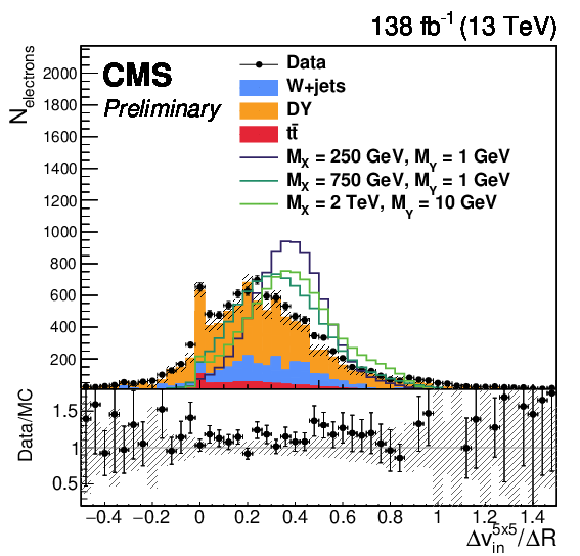
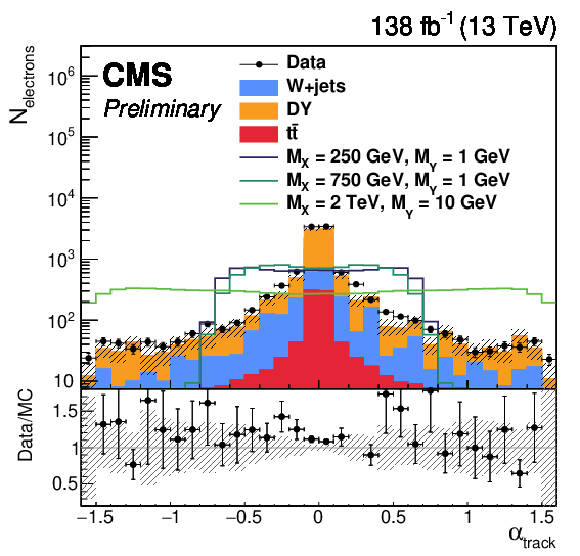
Figure 2:
The distribution of (upper left) $ \Delta v_{in}^{5\times5}/\Delta R $, (upper right) $ \alpha_{track} $, (lower left) $ E/p $, and (lower right) $ \Delta\phi_{in} $. The upper (lower) row shows distributions for the electrons with (without) an additional track. The shaded band represents statistical uncertainty of the MC. Each lined signal histogram is normalized to have an equal number of events to the total background yield. |
png pdf |
Figure 2-a:
The distribution of (upper left) $ \Delta v_{in}^{5\times5}/\Delta R $, (upper right) $ \alpha_{track} $, (lower left) $ E/p $, and (lower right) $ \Delta\phi_{in} $. The upper (lower) row shows distributions for the electrons with (without) an additional track. The shaded band represents statistical uncertainty of the MC. Each lined signal histogram is normalized to have an equal number of events to the total background yield. |
png pdf |
Figure 2-b:
The distribution of (upper left) $ \Delta v_{in}^{5\times5}/\Delta R $, (upper right) $ \alpha_{track} $, (lower left) $ E/p $, and (lower right) $ \Delta\phi_{in} $. The upper (lower) row shows distributions for the electrons with (without) an additional track. The shaded band represents statistical uncertainty of the MC. Each lined signal histogram is normalized to have an equal number of events to the total background yield. |
png pdf |
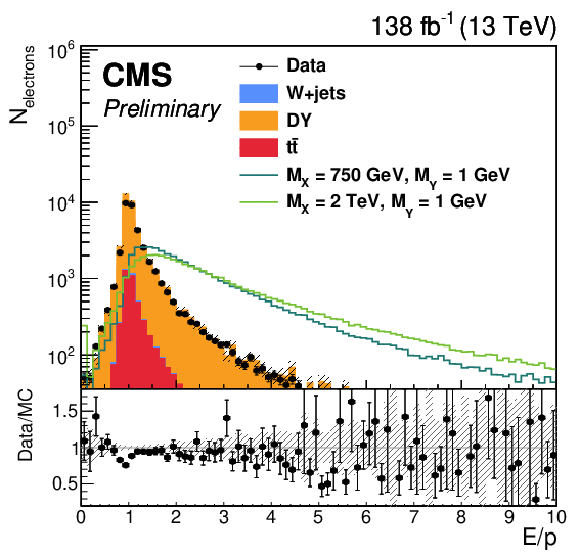
Figure 2-c:
The distribution of (upper left) $ \Delta v_{in}^{5\times5}/\Delta R $, (upper right) $ \alpha_{track} $, (lower left) $ E/p $, and (lower right) $ \Delta\phi_{in} $. The upper (lower) row shows distributions for the electrons with (without) an additional track. The shaded band represents statistical uncertainty of the MC. Each lined signal histogram is normalized to have an equal number of events to the total background yield. |
png pdf |
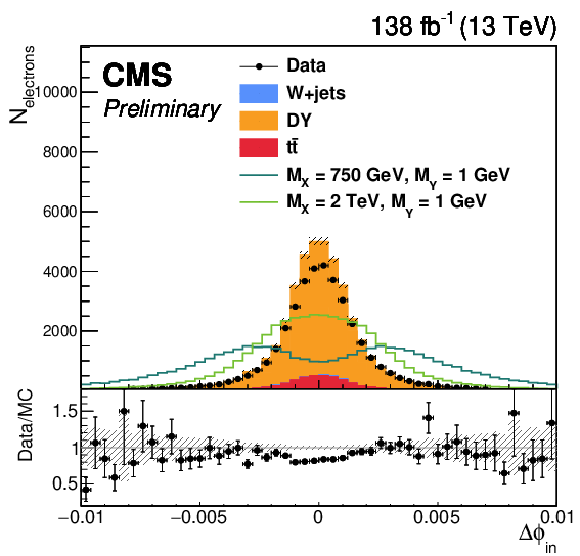
Figure 2-d:
The distribution of (upper left) $ \Delta v_{in}^{5\times5}/\Delta R $, (upper right) $ \alpha_{track} $, (lower left) $ E/p $, and (lower right) $ \Delta\phi_{in} $. The upper (lower) row shows distributions for the electrons with (without) an additional track. The shaded band represents statistical uncertainty of the MC. Each lined signal histogram is normalized to have an equal number of events to the total background yield. |
png pdf |
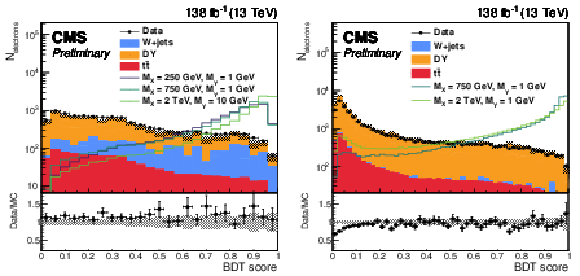
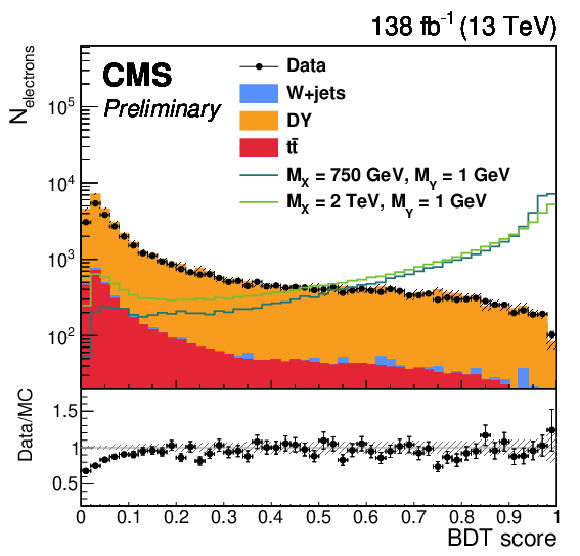
Figure 3:
The BDT score distributions of the model (left) with secondary tracks and (right) without any secondary track. The shaded band represents statistical uncertainty of the MC. Each lined signal histogram is normalized to have an equal number of events to the total background yield. |
png pdf |
Figure 3-a:
The BDT score distributions of the model (left) with secondary tracks and (right) without any secondary track. The shaded band represents statistical uncertainty of the MC. Each lined signal histogram is normalized to have an equal number of events to the total background yield. |
png pdf |
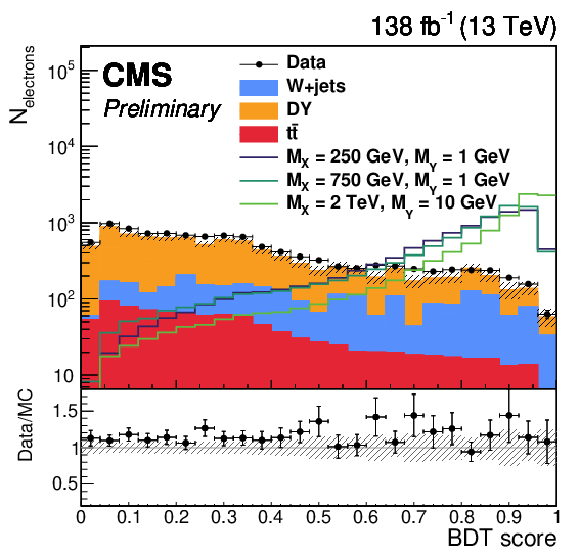
Figure 3-b:
The BDT score distributions of the model (left) with secondary tracks and (right) without any secondary track. The shaded band represents statistical uncertainty of the MC. Each lined signal histogram is normalized to have an equal number of events to the total background yield. |
png pdf |
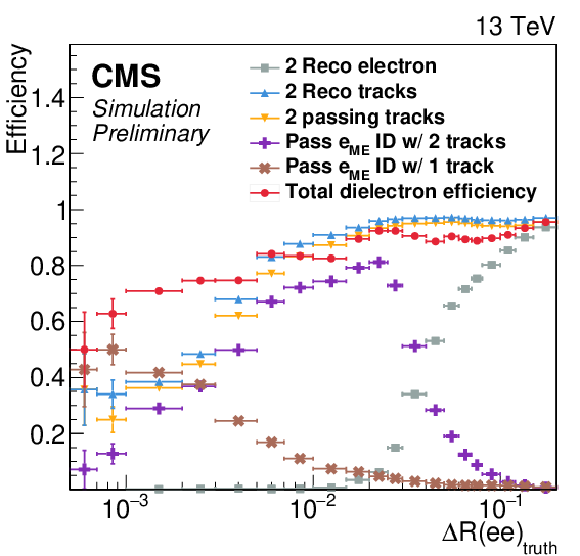
Figure 4:
The signal dielectron selection efficiency as a function of $ \Delta R $. The ID efficiencies incorporate the effects of all prerequisite selections. For instance, the $ \mathrm{e}_{\textrm{ME}} $ ID efficiency with two tracks (purple) includes the efficiency of the track selection described in Table 1 (yellow). The total dielectron efficiency is a sum of the $ \mathrm{e}_{\textrm{ME}} $ ID efficiency with two tracks (purple), one track (brown), and the standard reconstruction efficiency of two electrons (gray). |
png pdf |
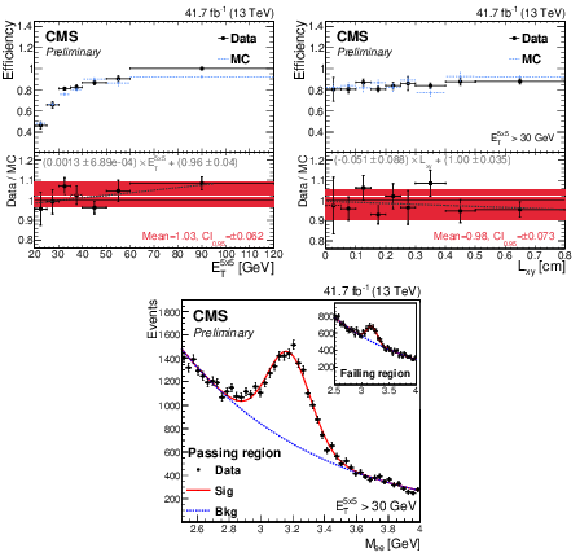
Figure 5:
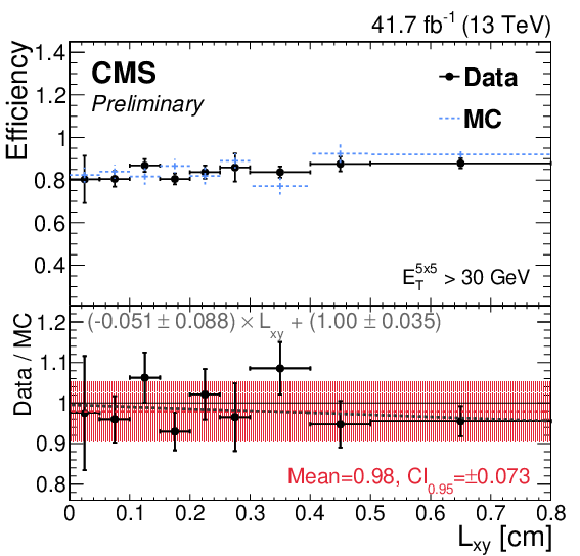
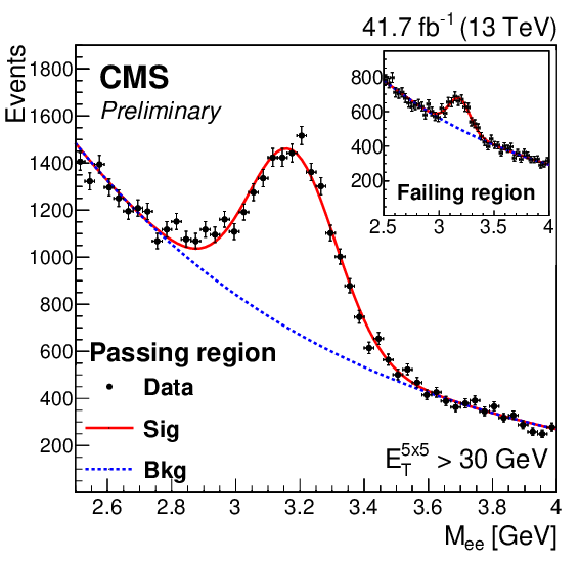
Efficiency and SF for the model with secondary tracks as a function of (upper left) $ E_{T}^{5\times5} $ and (upper right) $ L_{xy} $ with $ E_{\mathrm{T}}^{5\times5} > $ 30 GeV. The red and gray dashed lines depict the constant and first-order polynomial fit, respectively. (lower) The nominal dielectron mass distribution of $ \mathrm{J}/\psi $ candidates in data with $ {E_{\mathrm{T}}}^{5\times5} > $ 30 GeV that pass or fail the merged electron ID. The dielectron mass is reconstructed using tracks of electron candidates. |
png pdf |
Figure 5-a:
Efficiency and SF for the model with secondary tracks as a function of (upper left) $ E_{T}^{5\times5} $ and (upper right) $ L_{xy} $ with $ E_{\mathrm{T}}^{5\times5} > $ 30 GeV. The red and gray dashed lines depict the constant and first-order polynomial fit, respectively. (lower) The nominal dielectron mass distribution of $ \mathrm{J}/\psi $ candidates in data with $ {E_{\mathrm{T}}}^{5\times5} > $ 30 GeV that pass or fail the merged electron ID. The dielectron mass is reconstructed using tracks of electron candidates. |
png pdf |
Figure 5-b:
Efficiency and SF for the model with secondary tracks as a function of (upper left) $ E_{T}^{5\times5} $ and (upper right) $ L_{xy} $ with $ E_{\mathrm{T}}^{5\times5} > $ 30 GeV. The red and gray dashed lines depict the constant and first-order polynomial fit, respectively. (lower) The nominal dielectron mass distribution of $ \mathrm{J}/\psi $ candidates in data with $ {E_{\mathrm{T}}}^{5\times5} > $ 30 GeV that pass or fail the merged electron ID. The dielectron mass is reconstructed using tracks of electron candidates. |
png pdf |
Figure 5-c:
Efficiency and SF for the model with secondary tracks as a function of (upper left) $ E_{T}^{5\times5} $ and (upper right) $ L_{xy} $ with $ E_{\mathrm{T}}^{5\times5} > $ 30 GeV. The red and gray dashed lines depict the constant and first-order polynomial fit, respectively. (lower) The nominal dielectron mass distribution of $ \mathrm{J}/\psi $ candidates in data with $ {E_{\mathrm{T}}}^{5\times5} > $ 30 GeV that pass or fail the merged electron ID. The dielectron mass is reconstructed using tracks of electron candidates. |
png pdf |
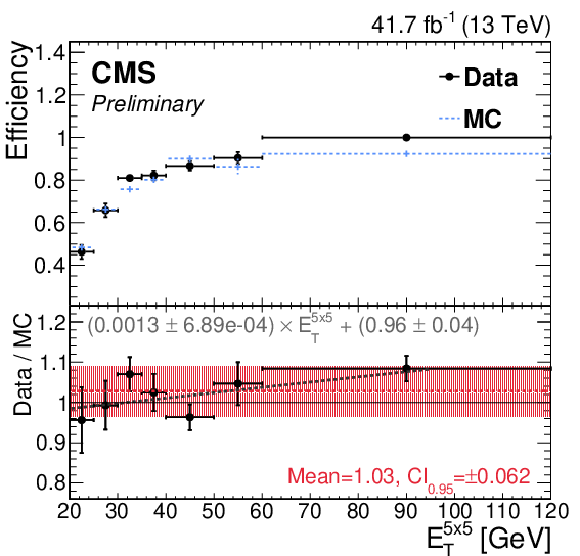
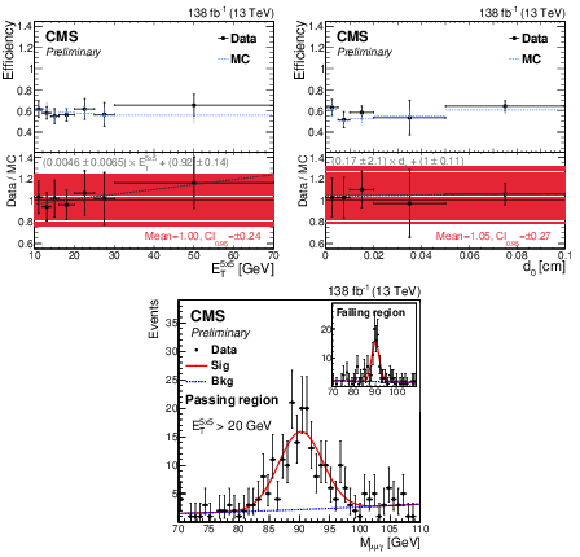
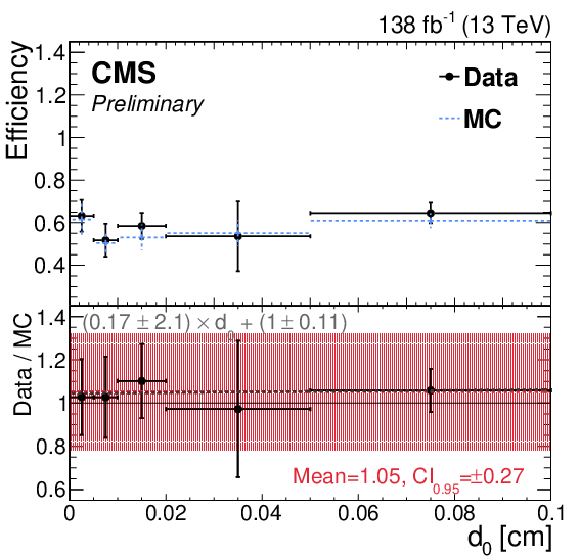
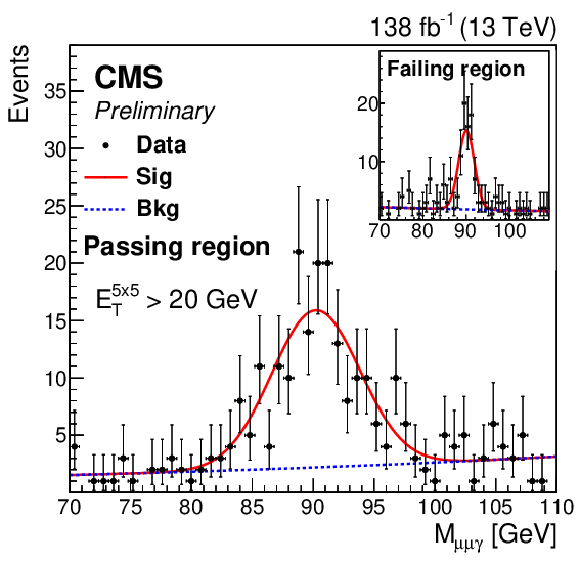
Figure 6:
Efficiency and SF as a function of (upper left) $ {E_{\mathrm{T}}}^{5\times5} $ and (upper right) $ d_{0} $ for the model without secondary tracks. The red and gray dashed lines depict the constant and first-order polynomial fit, respectively. (lower) The nominal Z boson candidate mass distribution in data using $ \mu\mu\gamma $ events with $ {E_{\mathrm{T}}}^{5\times 5} > $ 20 GeV. The passing and failing regions represent the Z boson candidate mass distributions with $ \mathrm{e}_{\mathrm{ME}} $ candidates that pass or fail the $ \mathrm{e}_{\mathrm{ME}} $ ID. |
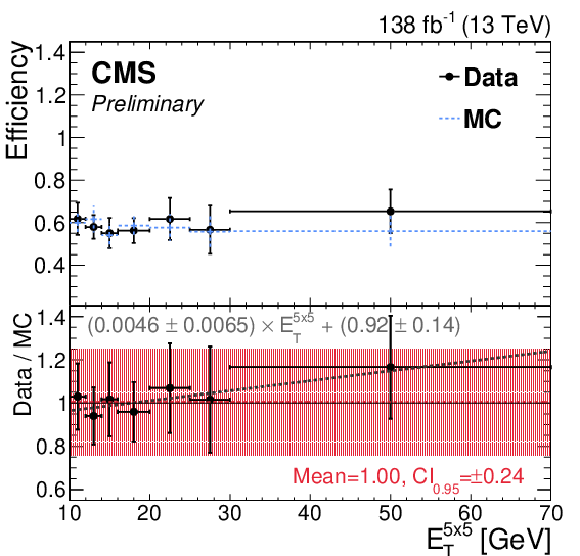
png pdf |
Figure 6-a:
Efficiency and SF as a function of (upper left) $ {E_{\mathrm{T}}}^{5\times5} $ and (upper right) $ d_{0} $ for the model without secondary tracks. The red and gray dashed lines depict the constant and first-order polynomial fit, respectively. (lower) The nominal Z boson candidate mass distribution in data using $ \mu\mu\gamma $ events with $ {E_{\mathrm{T}}}^{5\times 5} > $ 20 GeV. The passing and failing regions represent the Z boson candidate mass distributions with $ \mathrm{e}_{\mathrm{ME}} $ candidates that pass or fail the $ \mathrm{e}_{\mathrm{ME}} $ ID. |
png pdf |
Figure 6-b:
Efficiency and SF as a function of (upper left) $ {E_{\mathrm{T}}}^{5\times5} $ and (upper right) $ d_{0} $ for the model without secondary tracks. The red and gray dashed lines depict the constant and first-order polynomial fit, respectively. (lower) The nominal Z boson candidate mass distribution in data using $ \mu\mu\gamma $ events with $ {E_{\mathrm{T}}}^{5\times 5} > $ 20 GeV. The passing and failing regions represent the Z boson candidate mass distributions with $ \mathrm{e}_{\mathrm{ME}} $ candidates that pass or fail the $ \mathrm{e}_{\mathrm{ME}} $ ID. |
png pdf |
Figure 6-c:
Efficiency and SF as a function of (upper left) $ {E_{\mathrm{T}}}^{5\times5} $ and (upper right) $ d_{0} $ for the model without secondary tracks. The red and gray dashed lines depict the constant and first-order polynomial fit, respectively. (lower) The nominal Z boson candidate mass distribution in data using $ \mu\mu\gamma $ events with $ {E_{\mathrm{T}}}^{5\times 5} > $ 20 GeV. The passing and failing regions represent the Z boson candidate mass distributions with $ \mathrm{e}_{\mathrm{ME}} $ candidates that pass or fail the $ \mathrm{e}_{\mathrm{ME}} $ ID. |
png pdf |
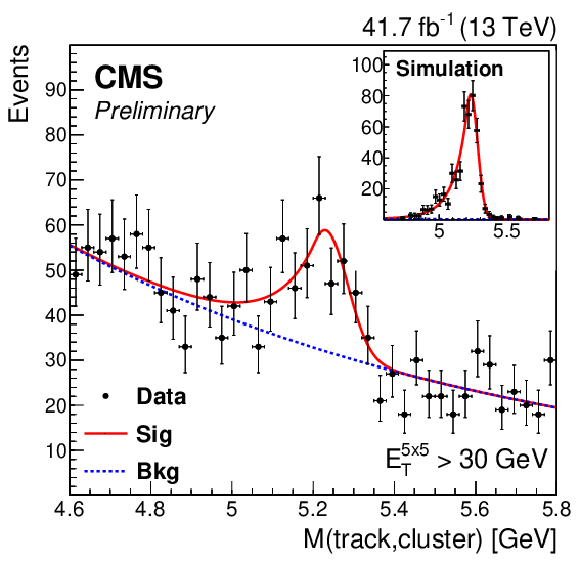
Figure 7:
The invariant mass distribution between the $ \textrm{U}_{5\times5} $ cluster and the kaon candidate with $ {E_{\mathrm{T}}}^{5\times5} > $ 30 GeV. The signal (background) contribution is modeled with a Crystal ball (exponential) function, represented with a red (blue) line. The subfigure on top right illustrates the distribution with a $ {\mathrm{B}^{\pm}}\rightarrow\mathrm{J}/\psi\mathrm{K^{\pm}}\rightarrow\mathrm{e}^+\mathrm{e}^-\mathrm{K^{\pm}} $ MC sample. |
| Tables | |

png pdf |
Table 1:
Secondary track selection criteria |

png pdf |
Table 2:
List of variables used to train the model with secondary tracks |

png pdf |
Table 3:
List of variables used to train the model without secondary tracks |
png pdf |
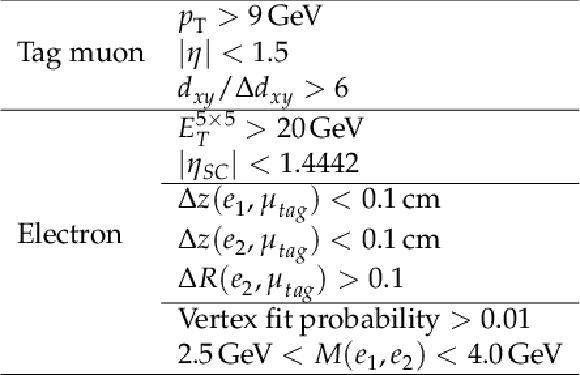
Table 4:
Selection criteria for $ \mathrm{J}/\psi\rightarrow\mathrm{e}^+\mathrm{e}^- $ control region. |

png pdf |
Table 5:
Selection criteria for the $ \mathrm{Z}\rightarrow\mu\mu\gamma $ control region. |

png pdf |
Table 6:
Selection criteria (in addition to Table 4) for the $ {\mathrm{B}^{\pm}}\rightarrow\mathrm{J}/\psi\mathrm{K^{\pm}}\rightarrow\mathrm{e}^+\mathrm{e}^-\mathrm{K^{\pm}} $ control region. |
| Summary |
| A number of BSM models predict light bosons that subsequently decay into a pair of leptons. In such models, the light boson can be significantly boosted, and the standard clustering and reconstruction algorithm may fail to resolve the electron pair. Moreover, a further Lorentz boost can lead to the absence of either of the electron tracks due to shared hits in the inner tracker. Therefore, a novel algorithm is developed to identify highly boosted electron pairs under the hypothesis of extreme Lorentz boosts with a merged cluster or cleaned inner track. The algorithm is trained using a BDT based on the compatibility between the merged cluster and electron tracks. The ID efficiency is validated using boosted $ \mathrm{J}/\psi\rightarrow\mathrm{e}^+\mathrm{e}^- $ decays in data for the model with secondary tracks. The overall efficiency is about 90% for $ {E_{\mathrm{T}}}^{5\times5} > $ 50 GeV. For the model without secondary tracks, $ \mathrm{Z}\rightarrow\mu\mu\gamma $ events with converted photons are used to validate the efficiency in data, which is approximately 60%. Due to the incapability of capturing all energy deposits from $ \mathrm{e}_{\mathrm{ME}} $ candidates, the $ \textrm{U}_{5\times5} $ cluster is used to estimate the energy of the $ \mathrm{e}_{\mathrm{ME}} $ instead of the SC. The $ \mathrm{U}_{5\times5} $ cluster's energy scale and resolution in data are measured with $ {\mathrm{B}^{\pm}}\rightarrow\mathrm{J}/\psi\mathrm{K^{\pm}}\rightarrow\mathrm{e}^+\mathrm{e}^-\mathrm{K^{\pm}} $ decays by reconstructing invariant mass between the $ \mathrm{U}_{5\times5} $ cluster and a track. A dedicated energy correction for the $ \mathrm{U}_{5\times5} $ cluster is also derived to match the energy description of the simulation to that of the data. |
| References | ||||
| 1 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |
| 2 | V. Barger and H.-S. Lee | Four-lepton resonance at the Large Hadron Collider | PRD 85 (2012) 055030 | |
| 3 | G. C. Branco et al. | Theory and phenomenology of two-higgs-doublet models | Physics Reports 516 (2012) 1 | |
| 4 | D. Curtin, R. Essig, S. Gori, and J. Shelton | Illuminating dark photons with high-energy colliders | JHEP 15 (2015) 157 | |
| 5 | ATLAS Collaboration | A search for new resonances in multiple final states with a high transverse momentum z boson in $ \sqrt{s} = $ 13 TeV pp collisions with the atlas detector | JHEP 23 (2023) 36 | |
| 6 | CMS Collaboration | Reconstruction of decays to merged photons using end-to-end deep learning with domain continuation in the CMS detector | PRD 108 (2023) 052002 | |
| 7 | CMS Collaboration | Search for new resonances decaying to pairs of merged diphotons in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PRL 134 (2025) 041801 | |
| 8 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 9 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 10 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 11 | CMS Tracker Group Collaboration | The CMS phase-1 pixel detector upgrade | JINST 16 (2021) P02027 | 2012.14304 |
| 12 | CMS Collaboration | Track impact parameter resolution for the full pseudo rapidity coverage in the 2017 dataset with the CMS phase-1 pixel detector | CMS Detector Performance Summary CMS-DP-2020-049, 2020 CDS |
|
| 13 | CMS Collaboration | 2017 tracking performance plots | CMS Detector Performance Summary CMS-DP-2017-015, 2017 CDS |
|
| 14 | CMS Collaboration | ECAL 2016 refined calibration and Run2 summary plots | CMS Detector Performance Summary CMS-DP-2020-021, 2020 CDS |
|
| 15 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13\,TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 16 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 17 | T. Sjöstrand et al. | An introduction to PYTHIA 8.2 | Computer Physics Communications 191 (2015) 159 | |
| 18 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 14 (2014) 79 | |
| 19 | D. J. Lange | The EvtGen particle decay simulation package | NIMA 462 (2001) 152 | |
| 20 | P. F. Monni et al. | MiNNLO$ _{PS} $: a new method to match NNLO QCD to parton showers | JHEP 05 (2020) 143 | 1908.06987 |
| 21 | P. F. Monni, E. Re, and M. Wiesemann | MiNNLO$ _{\text {PS}} $: optimizing 2 $ \rightarrow $ 1 hadronic processes | no. 11, 2020 EPJC 80 (2020) 1075 |
2006.04133 |
| 22 | E. Barberio and Z. Was | PHOTOS: A Universal Monte Carlo for QED radiative corrections. Version 2.0 | Comput. Phys. Commun. 79 (1994) 291 | |
| 23 | CMS Collaboration | Extraction and validation of a new set of cms pythia8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | |
| 24 | R. D. Ball et al. | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | |
| 25 | S. Agostinelli et al. | Geant4-a simulation toolkit | NIM A 506 (2003) 250 | |
| 26 | W. Adam, R. Frühwirth, A. Strandlie, and T. Todorov | Reconstruction of electrons with the Gaussian-sum filter in the CMS tracker at the LHC | J. Phys. G: Nucl. Part. Phys. 31 (2005) N9 | |
| 27 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s}= $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 28 | CMS Collaboration | CMS luminosity measurement for the 2017 data-taking period at $ \sqrt{s}= $ 13 TeV | CMS Physics Analysis Summary, 2018 CMS-PAS-LUM-17-004 |
CMS-PAS-LUM-17-004 |
| 29 | CMS Collaboration | CMS luminosity measurement for the 2018 data-taking period at $ \sqrt{s}= $ 13 TeV | CMS Physics Analysis Summary, 2019 CMS-PAS-LUM-18-002 |
CMS-PAS-LUM-18-002 |
| 30 | T. Chen and C. Guestrin | XGBoost: A scalable tree boosting system | in Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD '16, . ACM, New York, NY, USA, 2016 link |
|
| 31 | CMS Collaboration | Recording and reconstructing 10 billion unbiased $ {\mathrm{B}} $ hadron decays in CMS | CMS Detector Performance Summaries CMS-DP-2019-043, 2019 CDS |
|
| 32 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 33 | CMS Collaboration | Performance of the cms muon trigger system in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 16 (2021) P07001 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|