

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-TOP-21-008 | ||
| Measurement of the top quark pole mass using $\text{t}\overline{\text{t}}$+jet events in the dilepton final state at $\sqrt{s}=$ 13 TeV | ||
| CMS Collaboration | ||
| March 2022 | ||
| Abstract: A measurement of the top quark pole mass $m_{\text{t}}^{\text{pole}}$ in events where a top quark-antiquark pair ($\text{t}\overline{\text{t}}$) is produced in association with one additional jet ($\text{t}\overline{\text{t}}$+jet) is presented. This analysis is performed using proton-proton collision data at $\sqrt{s}=$ 13 TeV collected by the CMS experiment at the CERN LHC, corresponding to a total integrated luminosity of 36.3fb$^{-1}$. Events with two opposite charge leptons in the final state ($\text{e}^{+}\text{e}^{-}$, $\mu^{+}\mu^{-}$, $\text{e}^{\pm}\mu^{\mp}$) are analyzed. Using multivariate analysis techniques based on machine learning, the reconstruction of the main observable and the event selection are optimized. The production cross section is measured as a function of the inverse invariant mass of the $\text{t}\overline{\text{t}}$+jet system at the parton level, using a maximum likelihood unfolding. The top quark pole mass is extracted using the theory predictions at next-to-leading order, resulting in $m_{\text{t}}^{\text{pole}}=$ 172.94 $\pm$ 1.37 GeV when using the ABMP16NLO parton distribution functions. | ||
|
Links:
CDS record (PDF) ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, Submitted to JHEP. The superseded preliminary plots can be found here. |
||
| Figures | |

png pdf |
Figure 1:
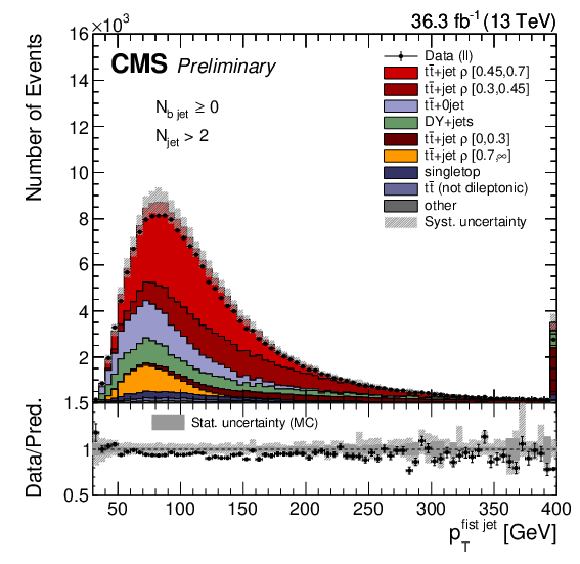
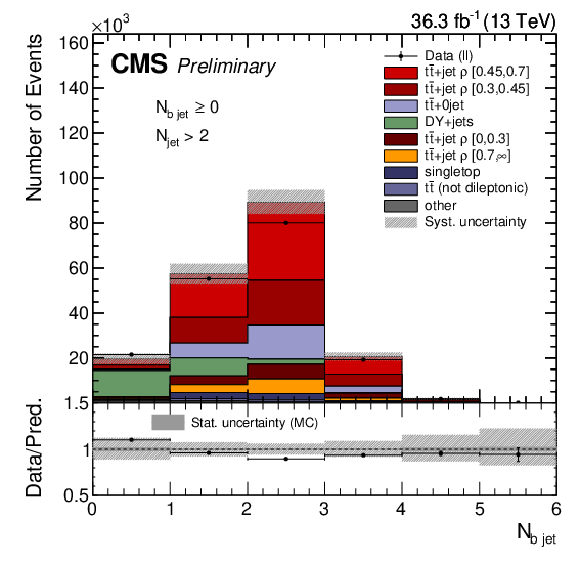
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the number of leading (upper left) and trailing (upper middle) lepton ${p_{\mathrm {T}}}$, leading (upper right) and third hardest (lower left) jet ${p_{\mathrm {T}}}$, the jet multiplicity (lower middle), and b tagged jet multiplicity (lower right), after applying the signal selection. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |

png pdf |
Figure 1-a:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the number of leading (upper left) and trailing (upper middle) lepton ${p_{\mathrm {T}}}$, leading (upper right) and third hardest (lower left) jet ${p_{\mathrm {T}}}$, the jet multiplicity (lower middle), and b tagged jet multiplicity (lower right), after applying the signal selection. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |
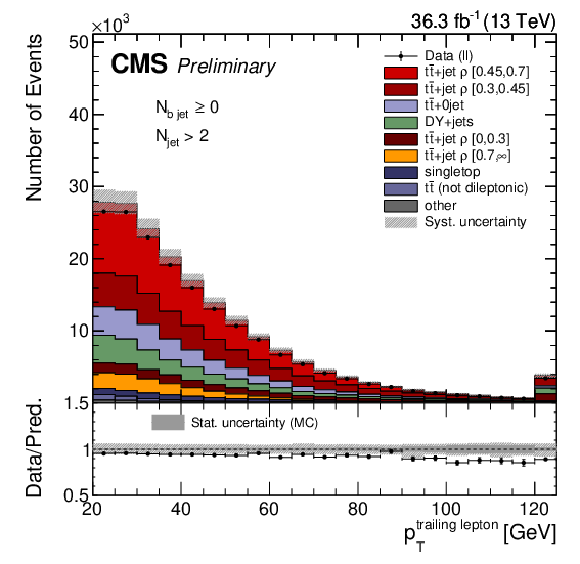
png pdf |
Figure 1-b:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the number of leading (upper left) and trailing (upper middle) lepton ${p_{\mathrm {T}}}$, leading (upper right) and third hardest (lower left) jet ${p_{\mathrm {T}}}$, the jet multiplicity (lower middle), and b tagged jet multiplicity (lower right), after applying the signal selection. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |
png pdf |
Figure 1-c:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the number of leading (upper left) and trailing (upper middle) lepton ${p_{\mathrm {T}}}$, leading (upper right) and third hardest (lower left) jet ${p_{\mathrm {T}}}$, the jet multiplicity (lower middle), and b tagged jet multiplicity (lower right), after applying the signal selection. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |

png pdf |
Figure 1-d:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the number of leading (upper left) and trailing (upper middle) lepton ${p_{\mathrm {T}}}$, leading (upper right) and third hardest (lower left) jet ${p_{\mathrm {T}}}$, the jet multiplicity (lower middle), and b tagged jet multiplicity (lower right), after applying the signal selection. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |

png pdf |
Figure 1-e:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the number of leading (upper left) and trailing (upper middle) lepton ${p_{\mathrm {T}}}$, leading (upper right) and third hardest (lower left) jet ${p_{\mathrm {T}}}$, the jet multiplicity (lower middle), and b tagged jet multiplicity (lower right), after applying the signal selection. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |
png pdf |
Figure 1-f:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the number of leading (upper left) and trailing (upper middle) lepton ${p_{\mathrm {T}}}$, leading (upper right) and third hardest (lower left) jet ${p_{\mathrm {T}}}$, the jet multiplicity (lower middle), and b tagged jet multiplicity (lower right), after applying the signal selection. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |

png pdf |
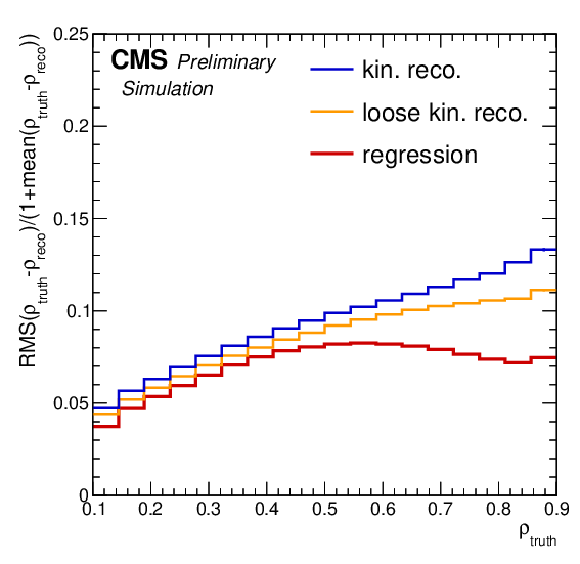
Figure 2:
The correlation between $\rho _{\text {true}}$ and $\rho _{\text {reco}}$ is shown for the regression NN reconstruction method (left). The distribution of the response corrected RMS (right) of $\rho _{\text {true}}-\rho _{\text {reco}}$ versus $\rho _{\text {true}}$ is shown, compared for the kinematic reconstruction (blue), the loose kinematic reconstruction (orange), and the regression NN (red). |
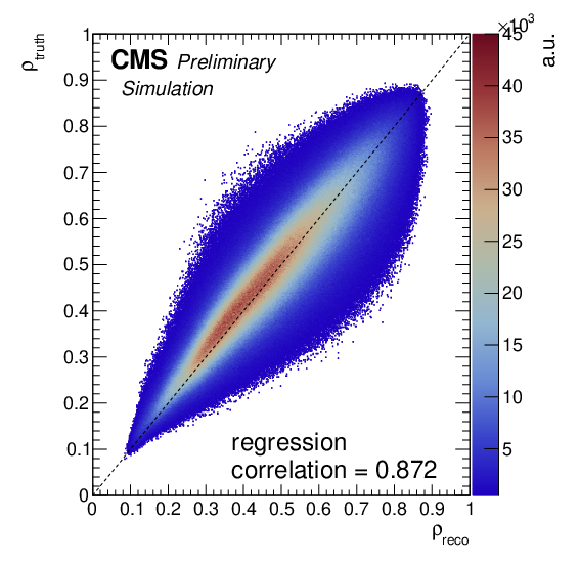
png pdf |
Figure 2-a:
The correlation between $\rho _{\text {true}}$ and $\rho _{\text {reco}}$ is shown for the regression NN reconstruction method (left). The distribution of the response corrected RMS (right) of $\rho _{\text {true}}-\rho _{\text {reco}}$ versus $\rho _{\text {true}}$ is shown, compared for the kinematic reconstruction (blue), the loose kinematic reconstruction (orange), and the regression NN (red). |
png pdf |
Figure 2-b:
The correlation between $\rho _{\text {true}}$ and $\rho _{\text {reco}}$ is shown for the regression NN reconstruction method (left). The distribution of the response corrected RMS (right) of $\rho _{\text {true}}-\rho _{\text {reco}}$ versus $\rho _{\text {true}}$ is shown, compared for the kinematic reconstruction (blue), the loose kinematic reconstruction (orange), and the regression NN (red). |
png pdf |
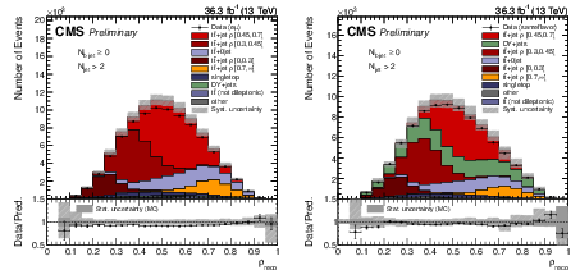
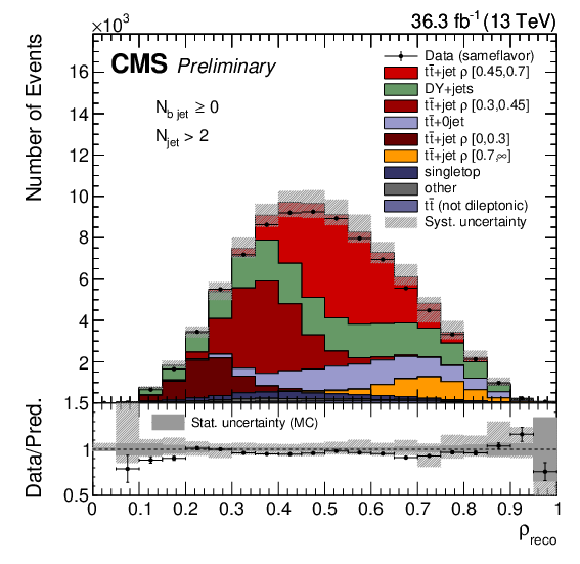
Figure 3:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function $\rho $ as reconstructed by the NN reconstruction method for the $\mathrm{e^{\pm}} {\mu ^\mp} $ (left) and same flavor channels (right). The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |

png pdf |
Figure 3-a:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function $\rho $ as reconstructed by the NN reconstruction method for the $\mathrm{e^{\pm}} {\mu ^\mp} $ (left) and same flavor channels (right). The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |
png pdf |
Figure 3-b:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function $\rho $ as reconstructed by the NN reconstruction method for the $\mathrm{e^{\pm}} {\mu ^\mp} $ (left) and same flavor channels (right). The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |
png pdf |
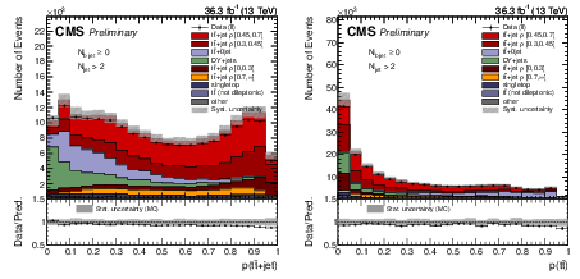
Figure 4:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the signal (left) and $\mathrm{t\bar{t}}$+jet background (right) output node probability of the classifier NN. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |

png pdf |
Figure 4-a:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the signal (left) and $\mathrm{t\bar{t}}$+jet background (right) output node probability of the classifier NN. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |

png pdf |
Figure 4-b:
The observed (points) and the predicted (stacked histograms) signal and background yields as a function of the signal (left) and $\mathrm{t\bar{t}}$+jet background (right) output node probability of the classifier NN. The shaded area indicates the total uncertainties on the signal and total background, while the dark gray area represents the statistical uncertainty from the limited amount of events simulated. |
png pdf |
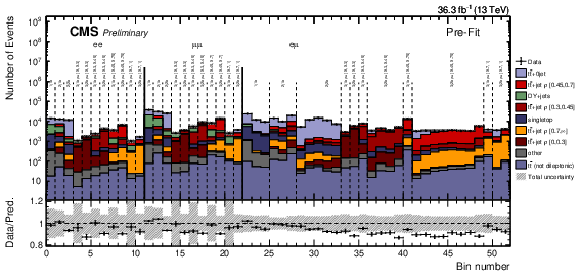
Figure 5:
Comparison between data (points) and pre-fit distributions of the expected signal and backgrounds from simulation (histograms) used in the simultaneous fit. The hatched bands corresponds to the total uncertainty. |
png pdf |
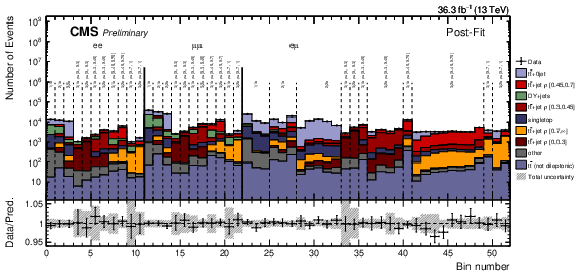
Figure 6:
Comparison between data (points) and post-fit distributions of the expected signal and backgrounds from simulation (histograms) used in the simultaneous fit. The hatched bands corresponds to the total uncertainty. |

png pdf |
Figure 7:
Post-fit pull of the nuisance parameters as well as their impacts on the signal strengths $r_k$, ordered by their relative summed impact. Only the 30 highest ranked parameters are shown. The pulls of the nuisance parameters (black markers) are computed relative to their pre-fit values $\theta _0$ and uncertainties $\Delta \theta $. The impact $\Delta r_{k}$ are computed as the difference of the nominal best fit value of $r_k$ and the best fit value obtained when fixing the nuisance parameter under scrutiny to its bestfit value $\hat{\theta}$ plus/minus its post-fit uncertainty (colored areas). The shaded areas correspond to the expected pulls, constraints, and impacts. |
png pdf |
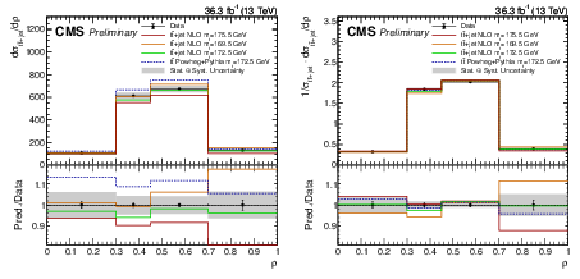
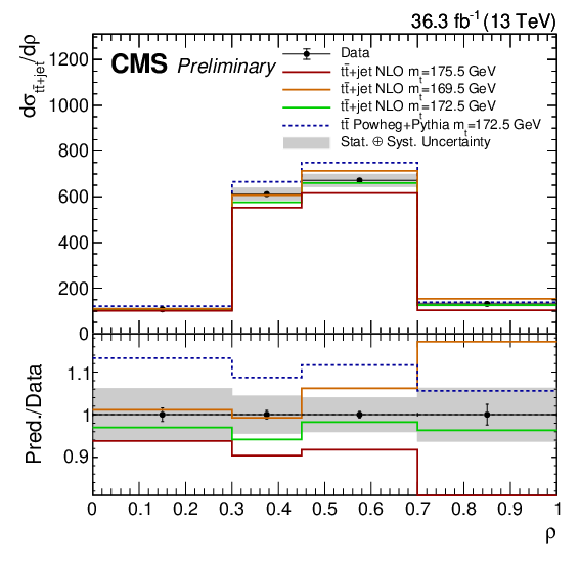
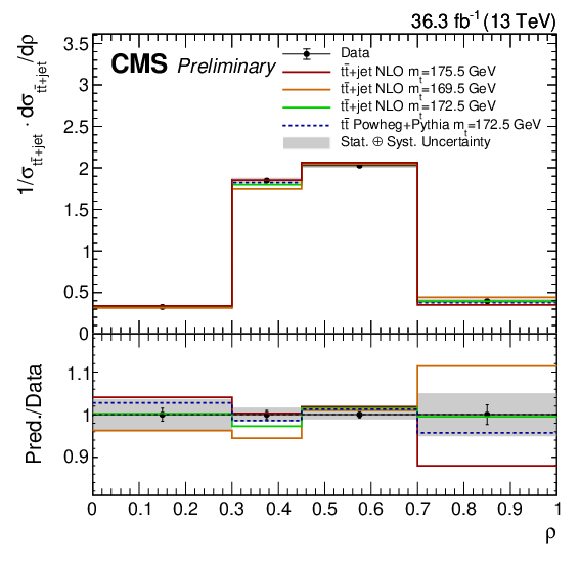
Figure 8:
The absolute (left) and normalized (right) differential cross section as a function of $\rho $. The gray bands correspond to the total uncertainty, while the errors of the data points correspond to the statistical only uncertainty. The blue line shows the expected result using the nominal POWHEG+PYTHIA-8 simulation, while the red, orange, and green lines correspond to the expectation from NLO fixed order theory prediction for top mass assumptions of 169.5, 172.5, and 175.5 GeV, respectively. |
png pdf |
Figure 8-a:
The absolute (left) and normalized (right) differential cross section as a function of $\rho $. The gray bands correspond to the total uncertainty, while the errors of the data points correspond to the statistical only uncertainty. The blue line shows the expected result using the nominal POWHEG+PYTHIA-8 simulation, while the red, orange, and green lines correspond to the expectation from NLO fixed order theory prediction for top mass assumptions of 169.5, 172.5, and 175.5 GeV, respectively. |
png pdf |
Figure 8-b:
The absolute (left) and normalized (right) differential cross section as a function of $\rho $. The gray bands correspond to the total uncertainty, while the errors of the data points correspond to the statistical only uncertainty. The blue line shows the expected result using the nominal POWHEG+PYTHIA-8 simulation, while the red, orange, and green lines correspond to the expectation from NLO fixed order theory prediction for top mass assumptions of 169.5, 172.5, and 175.5 GeV, respectively. |
png pdf |
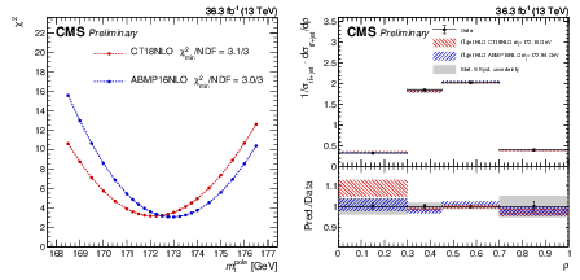
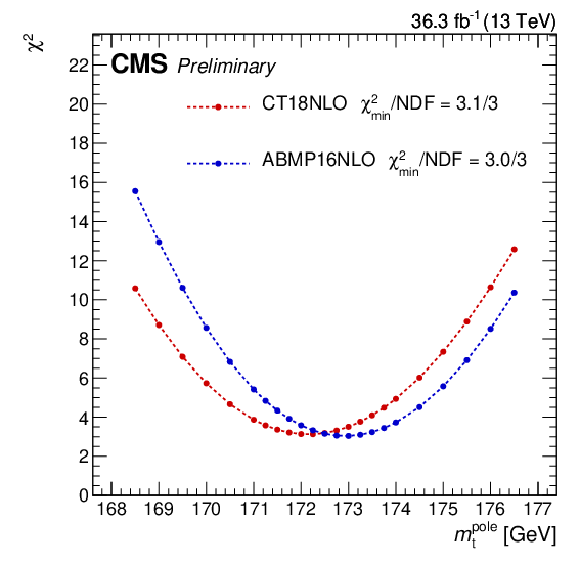
Figure 9:
Left: ${\chi ^2}$ fit of the top quark pole mass using the measured normalized differential cross section and NLO fixed order theory prediction using the ABMP16NLO (blue) and the CT18NLO PDF set (red) The ${\chi ^2}$ values at the minimum are given divided by the number of degrees of freedom (NDF). Right: The normalized differential cross section as a function of $\rho $, same as in Fig. 8, compared to predictions for top quark pole mass values as determined in the ${\chi ^2}$ fit including scale and PDF uncertainties (hatched bands). The gray bands correspond to the total fit uncertainty. |
png pdf |
Figure 9-a:
Left: ${\chi ^2}$ fit of the top quark pole mass using the measured normalized differential cross section and NLO fixed order theory prediction using the ABMP16NLO (blue) and the CT18NLO PDF set (red) The ${\chi ^2}$ values at the minimum are given divided by the number of degrees of freedom (NDF). Right: The normalized differential cross section as a function of $\rho $, same as in Fig. 8, compared to predictions for top quark pole mass values as determined in the ${\chi ^2}$ fit including scale and PDF uncertainties (hatched bands). The gray bands correspond to the total fit uncertainty. |

png pdf |
Figure 9-b:
Left: ${\chi ^2}$ fit of the top quark pole mass using the measured normalized differential cross section and NLO fixed order theory prediction using the ABMP16NLO (blue) and the CT18NLO PDF set (red) The ${\chi ^2}$ values at the minimum are given divided by the number of degrees of freedom (NDF). Right: The normalized differential cross section as a function of $\rho $, same as in Fig. 8, compared to predictions for top quark pole mass values as determined in the ${\chi ^2}$ fit including scale and PDF uncertainties (hatched bands). The gray bands correspond to the total fit uncertainty. |
| Tables | |

png pdf |
Table 1:
Overview about categories and distributions implemented in the maximum likelihood fit. The symbol ${R_{\text {NN}}}$ is defined as $ R_{\text {NN}} = {p({\mathrm{t\bar{t}}\text{+jet})}}/{[p({\mathrm{t\bar{t}}\text{+jet})+p({\mathrm{t\bar{t}}+jet)}}]} $. |

png pdf |
Table 2:
The relative uncertainties on the parton-level cross section values $\sigma _{\mathrm{t\bar{t}}\text{+jet}}^{k}$ and their sources. The statistical uncertainty is evaluated by keeping all nuisance parameters fixed to their post-fit values. All other quoted uncertainties are obtained by fixing all but the listed sources of uncertainties to their post-fit values and subtracting the result quadratically from a fit with all nuisance parameters fixed to their post-fit values. The quadratic sum of the contributions varies from the total uncertainty because of correlations between the nuisance parameters. |
| Summary |
| In this note, a measurement of the normalized differential cross section of top quark-antiquark pair ($\mathrm{t\bar{t}}$) production in association with at least one additional jet as a function of the inverse invariant mass of the $\mathrm{t\bar{t}}$+jet system $\rho=m_0/m_{\mathrm{t\bar{t}}\text{+jet}}$, with $m_0 = $ 170 GeV, is presented. Proton-proton collision data collected by the CMS experiment at the CERN LHC at a center-of-mass energy of 13 TeV are used, corresponding to an integrated luminosity of 36.3 fb$^{-1}$. Events in the dileptonic decay channel are considered, and a novel multivariate analysis technique is applied to maximize the sensitivity to the signal process. The measured differential cross section is unfolded to the parton level by using a maximum likelihood fit to final-state observables, where all systematic uncertainties are profiled. From a comparison to next-to-leading order prediction in quantum chromodynamics in the pole mass renormalization scheme, the top quark pole mass is extracted using two sets of parton distribution functions. Dynamical scales are used here for the first time for the $\mathrm{t\bar{t}}$+jet process, and the top quark pole mass is determined to be ${m_{\mathrm{t}}^{\text{pole}}} = $ 172.94$^{+1.37}_{-1.34}$ GeV using the ABMP16NLO PDF set, and ${m_{\mathrm{t}}^{\text{pole}}} = $ 172.16$^{+1.44}_{-1.41}$ GeV using the CT18NLO PDF set. |
| References | ||||
| 1 | G. Degrassi et al. | Higgs mass and vacuum stability in the standard model at NNLO | JHEP 08 (2012) 098 | 1205.6497 |
| 2 | S. Alekhin, A. Djouadi, and S. Moch | The top quark and Higgs boson masses and the stability of the electroweak vacuum | PLB 716 (2012) 214 | 1207.0980 |
| 3 | Gfitter Group Collaboration | The global electroweak fit at NNLO and prospects for the LHC and ILC | EPJC 74 (2014) 3046 | 1407.3792 |
| 4 | J. de Blas et al. | Electroweak precision observables and Higgs-boson signal strengths in the standard model and beyond: present and future | JHEP 12 (2016) 135 | 1608.01509 |
| 5 | S. Alekhin, J. Blumlein, S. Moch, and R. Placakyte | Parton distribution functions, $ {\alpha_S}, $ and heavy-quark masses for LHC Run II | PRD 96 (2017) 014011 | 1701.05838 |
| 6 | Particle Data Group Collaboration | Review of particle physics | PTEP 2020 (2020) 083C01 | |
| 7 | ATLAS Collaboration | Measurement of the top quark mass in the $ \mathrm{t\bar{t}}\to $ dilepton channel from $ \sqrt{s}= $ 8 TeV ATLAS data | PLB 761 (2016) 350 | 1606.02179 |
| 8 | ATLAS Collaboration | Top-quark mass measurement in the all-hadronic $ \mathrm{t\bar{t}} $ decay channel at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | JHEP 09 (2017) 118 | 1702.07546 |
| 9 | ATLAS Collaboration | Measurement of the top quark mass in the $ \mathrm{t\bar{t}}\to $ lepton+jets channel from $ \sqrt{s}= $ 8 TeV ATLAS data and combination with previous results | EPJC 79 (2019) 290 | 1810.01772 |
| 10 | CMS Collaboration | Measurement of the top quark mass using proton-proton data at $ \sqrt{s}= $ 7 and 8 TeV | PRD 93 (2016) 072004 | CMS-TOP-14-022 1509.04044 |
| 11 | CMS Collaboration | Measurement of the top quark mass in the dileptonic $ \mathrm{t\bar{t}} $ decay channel using the mass observables $ m_{\mathrm{b}\ell} $, $ m_{\text{T2}} $, and $ m_{\mathrm{b}\ell\nu} $ in pp collisions at $ \sqrt{s}= $ 8 TeV | PRD 96 (2017) 032002 | CMS-TOP-15-008 1704.06142 |
| 12 | CMS Collaboration | Measurement of the top quark mass with lepton+jets final states using pp collisions at $ \sqrt{s}= $ 13 TeV | EPJC 78 (2018) 891 | CMS-TOP-17-007 1805.01428 |
| 13 | CMS Collaboration | Measurement of the top quark mass in the all-jets final state at $ \sqrt{s}= $ 13 TeV and combination with the lepton+jets channel | EPJC 79 (2019) 313 | CMS-TOP-17-008 1812.10534 |
| 14 | CMS Collaboration | Measurement of the top quark mass using events with a single reconstructed top quark in pp collisions at $ \sqrt{s}= $ 13 TeV | JHEP 12 (2021) 161 | CMS-TOP-19-009 2108.10407 |
| 15 | S. Ferrario Ravasio, T. Ježo, P. Nason, and C. Oleari | A theoretical study of top-mass measurements at the LHC using NLO+PS generators of increasing accuracy | EPJC 78 (2018) 458 | 1906.09166 |
| 16 | M. Butenschoen et al. | Top quark mass calibration for Monte Carlo event generators | PRL 117 (2016) 232001 | 1608.01318 |
| 17 | ATLAS, CDF, CMS, D0 Collaborations | First combination of Tevatron and LHC measurements of the top-quark mass | 2014 | 1403.4427 |
| 18 | High precision fundamental constants at the TeV scale | 2014 | 1405.4781 | |
| 19 | A. Juste et al. | Determination of the top quark mass circa 2013: methods, subtleties, perspectives | EPJC 74 (2014) 3119 | 1310.0799 |
| 20 | P. Nason | The top mass in hadronic collisions | p. 123 2019 | 1712.02796 |
| 21 | A. H. Hoang | The top mass: interpretation and theoretical uncertainties | in 7th International Workshop on Top Quark Physics 2014 | 1412.3649 |
| 22 | CMS Collaboration | Measurement of the $ \mathrm{t\bar{t}} $ production cross section, the top quark mass, and the strong coupling constant using dilepton events in pp collisions at $ \sqrt{s} = $ 13 TeV | EPJC 79 (2019) 368 | CMS-TOP-17-001 1812.10505 |
| 23 | ATLAS Collaboration | Measurement of the $ \mathrm{t\bar{t}} $ production cross-section using $ \mathrm{e}\mu $ events with b-tagged jets in pp collisions at $ \sqrt{s}= $ 7 and 8 TeV with the ATLAS detector | EPJC 74 (2014) 3109 | 1406.5375 |
| 24 | CMS Collaboration | Measurement of the $ \mathrm{t\bar{t}} $ production cross section in the $ \mathrm{e}\mu $ channel in proton-proton collisions at $ \sqrt{s}= $ 7 and 8 TeV | JHEP 08 (2016) 029 | CMS-TOP-13-004 1603.02303 |
| 25 | CMS Collaboration | Measurement of the $ \mathrm{t\bar{t}} $ production cross section using events with one lepton and at least one jet in pp collisions at $ \sqrt{s}= $ 13 TeV | JHEP 09 (2017) 051 | CMS-TOP-16-006 1701.06228 |
| 26 | ATLAS Collaboration | Determination of the top-quark pole mass using $ \mathrm{t\bar{t}} $+1-jet events collected with the ATLAS experiment in 7 $ TeV pp $ collisions | JHEP 10 (2015) 121 | 1507.01769 |
| 27 | D0 Collaboration | Measurement of the inclusive $ \mathrm{t\bar{t}} $ production cross section in pp collisions at $ \sqrt{s}= $ 1.96 TeV and determination of the top quark pole mass | PRD 94 (2016) 092004 | 1605.06168 |
| 28 | ATLAS Collaboration | Measurement of lepton differential distributions and the top quark mass in $ \mathrm{t\bar{t}} $ production in pp collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | EPJC 77 (2017) 804 | 1709.09407 |
| 29 | CMS Collaboration | Measurement of $ \mathrm{t\bar{t}} $ normalised multi-differential cross sections in pp collisions at $ \sqrt{s}= $ 13 TeV, and simultaneous determination of the strong coupling strength, top quark pole mass, and parton distribution functions | EPJC 80 (2020) 658 | CMS-TOP-18-004 1904.05237 |
| 30 | U. Langenfeld, S. Moch, and P. Uwer | Measuring the running top-quark mass | PRD 80 (2009) 054009 | 0906.5273 |
| 31 | J. Fuster et al. | Extracting the top-quark running mass using $ \mathrm{t\bar{t}} $+1-jet events produced at the Large Hadron Collider | EPJC 77 (2017) 794 | 1704.00540 |
| 32 | CMS Collaboration | Running of the top quark mass from proton-proton collisions at $ \sqrt{s} = $ 13 TeV | PLB 803 (2020) 135263 | CMS-TOP-19-007 1909.09193 |
| 33 | S. Alioli et al. | A new observable to measure the top-quark mass at hadron colliders | EPJC 73 (2013) 2438 | 1303.6415 |
| 34 | G. Bevilacqua et al. | Top quark mass studies with $ \mathrm{t\bar{t}}\text{j} $ at the LHC | JHEP 03 (2018) 169 | 1710.07515 |
| 35 | ATLAS Collaboration | Measurement of the top-quark mass in $ \mathrm{t\bar{t}} $+1-jet events collected with the ATLAS detector in pp collisions at $ \sqrt{s}= $ 8 TeV | JHEP 11 (2019) 150 | 1905.02302 |
| 36 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 37 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 38 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 39 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 40 | CMS Collaboration | Performance of missing transverse momentum reconstruction in proton-proton collisions at $ \sqrt{s} = $ 13 TeV using the CMS detector | JINST 14 (2019) P07004 | CMS-JME-17-001 1903.06078 |
| 41 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 42 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 43 | CMS Collaboration | Performance of the CMS muon detector and muon reconstruction with proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 13 (2018) P06015 | CMS-MUO-16-001 1804.04528 |
| 44 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 45 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 46 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG box | JHEP 06 (2010) 043 | 1002.2581 |
| 47 | NNPDF Collaboration | Unbiased global determination of parton distributions and their uncertainties at NNLO and at LO | NPB 855 (2012) 153 | 1107.2652 |
| 48 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 49 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 50 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA 8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 51 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 52 | R. Frederix and S. Frixione | Merging meets matching in MCatNLO | JHEP 12 (2012) 061 | 1209.6215 |
| 53 | P. Artoisenet, R. Frederix, O. Mattelaer, and R. Rietkerk | Automatic spin-entangled decays of heavy resonances in Monte Carlo simulations | JHEP 03 (2013) 015 | 1212.3460 |
| 54 | E. Re | Single-top tW-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 55 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in $ POWHEG: $ s-~and t-channel contributions | JHEP 09 (2009) 111 | 0907.4076 |
| 56 | CMS Collaboration | Investigations of the impact of the parton shower tuning in PYTHIA 8 in the modelling of $ \mathrm{t\bar{t}} $ at $ \sqrt{s}= $ 8 TeV and 13 TeV | 2016 CMS-PAS-TOP-16-021 | |
| 57 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 58 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA8.1: the monash 2013 tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 59 | M. L. Mangano, M. Moretti, F. Piccinini, and M. Treccani | Matching matrix elements and shower evolution for top-quark production in hadronic collisions | JHEP 01 (2007) 013 | hep-ph/0611129 |
| 60 | S. Mrenna and P. Richardson | Matching matrix elements and parton showers with HERWIG and PYTHIA | JHEP 05 (2004) 040 | hep-ph/0312274 |
| 61 | M. Czakon and A. Mitov | Top++: a program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 62 | M. Cacciari et al. | Top-pair production at hadron colliders with next-to-next-to-leading logarithmic soft-gluon resummation | PLB 710 (2012) 612 | 1111.5869 |
| 63 | P. Barnreuther, M. Czakon, and A. Mitov | Percent level precision physics at the tevatron: First genuine NNLO QCD corrections to $ \mathrm{q\bar{q}}\to\mathrm{t\bar{t}}$+X | PRL 109 (2012) 132001 | 1204.5201 |
| 64 | M. Czakon and A. Mitov | NNLO corrections to top-pair production at hadron colliders: the all-fermionic scattering channels | JHEP 12 (2012) 054 | 1207.0236 |
| 65 | M. Czakon and A. Mitov | NNLO corrections to top pair production at hadron colliders: the quark-gluon reaction | JHEP 01 (2013) 080 | 1210.6832 |
| 66 | M. Beneke, P. Falgari, S. Klein, and C. Schwinn | Hadronic top-quark pair production with NNLL threshold resummation | NPB 855 (2012) 695 | 1109.1536 |
| 67 | M. Czakon, P. Fiedler, and A. Mitov | Total top-quark pair-production cross section at hadron colliders through $ \mathcal{O}({\alpha_S}^{4}) $ | PRL 110 (2013) 252004 | 1303.6254 |
| 68 | N. Kidonakis | Two-loop soft anomalous dimensions for single top quark associated production with a $ \mathrm{W^{-}} $ or $ \mathrm{H}^{-} $ | PRD 82 (2010) 054018 | 1005.4451 |
| 69 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 70 | J. M. Campbell, R. K. Ellis, and C. Williams | Vector boson pair production at the LHC | JHEP 07 (2011) 018 | 1105.0020 |
| 71 | S. Agostinelli et al. | GEANT4--a simulation toolkit | Nucl. Instrum. Methods. Phys. Res. A 506 (2003) 250 | |
| 72 | ATLAS Collaboration | Measurement of the inelastic proton-proton cross section at $ \sqrt{s} = $ 13 TeV with the ATLAS detector at the LHC | PRL 117 (2016) 182002 | 1606.02625 |
| 73 | CMS Collaboration | Pileup jet identification | CMS-PAS-JME-13-005 | CMS-PAS-JME-13-005 |
| 74 | CMS Collaboration | Identification of heavy-flavour jets with the CMS detector in pp collisions at 13 TeV | JINST 13 (2018) P05011 | CMS-BTV-16-002 1712.07158 |
| 75 | CMS Collaboration | A deep neural network for simultaneous estimation of b jet energy and resolution | Comput. Softw. Big Sci. 4 (2020) 10 | CMS-HIG-18-027 1912.06046 |
| 76 | CMS Collaboration | Measurement of the differential cross section for top quark pair production in pp collisions at $ \sqrt{s} = $ 8 TeV | EPJC 75 (2015) 542 | CMS-TOP-12-028 1505.04480 |
| 77 | CMS Collaboration | Measurement of double-differential cross sections for top quark pair production in pp collisions at $ \sqrt{s} = $ 8 TeV and impact on parton distribution functions | EPJC 77 (2017) 459 | CMS-TOP-14-013 1703.01630 |
| 78 | CMS Collaboration | Measurement of normalized differential $ \mathrm{t\bar{t}} $ cross sections in the dilepton channel from pp collisions at $ \sqrt{s}= $ 13 TeV | JHEP 04 (2018) 060 | CMS-TOP-16-007 1708.07638 |
| 79 | CMS Collaboration | Measurements of $ \mathrm{t\bar{t}} $ differential cross sections in proton-proton collisions at $ \sqrt{s}= $ 13 TeV using events containing two leptons | JHEP 02 (2019) 149 | CMS-TOP-17-014 1811.06625 |
| 80 | L. Sonnenschein | Analytical solution of $ \mathrm{t\bar{t}} $ dilepton equations | PRD 73 (2006) 054015 | hep-ph/0603011 |
| 81 | M. Abadi et al. | TensorFlow: large-scale machine learning on heterogeneous systems | 2015 Software available from tensorflow.org | |
| 82 | F. Chollet et al. | KERAS | link | |
| 83 | J. Snoek, H. Larochelle, and R. P. Adams | Practical bayesian optimization of machine learning algorithms | 2012 | 1206.2944 |
| 84 | E. Brochu, V. M. Cora, and N. de Freitas | A tutorial on bayesian optimization of expensive cost functions, with application to active user modeling and hierarchical reinforcement learning | 2010 | 1012.2599 |
| 85 | F. Nogueira | Bayesian optimization: ppen source constrained global optimization tool for Python | link | |
| 86 | R. D. Cousins | Generalization of chisquare goodness-of-fit test for binned data using saturated models, with application to histograms | 2013 | |
| 87 | Y. Ganin and V. Lempitsky | Unsupervised domain adaptation by backpropagation | 2015 | 1409.7495 |
| 88 | J. Kieseler, K. Lipka, and S. Moch | Calibration of the top-quark Monte Carlo mass | PRL 116 (2016) 162001 | 1511.00841 |
| 89 | F. James and M. Roos | MINUIT - a system for function minimization and analysis of the parameter errors and correlations | Computer Physics Communications 10 (1975) 343 | |
| 90 | ATLAS, CMS Collaborations, LHC Higgs combination group | Procedure for the LHC Higgs boson search combination in summer 2011 | technical report, CERN, Geneva | |
| 91 | CMS Collaboration | Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV | EPJC 75 (2015) 212 | CMS-HIG-14-009 1412.8662 |
| 92 | ATLAS, CMS Collaboration | Measurements of the Higgs boson production and decay rates and constraints on its couplings from a combined ATLAS and CMS analysis of the LHC pp collision data at $ \sqrt{s}= $ 7 and 8 TeV | JHEP 08 (2016) 045 | 1606.02266 |
| 93 | J. S. Conway | Incorporating nuisance parameters in likelihoods for multisource spectra | in PHYSTAT 2011, p. 115 2011 | 1103.0354 |
| 94 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC (2021) | CMS-LUM-17-003 2104.01927 |
| 95 | CMS Collaboration | Electron and photon reconstruction and identification with the CMS experiment at the CERN LHC | JINST 16 (2021) P05014 | CMS-EGM-17-001 2012.06888 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|