Compact Muon Solenoid
LHC, CERN

Visit us: CMS Public Website, CMS Physics ; Contact us: CMS Publications Committee

CMS-SUS-16-046 ; CERN-EP-2017-284

Search for gauge-mediated supersymmetry in events with at least one photon and missing transverse momentum in pp collisions at $\sqrt{s} = $ 13 TeV

CMS Collaboration

21 November 2017

Phys. Lett. B 780 (2018) 118

Abstract: A search for gauge-mediated supersymmetry (SUSY) in final states with photons and large missing transverse momentum is presented. The data sample of pp collisions at $\sqrt{s} = $ 13 TeV was collected with the CMS detector at the CERN LHC and corresponds to an integrated luminosity of 35.9 fb$^{-1}$. Data are compared with models in which the lightest neutralino has bino- or wino-like components, resulting in decays to photons and gravitinos, where the gravitinos escape detection. The event selection is optimized for both electroweak (EWK) and strong production SUSY scenarios. The observed data are consistent with standard model predictions, and limits are set in the context of a general gauge mediation model in which gaugino masses up to 980 GeV are excluded at 95% confidence level. Gaugino masses below 780 and 950 GeV are excluded in two simplified models with EWK production of mass-degenerate charginos and neutralinos. Stringent limits are set on simplified models based on gluino and squark pair production, excluding gluino (squark) masses up to 2100 (1750) GeV depending on the assumptions made for the decay modes and intermediate particle masses. This analysis sets the highest mass limits to date in the studied EWK models, and in the considered strong production models when the mass difference between the gauginos and the squarks or gluinos is small.

Links: e-print arXiv:1711.08008 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ;

Additional information on efficiencies needed for reinterpretation of these results are available here Additional technical material for CMS speakers can be found here

Figures
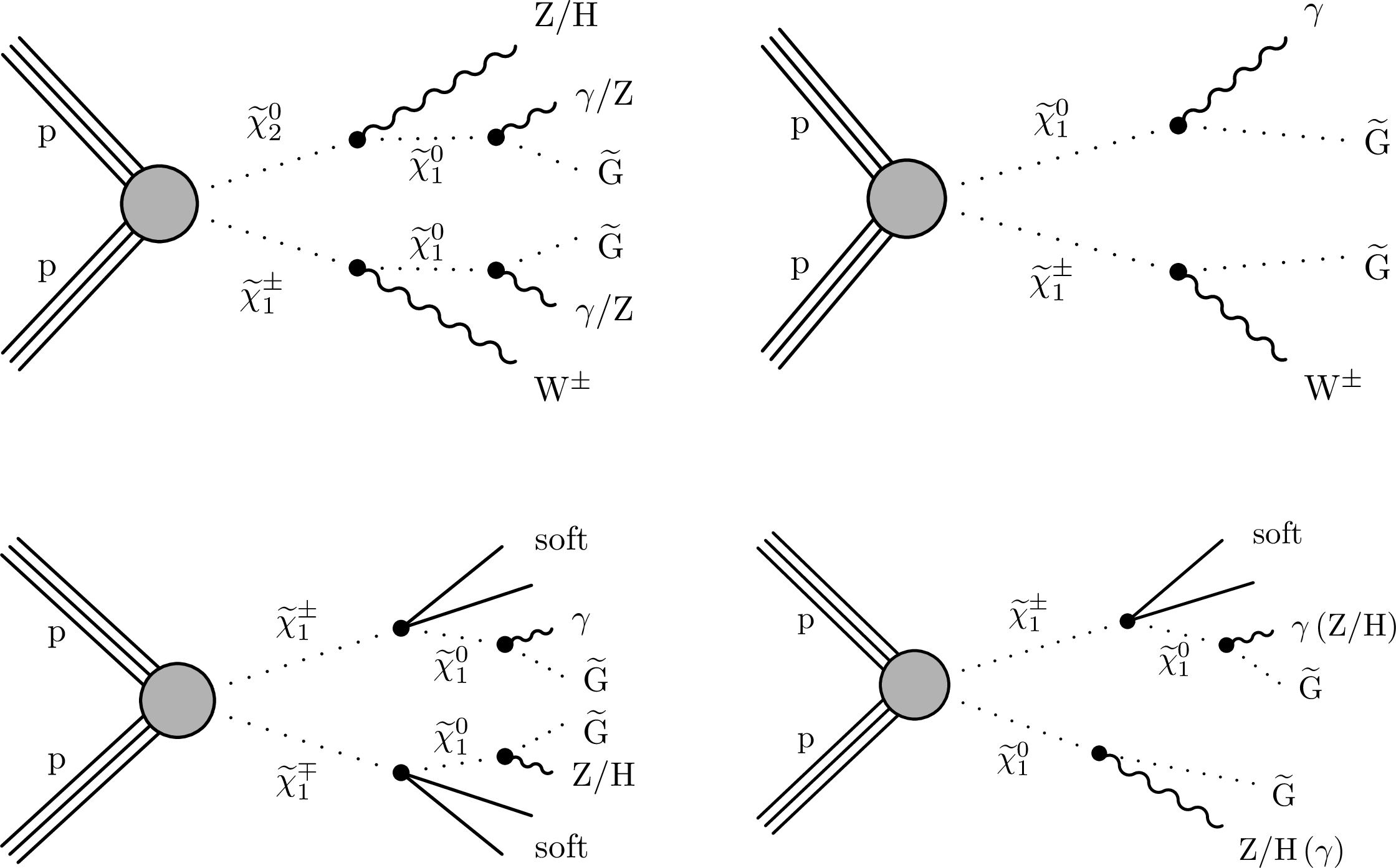
png pdf	Figure 1: In the context of GGM, several production and decay channels are possible. The diagram of the dominant process $ \tilde{\chi}^0 _2$-$ \tilde{\chi}^{\pm} _1$ production is shown (upper left), where the gaugino decays depend on the mass configuration under study. In the TChiWg model (upper right), the gauginos are mass degenerate. The TChiNg model comprises $ \tilde{\chi}^{\pm} _1$ pair production (lower left) and $ \tilde{\chi}^{\pm} _1 \tilde{\chi}^0 _1$ production (lower right), where the $ \tilde{\chi}^{\pm} _1$ is only slightly heavier than the $ \tilde{\chi}^0 _1$, so only low-momentum (soft) particles appear in the decay of $ \tilde{\chi}^{\pm} _1$ to $ \tilde{\chi}^0 _1$.
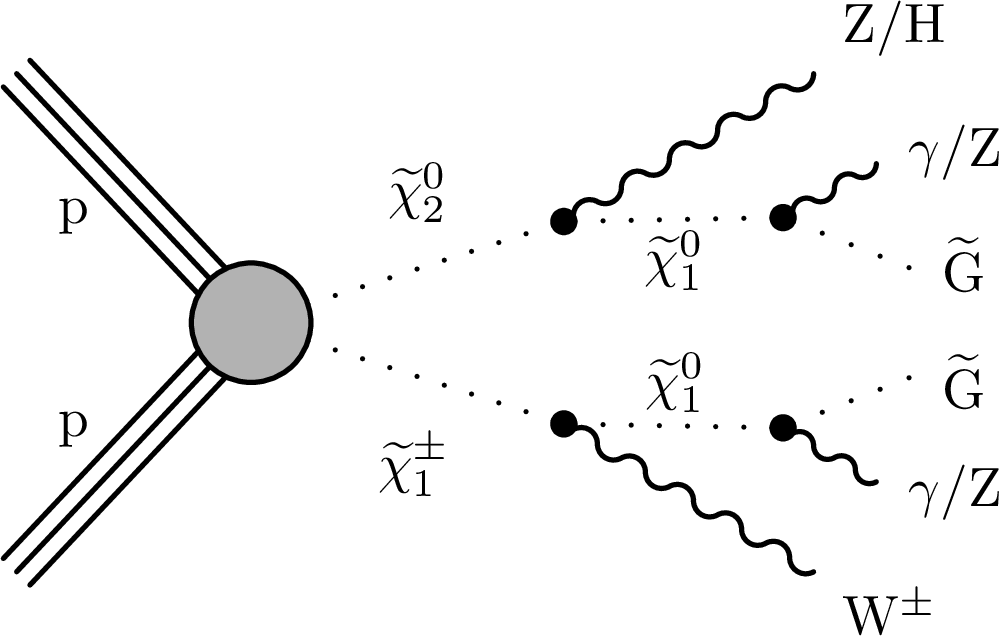
png pdf	Figure 1-a: In the context of GGM, several production and decay channels are possible. The diagram of the dominant process $ \tilde{\chi}^0 _2$-$ \tilde{\chi}^{\pm} _1$ production, where the gaugino decays depend on the mass configuration under study.
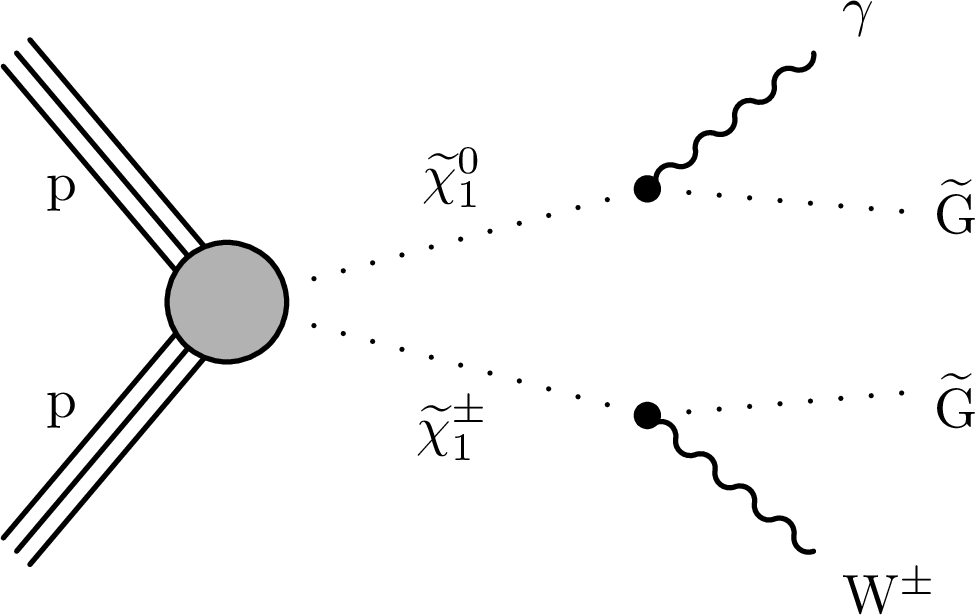
png pdf	Figure 1-b: The TChiWg model, where the gauginos are mass degenerate.
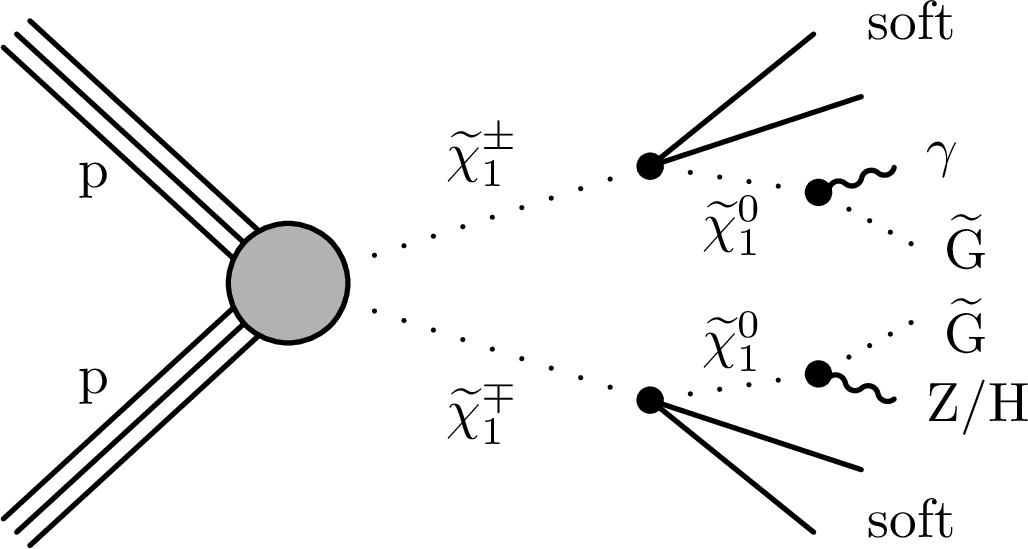
png pdf	Figure 1-c: The TChiNg model, which comprises $ \tilde{\chi}^{\pm} _1$ pair production, where the $ \tilde{\chi}^{\pm} _1$ is only slightly heavier than the $ \tilde{\chi}^0 _1$, so only low-momentum (soft) particles appear in the decay of $ \tilde{\chi}^{\pm} _1$ to $ \tilde{\chi}^0 _1$.
png pdf	Figure 1-d: The TChiNg model, which comprises $ \tilde{\chi}^{\pm} _1 \tilde{\chi}^0 _1$ production, where the $ \tilde{\chi}^{\pm} _1$ is only slightly heavier than the $ \tilde{\chi}^0 _1$, so only low-momentum (soft) particles appear in the decay of $ \tilde{\chi}^{\pm} _1$ to $ \tilde{\chi}^0 _1$.
png pdf	Figure 2: For strong gluino pair-production the simplified scenarios T5gg (upper left) and T5Wg (upper right) and for squark pair-production the simplified scenarios T6gg (lower left) and T6Wg (lower right) are studied. In the T5Wg (T6Wg) scenario, a branching fraction of 50% is assumed for the decays $\tilde{\mathrm{g}}\rightarrow {\mathrm {q}} {\overline {\mathrm {q}}} \tilde{\chi}^{\pm} _1$ and $\tilde{\mathrm{g}}\rightarrow {\mathrm {q}} {\overline {\mathrm {q}}} \tilde{\chi}^0 _1$ ($\tilde{\mathrm{q}}\rightarrow {\mathrm {q}} \tilde{\chi}^{\pm} _1$ and $\tilde{\mathrm{q}}\rightarrow {\mathrm {q}} \tilde{\chi}^0 _1$), resulting in final states with zero, one, or two photons.
png pdf	Figure 2-a: The strong gluino pair-production simplified scenario T5gg.
png pdf	Figure 2-b: The strong gluino pair-production simplified scenario T5Wg. A branching fraction of 50% is assumed for the decays $\tilde{\mathrm{g}}\rightarrow {\mathrm {q}} {\overline {\mathrm {q}}} \tilde{\chi}^{\pm} _1$ and $\tilde{\mathrm{g}}\rightarrow {\mathrm {q}} {\overline {\mathrm {q}}} \tilde{\chi}^0 _1$ ($\tilde{\mathrm{q}}\rightarrow {\mathrm {q}} \tilde{\chi}^{\pm} _1$ and $\tilde{\mathrm{q}}\rightarrow {\mathrm {q}} \tilde{\chi}^0 _1$), resulting in final states with zero, one, or two photons.
png pdf	Figure 2-c: The quark pair-production simplified scenario T6gg.
png pdf	Figure 2-d: The quark pair-production simplified scenario T6Wg. A branching fraction of 50% is assumed for the decays $\tilde{\mathrm{g}}\rightarrow {\mathrm {q}} {\overline {\mathrm {q}}} \tilde{\chi}^{\pm} _1$ and $\tilde{\mathrm{g}}\rightarrow {\mathrm {q}} {\overline {\mathrm {q}}} \tilde{\chi}^0 _1$ ($\tilde{\mathrm{q}}\rightarrow {\mathrm {q}} \tilde{\chi}^{\pm} _1$ and $\tilde{\mathrm{q}}\rightarrow {\mathrm {q}} \tilde{\chi}^0 _1$), resulting in final states with zero, one, or two photons.
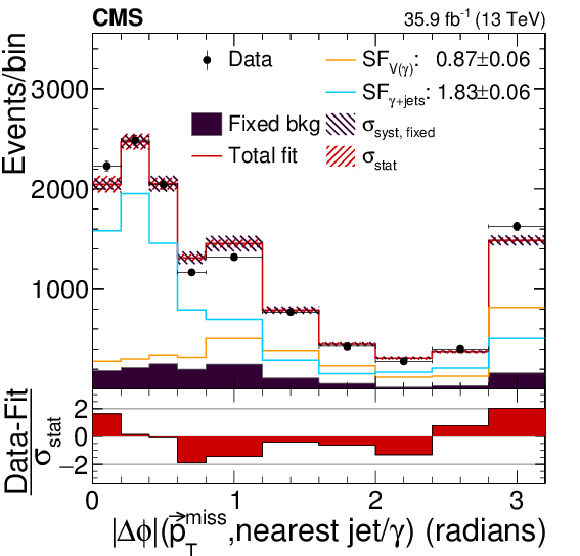
png pdf	Figure 3: The post-fit distributions for the $ \gamma $+jets (blue) and V($\gamma $) (orange) background in the control region together with the fixed background (dark magenta) and the total fit distribution stacked onto the fixed backgrounds (red) are shown. The statistical uncertainty ($\sigma _{\text {stat}}$) of the post-fit distribution is shown in the red hatched area and the systematic uncertainty of the fixed background ($\sigma _{\text {syst, fixed}}$) is indicated with the dark magenta hatched area. The values SF$_{{{\rm V}(\gamma)}}$ and SF$_{\gamma{+}{\text{jets}}}$ in the legend are the resulting scale factors. The pull distribution only considers the statistical uncertainty.
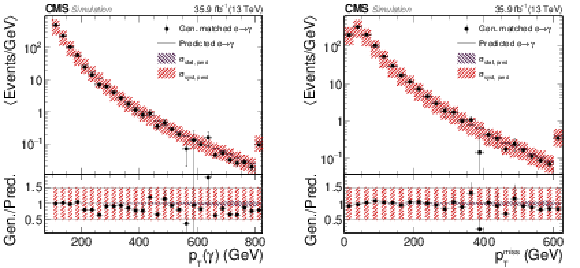
png pdf	Figure 4: Validation of the electron misidentification background estimation method using MC simulation. In the selection with at least one photon with $ {p_{\mathrm {T}}} > $ 100 GeV, the prediction of the $ {\mathrm {e}}\to \gamma $ misidentification estimation method is compared to direct simulation in the photon ${p_{\mathrm {T}}}$ (left) and the ${p_{\mathrm {T}}^{\, miss}}$ (right) distributions. The black and red hatched areas represent the statistical ($\sigma _{\text {stat, pred}}$) and the 50% systematic ($\sigma _{\text {syst, pred}}$) uncertainties of the prediction, respectively. Events populating the phase space beyond the shown range are included in the last bin.
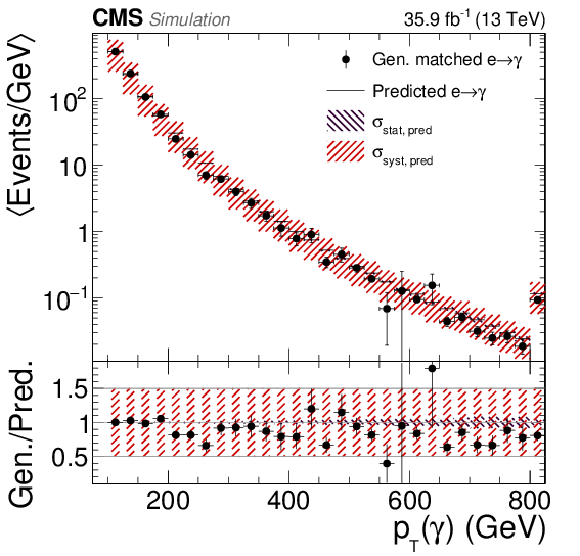
png pdf	Figure 4-a: Validation of the electron misidentification background estimation method using MC simulation. In the selection with at least one photon with $ {p_{\mathrm {T}}} > $ 100 GeV, the prediction of the $ {\mathrm {e}}\to \gamma $ misidentification estimation method is compared to direct simulation in the photon ${p_{\mathrm {T}}}$ distribution. The black and red hatched areas represent the statistical ($\sigma _{\text {stat, pred}}$) and the 50% systematic ($\sigma _{\text {syst, pred}}$) uncertainties of the prediction, respectively. Events populating the phase space beyond the shown range are included in the last bin.
png pdf	Figure 4-b: Validation of the electron misidentification background estimation method using MC simulation. In the selection with at least one photon with $ {p_{\mathrm {T}}} > $ 100 GeV, the prediction of the $ {\mathrm {e}}\to \gamma $ misidentification estimation method is compared to direct simulation in the ${p_{\mathrm {T}}^{\, miss}}$ distribution. The black and red hatched areas represent the statistical ($\sigma _{\text {stat, pred}}$) and the 50% systematic ($\sigma _{\text {syst, pred}}$) uncertainties of the prediction, respectively. Events populating the phase space beyond the shown range are included in the last bin.
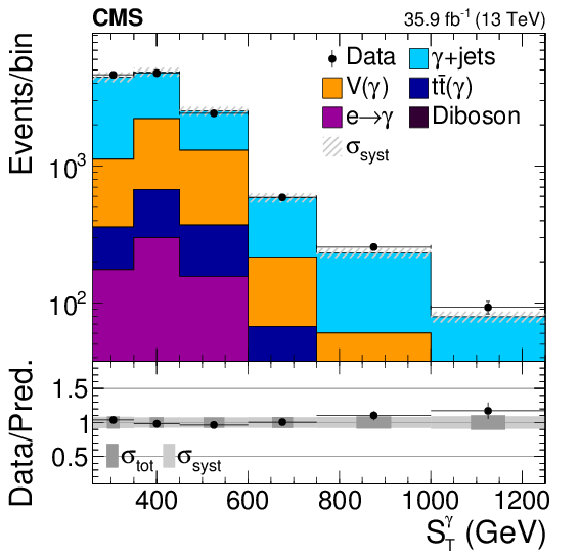
png pdf	Figure 5: Data to simulation comparisons in the control region (left) and the validation region (right). Events with ${S_{\mathrm {T}}^{\gamma}}$ beyond the shown range are included in the last bin. The hatched light gray band in the upper panel, as well as the solid light gray band in the lower panel represent the total systematic uncertainty ($\sigma _{\text {syst}}$). The dark gray band in the lower panel indicates the quadratic sum of the statistical and systematic uncertainties ($\sigma _{\text {tot}}$).
png pdf	Figure 5-a: Data to simulation comparisons in the control region. Events with ${S_{\mathrm {T}}^{\gamma}}$ beyond the shown range are included in the last bin. The hatched light gray band in the upper panel, as well as the solid light gray band in the lower panel represent the total systematic uncertainty ($\sigma _{\text {syst}}$). The dark gray band in the lower panel indicates the quadratic sum of the statistical and systematic uncertainties ($\sigma _{\text {tot}}$).
png pdf	Figure 5-b: Data to simulation comparisons in the validation region. Events with ${S_{\mathrm {T}}^{\gamma}}$ beyond the shown range are included in the last bin. The hatched light gray band in the upper panel, as well as the solid light gray band in the lower panel represent the total systematic uncertainty ($\sigma _{\text {syst}}$). The dark gray band in the lower panel indicates the quadratic sum of the statistical and systematic uncertainties ($\sigma _{\text {tot}}$).
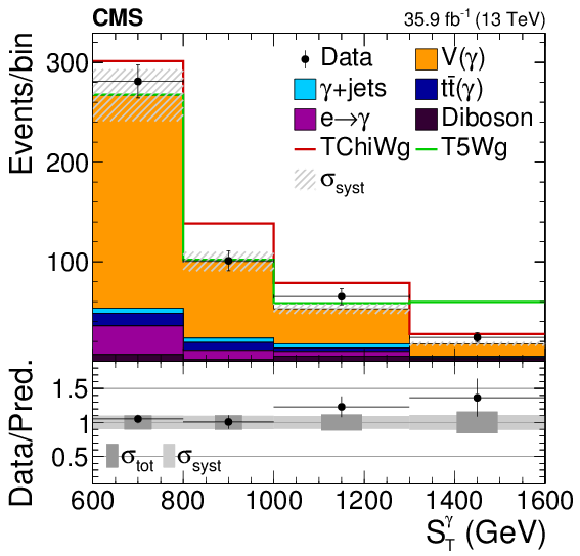
png pdf	Figure 6: Comparison of the measurement and prediction in the signal region in four exclusive bins of ${S_{\mathrm {T}}^{\gamma}}$. For guidance, two SUSY benchmark signal points are stacked on the SM background prediction, where the TChiWg signal point corresponds to a NLSP mass of 700 GeV and the T5Wg signal point corresponds to a gluino mass of 1750 GeV and a NLSP mass of 1700 GeV. Events with values of ${S_{\mathrm {T}}^{\gamma}}$ beyond the shown range are included in the last bin. The hatched light gray band in the upper panel, as well as the solid light gray band in the lower panel represent the total systematic uncertainty ($\sigma _{\text {syst}}$). The dark gray band in the lower panel indicates the quadratic sum of the statistical and systematic uncertainties ($\sigma _{\text {tot}}$).
png pdf root	Figure 7: Observed upper cross section limit at 95%CL for the EWK GGM signal in the wino-bino mass plane. The thick lines represent the observed (black) and expected (red) exclusion contours, where the phase space closer to the diagonal is excluded by the analysis. The thin dotted red curves indicate the region containing 68% of the distribution of limits expected under the background-only hypothesis. The thin solid black curves show the change in the observed limit due to variation of the signal cross sections within their theoretical uncertainties.
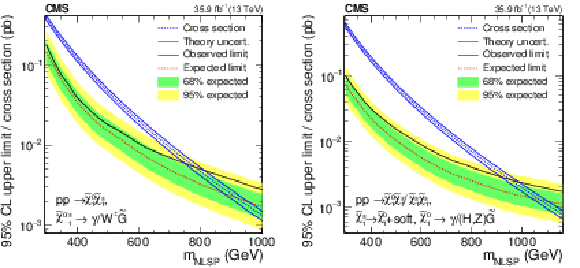
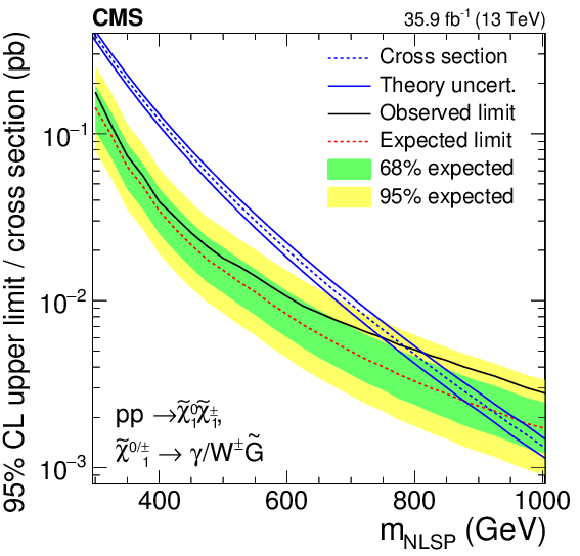
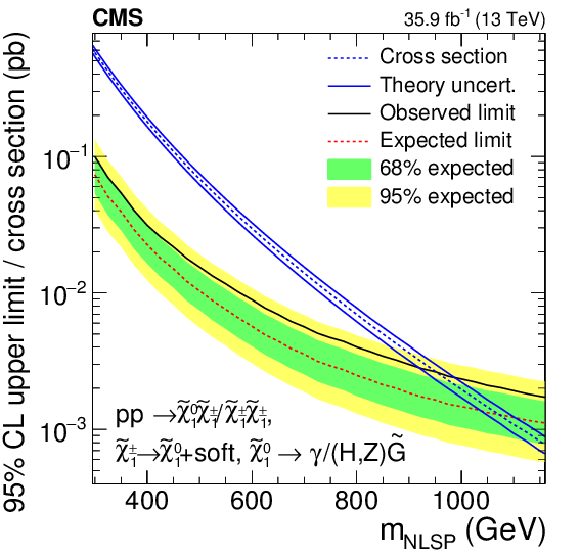
png pdf	Figure 8: Observed (black) and expected (red) upper cross section limits as a function of the NLSP mass for the TChiWg (left) and TChiNg (right) model together with the corresponding theoretical cross section (blue). The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. The solid blue lines represent the theoretical uncertainty in the signal cross section.
png pdf root	Figure 8-a: Observed (black) and expected (red) upper cross section limits as a function of the NLSP mass for the TChiWg model together with the corresponding theoretical cross section (blue). The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. The solid blue lines represent the theoretical uncertainty in the signal cross section.
png pdf root	Figure 8-b: Observed (black) and expected (red) upper cross section limits as a function of the NLSP mass for the TChiNg model together with the corresponding theoretical cross section (blue). The inner (green) band and the outer (yellow) band indicate the regions containing 68 and 95%, respectively, of the distribution of limits expected under the background-only hypothesis. The solid blue lines represent the theoretical uncertainty in the signal cross section.
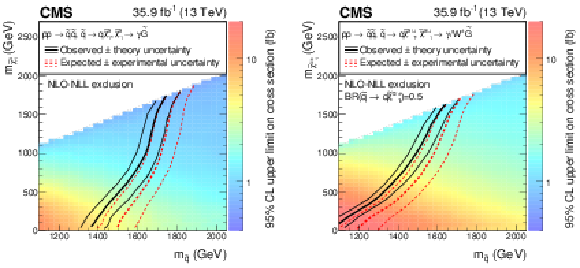
png pdf	Figure 9: The 95% CL limits for the T5gg (left) and T5Wg (right) SMS models in the gluino-neutralino/chargino mass plane. The color scale encodes the observed upper cross section limit for each point. The thick lines represent the observed (black) and expected (red) exclusion contours, where the phase space of lower masses is excluded by the analysis. The thin dotted red curves indicate the region containing 68% of the distribution of limits expected under the background-only hypothesis. The thin solid black curves show the change in the observed limit due to variation of the signal cross sections within their theoretical uncertainties.
png pdf root	Figure 9-a: The 95% CL limits for the T5gg SMS model in the gluino-neutralino/chargino mass plane. The color scale encodes the observed upper cross section limit for each point. The thick lines represent the observed (black) and expected (red) exclusion contours, where the phase space of lower masses is excluded by the analysis. The thin dotted red curves indicate the region containing 68% of the distribution of limits expected under the background-only hypothesis. The thin solid black curves show the change in the observed limit due to variation of the signal cross sections within their theoretical uncertainties.
png pdf root	Figure 9-b: The 95% CL limits for the T5Wg SMS model in the gluino-neutralino/chargino mass plane. The color scale encodes the observed upper cross section limit for each point. The thick lines represent the observed (black) and expected (red) exclusion contours, where the phase space of lower masses is excluded by the analysis. The thin dotted red curves indicate the region containing 68% of the distribution of limits expected under the background-only hypothesis. The thin solid black curves show the change in the observed limit due to variation of the signal cross sections within their theoretical uncertainties.
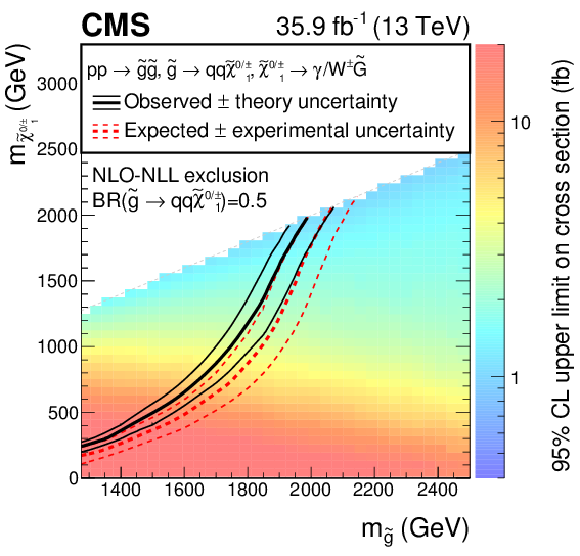
png pdf	Figure 10: The 95% CL limits for the T6gg (left) and T6Wg (right) SMS models in the squark-neutralino/chargino mass plane. The color scale encodes the observed upper cross section limit for each point. The thick lines represent the observed (black) and expected (red) exclusion contours, where the phase space of lower masses is excluded by the analysis. The thin dotted red curves indicate the region containing 68% of the distribution of limits expected under the background-only hypothesis. The thin solid black curves show the change in the observed limit due to variation of the signal cross sections within their theoretical uncertainties. For the signal production cross section five accessible mass-degenerate squark flavors for $\tilde{\mathrm{q}}_{\text {L}}$ and $\tilde{\mathrm{q}}_{\text {R}}$ were assumed.
png pdf root	Figure 10-a: The 95% CL limits for the T6gg SMS model in the squark-neutralino/chargino mass plane. The color scale encodes the observed upper cross section limit for each point. The thick lines represent the observed (black) and expected (red) exclusion contours, where the phase space of lower masses is excluded by the analysis. The thin dotted red curves indicate the region containing 68% of the distribution of limits expected under the background-only hypothesis. The thin solid black curves show the change in the observed limit due to variation of the signal cross sections within their theoretical uncertainties. For the signal production cross section five accessible mass-degenerate squark flavors for $\tilde{\mathrm{q}}_{\text {L}}$ and $\tilde{\mathrm{q}}_{\text {R}}$ were assumed.
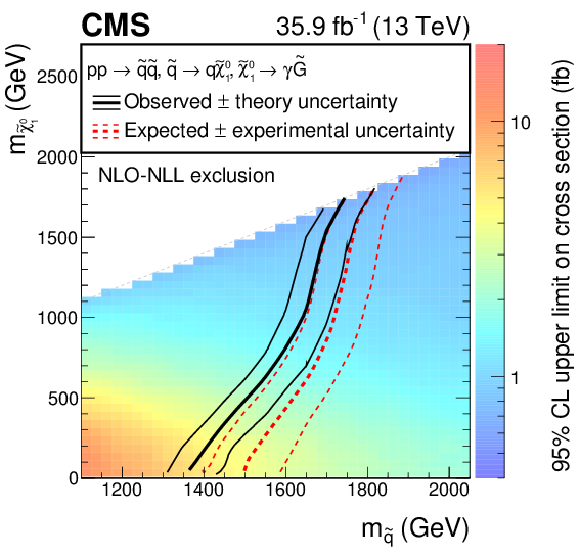
png pdf root	Figure 10-b: The 95% CL limits for the T6Wg SMS model in the squark-neutralino/chargino mass plane. The color scale encodes the observed upper cross section limit for each point. The thick lines represent the observed (black) and expected (red) exclusion contours, where the phase space of lower masses is excluded by the analysis. The thin dotted red curves indicate the region containing 68% of the distribution of limits expected under the background-only hypothesis. The thin solid black curves show the change in the observed limit due to variation of the signal cross sections within their theoretical uncertainties. For the signal production cross section five accessible mass-degenerate squark flavors for $\tilde{\mathrm{q}}_{\text {L}}$ and $\tilde{\mathrm{q}}_{\text {R}}$ were assumed.

Tables
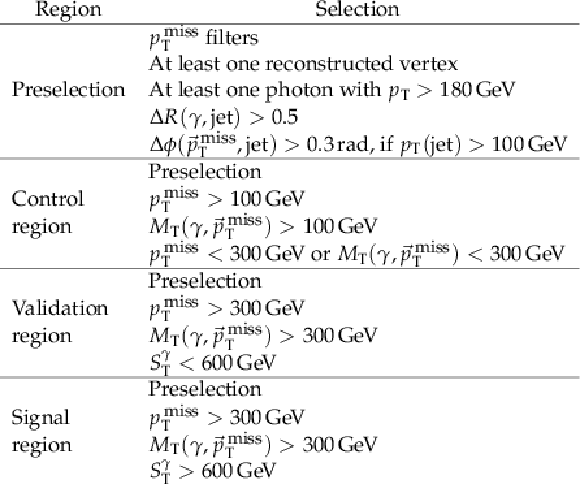
png pdf	Table 1: Summary of the event selection criteria required for the control, validation, and signal regions.
png pdf	Table 2: Systematic uncertainties in the background prediction in percent.
png pdf	Table 3: Systematic uncertainties in the signal predictions in percent.
png pdf	Table 4: Background and data yields, as well as the statistical and systematic uncertainties for the separate signal region bins. For the total background uncertainty the uncertainties of the individual background components are summed quadratically.

Summary

A search for electroweak (EWK) and strong production of gauginos in the framework of gauge mediated supersymmetry breaking in final states with photons and large missing transverse momentum has been performed. A data set recorded by the CMS experiment at a center-of-mass energy of 13 TeV, corresponding to an integrated luminosity of 35.9 fb$^{-1}$, was analyzed. The data were found to agree with the expectation from the standard model, without any indication of new physics. The analysis is sensitive to EWK production of gauginos and to strong production of gluinos and squarks in particular if the mass difference between gauginos and gluinos or squarks is small. A two-dimensional EWK signal scan in the framework of general gauge mediation is used to interpret the results. In the case of similar wino and bino masses, the analysis excludes masses below 980 GeV at 95% confidence level, improving on the current best limit by 270 GeV [26]. Two EWK simplified models are also used for the interpretation. The analysis excludes masses of the next-to-lightest supersymmetric particle $\tilde{\chi}^0_1$ below 780 (950) GeV in the TChiWg (TChiNg) scenario. Additionally, limits are set for strong production simplified models based on gluino (T5gg, T5Wg) and squark (T6gg, T6Wg) pair production, excluding gluino (squark) masses up to 2100 (1750) GeV. This analysis complements searches in the photon+jets, diphoton, and photon+leptons final states, and sets the most stringent limits to date in the EWK production models, and in the strong production models when the gauginos are degenerate in mass with the gluino or squarks.

Additional Figures
png pdf	Additional Figure 1: Sketch of the control region and signal region definition. The blue area indicates the phase space of the validation region.

Additional Tables
png pdf	Additional Table 1: Cutflow of the TChiWg benchmark signal point with a wino NLSP with a mass of 700 GeV. The preselection cut comprises the requirement of at least one loosely isolated photon with ${p_{\mathrm {T}}} > $ 180 GeV and a seed crystal energy fraction of at least 30% wrt. the full corrected photon ${p_{\mathrm {T}}}$, which was accepted by the trigger and was measured in the ECAL barrel. Furthermore, for the photon a minimal distance in $\Delta \mathrm{R}$ of 0.5 is required wrt. to the nearest jet. Also $\Delta \phi (p_{\mathrm{T}}^{\, {\text{miss}}}, \text{jet}) > $ 0.3 is required for all jets with $ {p_{\mathrm {T}}} > $ 100 GeV. The yields correspond to a center-of-mass energy of 13 TeV and an integrated luminosity of 35.9 fb$^{-1}$.
png pdf	Additional Table 2: Cutflow of the T5Wg benchmark signal point with a gluino mass of 1750 GeV and a gaugino mass of 1700 GeV. The preselection cut comprises the requirement of at least one loosely isolated photon with ${p_{\mathrm {T}}} > $ 180 GeV and a seed crystal energy fraction of at least 30% wrt. the full corrected photon ${p_{\mathrm {T}}}$, which was accepted by the trigger and was measured in the ECAL barrel. Furthermore, for the photon a minimal distance in $\Delta \mathrm{R}$ of 0.5 is required wrt. to the nearest jet. Also $\Delta \phi (p_{\mathrm{T}}^{\, {\text{miss}}}, \text{jet}) > $ 0.3 is required for all jets with ${p_{\mathrm {T}}} > $ 100 GeV. The yields correspond to a center-of-mass energy of 13 TeV and an integrated luminosity of 35.9 fb$^{-1}$.

References
1	ATLAS Collaboration	Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC	PLB 716 (2012) 1	1207.7214
2	CMS Collaboration	Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC	PLB 716 (2012) 30	CMS-HIG-12-028 1207.7235
3	CMS Collaboration	Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV	EPJC 75 (2015) 212	CMS-HIG-14-009 1412.8662
4	P. Ramond	Dual theory for free fermions	PRD 3 (1971) 2415
5	P. Ramond	An interpretation of dual theories	Nuovo Cim. A 4 (1971) 544
6	Yu. A. Golfand and E. P. Likhtman	Extension of the algebra of Poincare group generators and violation of P invariance	JEPTL 13 (1971) 323
7	D. V. Volkov and V. P. Akulov	Possible universal neutrino interaction	JEPTL 16 (1972) 438
8	J. Wess and B. Zumino	Supergauge transformations in four-dimensions	NPB 70 (1974) 39
9	D. Z. Freedman, P. van Nieuwenhuizen, and S. Ferrara	Progress toward a theory of supergravity	PRD 13 (1976) 3214
10	S. Deser and B. Zumino	Consistent supergravity	PLB 62 (1976) 335
11	D. Z. Freedman and P. van Nieuwenhuizen	Properties of supergravity theory	PRD 14 (1976) 912
12	S. Ferrara and P. van Nieuwenhuizen	Consistent supergravity with complex spin 3/2 gauge fields	PRL 37 (1976) 1669
13	P. Fayet	Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino	NPB 90 (1975) 104
14	A. H. Chamseddine, R. L. Arnowitt, and P. Nath	Locally supersymmetric grand unification	PRL 49 (1982) 970
15	R. Barbieri, S. Ferrara, and C. A. Savoy	Gauge models with spontaneously broken local supersymmetry	PLB 119 (1982) 343
16	L. J. Hall, J. D. Lykken, and S. Weinberg	Supergravity as the messenger of supersymmetry breaking	PRD 27 (1983) 2359
17	G. L. Kane, C. F. Kolda, L. Roszkowski, and J. D. Wells	Study of constrained minimal supersymmetry	PRD 49 (1994) 6173	hep-ph/9312272
18	P. Fayet	Mixing between gravitational and weak interactions through the massive gravitino	PLB 70 (1977) 461
19	H. Baer, M. Brhlik, C. H. Chen, and X. Tata	Signals for the minimal gauge-mediated supersymmetry breaking model at the Fermilab Tevatron collider	PRD 55 (1997) 4463	hep-ph/9610358
20	H. Baer, P. G. Mercadante, X. Tata, and Y. L. Wang	Reach of Tevatron upgrades in gauge-mediated supersymmetry breaking models	PRD 60 (1999) 055001	hep-ph/9903333
21	S. Dimopoulos, S. Thomas, and J. D. Wells	Sparticle spectroscopy and electroweak symmetry breaking with gauge-mediated supersymmetry breaking	NPB 488 (1997) 39	hep-ph/9609434
22	J. R. Ellis, J. L. Lopez, and D. V. Nanopoulos	Analysis of LEP constraints on supersymmetric models with a light gravitino	PLB 394 (1997) 354	hep-ph/9610470
23	M. Dine, A. E. Nelson, Y. Nir, and Y. Shirman	New tools for low energy dynamical supersymmetry breaking	PRD 53 (1996) 2658	hep-ph/9507378
24	G. F. Giudice and R. Rattazzi	Gauge-mediated supersymmetry breaking	in Perspectives on supersymmetry, p. 355 World Scientific, Singapore
25	G. R. Farrar and P. Fayet	Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry	PLB 76 (1978) 575
26	CMS Collaboration	Search for supersymmetry in electroweak production with photons and large missing transverse energy in pp collisions at $ \sqrt{s} = $ 8 TeV	PLB 759 (2016) 479	CMS-SUS-14-016 1602.08772
27	CMS Collaboration	Data parking and data scouting at the CMS experiment	CDS
28	CMS Collaboration	Search for supersymmetry in events with a photon, a lepton, and missing transverse momentum in pp collisions at $ \sqrt{s} = $ 8 TeV	PLB 757 (2016) 6	CMS-SUS-14-013 1508.01218
29	ATLAS Collaboration	Search for photonic signatures of gauge-mediated supersymmetry in 8 TeV pp collisions with the ATLAS detector	PRD 92 (2015) 072001	1507.05493
30	CMS Collaboration	Search for new physics in events with photons, jets, and missing transverse energy in pp collisions at $ \sqrt{s} = $ 7 TeV	JHEP 03 (2013) 111	CMS-SUS-12-001 1211.4784
31	CMS Collaboration	Search for supersymmetry with photons in pp collisions at $ \sqrt{s} = $ 8 TeV	PRD 92 (2015) 072006	CMS-SUS-14-004 1507.02898
32	P. Meade, N. Seiberg, and D. Shih	General gauge mediation	Prog. Theor. Phys. Suppl. 177 (2009) 143	0801.3278
33	M. Buican, P. Meade, N. Seiberg, and D. Shih	Exploring general gauge mediation	JHEP 03 (2009) 016	0812.3668
34	J. T. Ruderman and D. Shih	General neutralino NLSPs at the early LHC	JHEP 08 (2012) 159	1103.6083
35	Y. Kats, P. Meade, M. Reece, and D. Shih	The status of GMSB after 1 fb$^{-1}$ at the LHC	JHEP 02 (2012) 115	1110.6444
36	Y. Kats and M. J. Strassler	Probing colored particles with photons, leptons, and jets	JHEP 11 (2012) 097	1204.1119
37	P. Grajek, A. Mariotti, and D. Redigolo	Phenomenology of general gauge mediation in light of a 125 GeV Higgs	JHEP 07 (2013) 109	1303.0870
38	CMS Collaboration	Interpretation of searches for supersymmetry with simplified models	PRD 88 (2013) 052017	CMS-SUS-11-016 1301.2175
39	CMS Collaboration	Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV	JINST 10 (2015) P08010	CMS-EGM-14-001 1502.02702
40	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
41	CMS Collaboration	Particle-flow reconstruction and global event description with the CMS detector	JINST 12 (2017) P10003	CMS-PRF-14-001 1706.04965
42	CMS Collaboration	Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV	JINST 10 (2015) P06005	CMS-EGM-13-001 1502.02701
43	M. Cacciari, G. P. Salam, and G. Soyez	The anti-$ k_t $ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
44	M. Cacciari, G. P. Salam, and G. Soyez	FastJet user manual	EPJC 72 (2012) 1896	1111.6097
45	M. Cacciari and G. P. Salam	Pileup subtraction using jet areas	PLB 659 (2008) 119	0707.1378
46	CMS Collaboration	Determination of jet energy calibration and transverse momentum resolution in CMS	JINST 6 (2011) 11002	CMS-JME-10-011 1107.4277
47	CMS Collaboration	Performance of the CMS missing transverse momentum reconstruction in pp data at $ \sqrt{s} = $ 8 TeV	JINST 10 (2015) P02006	CMS-JME-13-003 1411.0511
48	J. Alwall et al.	The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations	JHEP 07 (2014) 079	1405.0301
49	J. Alwall et al.	Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions	EPJC 53 (2008) 473	0706.2569
50	R. Frederix and S. Frixione	Merging meets matching in MC@NLO	JHEP 12 (2012) 061	1209.6215
51	P. Nason	A new method for combining NLO QCD with shower Monte Carlo algorithms	JHEP 11 (2004) 040	hep-ph/0409146
52	S. Frixione, P. Nason, and C. Oleari	Matching NLO QCD computations with parton shower simulations: the POWHEG method	JHEP 11 (2007) 070	0709.2092
53	S. Alioli, P. Nason, C. Oleari, and E. Re	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX	JHEP 06 (2010) 043	1002.2581
54	T. Melia, P. Nason, R. Rontsch, and G. Zanderighi	W$ ^+ $W$ ^- $, WZ and ZZ production in the POWHEG BOX	JHEP 11 (2011) 078	1107.5051
55	P. Nason and G. Zanderighi	W$ ^+ $W$ ^- $, WZ and ZZ production in the POWHEG-BOX-V2	EPJC 74 (2014) 2702	1311.1365
56	T. Sjostrand, S. Mrenna, and P. Z. Skands	PYTHIA 6.4 physics and manual	JHEP 05 (2006) 026	hep-ph/0603175
57	G. Bozzi et al.	Production of Drell--Yan lepton pairs in hadron collisions: Transverse-momentum resummation at next-to-next-to-leading logarithmic accuracy	PLB 696 (2011) 207	1007.2351
58	T. Gehrmann et al.	W$ ^+ $W$ ^- $ production at hadron colliders in next-to-next-to leading order QCD	PRL 113 (2014) 212001	1408.5243
59	W. Beenakker, R. Hopker, M. Spira, and P. M. Zerwas	Squark and gluino production at hadron colliders	NPB 492 (1997) 51	hep-ph/9610490
60	A. Kulesza and L. Motyka	Threshold resummation for squark-antisquark and gluino-pair production at the LHC	PRL 102 (2009) 111802	0807.2405
61	A. Kulesza and L. Motyka	Soft gluon resummation for the production of gluino-gluino and squark-antisquark pairs at the LHC	PRD 80 (2009) 095004	0905.4749
62	W. Beenakker et al.	Soft-gluon resummation for squark and gluino hadroproduction	JHEP 12 (2009) 041	0909.4418
63	W. Beenakker et al.	Squark and gluino hadroproduction	Int. J. Mod. Phys. A 26 (2011) 2637	1105.1110
64	C. Borschensky et al.	Squark and gluino production cross sections in pp collisions at $ \sqrt{s} = $ 13, 14, 33 and 100 TeV	EPJC 74 (2014) 3174	1407.5066
65	W. Beenakker et al.	Production of charginos, neutralinos, and sleptons at hadron colliders	PRL 83 (1999) 3780	hep-ph/9906298
66	B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering	Gaugino production in proton-proton collisions at a center-of-mass energy of 8 TeV	JHEP 10 (2012) 081	1207.2159
67	B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering	Precision predictions for electroweak superpartner production at hadron colliders with $ \sc $ Resummino	EPJC 73 (2013) 2480	1304.0790
68	NNPDF Collaboration	Parton distributions for the LHC Run II	JHEP 04 (2015) 040	1410.8849
69	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2016) 155	CMS-GEN-14-001 1512.00815
70	GEANT4 Collaboration	GEANT4---a simulation toolkit	NIMA 506 (2003) 250
71	CMS CollaborationS. Abdullin, et al.	The fast simulation of the CMS detector at LHC	volume 331, p. 032049 2011
72	CMS Collaboration, S. Sekmen	Recent developments in CMS fast simulation	in Proceedings, 38th International Conference on High Energy Physics (ICHEP 2016), p. 181 Chicago, Illinois, USA, August, 2016 [PoS(ICHEP2016)181]	1701.03850
73	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020
74	CMS Collaboration	Technical proposal for the Phase-II upgrade of the Compact Muon Solenoid	CMS-PAS-TDR-15-002	CMS-PAS-TDR-15-002
75	CMS Collaboration	Measurement of the inclusive $ w $ and $ z $ production cross sections in pp collisions at $ \sqrt{s} = $ 7 TeV	JHEP 10 (2011) 132	CMS-EWK-10-005 1107.4789
76	J. Butterworth et al.	PDF4LHC recommendations for LHC Run II	JPG 43 (2016) 023001	1510.03865
77	CMS Collaboration	Measurement of the semileptonic $ \mathrm{t\bar{t}} $+$ \gamma $ production cross section in pp collisions at $ \sqrt{s} = $ 8 TeV	JHEP 10 (2017) 006	CMS-TOP-14-008 1706.08128
78	CMS Collaboration	CMS luminosity measurements for the 2016 data taking period	CMS-PAS-LUM-17-001	CMS-PAS-LUM-17-001
79	CMS Collaboration	Search for top-squark pair production in the single-lepton final state in pp collisions at $ \sqrt{s} = $ 8 TeV	EPJC 73 (2013) 2677	CMS-SUS-13-011 1308.1586
80	T. Junk	Confidence level computation for combining searches with small statistics	NIMA 434 (1999) 435	hep-ex/9902006
81	A. L. Read	Presentation of search results: the CLs technique	JPG 28 (2002) 2693
82	ATLAS, CMS, and LHC Higgs Combination Group collaborations	Procedure for the LHC Higgs boson search combination in Summer 2011	CMS-NOTE-2011-005
83	G. Cowan, K. Cranmer, E. Gross, and O. Vitells	Asymptotic formulae for likelihood-based tests of new physics	EPJC 71 (2011) 1554	1007.1727

Compact Muon Solenoid LHC, CERN

© Copyright CERN 2018 for the benefit of the CMS Collaboration