

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-16-047 ; CERN-EP-2018-027 | ||
| Search for high-mass resonances in dilepton final states in proton-proton collisions at $\sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 16 March 2018 | ||
| JHEP 06 (2018) 120 | ||
| Abstract: A search is presented for new high-mass resonances decaying into electron or muon pairs. The search uses proton-proton collision data at a centre-of-mass energy of 13 TeV collected by the CMS experiment at the LHC in 2016, corresponding to an integrated luminosity of 36 fb$^{-1}$. Observations are in agreement with standard model expectations. Upper limits on the product of a new resonance production cross section and branching fraction to dileptons are calculated in a model-independent manner. This permits the interpretation of the limits in models predicting a narrow dielectron or dimuon resonance. A scan of different intrinsic width hypotheses is performed. Limits are set on the masses of various hypothetical particles. For the $ \mathrm{Z}'_{\text{SSM}} $ ($\mathrm{Z}'_{\psi}$) particle, which arises in the sequential standard model (superstring-inspired model), a lower mass limit of 4.50 (3.90) TeV is set at 95% confidence level. The lightest Kaluza-Klein graviton arising in the Randall-Sundrum model of extra dimensions, with coupling parameters $k/\overline{M}_\mathrm{Pl}$ of 0.01, 0.05, and 0.10, is excluded at 95% confidence level below 2.10, 3.65, and 4.25 TeV, respectively. In a simplified model of dark matter production via a vector or axial vector mediator, limits at 95% confidence level are obtained on the masses of the dark matter particle and its mediator. | ||
| Links: e-print arXiv:1803.06292 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
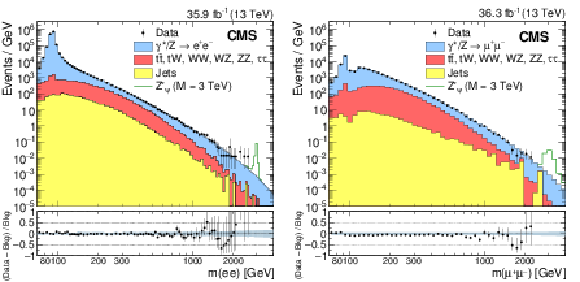
Figure 1:
The invariant mass spectra of dielectron (left) and dimuon (right) events. The points with error bars represent the observed yield. The histograms represent the expectations from the SM processes. The bins have equal width in logarithmic scale so that the width in GeV becomes larger with increasing mass. Example signal shapes for a narrow resonance with a mass of 3 TeV are shown by the stacked open histograms. The uncertainty bands in the ratio plots represent the systematic uncertainty in the background yields. |

png pdf |
Figure 1-a:
The invariant mass spectrum of dielectron events. The points with error bars represent the observed yield. The histograms represent the expectations from the SM processes. The bins have equal width in logarithmic scale so that the width in GeV becomes larger with increasing mass. Example signal shape for a narrow resonance with a mass of 3 TeV is shown by the stacked open histogram. The uncertainty band in the ratio plot represents the systematic uncertainty in the background yields. |
png pdf |
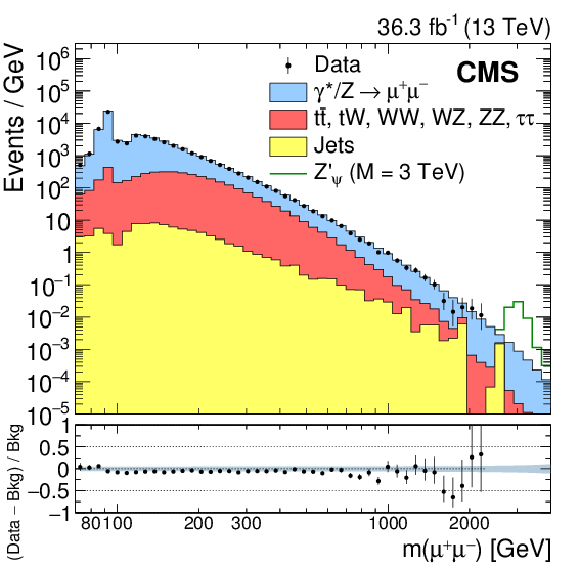
Figure 1-b:
The invariant mass spectrum of dimuon events. The points with error bars represent the observed yield. The histograms represent the expectations from the SM processes. The bins have equal width in logarithmic scale so that the width in GeV becomes larger with increasing mass. Example signal shape for a narrow resonance with a mass of 3 TeV is shown by the stacked open histogram. The uncertainty band in the ratio plot represents the systematic uncertainty in the background yields. |

png pdf |
Figure 2:
The cumulative distributions, where all events above the specified mass on the $x$ axis are summed, of the invariant mass spectra of dielectron (left) and dimuon (right) events. The points with error bars represent the observed yield. The histograms represent the expectations from SM processes. The uncertainty bands in the ratio plots represent the systematic uncertainty in the background yields. |

png pdf |
Figure 2-a:
The cumulative distribution, where all events above the specified mass on the $x$ axis are summed, of the invariant mass spectrum of dielectron events. The points with error bars represent the observed yield. The histograms represent the expectations from SM processes. The uncertainty band in the ratio plot represents the systematic uncertainty in the background yields. |
png pdf |
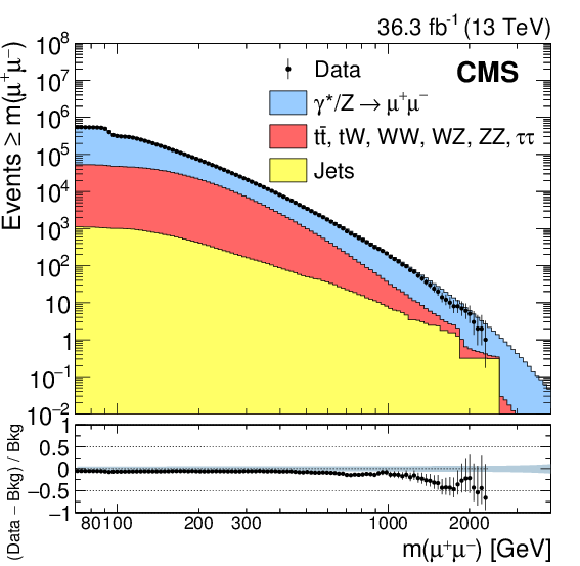
Figure 2-b:
The cumulative distribution, where all events above the specified mass on the $x$ axis are summed, of the invariant mass spectrum of dimuon events. The points with error bars represent the observed yield. The histograms represent the expectations from SM processes. The uncertainty band in the ratio plot represents the systematic uncertainty in the background yields. |

png pdf |
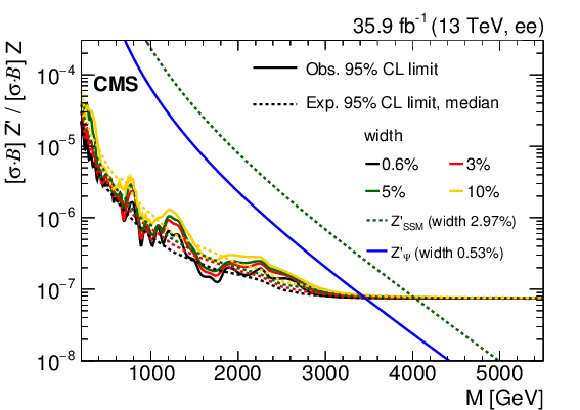
Figure 3:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction of a Z boson, for the dielectron channel (left), dimuon channel (right), and their combination (lower). The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ resonances are shown for comparison. |

png pdf |
Figure 3-a:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction of a Z boson, for the dielectron channel. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ resonances are shown for comparison. |

png pdf |
Figure 3-b:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction of a Z boson, for the dimuon channel. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ resonances are shown for comparison. |

png pdf |
Figure 3-c:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction of a Z boson, for the combination of dielectron and dimuon channels. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ resonances are shown for comparison. |

png pdf |
Figure 4:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-1 resonance, for widths equal to 0.6, 3, 5, and 10% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the dielectron channel (left), dimuon channel (right), and their combination (lower). Theoretical predictions for the spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ resonances are also shown. |
png pdf |
Figure 4-a:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-1 resonance, for widths equal to 0.6, 3, 5, and 10% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the dielectron channel. Theoretical predictions for the spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ resonances are also shown. |

png pdf |
Figure 4-b:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-1 resonance, for widths equal to 0.6, 3, 5, and 10% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the dimuon channel. Theoretical predictions for the spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ resonances are also shown. |

png pdf |
Figure 4-c:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-1 resonance, for widths equal to 0.6, 3, 5, and 10% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the combination of dielectron and dimuon channels. Theoretical predictions for the spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ resonances are also shown. |
png pdf |
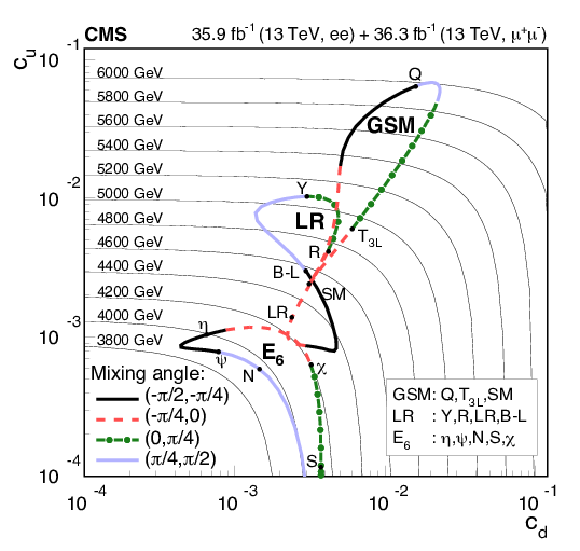
Figure 5:
Limits in the $(c_{{\mathrm {d}}},c_{{\mathrm {u}}})$ plane obtained by recasting the combined limit at 95% CL on the $ {{\mathrm {Z}^\prime}} $ boson cross section from dielectron and dimuon channels. For a given $ {{\mathrm {Z}^\prime}} $ boson mass, the cross section limit results in a solid thin black line. These lines are labelled with the relevant $ {{\mathrm {Z}^\prime}} $ boson masses. The closed contours representing the GSM, LR, and E$_6$ model classes are composed of thick line segments. Each point on a segment corresponds to a particular model, and the location of the point gives the mass limit on the relevant $ {{\mathrm {Z}^\prime}} $ boson. As indicated in the bottom left legend, the segment line styles correspond to ranges of the particular mixing angle for each considered model. The bottom right legend indicates the constituents of each model class. |
png pdf |
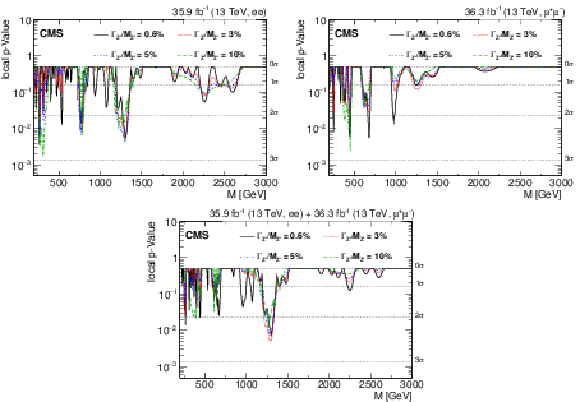
Figure 6:
The observed local $p$-value for the dielectron channel (left), dimuon channel (right), and their combination (lower) as a function of the dilepton invariant mass. |
png pdf |
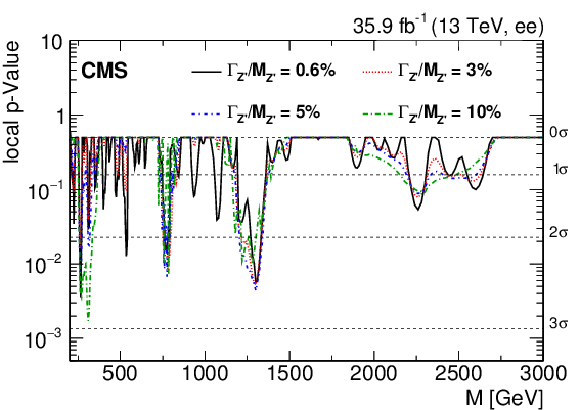
Figure 6-a:
The observed local $p$-value for the dielectron channel as a function of the dilepton invariant mass. |

png pdf |
Figure 6-b:
The observed local $p$-value for the dimuon channel as a function of the dilepton invariant mass. |

png pdf |
Figure 6-c:
The observed local $p$-value for the combination of dielectron and dimuon channels as a function of the dilepton invariant mass. |

png pdf |
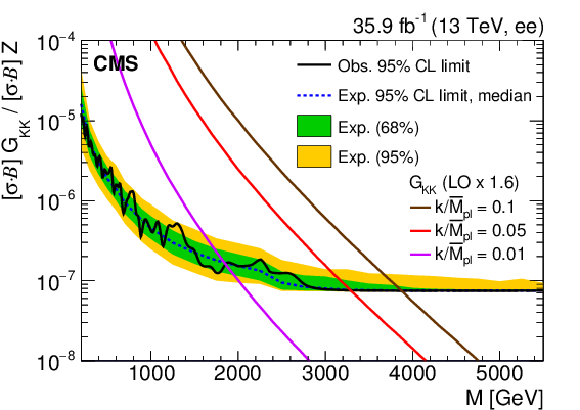
Figure 7:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-2 resonance, relative to the product of production cross section and branching fraction of a Z boson, for the dielectron channel (left), dimuon channel (right), and their combination (lower). The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-2 resonances with widths equal to 0.01, 0.36, and 1.42 GeV corresponding to coupling parameters $k/\overline {M}_\mathrm {Pl}$ of 0.01, 0.05, and 0.10 are shown for comparison. |
png pdf |
Figure 7-a:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-2 resonance, relative to the product of production cross section and branching fraction of a Z boson, for the dielectron channel. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-2 resonances with widths equal to 0.01, 0.36, and 1.42 GeV corresponding to coupling parameters $k/\overline {M}_\mathrm {Pl}$ of 0.01, 0.05, and 0.10 are shown for comparison. |
png pdf |
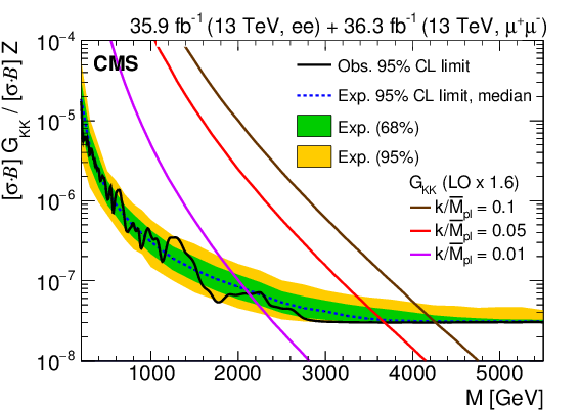
Figure 7-b:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-2 resonance, relative to the product of production cross section and branching fraction of a Z boson, for the dimuon channel. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-2 resonances with widths equal to 0.01, 0.36, and 1.42 GeV corresponding to coupling parameters $k/\overline {M}_\mathrm {Pl}$ of 0.01, 0.05, and 0.10 are shown for comparison. |
png pdf |
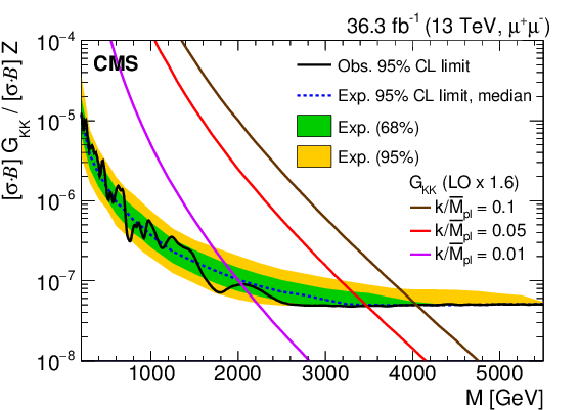
Figure 7-c:
The upper limits at 95% CL on the product of production cross section and branching fraction for a spin-2 resonance, relative to the product of production cross section and branching fraction of a Z boson, for the combination of dielectron and dimuon channels. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-2 resonances with widths equal to 0.01, 0.36, and 1.42 GeV corresponding to coupling parameters $k/\overline {M}_\mathrm {Pl}$ of 0.01, 0.05, and 0.10 are shown for comparison. |

png pdf |
Figure 8:
Limits at 95% confidence level for the masses of the DM particle, which is assumed to be Dirac fermion, and its associated mediator, in a simplified model of DM production via a vector (left) or axial vector (right) mediator. The parameter exclusion is obtained by comparing the limits on product of the production cross section and the branching fraction for decay to a Z boson, with the values obtained from calculations in the simplified model. For each combination of the DM particle and mediator mass values, the width of the mediator is taken into account in the limit calculation. The lines with the hatching represents the excluded regions. The solid grey lines, marked as "$\Omega h^{2} \ge 0.12$'', correspond to parameter regions that reproduce the observed DM relic density in the universe [62,63,4,26], with the hatched area indicating the region where the DM relic abundance exceeds the observed value. |

png pdf |
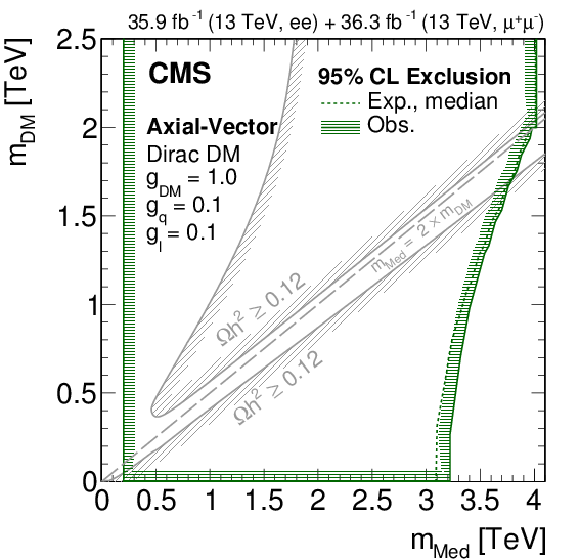
Figure 8-a:
Limits at 95% confidence level for the masses of the DM particle, which is assumed to be Dirac fermion, and its associated mediator, in a simplified model of DM production via a vector mediator. The parameter exclusion is obtained by comparing the limits on product of the production cross section and the branching fraction for decay to a Z boson, with the values obtained from calculations in the simplified model. For each combination of the DM particle and mediator mass values, the width of the mediator is taken into account in the limit calculation. The lines with the hatching represents the excluded regions. The solid grey lines, marked as "$\Omega h^{2} \ge 0.12$'', correspond to parameter regions that reproduce the observed DM relic density in the universe [62,63,4,26], with the hatched area indicating the region where the DM relic abundance exceeds the observed value. |
png pdf |
Figure 8-b:
Limits at 95% confidence level for the masses of the DM particle, which is assumed to be Dirac fermion, and its associated mediator, in a simplified model of DM production via a axial vector mediator. The parameter exclusion is obtained by comparing the limits on product of the production cross section and the branching fraction for decay to a Z boson, with the values obtained from calculations in the simplified model. For each combination of the DM particle and mediator mass values, the width of the mediator is taken into account in the limit calculation. The lines with the hatching represents the excluded regions. The solid grey lines, marked as "$\Omega h^{2} \ge 0.12$'', correspond to parameter regions that reproduce the observed DM relic density in the universe [62,63,4,26], with the hatched area indicating the region where the DM relic abundance exceeds the observed value. |
| Tables | |
png pdf |
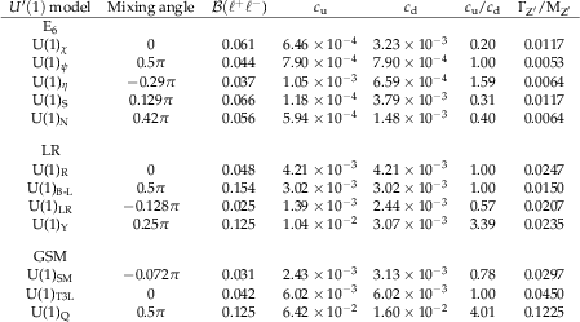
Table 1:
Various benchmark models with their corresponding mixing angles, their branching fraction ($\mathcal {B}$) to dileptons, the $c_{{\mathrm {u}}}$ and $c_{{\mathrm {d}}}$ parameter values and their ratio, and the width to mass ratio of the associated $ {{\mathrm {Z}^\prime}} $ boson. |

png pdf |
Table 2:
The number of dielectron events in various invariant mass ranges. The total background is the sum of the events for the SM processes listed. The yields from simulation are normalized relative to the expected cross sections, and overall the simulation is normalized to the observed yield using the number of events in the mass window 60-120 GeV. Uncertainties include both statistical and systematic components, summed in quadrature. |

png pdf |
Table 3:
The number of dimuon events in various invariant mass ranges. The total background is the sum of the events for the SM processes listed. The yields from simulation are normalized relative to the expected cross sections, and overall the simulation is normalized to the observed yield using the number of events in the mass window 60-120 GeV, acquired using a prescaled low threshold trigger. Uncertainties include both statistical and systematic components, summed in quadrature. |

png pdf |
Table 4:
The observed and expected 95% CL lower limits on the masses of spin-1 $ {{\mathrm {Z}'}_\mathrm {SSM}} $ and $ {{\mathrm {Z}'}_\psi} $ bosons, assuming a signal width of 0.6% (3.0%) of the resonance mass for $ {{\mathrm {Z}'}_\psi} $ ($ {{\mathrm {Z}'}_\mathrm {SSM}} $). |

png pdf |
Table 5:
The observed and expected 95% CL lower limits on the masses of spin-2 resonances with widths equal to 0.01, 0.36 and 1.42 GeV corresponding to coupling parameters $k/\overline {M}_\mathrm {Pl}$ of 0.01, 0.05, and 0.10. |
| Summary |
|
A search for narrow resonances in dielectron and dimuon invariant mass spectra has been performed using data recorded in 2016 from proton-proton collisions at $\sqrt{s} = $ 13 TeV. The integrated luminosity for the dielectron sample is 35.9 fb$^{-1}$ and for the dimuon sample is 36.3 fb$^{-1}$. Observations are in agreement with standard model expectations. Upper limits at 95% confidence level on the product of a narrow-resonance production cross section and branching fraction to dileptons have been calculated in a model-independent manner to enable interpretation in the framework of models predicting a narrow dielectron or dimuon resonance. A scan of different intrinsic width hypotheses is performed. Limits are set on the masses of various hypothetical particles. For the $\mathrm{Z}'_{\text{SSM}}$ particle, which arises in the sequential standard model, and for the superstring-inspired $\mathrm{Z}'_{\psi}$ particle, 95% confidence level lower mass limits for the combined channels are found to be 4.50 and 3.90 TeV, respectively. These limits extend the previous ones from CMS by 1.1 TeV in both models. The corresponding limits for Kaluza-Klein gravitons arising in the Randall-Sundrum model of extra dimensions with coupling parameters $k/\overline{M}_\mathrm{Pl}$ of 0.01, 0.05, and 0.10 are 2.10, 3.65, and 4.25 TeV, respectively. The limits extend previous published CMS results by 0.6 (1.1) TeV for a $k/\overline{M}_\mathrm{Pl}$ value of 0.01 (0.10). Finally, limits at 95% confidence level are obtained for the masses of the dark matter particle and its associated mediator, in a simplified model of dark matter production via a vector or axial vector mediator. |
| References | ||||
| 1 | A. Leike | The phenomenology of extra neutral gauge bosons | PR 317 (1999) 143 | hep-ph/9805494 |
| 2 | P. Langacker | The physics of heavy Z' gauge bosons | Rev. Mod. Phys. 81 (2009) 1199 | 0801.1345 |
| 3 | L. Randall and R. Sundrum | A large mass hierarchy from a small extra dimension | PRL 83 (1999) 3370 | hep-ph/9905221 |
| 4 | Planck Collaboration | Planck 2015 results. XIII. Cosmological parameters | Astron. Astrophys. 594 (2016) A13 | 1502.01589 |
| 5 | M. S. Carena, A. Daleo, B. A. Dobrescu, and T. M. P. Tait | Z' gauge bosons at the Tevatron | PRD 70 (2004) 093009 | hep-ph/0408098 |
| 6 | E. Accomando et al. | Z' physics with early LHC data | PRD 83 (2011) 075012 | 1010.6058 |
| 7 | G. Altarelli, B. Mele, and M. Ruiz-Altaba | Searching for new heavy vector bosons in $ {\mathrm{p}}\mathrm{\bar{p}} $ colliders | Z. Phys. C 45 (1989) 109, . [Erratum: Z. Phys. C 47 (1990) 676] | |
| 8 | J. L. Hewett and T. G. Rizzo | Low-energy phenomenology of superstring-inspired E$ _6 $ models | PR 183 (1989) 193 | |
| 9 | E. Accomando et al. | Z' at the LHC: Interference and Finite Width Effects in Drell-Yan | JHEP 10 (2013) 153 | 1304.6700 |
| 10 | CMS Collaboration | Search for resonances in the dilepton mass distribution in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s}= $ 7 TeV | JHEP 05 (2011) 093 | CMS-EXO-10-013 1103.0981 |
| 11 | CMS Collaboration | Search for narrow resonances in dilepton mass spectra in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s}= $ 7 TeV | PLB 714 (2012) 158 | CMS-EXO-11-019 1206.1849 |
| 12 | CMS Collaboration | Search for heavy narrow dilepton resonances in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s}= $ 7 TeV and $ \sqrt{s}= $ 8 TeV | PLB 720 (2013) 63 | CMS-EXO-12-015 1212.6175 |
| 13 | CMS Collaboration | Search for physics beyond the standard model in dilepton mass spectra in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | JHEP 04 (2015) 025 | CMS-EXO-12-061 1412.6302 |
| 14 | CMS Collaboration | Search for narrow resonances in dilepton mass spectra in proton-proton collisions at $ \sqrt{s} = $ 13 TeV and combination with 8 TeV data | PLB 768 (2017) 57 | CMS-EXO-15-005 1609.05391 |
| 15 | ATLAS Collaboration | Search for high mass dilepton resonances in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s}= $ 7 TeV with the ATLAS experiment | PLB 700 (2011) 163 | 1103.6218 |
| 16 | ATLAS Collaboration | Search for high-mass resonances decaying to dilepton final states in $ {\mathrm{p}}{\mathrm{p}} $ collisions at $ \sqrt{s} = $ 7 TeV with the ATLAS detector | JHEP 11 (2012) 138 | 1209.2535 |
| 17 | ATLAS Collaboration | Search for high-mass dilepton resonances in pp collisions at $ \sqrt{s}= $ 8 TeV with the ATLAS detector | PRD 90 (2014) 052005 | 1405.4123 |
| 18 | ATLAS Collaboration | Search for new high-mass phenomena in the dilepton final state using 36.1 fb$ ^{-1} $ of proton-proton collision data at $ \sqrt{s} = $ 13 TeV with the ATLAS detector | JHEP 10 (2017) 182 | 1707.02424 |
| 19 | L. Randall and R. Sundrum | An alternative to compactification | PRL 83 (1999) 4690 | hep-th/9906064 |
| 20 | CDF Collaboration | Search for high-mass $ e^+e^- $ resonances in $ {\mathrm{p}}\mathrm{\bar{p}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PRL 102 (2009) 031801 | 0810.2059 |
| 21 | CDF Collaboration | A search for high-mass resonances decaying to dimuons at CDF | PRL 102 (2009) 091805 | 0811.0053 |
| 22 | D0 Collaboration | Search for Randall--Sundrum gravitons in the dielectron and diphoton final states with 5.4 fb$ ^{-1} $ of data from $ {\mathrm{p}}\mathrm{\bar{p}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PRL 104 (2010) 241802 | 1004.1826 |
| 23 | D0 Collaboration | Search for a heavy neutral gauge boson in the dielectron channel with 5.4 fb$ ^{-1} $ of $ {\mathrm{p}}\mathrm{\bar{p}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PLB 695 (2011) 88 | 1008.2023 |
| 24 | CDF Collaboration | Search for high mass resonances decaying to muon pairs in $ \sqrt{s} = $ 1.96 TeV ${\mathrm{p}}\mathrm{\bar{p}} $ collisions | PRL 106 (2011) 121801 | 1101.4578 |
| 25 | CDF Collaboration | Search for new dielectron resonances and Randall--Sundrum gravitons at the Collider Detector at Fermilab | PRL 107 (2011) 051801 | 1103.4650 |
| 26 | A. Albert et al. | Recommendations of the LHC Dark Matter Working Group: Comparing LHC searches for heavy mediators of dark matter production in visible and invisible decay channels | 1703.05703 | |
| 27 | M. Backovi\'c et al. | Higher-order QCD predictions for dark matter production at the LHC in simplified models with $ s $ channel mediators | EPJC 75 (2015) 482 | 1508.05327 |
| 28 | C. Battilana | The CMS muon system: status and upgrades for LHC Run-2 and performance of muon reconstruction with 13 TeV data | JINST 12 (2017) C01048 | |
| 29 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 30 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 31 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 32 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 33 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 34 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO vector-boson production matched with shower in POWHEG | JHEP 07 (2008) 060 | 0805.4802 |
| 35 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 36 | E. Re | Single-top $ \mathrm{W}\mathrm{t} $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 37 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 38 | T. Sjostrand et al. | An Introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 39 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 40 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 41 | A. Manohar, P. Nason, G. P. Salam, and G. Zanderighi | How bright is the proton? A precise determination of the photon parton distribution function | PRL 117 (2016) 242002 | 1607.04266 |
| 42 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 43 | D. Bourilkov | Photon-induced background for dilepton searches and measurements in pp collisions at 13 TeV | 1606.00523 | |
| 44 | D. Bourilkov | Exploring the LHC Landscape with dileptons | 1609.08994 | |
| 45 | M. Czakon and A. Mitov | Top++: a program for the calculation of the top-pair cross-section at hadron colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 46 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 47 | M. R. Whalley, D. Bourilkov, and R. C. Group | The Les Houches accord PDFs (LHAPDF) and LHAGLUE | in HERA and the LHC: A Workshop on the implications of HERA for LHC physics. Proceedings, Part B 2005 | hep-ph/0508110 |
| 48 | D. Bourilkov, R. C. Group, and M. R. Whalley | LHAPDF: PDF use from the Tevatron to the LHC | in TeV4LHC Workshop - 4th meeting Batavia, Illinois, October 20-22, 2005 (2006) | hep-ph/0605240 |
| 49 | A. Buckley et al. | LHAPDF6: parton density access in the LHC precision era | EPJC 75 (2015) 132 | 1412.7420 |
| 50 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 51 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 52 | CMS Collaboration | Performance of CMS muon reconstruction in $ {\mathrm{p}}{\mathrm{p}} $ collision events at $ \sqrt{s} = $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 53 | ATLAS and CMS Collaborations | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 54 | L. Moneta et al. | The RooStats Project | in 13$^\textth$ International Workshop on Advanced Computing and Analysis Techniques in Physics Research (ACAT2010) SISSA, 2010 PoS(ACAT2010)057 | 1009.1003 |
| 55 | BaBar Collaboration | Study of $ B \to X\gamma $ decays and determination of $ |V_{td}/V_{ts}| $ | PRD 82 (2010) 051101 | 1005.4087 |
| 56 | M. J. Oreglia | A study of the reactions $\psi' \to \gamma\gamma \psi$ | PhD thesis, Stanford University, 1980 SLAC Report SLAC-R-236, see Appendix D | |
| 57 | NNPDF Collaboration | Parton distributions with LHC data | NPB 867 (2013) 244 | 1207.1303 |
| 58 | E. Gross and O. Vitells | Trial factors or the look elsewhere effect in high energy physics | EPJC 70 (2010) 525 | 1005.1891 |
| 59 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 60 | P. Mathews, V. Ravindran, and K. Sridhar | NLO-QCD corrections to dilepton production in the Randall--Sundrum model | JHEP 10 (2005) 031 | hep-ph/0506158 |
| 61 | J. Alwall et al. | Computing decay rates for new physics theories with FeynRules and $ MadGraph5\_aMCatNLO $ | CPC 197 (2015) 312 | 1402.1178 |
| 62 | M. Backovi\'c et al. | MadDM: New dark matter tool in the LHC era | AIP Conf. Proc. 1743 (2016) 060001 | 1509.03683 |
| 63 | M. Backovi\'c, K. Kong, and M. McCaskey | MadDM v.1.0: Computation of Dark Matter Relic Abundance using $ MadGraph5 $ | Phys. Dark Univ. 5-6 (2014) 18 | 1308.4955 |
| 64 | CMS Collaboration | Search for dark matter produced with an energetic jet or a hadronically decaying W or Z boson at $ \sqrt{s}= $ 13 TeV | JHEP 07 (2017) 014 | CMS-EXO-16-037 1703.01651 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|