

Compact Muon Solenoid
LHC, CERN
| CMS-EXO-15-005 ; CERN-EP-2016-209 | ||
| Search for narrow resonances in dilepton mass spectra in proton-proton collisions at $ \sqrt{s} = $ 13 TeV and combination with 8 TeV data | ||
| CMS Collaboration | ||
| 18 September 2016 | ||
| Phys. Lett. B 768 (2017) 57 | ||
| Abstract: A search for narrow resonances in dielectron and dimuon invariant mass spectra has been performed using data obtained from proton-proton collisions at $ \sqrt{s} = $ 13 TeV collected with the CMS detector. The integrated luminosity for the dielectron sample is 2.7 fb$^{-1}$ and for the dimuon sample 2.9 fb$^{-1}$. The sensitivity of the search is increased by combining these data with a previously analysed set of data obtained at $ \sqrt{s} = $ 8 TeV and corresponding to a luminosity of 20 fb$^{-1}$. No evidence for non-standard-model physics is found, either in the 13 TeV data set alone, or in the combined data set. Upper limits on the product of production cross section and branching fraction have also been calculated in a model-independent manner to enable interpretation in models predicting a narrow dielectron or dimuon resonance structure. Limits are set on the masses of hypothetical particles that could appear in new-physics scenarios. For the $\mathrm{Z}'_{\text{SSM}}$ particle, which arises in the sequential standard model, and for the superstring inspired $\mathrm{Z}'_{\psi}$ particle, 95% confidence level lower mass limits for the combined data sets and combined channels are found to be 3.37 and 2.82 TeV, respectively. The corresponding limits for Kaluza-Klein gravitons arising in the Randall-Sundrum model of extra dimensions with coupling parameters 0.01 and 0.10 are 1.46 and 3.11 TeV, respectively. These results significantly extend previous limits. | ||
| Links: e-print arXiv:1609.05391 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
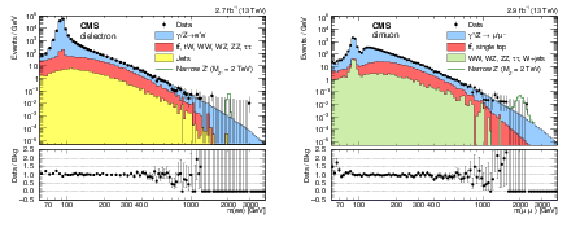
Figure 1:
The invariant mass spectrum of (left) dielectron and (right) dimuon events at $ \sqrt{s} = $ 13 TeV. The points with error bars represent the data. The histograms represent the expectations from SM processes. The bins have equal width in logarithmic scale but the width in GeV becomes larger with increasing mass. Example signal shapes for a narrow resonance with a mass of 2 TeV are shown by the stacked open histograms. |

png pdf |
Figure 1-a:
The invariant mass spectrum of dielectron events at $ \sqrt{s} = $ 13 TeV. The points with error bars represent the data. The histograms represent the expectations from SM processes. The bins have equal width in logarithmic scale but the width in GeV becomes larger with increasing mass. Example signal shapes for a narrow resonance with a mass of 2 TeV are shown by the stacked open histograms. |
png pdf |
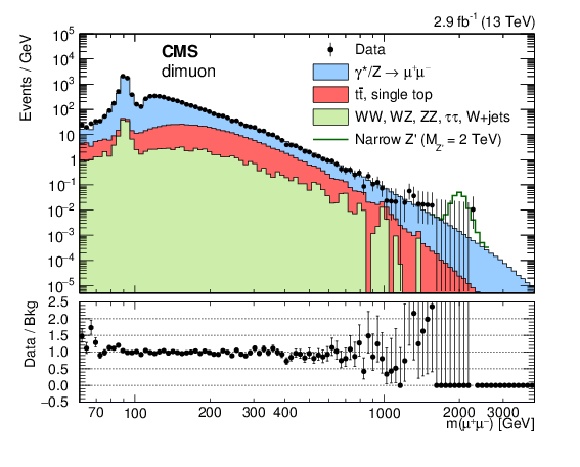
Figure 1-b:
The invariant mass spectrum of dimuon events at $ \sqrt{s} = $ 13 TeV. The points with error bars represent the data. The histograms represent the expectations from SM processes. The bins have equal width in logarithmic scale but the width in GeV becomes larger with increasing mass. Example signal shapes for a narrow resonance with a mass of 2 TeV are shown by the stacked open histograms. |

png pdf |
Figure 2:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the (left) dielectron and (right) dimuon channels in the 13 TeV data. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are shown for comparison. |
png pdf |
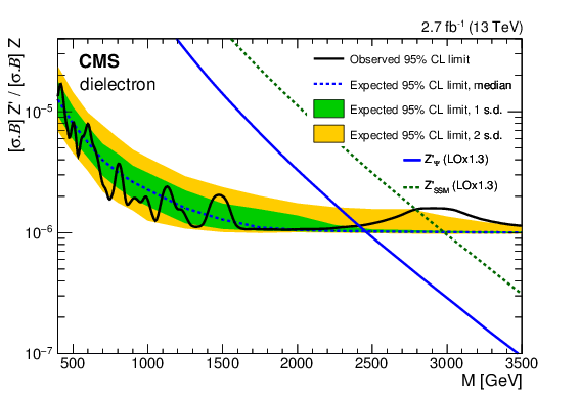
Figure 2-a:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the dielectron channel in the 13 TeV data. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are shown for comparison. |

png pdf |
Figure 2-b:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the dimuon channel in the 13 TeV data. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are shown for comparison. |
png pdf |
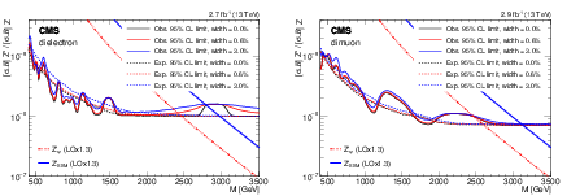
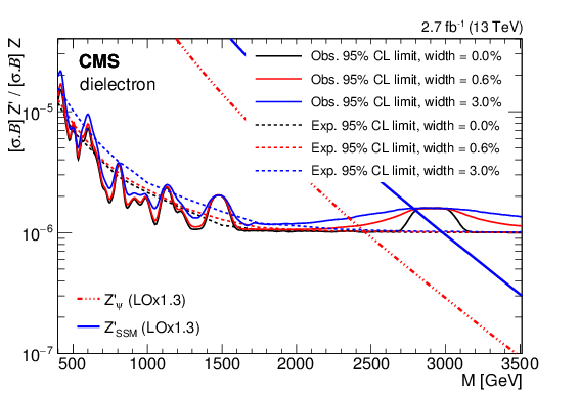
Figure 3:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance for widths equal to 0, 0.6, and 3.0% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the (left) dielectron and (right) dimuon channels in the 13 TeV data. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |
png pdf |
Figure 3-a:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance for widths equal to 0, 0.6, and 3.0% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the dielectron channel in the 13 TeV data. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |

png pdf |
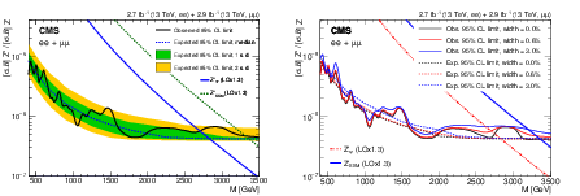
Figure 3-b:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance for widths equal to 0, 0.6, and 3.0% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the dimuon channel in the 13 TeV data. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |
png pdf |
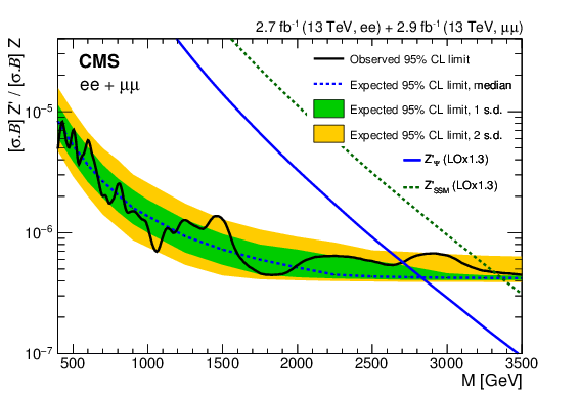
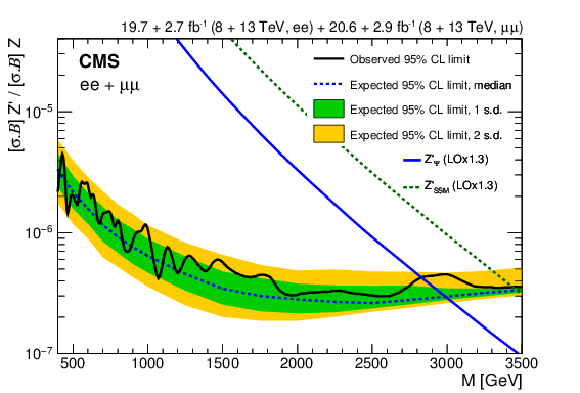
Figure 4:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance, relative to the product of production cross section and branching fraction for a Z boson, for the combined dielectron and dimuon channels in the 13 TeV data, (left) for a resonance width equal to 0.6% of the resonance mass and (right) for resonance widths equal to 0, 0.6, and 3.0% of the resonance mass. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |
png pdf |
Figure 4-a:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance, relative to the product of production cross section and branching fraction for a Z boson, for the combined dielectron and dimuon channels in the 13 TeV data, for a resonance width equal to 0.6% of the resonance mass. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |

png pdf |
Figure 4-b:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance, relative to the product of production cross section and branching fraction for a Z boson, for the combined dielectron and dimuon channels in the 13 TeV data, for resonance widths equal to 0, 0.6, and 3.0% of the resonance mass. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |
png pdf |
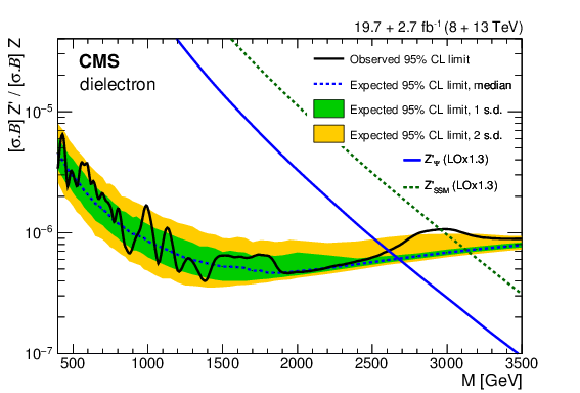
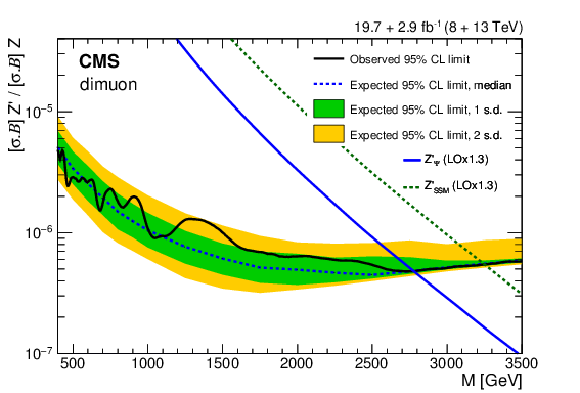
Figure 5:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the combined 8 and 13 TeV data in the (left) dielectron and (right) dimuon channel. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |
png pdf |
Figure 5-a:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the combined 8 and 13 TeV data in the dielectron channel. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |
png pdf |
Figure 5-b:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the combined 8 and 13 TeV data in the dimuon channel. The shaded bands correspond to the 68 and 95% quantiles for the expected limits. Theoretical predictions for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances are also shown. |
png pdf |
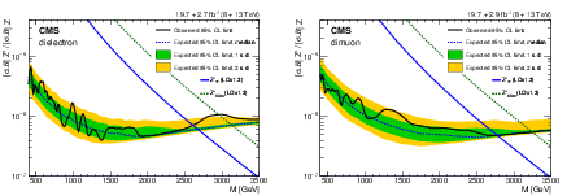
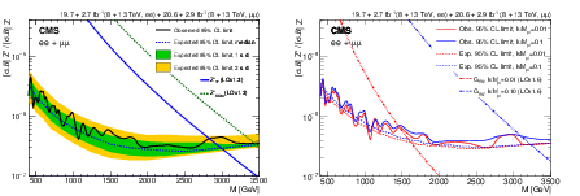
Figure 6:
The 95% CL upper limits on the product of production cross section and branching fraction for (left) a spin-1 resonance with a width equal to 0.6% of the resonance mass and (right) for a spin-2 RS graviton, both relative to the product of production cross section and branching fraction for a Z boson, for the combined dielectron and dimuon channels and combined 8 and 13 TeV data. For the spin-1 results (left plot), the shaded bands correspond to the 68 and 95% quantiles for the expected limits, and theoretical predictions are shown for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances. For the spin-2 results (right plot), observed limits, expected limits, and theoretical predictions are shown for values of the coupling parameter $k/\overline {M}_\mathrm {Pl}= $ 0.01 and 0.10. |
png pdf |
Figure 6-a:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-1 resonance with a width equal to 0.6% of the resonance mass, relative to the product of production cross section and branching fraction for a Z boson, for the combined dielectron and dimuon channels and combined 8 and 13 TeV data. The shaded bands correspond to the 68 and 95% quantiles for the expected limits, and theoretical predictions are shown for the spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ resonances. |
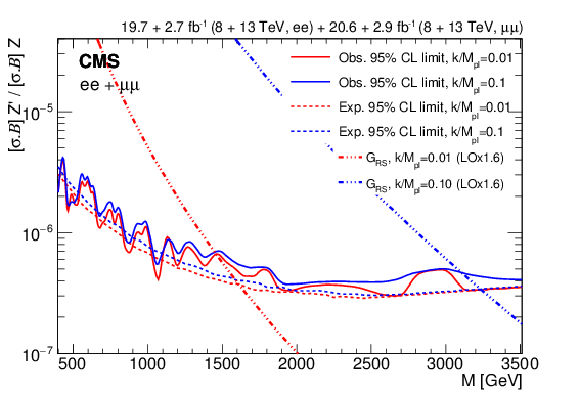
png pdf |
Figure 6-b:
The 95% CL upper limits on the product of production cross section and branching fraction for a spin-2 RS graviton, relative to the product of production cross section and branching fraction for a Z boson, for the combined dielectron and dimuon channels and combined 8 and 13 TeV data. Observed limits, expected limits, and theoretical predictions are shown for values of the coupling parameter $k/\overline {M}_\mathrm {Pl}= $ 0.01 and 0.10. |
| Tables | |

png pdf |
Table 1:
The observed and expected 95% CL lower limits on the masses of spin-1 $\mathrm{Z}'_{\text{SSM}}$ and $\mathrm{Z}'_{\psi}$ bosons for the combination of the 8 and 13 TeV data, assuming a signal width of 0.6% of the resonance mass for $\mathrm{Z}'_{\psi}$ and 3% for $\mathrm{Z}'_{\text{SSM}}$ . |

png pdf |
Table 2:
The observed and expected 95% CL lower limits on the masses of spin-2 Kaluza-Klein gravitons in the Randall-Sundrum model, for two values of the coupling parameter, $k/\overline {M}_\mathrm {Pl}$. |
| Summary |
| A search for narrow resonances in dielectron and dimuon invariant mass spectra has been performed using data obtained from proton-proton collisions at $ \sqrt{s} = $ 13 TeV. The integrated luminosity for the dielectron sample is 2.7 fb$^{-1}$ and for the dimuon sample 2.9 fb$^{-1}$. The sensitivity of the search is increased by combining these data with a previously analysed set of data obtained at $ \sqrt{s} = $ 8 TeV and corresponding to a luminosity of 20 fb$^{-1}$. No evidence for non-standard-model physics is found, either in the 13 TeV data set alone, or in the combined data set. Upper limits at 95% confidence level on the product of production cross section and branching fraction have also been calculated in a model-independent manner to enable interpretation in models predicting a narrow dielectron or dimuon resonance structure. Limits are set on the masses of hypothetical particles that could appear in new-physics scenarios. For the $\mathrm{Z}'_{\text{SSM}}$ particle, which arises in the sequential standard model, and for the superstring inspired $\mathrm{Z}'_{\psi}$ particle, 95% confidence level lower mass limits for the combined data sets and combined channels are found to be 3.37 and 2.82 TeV, respectively. The corresponding limits for Kaluza-Klein gravitons arising in the Randall-Sundrum model of extra dimensions with coupling parameters 0.01 and 0.10 are 1.46 and 3.11 TeV, respectively. These results significantly extend previous limits. |
| References | ||||
| 1 | J. Ellis | Outstanding questions: physics beyond the standard model | Phil. Trans. R. Soc. A 370 (2012) 818 | |
| 2 | D. Kazakov | The Higgs boson is found: what is next? | Phys.-Usp. 57 (2014) 930 | hep-ph |
| 3 | G. Altarelli, B. Mele, and M. Ruiz-Altaba | Searching for new heavy vector bosons in $ \mathrm{ p }\Pap $ colliders | Z. Phys. C 45 (1989) 109 | |
| 4 | A. Leike | The phenomenology of extra neutral gauge bosons | PR 317 (1999) 143 | hep-ph/9805494 |
| 5 | J. L. Hewett and T. G. Rizzo | Low-energy phenomenology of superstring-inspired E$ _6 $ models | PR 183 (1989) 193 | |
| 6 | L. Randall and R. Sundrum | An alternative to compactification | PRL 83 (1999) 4690 | hep-th/9906064 |
| 7 | L. Randall and R. Sundrum | A large mass hierarchy from a small extra dimension | PRL 83 (1999) 3370 | hep-ph/9905221 |
| 8 | ATLAS Collaboration | Search for high-mass dilepton resonances in pp collisions at $ \sqrt{s}= $ 8 ~TeV with the ATLAS detector | PRD 90 (2014) 052005 | 1405.4123 |
| 9 | CMS Collaboration | Search for physics beyond the standard model in dilepton mass spectra in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | JHEP 04 (2015) 025 | CMS-EXO-12-061 1412.6302 |
| 10 | ATLAS Collaboration | Search for high-mass new phenomena in the dilepton final state using proton-proton collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | PLB 761 (2016) 372 | 1607:03669 |
| 11 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 12 | CMS Collaboration | The TriDAS project technical design report, volume i: The trigger systems | CDS | |
| 13 | CMS Collaboration | The TriDAS project technical design report, volume ii: Data acquisition and high-level trigger | CDS | |
| 14 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s} = $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 15 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 16 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 17 | D. Bourilkov | Photon-induced Background for Dilepton Searches and Measurements in pp Collisions at 13 TeV | 1606.00523 | |
| 18 | NNPDF Collaboration | Parton distributions with QED corrections | NPB 877 (2013) 290 | 1308.0598 |
| 19 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 20 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 21 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 22 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO vector-boson production matched with shower in POWHEG | JHEP 07 (2008) 060 | 0805.4802 |
| 23 | S. Frixione, P. Nason, and G. Ridolfi | A positive-weight next-to-leading-order Monte Carlo for heavy flavour hadroproduction | JHEP 09 (2007) 126 | 0707.3088 |
| 24 | E. Re | Single-top $ \mathrm{ W }\mathrm{t } $-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 25 | T. Sjostrand et al. | An Introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 26 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 27 | R. D. Ball et al. | Parton distributions with LHC data | NPB 867 (2013) 244 | 1207.1303 |
| 28 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 29 | M. R. Whalley, D. Bourilkov, and R. C. Group | The Les Houches accord PDFs (LHAPDF) and LHAGLUE | in HERA and the LHC: A Workshop on the implications of HERA for LHC physics. Proceedings, Part B 2005 | hep-ph/0508110 |
| 30 | D. Bourilkov, R. C. Group, and M. R. Whalley | LHAPDF: PDF use from the Tevatron to the LHC | hep-ph/0605240 | |
| 31 | A. Buckley et al. | LHAPDF6: parton density access in the LHC precision era | EPJC 75 (2015) 132 | 1412.7420 |
| 32 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 33 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 34 | E. Accomando et al. | Z' at the LHC: Interference and Finite Width Effects in Drell-Yan | JHEP 10 (2013) 153 | 1304.6700 |
| 35 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 36 | P. Mathews, V. Ravindran, and K. Sridhar | NLO-QCD corrections to dilepton production in the Randall--Sundrum model | JHEP 10 (2005) 031 | hep-ph/0506158 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|