Loading [MathJax]/jax/output/CommonHTML/jax.js

Compact Muon Solenoid
LHC, CERN

Visit us: CMS Public Website, CMS Physics ; Contact us: CMS Publications Committee

CMS-BPH-23-005 ; CERN-EP-2024-120

Search for CP violation in $\mathrm{D^0}\to\mathrm{K^0_S}\mathrm{K^0_S}$ decays in proton-proton collisions at $\sqrt{s} =$ 13 TeV

CMS Collaboration

19 May 2024

Eur. Phys. J. C 84 (2024) 1264

Abstract: A search is reported for charge-parity CP violation in $\mathrm{D^0}\to\mathrm{K^0_S}\mathrm{K^0_S}$ decays, using data collected in proton-proton collisions at $\sqrt{s} =$ 13 TeV recorded by the CMS experiment in 2018. The analysis uses a dedicated data set that corresponds to an integrated luminosity of 41.6 fb$^{-1}$, which consists of about 10 billion events containing a pair of b hadrons, nearly all of which decay to charm hadrons. The flavor of the neutral $\mathrm{D}$ meson is determined by the pion charge in the reconstructed decays $\mathrm{D}^{*+}\to\mathrm{D^0}\pi^{+}$ and $\mathrm{D}^{*-}\to\overline{\mathrm{D}}^{0}\pi^{-}$. The CP asymmetry in $\mathrm{D^0}\to\mathrm{K^0_S}\mathrm{K^0_S}$ is measured to be $A_{CP}(\mathrm{K^0_S}\mathrm{K^0_S}) =$ (6.2 $\pm$ 3.0 $\pm$ 0.2 $\pm$ 0.8)%, where the three uncertainties represent the statistical uncertainty, the systematic uncertainty, and the uncertainty in the measurement of the CP asymmetry in the $\mathrm{D^0}\to\mathrm{K^0_S}\pi^{+}\pi^{-}$ decay. This is the first CP asymmetry measurement by CMS in the charm sector as well as the first to utilize a fully hadronic final state.

Links: e-print arXiv:2405.11606 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ;

Figures
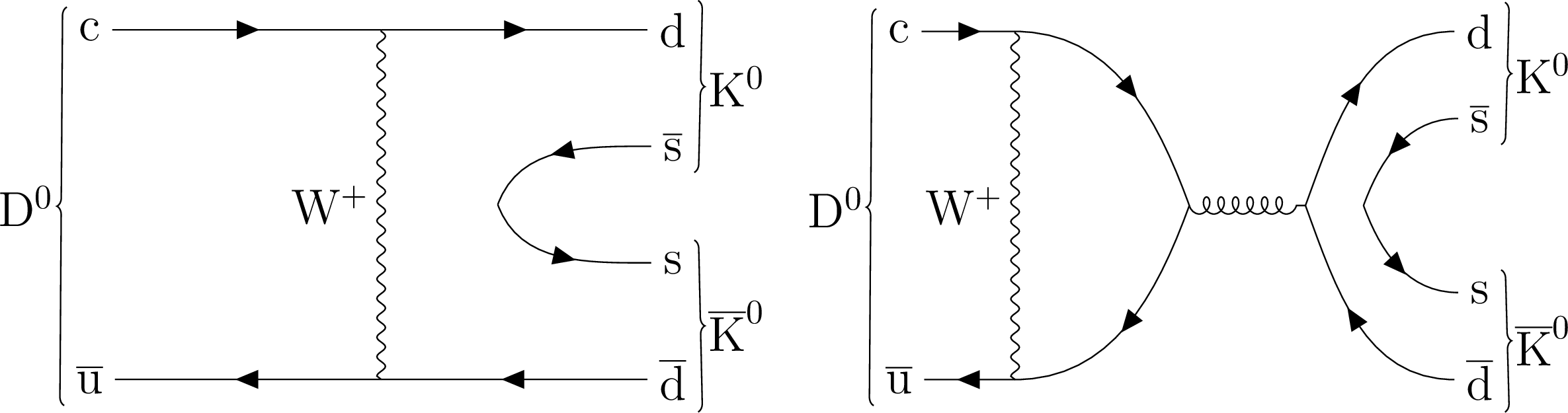
png pdf	Figure 1: The decay of neutral charm meson to two neutral kaons: exchange (left) and penguin annihilation (right) diagrams.
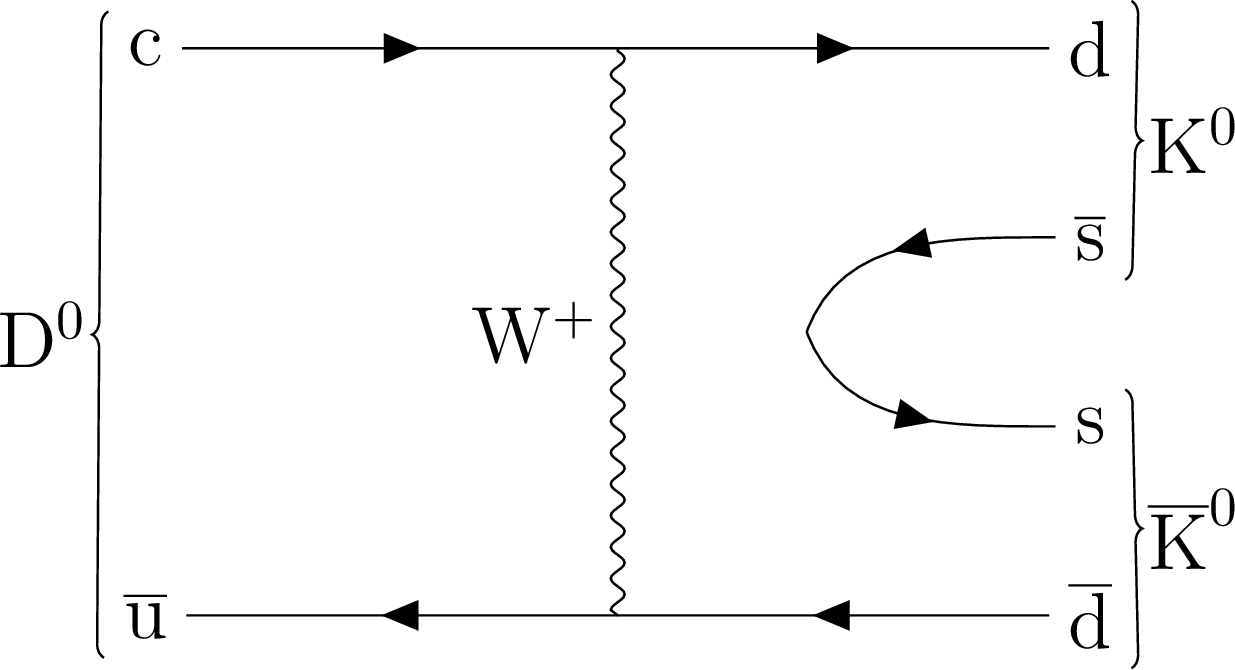
png pdf	Figure 1-a: The decay of neutral charm meson to two neutral kaons: exchange (left) and penguin annihilation (right) diagrams.
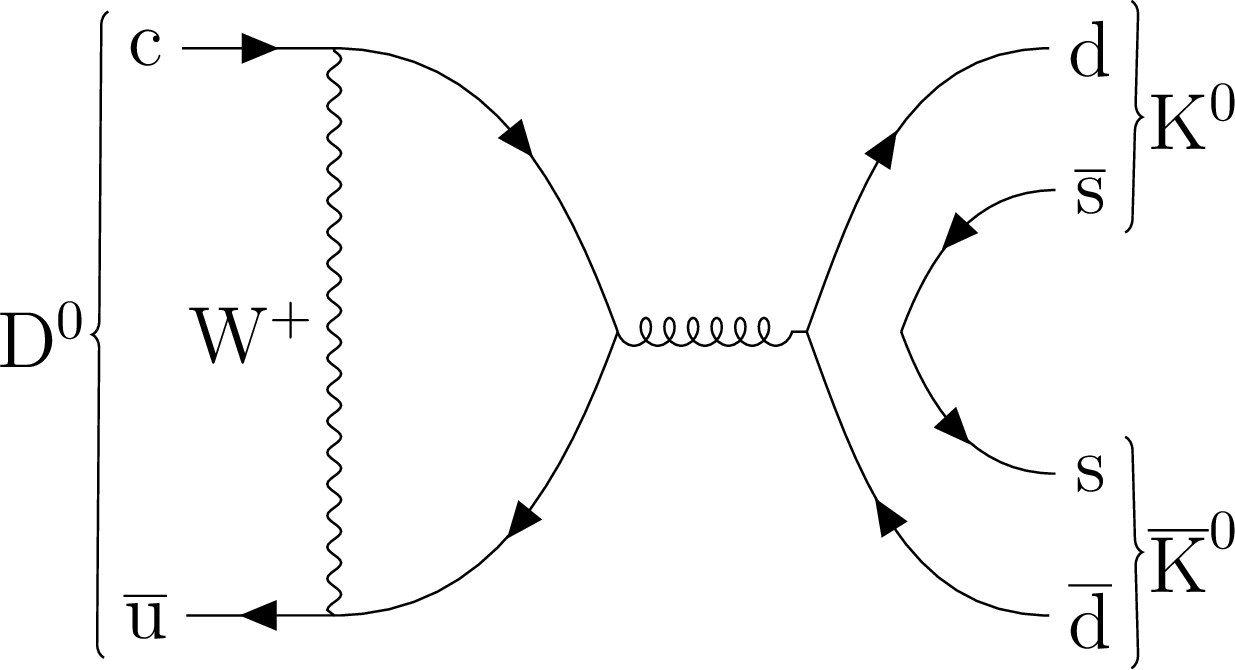
png pdf	Figure 1-b: The decay of neutral charm meson to two neutral kaons: exchange (left) and penguin annihilation (right) diagrams.
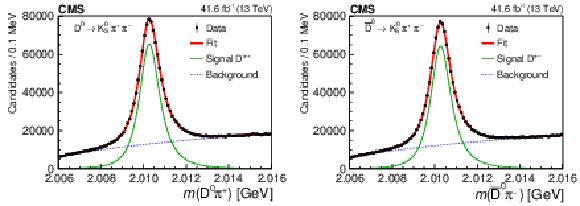
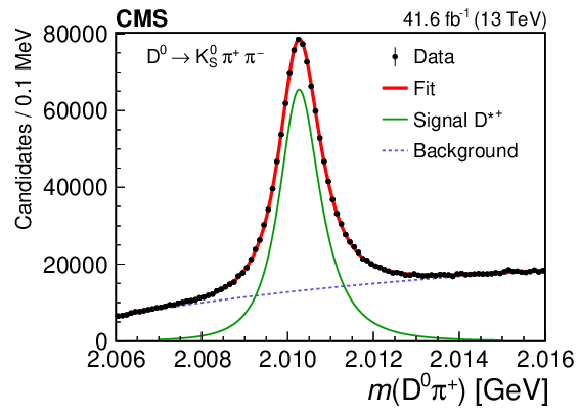
png pdf	Figure 2: The $\mathrm{D^0}\pi^{+}$ (left) and $\overline{\mathrm{D}}^{0}\pi^{-}$ (right) invariant mass distributions for the $\mathrm{K^0_S}\pi^{+}\pi^{-}$ channel, with the result of the fit to both distributions.
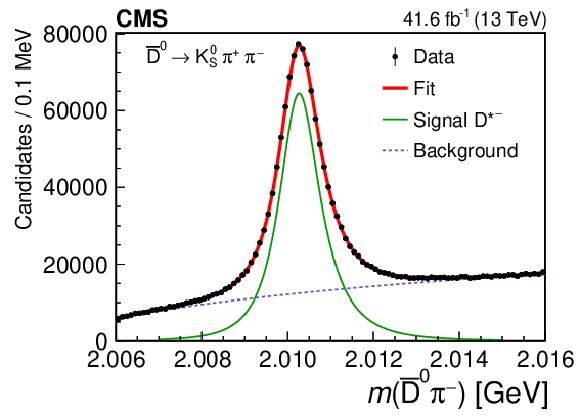
png pdf	Figure 2-a: The $\mathrm{D^0}\pi^{+}$ (left) and $\overline{\mathrm{D}}^{0}\pi^{-}$ (right) invariant mass distributions for the $\mathrm{K^0_S}\pi^{+}\pi^{-}$ channel, with the result of the fit to both distributions.
png pdf	Figure 2-b: The $\mathrm{D^0}\pi^{+}$ (left) and $\overline{\mathrm{D}}^{0}\pi^{-}$ (right) invariant mass distributions for the $\mathrm{K^0_S}\pi^{+}\pi^{-}$ channel, with the result of the fit to both distributions.
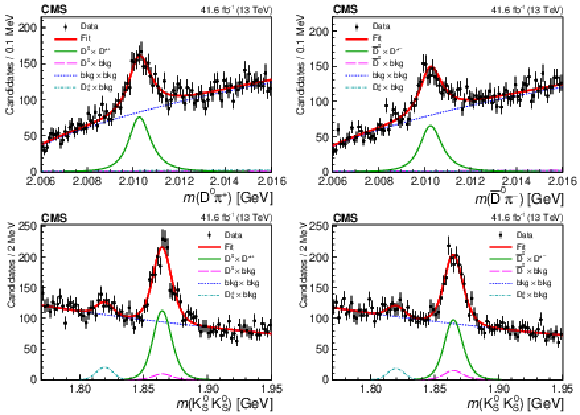
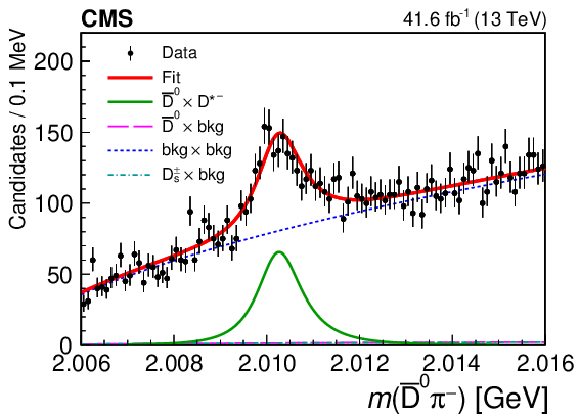
png pdf	Figure 3: The invariant mass distributions for $\mathrm{D}^{*+}$ candidates (left) and $\mathrm{D}^{*-}$ candidates (right), with the $m(\mathrm{D}\pi^{\pm})$ distributions in the upper row and the $m(\mathrm{K^0_S}\mathrm{K^0_S})$ distributions in the lower row. Projections of the simultaneous 2D fit are also shown.
png pdf	Figure 3-a: The invariant mass distributions for $\mathrm{D}^{*+}$ candidates (left) and $\mathrm{D}^{*-}$ candidates (right), with the $m(\mathrm{D}\pi^{\pm})$ distributions in the upper row and the $m(\mathrm{K^0_S}\mathrm{K^0_S})$ distributions in the lower row. Projections of the simultaneous 2D fit are also shown.
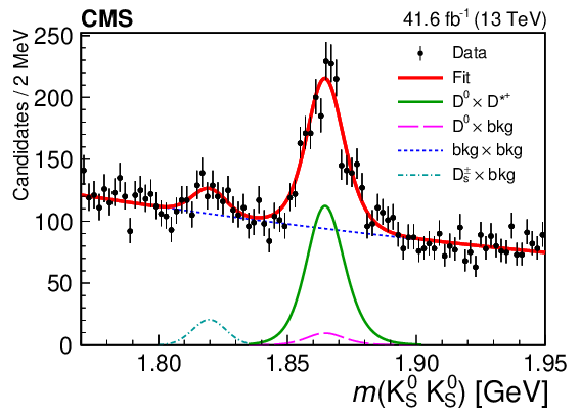
png pdf	Figure 3-b: The invariant mass distributions for $\mathrm{D}^{*+}$ candidates (left) and $\mathrm{D}^{*-}$ candidates (right), with the $m(\mathrm{D}\pi^{\pm})$ distributions in the upper row and the $m(\mathrm{K^0_S}\mathrm{K^0_S})$ distributions in the lower row. Projections of the simultaneous 2D fit are also shown.
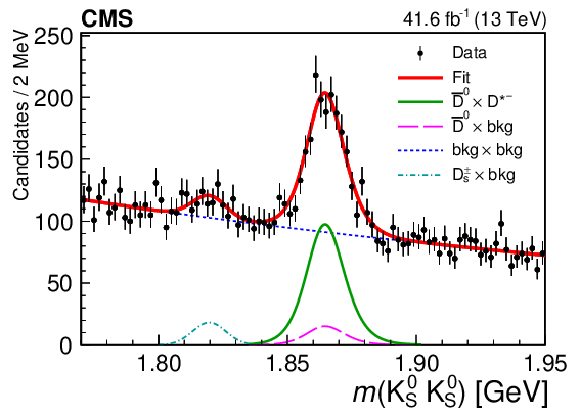
png pdf	Figure 3-c: The invariant mass distributions for $\mathrm{D}^{*+}$ candidates (left) and $\mathrm{D}^{*-}$ candidates (right), with the $m(\mathrm{D}\pi^{\pm})$ distributions in the upper row and the $m(\mathrm{K^0_S}\mathrm{K^0_S})$ distributions in the lower row. Projections of the simultaneous 2D fit are also shown.
png pdf	Figure 3-d: The invariant mass distributions for $\mathrm{D}^{*+}$ candidates (left) and $\mathrm{D}^{*-}$ candidates (right), with the $m(\mathrm{D}\pi^{\pm})$ distributions in the upper row and the $m(\mathrm{K^0_S}\mathrm{K^0_S})$ distributions in the lower row. Projections of the simultaneous 2D fit are also shown.
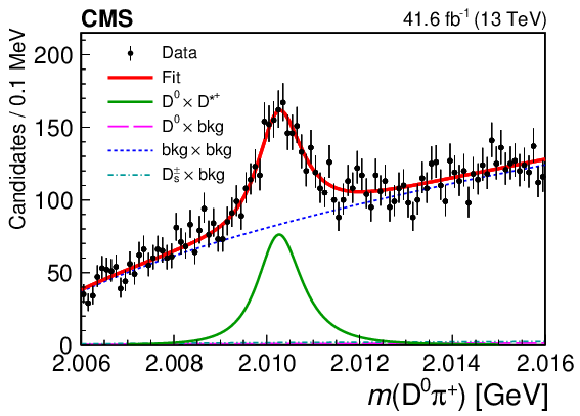
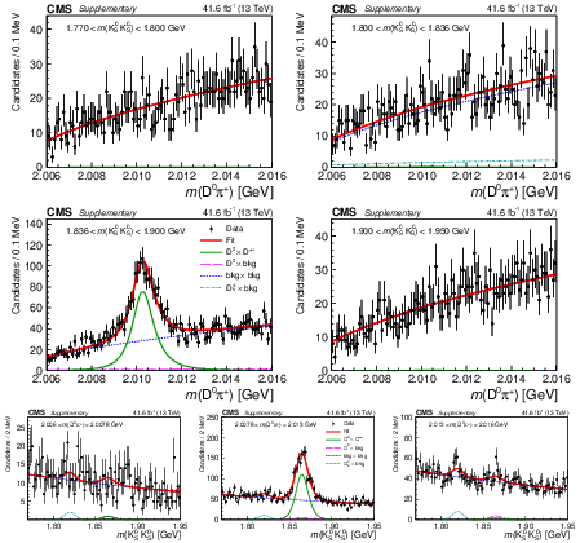
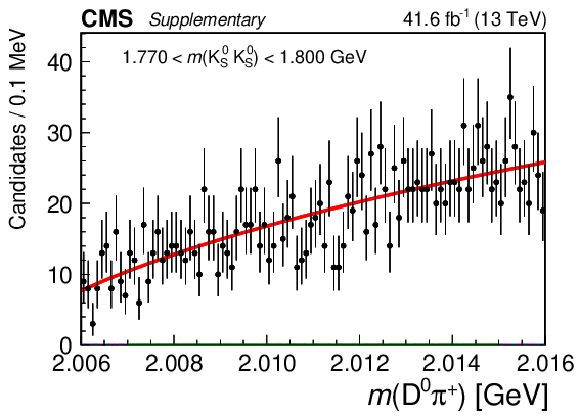
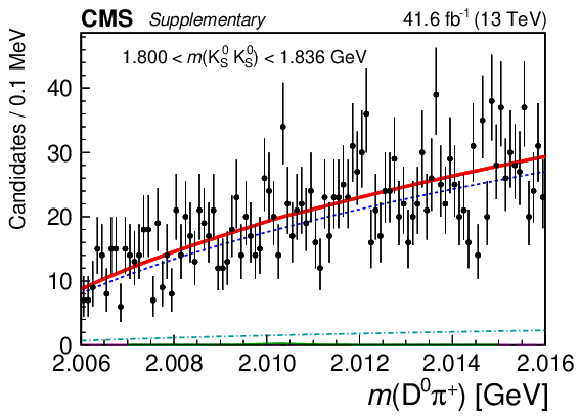
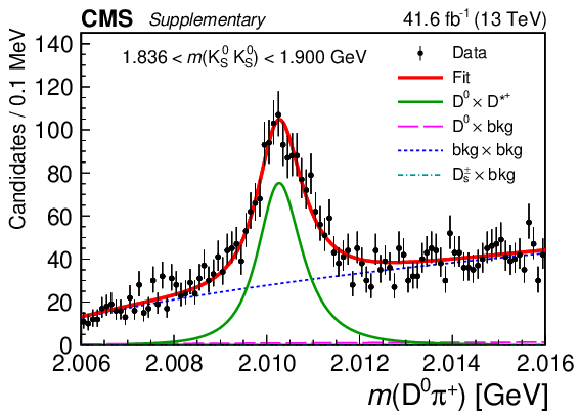
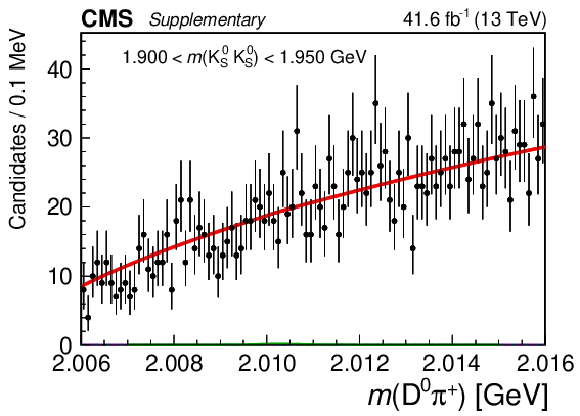
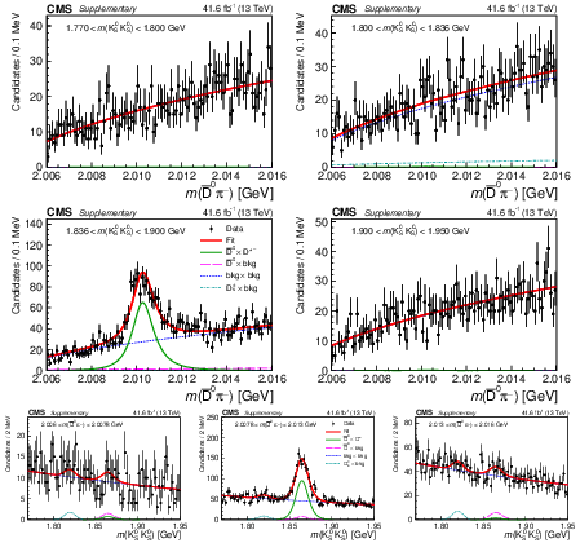
png pdf	Figure 4: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*+}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\mathrm{D^0}\pi^{+})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\mathrm{D^0}\pi^{+})$: left sideband (left), signal region of $\mathrm{D^0}\pi^{+}$ (center), and right sideband (right).
png pdf	Figure 4-a: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*+}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\mathrm{D^0}\pi^{+})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\mathrm{D^0}\pi^{+})$: left sideband (left), signal region of $\mathrm{D^0}\pi^{+}$ (center), and right sideband (right).
png pdf	Figure 4-b: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*+}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\mathrm{D^0}\pi^{+})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\mathrm{D^0}\pi^{+})$: left sideband (left), signal region of $\mathrm{D^0}\pi^{+}$ (center), and right sideband (right).
png pdf	Figure 4-c: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*+}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\mathrm{D^0}\pi^{+})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\mathrm{D^0}\pi^{+})$: left sideband (left), signal region of $\mathrm{D^0}\pi^{+}$ (center), and right sideband (right).
png pdf	Figure 4-d: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*+}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\mathrm{D^0}\pi^{+})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\mathrm{D^0}\pi^{+})$: left sideband (left), signal region of $\mathrm{D^0}\pi^{+}$ (center), and right sideband (right).
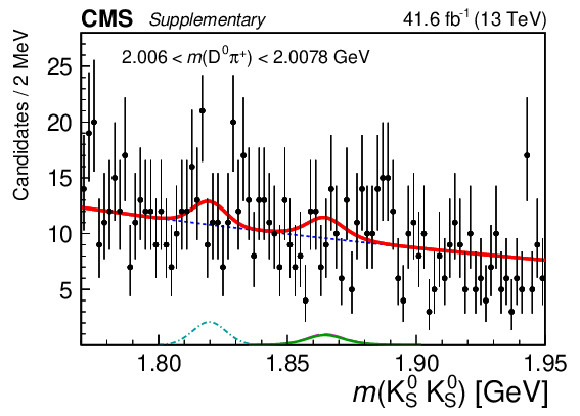
png pdf	Figure 4-e: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*+}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\mathrm{D^0}\pi^{+})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\mathrm{D^0}\pi^{+})$: left sideband (left), signal region of $\mathrm{D^0}\pi^{+}$ (center), and right sideband (right).
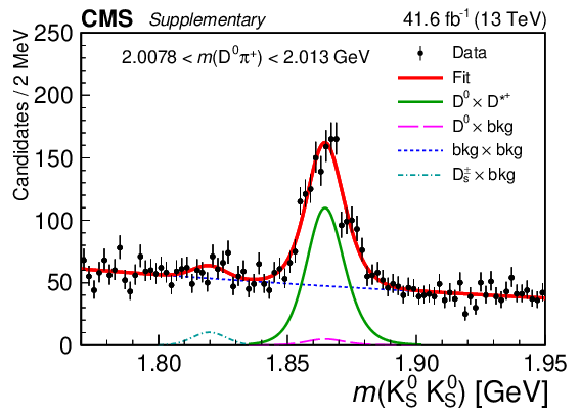
png pdf	Figure 4-f: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*+}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\mathrm{D^0}\pi^{+})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\mathrm{D^0}\pi^{+})$: left sideband (left), signal region of $\mathrm{D^0}\pi^{+}$ (center), and right sideband (right).
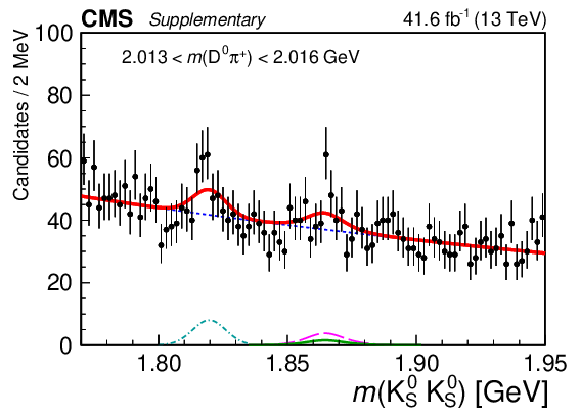
png pdf	Figure 4-g: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*+}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\mathrm{D^0}\pi^{+})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\mathrm{D^0}\pi^{+})$: left sideband (left), signal region of $\mathrm{D^0}\pi^{+}$ (center), and right sideband (right).
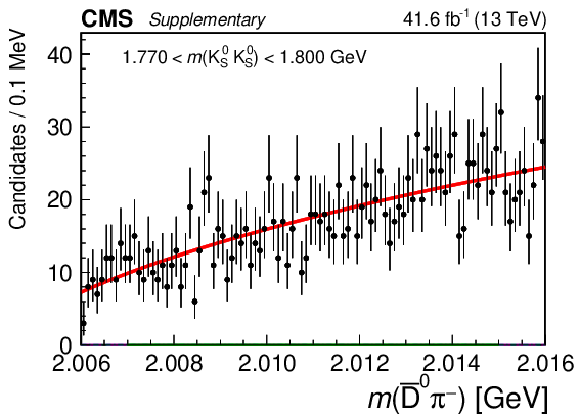
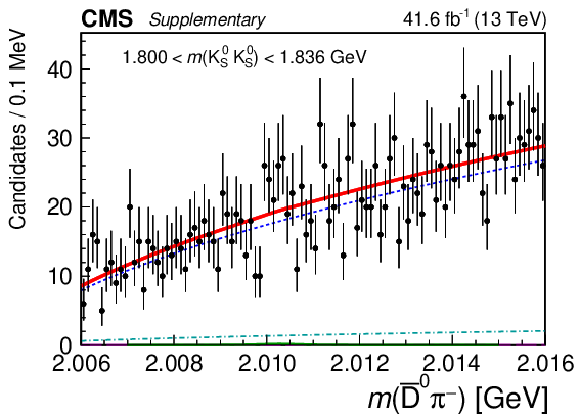
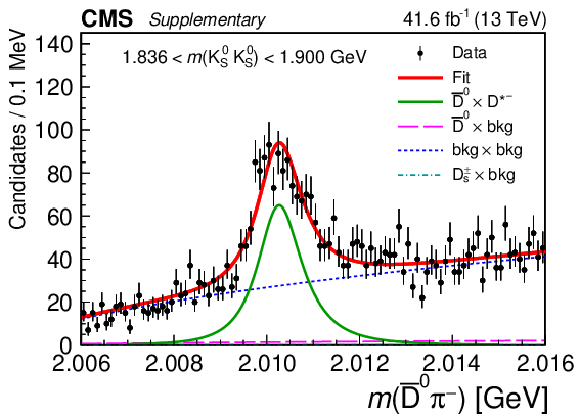
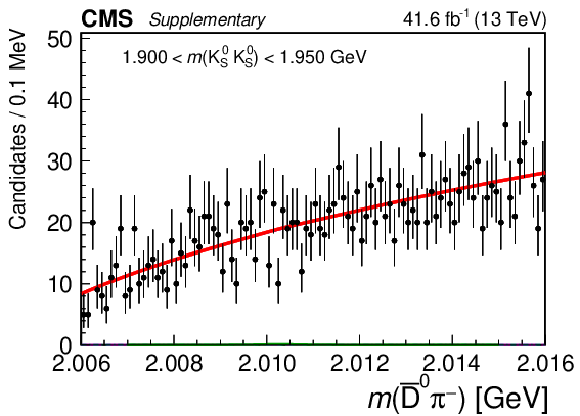
png pdf	Figure 5: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*-}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\overline{\mathrm{D}}^{0}\pi^{-})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\overline{\mathrm{D}}^{0}\pi^{-})$: left sideband (left), signal region of $\overline{\mathrm{D}}^{0}\pi^{-}$ (center), and right sideband (right).
png pdf	Figure 5-a: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*-}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\overline{\mathrm{D}}^{0}\pi^{-})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\overline{\mathrm{D}}^{0}\pi^{-})$: left sideband (left), signal region of $\overline{\mathrm{D}}^{0}\pi^{-}$ (center), and right sideband (right).
png pdf	Figure 5-b: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*-}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\overline{\mathrm{D}}^{0}\pi^{-})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\overline{\mathrm{D}}^{0}\pi^{-})$: left sideband (left), signal region of $\overline{\mathrm{D}}^{0}\pi^{-}$ (center), and right sideband (right).
png pdf	Figure 5-c: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*-}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\overline{\mathrm{D}}^{0}\pi^{-})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\overline{\mathrm{D}}^{0}\pi^{-})$: left sideband (left), signal region of $\overline{\mathrm{D}}^{0}\pi^{-}$ (center), and right sideband (right).
png pdf	Figure 5-d: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*-}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\overline{\mathrm{D}}^{0}\pi^{-})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\overline{\mathrm{D}}^{0}\pi^{-})$: left sideband (left), signal region of $\overline{\mathrm{D}}^{0}\pi^{-}$ (center), and right sideband (right).
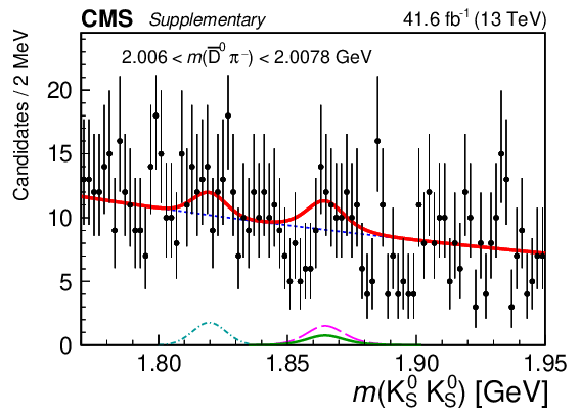
png pdf	Figure 5-e: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*-}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\overline{\mathrm{D}}^{0}\pi^{-})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\overline{\mathrm{D}}^{0}\pi^{-})$: left sideband (left), signal region of $\overline{\mathrm{D}}^{0}\pi^{-}$ (center), and right sideband (right).
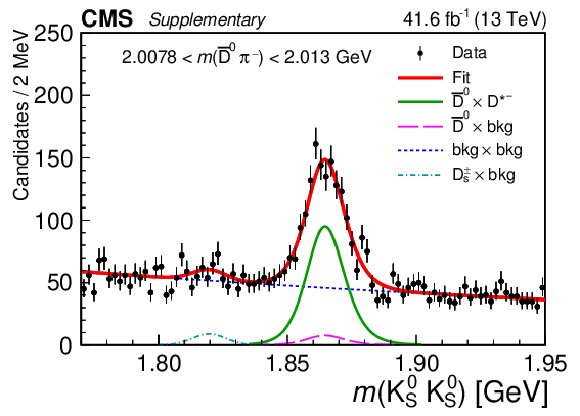
png pdf	Figure 5-f: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*-}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\overline{\mathrm{D}}^{0}\pi^{-})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\overline{\mathrm{D}}^{0}\pi^{-})$: left sideband (left), signal region of $\overline{\mathrm{D}}^{0}\pi^{-}$ (center), and right sideband (right).
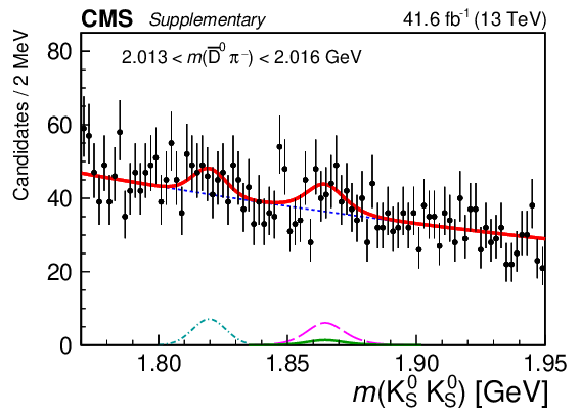
png pdf	Figure 5-g: Results of the 2D fit to the $m(\mathrm{D}\pi^{\pm}) \times m(\mathrm{K^0_S}\mathrm{K^0_S})$ for the signal channel, $\mathrm{D}^{*-}$ candidates. Upper and middle rows show 1D projections of the 2D fit on $m(\overline{\mathrm{D}}^{0}\pi^{-})$ in ranges of $m(\mathrm{K^0_S}\mathrm{K^0_S})$: left sideband (upper left), region of $\mathrm{D}_{s}^{\pm}\to\mathrm{K^0_S}\mathrm{K^0_S}\pi^{\pm}$ contamination (upper right), signal region of $\mathrm{K^0_S}\mathrm{K^0_S}$ (middle left), and right sideband (middle right). Lower row shows 1D projections of the 2D fit on $m(\mathrm{K^0_S}\mathrm{K^0_S})$ in ranges of $m(\overline{\mathrm{D}}^{0}\pi^{-})$: left sideband (left), signal region of $\overline{\mathrm{D}}^{0}\pi^{-}$ (center), and right sideband (right).

Tables
png pdf	Table 1: Optimized selection criteria in the signal channel $\mathrm{K^0_S}\mathrm{K^0_S}$. The requirements on the $\mathrm{K^0_S}$ candidates in the third and fourth lines are given first for the $\mathrm{K^0_S}$ with larger $p_{\mathrm{T}}$, then for the $\mathrm{K^0_S}$ with lower $p_{\mathrm{T}}$.
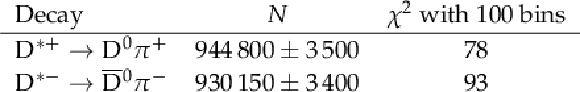
png pdf	Table 2: Results of the fit to the selected $\mathrm{D}^{*+}\to\mathrm{D^0}\pi^{+}$ and $\mathrm{D}^{*-}\to\overline{\mathrm{D}}^{0}\pi^{-}$ candidates, where $\mathrm{D^0}\,(\overline{\mathrm{D}}^{0}) \to\mathrm{K^0_S}\pi^{+}\pi^{-}$. The ${\mathrm{D}^{\ast}(2010)^{\pm}}$ signal yields $N$ given in the second column are used in the evaluation of $A_{CP}^{\text{raw}}$. The uncertainties are statistical only.
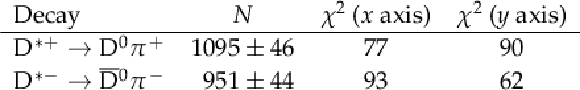
png pdf	Table 3: Results of the 2D fit to the selected $\mathrm{D}^{*+}\to\mathrm{D^0}\pi^{+}$ and $\mathrm{D}^{*-}\to\overline{\mathrm{D}}^{0}\pi^{-}$ candidates, where $\mathrm{D^0}\,(\overline{\mathrm{D}}^{0}) \to\mathrm{K^0_S}\mathrm{K^0_S}$. The ${\mathrm{D}^{\ast}(2010)^{\pm}}$ signal yields $N$ given in the second column are used in the evaluation of $A_{CP}^{\text{raw}}$. The $\chi^2$ corresponds to the fit projection with 100 bins in the $x = m(\mathrm{D}\pi^{\pm})$ axis and 90 bins in the $y = m(\mathrm{K^0_S}\mathrm{K^0_S})$ axis, as shown in Fig 3. The uncertainties are statistical only.
png pdf	Table 4: Absolute systematic uncertainties in the measurement of $\Delta A_{CP}$.

Summary

A measurement of CP violation in $\mathrm{D^0}$ decays is reported, using proton-proton collision data collected at $\sqrt{s} =$ 13 TeV with a novel high-rate data stream (B parking). These data correspond to an integrated luminosity of 41.6 fb$^{-1}$ and include about 10 billion events containing beauty hadron decays. The difference in the CP asymmetries between $\mathrm{D^0}\to\mathrm{K^0_S}\mathrm{K^0_S}$ and $\mathrm{D^0}\to\mathrm{K^0_S}\pi^{+}\pi^{-}$ is measured to be: $\Delta A_{CP} \equiv A_{CP}(\mathrm{K^0_S}\mathrm{K^0_S})-A_{CP}(\mathrm{K^0_S}\pi^{+}\pi^{-}) =$ (6.3 $\pm$ 3.0 (stat) $\pm$ 0.2 (syst) )%. Using the world-average value of $A_{CP}(\mathrm{K^0_S}\pi^{+}\pi^{-}) = (-$ 0.1 $\pm$ 0.8 $)%$ [18,35,4], we report the measurement, $A_{CP}(\mathrm{K^0_S}\mathrm{K^0_S}) =$(6.2 $\pm$ 3.0 $\pm$ 0.2 $\pm$ 0.8)%, where the three uncertainties represent the statistical uncertainty, the systematic uncertainty, and the uncertainty in the measurement of the CP asymmetry in the $\mathrm{D^0}\to\mathrm{K^0_S}\pi^{+}\pi^{-}$ decay. The measured value is consistent with no CP violation within 2.0 standard deviations. Likewise, it is consistent with the LHCb [16] and the Belle measurements [17] at the level of 2.7 and 1.8 standard deviations, respectively. Tabulated results are provided in the HEPData record for this analysis [36]. This is the first CMS search for CP violation in the charm sector, paving the way for future measurements with more data, using new techniques, and in other channels.

References
1	A. D. Sakharov	Violation of CP invariance, C asymmetry, and baryon asymmetry of the universe	Pisma Zh. Eksp. Teor. Fiz. 5 (1967) 32
2	N. Cabibbo et al.	Unitary symmetry and leptonic decays	PRL 10 (1963) 531
3	M. Kobayashi and T. Maskawa	CP-violation in the renormalizable theory of weak interaction	Prog. Theor. Phys. 49 (1973) 652
4	Particle Data Group	Review of particle physics	PTEP 2022 (2022) 083C01
5	A. G. Cohen, D. B. Kaplan, and A. E. Nelson	Progress in electroweak baryogenesis	Ann. Rev. Nucl. Part. Sci. 43 (1993) 27	hep-ph/9302210
6	A. Riotto and M. Trodden	Recent progress in baryogenesis	Ann. Rev. Nucl. Part. Sci. 49 (1999) 35	hep-ph/9901362
7	W.-S. Hou	Source of CP violation for the baryon asymmetry of the Universe	Chin. J. Phys. 47 (2009) 134	0803.1234
8	S. L. Glashow, J. Iliopoulos, and L. Maiani	Weak interactions with lepton-hadron symmetry	PRD 2 (1970) 1285
9	LHCb Collaboration	Observation of CP violation in charm decays	PRL 122 (2019) 211803	1903.08726
10	A. Lenz and G. Wilkinson	Mixing and CP violation in the charm system	Ann. Rev. Nucl. Part. Sci. 71 (2021) 59	2011.04443
11	U. Nierste and S. Schacht	$CP$ violation in ${D}^{0}\to{K}_{S}{K}_{S}$	PRD 92 (2015) 054036	1508.00074
12	H.-n. Li, C.-D. Lu, and F.-S. Yu	Branching ratios and direct $CP$ asymmetries in $D\to \pi^{+}\pi^{-}$ decays	PRD 86 (2012) 036012	1203.3120
13	H.-Y. Cheng and C.-W. Chiang	Revisiting $CP$ violation in $D\to \pi^{+}\pi^{-}$ and $VP$ decays	PRD 100 (2019) 093002	1909.03063
14	F. Buccella, A. Paul, and P. Santorelli	$SU(3{)}_{F}$ breaking through final state interactions and $CP$ asymmetries in $D\to \pi^{+}\pi^{-}$ decays	PRD 99 (2019) 113001	1902.05564
15	J. Brod, A. L. Kagan, and J. Zupan	Size of direct $CP$ violation in singly Cabibbo-suppressed $D$ decays	PRD 86 (2012) 014023	1111.5000
16	LHCb Collaboration	Measurement of $CP$ asymmetry in $D^0 \to K^0_S K^0_S$ decays	PRD 104 (2021) L031102	2105.01565
17	Belle Collaboration	Search for $CP$ violation and measurement of the branching fraction in the decay $D^{0} \to K^0_S K^0_S$	PRL 119 (2017) 171801	1705.05966
18	CDF Collaboration	Measurement of CP-violation asymmetries in $D^{0} \to K^{0}_{S} \pi^+ \pi^-$	PRD 86 (2012) 032007	1207.0825
19	CMS Collaboration	Test of lepton flavor universality in ${\mathrm{B}^{\pm}}\to\mathrm{K^{\pm}}\mu^{+}\mu^{-}$ and ${\mathrm{B}^{\pm}}\to\mathrm{K^{\pm}}\mathrm{e}^+\mathrm{e}^-$ decays in proton-proton collisions at $\sqrt{s}$ = 13 TeV	Submitted to Phys. Rep., 2024	CMS-BPH-22-005 2401.07090
20	CMS Collaboration	Enriching the physics program of the CMS experiment via data scouting and data parking	Submitted to Phys. Rep., 2024	CMS-EXO-23-007 2403.16134
21	CMS Tracker Group Collaboration	The CMS Phase-1 pixel detector upgrade	JINST 16 (2021) P02027	2012.14304
22	CMS Collaboration	Track impact parameter resolution for the full pseudo rapidity coverage in the 2017 dataset with the CMS Phase-1 pixel detector	CMS Detector Performance Note CMS-DP-2020-049, 2020 CDS
23	CMS Collaboration	Performance of the CMS Level-1 trigger in proton-proton collisions at $\sqrt{s} =$ 13 TeV	JINST 15 (2020) P10017	CMS-TRG-17-001 2006.10165
24	CMS Collaboration	The CMS trigger system	JINST 12 (2017) P01020	CMS-TRG-12-001 1609.02366
25	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004
26	T. Sjöstrand et al.	An introduction to PYTHIA 8.2	Comput. Phys. Commun. 191 (2015) 159	1410.3012
27	D. J. Lange	The EvtGen particle decay simulation package	NIM A 462 (2001) 152
28	CMS Collaboration	Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements	EPJC 80 (2020) 4	CMS-GEN-17-001 1903.12179
29	E. Barberio and Z. Was	PHOTOS --- a universal Monte Carlo for QED radiative corrections: version 2.0	Comput. Phys. Commun. 79 (1994) 291
30	GEANT4 Collaboration	GEANT 4 --- a simulation toolkit	NIM A 506 (2003) 250
31	CMS Collaboration	CMS tracking performance results from early LHC operation	EPJC 70 (2010) 1165	CMS-TRK-10-001 1007.1988
32	CMS Collaboration	Description and performance of track and primary-vertex reconstruction with the CMS tracker	JINST 9 (2014) P10009	CMS-TRK-11-001 1405.6569
33	N. L. Johnson	Systems of frequency curves generated by methods of translation	Biometrika 36 (1949) 149
34	M. J. Oreglia	A study of the reactions $\psi^\prime \to \gamma \gamma \psi$	PhD thesis, Stanford University, SLAC Report SLAC-R-236, 1980 link
35	CLEO Collaboration	Search for CP violation in $\mathrm{D^0}\to\mathrm{K^0_S}\pi^{+}\pi^{-}$	PRD 70 (2004) 091101	hep-ex/0311033
36	CMS Collaboration	HEPData record for this analysis	link

Compact Muon Solenoid LHC, CERN

© Copyright CERN 2024 for the benefit of the CMS Collaboration