

Compact Muon Solenoid
LHC, CERN
| CMS-B2G-16-023 ; CERN-EP-2017-279 | ||
| Search for ZZ resonances in the $ 2 \ell 2 \nu $ final state in proton-proton collisions at 13 TeV | ||
| CMS Collaboration | ||
| 13 November 2017 | ||
| JHEP 03 (2018) 003 | ||
| Abstract: A search for heavy resonances decaying to a pair of Z bosons is performed using data collected with the CMS detector at the LHC. Events are selected by requiring two oppositely charged leptons (electrons or muons), consistent with the decay of a Z boson, and large missing transverse momentum, which is interpreted as arising from the decay of a second Z boson to two neutrinos. The analysis uses data from proton-proton collisions at a center-of-mass energy of 13 TeV, corresponding to an integrated luminosity of 35.9 fb$^{-1}$. The hypothesis of a spin-2 bulk graviton (X) decaying to a pair of Z bosons is examined for 600 $ \le{m_{\mathrm{X}}} \le $ 2500 GeV and upper limits at 95% confidence level are set on the product of the production cross section and branching fraction of $\mathrm{X}\to \mathrm{Z}\mathrm{Z}$ ranging from 100 to 4 fb. For bulk graviton models characterized by a curvature scale parameter $\tilde{k}= $ 0.5 in the extra dimension, the region ${m_{\mathrm{X}}} < $ 800 GeV is excluded, providing the most stringent limit reported to date. Variations of the model considering the possibility of a wide resonance produced exclusively via gluon-gluon fusion or $\mathrm{q\bar{q}}$ annihilation are also examined. | ||
| Links: e-print arXiv:1711.04370 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Leading order Feynman diagram for the production of a generic resonance X via gluon-gluon fusion decaying to the ZZ final state. |
png pdf |
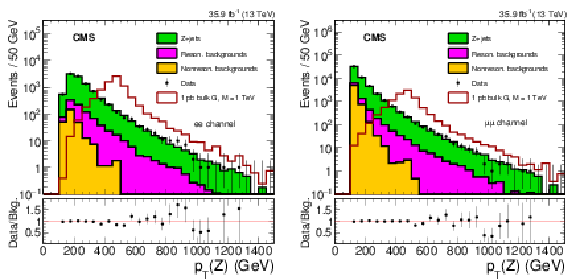
Figure 2:
The $ {p_{\mathrm {T}}} ^{\mathrm{Z}}$ distributions for electron (left) and muon (right) channels comparing the data and background model based on control samples in data. The lower panels give the ratio of data to the prediction for the background with only statistical uncertainties shown. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of cross section and branching fraction $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. |
png pdf |
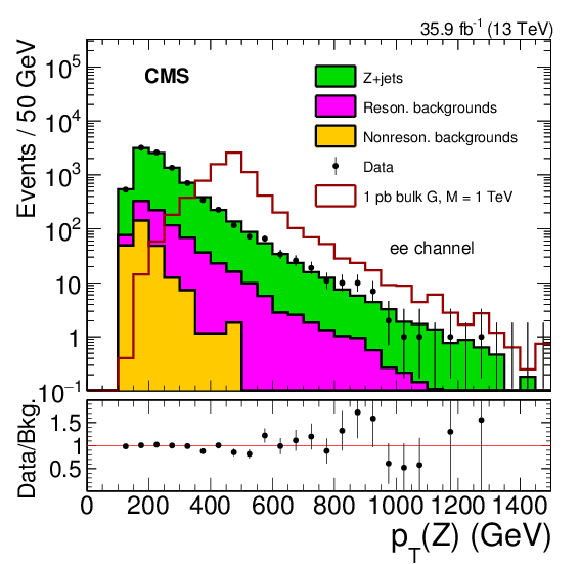
Figure 2-a:
The $ {p_{\mathrm {T}}} ^{\mathrm{Z}}$ distributions for the electron channel comparing the data and background model based on control samples in data. The lower panel gives the ratio of data to the prediction for the background with only statistical uncertainties shown. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of cross section and branching fraction $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. |
png pdf |
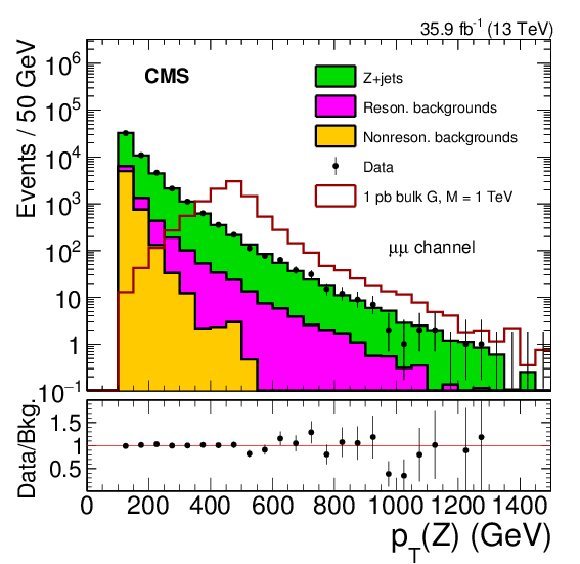
Figure 2-b:
The $ {p_{\mathrm {T}}} ^{\mathrm{Z}}$ distributions for the muon channel comparing the data and background model based on control samples in data. The lower panel gives the ratio of data to the prediction for the background with only statistical uncertainties shown. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of cross section and branching fraction $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. |
png pdf |
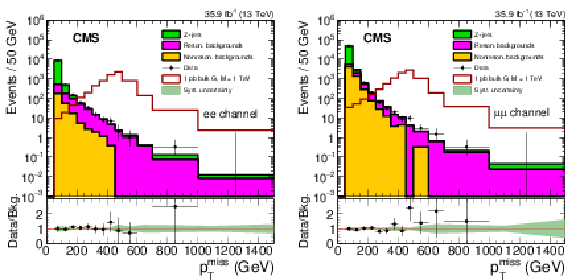
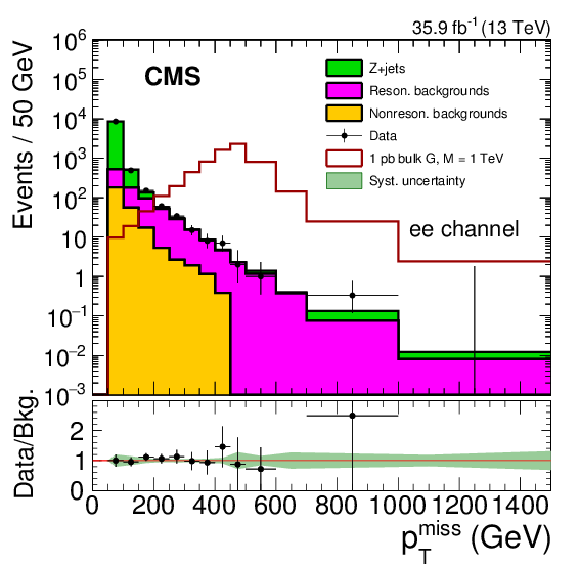
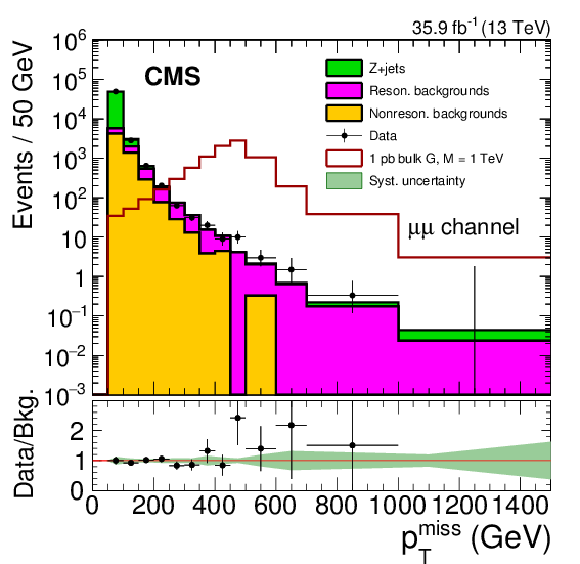
Figure 3:
The ${{p_{\mathrm {T}}} ^\text {miss}}$ for electron (left) and muon (right) channels comparing the data and background model based on control samples in data. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of cross section and branching fraction $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. The lower panels show the ratio of data to the prediction for the background. The shaded band shows the systematic uncertainties in background, while the statistical uncertainty in the data is shown by the error bars. |
png pdf |
Figure 3-a:
The ${{p_{\mathrm {T}}} ^\text {miss}}$ for the electron channel comparing the data and background model based on control samples in data. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of cross section and branching fraction $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. The lower panel shows the ratio of data to the prediction for the background. The shaded band shows the systematic uncertainties in background, while the statistical uncertainty in the data is shown by the error bars. |
png pdf |
Figure 3-b:
The ${{p_{\mathrm {T}}} ^\text {miss}}$ for the muon channel comparing the data and background model based on control samples in data. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of cross section and branching fraction $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. The lower panel shows the ratio of data to the prediction for the background. The shaded band shows the systematic uncertainties in background, while the statistical uncertainty in the data is shown by the error bars. |
png pdf |
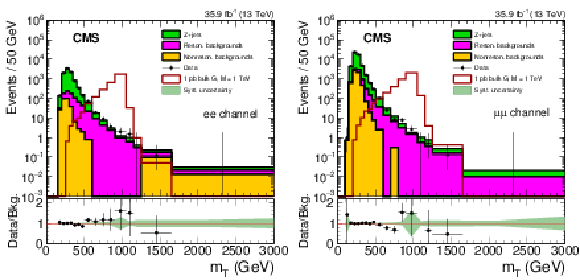
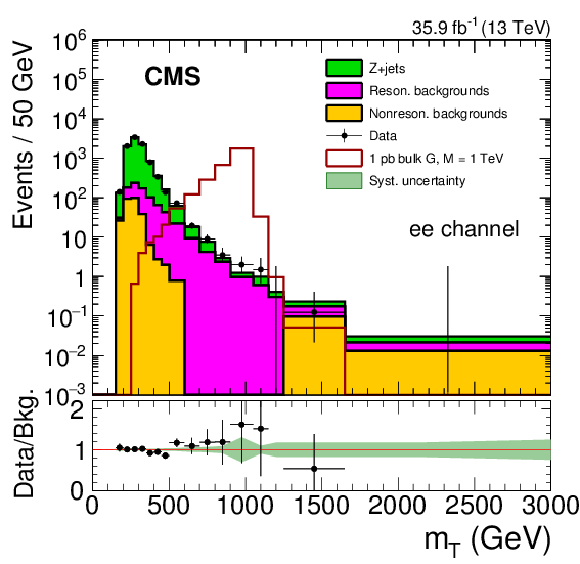
Figure 4:
The $ {m_\mathrm {T}} $ distributions for electron (left) and muon (right) channels comparing the data and background model based on control samples in data, after fitting the background-only model to the data. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of branching fraction and cross section $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. The lower panels show the ratio of data to the prediction for the background. The shaded bands show the systematic uncertainties in the background, while the statistical uncertainty in the data is shown by the error bars. |
png pdf |
Figure 4-a:
The $ {m_\mathrm {T}} $ distributions for the electron muon channel comparing the data and background model based on control samples in data, after fitting the background-only model to the data. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of branching fraction and cross section $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. The lower panel shows the ratio of data to the prediction for the background. The shaded bands show the systematic uncertainties in the background, while the statistical uncertainty in the data is shown by the error bars. |
png pdf |
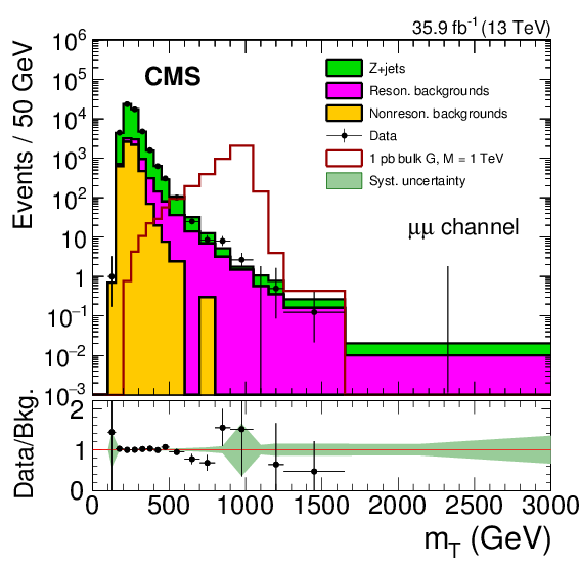
Figure 4-b:
The $ {m_\mathrm {T}} $ distributions for the electron muon channel comparing the data and background model based on control samples in data, after fitting the background-only model to the data. The expected distribution for a zero width bulk graviton resonance with a mass of 1 TeV is also shown for a value of 1 pb for the product of branching fraction and cross section $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z}) + \mathcal {B} (\mathrm{Z} \mathrm{Z} \to 2\ell 2\nu)$. The lower panel shows the ratio of data to the prediction for the background. The shaded bands show the systematic uncertainties in the background, while the statistical uncertainty in the data is shown by the error bars. |
png pdf |
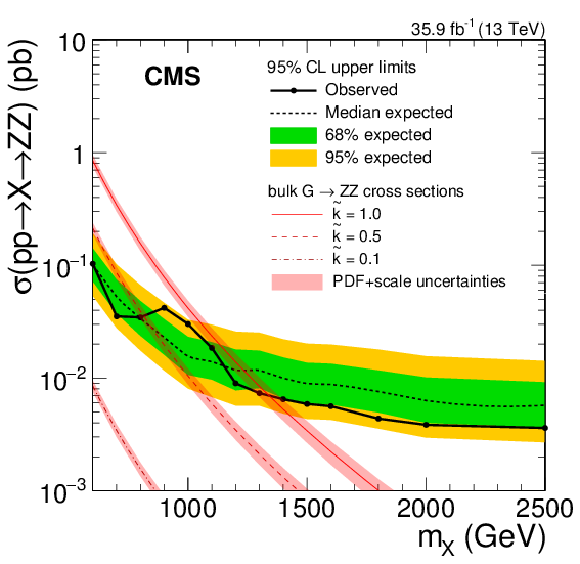
Figure 5:
Expected and observed limits on the product of cross section and branching fraction of a new spin-2 heavy resonance $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} $, assuming zero width, based on the combined analysis of the electron and muon channels. Expectations for the production cross section $\sigma ({\mathrm{p}} {\mathrm{p}} \to {\mathrm {X}} \to \mathrm{Z} \mathrm{Z})$ are also shown for the benchmark bulk graviton model for three values of the curvature scale parameter $\tilde{k}$. |
png pdf |
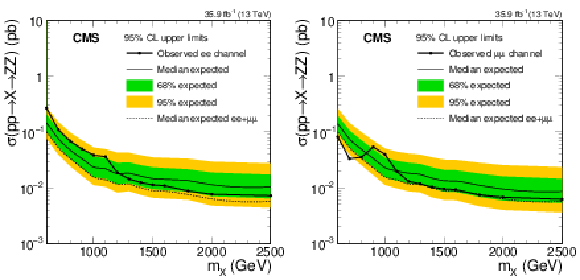
Figure 6:
Expected and observed limits on the product of cross section and branching fraction of a new spin-2 bulk heavy resonance $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} $, assuming zero width, shown separately for searches $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} \to \ell \ell \nu \nu $ in the electron (left) and muon (right) final states. The median expected 95% CL limits from the combined analysis (Fig. 5) are also shown. |
png pdf |
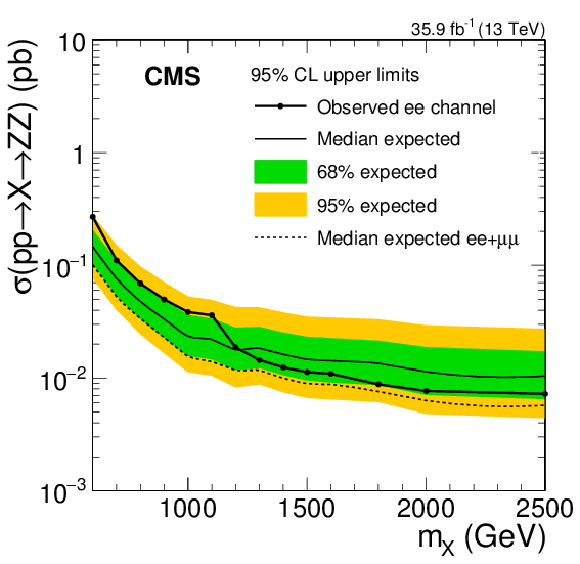
Figure 6-a:
Expected and observed limits on the product of cross section and branching fraction of a new spin-2 bulk heavy resonance $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} $, assuming zero width, shown separately for searches $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} \to \ell \ell \nu \nu $ in the electron final state. The median expected 95% CL limits from the combined analysis (Fig. 5) are also shown. |
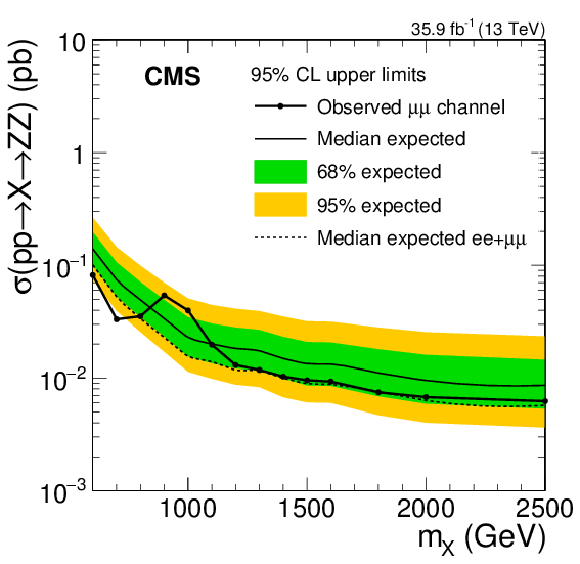
png pdf |
Figure 6-b:
Expected and observed limits on the product of cross section and branching fraction of a new spin-2 bulk heavy resonance $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} $, assuming zero width, shown separately for searches $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} \to \ell \ell \nu \nu $ in the muon final state. The median expected 95% CL limits from the combined analysis (Fig. 5) are also shown. |
png pdf |
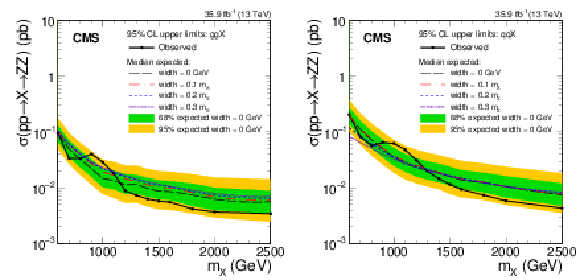
Figure 7:
Expected and observed limits on the product of cross section and branching fraction of a new spin-2 heavy resonance $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} $ based on a combined analysis of the electron and muon channels. The more generic version of the bulk graviton model is considered, assuming either gluon-gluon fusion (left) or ${\mathrm{q} \mathrm{\bar{q}}}$ annihilation (right) processes. Expected limits are also shown for models having various decay widths relative to the mass of the resonance. |

png pdf |
Figure 7-a:
Expected and observed limits on the product of cross section and branching fraction of a new spin-2 heavy resonance $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} $ based on a combined analysis of the electron and muon channels. The more generic version of the bulk graviton model is considered, assuming the gluon-gluon fusion process. Expected limits are also shown for models having various decay widths relative to the mass of the resonance. |
png pdf |
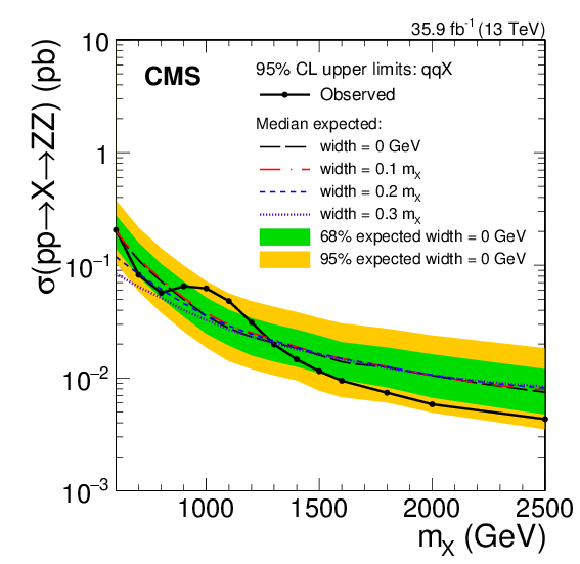
Figure 7-b:
Expected and observed limits on the product of cross section and branching fraction of a new spin-2 heavy resonance $ {\mathrm {X}} \to \mathrm{Z} \mathrm{Z} $ based on a combined analysis of the electron and muon channels. The more generic version of the bulk graviton model is considered, assuming the ${\mathrm{q} \mathrm{\bar{q}}}$ annihilation process. Expected limits are also shown for models having various decay widths relative to the mass of the resonance. |
| Tables | |

png pdf |
Table 1:
Summary of the normalization uncertainties that are included in the statistical procedure for the electron and muon channels. All values are listed in percentage units and similar categories are grouped for brevity. Sources that do not apply or are found to be negligibly small are marked "--" or "(--),'' respectively. Integrated luminosity and theoretical uncertainties are evaluated separately for effects on normalizations, while all the other uncertainties are considered simultaneously with shape variations in the statistical analysis. Values in the signal column refer to the hypothetical spin-2 bulk graviton signal with a mass of 1 TeV. |

png pdf |
Table 2:
Event yields for different background contributions and those observed in data in the electron and muon channels. |
| Summary |
| A search for the production of new resonances has been performed in events with a leptonically decaying Z boson and missing transverse momentum, using data corresponding to an integrated luminosity of 35.9 fb$^{-1}$ of proton-proton collisions at a center-of-mass energy of 13 TeV. The data are consistent with expectations from standard model processes. The hypothesis of a spin-2 bulk graviton, X, decaying to a pair of Z bosons is examined for 600 $ \le {m_{\mathrm{X}}} \le $ 2500 GeV, and upper limits are set at 95% confidence level on the product of the cross section and branching fraction $\sigma({\mathrm{p}}{\mathrm{p}} \to \mathrm{X}\to \mathrm{Z}\mathrm{Z})$ ranging from 100 to 4 fb. For bulk graviton models characterized by a curvature scale parameter $\tilde{k}= $ 0.5 in the extra dimension, the region ${m_{\mathrm{X}}} < 800$ GeV is excluded, providing the most stringent limit reported to date. The analysis is repeated considering variations of the bulk graviton model to include a large mass-dependent width. Exclusion limits are provided separately for gluon-gluon fusion and $\mathrm{q\bar{q}}$ annihilation production processes. |
| References | ||||
| 1 | F. Englert and R. Brout | Broken symmetry and the mass of gauge vector mesons | PRL 13 (%%Aug%%, 1964) 321 | |
| 2 | P. W. Higgs | Broken symmetries, massless particles and gauge fields | PL12 (1964) 132 | |
| 3 | P. W. Higgs | Broken symmetries and the masses of gauge bosons | PRL 13 (1964) 508 | |
| 4 | G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble | Global conservation laws and massless particles | PRL 13 (1964) 585 | |
| 5 | P. W. Higgs | Spontaneous symmetry breakdown without massless bosons | PR145 (1966) 1156 | |
| 6 | T. W. B. Kibble | Symmetry breaking in non-abelian gauge theories | PR155 (1967) 1554 | |
| 7 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 8 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 9 | CMS Collaboration | Observation of a new boson with mass near 125 GeV in pp collisions at $ \sqrt{s} = $ 7 and 8 TeV | JHEP 06 (2013) 081 | CMS-HIG-12-036 1303.4571 |
| 10 | S. Weinberg | Implications of dynamical symmetry breaking | PRD 13 (1976) 974 | |
| 11 | S. Weinberg | Implications of dynamical symmetry breaking: An addendum | PRD 19 (1979) 1277 | |
| 12 | L. Susskind | Dynamics of spontaneous symmetry breaking in the Weinberg--Salam theory | PRD 20 (1979) 2619 | |
| 13 | D. B. Kaplan and H. Georgi | SU(2) x U(1) breaking by vacuum misalignment | PLB 136 (1984) 183 | |
| 14 | R. Contino, T. Kramer, M. Son, and R. Sundrum | Warped/composite phenomenology simplified | JHEP 05 (2007) 074 | hep-ph/0612180 |
| 15 | G. F. Giudice, C. Grojean, A. Pomarol, and R. Rattazzi | The strongly-interacting light Higgs | JHEP 06 (2007) 045 | hep-ph/0703164 |
| 16 | N. Arkani-Hamed, S. Dimopoulos, and G. R. Dvali | The hierarchy problem and new dimensions at a millimeter | PLB 429 (1998) 263 | hep-ph/9803315 |
| 17 | I. Antoniadis, N. Arkani-Hamed, S. Dimopoulos, and G. R. Dvali | New dimensions at a millimeter to a Fermi and superstrings at a TeV | PLB 436 (1998) 257 | hep-ph/9804398 |
| 18 | L. Randall and R. Sundrum | A large mass hierarchy from a small extra dimension | PRL 83 (1999) 3370 | hep-ph/9905221 |
| 19 | A. L. Fitzpatrick, J. Kaplan, L. Randall, and L.-T. Wang | Searching for the Kaluza-Klein graviton in bulk RS models | JHEP 09 (2007) 013 | hep-ph/0701150 |
| 20 | O. Antipin, D. Atwood, and A. Soni | Search for RS gravitons via $ W_L W_L $ decays | PLB 666 (2008) 155 | 0711.3175 |
| 21 | K. Agashe, H. Davoudiasl, G. Perez, and A. Soni | Warped gravitons at the LHC and beyond | PRD 76 (2007) 036006 | hep-ph/0701186 |
| 22 | ATLAS Collaboration | Search for new phenomena in the WW to $ \ell \nu \ell^\prime\nu^\prime $ final state in pp collisions at $ \sqrt{s}= $ 7 TeV with the ATLAS detector | PLB 718 (2013) 860 | 1208.2880 |
| 23 | ATLAS Collaboration | Search for resonant diboson production in the $ \ell\nu jj $ decay channels with the ATLAS detector at 7 TeV | PRD 87 (2013) 112006 | 1305.0125 |
| 24 | ATLAS Collaboration | Search for resonant diboson production in the $ {\ell \ell}{\text q\bar{\text q}} $ final state in pp collisions at $ \sqrt{s} = $ 8 TeV with the ATLAS detector | EPJC 75 (2015) 69 | 1409.6190 |
| 25 | CMS Collaboration | Search for a narrow spin-2 resonance decaying to a pair of Z vector bosons in the semileptonic final state | PLB 718 (2013) 1208 | CMS-EXO-11-102 1209.3807 |
| 26 | CMS Collaboration | Search for massive resonances decaying into pairs of boosted bosons in semi-leptonic final states at $ \sqrt{s}= $ 8 TeV | JHEP 08 (2014) 174 | CMS-EXO-13-009 1405.3447 |
| 27 | ATLAS Collaboration | Searches for heavy diboson resonances in pp collisions at $ \sqrt{s}= $ 13 TeV with the ATLAS detector | JHEP 09 (2016) 173 | 1606.04833 |
| 28 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 29 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 30 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 31 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 32 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 33 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 34 | CMS Collaboration | Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P08010 | CMS-EGM-14-001 1502.02702 |
| 35 | CMS Collaboration | Performance of CMS muon reconstruction in pp collision events at $ \sqrt{s}= $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 36 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 37 | Particle Data Group, C. Patrignani et al. | Review of Particle Physics | CPC 40 (2016) 100001 | |
| 38 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 39 | A. Oliveira | Gravity particles from warped extra dimensions, predictions for LHC | 1404.0102 | |
| 40 | Y. Gao et al. | Spin determination of single-produced resonances at hadron colliders | PRD 81 (2010) 075022 | 1001.3396 |
| 41 | S. Bolognesi et al. | On the spin and parity of a single-produced resonance at the LHC | PRD 86 (2012) 095031 | 1208.4018 |
| 42 | M. Chen et al. | The role of interference in unraveling the ZZ-couplings of the newly discovered boson at the LHC | PRD 89 (2014) 034002 | 1310.1397 |
| 43 | CMS Collaboration | Measurement of the properties of a Higgs boson in the four-lepton final state | PRD 89 (2014) 092007 | CMS-HIG-13-002 1312.5353 |
| 44 | CMS Collaboration | Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV | PRD 92 (2015) 012004 | CMS-HIG-14-018 1411.3441 |
| 45 | T. Sjostrand, S. Mrenna, and P. Skands | PYTHIA 6.4 physics and manual | JHEP 05 (2006) 026 | hep-ph/0603175 |
| 46 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 47 | GEANT4 Collaboration | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 48 | J. Allison et al. | Geant4 developments and applications | IEEE Trans. Nucl. Sci. 53 (2006) 270 | |
| 49 | Geant4 Collaboration | Recent developments in Geant4 | Annals Nucl. Energy 82 (2015) 19 | |
| 50 | Y. Li and F. Petriello | Combining QCD and electroweak corrections to dilepton production in FEWZ | PRD 86 (2012) 094034 | 1208.5967 |
| 51 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 52 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 53 | M. Grazzini, S. Kallweit, and D. Rathlev | ZZ production at the LHC: fiducial cross sections and distributions in NNLO QCD | PLB 750 (2015) 407 | 1507.06257 |
| 54 | A. Bierweiler, T. Kasprzik, and J. H. Kuhn | Vector-boson pair production at the LHC to $ \mathcal{O}(\alpha^3) $ accuracy | JHEP 12 (2013) 071 | 1305.5402 |
| 55 | S. Gieseke, T. Kasprzik, and J. H. Kuhn | Vector-boson pair production and electroweak corrections in HERWIG++ | EPJC 74 (2014) 2988 | 1401.3964 |
| 56 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 57 | CMS Collaboration | CMS luminosity measurements for the 2016 data taking period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 58 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 59 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 60 | A. L. Read | Presentation of search results: the $ CL_s $ technique | in Durham IPPP Workshop: Advanced Statistical Techniques in Particle Physics, p. 2693 Durham, UK, March, 2002 [JPG 28 (2002) 2693] | |
| 61 | ATLAS, CMS, and the LHC Higgs Combination Group Collaboration | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|