

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SUS-16-023 | ||
| Search for supersymmetry in final states with at least one photon and $E_{\mathrm{T}}^{\text{miss}}$ in pp collisions at $\sqrt{s}=$ 13 TeV | ||
| CMS Collaboration | ||
| August 2016 | ||
| Abstract: A search for electroweak production of gauginos is presented using the first LHC Run II data at a center-of-mass energy of 13 TeV. The used data set has been recorded with the CMS detector and corresponds to an integrated luminosity of 2.3 fb$^{-1}$. In gauge-mediated supersymmetry breaking (GMSB) models the gauginos can decay to photons, or other standard model bosons, and gravitinos. The final state considered in this search is characterized by photons and missing transverse energy. Since in electroweak production scenarios the expected hadronic activity is low compared to strong production, no jet requirements are used. Additionally, gluino pair production models are considered, where the analysis does not lose sensitivity in scenarios with compressed mass spectra. The observed data are in agreement with the standard model prediction and limits are set on different models of GMSB. | ||
| Links: CDS record (PDF) ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Feynman diagram of the dominant ${\tilde{\chi}^\pm _{1}} - {\tilde{\chi}^{0}_{2}}$ production mechanism and a typical decay chain in scenarios with a bino-like ${\tilde{\chi}^{0}_{1}}$ and wino-like ${\tilde{\chi}^{0}_{2}}$ and ${\tilde{\chi}^\pm _{1}} $. |

png pdf |
Figure 2:
Feynman diagram corresponding to the TChiWg simplified model. |

png pdf |
Figure 3-a:
Feynman diagrams of the T5gg (a) and T5Wg (b) simplified models. |
png pdf |
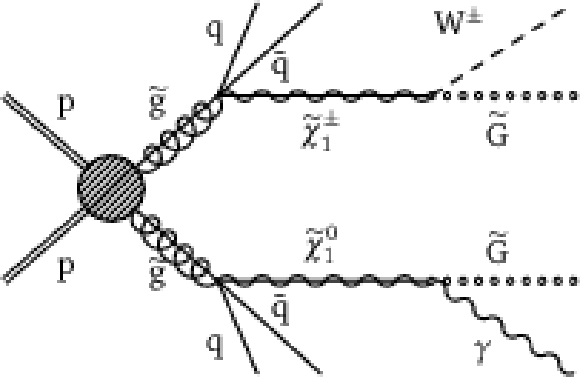
Figure 3-b:
Feynman diagrams of the T5gg (a) and T5Wg (b) simplified models. |
png pdf |
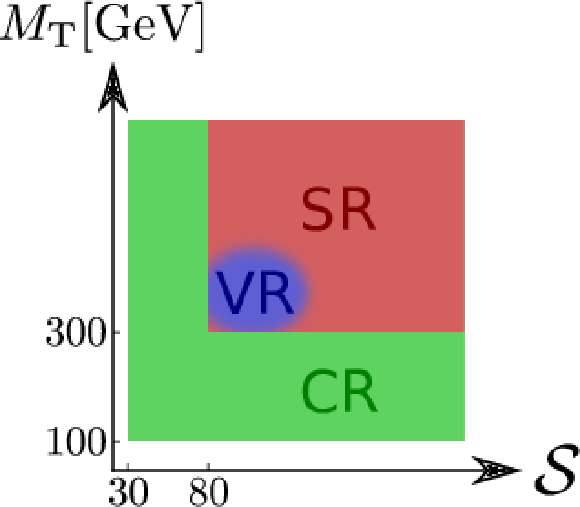
Figure 4:
Sketch of the control (CR) and signal region (SR) definitions. The validation region (VR) is not defined in the ${\mathcal {S}}- {M_\mathrm {T}}$ plane, but embedded in the SR with the additional condition $ { S_\mathrm {T}^{ {\gamma }}}<$ 600 GeV. This corresponds approximately to the bottom-left corner of the SR, which is therefore illustrated as a blurred region. |
png pdf |
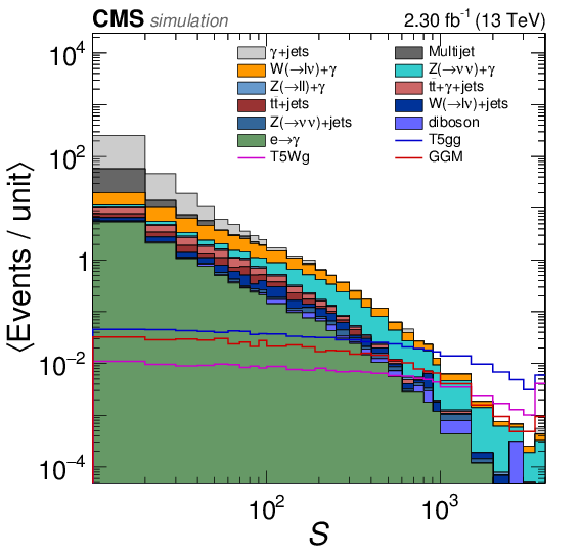
Figure 5-a:
The ${\mathcal {S}}$ and ${M_\mathrm {T}}$ distributions after the preselection. The overflow is contained in the last bin shown and the bin contents are divided by the bin widths. |
png pdf |
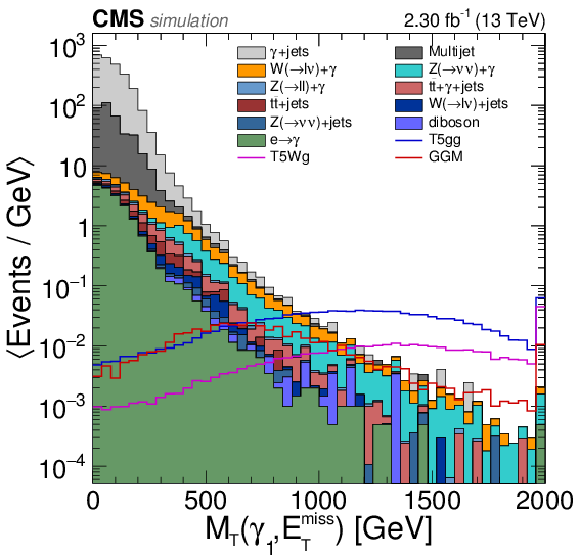
Figure 5-b:
The ${\mathcal {S}}$ and ${M_\mathrm {T}}$ distributions after the preselection. The overflow is contained in the last bin shown and the bin contents are divided by the bin widths. |

png pdf |
Figure 6:
Template fit result: The post-fit distributions for ($\gamma +$)jets and V($+\gamma $) together with the total fit distribution stacked onto the fixed backgrounds. Events containing zero jets are counted in the last shown bin. The values in the legend are the resulting scale factors. |

png pdf |
Figure 7-a:
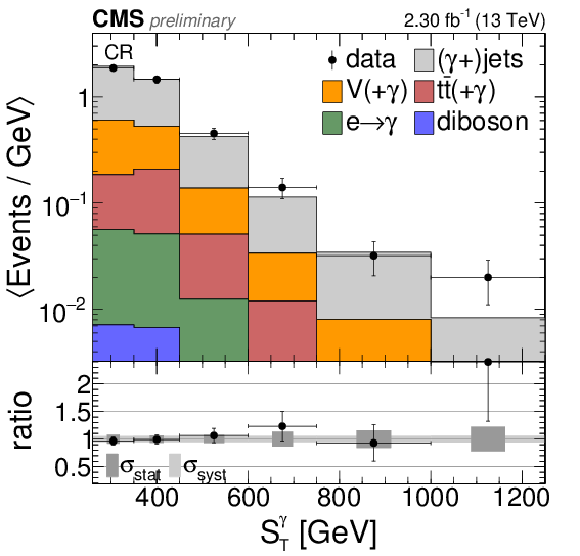
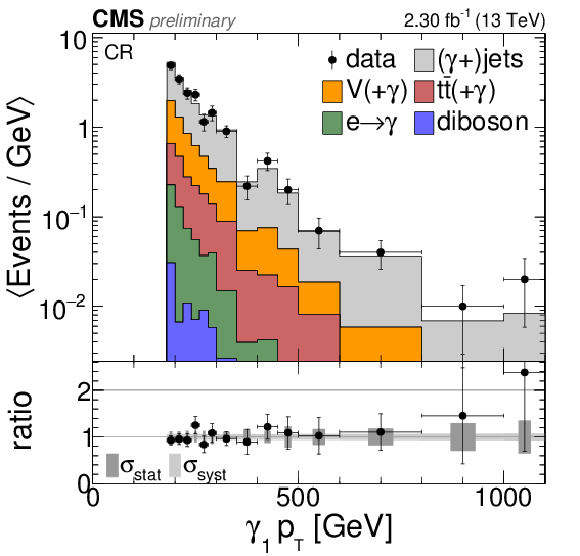
Comparison of the total background prediction to data in the control region without a b-jet veto. a,b: ${E_{\mathrm {T}}^{\text {miss}}} $ significance (a) and transverse mass (b). c,d: ${ S_\mathrm {T}^{ {\gamma }}}$ (c) and leading photon ${p_{\mathrm {T}}} $ (d). The overflow is contained in the last bin. The bin contents are divided by the bin widths. |

png pdf |
Figure 7-b:
Comparison of the total background prediction to data in the control region without a b-jet veto. a,b: ${E_{\mathrm {T}}^{\text {miss}}} $ significance (a) and transverse mass (b). c,d: ${ S_\mathrm {T}^{ {\gamma }}}$ (c) and leading photon ${p_{\mathrm {T}}} $ (d). The overflow is contained in the last bin. The bin contents are divided by the bin widths. |
png pdf |
Figure 7-c:
Comparison of the total background prediction to data in the control region without a b-jet veto. a,b: ${E_{\mathrm {T}}^{\text {miss}}} $ significance (a) and transverse mass (b). c,d: ${ S_\mathrm {T}^{ {\gamma }}}$ (c) and leading photon ${p_{\mathrm {T}}} $ (d). The overflow is contained in the last bin. The bin contents are divided by the bin widths. |
png pdf |
Figure 7-d:
Comparison of the total background prediction to data in the control region without a b-jet veto. a,b: ${E_{\mathrm {T}}^{\text {miss}}} $ significance (a) and transverse mass (b). c,d: ${ S_\mathrm {T}^{ {\gamma }}}$ (c) and leading photon ${p_{\mathrm {T}}} $ (d). The overflow is contained in the last bin. The bin contents are divided by the bin widths. |
png pdf |
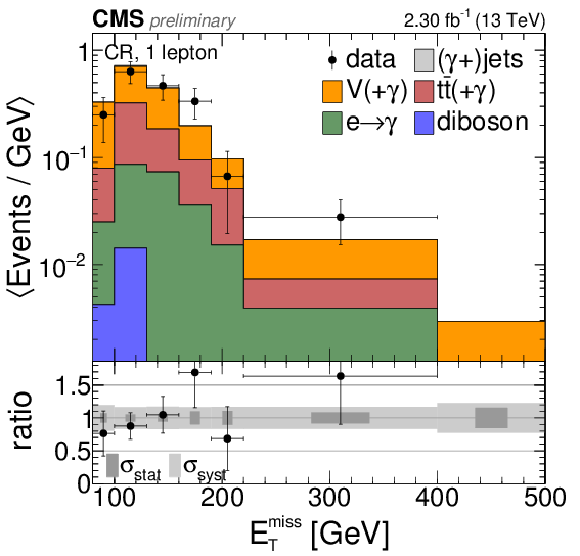
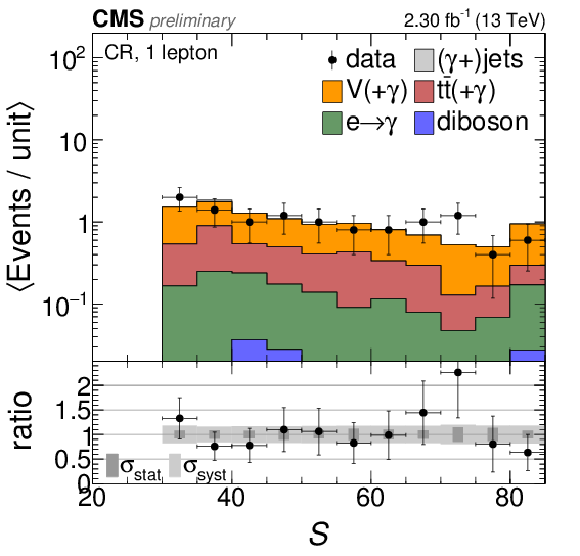
Figure 8-a:
Comparison of the total background prediction to data in the control region with the additional requirement of exactly one lepton. a: missing transverse energy. b: ${E_{\mathrm {T}}^{\text {miss}}}$ significance. The overflow is contained in the last bin. The bin contents are divided by the bin widths. |
png pdf |
Figure 8-b:
Comparison of the total background prediction to data in the control region with the additional requirement of exactly one lepton. a: missing transverse energy. b: ${E_{\mathrm {T}}^{\text {miss}}}$ significance. The overflow is contained in the last bin. The bin contents are divided by the bin widths. |
png pdf |
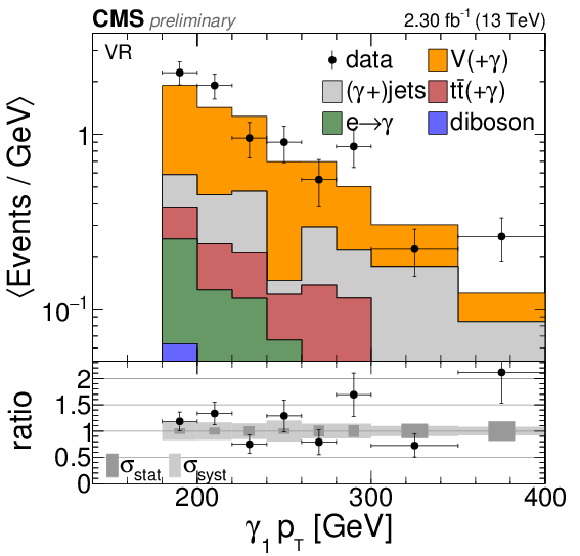
Figure 9-a:
Comparison of the total background prediction to data in the validation region. a: leading photon ${p_{\mathrm {T}}} $. b: ${ S_\mathrm {T}^{ {\gamma }}}$. The overflow is contained in the last bin. The bin contents are divided by the bin widths. |
png pdf |
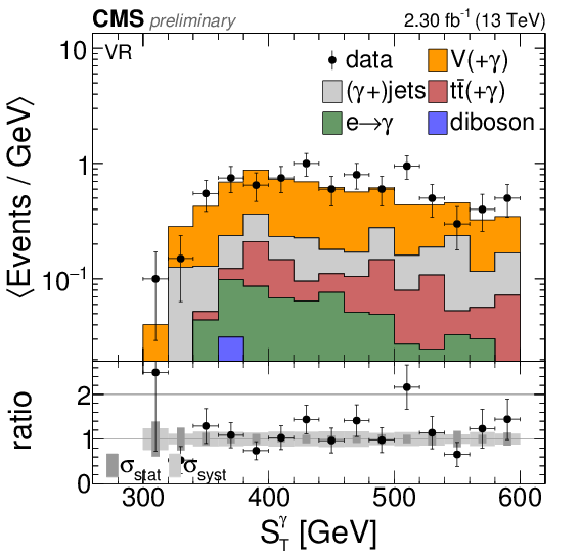
Figure 9-b:
Comparison of the total background prediction to data in the validation region. a: leading photon ${p_{\mathrm {T}}} $. b: ${ S_\mathrm {T}^{ {\gamma }}}$. The overflow is contained in the last bin. The bin contents are divided by the bin widths. |
png pdf |
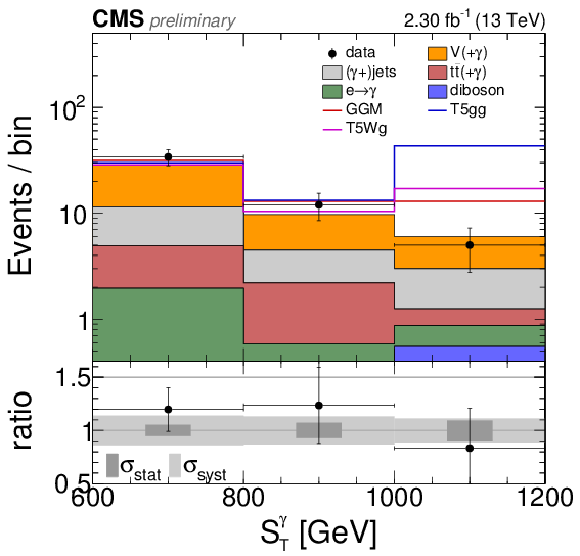
Figure 10:
Background and data distributions in the signal region using the final binning in ${ S_\mathrm {T}^{ {\gamma }}}$. The last bin contains the overflow. The background and signal histograms are stacked. |
png pdf |
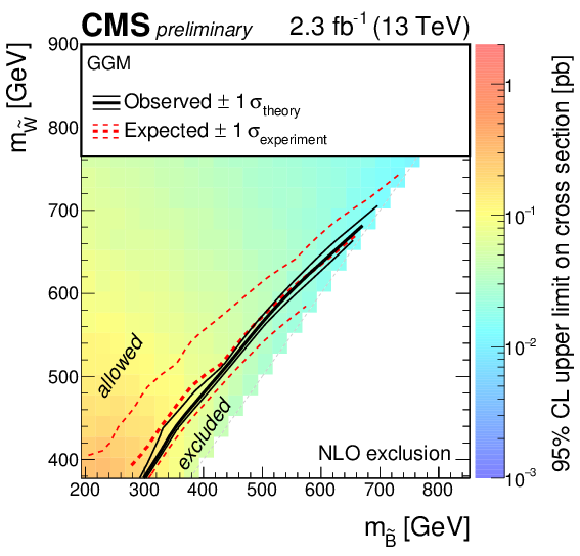
Figure 11:
The 95% CL limits for the GGM model in the bino-wino mass plane. The color scale encodes the observed upper cross section limit for each point. The lines represent the observed (black) and expected (red) exclusion contours and their uncertainties. |
png pdf |
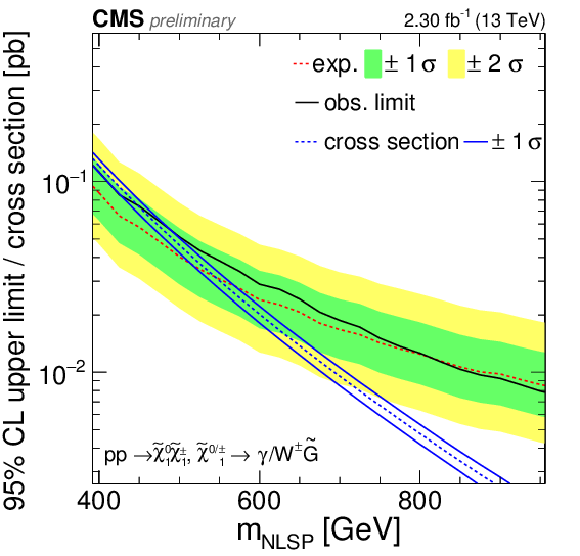
Figure 12:
Observed and expected upper cross section limits as a function of the NLSP mass for the TChiWg model together with the theoretical cross section. |
png pdf |
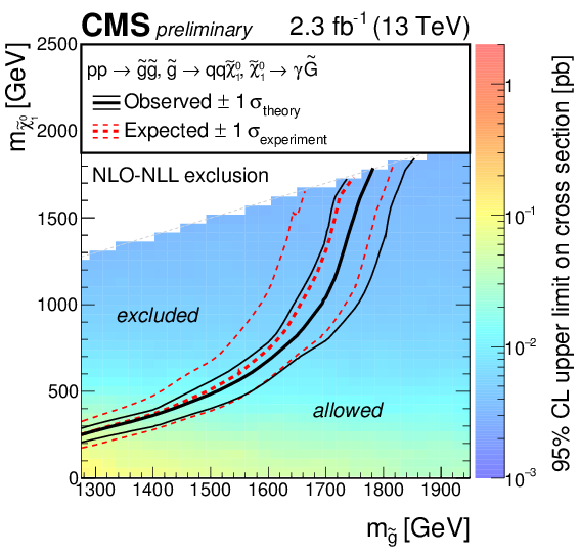
Figure 13:
The 95% CL limits for the T5gg model in the gluino-neutralino mass plane. The color scale encodes the observed upper cross section limit for each point. The lines represent the observed (black) and expected (red) exclusion contours and their uncertainties. |

png pdf |
Figure 14:
The 95% CL limits for the T5Wg model in the gluino-neutralino mass plane. The color scale encodes the observed upper cross section limit for each point. The lines represent the observed (black) and expected (red) exclusion contours and their uncertainties. |
| Tables | |
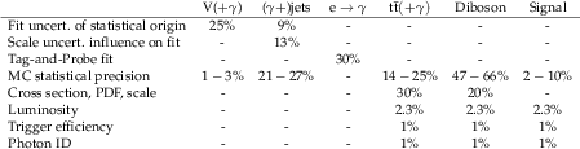
png pdf |
Table 1:
Systematic uncertainties of the separate backgrounds. The uncertainties are relative to the respective backgrounds. |
png pdf |
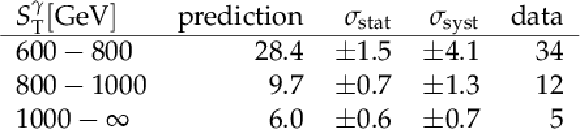
Table 2:
Yields for the individual SR bins. For the total systematic uncertainties the correlation term for the systematic uncertainties of ${\mathrm {V}(+ {\gamma })}$ and ${( {\gamma }+)\text {jets}}$ has been considered. |

png pdf |
Table 3:
Individual background yields for the separate signal region bins. The statistical uncertainty of the ${ {\mathrm {e}}\to {\gamma }}$ background is due to the limited size of the collected data sample. All other statistical uncertainties are due to the limited number of simulated events. |
| Summary |
| A search for the production of supersymmetric particles decaying to photons is presented. The data sample used corresponds to 2.3 fb$^{-1}$ of pp collisions recorded with the CMS detector in 2015 at $ \sqrt{s} = $ 13 TeV. A cut-and-count experiment is performed in three exclusive search bins. The observed event counts are in agreement with the SM prediction. Exclusion limits at the 95% CL are set for a general gauge mediation model of electroweak production and the simplified model TChiWg. The limits for the electroweak production models cannot be improved with respect to the 8 TeV search. A much larger sensitivity is expected with more integrated luminosity collected at $ \sqrt{s} = $ 13 TeV. Additionally, limits are set for two simplified models (T5gg, T5Wg) assuming gluino pair production. The currently best CMS limits are improved in regions with large NLSP masses. |
| References | ||||
| 1 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 2 | J. Wess and B. Zumino | Supergauge transformations in four-dimensions | Nucl. Phys. B 70 (1974) 39 | |
| 3 | D. Z. Freedman, P. van Nieuwenhuizen, and S. Ferrara | Progress toward a theory of supergravity | PRD 13 (1976) 3214 | |
| 4 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | Nucl. Phys. B 90 (1975) 104 | |
| 5 | A. H. Chamseddine, R. L. Arnowitt, and P. Nath | Locally supersymmetric grand unification | PRL 49 (1982) 970 | |
| 6 | L. J. Hall, J. D. Lykken, and S. Weinberg | Supergravity as the messenger of supersymmetry breaking | PRD 27 (1983) 2359 | |
| 7 | G. L. Kane, C. F. Kolda, L. Roszkowski, and J. D. Wells | Study of constrained minimal supersymmetry | PRD 49 (1994) 6173 | hep-ph/9312272 |
| 8 | R. Barbieri and G. F. Giudice | Upper bounds on supersymmetric particle masses | Nucl. Phys. B 306 (1988) 63 | |
| 9 | P. Fayet | Mixing between gravitational and weak interactions through the massive gravitino | PLB 70 (1977) 461 | |
| 10 | H. Baer, M. Brhlik, C. H. Chen, and X. Tata | Signals for the minimal gauge-mediated supersymmetry breaking model at the Fermilab Tevatron collider | PRD 55 (1997) 4463 | hep-ph/9610358 |
| 11 | H. Baer, P. G. Mercadante, X. Tata, and Y. L. Wang | Reach of Tevatron upgrades in gauge-mediated supersymmetry breaking models | PRD 60 (1999) 055001 | hep-ph/9903333 |
| 12 | S. Dimopoulos, S. Thomas, and J. D. Wells | Sparticle spectroscopy and electroweak symmetry breaking with gauge-mediated supersymmetry breaking | Nucl. Phys. B 488 (1997) 39 | hep-ph/9609434 |
| 13 | J. R. Ellis, J. L. Lopez, and D. V. Nanopoulos | Analysis of LEP constraints on supersymmetric models with a light gravitino | PLB 394 (1997) 354 | hep-ph/9610470 |
| 14 | M. Dine, A. E. Nelson, Y. Nir, and Y. Shirman | New tools for low energy dynamical supersymmetry breaking | PRD 53 (1996) 2658 | hep-ph/9507378 |
| 15 | G. F. Giudice and R. Rattazzi | Gauge-mediated supersymmetry breaking | in Perspectives on supersymmetry, p. 355 World Scientific, Singapore | |
| 16 | R. Barbier et al. | R-parity violating supersymmetry | Phys.Rept. 420 (2005) 1 | hep-ph/0406039 |
| 17 | G. R. Farrar and P. Fayet | Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry | PLB 76 (1978) 575 | |
| 18 | P. Meade, N. Seiberg, and D. Shih | General gauge mediation | Prog. Theor. Phys. Suppl. 177 (2009) 143 | 0801.3278 |
| 19 | M. Buican, P. Meade, N. Seiberg, and D. Shih | Exploring general gauge mediation | JHEP 03 (2009) 016 | 0812.3668 |
| 20 | J. T. Ruderman and D. Shih | General neutralino NLSPs at the early LHC | JHEP 08 (2012) 159 | 1103.6083 |
| 21 | Y. Kats, P. Meade, M. Reece, and D. Shih | The status of GMSB after 1/fb at the LHC | JHEP 02 (2012) 115 | 1110.6444 |
| 22 | Y. Kats and M. J. Strassler | Probing colored particles with photons, leptons, and jets | JHEP 11 (2012) 097 | 1204.1119 |
| 23 | P. Grajek, A. Mariotti, and D. Redigolo | Phenomenology of general gauge mediation in light of a 125$ GeV $ Higgs | JHEP 07 (2013) 109 | 1303.0870 |
| 24 | CMS Collaboration | Search for supersymmetry in electroweak production with photons and large missing transverse energy in pp collisions at $ \sqrt{s} $ = 8 TeV | PLB 759 (2016) 479 | CMS-SUS-14-016 1602.08772 |
| 25 | CMS Collaboration | Data parking and data scouting at the CMS experiment | CDS | |
| 26 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 27 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 28 | CMS Collaboration | Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P08010 | CMS-EGM-14-001 1502.02702 |
| 29 | CMS Collaboration | Identification of b-quark jets with the CMS experiment | JINST 8 (2013) P04013 | CMS-BTV-12-001 1211.4462 |
| 30 | CMS Collaboration | Identification of b quark jets at the CMS Experiment in the LHC Run 2 | CMS-PAS-BTV-15-001 | CMS-PAS-BTV-15-001 |
| 31 | C. J. Clopper and E. S. Pearson | The use of confidence or fiducial limits illustrated in the case of the binomial | Biometrika 26 (1934), no. 4, 404 | |
| 32 | CMS Collaboration | Missing transverse energy performance of the CMS detector | JINST 6 (2011) P09001 | CMS-JME-10-009 1106.5048 |
| 33 | CMS Collaboration | Performance of the CMS missing transverse momentum reconstruction in pp data at $ \sqrt{s} $ = 8 TeV | JINST 10 (2015), no. 02, P02006 | CMS-JME-13-003 1411.0511 |
| 34 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 35 | P. Nason | A New method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 36 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 37 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 38 | T. Melia, P. Nason, R. Rontsch, and G. Zanderighi | W+W-, WZ and ZZ production in the POWHEG BOX | JHEP 11 (2011) 078 | 1107.5051 |
| 39 | P. Nason and G. Zanderighi | $ W^+ W^- $ , $ W Z $ and $ Z Z $ production in the POWHEG-BOX-V2 | EPJC 74 (2014), no. 1 | 1311.1365 |
| 40 | T. Sj\"ostrand, S. Mrenna, and P. Skands | PYTHIA 6.4 physics and manual | JHEP 05 (2006) 026 | hep-ph/0603175 |
| 41 | T. Sjostrand, S. Mrenna, and P. Z. Skands | A Brief Introduction to PYTHIA 8.1 | CPC 178 (2008) 852--867 | 0710.3820 |
| 42 | GEANT4 Collaboration | GEANT4: A Simulation toolkit | Nucl.Instrum.Meth. A 506 (2003) 250 | |
| 43 | G. Bozzi et al. | Production of Drell-Yan lepton pairs in hadron collisions: Transverse-momentum resummation at next-to-next-to-leading logarithmic accuracy | PLB 696 (2011) 207 | 1007.2351 |
| 44 | T. Gehrmann et al. | $ W^+W^- $ Production at Hadron Colliders in Next to Next to Leading Order QCD | PRL 113 (2014), no. 21, 212001 | 1408.5243 |
| 45 | C. Borschensky et al. | Squark and gluino production cross sections in pp collisions at $ \sqrt{s} $ = 13, 14, 33 and 100 TeV | EPJC 74 (2014), no. 12 | 1407.5066 |
| 46 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Gaugino production in proton-proton collisions at a center-of-mass energy of 8 TeV | JHEP 10 (2012) 081 | 1207.2159 |
| 47 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Precision predictions for electroweak superpartner production at hadron colliders with Resummino | EPJC 73 (2013) 2480 | 1304.0790 |
| 48 | W. Beenakker et al. | The Production of charginos / neutralinos and sleptons at hadron colliders | PRL 83 (1999) 3780--3783, , [Erratum: PRLett.100,029901(2008)] | hep-ph/9906298 |
| 49 | CMS Collaboration | Measurement of the inclusive top-quark pair + photon production cross section in the muon + jets channel in pp collisions at 8 TeV | CDS | |
| 50 | CMS Collaboration | Measurement of the WW cross section pp collisions at sqrt(s)=13 TeV | CMS-PAS-SMP-16-006 | CMS-PAS-SMP-16-006 |
| 51 | CMS Collaboration | Measurement of the WZ production cross section in pp collisions at sqrt(s) = 13 TeV | CMS-PAS-SMP-16-002 | CMS-PAS-SMP-16-002 |
| 52 | CMS Collaboration | Measurement of the ZZ production cross section and $ \mathrm{Z} \to \ell\ell\ell'\ell' $ branching fraction in pp collisions at $ \sqrt{s}=13 \mathrm{TeV} $ | CMS-PAS-SMP-16-001 | CMS-PAS-SMP-16-001 |
| 53 | T. Junk | Confidence level computation for combining searches with small statistics | Nucl.Instrum.Meth. A 434 (1999) 435 | hep-ex/9902006 |
| 54 | A. L. Read | Presentation of search results: the CLs technique | JPG 28 (2002) 2693 | |
| 55 | ATLAS Collaboration, CMS Collaboration, LHC Higgs Combination Group Collaboration | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |
| 56 | E. Gross and O. Vitells | Trial factors or the look elsewhere effect in high energy physics | EPJC 70 (2010) 525 | 1005.1891 |
| 57 | CMS Collaboration | Search for supersymmetry in events with photons and missing transverse energy | CMS-PAS-SUS-15-012 | CMS-PAS-SUS-15-012 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|