

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-17-001 | ||
| Search for lepton flavour violating decays of the Higgs boson to $\mu\tau$ and $\textrm{e}\tau$ in proton-proton collisions at $\sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| May 2017 | ||
| Abstract: A search for lepton flavor violating decays of the 125 GeV Higgs boson in the $\mu\tau$ and $\textrm{e}\tau$ decay modes is presented. The search is based on a dataset of 35.9 fb$^{-1}$ of proton-proton collisions collected with the CMS detector in 2016, at a center-of-mass energy of 13 TeV. The tau leptons are reconstructed in the leptonic and hadronic decay modes. No significant excess over the standard model background expectation is observed. The observed (expected) upper limits on the branching fraction of the Higgs boson are found to be $\mathcal{B}(\textrm{H}\rightarrow\mu\tau)< $ 0.25(0.25)% and $\mathcal{B}(\textrm{H}\rightarrow\textrm{e}\tau)< $ 0.61(0.37)% at 95% confidence level. These results are used to derive upper limits on the off-diagonal $\mu\tau$ and $\textrm{e}\tau$ Yukawa couplings, $\sqrt{|{Y_{\mu\tau}}|^{2}+|{Y_{\tau\mu}}|^{2}}<1.43\times 10^{-3}$ and $\sqrt{|{Y_{\textrm{e}\tau}}|^{2}+|{Y_{\tau\textrm{e}}}|^{2}}<2.26\times 10^{-3}$ at 95% CL. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JHEP 06 (2018) 001. The superseded preliminary plots can be found here. |
||
| Figures & Tables | Summary | Additional Figures | References | CMS Publications |
|---|
| Figures | |
png pdf |
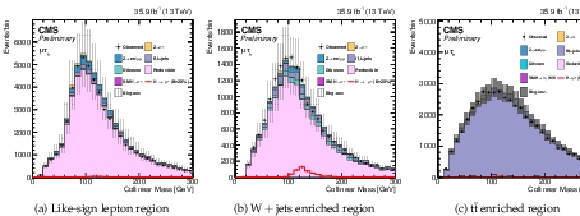
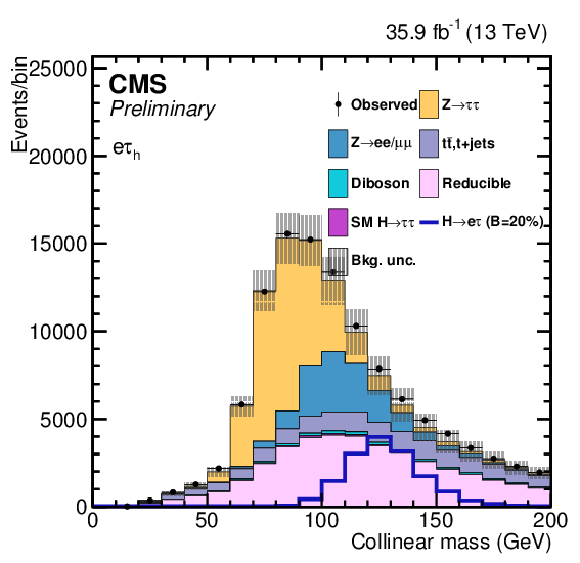
Figure 1:
$ {M_{col}} $ in different control regions defined in the text. The distributions are pre-fit and include both statistical and systematic uncertainties. |
png pdf |
Figure 1-a:
$ {M_{col}} $ in the like-sign lepton control region. The distribution is pre-fit and includes both statistical and systematic uncertainties. |
png pdf |
Figure 1-b:
$ {M_{col}} $ in the W+jets enriched control region. The distribution is pre-fit and includes both statistical and systematic uncertainties. |
png pdf |
Figure 1-c:
$ {M_{col}} $ in the $\mathrm{t \bar{t}}$ enriched control region. The distribution is pre-fit and includes both statistical and systematic uncertainties. |
png pdf |
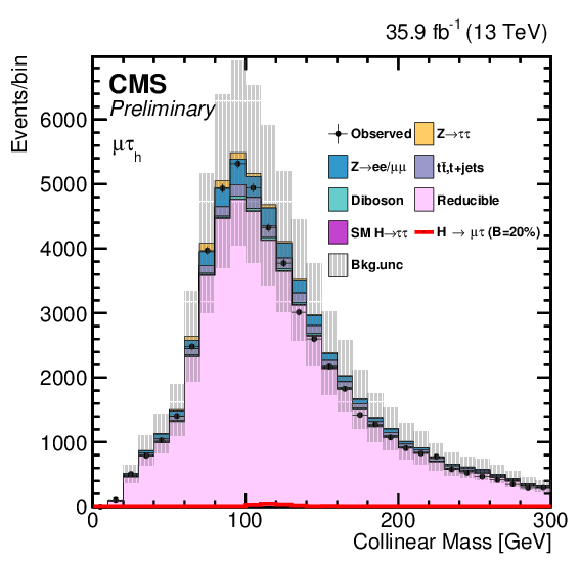
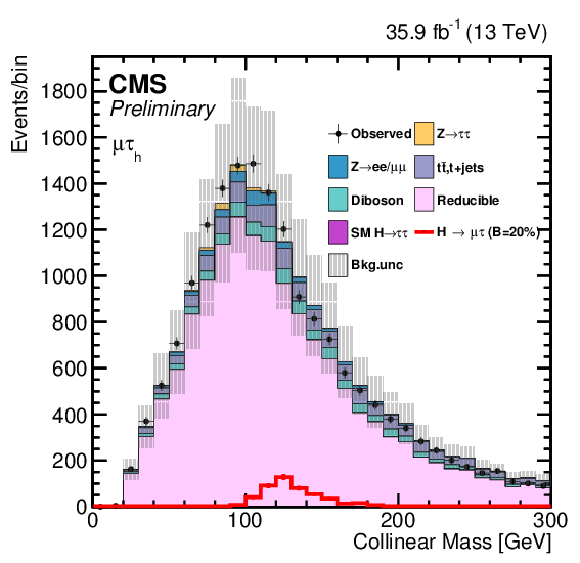
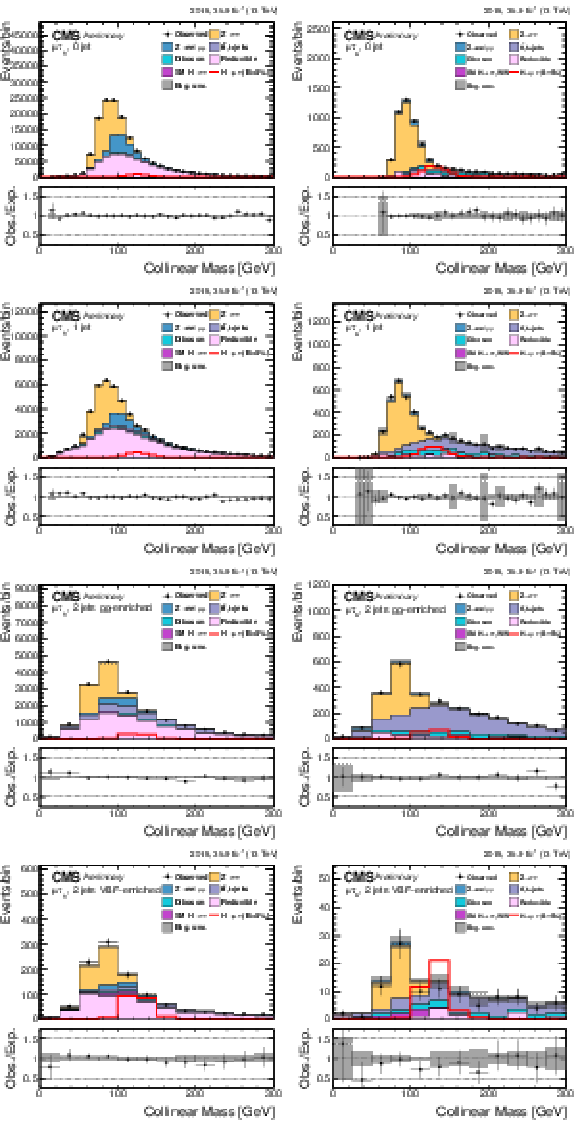
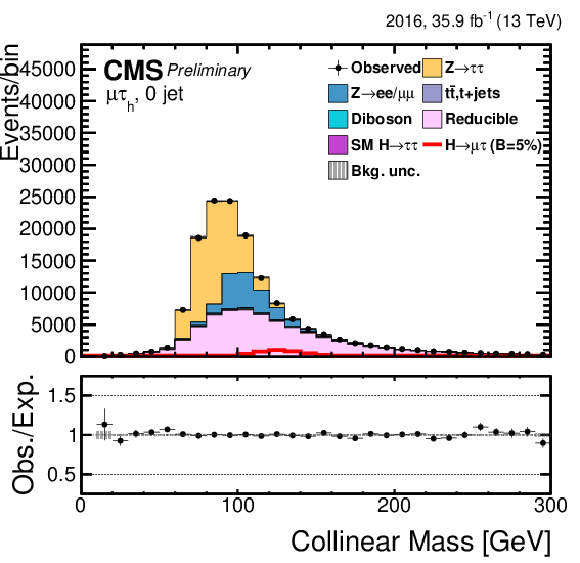
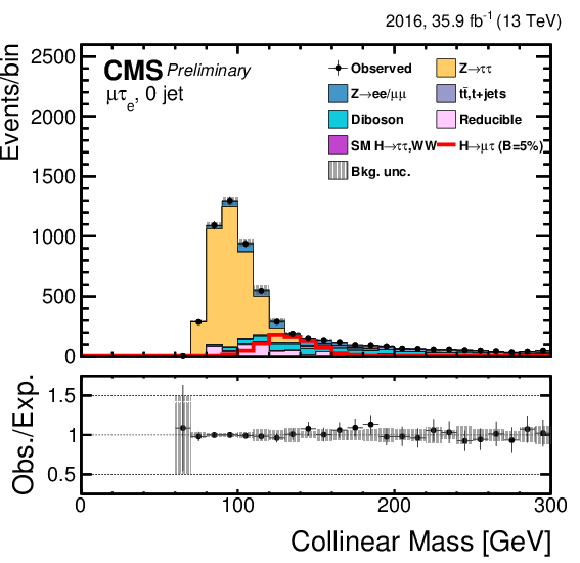
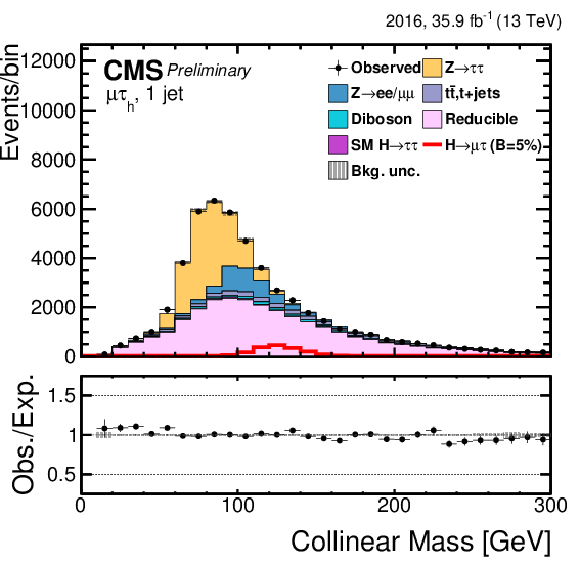
Figure 2:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis, in the different channels and categories compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in each plot shows the fractional difference between the observed data and the fitted background. The left column of plots corresponds to the $\mathrm{ H } \to \mu {\tau _{h}} $ categories, from 0-jets (first row) to 2-jets VBF (fourth row). The right one to their $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ counterparts. |
png pdf |
Figure 2-a:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis in the $\mathrm{ H } \to \mu {\tau _{h}} $ 0-jet category compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
Figure 2-b:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis in the $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ 0-jet category compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
Figure 2-c:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis in the $\mathrm{ H } \to \mu {\tau _{h}} $ 1-jet category compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
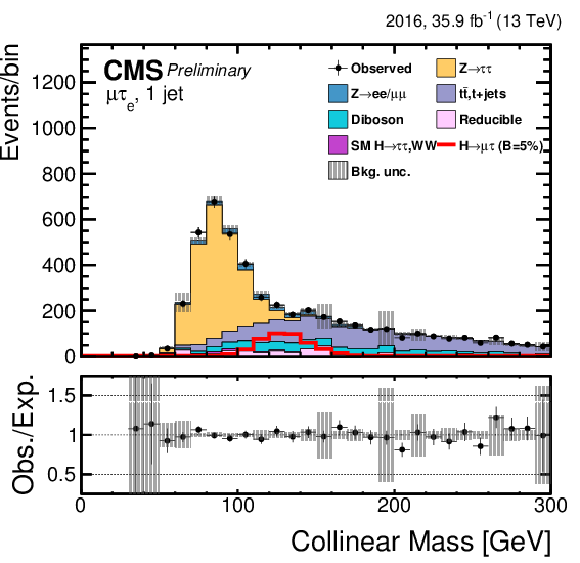
png pdf |
Figure 2-d:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis in the $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ 1-jet category compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
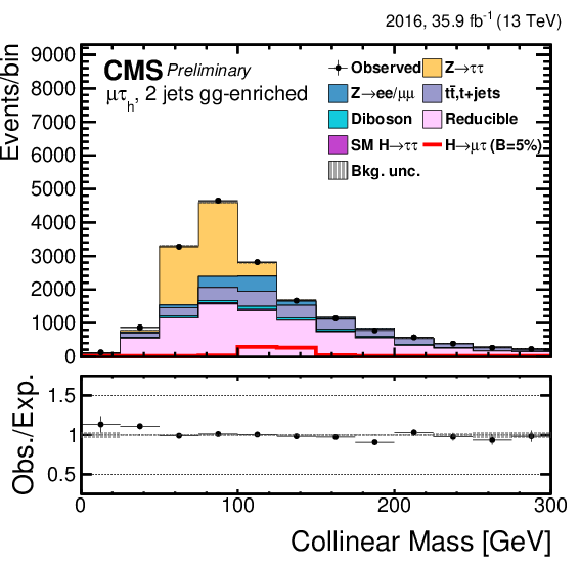
png pdf |
Figure 2-e:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis in the $\mathrm{ H } \to \mu {\tau _{h}} $ 2-jets gg category compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
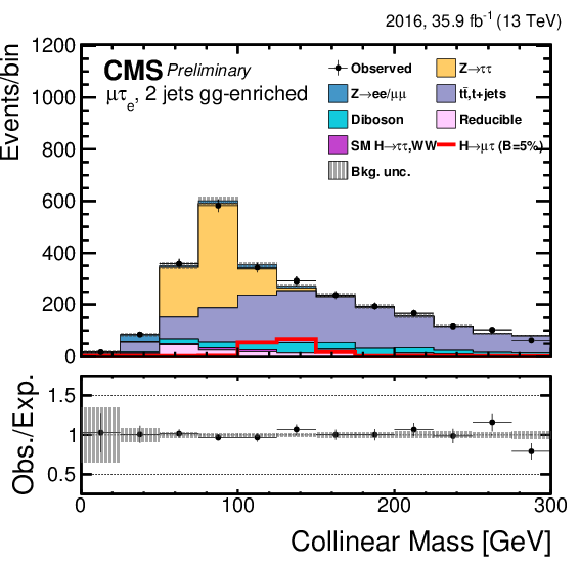
png pdf |
Figure 2-f:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis in the $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ 2-jets gg category compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |

png pdf |
Figure 2-g:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis in the $\mathrm{ H } \to \mu {\tau _{h}} $ 2-jets VBF category compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
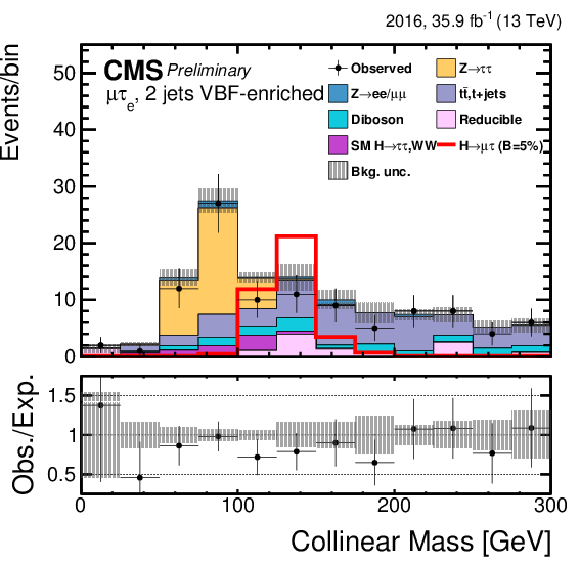
png pdf |
Figure 2-h:
Distribution of the collinear mass $ {M_{col}} $ for the $\mathrm{ H } \rightarrow \mu \tau $ process in $ {M_{col}} $-fit analysis in the $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ 2-jets VBF category compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the overlayed simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=5%$. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |

png pdf |
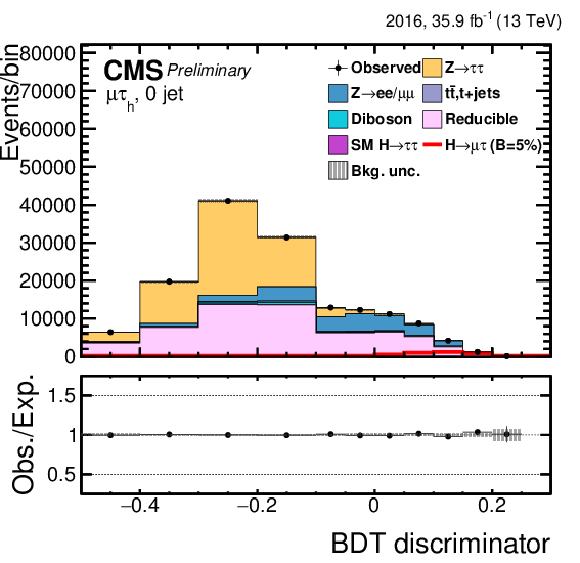
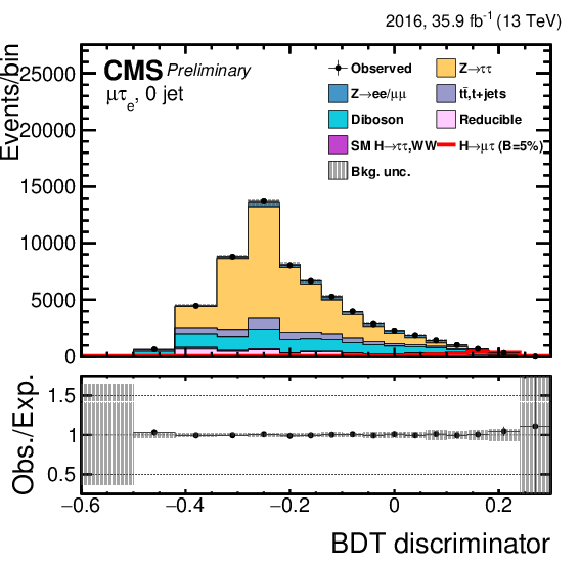
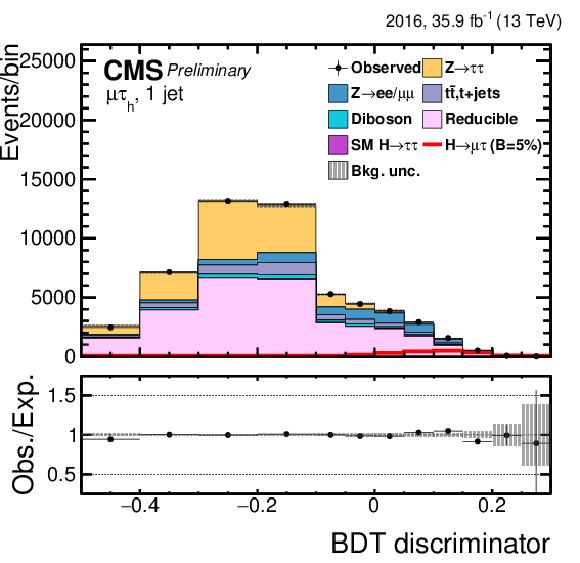
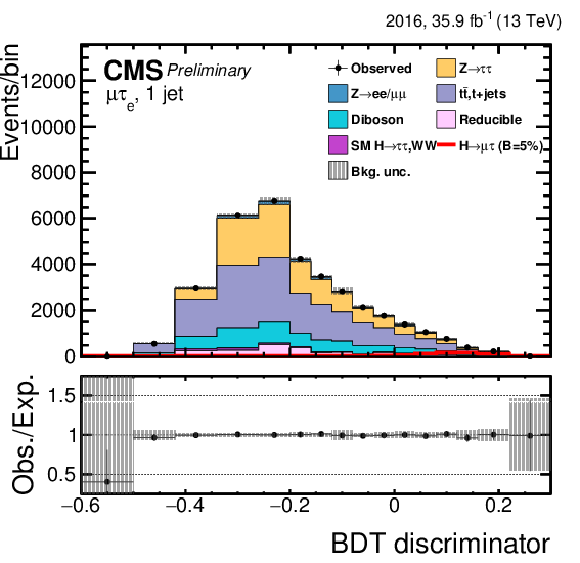
Figure 3:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis, in the different channels and categories compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in each plot shows the fractional difference between the observed data and the fitted background. The left column of plots corresponds to the $\mathrm{ H } \to \mu {\tau _{h}} $ categories, from 0-jets (first row) to 2-jets VBF (fourth row). The right one to their $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ counterparts. |
png pdf |
Figure 3-a:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis in the $\mathrm{ H } \to \mu {\tau _{h}} $ 0-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
Figure 3-b:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis in the $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ 0-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
Figure 3-c:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis in the $\mathrm{ H } \to \mu {\tau _{h}} $ 1-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
Figure 3-d:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis in the $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ 1-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
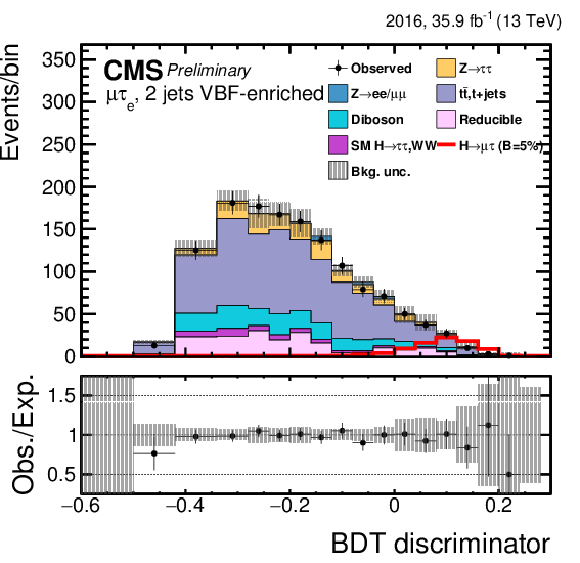
png pdf |
Figure 3-e:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis in the $\mathrm{ H } \to \mu {\tau _{h}} $ 2-jets gg category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
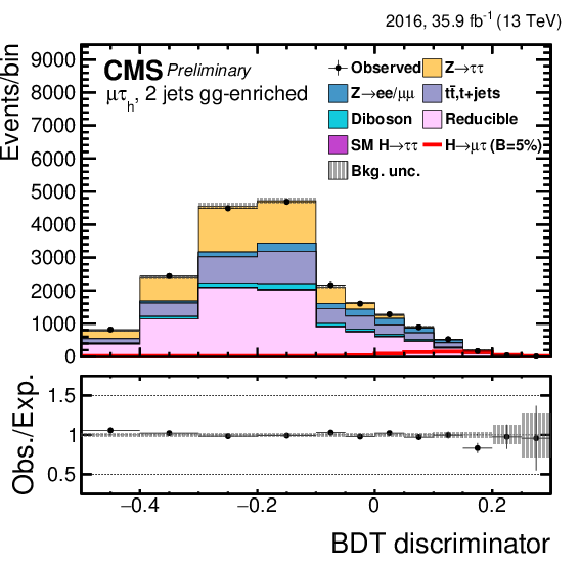
png pdf |
Figure 3-f:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis in the $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ 2-jets gg category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
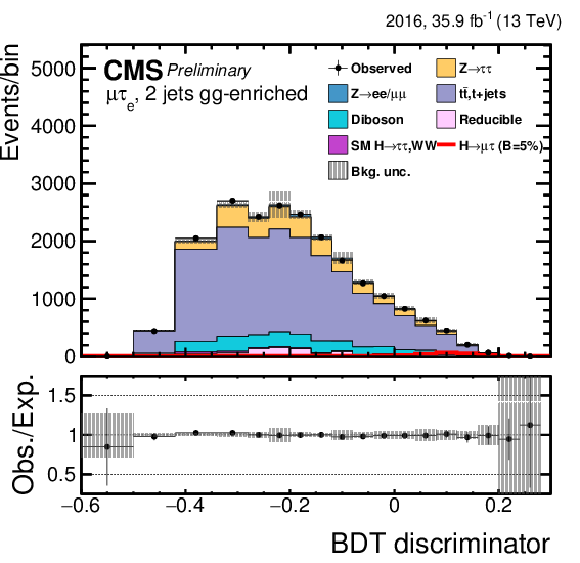
png pdf |
Figure 3-g:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis in the $\mathrm{ H } \to \mu {\tau _{h}} $ 2-jets VBF category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
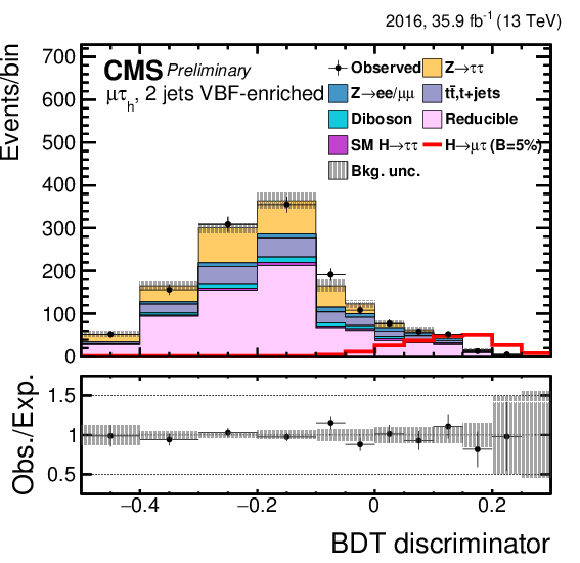
png pdf |
Figure 3-h:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mu \tau $ process in the BDT-fit analysis in the $\mathrm{ H } \to \mu \tau _{\mathrm{ e } }$ 2-jets VBF category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mu \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
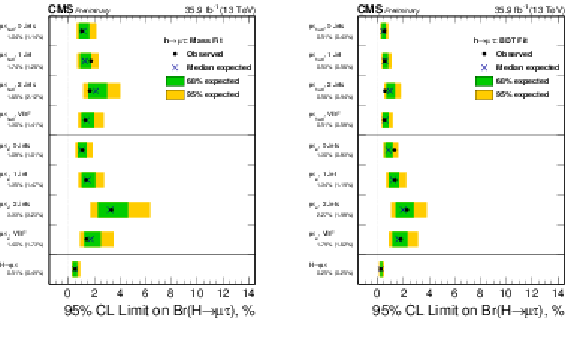
Figure 4:
Observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mu \tau )$ for each individual category and combined. Left: $ {M_{col}} $-fit analysis. Right: BDT-fit analysis. |

png pdf |
Figure 4-a:
Observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mu \tau )$ for each individual category and combined: $ {M_{col}} $-fit analysis. |
png pdf |
Figure 4-b:
Observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mu \tau )$ for each individual category and combined: BDT-fit analysis. |

png pdf |
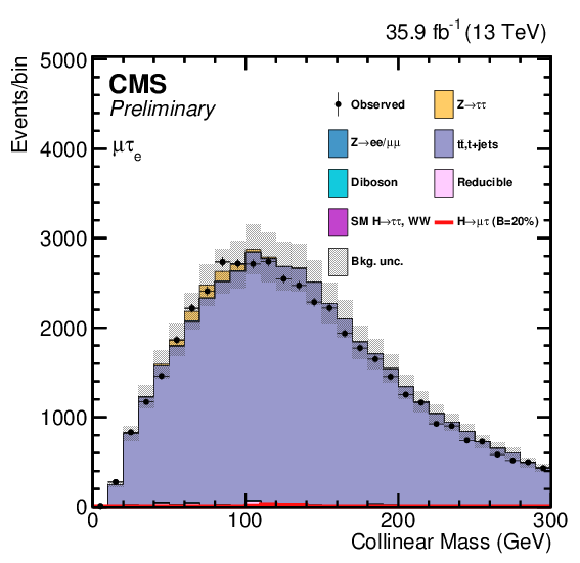
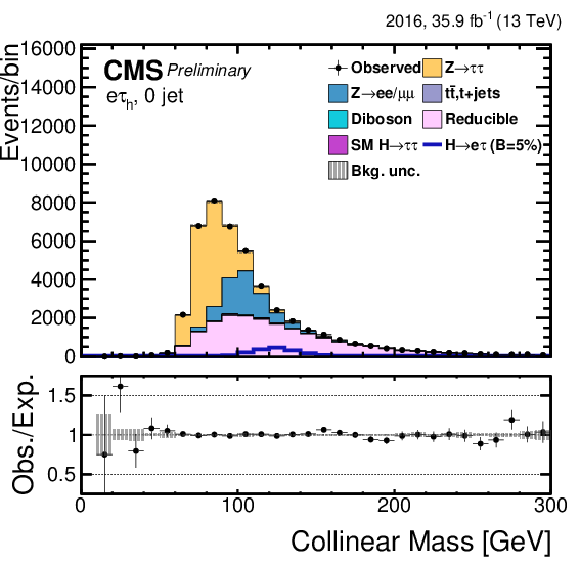
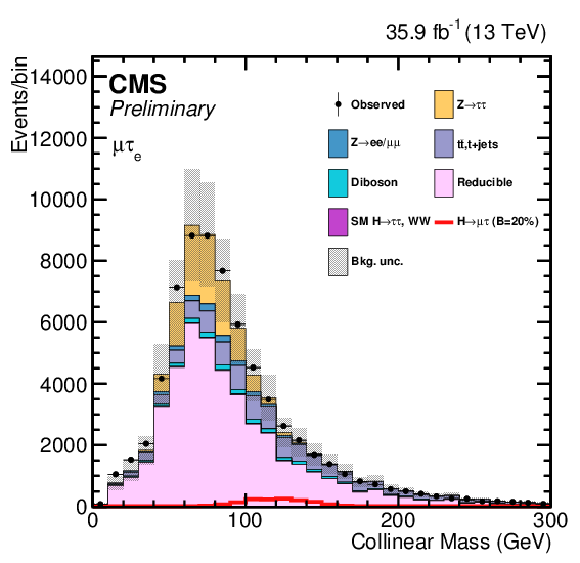
Figure 5:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the different channels and categories compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in each plot shows the fractional difference between the observed data and the fitted background. The left column of plots correspond to the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ categories, from 0-jets (first row) to 2 jets VBF (fourth row). The right one to their $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ counterparts. |
png pdf |
Figure 5-a:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ 0-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
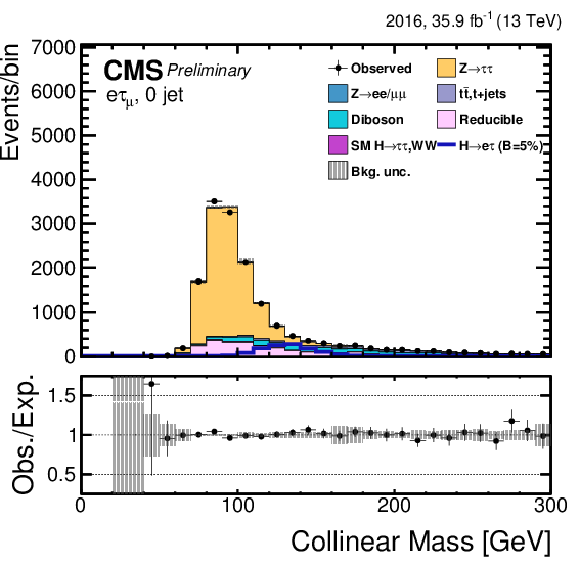
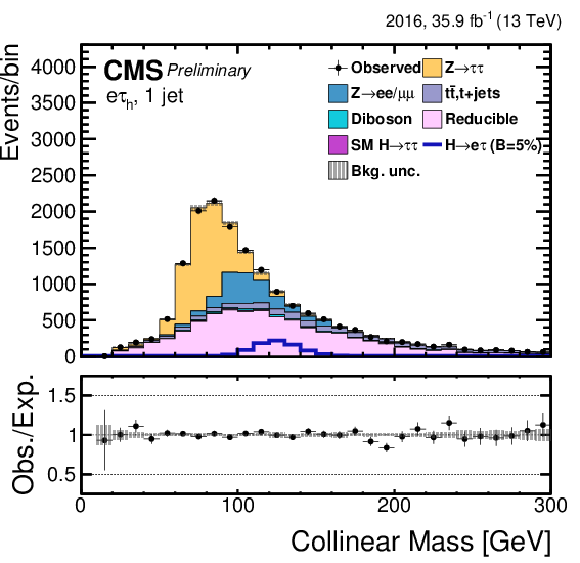
Figure 5-b:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ 0-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
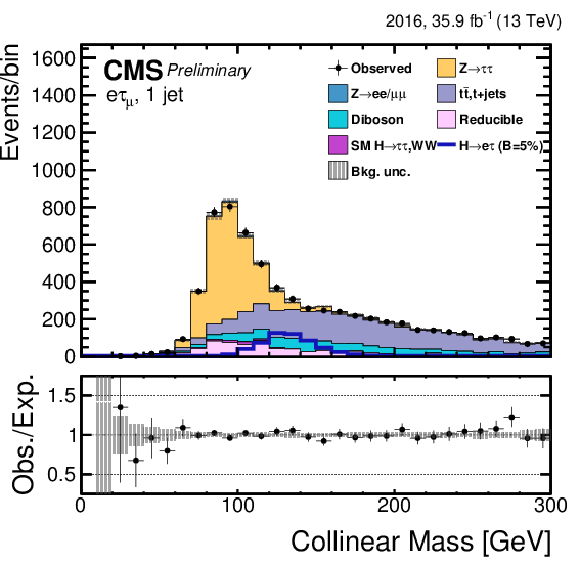
Figure 5-c:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ 1-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
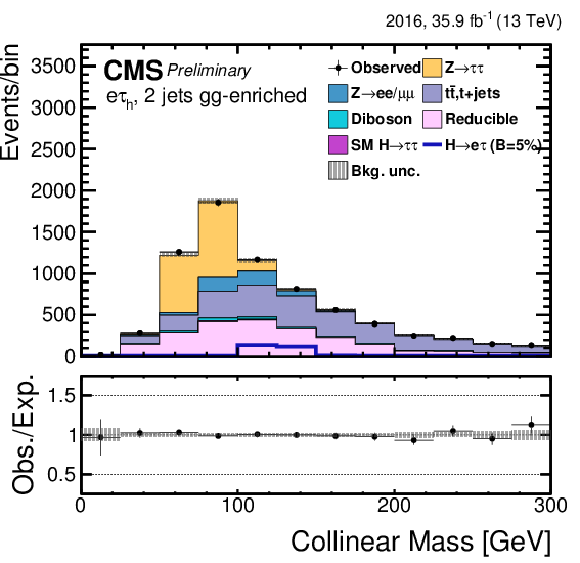
Figure 5-d:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ 1-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
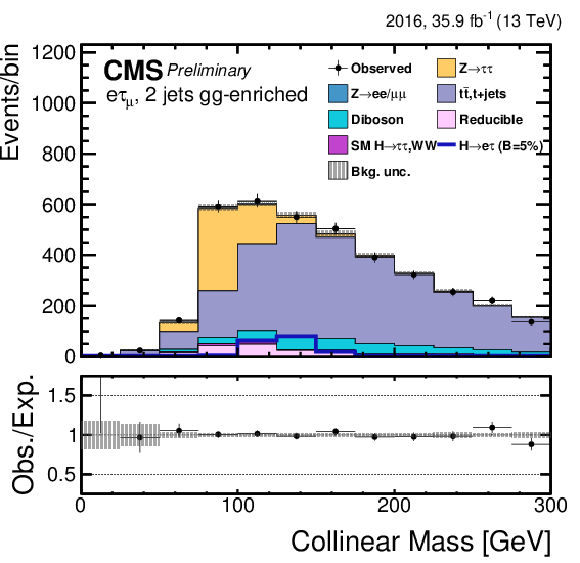
Figure 5-e:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ 2-jets gg category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
Figure 5-f:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ 2-jets gg category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
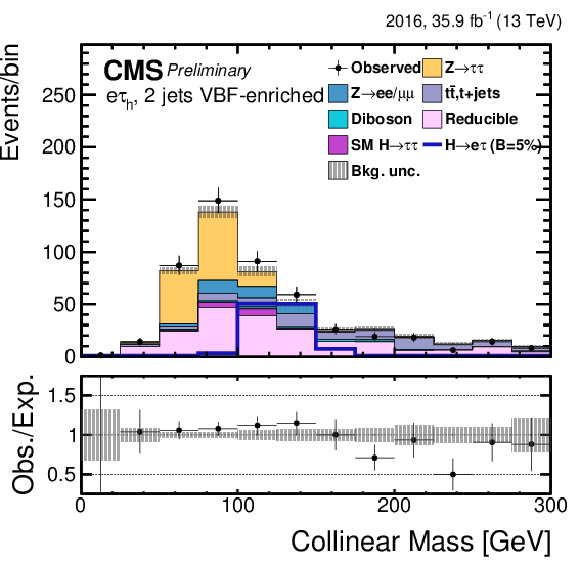
Figure 5-g:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ 2-jets VBF category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
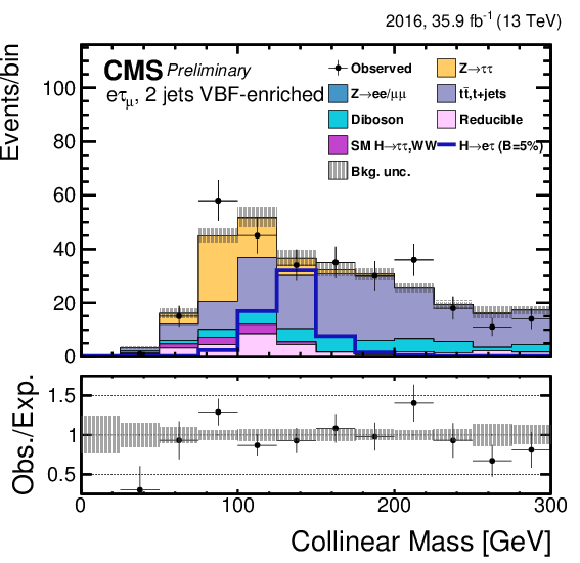
Figure 5-h:
Distribution of the collinear mass $M_\text {col}$ for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process in the $ {M_{col}} $-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ 2-jets VBF category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=5%$. The lower panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
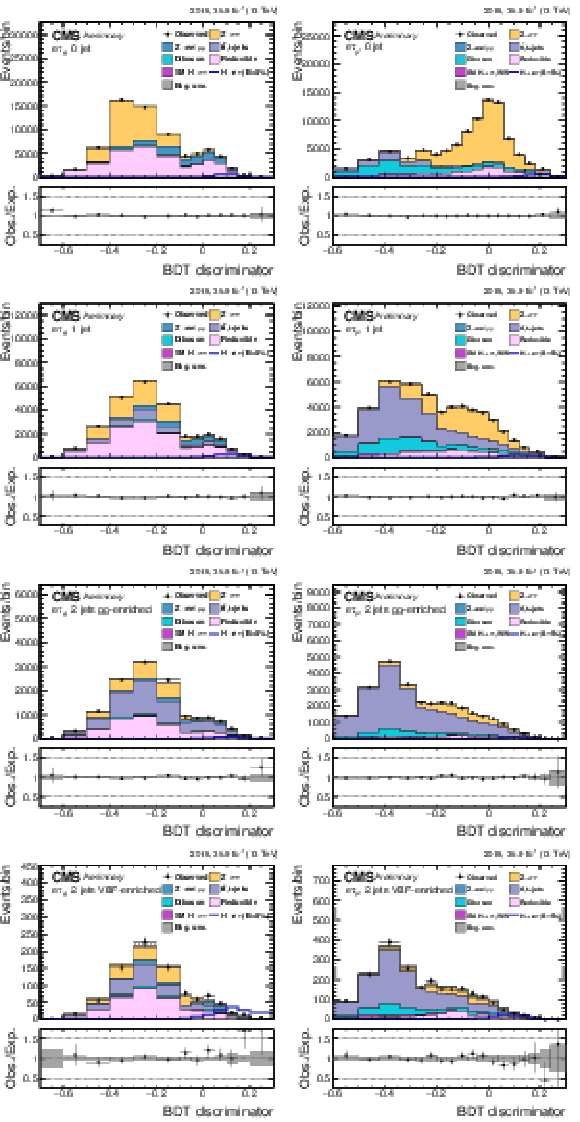
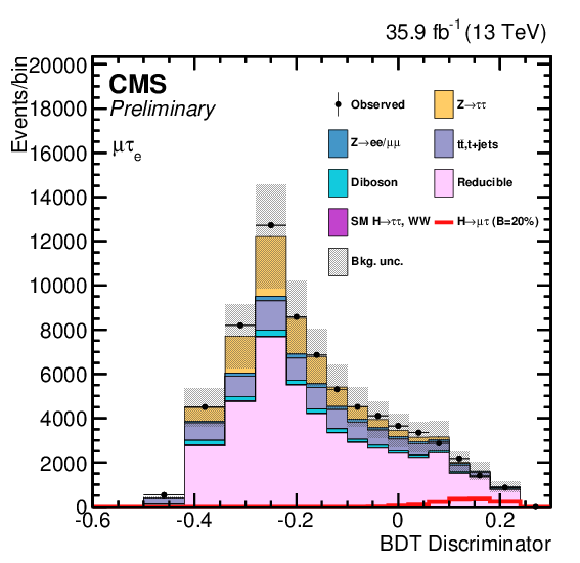
Figure 6:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the different channels and categories compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in each plot shows the fractional difference between the observed data and the fitted background. The left column of plots corresponds to the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ categories, from 0-jets (first row) to 2-jets VBF (fourth row). The right one to their $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ counterparts. |
png pdf |
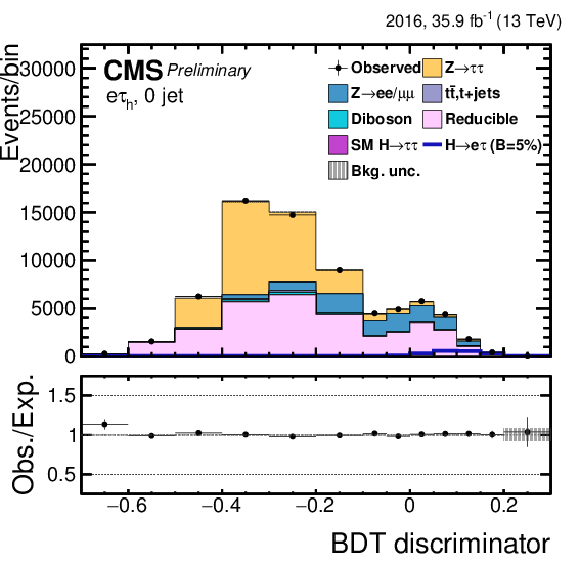
Figure 6-a:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ 0-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
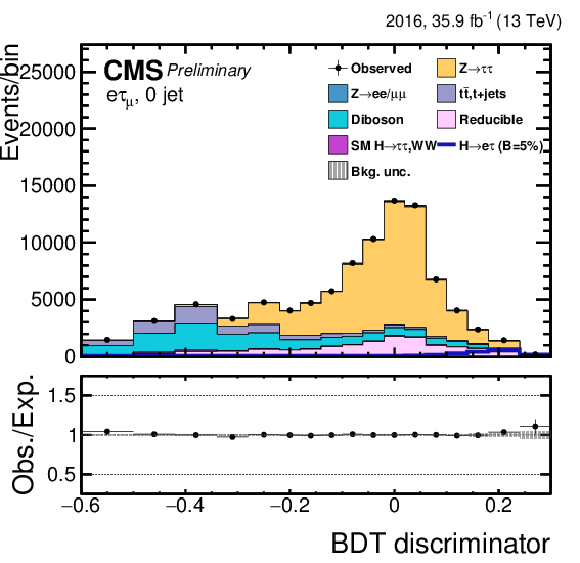
png pdf |
Figure 6-b:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ 0-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
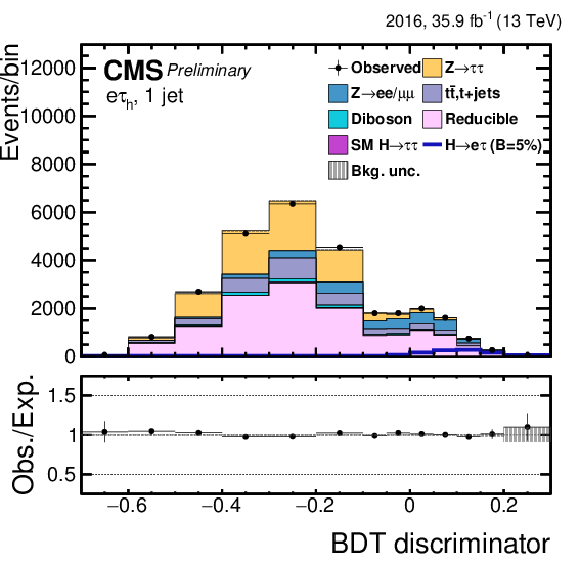
png pdf |
Figure 6-c:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ 1-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
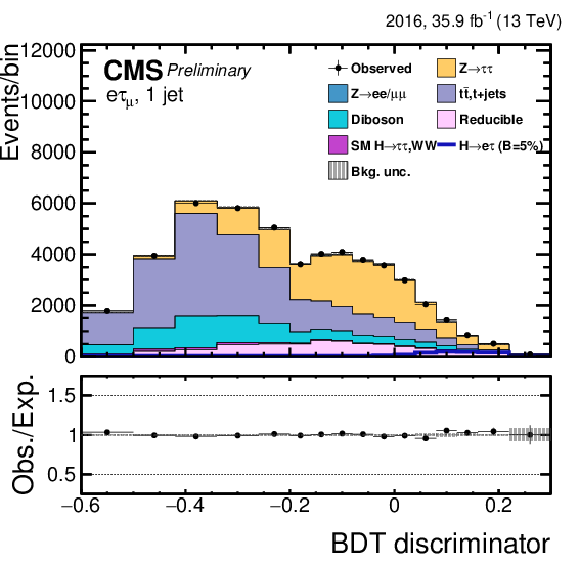
png pdf |
Figure 6-d:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ 1-jet category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
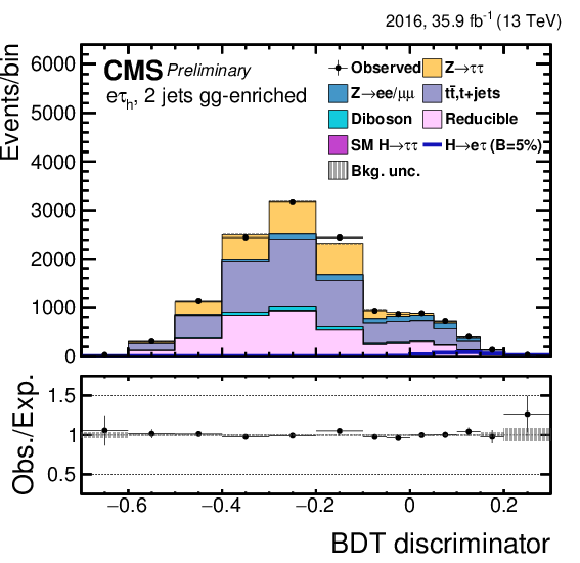
png pdf |
Figure 6-e:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ 2-jets gg category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |

png pdf |
Figure 6-f:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ 2-jets gg category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
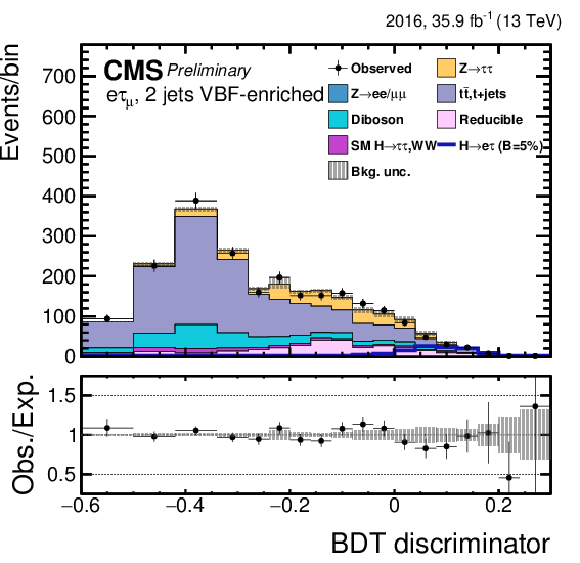
Figure 6-g:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } {\tau _{h}} $ 2-jets VBF category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
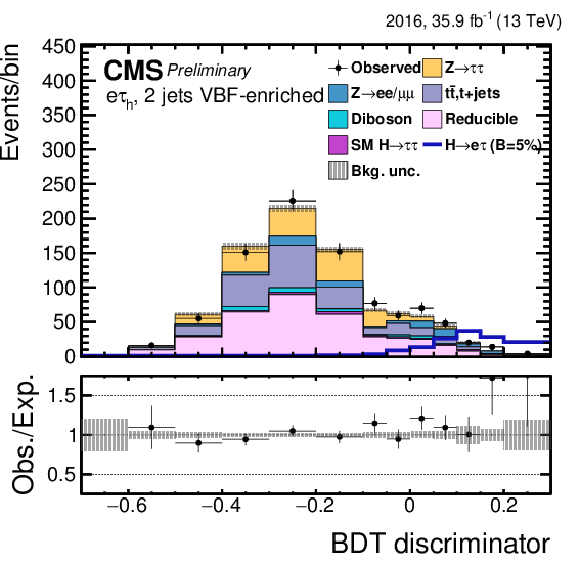
Figure 6-h:
Distribution of the BDT output for the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process for the BDT-fit analysis, in the $\mathrm{ H } \to \mathrm{ e } \tau _{\mu }$ 2-jets VBF category, compared to the signal and background estimation. The background is normalized to the best-fit values from the signal plus background fit while the simulated signal corresponds to $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )=$ 5%. The bottom panel in the plot shows the fractional difference between the observed data and the fitted background. |
png pdf |
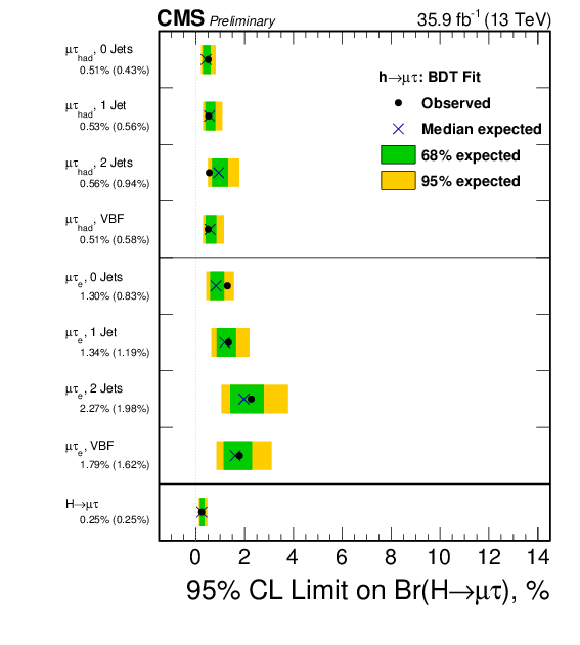
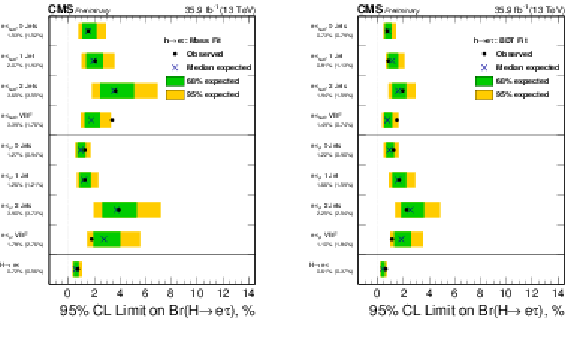
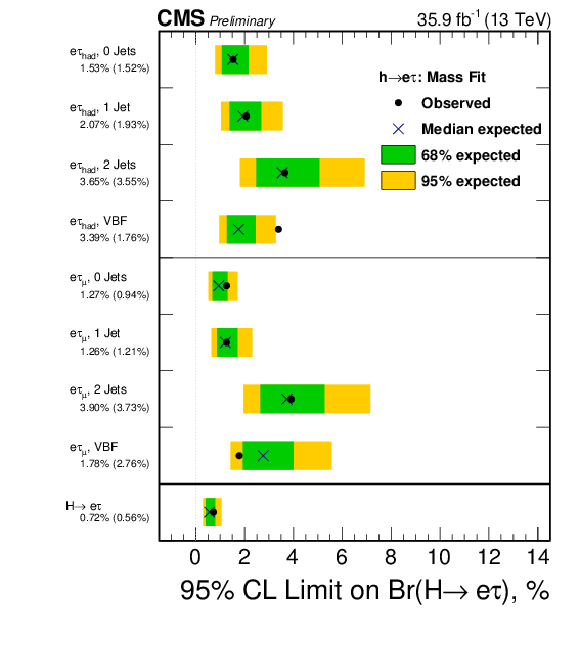
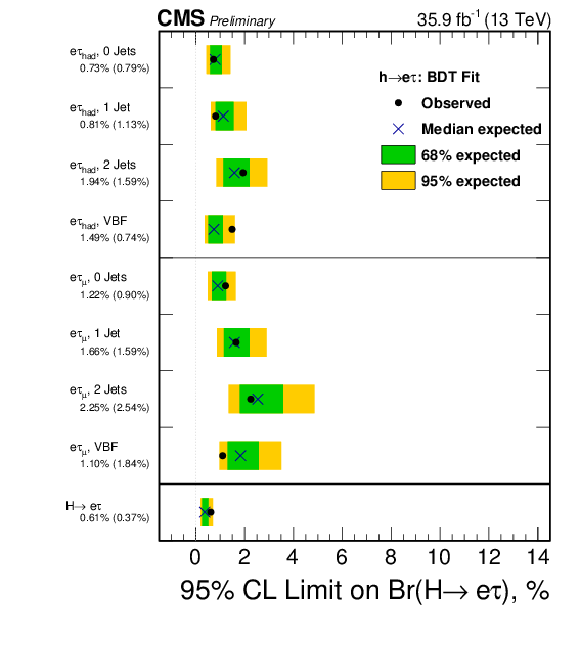
Figure 7:
Observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )$ for each individual category and combined. Left: $ {M_{col}} $-fit analysis. Right: BDT-fit analysis. |
png pdf |
Figure 7-a:
Observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )$ for each individual category and combined: $ {M_{col}} $-fit analysis. |
png pdf |
Figure 7-b:
Observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )$ for each individual category and combined: BDT-fit analysis. |
png pdf |
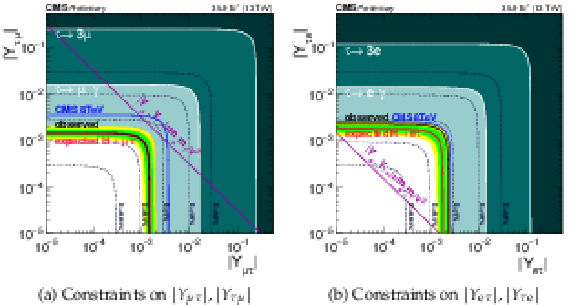
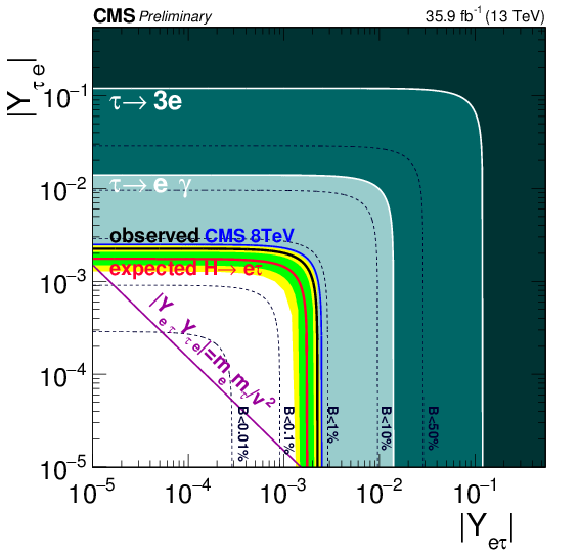
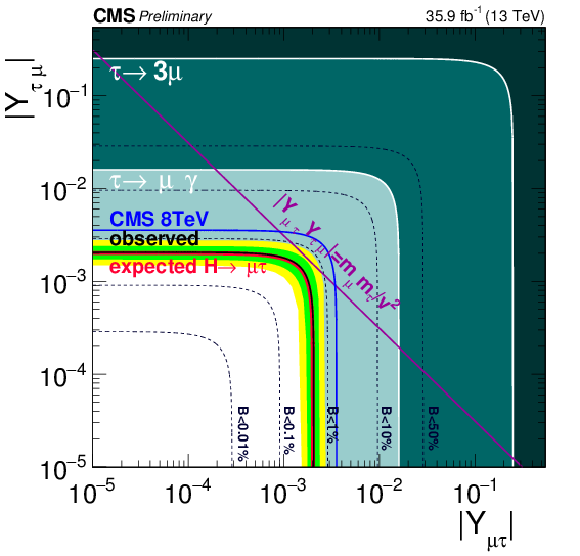
Figure 8:
Constraints on the flavour violating Yukawa couplings, $|Y_{\mu \tau }|,|Y_{\tau \mu }|$ and $|Y_{\mathrm{ e } \tau }|,|Y_{\tau \mathrm{ e } }|$, from the BDT result. The expected (red solid line) and observed (black solid line) limits are derived from the limit on $B(\mathrm{ H } \to \mu \tau )$ and $B(\mathrm{ H } \to \mathrm{ e } \tau )$ from the present analysis. The flavour diagonal Yukawa couplings are approximated by their SM values. The green (yellow) band indicates the range that is expected to contain 68% (95%) of all observed limit excursions from the expected limit. The shaded regions are derived constraints from null searches for $\tau \to 3\mu $ or $\tau \to 3\mathrm{ e } $ (dark green) and $\tau \to \mu \gamma $ or $\tau \to \mathrm{ e } \gamma $ (lighter green).The purple diagonal line is the theoretical naturalness limit $Y_{ij}Y_{ji} \leq m_im_j/v^2$. |

png pdf |
Figure 8-a:
Constraints on the flavour violating Yukawa couplings, $|Y_{\mu \tau }|,|Y_{\tau \mu }|$, from the BDT result. The expected (red solid line) and observed (black solid line) limits are derived from the limit on $B(\mathrm{ H } \to \mu \tau )$ from the present analysis. The flavour diagonal Yukawa couplings are approximated by their SM values. The green (yellow) band indicates the range that is expected to contain 68% (95%) of all observed limit excursions from the expected limit. The shaded regions are derived constraints from null searches for $\tau \to 3\mu $ (dark green) and $\tau \to \mu \gamma $ (lighter green).The purple diagonal line is the theoretical naturalness limit $Y_{ij}Y_{ji} \leq m_im_j/v^2$. |
png pdf |
Figure 8-b:
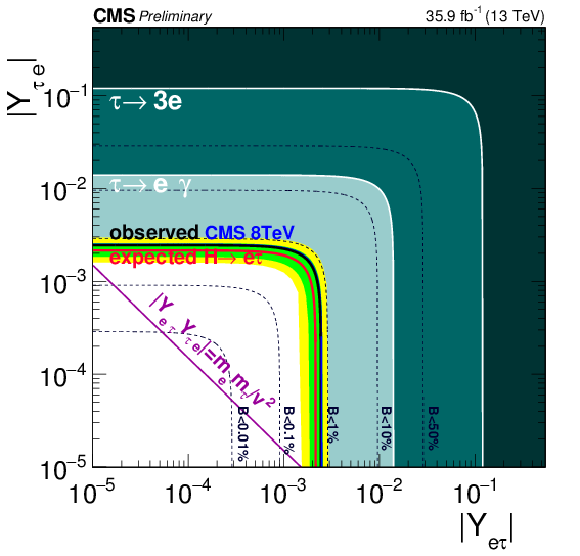
Constraints on the flavour violating Yukawa couplings, $|Y_{\mathrm{ e } \tau }|,|Y_{\tau \mathrm{ e } }|$, from the BDT result. The expected (red solid line) and observed (black solid line) limits are derived from the limit on $B(\mathrm{ H } \to \mathrm{ e } \tau )$ from the present analysis. The flavour diagonal Yukawa couplings are approximated by their SM values. The green (yellow) band indicates the range that is expected to contain 68% (95%) of all observed limit excursions from the expected limit. The shaded regions are derived constraints from null searches for $\tau \to 3\mathrm{ e } $ (dark green) and $\tau \to \mathrm{ e } \gamma $ (lighter green).The purple diagonal line is the theoretical naturalness limit $Y_{ij}Y_{ji} \leq m_im_j/v^2$. |
| Tables | |
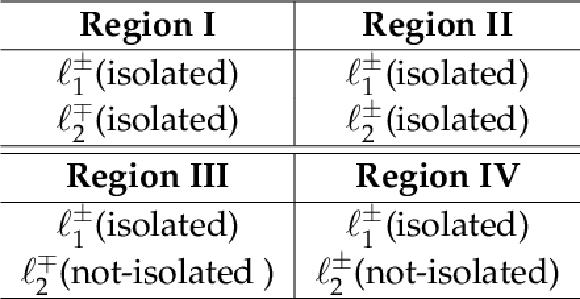
png pdf |
Table 1:
Definition of the samples used to estimate the misidentified lepton ($\ell $) background. They are defined by the charge of the two leptons and by the isolation requirements on each. The definition of not-isolated differs in each channel. |
png pdf |
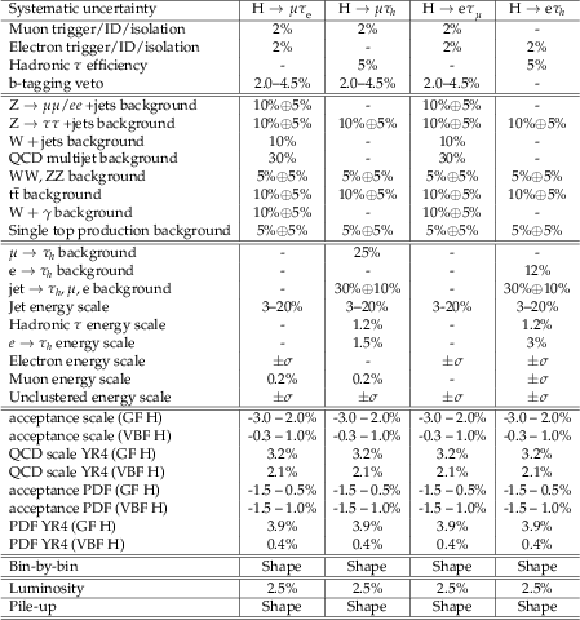
Table 2:
The systematic uncertainties in the expected event yield. All uncertainties are treated as correlated between the categories, except those which have two values. In this case the first value is the correlated uncertainty and the second value is the uncorrelated uncertainty for each individual category. Anticorrelations arise due to migration of events between the categories and are expressed as negative numbers. |
png pdf |
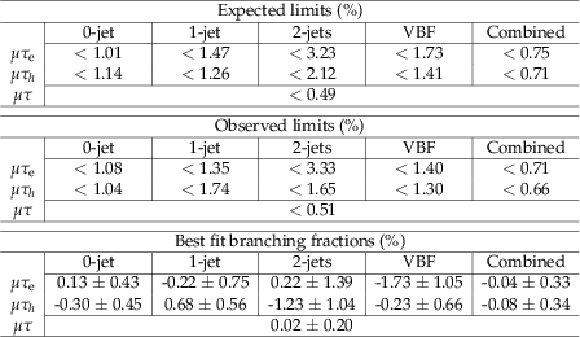
Table 3:
The expected and observed upper limits at 95% CL, and best fit branching fractions in percent for the different jet categories for the $\mathrm{ H } \rightarrow \mu \tau $ process obtained with the $ {M_{col}} $-fit analysis. |
png pdf |
Table 4:
The expected and observed upper limits at 95% CL, and the best fit branching fractions in percent for each individual jet category, and combined, in the $\mathrm{ H } \rightarrow \mu \tau $ process obtained with the BDT-fit analysis. |
png pdf |
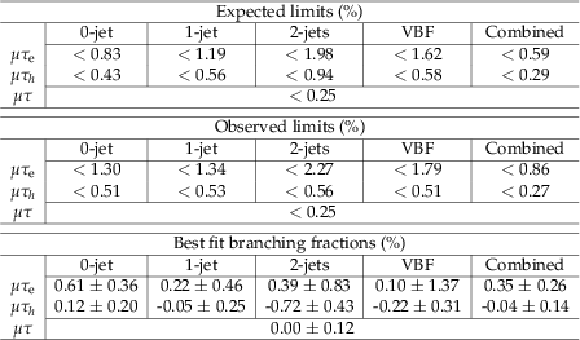
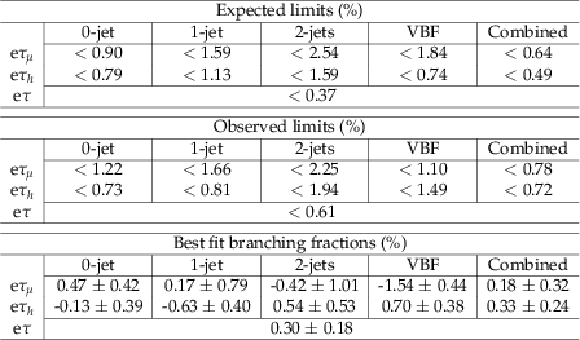
Table 5:
The expected and observed upper limits at 95% CL and best fit branching fractions in percent for each individual jet category, and combined, in the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process obtained with the $ {M_{col}} $-fit analysis. |
png pdf |
Table 6:
The observed and expected upper limits at 95% CL and the best fit branching fractions in percent for the different jet categories in the $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ process obtained with the BDT-fit analysis. |

png pdf |
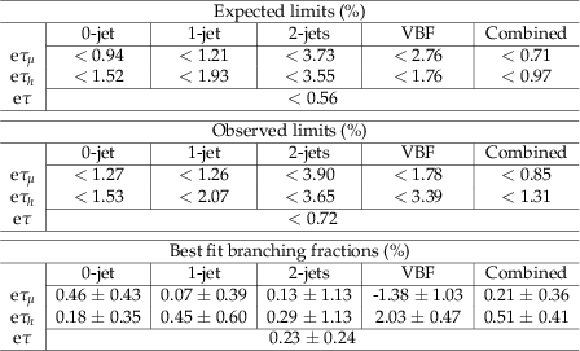
Table 7:
The observed and expected upper limits at the 95% CL and the best fit branching fractions in percent for the $\mathrm{ H } \rightarrow \mu \tau $ and $\mathrm{ H } \rightarrow \mathrm{ e } \tau $ processes, with the different selections. |
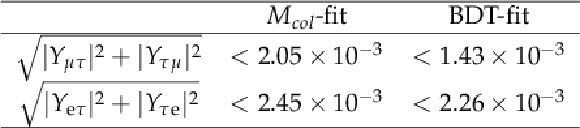
png pdf |
Table 8:
95% CL upper limit on the Yukawa couplings |
| Summary |
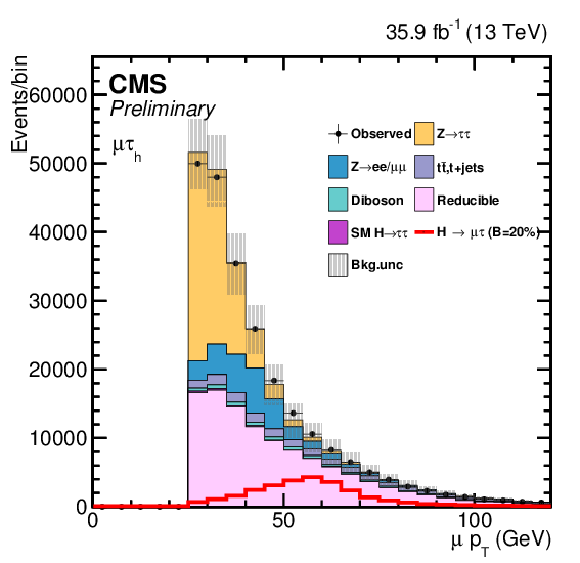
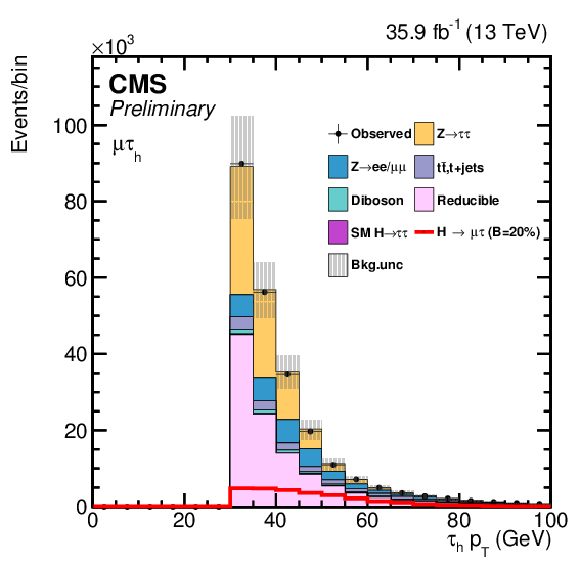
| This article presents the search for LFV decays of the Higgs boson in the $\mu\tau$ and $\textrm{e}\tau$ final states, with the 2016 data collected by the CMS detector. The dataset analyzed corresponds to an integrated luminosity of 35.9 fb$^{-1}$ of proton-proton collision data recorded at $ \sqrt{s} = $ 13 TeV. The results are extracted by a fit to the output of a BDT trained to discriminate the signal from backgrounds. The results are cross-checked with alternate analysis that fits the $ {M_{col}} $ distribution after applying selection criteria on kinematic variables. No evidence is found for LFV Higgs boson decays. The observed (expected) limits on the branching fraction of the Higgs boson to $\mu\tau$ and to $\mathrm{ e }\tau$ are found to be less than 0.25(0.25)% and 0.61(0.37)%, respectively, at 95% confidence level, and constitute a significant improvement with respect to the previously obtained limits by CMS and ATLAS using 20 fb$^{-1}$ of 8 TeV proton-proton collision data. Upper limits on the off-diagonal $\mu\tau$ and $\mathrm{ e }\tau$ Yukawa couplings are derived from these constraints on the branching ratios, and found to be $\sqrt{ | {Y_{\mu\tau}} | ^{2}+ | {Y_{\tau\mu}} | ^{2}}<1.43\times 10^{-3}$ and $\sqrt{ | {Y_{\mathrm{ e }\tau}}| ^{2}+ | {Y_{\tau\mathrm{ e }}} | ^{2}}<2.26\times 10^{-3}$ at 95% CL. |
| Additional Figures | |
png pdf |
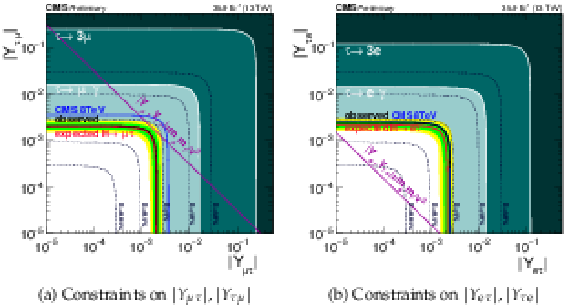
Additional Figure 1:
Constraints on the flavour violating Yukawa couplings, $|Y_{\mu \tau }|,|Y_{\tau \mu }|$ and $|Y_{\mathrm{ e } \tau }|,|Y_{\tau \mathrm{ e } }|$, from the $ {M_{col}} $-fit result. The expected (red solid line) and observed (black solid line) limits are derived from the limit on $B(\mathrm{ H } \to \mu \tau )$ and $B(\mathrm{ H } \to \mathrm{ e } \tau )$ from the present analysis. The flavour diagonal Yukawa couplings are approximated by their SM values. The green (yellow) band indicates the range that is expected to contain 68% (95%) of all observed limit excursions from the expected limit. The shaded regions are derived constraints from null searches for $\tau \to 3\mu $ or $\tau \to 3\mathrm{ e } $ (dark green) and $\tau \to \mu \gamma $ or $\tau \to \mathrm{ e } \gamma $ (lighter green). The purple diagonal line is the theoretical naturalness limit $Y_{ij}Y_{ji} \leq m_im_j/v^2$. |
png pdf |
Additional Figure 1-a:
Constraints on the flavour violating Yukawa coupling, $|Y_{\mu \tau }|,|Y_{\tau \mu }|$, from the $ {M_{col}} $-fit result. The expected (red solid line) and observed (black solid line) limits are derived from the limit on $B(\mathrm{ H } \to \mu \tau )$ from the present analysis. The flavour diagonal Yukawa couplings are approximated by their SM values. The green (yellow) band indicates the range that is expected to contain 68% (95%) of all observed limit excursions from the expected limit. The shaded regions are derived constraints from null searches for $\tau \to 3\mu $ (dark green) and $\tau \to \mu \gamma $ (lighter green). The purple diagonal line is the theoretical naturalness limit $Y_{ij}Y_{ji} \leq m_im_j/v^2$. |
png pdf |
Additional Figure 1-b:
Constraints on the flavour violating Yukawa coupling, $|Y_{\mathrm{ e } \tau }|,|Y_{\tau \mathrm{ e } }|$, from the $ {M_{col}} $-fit result. The expected (red solid line) and observed (black solid line) limits are derived from the limit on $B(\mathrm{ H } \to \mathrm{ e } \tau )$ from the present analysis. The flavour diagonal Yukawa couplings are approximated by their SM values. The green (yellow) band indicates the range that is expected to contain 68% (95%) of all observed limit excursions from the expected limit. The shaded regions are derived constraints from null searches for $\tau \to 3\mathrm{ e } $ (dark green) and $\tau \to \mu \gamma $ or $\tau \to \mathrm{ e } \gamma $ (lighter green).The purple diagonal line is the theoretical naturalness limit $Y_{ij}Y_{ji} \leq m_im_j/v^2$. |
png pdf |
Additional Figure 2:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (1/2) |
png pdf |
Additional Figure 2-a:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 2-b:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
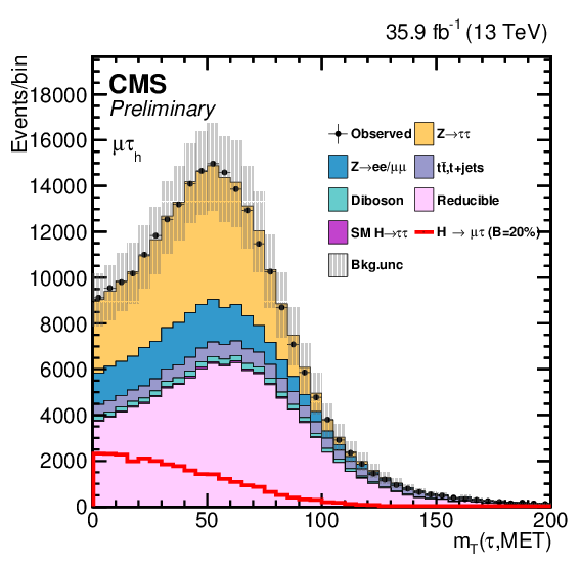
png pdf |
Additional Figure 2-c:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
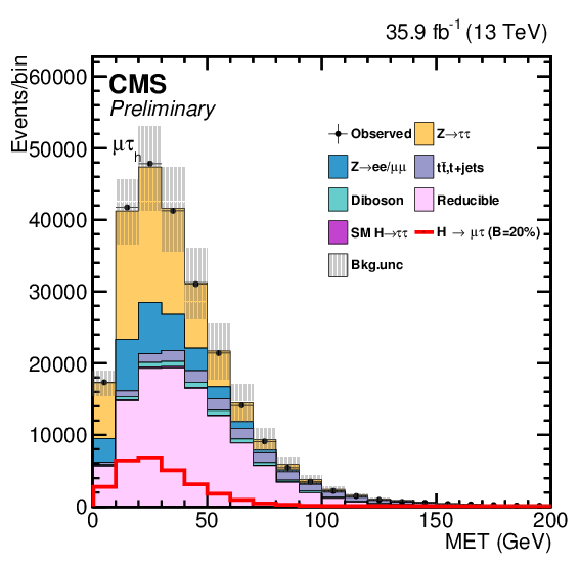
png pdf |
Additional Figure 2-d:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
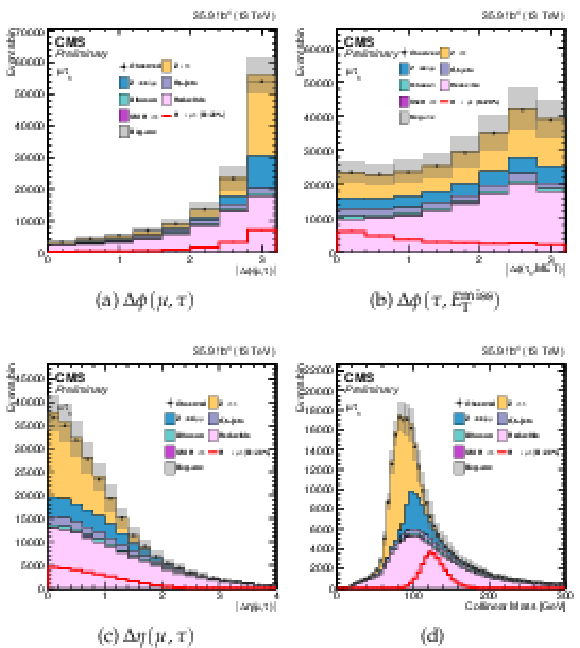
png pdf |
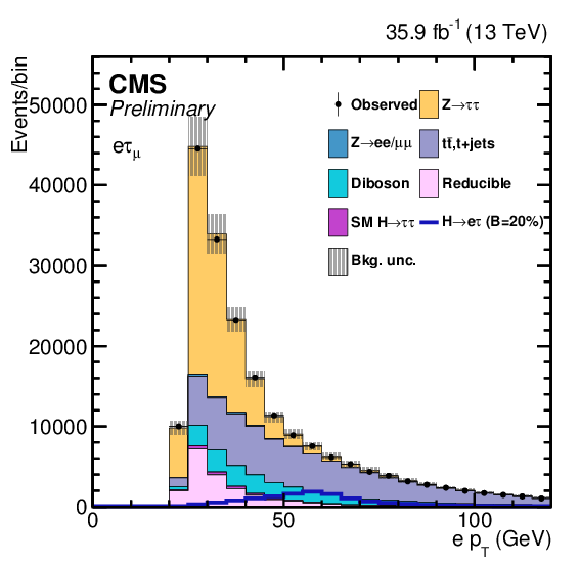
Additional Figure 3:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (2/2) |
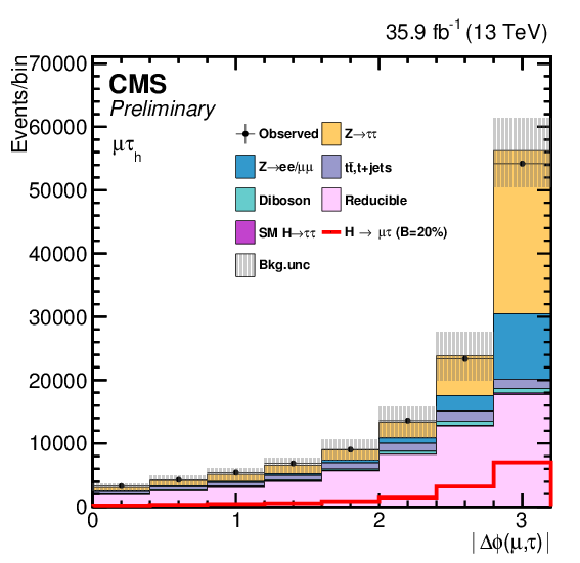
png pdf |
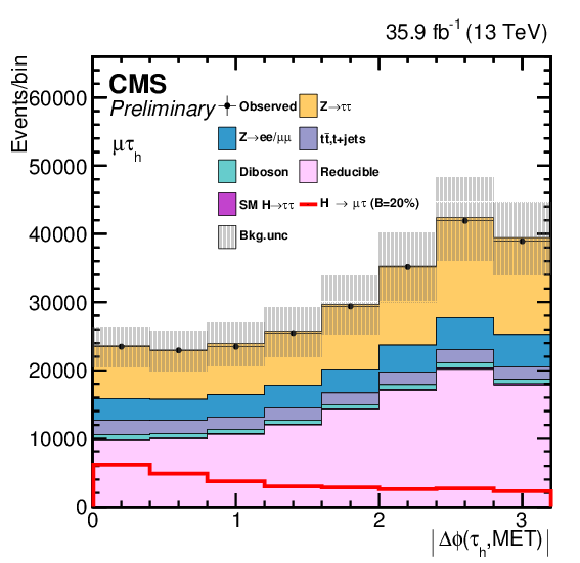
Additional Figure 3-a:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 3-b:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |

png pdf |
Additional Figure 3-c:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
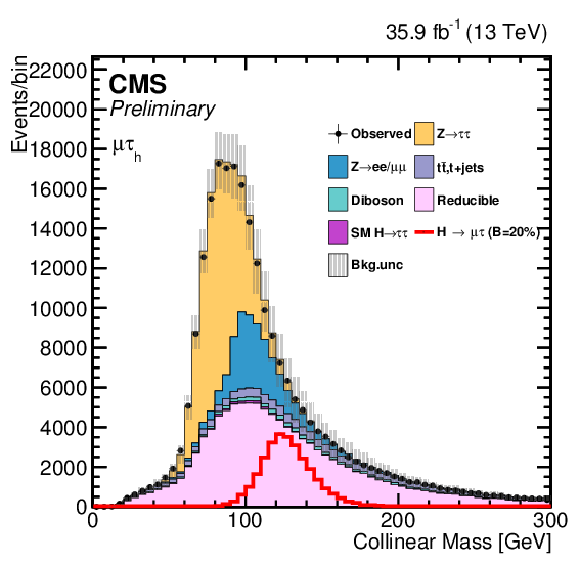
png pdf |
Additional Figure 3-d:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
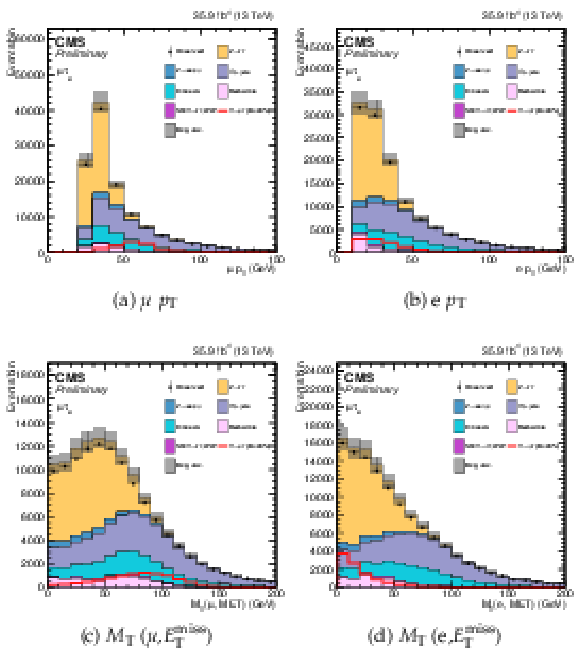
Additional Figure 4:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (1/2) |
png pdf |
Additional Figure 4-a:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
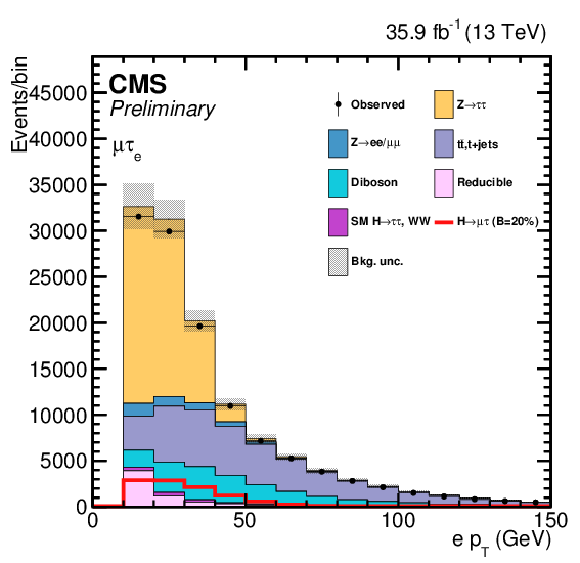
png pdf |
Additional Figure 4-b:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
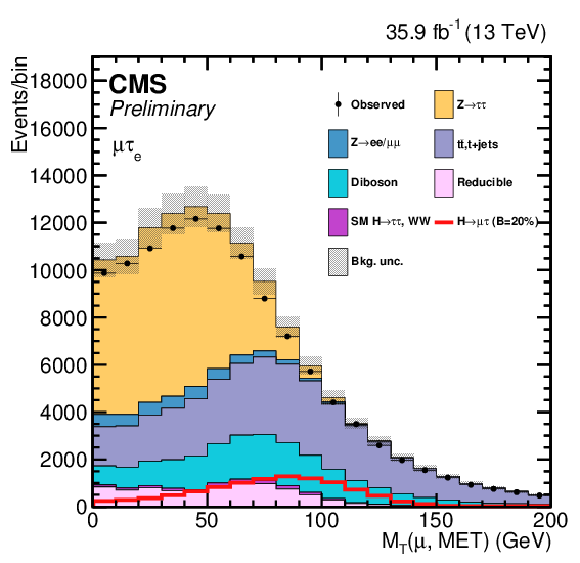
png pdf |
Additional Figure 4-c:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (1/2) |
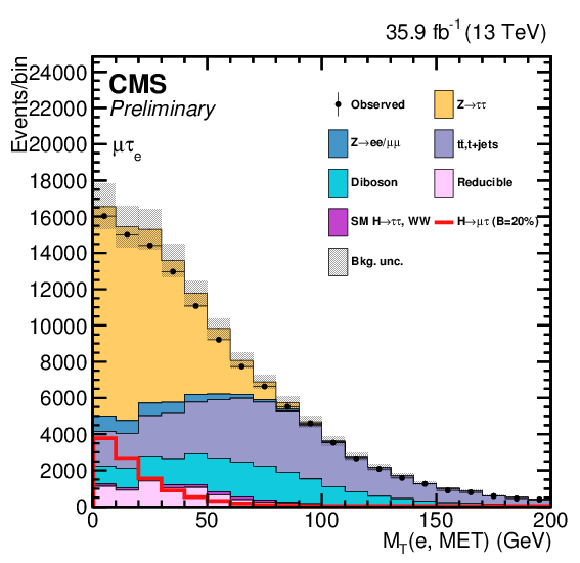
png pdf |
Additional Figure 4-d:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
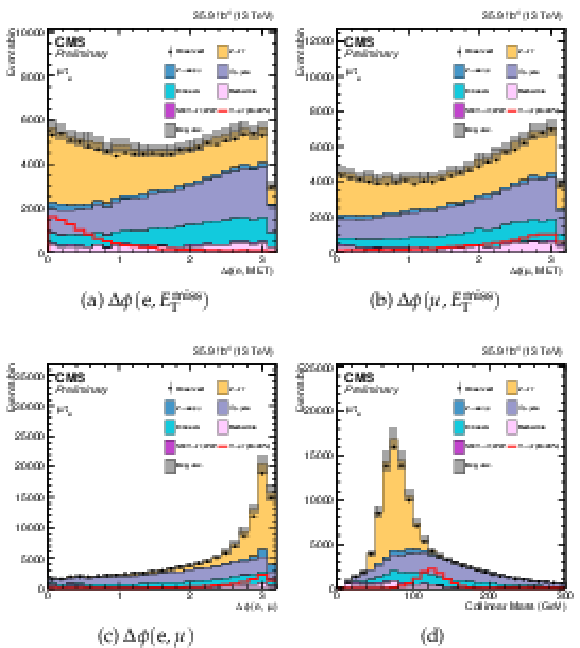
png pdf |
Additional Figure 5:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (2/2) |
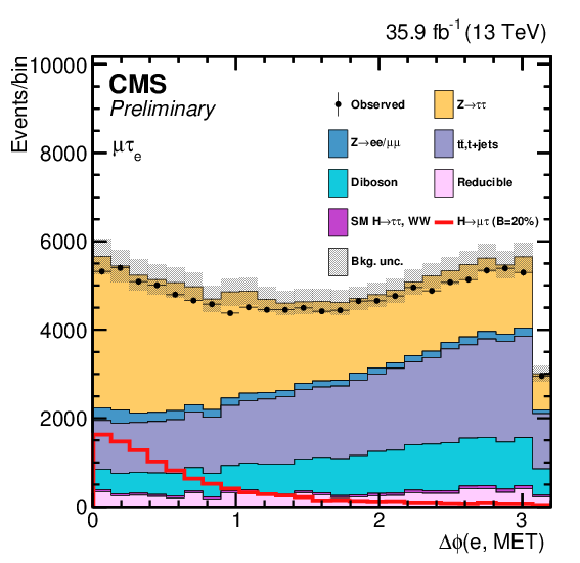
png pdf |
Additional Figure 5-a:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
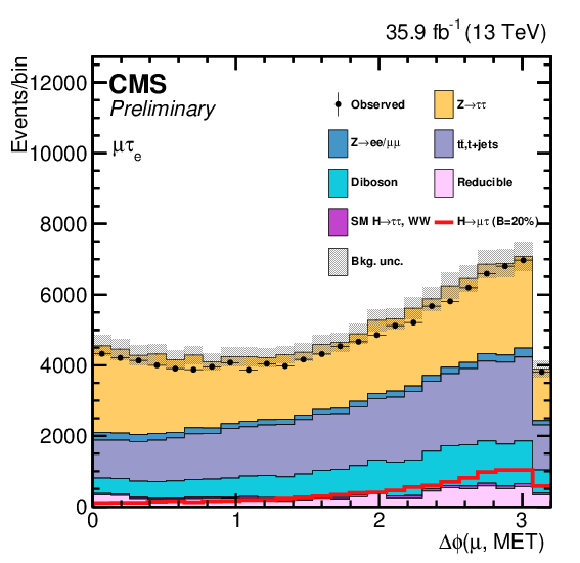
png pdf |
Additional Figure 5-b:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
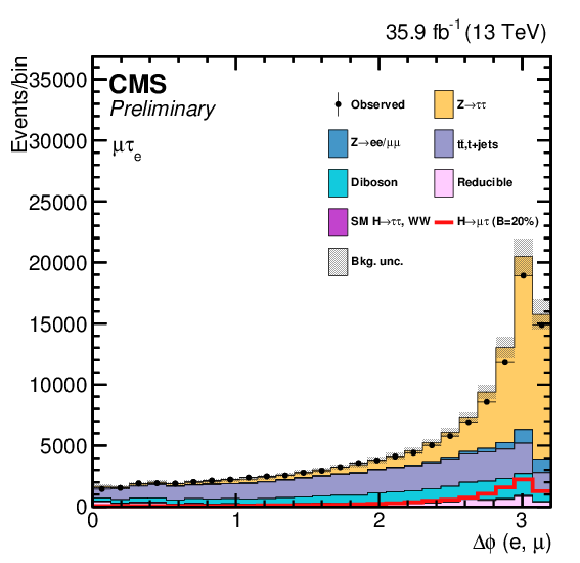
png pdf |
Additional Figure 5-c:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (2/2) |
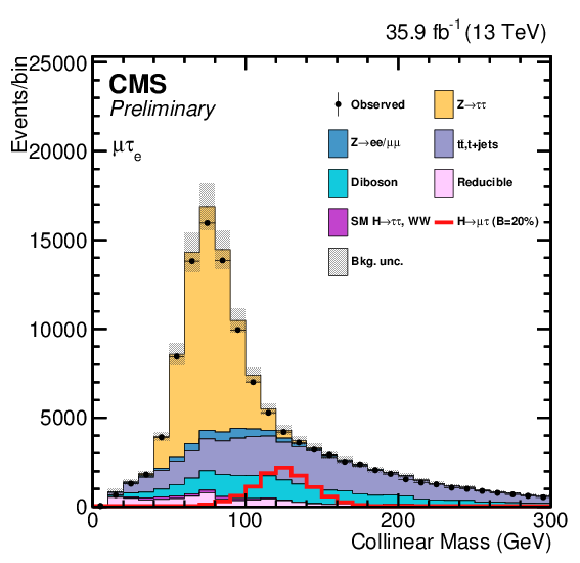
png pdf |
Additional Figure 5-d:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
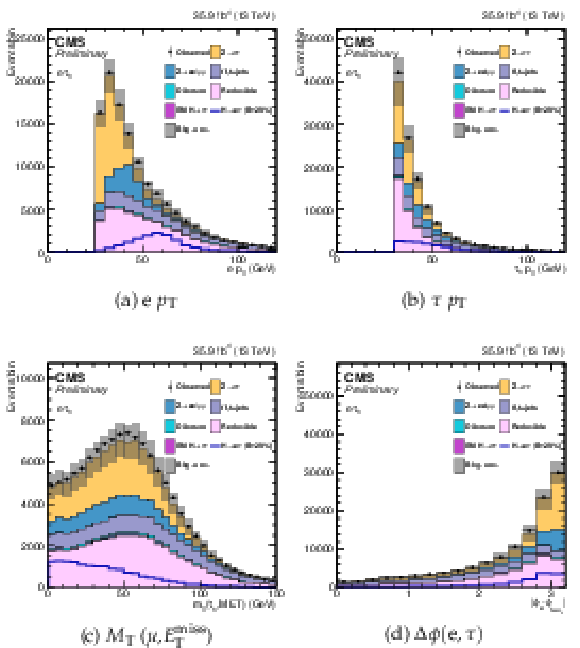
png pdf |
Additional Figure 6:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (1/2). |
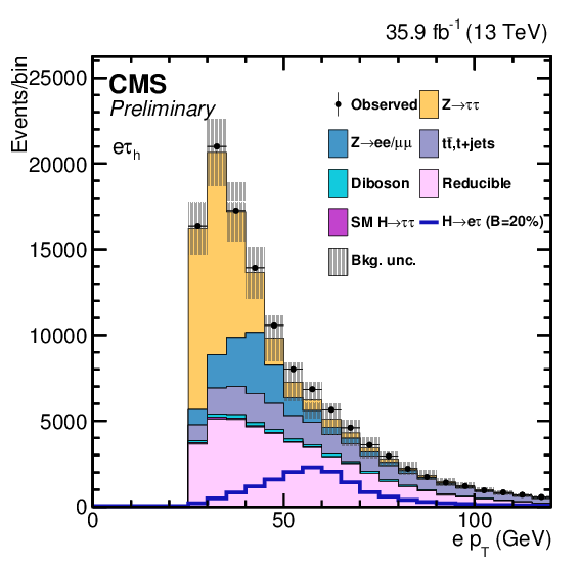
png pdf |
Additional Figure 6-a:
Ons of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
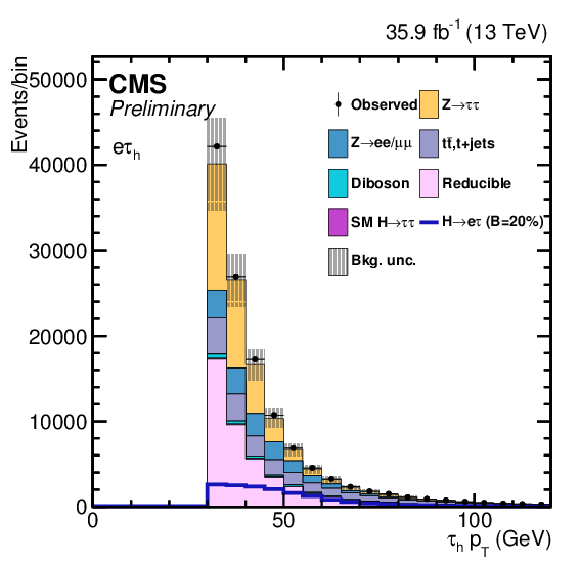
png pdf |
Additional Figure 6-b:
Ons of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
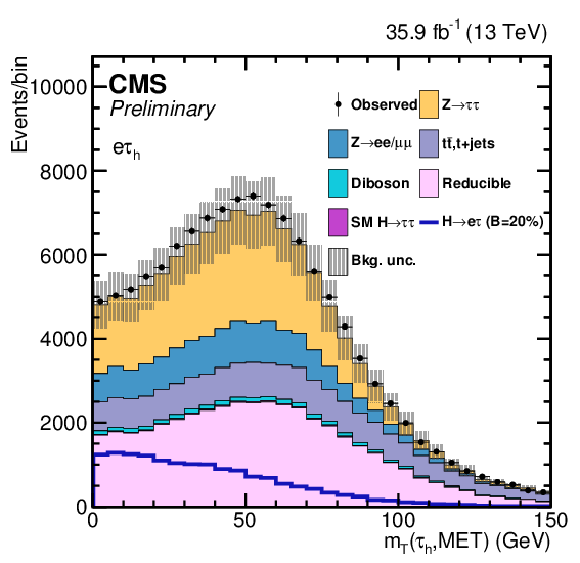
png pdf |
Additional Figure 6-c:
Ons of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
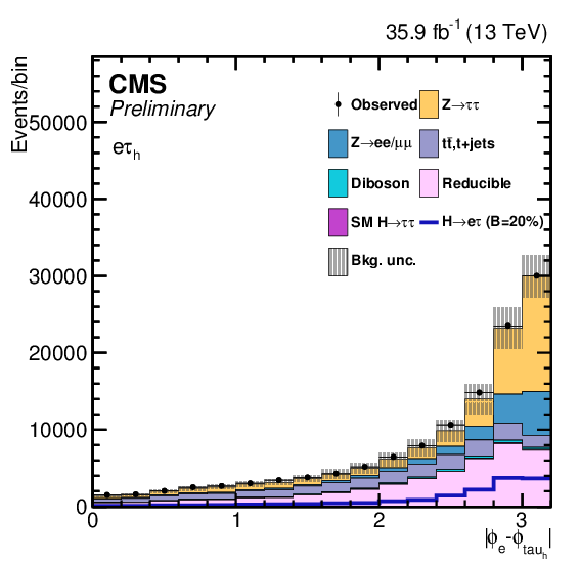
png pdf |
Additional Figure 6-d:
Ons of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
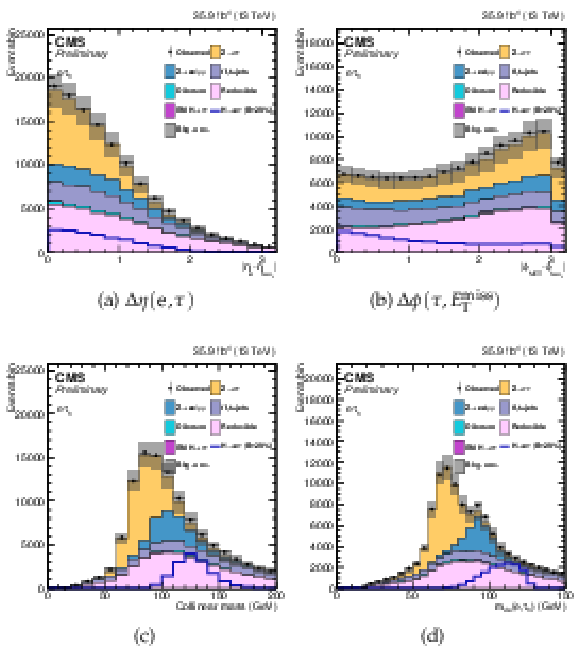
png pdf |
Additional Figure 7:
Variables used as input in the BDT analysis of the $ {\mathrm{ H } \to \mathrm{ e } \tau _{h}} $ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (2/2). |
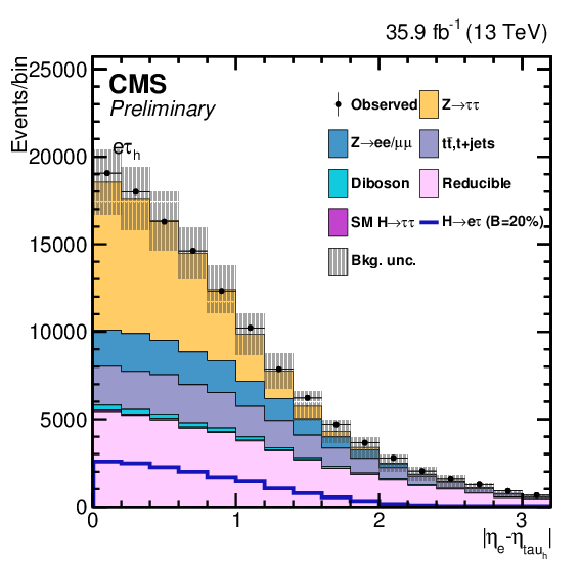
png pdf |
Additional Figure 7-a:
Ons of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
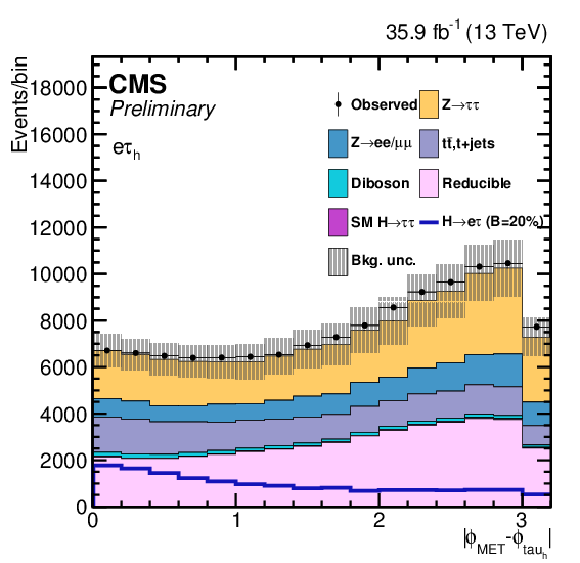
png pdf |
Additional Figure 7-b:
Ons of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 7-c:
Ons of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 7-d:
Ons of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{h}}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
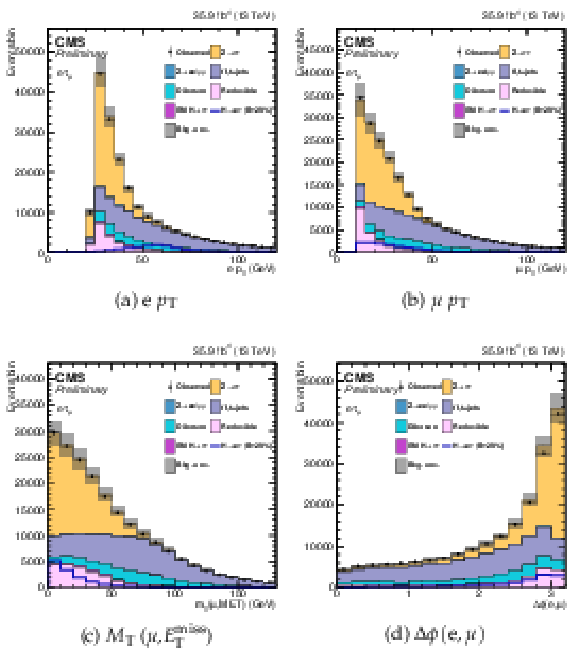
Additional Figure 8:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (1/2). |
png pdf |
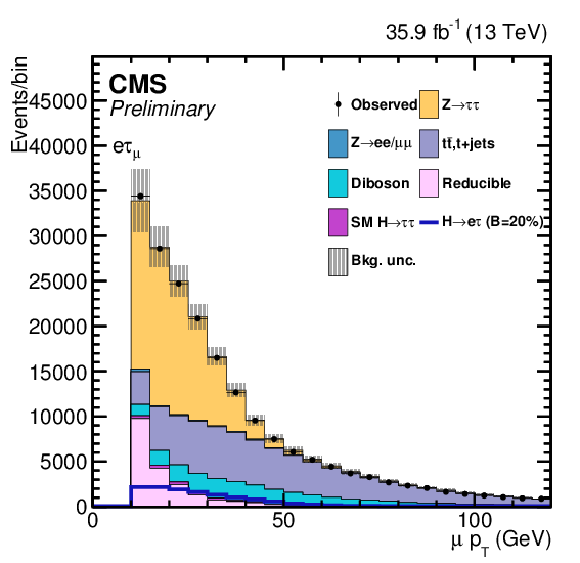
Additional Figure 8-a:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
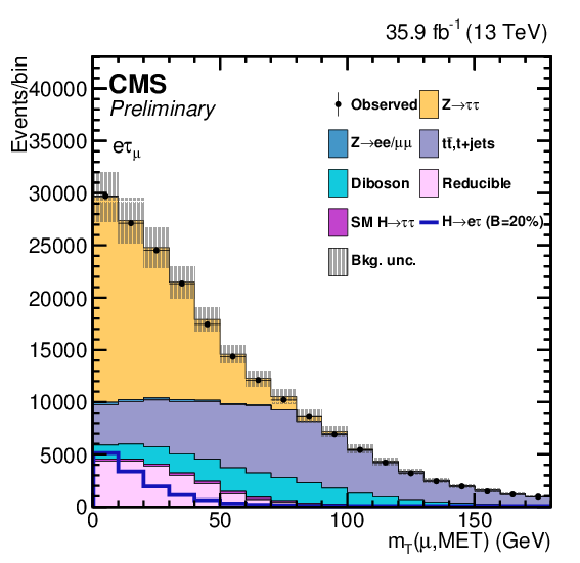
Additional Figure 8-b:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
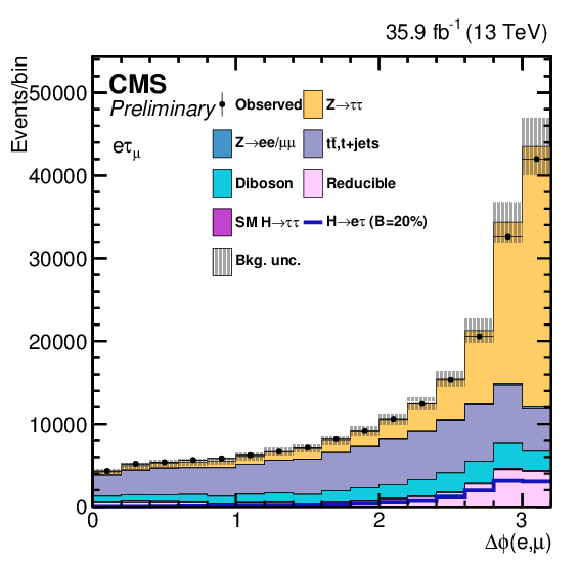
Additional Figure 8-c:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
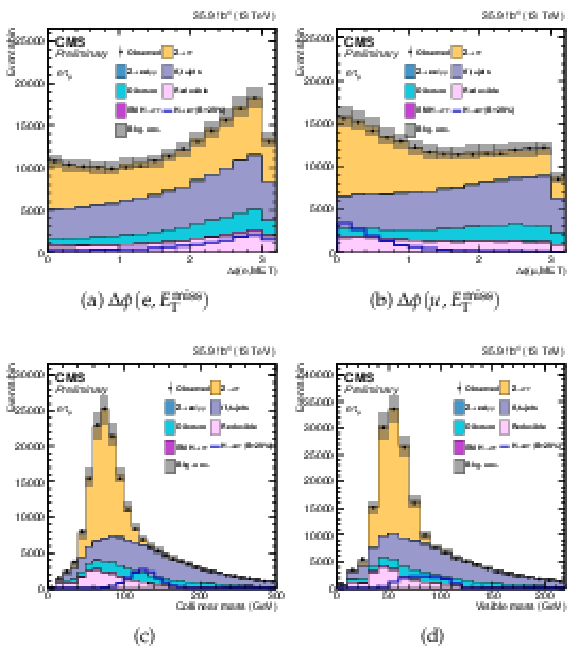
Additional Figure 8-d:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 9:
Variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. (2/2). |
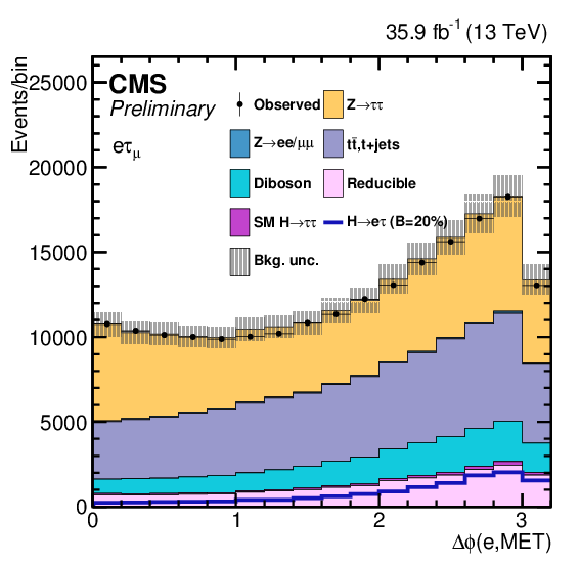
png pdf |
Additional Figure 9-a:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
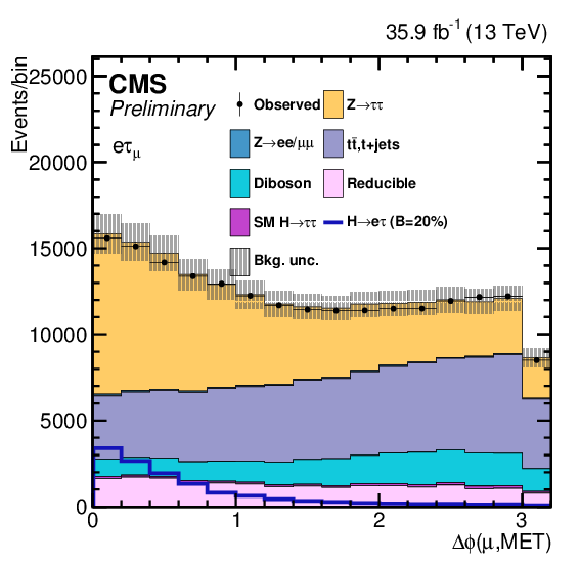
png pdf |
Additional Figure 9-b:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
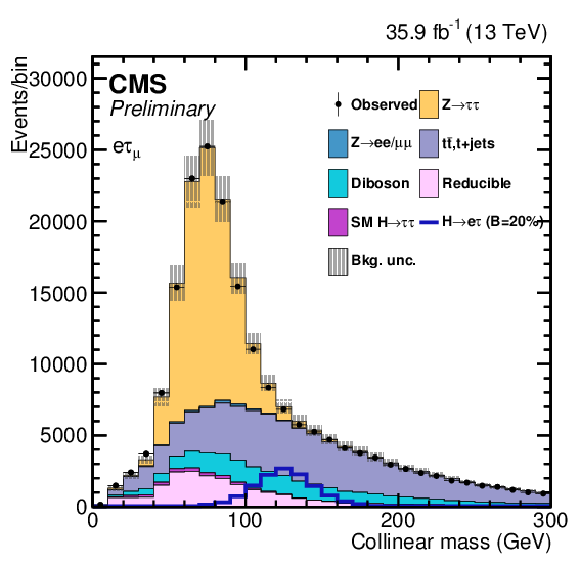
png pdf |
Additional Figure 9-c:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
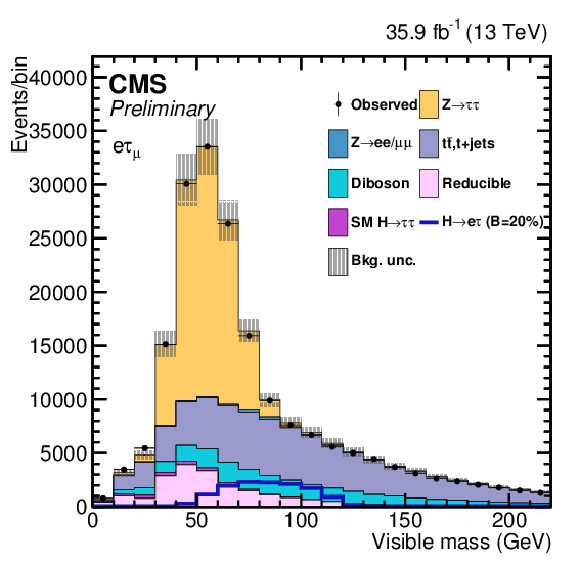
png pdf |
Additional Figure 9-d:
One of the variables used as input in the BDT analysis of the ${\mathrm{ H } \to \mathrm{ e } \tau _{\mu }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |

png pdf |
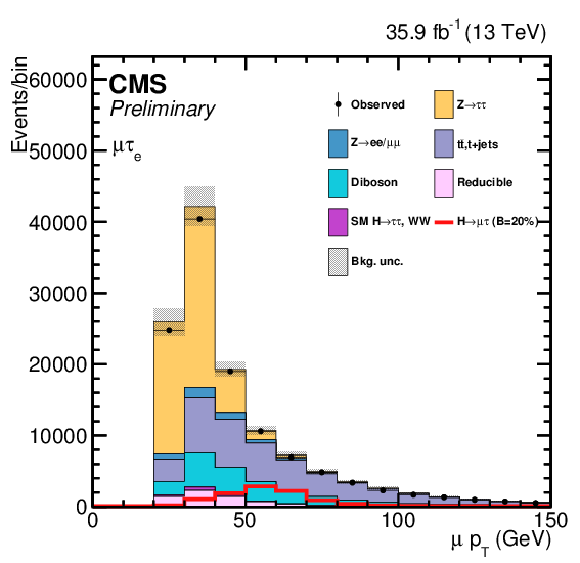
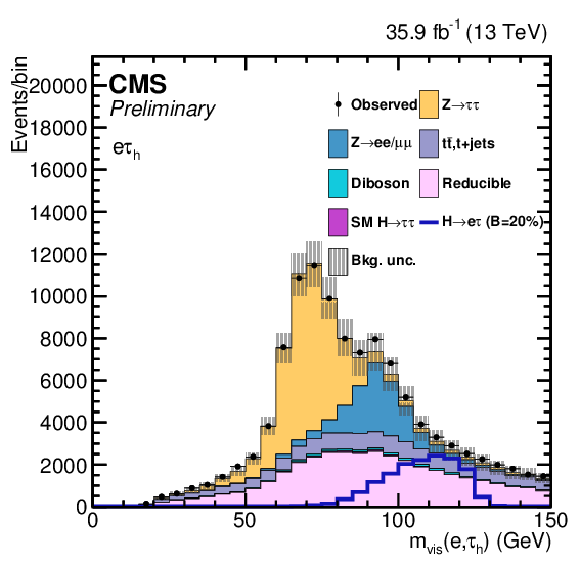
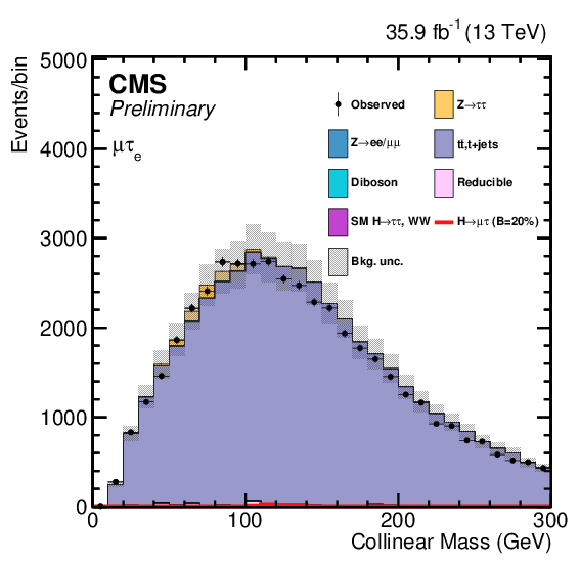
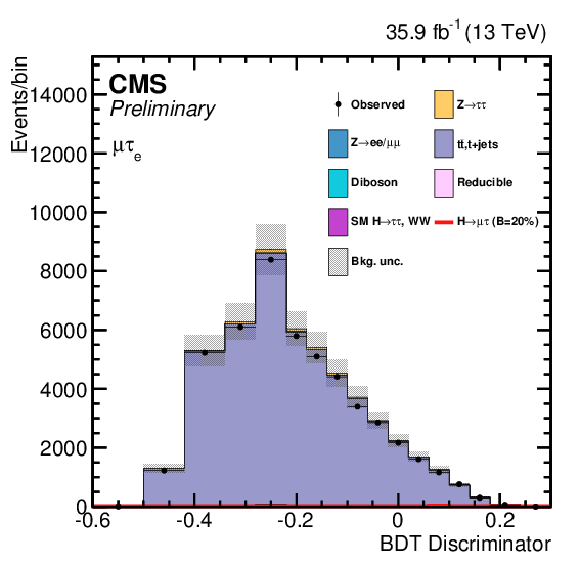
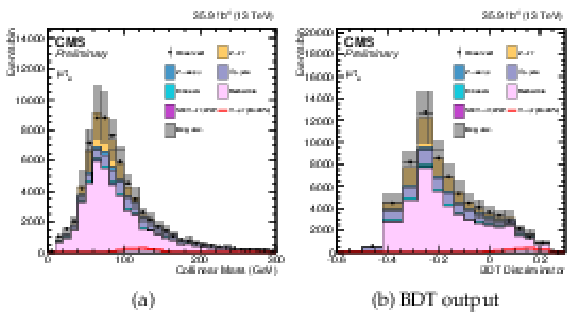
Additional Figure 10:
$ {M_{col}} $ and BDT output distributions from ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ control region (at least 1 b-jet in the event) after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. |
png pdf |
Additional Figure 10-a:
$ {M_{col}} $ output distribution from ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ control region (at least 1 b-jet in the event) after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 10-b:
BDT output distribution from ${\mathrm{ t } {}\mathrm{ \bar{t} } } $ control region (at least 1 b-jet in the event) after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
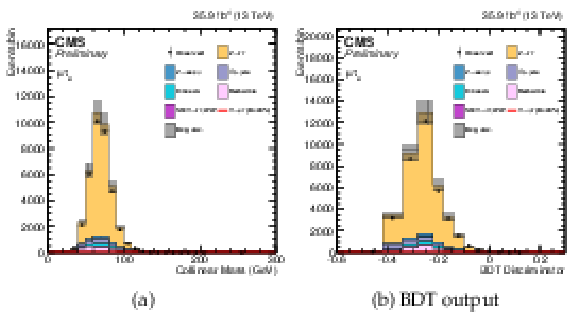
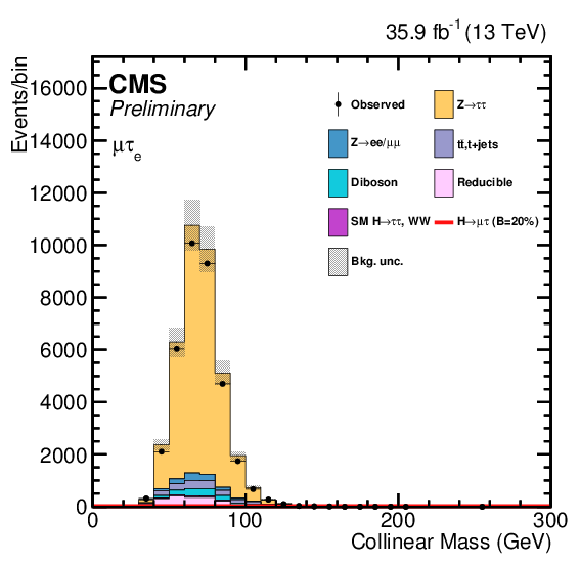
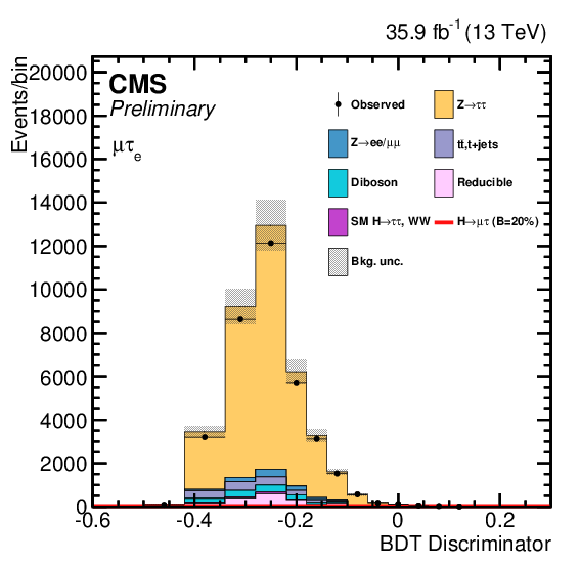
Additional Figure 11:
$ {M_{col}} $ and BDT output distributions from $\mathrm{ Z } \to \tau \tau $ control region after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. |
png pdf |
Additional Figure 11-a:
$ {M_{col}} $ distribution from $\mathrm{ Z } \to \tau \tau $ control region after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 11-b:
BDT output distribution from $\mathrm{ Z } \to \tau \tau $ control region after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 12:
$ {M_{col}} $ and BDT output distributions from QCD multijet control region after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distributions are shown before fitting, and include both statistical and systematics uncertainties. |
png pdf |
Additional Figure 12-a:
$ {M_{col}} $ distribution from QCD multijet control region after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
Additional Figure 12-b:
BDT output distribution from QCD multijet control region after loose selection for the ${\mathrm{ H } \to \mu \tau _{\mathrm{ e } }}$ channel. The distribution is shown before fitting, and includes both statistical and systematics uncertainties. |
png pdf |
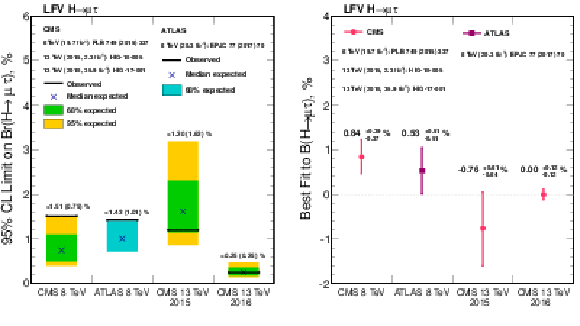
Additional Figure 13:
Comparison of observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mu \tau )$ (left) and best fit values on $\mathcal {B}(\mathrm{ H } \to \mu \tau )$ (right) of the 8 TeV publications by ATLAS and CMS, the preliminary result by CMS at 13 TeV using the 2015 2.3 fb$^{-1}$ data set, and the result from the BDT analysis of the 2016 13 TeV data set. |
png pdf |
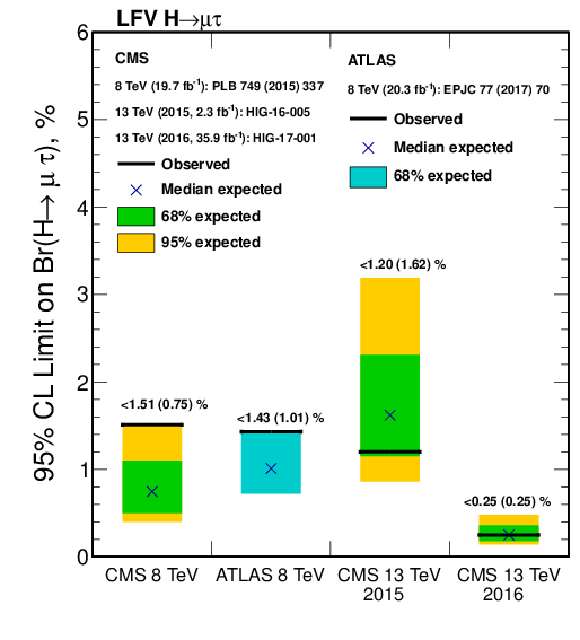
Additional Figure 13-a:
Comparison of observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mu \tau )$ of the 8 TeV publications by ATLAS and CMS, the preliminary result by CMS at 13 TeV using the 2015 2.3 fb$^{-1}$ data set, and the result from the BDT analysis of the 2016 13 TeV data set. |
png pdf |
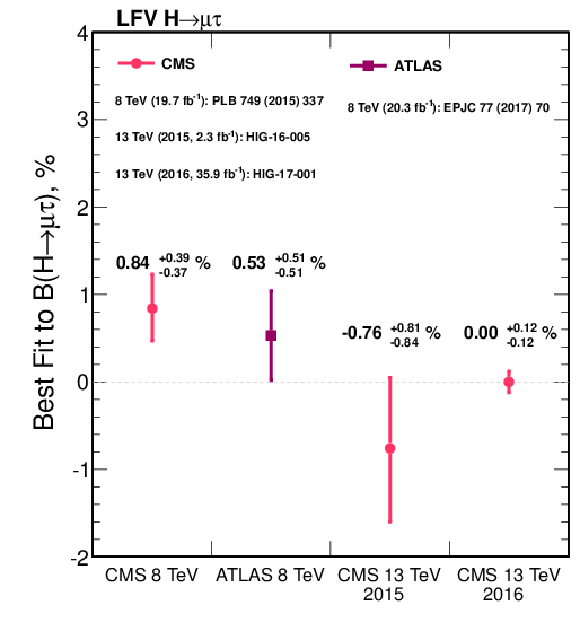
Additional Figure 13-b:
Best fit values on $\mathcal {B}(\mathrm{ H } \to \mu \tau )$ of the 8 TeV publications by ATLAS and CMS, the preliminary result by CMS at 13 TeV using the 2015 2.3 fb$^{-1}$ data set, and the result from the BDT analysis of the 2016 13 TeV data set. |
png pdf |
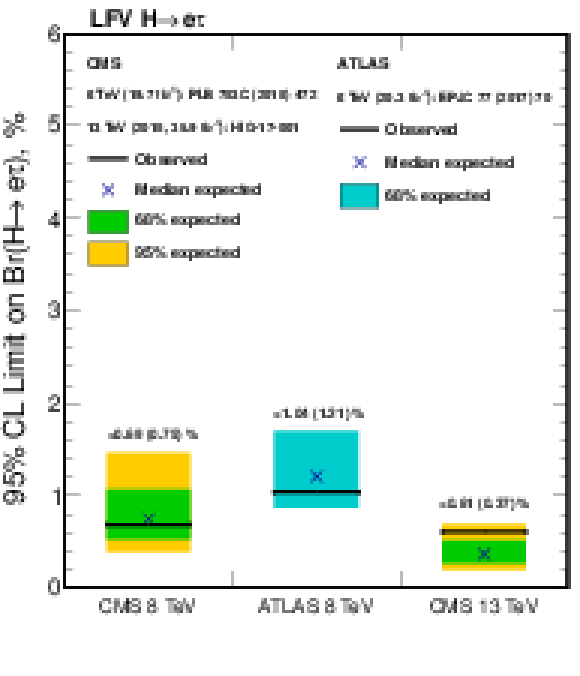
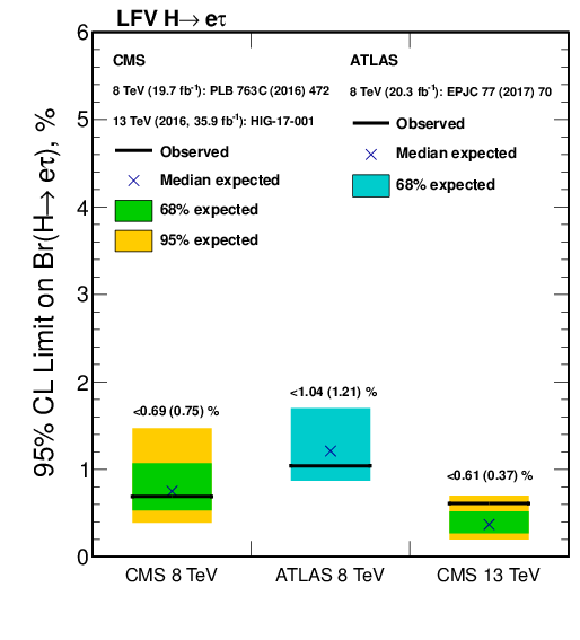
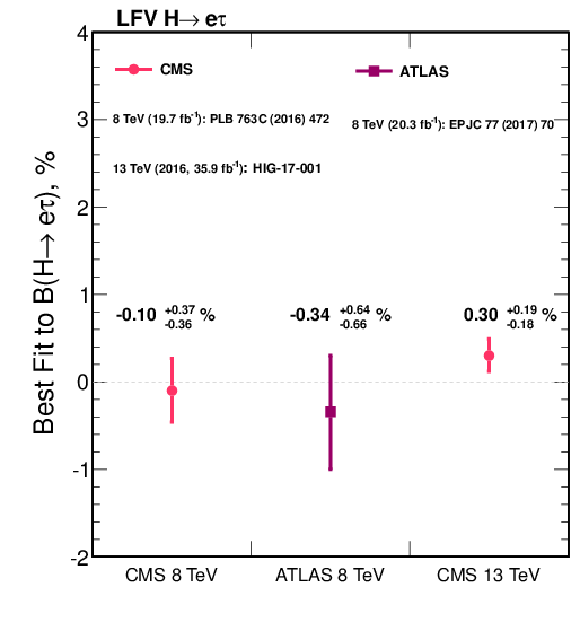
Additional Figure 14:
Comparison of observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )$ (left) and best fit values on $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )$ (right) of the 8 TeV publications by ATLAS and CMS and the result from the BDT analysis of the 2016 13 TeV data set. |
png pdf |
Additional Figure 14-a:
Comparison of observed and expected 95% CL upper limits on the $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )$ of the 8 TeV publications by ATLAS and CMS and the result from the BDT analysis of the 2016 13 TeV data set. |
png pdf |
Additional Figure 14-b:
Best fit values on $\mathcal {B}(\mathrm{ H } \to \mathrm{ e } \tau )$ of the 8 TeV publications by ATLAS and CMS and the result from the BDT analysis of the 2016 13 TeV data set. |
| References | ||||
| 1 | ATLAS Collaboration | Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 2 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 3 | CMS Collaboration | Observation of a new boson with mass near 125 GeV in pp collisions at $ \sqrt{s} $ = 7 and 8 TeV | JHEP 06 (2013) 081 | CMS-HIG-12-036 1303.4571 |
| 4 | J. D. Bjorken and S. Weinberg | Mechanism for Nonconservation of Muon Number | PRL 38 (1977) 622 | |
| 5 | J. L. Diaz-Cruz and J. J. Toscano | Lepton flavor violating decays of Higgs bosons beyond the standard model | PRD 62 (2000) 116005 | hep-ph/9910233 |
| 6 | T. Han and D. Marfatia | $ h \to \mu \tau $ at Hadron Colliders | PRL 86 (2001) 1442 | hep-ph/0008141 |
| 7 | E. Arganda, A. M. Curiel, M. J. Herrero, and D. Temes | Lepton flavor violating Higgs boson decays from massive seesaw neutrinos | PRD 71 (2005) 035011 | hep-ph/0407302 |
| 8 | A. Arhrib, Y. Cheng, and O. C. W. Kong | Comprehensive analysis on lepton flavor violating Higgs boson to $ \mu\bar{\tau} + \tau \bar{\mu} $ decay in supersymmetry without R parity | PRD 87 (2013) 015025 | 1210.8241 |
| 9 | M. Arana-Catania, E. Arganda, and M. J. Herrero | Non-decoupling SUSY in LFV Higgs decays: a window to new physics at the LHC | JHEP 09 (2013) 160 | 1304.3371 |
| 10 | E. Arganda, M. J. Herrero, R. Morales, and A. Szynkman | Analysis of the $ h, H, A \to\tau\mu $ decays induced from SUSY loops within the Mass Insertion Approximation | JHEP 03 (2016) 055 | 1510.04685 |
| 11 | E. Arganda, M. J. Herrero, X. Marcano, and C. Weiland | Enhancement of the lepton flavor violating Higgs boson decay rates from SUSY loops in the inverse seesaw model | PRD 93 (2016), no. 5, 055010 | 1508.04623 |
| 12 | K. Agashe and R. Contino | Composite Higgs-mediated flavor-changing neutral current | PRD 80 (2009) 075016 | 0906.1542 |
| 13 | A. Azatov, M. Toharia, and L. Zhu | Higgs mediated flavor changing neutral currents in warped extra dimensions | PRD 80 (2009) 035016 | 0906.1990 |
| 14 | H. Ishimori et al. | Non-Abelian Discrete Symmetries in Particle Physics | Prog. Theor. Phys. Suppl. 183 (2010) 1 | 1003.3552 |
| 15 | G. Perez and L. Randall | Natural neutrino masses and mixings from warped geometry | JHEP 01 (2009) 077 | 0805.4652 |
| 16 | S. Casagrande et al. | Flavor physics in the Randall-Sundrum model I. Theoretical setup and electroweak precision tests | JHEP 10 (2008) 094 | 0807.4937 |
| 17 | A. J. Buras, B. Duling, and S. Gori | The impact of Kaluza-Klein fermions on Standard Model fermion couplings in a RS model with custodial protection | JHEP 09 (2009) 076 | 0905.2318 |
| 18 | M. Blanke et al. | $ \Delta F=2 $ observables and fine-tuning in a warped extra dimension with custodial protection | JHEP 03 (2009) 001 | 0809.1073 |
| 19 | G. F. Giudice and O. Lebedev | Higgs-dependent Yukawa couplings | PLB 665 (2008) 79 | 0804.1753 |
| 20 | J. A. Aguilar-Saavedra | A minimal set of top-Higgs anomalous couplings | Nucl. Phys. B 821 (2009) 215 | 0904.2387 |
| 21 | M. E. Albrecht et al. | Electroweak and flavour structure of a warped extra dimension with custodial protection | JHEP 09 (2009) 064 | 0903.2415 |
| 22 | A. Goudelis, O. Lebedev, and J. H. Park | Higgs-induced lepton flavor violation | PLB 707 (2012) 369 | 1111.1715 |
| 23 | D. McKeen, M. Pospelov, and A. Ritz | Modified Higgs branching ratios versus CP and lepton flavor violation | PRD 86 (2012) 113004 | 1208.4597 |
| 24 | A. Pilaftsis | Lepton flavour nonconservation in $ \mathrm{ H }^0 $ decays | PLB 285 (1992) 68 | |
| 25 | J. G. Korner, A. Pilaftsis, and K. Schilcher | Leptonic $ \mathrm{CP} $ asymmetries in flavor-changing $ \mathrm{ H }^{0} $ decays | PRD 47 (1993) 1080 | |
| 26 | E. Arganda, M. J. Herrero, X. Marcano, and C. Weiland | Imprints of massive inverse seesaw model neutrinos in lepton flavor violating Higgs boson decays | PRD 91 (2015), no. 1, 015001 | 1405.4300 |
| 27 | CMS Collaboration | Search for lepton-flavour-violating decays of the Higgs boson | PLB 749 (2015) 337 | CMS-HIG-14-005 1502.07400 |
| 28 | CMS Collaboration | Search for lepton flavour violating decays of the Higgs boson to e$ \tau $ and e$ \mu $ in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | Physics Letters B 763 (2016) 472 | |
| 29 | ATLAS Collaboration | Search for lepton-flavour-violating decays of the Higgs and $ Z $ bosons with the ATLAS detector | EPJC77 (2017), no. 2, 70 | 1604.07730 |
| 30 | ATLAS Collaboration | Search for lepton-flavour-violating $ \mathrm{ H }\to\mu\tau $ decays of the Higgs boson with the ATLAS detector | JHEP 11 (2015) 211 | 1508.03372 |
| 31 | B. McWilliams and L.-F. Li | Virtual effects of Higgs particles | Nucl. Phys. B 179 (1981) 62 | |
| 32 | O. U. Shanker | Flavour violation, scalar particles and leptoquarks | Nucl. Phys. B 206 (1982) 253 | |
| 33 | G. Blankenburg, J. Ellis, and G. Isidori | Flavour-changing decays of a 125 GeV Higgs-like particle | PLB 712 (2012) 386 | 1202.5704 |
| 34 | R. Harnik, J. Kopp, and J. Zupan | Flavor violating Higgs decays | JHEP 03 (2013) 26 | 1209.1397 |
| 35 | Particle Data Group, J. Beringer et al. | Review of Particle Physics | PRD 86 (2012) 010001 | |
| 36 | A. Celis, V. Cirigliano, and E. Passemar | Lepton flavor violation in the Higgs sector and the role of hadronic tau-lepton decays | PRD 89 (2014) 013008 | 1309.3564 |
| 37 | S. M. Barr and A. Zee | Electric Dipole Moment of the Electron and of the Neutron | PRL 65 (1990) 21 | |
| 38 | CMS Collaboration | Evidence for the direct decay of the 125 GeV Higgs boson to fermions | Nature Phys. 10 (2014) 557 | CMS-HIG-13-033 1401.6527 |
| 39 | CMS Collaboration | Evidence for the 125$ GeV $ Higgs boson decaying to a pair of $ \tau $ leptons | JHEP 05 (2014) 104 | CMS-HIG-13-004 1401.5041 |
| 40 | ATLAS Collaboration | Evidence for the Higgs-boson Yukawa coupling to tau leptons with the ATLAS detector | JHEP 04 (2015) 117 | 1501.04943 |
| 41 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 42 | H. M. Georgi, S. L. Glashow, M. E. Machacek, and D. V. Nanopoulos | Higgs Bosons from Two Gluon Annihilation in Proton Proton Collisions | PRL 40 (1978) 692 | |
| 43 | R. N. Cahn, S. D. Ellis, R. Kleiss, and W. J. Stirling | Transverse-momentum signatures for heavy Higgs bosons | PRD 35 (1987) 1626 | |
| 44 | S. L. Glashow, D. V. Nanopoulos, and A. Yildiz | Associated production of Higgs bosons and Z particles | PRD 18 (1978) 1724 | |
| 45 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 46 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 47 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 48 | S. Alioli et al. | Jet pair production in POWHEG | JHEP 04 (2011) 081 | 1012.3380 |
| 49 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO Higgs boson production via gluon fusion matched with shower in POWHEG | JHEP 04 (2009) 002 | 0812.0578 |
| 50 | J. Alwall et al. | MadGraph 5: going beyond | JHEP 06 (2011) 128 | 1106.0522 |
| 51 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | Journal of High Energy Physics 2014 (2014), no. 7, 79 | |
| 52 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC76 (2016), no. 3, 155 | CMS-GEN-14-001 1512.00815 |
| 53 | GEANT4 Collaboration | GEANT4 --- a simulation toolkit | NIMA 506 (2003) 250 | |
| 54 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014) P10009 | CMS-TRK-11-001 1405.6569 |
| 55 | CMS Collaboration | Particle--Flow Event Reconstruction in CMS and Performance for Jets, Taus, and $ E_{\mathrm{T}}^{\text{miss}} $ | CDS | |
| 56 | CMS Collaboration | Particle flow reconstruction of 0.9 TeV and 2.36 TeV collision events in CMS | CDS | |
| 57 | CMS Collaboration | Commissioning of the particle--flow event reconstruction with leptons from J/$ \psi $ and $ \mathrm{ W } $ decays at 7 TeV | CDS | |
| 58 | CMS Collaboration | Performance of the CMS missing transverse momentum reconstruction in pp data at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P02006 | CMS-JME-13-003 1411.0511 |
| 59 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 60 | CMS Collaboration | Performance of CMS muon reconstruction in $ pp $ collision events at $ \sqrt{s}= $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 61 | CMS Collaboration | Reconstruction and identification of tau lepton decays to hadrons and $ \nu_\tau $ at CMS | JINST 11 (2016) P01019 | CMS-TAU-14-001 1510.07488 |
| 62 | CMS Collaboration | Performance of reconstruction and identification of tau leptons in their decays to hadrons and tau neutrino in LHC Run-2 | ||
| 63 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 64 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 65 | CMS Collaboration | Determination of jet energy calibration and transverse momentum resolution in CMS | JINST 6 (2011) 11002 | CMS-JME-10-011 1107.4277 |
| 66 | R. K. Ellis, I. Hinchliffe, M. Soldate, and J. J. van der Bij | Higgs Decay to $ \tau^+\tau^- $: A possible signature of intermediate mass Higgs bosons at high energy hadron colliders | Nucl. Phys. B 297 (1988) 221 | |
| 67 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 68 | A. L. Read | Presentation of search results: the $ CL_s $ technique | JPG 28 (2002) 2693 | |
| 69 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector | 1610.07922 | |
| 70 | CMS Collaboration | Search for Lepton Flavour Violating Decays of the Higgs Boson in the mu-tau final state at 13 TeV | ||
| 71 | A. Denner et al. | Standard model Higgs-boson branching ratios with uncertainties | EPJC 71 (2011) 1753 | 1107.5909 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|