

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-EXO-17-011 | ||
| Search for a heavy right-handed W boson and a heavy neutrino in events with two same-flavor leptons and two jets at $\sqrt{s}= $ 13 TeV | ||
| CMS Collaboration | ||
| December 2017 | ||
| Abstract: A search for a heavy right-handed W gauge boson and a heavy right-handed neutrino at the CERN LHC has been conducted by the CMS collaboration in events with two same-flavor leptons (e or $\mu$) and two jets, using 2016 proton-proton collision data corresponding to an integrated luminosity of 35.9 fb$^{-1}$. No excess above the standard model expectation is seen in the invariant mass distribution of the dilepton plus dijet system. Assuming identical couplings and decay branching fractions as the standard model W gauge boson, and that only one heavy neutrino flavor ${\mathrm N}_R$ contributes significantly to the ${\mathrm W}_R$ decay width, the region in the two-dimensional ($m_{{\mathrm W}_R}$, $m_{{\mathrm N}_R}$) mass plane excluded at a 95% confidence level extends to approximately $m_{{\mathrm W}_R}= $ 4.4 TeV and covers a large range of neutrino masses below the ${\mathrm W}_R$ boson mass. This analysis provides the most stringent limits to date. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JHEP 05 (2018) 148. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
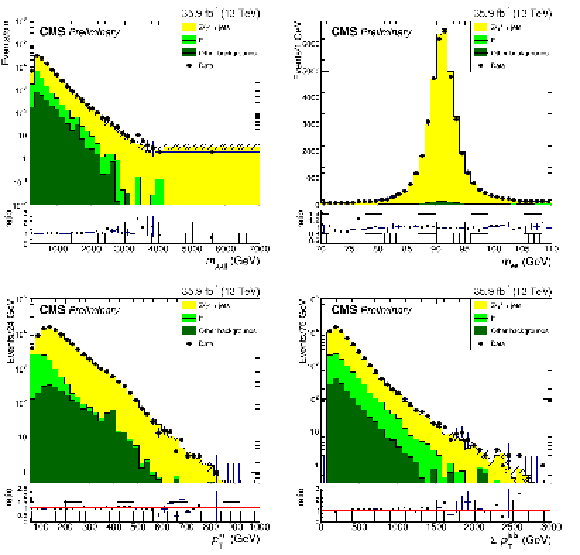
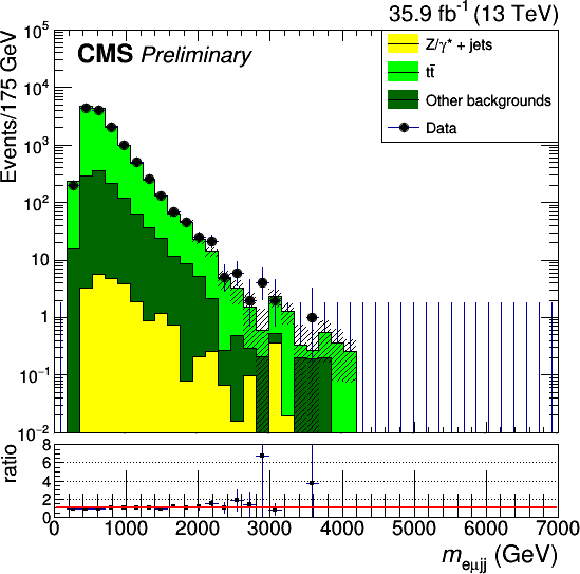
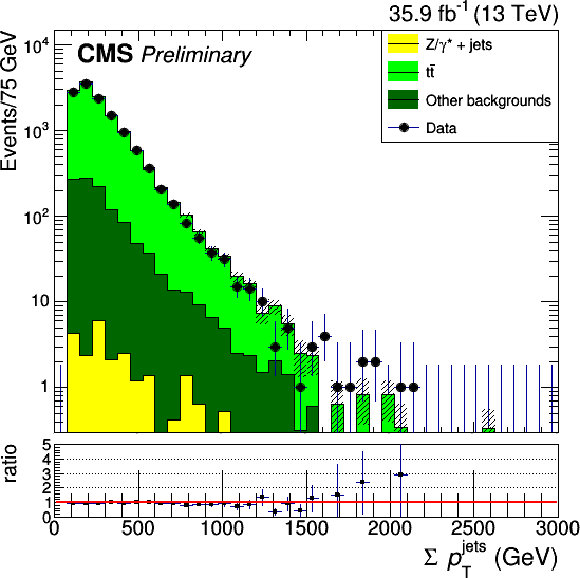
Figure 1:
Distribution of kinematic quantities for events in the low-dilepton mass control region. The four-object invariant mass (on the top) and the dilepton transverse momentum (on the bottom) for the DY $\mu \mu $ plus two jets selection are shown on the left. The dilepton mass (on the top) and the scalar sum of all jets $ {p_{\mathrm {T}}} $ (on the bottom) for the DY ee plus two jets selection are shown on the right. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png |
Figure 1-a:
Distribution of kinematic quantities for events in the low-dilepton mass control region. The four-object invariant mass (on the top) and the dilepton transverse momentum (on the bottom) for the DY $\mu \mu $ plus two jets selection are shown on the left. The dilepton mass (on the top) and the scalar sum of all jets $ {p_{\mathrm {T}}} $ (on the bottom) for the DY ee plus two jets selection are shown on the right. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png |
Figure 1-b:
Distribution of kinematic quantities for events in the low-dilepton mass control region. The four-object invariant mass (on the top) and the dilepton transverse momentum (on the bottom) for the DY $\mu \mu $ plus two jets selection are shown on the left. The dilepton mass (on the top) and the scalar sum of all jets $ {p_{\mathrm {T}}} $ (on the bottom) for the DY ee plus two jets selection are shown on the right. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |

png |
Figure 1-c:
Distribution of kinematic quantities for events in the low-dilepton mass control region. The four-object invariant mass (on the top) and the dilepton transverse momentum (on the bottom) for the DY $\mu \mu $ plus two jets selection are shown on the left. The dilepton mass (on the top) and the scalar sum of all jets $ {p_{\mathrm {T}}} $ (on the bottom) for the DY ee plus two jets selection are shown on the right. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png |
Figure 1-d:
Distribution of kinematic quantities for events in the low-dilepton mass control region. The four-object invariant mass (on the top) and the dilepton transverse momentum (on the bottom) for the DY $\mu \mu $ plus two jets selection are shown on the left. The dilepton mass (on the top) and the scalar sum of all jets $ {p_{\mathrm {T}}} $ (on the bottom) for the DY ee plus two jets selection are shown on the right. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png pdf |
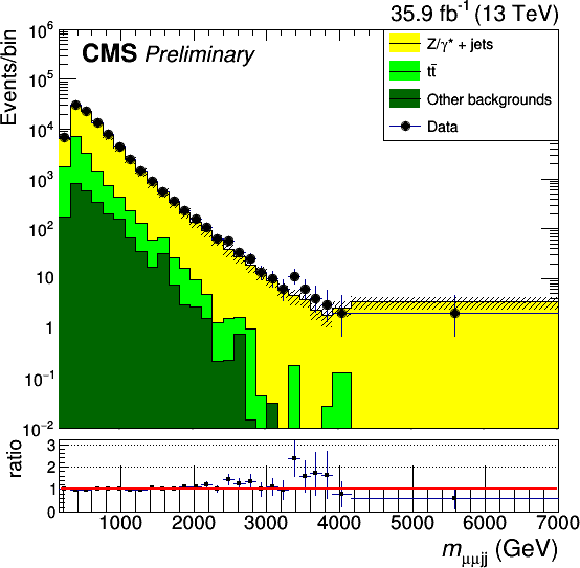
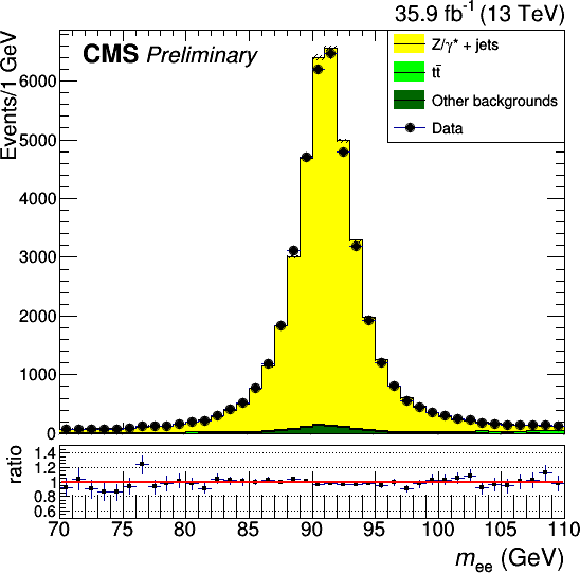
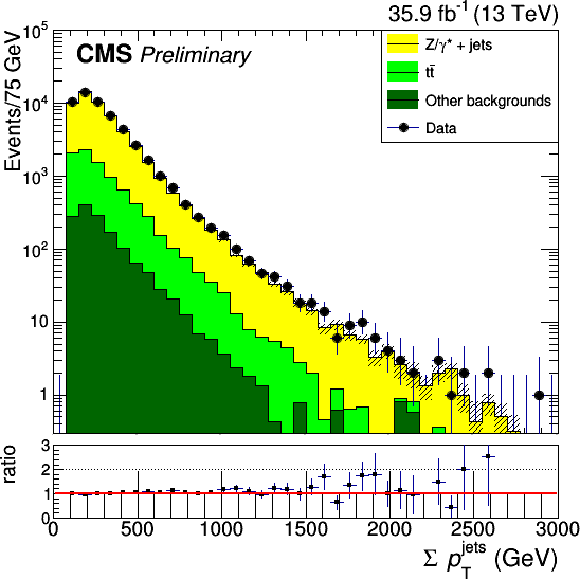
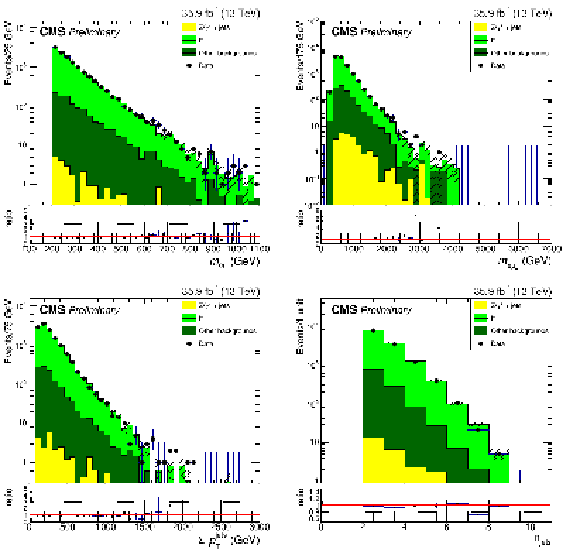
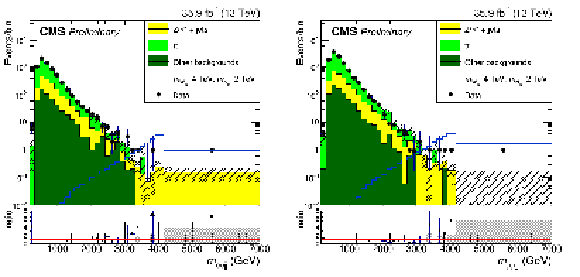
Figure 2:
Kinematic distributions for events in the flavor control region. The dilepton mass (top left), the four-object mass (top right), the scalar sum of all jets $ {p_{\mathrm {T}}} $ (bottom left) and the number of jets (bottom right) are shown. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png |
Figure 2-a:
Kinematic distributions for events in the flavor control region. The dilepton mass (top left), the four-object mass (top right), the scalar sum of all jets $ {p_{\mathrm {T}}} $ (bottom left) and the number of jets (bottom right) are shown. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png |
Figure 2-b:
Kinematic distributions for events in the flavor control region. The dilepton mass (top left), the four-object mass (top right), the scalar sum of all jets $ {p_{\mathrm {T}}} $ (bottom left) and the number of jets (bottom right) are shown. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png |
Figure 2-c:
Kinematic distributions for events in the flavor control region. The dilepton mass (top left), the four-object mass (top right), the scalar sum of all jets $ {p_{\mathrm {T}}} $ (bottom left) and the number of jets (bottom right) are shown. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png |
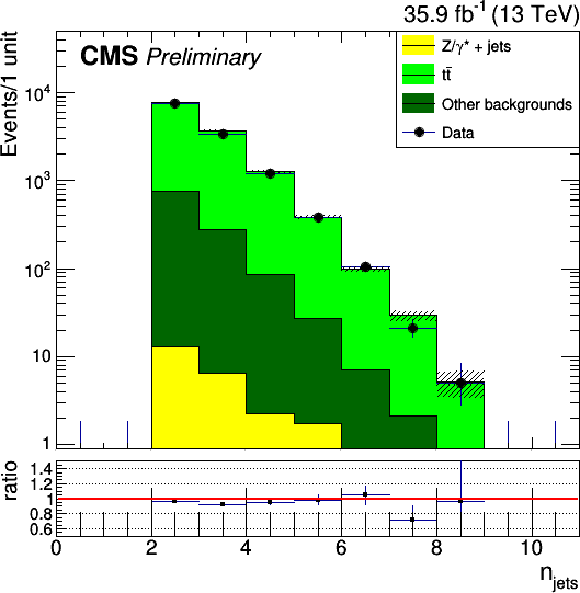
Figure 2-d:
Kinematic distributions for events in the flavor control region. The dilepton mass (top left), the four-object mass (top right), the scalar sum of all jets $ {p_{\mathrm {T}}} $ (bottom left) and the number of jets (bottom right) are shown. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. |
png pdf |
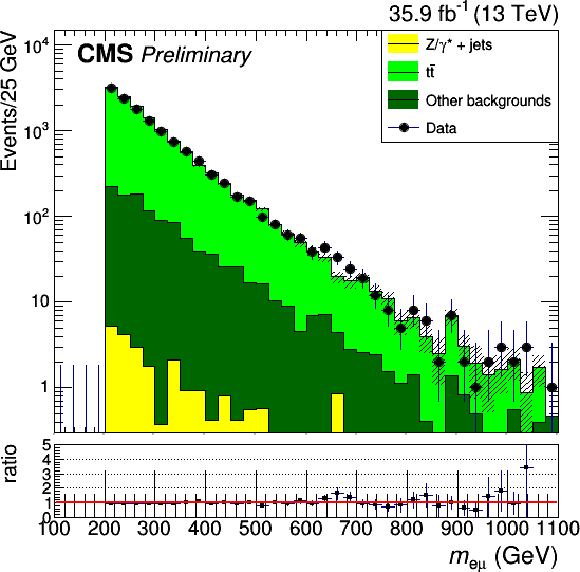
Figure 3:
Four-object mass distribution in the signal region for the electron channel on the left and for the muon channel on the right. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. The gray error band around 1 represents instead the systematic uncertainty of the simulation. |
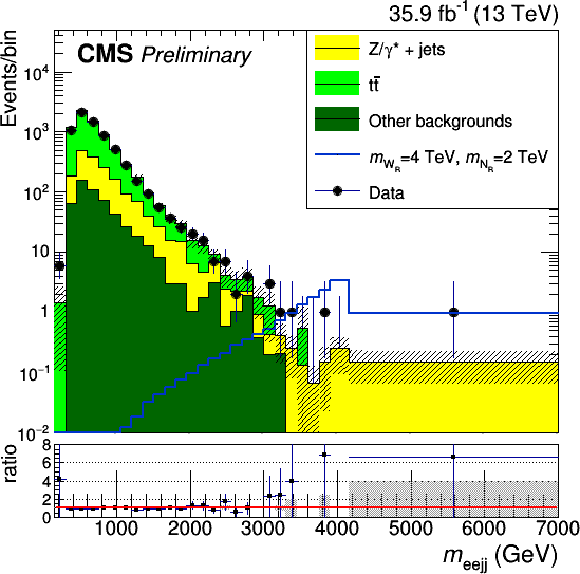
png |
Figure 3-a:
Four-object mass distribution in the signal region for the electron channel on the left and for the muon channel on the right. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. The gray error band around 1 represents instead the systematic uncertainty of the simulation. |
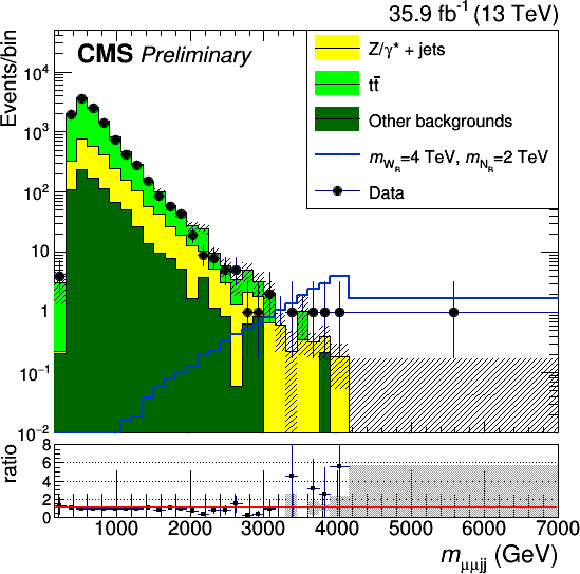
png |
Figure 3-b:
Four-object mass distribution in the signal region for the electron channel on the left and for the muon channel on the right. The error bands on the MC histograms only include statistical uncertainties. The error bars in the ratio represent the statistical uncertainties of data and MC calculated with the standard error propagation of $\frac {N_d}{N_s}$ given $N_d$ the number of data events in the bin and $N_s$ the number of simulated events in the bin. The gray error band around 1 represents instead the systematic uncertainty of the simulation. |
png pdf |
Figure 4:
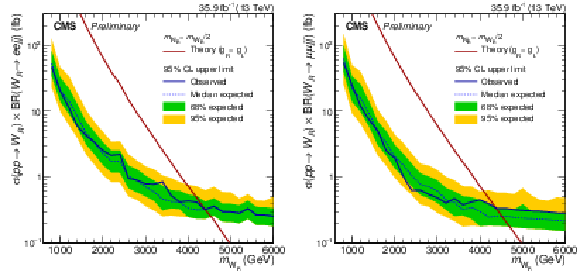
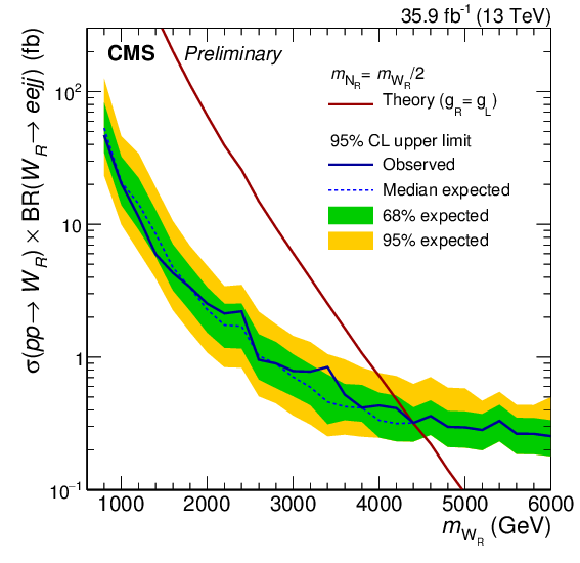
Limit on $\sigma (pp\rightarrow \mathrm{W}_{R}) \times BR(\mathrm{W}_{R} \rightarrow \ell \ell \text {jj})$ with systematic uncertainties for the electron channel on the left and for the muon channel on the right. The inner (green) band and the outer (yellow) band indicate the regions containing, respectively, the 68% and 95% of the distribution of limits expected under the signal plus background hypothesis. Right-handed bosons with $m_{\mathrm{W}_{R}} < $ 4.4 TeV are excluded. |
png pdf |
Figure 4-a:
Limit on $\sigma (pp\rightarrow \mathrm{W}_{R}) \times BR(\mathrm{W}_{R} \rightarrow \ell \ell \text {jj})$ with systematic uncertainties for the electron channel on the left and for the muon channel on the right. The inner (green) band and the outer (yellow) band indicate the regions containing, respectively, the 68% and 95% of the distribution of limits expected under the signal plus background hypothesis. Right-handed bosons with $m_{\mathrm{W}_{R}} < $ 4.4 TeV are excluded. |
png pdf |
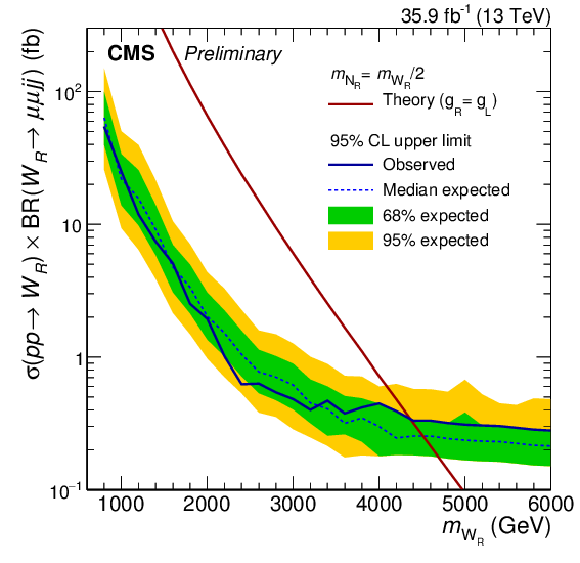
Figure 4-b:
Limit on $\sigma (pp\rightarrow \mathrm{W}_{R}) \times BR(\mathrm{W}_{R} \rightarrow \ell \ell \text {jj})$ with systematic uncertainties for the electron channel on the left and for the muon channel on the right. The inner (green) band and the outer (yellow) band indicate the regions containing, respectively, the 68% and 95% of the distribution of limits expected under the signal plus background hypothesis. Right-handed bosons with $m_{\mathrm{W}_{R}} < $ 4.4 TeV are excluded. |
png pdf |
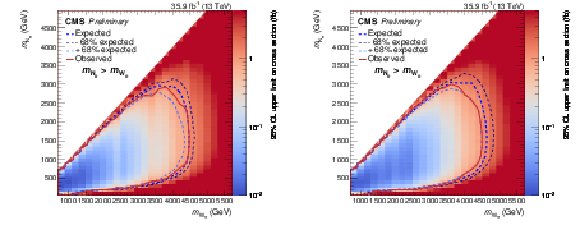
Figure 5:
Upper limit on the cross section for different $ \mathrm{W}_{R} $ and ${{{\mathrm N}_R}}$ mass hypothesis, for the electron channel on the left and for the muon channel on the right. The expected and observed exclusions are shown as the dotted (blue) curve and the solid (red) curve, respectively. The thin dotted (blue) curves indicate the region containing the 68% of the distribution of limits expected under the signal plus background hypothesys. |
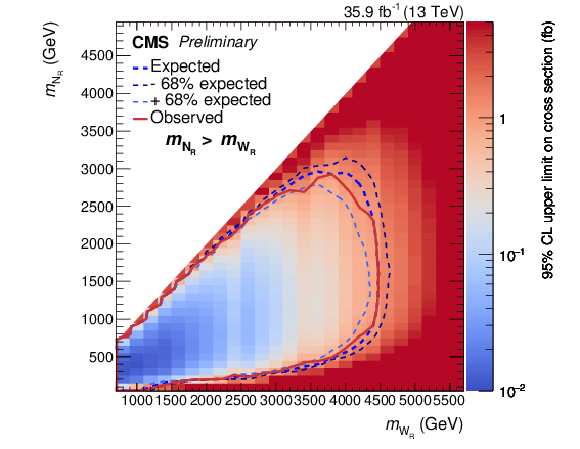
png pdf |
Figure 5-a:
Upper limit on the cross section for different $ \mathrm{W}_{R} $ and ${{{\mathrm N}_R}}$ mass hypothesis, for the electron channel on the left and for the muon channel on the right. The expected and observed exclusions are shown as the dotted (blue) curve and the solid (red) curve, respectively. The thin dotted (blue) curves indicate the region containing the 68% of the distribution of limits expected under the signal plus background hypothesys. |
png pdf |
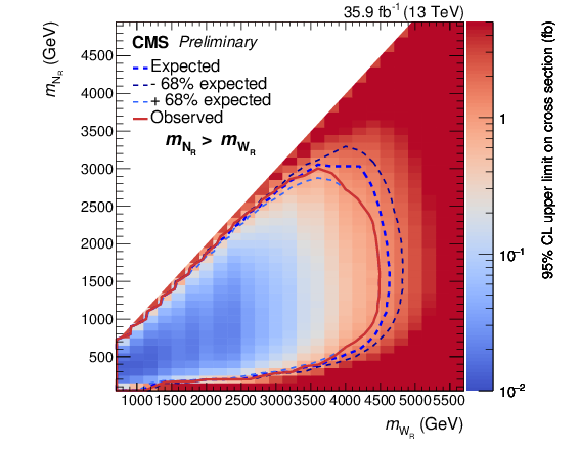
Figure 5-b:
Upper limit on the cross section for different $ \mathrm{W}_{R} $ and ${{{\mathrm N}_R}}$ mass hypothesis, for the electron channel on the left and for the muon channel on the right. The expected and observed exclusions are shown as the dotted (blue) curve and the solid (red) curve, respectively. The thin dotted (blue) curves indicate the region containing the 68% of the distribution of limits expected under the signal plus background hypothesys. |
| Tables | |

png pdf |
Table 1:
Transfer factor applied to the number of events in flavor control region to estimate the number of ${\mathrm{t} {}\mathrm{\bar{t}}}$ events in the $\mathrm{e} \mathrm{e} \text {jj}$ and $\mu \mu \text {jj}$ signal regions. |

png pdf |
Table 2:
Effect of object reconstruction's systematic uncertainties on signal and background yields. |

png pdf |
Table 3:
Uncertainties affecting $m_{\ell \ell \text {jj}}$ shape and normalization. The $ {\mathrm{t} {}\mathrm{\bar{t}}} $ SFs affect the $ {\mathrm{t} {}\mathrm{\bar{t}}} $ background, the DY PDF, factorization, and renormalization scales affect the DY + jets background and the luminosity affects both signal and backgrounds. |
png pdf |
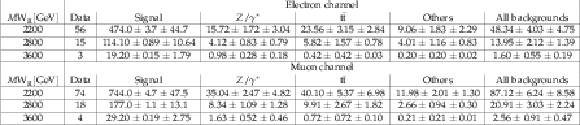
Table 4:
Observed number of events and magnitudes of systematic and statistical uncertainties for the expected events in different $ \mathrm{W}_{R} $ mass windows. All uncertainties are in number of events. In each table cell, the entry is of the form (mean $\pm $ stat. $\pm $ syst.). |
| Summary |
| In summary, a search for a right-handed W analogue to the W gauge boson in the decay channel of two leptons and two jets has been presented. No excess over standard model backgrounds are observed. A new W boson-like particle, with standard model couplings, decaying via a new heavy neutrino, up to a mass of 4.4 TeV, is excluded at 95% confidence level by the data, providing the most stringent limits to date. |
| References | ||||
| 1 | J. C. Pati and A. Salam | Lepton Number as the Fourth Color | PRD 10 (1974) 275, .[Erratum: Phys. Rev. D 11, 703 (1975)] | |
| 2 | R. N. Mohapatra and J. C. Pati | A Natural Left-Right Symmetry | PRD 11 (1975) 2558 | |
| 3 | G. Senjanovic and R. N. Mohapatra | Exact Left-Right Symmetry and Spontaneous Violation of Parity | PRD 12 (1975) 1502 | |
| 4 | W.-Y. Keung and G. Senjanovic | Majorana Neutrinos and the Production of the Right-handed Charged Gauge Boson | PRL 50 (1983) 1427 | |
| 5 | P. Adhya, D. R. Chaudhuri, and A. Raychaudhuri | Decay and decoupling of heavy right-handed Majorana neutrinos in the L-R model | EPJC19 (2001) 183--190 | hep-ph/0006260 |
| 6 | P. S. B. Dev, R. N. Mohapatra, and Y. Zhang | Heavy right-handed neutrino dark matter in left-right models | MPLA32 (2017) 1740007 | 1610.05738 |
| 7 | R. N. Mohapatra and G. Senjanovic | Neutrino Mass and Spontaneous Parity Violation | PRL 44 (1980) 912 | |
| 8 | M. Gell-Mann, P. Ramond, and R. Slansky | Complex Spinors and Unified Theories | Conf. Proc. C 790927 (1979) 315 | 1306.4669 |
| 9 | CMS Collaboration | Search for heavy neutrinos and $ \mathrm {W} $ bosons with right-handed couplings in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | EPJC 74 (2014) 3149 | CMS-EXO-13-008 1407.3683 |
| 10 | CMS Collaboration | Search for heavy neutrinos and $ \mathrm{W} $ bosons with right handed couplings in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | CMS-PAS-EXO-16-045 | CMS-PAS-EXO-16-045 |
| 11 | CMS Collaboration | Search for heavy neutrinos or third-generation leptoquarks in final states with two hadronically decaying $ \tau $ leptons and two jets in proton-proton collisions at $ \sqrt{s}= $ 13 TeV | JHEP 03 (2017) 077 | CMS-EXO-16-016 1612.01190 |
| 12 | CMS Collaboration | Search for the third-generation scalar leptoquarks and heavy right-handed neutrinos in final states with two tau leptons and two jets in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | CMS-EXO-16-023 1703.03995 |
|
| 13 | CMS Collaboration | Search for a heavy composite Majorana neutrino in the final state with two leptons and two quarks at sqrt(s) = 13 TeV | CMS-EXO-16-026 1706.08578 |
|
| 14 | ATLAS Collaboration | Search for heavy neutrinos and right-handed $ W $ bosons in events with two leptons and jets in $ pp $ collisions at $ \sqrt{s}= $ 7 TeV with the ATLAS detector | EPJC72 (2012) 2056 | 1203.5420 |
| 15 | ATLAS Collaboration | Search for third generation scalar leptoquarks in pp collisions at $ \sqrt{s} = $ 7 TeV with the ATLAS detector | JHEP 06 (2013) 033 | 1303.0526 |
| 16 | ATLAS Collaboration | Search for heavy Majorana neutrinos with the ATLAS detector in pp collisions at $ \sqrt{s}= $ 8 TeV | JHEP 07 (2015) 162 | 1506.06020 |
| 17 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 18 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 19 | CMS Collaboration | Particle-flow reconstruction and global event description with the cms detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 20 | CMS Collaboration | Commissioning of the particle-flow event reconstruction with the first LHC collisions recorded in the CMS detector | CMS-PAS-PFT-10-001 | |
| 21 | CMS Collaboration | Performance of CMS muon reconstruction in $ pp $ collision events at $ \sqrt{s} = $ 7 TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 22 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ k_t $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 23 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 24 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | CMS-PRF-14-001 1706.04965 |
|
| 25 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 26 | CMS Collaboration | Jet performance in pp collisions at $ \sqrt{s} = $ 7 TeV | CMS-PAS-JME-10-003 | |
| 27 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at $ \sqrt{s} = $ 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 28 | S. Agostinelli et al. | GEANT4---a simulation toolkit | NIMA 506 (2003) 250 | |
| 29 | T. Sjöstrand et al. | An Introduction to PYTHIA 8.2 | CPC 191 (2015) 159--177 | 1410.3012 |
| 30 | S. Frixione and B. R. Webber | Matching NLO QCD computations and parton shower simulations | JHEP 06 (2002) 029 | hep-ph/0204244 |
| 31 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 32 | J. Alwall et al. | MadGraph 5 : Going Beyond | JHEP 06 (2011) 128 | 1106.0522 |
| 33 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 34 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC71 (2011) 1547 | 1009.2450 |
| 35 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC76 (2016), no. 3, 155 | CMS-GEN-14-001 1512.00815 |
| 36 | L. Moneta et al. | The RooStats Project | PoS ACAT2010 (2010) 057 | 1009.1003 |
| 37 | CMS Collaboration | CMS Luminosity Measurements for the 2016 Data Taking Period | CMS-PAS-LUM-17-001 | CMS-PAS-LUM-17-001 |
| 38 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | JPG 43 (2016) 023001 | 1510.03865 |
| 39 | The ATLAS Collaboration, The CMS Collaboration, The LHC Higgs Combination Group Collaboration | Procedure for the LHC Higgs boson search combination in Summer 2011 | CMS-NOTE-2011-005 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|