CMS-PAS-EXO-16-045

CMS-PAS-EXO-16-045
Search for heavy neutrinos and W bosons with right handed couplings in proton-proton collisions at $\sqrt{s} =$ 13 TeV
CMS Collaboration
May 2017

Abstract: A search for heavy right handed neutrinos $\mathrm{N}_\ell$ ( $\ell = \mathrm{e}, \mu$ ), and right handed $W_R$ bosons, performed by the CMS experiment is summarized here. Using the 2.6 fb $^{-1}$ of integrated luminosity recorded by the CMS experiment in 2015 at a center-of-mass energy of 13 TeV, this search seeks evidence of $W_R$ bosons and $\mathrm{N}_\ell$ neutrinos in events with two leptons and two jets. The data do not significantly exceed expected backgrounds, and are consistent with expected results given uncertainties. For Standard Model extensions with strict left-right symmetry, and assuming only one $\mathrm{N}_\ell$ flavor contributes significantly to the $W_R$ decay width, mass limits are set in the two-dimensional $(M_{W_R}, M_{\mathrm{N}_\ell})$ plane at the ninety five percent confidence level. The limits extend to $M_{W_R}$ of 3.3 TeV (3.5 TeV) in the electron (muon) channel, and span a wide range of $M_{\mathrm{N}_\ell}$ values below $M_{W_R}$ .
Links: CDS record (PDF) ; inSPIRE record ; CADI line (restricted) ;

Figures & Tables	Summary	Additional Figures	References	CMS Publications

Figures
png pdf	Figure 1: Feynman diagram for the production of a ${W_R}$ boson and its decay to two charged leptons and two quarks through a heavy neutrino.
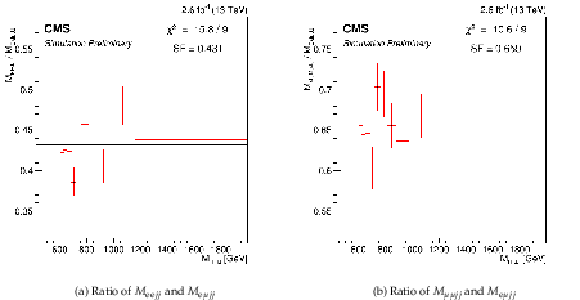
png pdf	Figure 2: Bin-by-bin ratio of ${M_{\ell \ell j j}}$ distribution and ${M_{\mathrm{ e } \mu j j}}$ from top quark background simulations, where $\ell$ is an electron (left) or a muon (right).
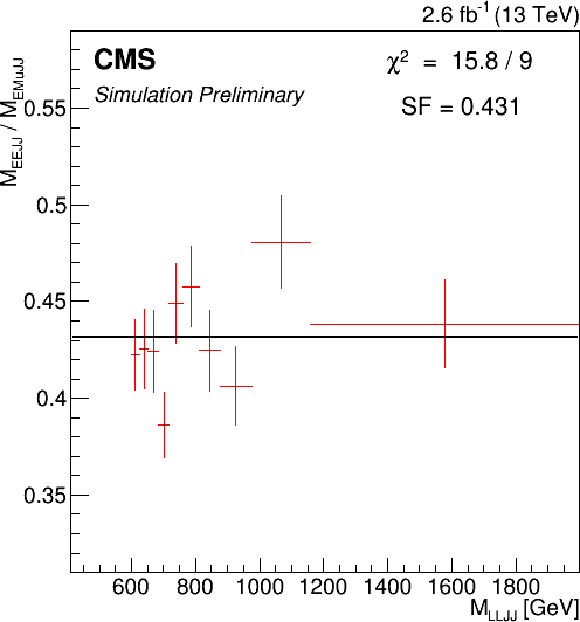
png	Figure 2-a: Bin-by-bin ratio of ${M_{\ell \ell j j}}$ distribution and ${M_{\mathrm{ e } \mu j j}}$ from top quark background simulations, where $\ell$ is an electron.
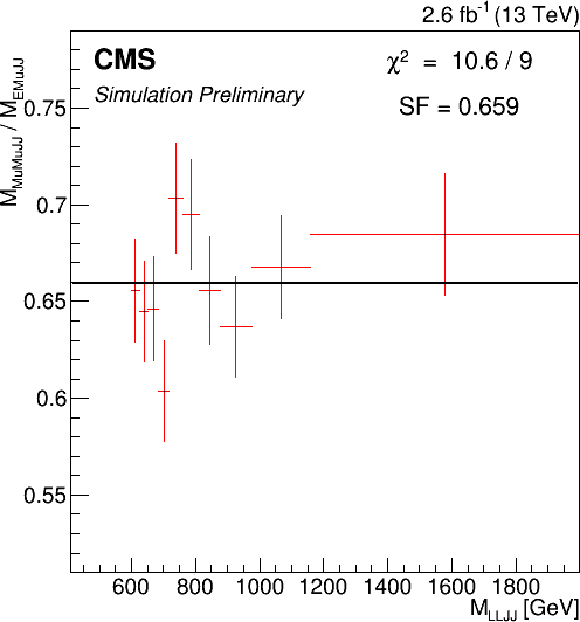
png	Figure 2-b: Bin-by-bin ratio of ${M_{\ell \ell j j}}$ distribution and ${M_{\mathrm{ e } \mu j j}}$ from top quark background simulations, where $\ell$ is a muon.
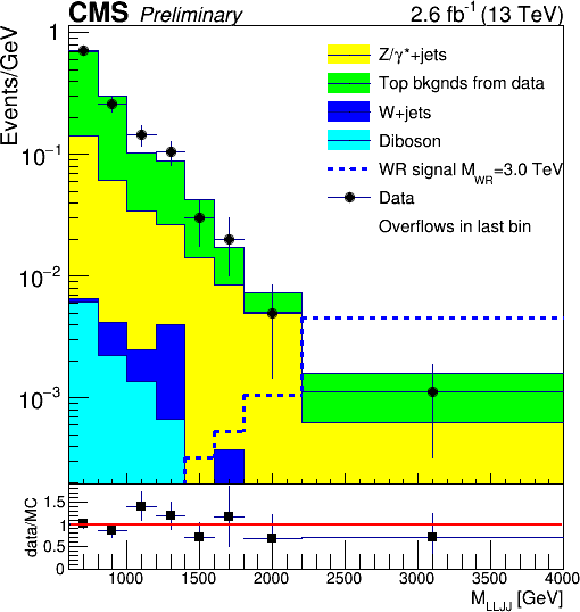
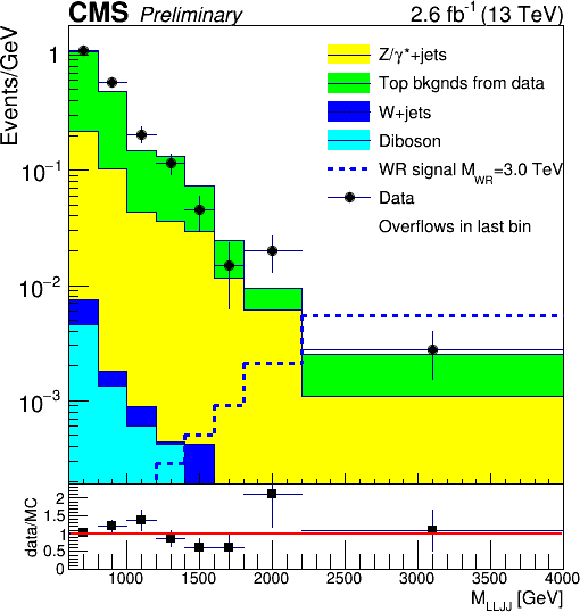
png pdf	Figure 3: ${M_{\ell \ell j j}}$ in the electron and muon channel signal regions. For the ${W_R}$ signal shown, $M_{ {\mathrm {N}_{\ell }} } = \frac {1}{2} {M_{\mathrm{ W } _{\mathrm {R}}}}$ . Both plots use 200 GeV wide bins from 600 to 1800 GeV, then one bin spans 1800 to 2200 GeV, and finally the last bin includes all events above 2200 GeV. In addition, the bin contents are divided by the bin widths.
png	Figure 3-a: ${M_{\ell \ell j j}}$ in the electron channel signal region. For the ${W_R}$ signal shown, $M_{ {\mathrm {N}_{\ell }} } = \frac {1}{2} {M_{\mathrm{ W } _{\mathrm {R}}}}$ . The plot uses 200 GeV wide bins from 600 to 1800 GeV, then one bin spans 1800 to 2200 GeV, and finally the last bin includes all events above 2200 GeV. In addition, the bin contents are divided by the bin widths.
png	Figure 3-b: ${M_{\ell \ell j j}}$ in the muon channel signal region. For the ${W_R}$ signal shown, $M_{ {\mathrm {N}_{\ell }} } = \frac {1}{2} {M_{\mathrm{ W } _{\mathrm {R}}}}$ . The plot uses 200 GeV wide bins from 600 to 1800 GeV, then one bin spans 1800 to 2200 GeV, and finally the last bin includes all events above 2200 GeV. In addition, the bin contents are divided by the bin widths.
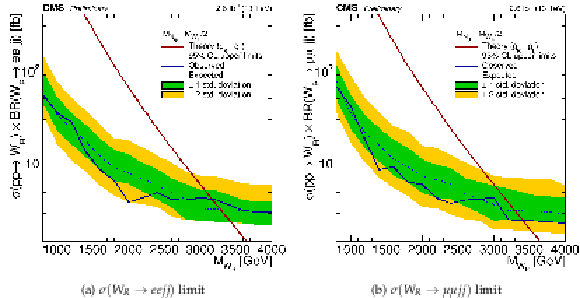
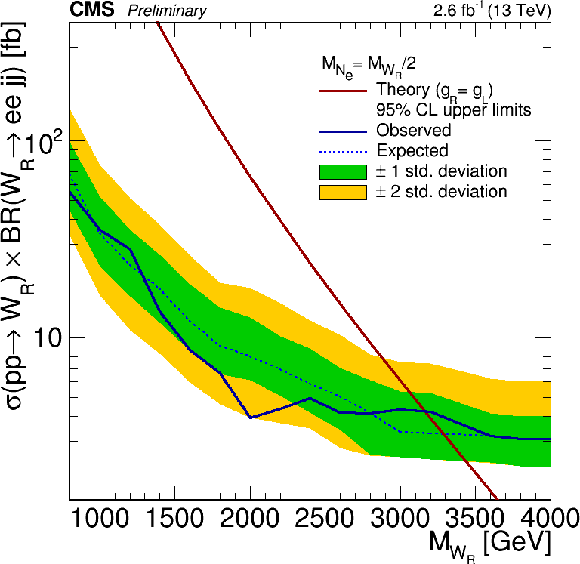
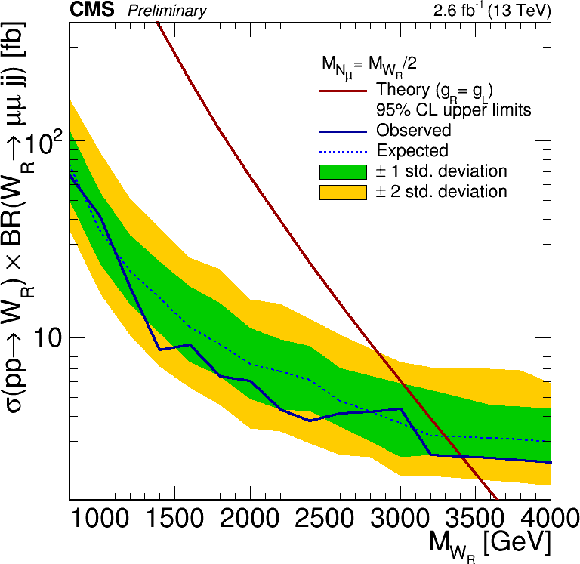
png pdf	Figure 4: ${W_R}$ cross section limits for $M_{ {\mathrm {N}_{\ell }} } = \frac {1}{2} {M_{\mathrm{ W } _{\mathrm {R}}}}$ .
png	Figure 4-a: ${W_R}$ cross section limits for $M_{ {\mathrm {N}_{\ell }} } = \frac {1}{2} {M_{\mathrm{ W } _{\mathrm {R}}}}$ . Electron channel.
png	Figure 4-b: ${W_R}$ cross section limits for $M_{ {\mathrm {N}_{\ell }} } = \frac {1}{2} {M_{\mathrm{ W } _{\mathrm {R}}}}$ . Muon channel.
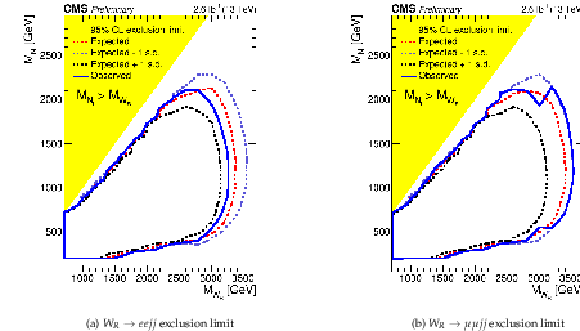
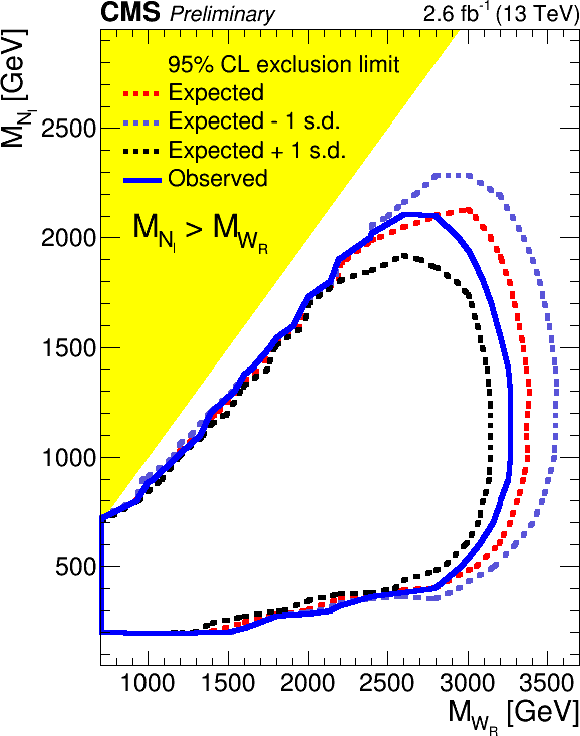
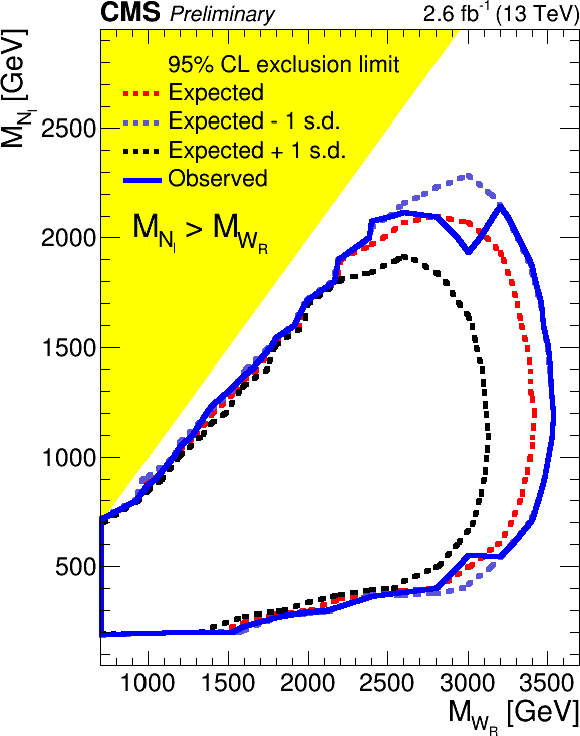
png pdf	Figure 5: 95% confidence level exclusion in the $( {M_{\mathrm{ W } _{\mathrm {R}}}} , M_{ {\mathrm {N}_{\ell }} })$ plane for ${W_R} \to eejj$ (left) and ${W_R} \to \mu \mu jj$ (right).
png	Figure 5-a: 95% confidence level exclusion in the $( {M_{\mathrm{ W } _{\mathrm {R}}}} , M_{ {\mathrm {N}_{\ell }} })$ plane for ${W_R} \to eejj$ .
png	Figure 5-b: 95% confidence level exclusion in the $( {M_{\mathrm{ W } _{\mathrm {R}}}} , M_{ {\mathrm {N}_{\ell }} })$ plane for ${W_R} \to \mu \mu jj$ .

Tables
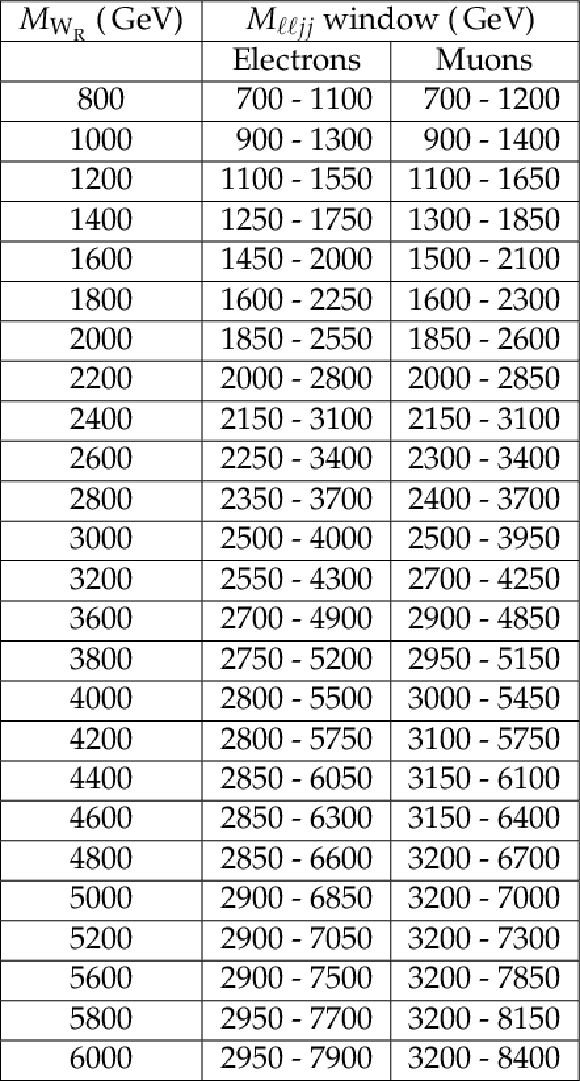
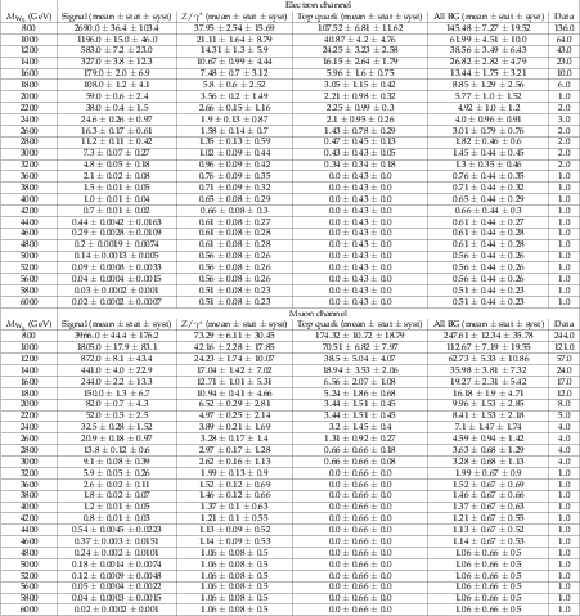
png pdf	Table 1: ${M_{\ell \ell j j}}$ windows that minimize the expected ${W_R}$ cross section limit at each ${M_{\mathrm{ W } _{\mathrm {R}}}}$ point.
png pdf	Table 2: For ${W_R}$ mass hypotheses with $M_{ {\mathrm {N}_{\ell }} } = \frac {1}{2} {M_{\mathrm{ W } _{\mathrm {R}}}}$ , these are the mean number of expected ${W_R}$ signal and background events, their statistical and systematic errors, and the number of observed events in data. All errors are given in number of events, and refer to the mean number of expected events. The analysis was run 3200 times to estimate the errors listed here, and the systematic errors from jet and lepton energy scale uncertainties are added in quadrature with systematic errors from luminosity, pileup and background normalization uncertainty. For the ${M_{\mathrm{ W } _{\mathrm {R}}}} =$ 2.6 TeV hypothesis, the electron channel top quark background estimate is higher than the muon channel because the electron channel ${M_{\mathrm{ W } _{\mathrm {R}}}}$ window extends lower in ${M_{\ell \ell j j}}$ (see Table {tab:masscuts}). In the $e\mu jj$ data used to estimate the top quark background, there is a deficit of events in the region 1.8 TeV $< {M_{\mathrm{ e } \mu j j}} <$ 2.1 TeV that, in both channels, results in little change in the top quark background going from the ${M_{\mathrm{ W } _{\mathrm {R}}}} =$ 2.0 TeV to the ${M_{\mathrm{ W } _{\mathrm {R}}}} =$ 2.2 TeV bin.

Summary

A search for right-handed bosons (

$W_R$ ) and heavy right-handed neutrinos (

$\mathrm{N}_\ell$ ) in the left-right symmetric extension of the standard model has been presented.

$W_R$ boson production is excluded at the 95% confidence level up to

$M_{W_R} <$ 3.5 (3.3) TeV in the muon (electron) channel. These results are consistent with expectations based on simulations of SM processes, and extend the mass limits in the muon (electron) channel 400 GeV (400 GeV) higher in

$M_{W_R}$ , and 150 GeV (300 GeV) higher in

$M_{\mathrm{N}_ell}$ relative to the Run I limits.

Additional Figures
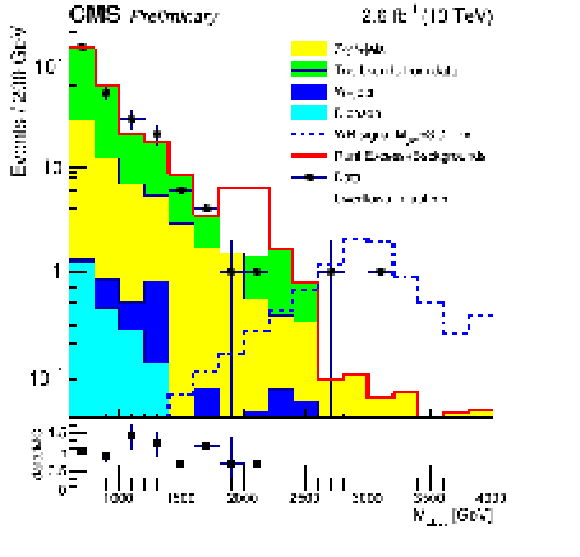
png pdf	Additional Figure 1: Data compared to the Run I excess plus expected backgrounds in the electron channel $M_{LLJJ}$ distribution. For the ${W_R}$ signal shown, $M_{N_{l}} = \frac {1}{2} M_{W_{R}}$ . The bins are 200 GeV wide.
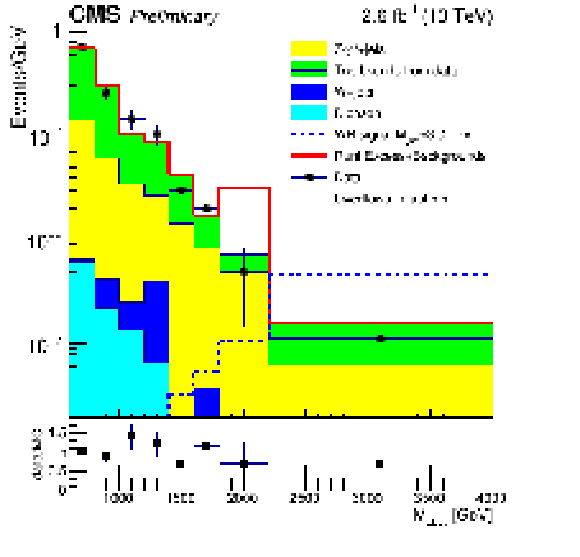
png pdf	Additional Figure 2: Data compared to the Run I excess plus expected backgrounds in the electron channel $M_{LLJJ}$ distribution. For the ${W_R}$ signal shown, $M_{N_{l}} = \frac {1}{2} M_{W_{R}}$ . The plot uses 200 GeV wide bins from 600 to 1800 GeV, then one bin spans 1800 to 2200 GeV, and finally the last bin includes all events above 2200 GeV. All bin contents are divided by the bin widths.

The results from 2015 data in the electron channel are compared to expected backgrounds plus the Run I electron channel excess in Additional Fig. 1 and Additional Fig. 2. The Run I excess normalization is rescaled to account for differences in integrated luminosity and

$W_{R}$ cross section between 2012 and 2015, and its shape is modeled using a Gaussian. Since the Run I excess spanned 1.8

$< M_{EEJJ} <$ 2.2 TeV, the mean of the Gaussian representing the excess was set to 2.0 TeV. Furthermore, the standard deviation of the Gaussian

$\sigma_{gaus}$ was chosen so that +3

$\sigma_{gaus}$ (-3

$\sigma_{gaus}$ ) away from the mean equaled 2.2 (1.8)

References
1	S. L. Glashow	Partial-symmetries of weak interactions	Nucl. Phys. 22 (1961) 579
2	S. Weinberg	A Model of Leptons	PRL 19 (1967) 1264
3	A. Salam	Weak and electromagnetic interactions	in Elementary particle physics: relativistic groups and analyticity, N. Svartholm, ed., p. 367 Almqvist \& Wiskell, 1968 Proceedings of the eighth Nobel symposium
4	J. C. Pati and A. Salam	Lepton number as the fourth "color"	PRD 10 (1974) 275
5	R. N. Mohapatra and J. C. Pati	A Natural Left-Right Symmetry	PRD 11 (1975) 2558
6	G. Senjanovi\'c and R. N. Mohapatra	Exact left-right symmetry and spontaneous violation of parity	PRD 12 (1975) 1502
7	W.-Y. Keung and G. Senjanovi\'c	Majorana Neutrinos and the Production of the Right-Handed Charged Gauge Boson	PRL 50 (1983) 1427
8	W. M. Alberico and S. M. Bilenky	Neutrino Oscillations, Masses and Mixing	Phys. Part. Nucl. 35 (2003) 297	hep-ph/0306239
9	C. Giunti and M. Laveder	Neutrino mixing	in Developments in Quantum Physics, F. Columbus and V. Krasnoholovets, eds Nova Science Publishers, Inc.	hep-ph/0310238
10	Particle Data Group Collaboration	Review of Particle Physics	CPC 40 (2016), no. 10, 100001
11	R. N. Mohapatra and G. Senjanovi\'c	Neutrino Mass and Spontaneous Parity Nonconservation	PRL 44 (1980) 912
12	M. Gell-Mann, P. Ramond, and R. Slansky	Complex Spinors and Unified Theories	in Supergravity, P. van Nieuwenhuizen and D. Z. Freedman, eds North Holland Publishing Co.	1306.4669
13	CMS Collaboration	Search for heavy neutrinos or third-generation leptoquarks in final states with two hadronically decaying tau leptons and two jets in proton-proton collisions at $\sqrt{s}$ = 13 TeV	JHEP 03 (2017) 077	CMS-EXO-16-016 1612.01190
14	CMS Collaboration	Search for the third-generation scalar leptoquarks and heavy right-handed neutrinos in $\tau_{l}\tau_{h} jj$ final states in pp collisions at 13 TeV	CDS
15	CMS Collaboration	Search for heavy composite Majorana neutrinos produced in association with a lepton and decaying into a same-flavour lepton plus two quarks at $\sqrt{s}$ = 13 TeV with the CMS detector	CDS
16	CMS Collaboration	Search for heavy neutrinos and $\mathrm {W}$ bosons with right-handed couplings in proton-proton collisions at $\sqrt{s} =$ 8 TeV	EPJC74 (2014), no. 11	CMS-EXO-13-008 1407.3683
17	E. Nardi, E. Roulet, and D. Tommasini	New Neutral Gauge Bosons and New Heavy Fermions in the Light of the New LEP Data	PLB 344 (1995) 225	hep-ph/9409310
18	G. Beall, M. Bander, and A. Soni	Constraint on the Mass Scale of a Left-Right-Symmetric Electroweak Theory from the KL-KS Mass Difference	PRL 48 (1982) 848
19	A. Maiezza, M. Nemev\vsek, F. Nesti, and G. Senjanovi\'c	Left-right symmetry at LHC	PRD 82 (2010) 055022	1005.5160
20	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 03 (2008) S08004	CMS-00-001
21	T. Sj\"ostrand, S. Mrenna, and P. Skands	PYTHIA 6.4 Physics and Manual	JHEP 05 (2006) 026	hep-ph/0603175
22	NNPDF Collaboration	Unbiased global determination of parton distributions and their uncertainties at NNLO and at LO	Nucl. Phys. B 855 (2012) 153	1107.2652
23	S. Alioli et al.	A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX	JHEP 06 (2010) 043	1002.2581
24	E. Re	Single-top Wt-channel production matched with parton showers using the POWHEG method	EPJC 71 (2010) 1547	1009.2450
25	S. Alioli, P. Nason, C. Oleari, and E. Re	NLO single-top production matched with shower in POWHEG: s- and t-channel contributions	JHEP 09 (2009) 111	0907.4076
26	J. Alwall et al.	MadGraph 5: Going Beyond	JHEP 06 (2011) 128	1106.0522
27	CMS Collaboration	Event generator tunes obtained from underlying event and multiparton scattering measurements	EPJC 76 (2016) 155	CMS-GEN-14-001 1512.00815
28	GEANT4 Collaboration	GEANT4 -- a simulation toolkit	NIMA 506 (2003) 250
29	CMS Collaboration	Search for a Narrow Resonance Produced in 13 TeV pp Collisions Decaying to Electron Pair or Muon Pair Final States	CDS
30	M. Cacciari and G. P. Salam	Pileup subtraction using jet areas	PLB 659 (2008) 119	0707.1378
31	CMS Collaboration	Commissioning of the Particle-Flow Event Reconstruction with the first LHC collisions recorded in the CMS detector	CDS
32	CMS Collaboration	Particle-Flow Event Reconstruction in CMS and Performance for Jets, Taus, and MET	CDS
33	M. Cacciari, G. P. Salam, and G. Soyez	The anti- $k_{t}$ jet clustering algorithm	JHEP 04 (2008) 063	0802.1189
34	M. Cacciari, G. P. Salam, and G. Soyez	The Catchment Area of Jets	JHEP 04 (2008) 005	0802.1188
35	CMS Collaboration	Study of Pileup Removal Algorithms for Jets	CMS-PAS-JME-14-001	CMS-PAS-JME-14-001
36	CMS Collaboration	Jet Performance in pp Collisions at $\sqrt{s} = 7$ TeV	CDS
37	CMS Collaboration	Determination of Jet Energy Calibration and Transverse Momentum Resolution in CMS	JINST 6 (2011) 11002	CMS-JME-10-011 1107.4277