

Compact Muon Solenoid
LHC, CERN
| CMS-SMP-20-007 ; CERN-EP-2021-171 | ||
| Measurement of double-parton scattering in inclusive production of four jets with low transverse momentum in proton-proton collisions at $\sqrt{s} = $ 13 TeV | ||
| CMS Collaboration | ||
| 29 September 2021 | ||
| JHEP 01 (2022) 177 | ||
| Abstract: A measurement of inclusive four-jet production in proton-proton collisions at a center-of-mass energy of 13 TeV is presented. The transverse momenta of jets within $| \eta | < $ 4.7 reach down to 35, 30, 25, and 20 GeV for the first-, second-, third-, and fourth-leading jet, respectively. Differential cross sections are measured as functions of the jet transverse momentum, jet pseudorapidity, and several other observables that describe the angular correlations between the jets. The measured distributions show sensitivity to different aspects of the underlying event, parton shower, and matrix element calculations. In particular, the interplay between angular correlations caused by parton shower and double-parton scattering contributions is shown to be important. The double-parton scattering contribution is extracted by means of a template fit to the data, using distributions for single-parton scattering obtained from Monte Carlo event generators and a double-parton scattering distribution constructed from inclusive single-jet events in data. The effective double-parton scattering cross section is calculated and discussed in view of previous measurements and of its dependence on the models used to describe the single-parton scattering background. | ||
| Links: e-print arXiv:2109.13822 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; HepData record ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
A schematic depiction of inclusive four-jet production through SPS (left) and DPS (right). In the case of SPS, one hard scattering produces the jets $a$ through $d$, whereas two independent hard scatterings create two jets each in the case of DPS. Since the two jet pairs are created independently in a DPS event, they are expected to show different kinematic correlations compared with the four jets originating from an SPS event. |

png pdf |
Figure 1-a:
A schematic depiction of inclusive four-jet production through SPS. One hard scattering produces the jets $a$ through $d$. |

png pdf |
Figure 1-b:
A schematic depiction of inclusive four-jet production through DPS. Two independent hard scatterings create two jets each. Since the two jet pairs are created independently, they are expected to show different kinematic correlations compared with the four jets originating from an SPS event. |
png pdf |
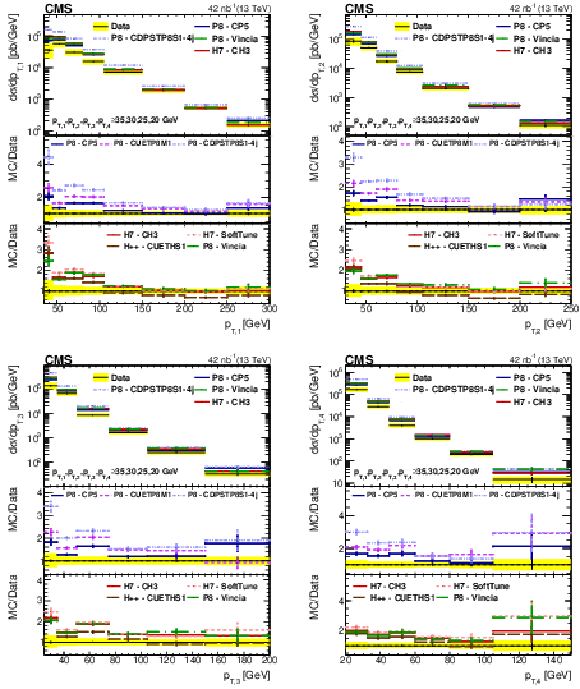
Figure 2:
Comparison of the ${p_{\mathrm {T}}}$ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the leading (upper left), subleading (upper right), third leading (lower left), and fourth leading (lower right) jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
Figure 2-a:
Comparison of the ${p_{\mathrm {T}}}$ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 2-b:
Comparison of the ${p_{\mathrm {T}}}$ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the subleading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 2-c:
Comparison of the ${p_{\mathrm {T}}}$ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the third leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
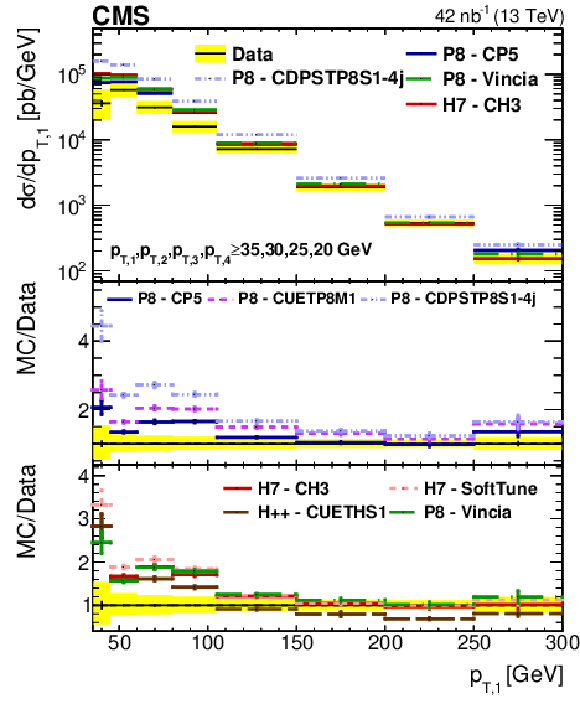
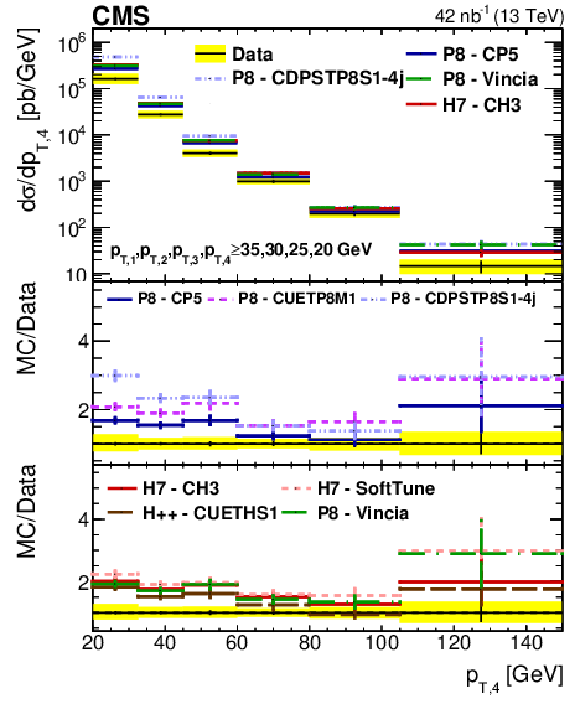
Figure 2-d:
Comparison of the ${p_{\mathrm {T}}}$ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the fourth leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
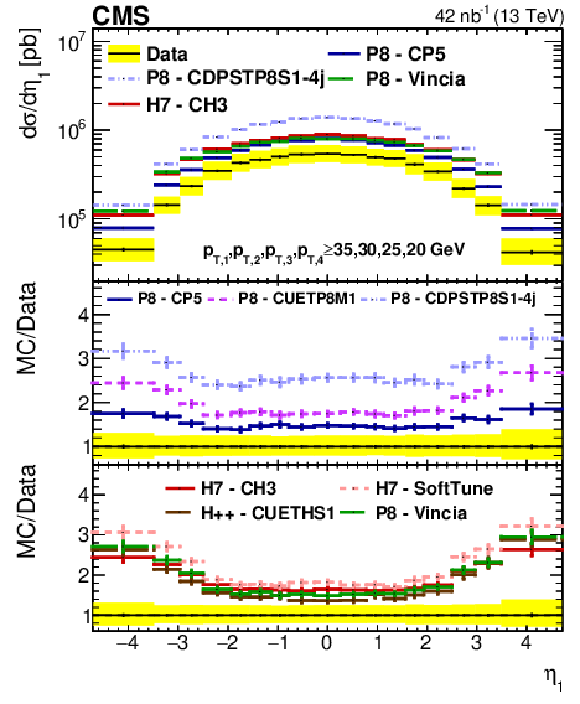
Figure 3:
Comparison of the $\eta $ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the leading (upper left), subleading (upper right), third leading (lower left), and fourth leading (lower right) jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
Figure 3-a:
Comparison of the $\eta $ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
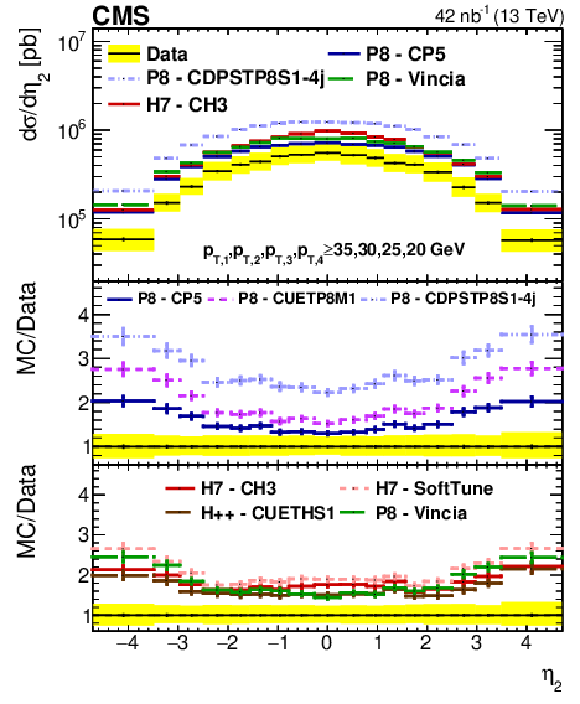
png pdf |
Figure 3-b:
Comparison of the $\eta $ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the subleading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 3-c:
Comparison of the $\eta $ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the third leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 3-d:
Comparison of the $\eta $ spectra from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes, for the fourth leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 4:
Comparison of the ${\Delta \phi _\text {Soft}}$, ${\Delta \phi _\mathrm {3j}^\text {min}}$, ${\Delta Y}$, and ${\phi _{ij}}$ distributions from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes in Region I. All distributions have been normalized to regions where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 4-a:
Comparison of the ${\Delta \phi _\text {Soft}}$ distribution from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes in Region I. All distributions have been normalized to regions where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
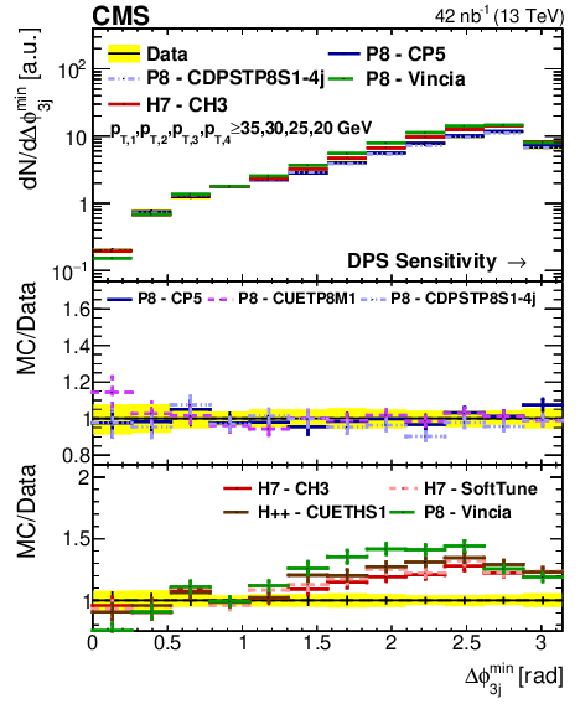
png pdf |
Figure 4-b:
Comparison of the ${\Delta \phi _\mathrm {3j}^\text {min}}$ distribution from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes in Region I. All distributions have been normalized to regions where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 4-c:
Comparison of the ${\Delta Y}$ distribution from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes in Region I. All distributions have been normalized to regions where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 4-d:
Comparison of the ${\phi _{ij}}$ distribution from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes in Region I. All distributions have been normalized to regions where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
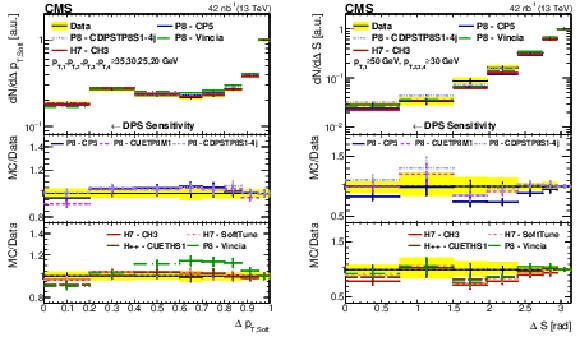
png pdf |
Figure 5:
Comparison of the ${\Delta p_{\text {T,Soft}}}$ and ${\Delta S}$ distributions from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes in Region I and Region II, respectively. All distributions have been normalized to regions where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
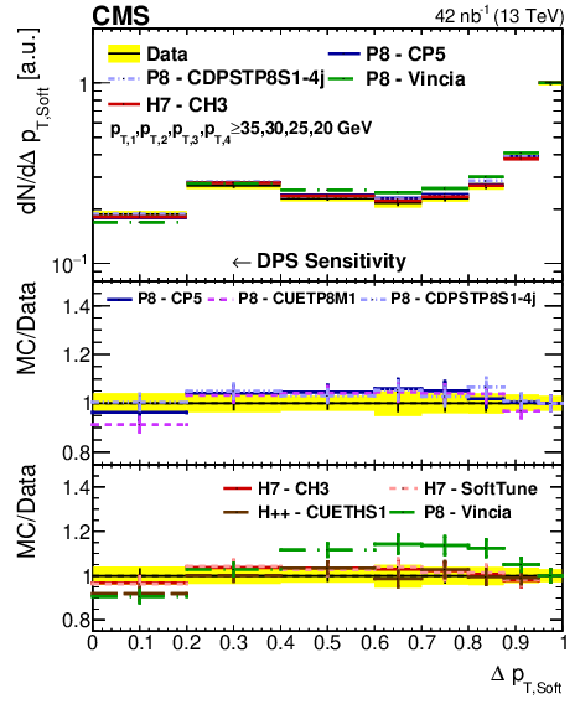
png pdf |
Figure 5-a:
Comparison of the ${\Delta p_{\text {T,Soft}}}$ distribution from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes in Region I. All distributions have been normalized to regions where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
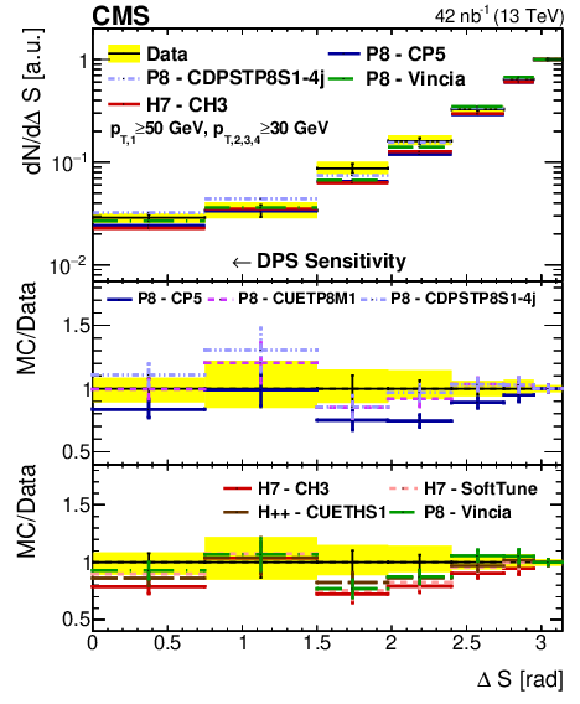
Figure 5-b:
Comparison of the ${\Delta S}$ distribution from data to different PYTHIA-8 (P8), HERWIG++ (H++), and HERWIG-7 (H7) tunes in Region II. All distributions have been normalized to regions where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
Figure 6:
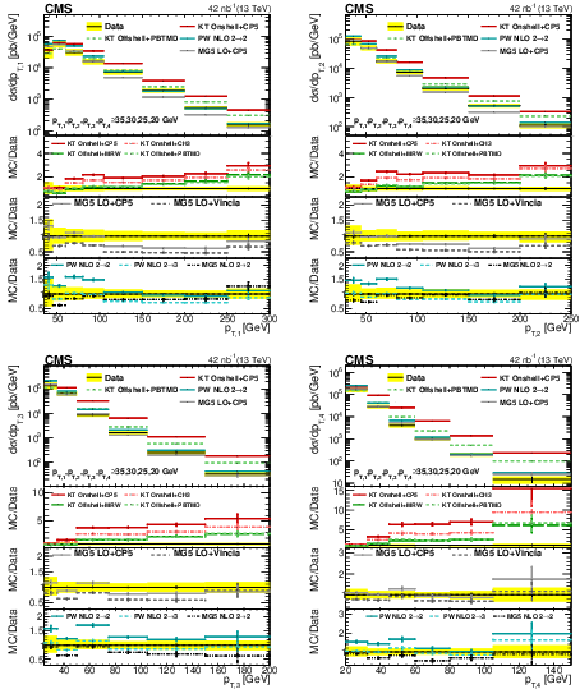
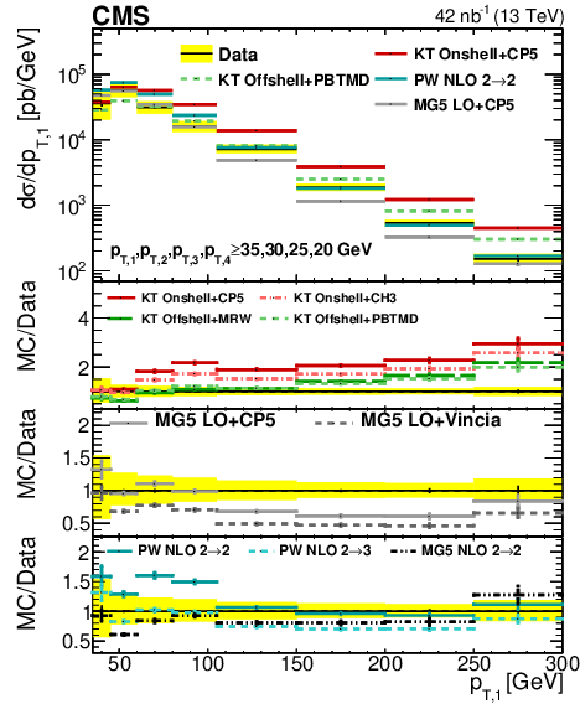
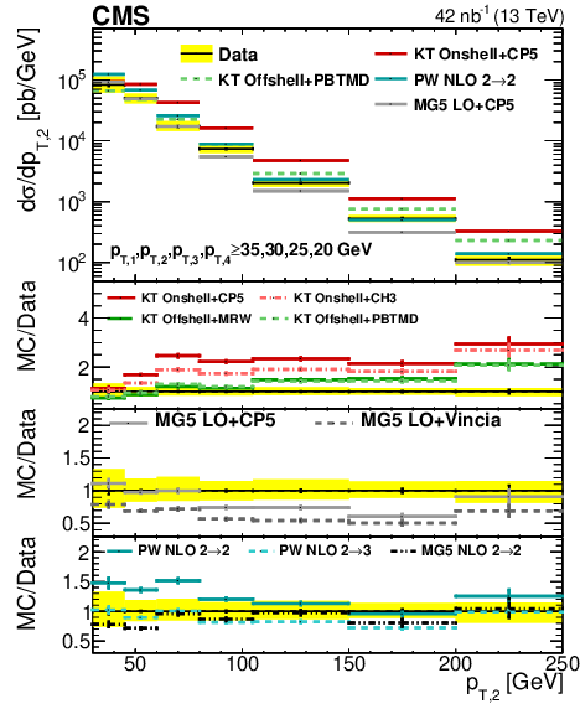
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the leading (upper left), subleading (upper right), third leading (lower left), and fourth leading (lower right) jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
Figure 6-a:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
Figure 6-b:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the subleading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
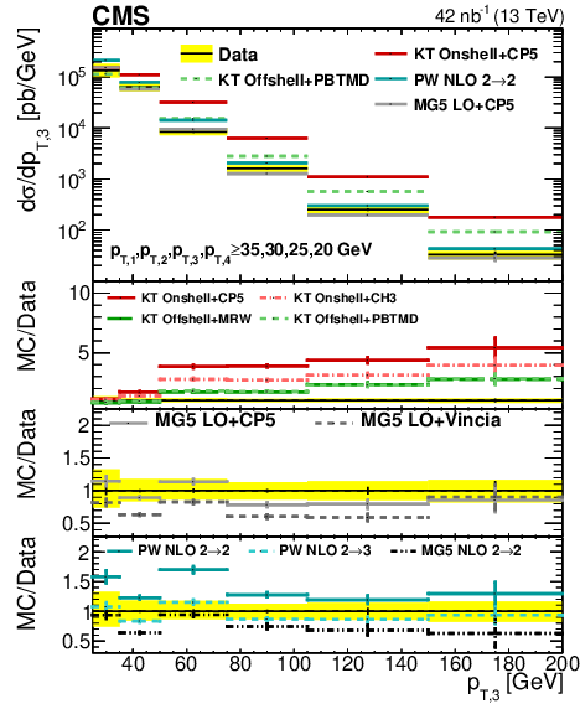
png pdf |
Figure 6-c:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the third leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 6-d:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the fourth leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
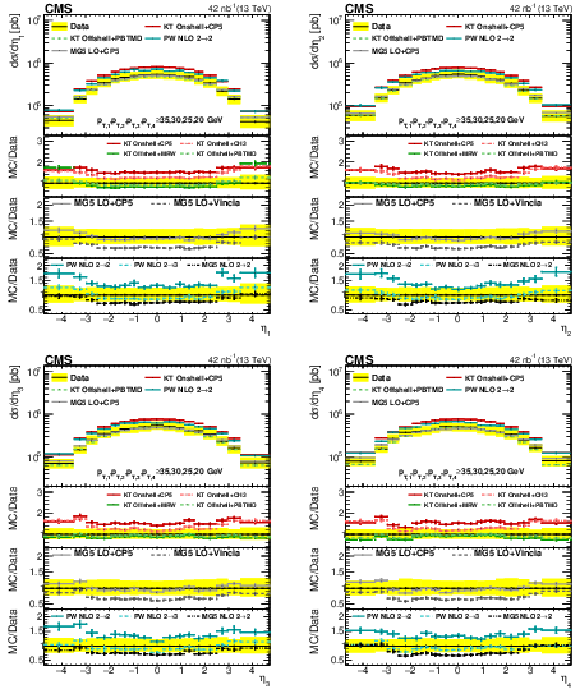
png pdf |
Figure 7:
Comparison of the unfolded $\eta $ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the leading (upper left), subleading (upper right), third leading (lower left), and fourth leading (lower right) jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 7-a:
Comparison of the unfolded $\eta $ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 7-b:
Comparison of the unfolded $\eta $ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the subleading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 7-c:
Comparison of the unfolded $\eta $ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the third leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 7-d:
Comparison of the unfolded $\eta $ spectra of data with different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) models, for the fourth leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
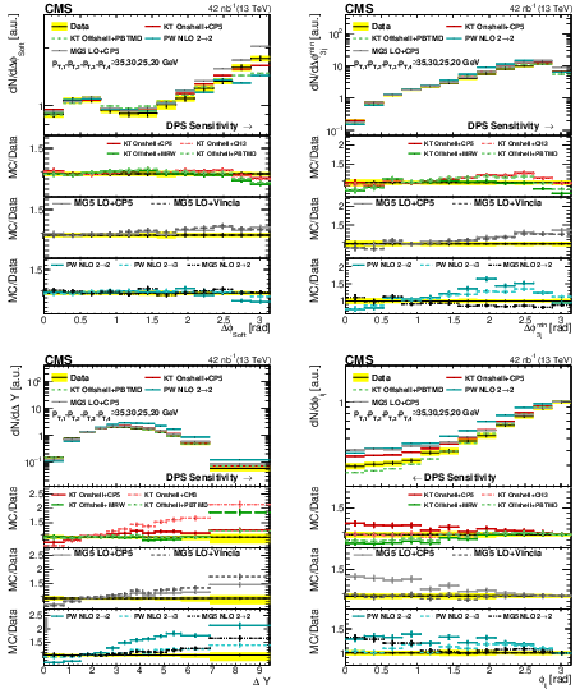
png pdf |
Figure 8:
Comparison of the ${\Delta \phi _\text {Soft}}$, ${\Delta \phi _\mathrm {3j}^\text {min}}$, ${\Delta Y}$, and ${\phi _{ij}}$ distributions from data to different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) implementations in Region I. All distributions have been normalized to regions where a reduced DPS sensitivity is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
Figure 8-a:
Comparison of the ${\Delta \phi _\text {Soft}}$ distribution from data to different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) implementations in Region I. All distributions have been normalized to regions where a reduced DPS sensitivity is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
Figure 8-b:
Comparison of the ${\Delta \phi _\mathrm {3j}^\text {min}}$ distribution from data to different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) implementations in Region I. All distributions have been normalized to regions where a reduced DPS sensitivity is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
Figure 8-c:
Comparison of the ${\Delta Y}$ distribution from data to different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) implementations in Region I. All distributions have been normalized to regions where a reduced DPS sensitivity is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
Figure 8-d:
Comparison of the ${\phi _{ij}}$ distribution from data to different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) implementations in Region I. All distributions have been normalized to regions where a reduced DPS sensitivity is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
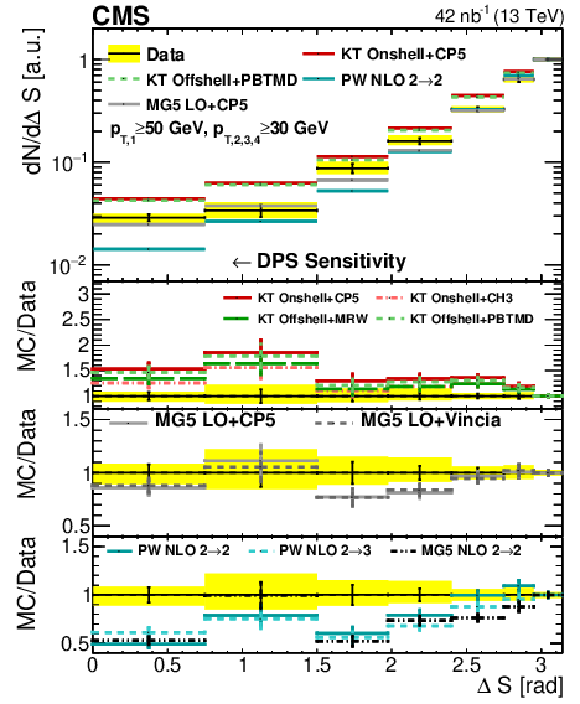
Figure 9:
Comparison of the ${\Delta p_{\text {T,Soft}}}$ and ${\Delta S}$ distributions from data to different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) implementations in Region I and Region II, respectively. All distributions have been normalized to regions where a reduced DPS sensitivity is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |
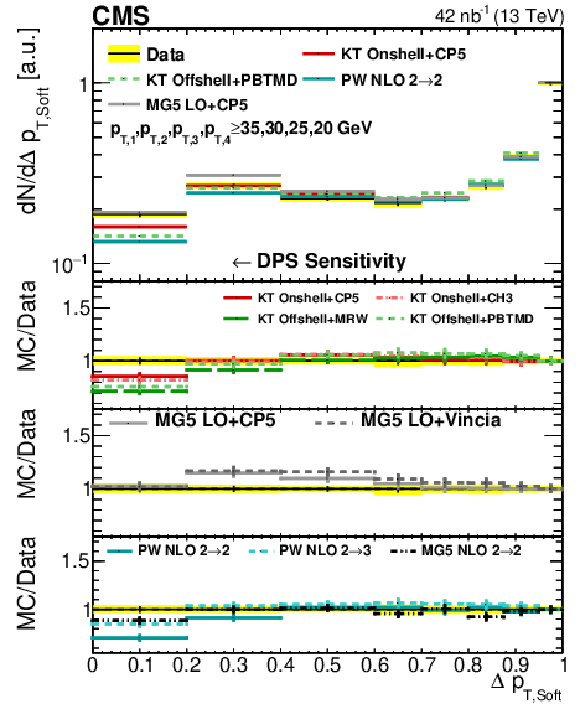
png pdf |
Figure 9-a:
Comparison of the ${\Delta p_{\text {T,Soft}}}$ distribution from data to different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) implementations in Region I. All distributions have been normalized to regions where a reduced DPS sensitivity is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |
png pdf |
Figure 9-b:
Comparison of the ${\Delta S}$ distribution from data to different KaTie (KT), MadGraph 5_aMC@NLO (MG5), and POWHEG (PW) implementations in Region II. All distributions have been normalized to regions where a reduced DPS sensitivity is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
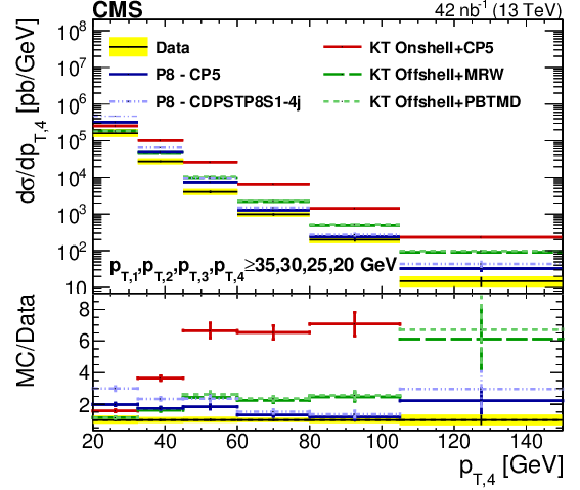
Figure 10:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectra of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the leading (upper left), subleading (upper right), third leading (lower left), and fourth leading (lower right) jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
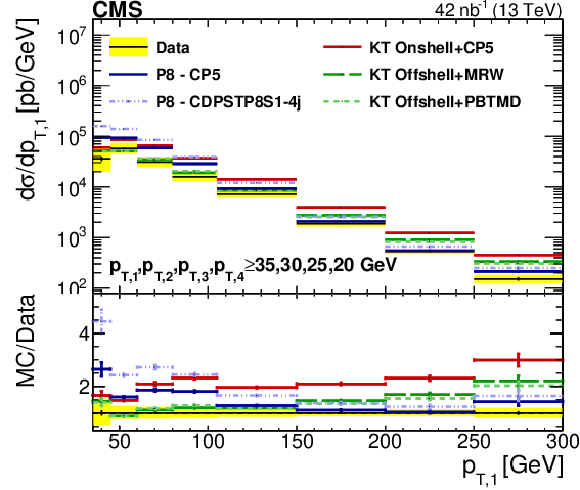
png pdf |
Figure 10-a:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectrum of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 10-b:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectrum of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the subleading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 10-c:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectrum of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the third leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
Figure 10-d:
Comparison of the unfolded ${p_{\mathrm {T}}}$ spectrum of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the fourth leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
png pdf |
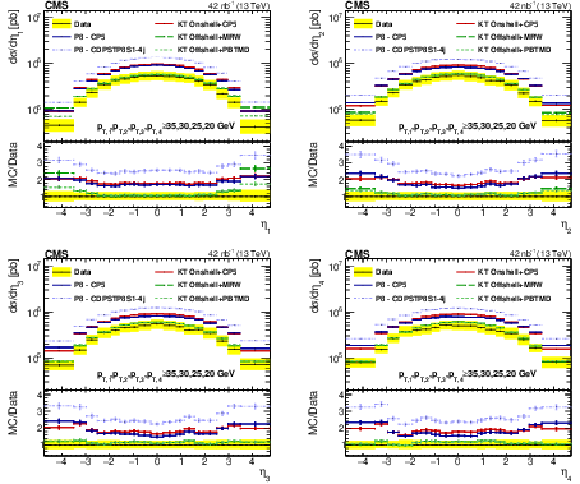
Figure 11:
Comparison of the unfolded $\eta $ spectra of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the leading (upper left), subleading (upper right), third leading (lower left), and fourth leading (lower right) jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 11-a:
Comparison of the unfolded $\eta $ spectra of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |
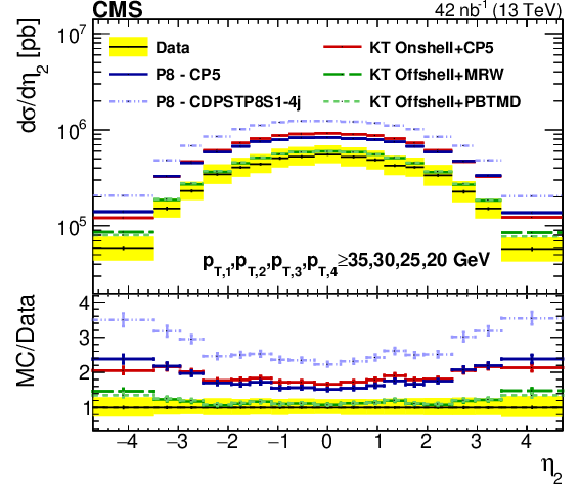
png pdf |
Figure 11-b:
Comparison of the unfolded $\eta $ spectra of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the subleading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 11-c:
Comparison of the unfolded $\eta $ spectra of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the third leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 11-d:
Comparison of the unfolded $\eta $ spectra of data with different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models, for the fourth leading jet in Region I. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty in the measurement. |

png pdf |
Figure 12:
Comparison of the distributions in DPS-sensitive observables obtained from data to different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models. All distributions have been determined in Region I, except for the ${\Delta S}$ distribution which has been measured in Region II. All distributions have been normalized to the region where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
Figure 12-a:
Comparison of the distribution in a DPS-sensitive observable obtained from data to different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models. The distributions have been determined in Region I and have been normalized to the region where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |
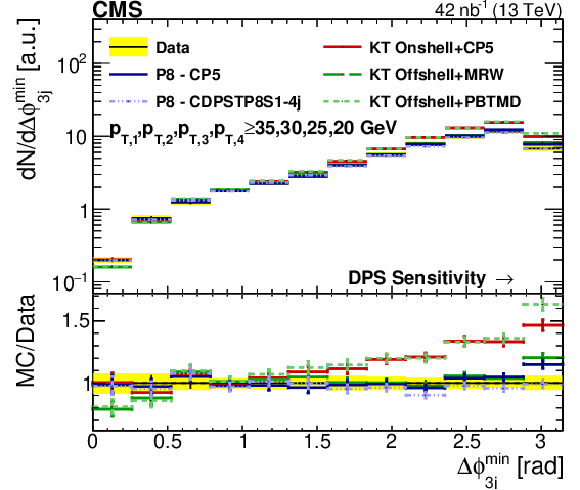
png pdf |
Figure 12-b:
Comparison of the distribution in a DPS-sensitive observable obtained from data to different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models. The distributions have been determined in Region I and have been normalized to the region where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |
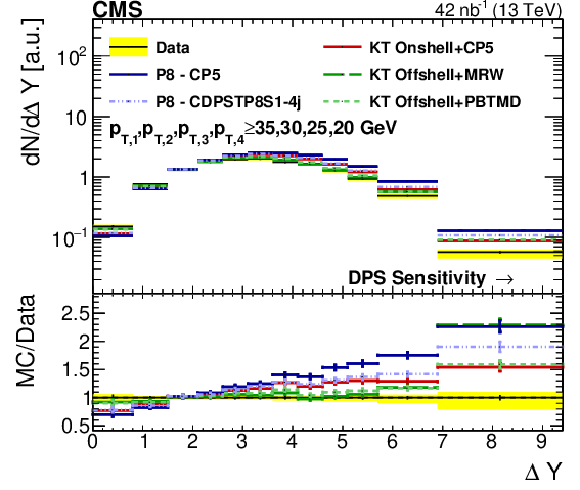
png pdf |
Figure 12-c:
Comparison of the distribution in a DPS-sensitive observable obtained from data to different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models. The distributions have been determined in Region I and have been normalized to the region where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
Figure 12-d:
Comparison of the distribution in a DPS-sensitive observable obtained from data to different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models. The distributions have been determined in Region I and have been normalized to the region where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
Figure 12-e:
Comparison of the distribution in a DPS-sensitive observable obtained from data to different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models. The distributions have been determined in Region I and have been normalized to the region where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |
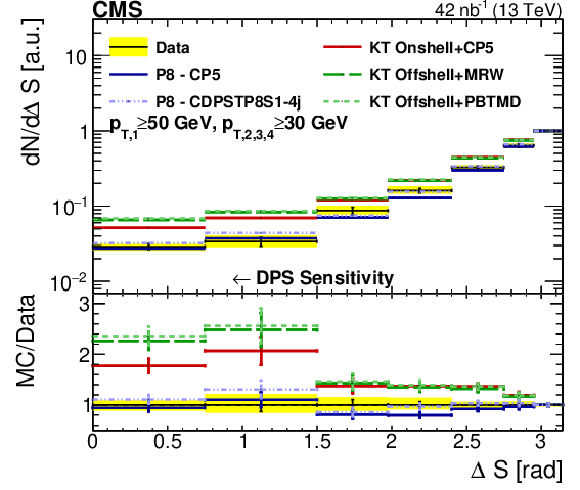
png pdf |
Figure 12-f:
Comparison of the distribution in a DPS-sensitive observable obtained from data to different SPS+DPS KaTie (KT) and PYTHIA-8 (P8) models. The distributions have been determined in Region II and have been normalized to the region where a reduced DPS contribution is expected. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the measurement. |

png pdf |
Figure 13:
The ${\Delta S}$ distribution obtained from the mixed data sample compared to predictions from the pure DPS sample in PYTHIA-8 (P8) and KaTie (KT). The distributions are normalized to unity. The error bars represent the statistical uncertainty, and the yellow band indicates the total (statistical+systematic) uncertainty on the data. |

png pdf |
Figure 14:
The results of the template fit for the POWHEG (PW) NLO 2 $\to$ 2 model without the hard MPI removed. The yellow bands represent the total uncertainty of the distribution. The ratio of the scaled MC model and of the total fitted result over the data are shown in the bottom plot. Since the ${\Delta S}$ distribution obtained from the mixed data sample carries a statistical and systematic uncertainty, so does the total fitted sample. The total uncertainty in the ratio is shown on the plot. |

png pdf |
Figure 15:
Comparison of the values for ${\sigma _\text {eff}}$ extracted from data using different SPS models where events that have generated one or more hard MPI partons with $ {p_{\mathrm {T}}} ^\text {parton} \geq $ 20 GeV, have been removed. The results from four-jet measurements performed at lower center-of-mass energies [20,6,24,51] are shown alongside the newly extracted values. The error bars in each of the values of ${\sigma _\text {eff}}$ represent the total (statistical+systematic) uncertainties. |
| Tables | |
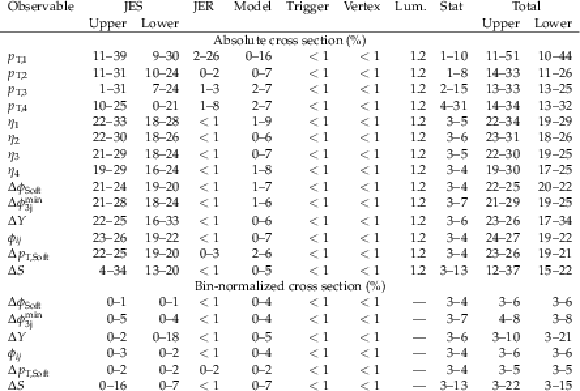
png pdf |
Table 1:
Systematic uncertainties, along with the statistical and the total uncertainties for the ${p_{\mathrm {T}}}$ spectra, the $\eta $ spectra, and the DPS sensitive observables, in percent. The JES uncertainty leads to asymmetric uncertainties (an upper and a lower error), while all other systematic uncertainties, as well as the statistical uncertainty, are symmetric. |

png pdf |
Table 2:
Systematic uncertainties, along with the statistical and the total uncertainties for the cross sections of the two phase space regions, along with the observables needed for the extraction of $ {\sigma _\mathrm {A,B}^\mathrm {DPS}} $, in percent. The JES uncertainty leads to asymmetric uncertainties (an upper and a lower error): all other systematic uncertainties, as well as the statistical uncertainty, are symmetric. An additional uncertainty in ${\epsilon _\mathrm {4j}}$ because of possible differences between generator- and detector-level events, is estimated to be 2%. |

png pdf |
Table 3:
Cross sections obtained from data and from the PYTHIA-8, HERWIG++, and HERWIG-7 models in Region I and Region II of the phase space, where ME stands for matrix element. |

png pdf |
Table 4:
Cross sections obtained from data and from KaTie, MadGraph 5_aMC@NLO, and POWHEG in region Region I and Region II of the phase space, where ME stands for matrix element. |

png pdf |
Table 5:
Cross sections obtained from data and from models with an explicit DPS contribution in Region I and Region II of the phase space, where ME stands for matrix element. |

png pdf |
Table 6:
The values of the DPS fraction $ {f_\mathrm {DPS}} $ extracted from data using different SPS models, along with their statistical and systematic uncertainties. The results are shown for the model where the full tune is used, and for the same models where the hard MPI have been removed. The last column shows the net difference between the two first columns, and is interpreted as the fraction of DPS inherent to the tune. |

png pdf |
Table 7:
The values of the DPS cross section $ {\sigma _\mathrm {A,B}^\mathrm {DPS}} $ extracted from data using different SPS models, along with their statistical and systematic uncertainties. The results are shown for the model where the full tune is used, and for the same models where the hard MPI have been removed The last column shows the net difference between the two first columns and is interpreted as the amount of DPS inherent to the tune. |
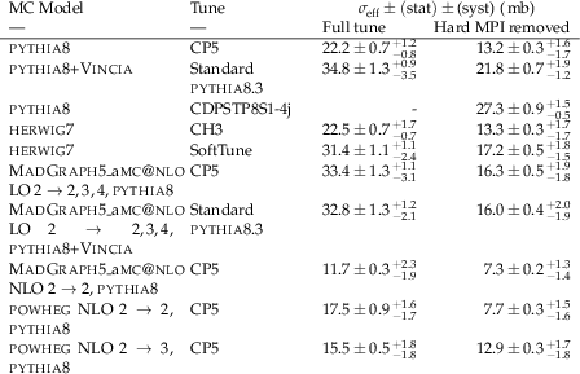
png pdf |
Table 8:
The values of the effective cross section $ {\sigma _\text {eff}} $ extracted from data using different SPS models, along with their statistical and systematic uncertainties. The results are shown for the model where the full tune is used, and for the same models where the hard MPI have been removed |
| Summary |
|
A study of the inclusive production of four-jet events at low transverse momentum has been presented based on data from proton-proton collisions collected with the CMS detector at a center-of-mass energy of 13 TeV. Various observables sensitive to double-parton scattering (DPS) are studied and values for its effective cross section have been extracted. Models based on leading order (LO) 2 $\to$ 2 matrix elements significantly overestimate the absolute four-jet cross section in the phase space domains studied in this paper. This excess is related to an abundance of low-${p_{\mathrm{T}}}$ and forward jets. The predictions of the absolute cross section generally improve when next-to-leading order (NLO) and/or higher-multiplicity matrix elements are used. The azimuthal angle between the jets with the largest separation in $\eta$, ${\phi_{ij}}$, has a strong discriminating power for different parton-shower approaches and the data favor the angular-ordered and dipole-antenna parton-shower models over those with a ${p_{\mathrm{T}}}$-ordered parton shower. The yield of jet pairs with large rapidity separation ${\Delta Y}$ is, however, overestimated by all models, although models based on NLO and/or higher-multiplicity matrix elements are closer to the data. The distribution of the minimal combined azimuthal angular range of three jets, ${\Delta \phi_\mathrm{3j}^\text{min}} $, also exhibits sensitivity to the parton-shower implementation, with data favoring ${p_{\mathrm{T}}}$-ordered parton showers with the LO 2 $\to$ 2 models for this observable. In the case of models based on NLO and/or higher-multiplicity matrix elements the comparisons are less conclusive. Other observables, such as the azimuthal angle between the two softest jets, ${\Delta \phi_\text{Soft}}$, and their transverse momentum balance, ${\Delta p_{\text{T,Soft}}}$, indicate the need for a DPS contribution in the models to various degrees, as confirmed by the extracted values of ${\sigma_\text{eff}}$. The distribution of the azimuthal angle between the hard and soft jet pairs, ${\Delta S}$, is the least sensitive to the details of the parton-shower modeling, and it is used for the extraction of the effective cross section, ${\sigma_\text{eff}}$. A dependence is observed of the extracted values of ${\sigma_\text{eff}}$ on the model used to describe the SPS contribution. Models based on NLO 2 $\to$ 2 matrix elements yield the smallest ($\sim$7 mb) values of ${\sigma_\text{eff}}$ and need the largest DPS contribution. However, models using a 2 $\to$ 2 matrix element along with older underlying event descriptions and older PDFs, tend to need the smallest DPS contribution. The sensitivity to the underlying event description, parton showers, and the PDFs is observed to be small when including higher-order matrix elements, since both models using the 2 $\to$ 2, 3, 4 matrix elements show agreement with each other. These results demonstrate the need for further development of models to accurately describe final states with multiple jets in phase space regions with large potential DPS contributions. |
| References | ||||
| 1 | CMS Collaboration | Measurement of the ratio of inclusive jet cross sections using the anti-$ {k_{\mathrm{T}}} $ algorithm with radius parameters R = 0.5 and 0.7 in pp collisions at $ \sqrt{s}= $ 7 TeV | PRD 90 (2014) 072006 | CMS-SMP-13-002 1406.0324 |
| 2 | CMS Collaboration | Measurement and QCD analysis of double-differential inclusive jet cross sections in pp collisions at $ \sqrt{s}= $ 8 TeV and cross section ratios to 2.76 and 7 TeV | JHEP 03 (2017) 156 | CMS-SMP-14-001 1609.05331 |
| 3 | CMS Collaboration | Measurement of the double-differential inclusive jet cross section in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | EPJC. 76 (2016) 451 | CMS-SMP-15-007 1605.04436 |
| 4 | M. Diehl, D. Ostermeier, and A. Schafer | Elements of a theory for multiparton interactions in QCD | JHEP 03 (2012) 089 | 1111.0910 |
| 5 | CDF Collaboration | Measurement of double parton scattering in $ \mathrm{\overline{p}p} $ collisions at $\sqrt{s} = $ 1.8 TeV | PRL 79 (1997) 584 | |
| 6 | CDF Collaboration | Double parton scattering in $ \mathrm{\overline{p}p} $ collisions at $ \sqrt{s}= $ 1.8 TeV | PRD 56 (1997) 3811 | |
| 7 | D0 Collaboration | Double parton interactions in $ {\gamma}+3 $ jet events in $ \mathrm{p\overline{p}} $ collisions at $ \sqrt{s}=1.96\text{}\text{}\mathrm{TeV} $ | PRD 81 (2010) 052012 | 0912.5104 |
| 8 | D0 Collaboration | Double parton interactions in $ \gamma+3 $ jet and $ \gamma+\mathrm{b/c jet}+2 $ jet events in $ \mathrm{p \bar p} $ collisions at $ \sqrt s= $ 1.96 TeV | PRD 89 (2014) 072006 | 1402.1550 |
| 9 | D0 Collaboration | Study of double parton interactions in diphoton + dijet events in $ \mathrm{p\bar{p}} $ collisions at $ \sqrt{s} = $ 1.96 TeV | PRD 93 (2016) 052008 | 1512.05291 |
| 10 | ATLAS Collaboration | Measurement of hard double-parton interactions in $ \mathrm{W}(\to \mathrm{l}\nu) $+ 2 jet events at $ \sqrt{s} = $ 7 TeV with the ATLAS detector | New J. Phys. 15 (2013) 033038 | 1301.6872 |
| 11 | CMS Collaboration | Study of double parton scattering using W + 2-jet events in proton-proton collisions at $ \sqrt{s} = $ 7 TeV | JHEP 03 (2014) 032 | CMS-FSQ-12-028 1312.5729 |
| 12 | CMS Collaboration | Constraints on the double-parton scattering cross section from same-sign W boson pair production in proton-proton collisions at $ \sqrt{s}= $ 8 TeV | JHEP 02 (2018) 032 | CMS-FSQ-16-005 1712.02280 |
| 13 | CMS Collaboration | Evidence for WW production from double-parton interactions in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | EPJC 80 (2020) 41 | CMS-SMP-18-015 1909.06265 |
| 14 | CMS Collaboration | Measurements of Z bosons plus jets using variables sensitive to double parton scattering in pp collisions at 13 TeV | Submitted to JHEP | CMS-SMP-20-009 2105.14511 |
| 15 | LHCb Collaboration | Observation of double charm production involving open charm in pp collisions at $ \sqrt{s} = $ 7 TeV | JHEP 06 (2012) 141 | 1205.0975 |
| 16 | LHCb Collaboration | Observation of associated production of a Z boson with a D meson in the forward region | JHEP 04 (2014) 091 | 1401.3245 |
| 17 | D0 Collaboration | Observation and studies of double $ \mathrm{J}/ {\psi} $ production at the Tevatron | PRD 90 (2014) 111101 | |
| 18 | LHCb Collaboration | Production of associated Y and open charm hadrons in pp collisions at $ \sqrt{s}= $ 7 and 8 TeV via double parton scattering | JHEP 07 (2016) 052 | 1510.05949 |
| 19 | LHCb Collaboration | Measurement of the J/$ \psi $ pair production cross-section in pp collisions at $ \sqrt{s}= $ 13 TeV | JHEP 06 (2017) 047 | 1612.07451 |
| 20 | UA2 Collaboration | A study of multi-jet events at the CERN pp collider and a search for double parton scattering | PLB 268 (1991) 145 | |
| 21 | CDF Collaboration | Study of four-jet events and evidence for double parton interactions in $ \mathrm{p\bar{p}} $ collisions at $ \sqrt{s} = $ 1.8 TeV | PRD 47 (1993) 4857 | |
| 22 | ATLAS Collaboration | Measurement of four-jet differential cross sections in $ \sqrt{s} = $ 8 TeV proton-proton collisions using the ATLAS detector | JHEP 12 (2015) 105 | 1509.07335 |
| 23 | I. Sadeh | Double parton scattering in four-jet events in pp collisions at 7 TeV with the ATLAS experiment at the LHC | PhD thesis, Tel Aviv U. | 1308.0587 |
| 24 | ATLAS Collaboration | Study of hard double-parton scattering in four-jet events in pp collisions at $ \sqrt{s}= $ 7 TeV with the ATLAS experiment | JHEP 11 (2016) 110 | 1608.01857 |
| 25 | CMS Collaboration | Measurement of four-jet production in proton-proton collisions at $ \sqrt{s}= $ 7 TeV | PRD 89 (2014) 092010 | CMS-FSQ-12-013 1312.6440 |
| 26 | CMS Collaboration | Studies of inclusive four-jet production with two $ \mathrm{b} $-tagged jets in proton-proton collisions at 7 TeV | PRD 94 (2016) 112005 | CMS-FSQ-13-010 1609.03489 |
| 27 | CMS Collaboration | HEPData record for this analysis | HEPData record for this analysis | |
| 28 | S. Domdey, H.-J. Pirner, and U. A. Wiedemann | Testing the scale dependence of the scale factor $ \sigma_\mathrm{eff} $ in double dijet production at the LHC | EPJC 65 (2010) 153 | 0906.4335 |
| 29 | E. L. Berger, C. B. Jackson, and G. Shaughnessy | Characteristics and estimates of double parton scattering at the Large Hadron Collider | PRD 81 (2010) 014014 | 0911.5348 |
| 30 | R. Maciu\la and A. Szczurek | Searching for and exploring double-parton scattering effects in four-jet production at the LHC | PLB 749 (2015) 57 | 1503.08022 |
| 31 | K. Kutak et al. | Four-jet production in single- and double-parton scattering within high-energy factorization | JHEP 04 (2016) 175 | 1602.06814 |
| 32 | K. Kutak | Four-jet production in single- and double-parton scattering within high-energy factorization | PoS ICHEP2016 (2016) 610 | 1701.00410 |
| 33 | K. Kutak et al. | Search for optimal conditions for exploring double-parton scattering in four-jet production: $ {k_{\mathrm{T}}}$-factorization approach | PRD 94 (2016) 014019 | 1605.08240 |
| 34 | CMS Collaboration | Performance of the CMS Level-1 trigger in proton-proton collisions at $ \sqrt{s} = $ 13 TeV | JINST 15 (2020) P10017 | CMS-TRG-17-001 2006.10165 |
| 35 | CMS Collaboration | The CMS trigger system | JINST 12 (2017) P01020 | CMS-TRG-12-001 1609.02366 |
| 36 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017) P10003 | CMS-PRF-14-001 1706.04965 |
| 37 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-$ {k_{\mathrm{T}}} $ jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 38 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 39 | CMS Collaboration | Jet energy scale and resolution in the CMS experiment in pp collisions at 8 TeV | JINST 12 (2017) P02014 | CMS-JME-13-004 1607.03663 |
| 40 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 41 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | CPC 191 (2015) 159 | 1410.3012 |
| 42 | M. Bahr et al. | Herwig++ physics and manual | EPJC 58 (2008) 639 | 0803.0883 |
| 43 | J. Bellm et al. | Herwig 7.0 / Herwig++ 3.0 release note | EPJC 76 (2015) 196 | 1512.0117 |
| 44 | V. N. Gribov and L. N. Lipatov | Deep inelastic e p scattering in perturbation theory | Sov. J. NP 15 (1972) 438 | |
| 45 | Y. L. Dokshitzer | Calculation of the structure functions for deep inelastic scattering and e+ e- annihilation by perturbation theory in quantum chromodynamics. | Sov. Phys. JETP 46 (1977) 641 | |
| 46 | G. Altarelli and G. Parisi | Asymptotic freedom in parton language | Nuclear Physics B 126 (1977) 298 | |
| 47 | B. Andersson, G. Gustafson, G. Ingelman, and T. Sjostrand | Parton fragmentation and string dynamics | Phys. Rep. 97 (1983) 31 | |
| 48 | D. Amati and G. Veneziano | Preconfinement as a property of perturbative QCD | PLB 83 (1979) 87 | |
| 49 | GEANT4 Collaboration | GEANT4--a simulation toolkit | NIMA 506 (2003) 250 | |
| 50 | P. Skands, S. Carrazza, and J. Rojo | Tuning PYTHIA 8.1: the Monash 2013 tune | EPJC 74 (2014) 3024 | 1404.5630 |
| 51 | CMS Collaboration | Event generator tunes obtained from underlying event and multiparton scattering measurements | EPJC 76 (2016) 155 | CMS-GEN-14-001 1512.00815 |
| 52 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020) 4 | CMS-GEN-17-001 1903.12179 |
| 53 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017) 663 | 1706.00428 |
| 54 | R. Corke and T. Sjostrand | Interleaved parton showers and tuning prospects | JHEP 03 (2011) 032 | 1011.1759 |
| 55 | J. Pumplin et al. | New generation of parton distributions with uncertainties from global QCD analysis | JHEP 07 (2002) 012 | hep-ph/0201195 |
| 56 | N. Fischer, S. Prestel, M. Ritzmann, and P. Skands | VINCIA for hadron colliders | EPJC 76 (2016) 589 | 1605.06142 |
| 57 | L. A. Harland-Lang, A. D. Martin, P. Motylinski, and R. S. Thorne | Parton distributions in the LHC era: MMHT 2014 PDFs | EPJC 75 (2015) 204 | 1412.3989 |
| 58 | CMS Collaboration | Development and validation of HERWIG 7 tunes from CMS underlying-event measurements | EPJC 81 (2021) 312 | CMS-GEN-19-001 2011.03422 |
| 59 | H. Jung et al. | The CCFM Monte Carlo generator CASCADE version 2.2.03 | EPJC 70 (2010) 1237 | 1008.0152 |
| 60 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 61 | J. Alwall et al. | Comparative study of various algorithms for the merging of parton showers and matrix elements in hadronic collisions | EPJC 53 (2008) 473 | 0706.2569 |
| 62 | P. Nason | A new method for combining NLO QCD with shower Monte Carlo algorithms | JHEP 11 (2004) 040 | hep-ph/0409146 |
| 63 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 64 | S. Alioli, P. Nason, C. Oleari, and E. Re | A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX | JHEP 06 (2010) 043 | 1002.2581 |
| 65 | S. Alioli et al. | Jet pair production in POWHEG | JHEP 04 (2011) 081 | 1012.3380 |
| 66 | A. Kardos, P. Nason, and C. Oleari | Three-jet production in POWHEG | JHEP 04 (2014) 043 | 1402.4001 |
| 67 | A. van Hameren | KaTie : For parton-level event generation with $ {k_{\mathrm{T}}}-dependent $ initial states | CPC 224 (2018) 371 | 1611.00680 |
| 68 | S. Catani and F. Hautmann | High-energy factorization and small-x deep inelastic scattering beyond leading order | NPB 427 (1994) 475 | hep-ph/9405388 |
| 69 | M. Deak, F. Hautmann, H. Jung, and K. Kutak | Forward jet production at the Large Hadron Collider | JHEP 09 (2009) 121 | 0908.0538 |
| 70 | S. Sapeta | QCD and jets at hadron colliders | Prog. Part. NP 89 (2016) 1 | 1511.09336 |
| 71 | M. Bury et al. | Calculations with off-shell matrix elements, TMD parton densities and TMD parton showers | EPJC 78 (2018) 137 | 1712.05932 |
| 72 | A. Bermudez Martinez et al. | Collinear and TMD parton densities from fits to precision DIS measurements in the parton branching method | PRD 99 (2019) 074008 | 1804.11152 |
| 73 | S. Schmitt | TUnfold, an algorithm for correcting migration effects in high energy physics | JINST 7 (2012) T10003 | 1205.6201 |
| 74 | S. Schmitt | Data unfolding methods in high energy physics | EPJ Web Conf. 137 (2017) 11008 | 1611.01927 |
| 75 | A. N. Tikhonov | Solution of incorrectly formulated problems and the regularization method | Soviet Math. Dokl. 4 (1963) 1035 | |
| 76 | R. Brun and F. Rademakers | ROOT- An object oriented data analysis framework | NIMA 389 (1997) 81 | |
| 77 | CMS Collaboration | Precision luminosity measurement in proton-proton collisions at $ \sqrt{s} = $ 13 TeV in 2015 and 2016 at CMS | EPJC 81 (2021) 800 | CMS-LUM-17-003 2104.01927 |
| 78 | M. H. Seymour and A. Siodmok | Extracting $ \sigma_\mathrm{effective} $ from the LHCb double-charm measurement | 1308.6749 | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|