CMS-FSQ-13-006

CMS-FSQ-13-006 ; CERN-PH-EP-2015-210
Measurement of the inelastic cross section in proton-lead collisions at $\sqrt{s_{_\mathrm{NN}}}=$ 5.02 TeV
CMS Collaboration
13 September 2015
Phys. Lett. B 759 (2016) 641
Abstract: The inelastic hadronic cross section in proton-lead collisions at a centre-of-mass energy per nucleon pair of 5.02 TeV is measured with the CMS detector at the LHC. The data sample, corresponding to an integrated luminosity of $ \mathcal{L} =$ 12.6 $\pm$ 0.4 nb$^{-1}$, has been collected with an unbiased trigger for inclusive particle production. The cross section is obtained from the measured number of proton-lead collisions with hadronic activity produced in the pseudorapidity ranges $ 3 < \eta < 5 $ and/or $-5 < \eta < -3 $, corrected for photon-induced contributions, experimental acceptance, and other instrumental effects. The inelastic cross section is measured to be $\sigma_{\text{inel}}(\text{pPb})= $ 2061 $\pm$ 3 (stat) $\pm$ 34 (syst) $\pm$ 72 (lumi) mb. Various Monte Carlo generators, commonly used in heavy ion and cosmic ray physics, are found to reproduce the data within uncertainties. The value of $\sigma_{\text{inel}}(\text{pPb})$ is compatible with that expected from the proton-proton cross section at 5.02 TeV scaled up within a simple Glauber approach to account for multiple scatterings in the lead nucleus, indicating that further net nuclear corrections are small.
Links: e-print arXiv:1509.03893 [hep-ex] (PDF) ; CDS record ; inSPIRE record ; CADI line (restricted) ;

Figures & Tables	Summary	References	CMS Publications

Figures
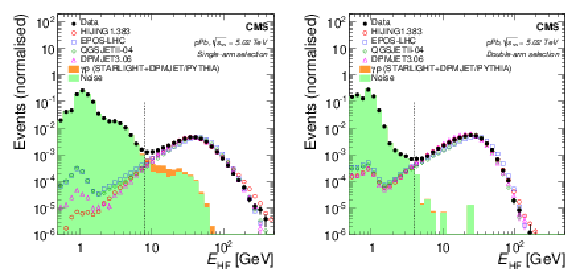
png pdf	Figure 1: Distribution of the energy deposited in the HF calorimeter ($ {E_{\mathrm {HF}}} $) for the single-arm (left) and double-arm (right) event selections. The data sample, shown exemplarily for one period with stable run conditions, comprises 1.31 nb$^{-1}$ recorded with an unbiased trigger. The contribution from noise is obtained from a random trigger normalised to the same number of triggers as that in the collision data. The average number of photon-proton processes simulated with STARLIGHT+DPMJET and STARLIGHT+PYTHIA is treated as background and stacked on top. Four hadronic interaction models (EPOS, DPMJET, HIJING, and QGSJETII) are overlaid and normalised to the number of data events with $ {E_{\mathrm {HF}}} > $ 10 GeV, where the contribution from the background is small. The vertical line represents the threshold energy of 8 GeV (4 GeV) for the single-arm (double-arm) selection used in this analysis.
png pdf	Figure 1-a: Distribution of the energy deposited in the HF calorimeter ($ {E_{\mathrm {HF}}} $) for the single-arm event selection. The data sample, shown exemplarily for one period with stable run conditions, comprises 1.31 nb$^{-1}$ recorded with an unbiased trigger. The contribution from noise is obtained from a random trigger normalised to the same number of triggers as that in the collision data. The average number of photon-proton processes simulated with STARLIGHT+DPMJET and STARLIGHT+PYTHIA is treated as background and stacked on top. Four hadronic interaction models (EPOS, DPMJET, HIJING, and QGSJETII) are overlaid and normalised to the number of data events with $ {E_{\mathrm {HF}}} > $ 10 GeV, where the contribution from the background is small. The vertical line represents the threshold energy of 8 GeV (4 GeV) for the single-arm (double-arm) selection used in this analysis.
png pdf	Figure 1-b: Distribution of the energy deposited in the HF calorimeter ($ {E_{\mathrm {HF}}} $) for the double-arm event selection. The data sample, shown exemplarily for one period with stable run conditions, comprises 1.31 nb$^{-1}$ recorded with an unbiased trigger. The contribution from noise is obtained from a random trigger normalised to the same number of triggers as that in the collision data. The average number of photon-proton processes simulated with STARLIGHT+DPMJET and STARLIGHT+PYTHIA is treated as background and stacked on top. Four hadronic interaction models (EPOS, DPMJET, HIJING, and QGSJETII) are overlaid and normalised to the number of data events with $ {E_{\mathrm {HF}}} > $ 10 GeV, where the contribution from the background is small. The vertical line represents the threshold energy of 8 GeV (4 GeV) for the single-arm (double-arm) selection used in this analysis.
png pdf	Figure 2: Acceptance versus purity of the two event selections, as derived from the EPOS and QGSJETII generators. The symbols indicate different values of the ${E_{\mathrm {HF}}}$ thresholds. The chosen thresholds are marked with squares.
png pdf	Figure 3: Inelastic hadronic cross sections for collisions as a function of the centre-of-mass energy. The measurement described here (circle, with error bars obtained from the quadratic sum of all uncertainties) is compared to lower energy data (squares and triangles) [39,2,40] and to different model predictions (curves).

Tables
png pdf	Table 1: Central values and uncertainties for the two event selections for noise cross section contribution ($ {N_{\text {noise}}} / {\mathcal {L}} $) and the fraction of noise events ($f_{\text {noise}}$) as derived from data. Additionally, the quantities acceptance ($\epsilon _{\text {acc}}$), electromagnetic cross section contribution ($ {N_{\gamma \mathrm{ p } }} / {\mathcal {L}} $), and hadron-level correction factor ($ {c_{\text {vis}}} $) as derived from simulations are listed.
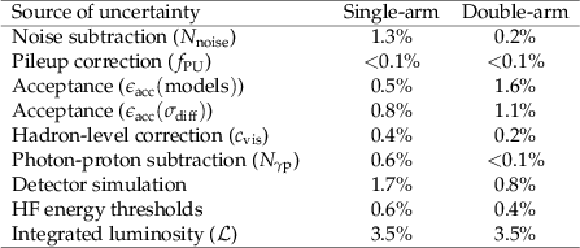
png pdf	Table 2: List of the systematic uncertainties, propagated into the final cross sections, for the two event selections.
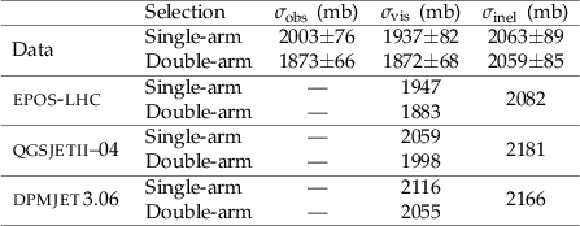
png pdf	Table 3: Summary of cross sections obtained from the two different event selections. The acceptance definition for ${\sigma _{\text {vis}}}$ is based on the production of stable particles within $ 3 < {\| \eta \| } < 5 $ with momentum $ p_{\rm HF} > $ 21.3 GeV/$c$ (11.3 GeV/$c$) for the single-arm (double-arm) event selections.

Summary

The measured cross sections for the single-arm and double-arm event selections are listed in Table 3, compared to the predictions of the hadronic interaction models DPMJET, EPOS, and QGSJETII. Due to the different acceptance, the extrapolations from the hadron-level to the inelastic cross section are of different magnitude, but the models reproduce well the approximately 65 mb difference between the two selections. The values of the inelastic cross sections obtained from the single-arm and double-arm methods agree well within the uncertainties.

The final $\sigma_{\text{inel}}$ value is obtained by taking the weighted average of the measured values in the two event selections. The statistical uncertainties and the uncertainty on the luminosity are correlated between the selections. The degree of correlation among the remaining systematic uncertainties is much smaller and they are taken as uncorrelated. This yields a final result for the inelastic hadronic cross section of

$\sigma_{\text{inel}}(\mathrm{pPb}) =$ 2061 $\pm$ 3 (stat) $\pm$ 34 (syst) $\pm$ 72 (lumi) mb.

This result is shown in Fig. 3 compared to other measurements at different centre-of-mass energies and to various theoretical predictions. A pPb cross section was also measured by the ALICE Collaboration, amounting to 2090?2120mb with an uncertainty of 70mb [41]. A direct comparison of this observed cross section to the one measured in the present analysis is not possible due to the unknown to us ALICE detector acceptance and possible contamination from noise and photon-proton interactions.

The inelastic cross section measured by the CMS experiment is compared to the Glauber-model prediction (solid curve in Fig. 3) obtained using a pp inelastic cross section at $\sqrt{s} = $ 5.02 TeV of 70.0 $\pm$ 1.5 mb, derived from the COMPETE parametrisation [42] including the measurement of the TOTEM Collaboration at $\sqrt{s} =$ 7 TeV [43] (where the assigned uncertainty is that measured by the latter). The Glauber calculation yields 2130 $\pm$ 40 mb and is compatible with the measurement presented here indicating that effects neglected by the calculation (such as nucleon correlations and screening) are either small or approximately cancel out. The experimental result is also consistent with the prediction of the DIPSY model [44, 45] based on a dipole-model approach including parton saturation and multiple-scattering. Among the Gribov?Regge models, the EPOS prediction is compatible with the measurement within uncertainties, whereas DPMJET and QGSJETII predict a value more than 1 standard deviation above the data, with a larger discrepancy appearing for the svis cross sections (Table 3). The EPOS and QGSJETII models are commonly used for cosmic ray air shower simulations. Thus, at the corresponding cosmic ray proton energies of $E_{\text{cr}} = s/(2m_{\mathrm{p}}) = $ 1016.1 eV, where $m_{\mathrm{p}}$ is the mass of the proton, there are no indications for data-model deviations above 5% in the proton-lead collisions studied here. Note, however, that our measurement deals with an ion much heavier than those involved in proton-air interactions. Corrections to the Glauber model are possibly larger in the latter case [3, 13]. In summary, the measurement of the cross sections in pPb collisions presented here is the first such fully corrected measurement at multi-TeV energies and, thus, provides important constraints on hadronic interaction models commonly used in high-energy heavy ion and cosmic ray physics.

References
1	R. Engel, T. K. Gaisser, P. Lipari, and T. Stanev	Proton proton cross-section at $ \sqrt{s} $ similar to 30~TeV	PRD 58 (1998) 014019	hep-ph/9802384
2	A. S. Carroll et al.	Absorption cross-sections of $ \pi^\pm $, K$ ^\pm $, p and $ \bar{\mathrm{p}} $ on nuclei between 60~GeV/$ c $ and 280~GeV/$ c $	PLB 80 (1979) 319
3	M. Alvioli et al.	Diffraction on nuclei: effects of nucleon correlations	PRC 81 (2010) 025204	0911.1382
4	I. Sarcevic, S. D. Ellis, and P. Carruthers	QCD minijet cross-sections	PRD 40 (1989) 1446
5	R. J. Glauber	Cross-sections in deuterium at high-energies	PR100 (1955) 242
6	R. J. Glauber and G. Matthiae	High-energy scattering of protons by nuclei	Nucl. Phys. B 21 (1970) 135
7	V. N. Gribov	A reggeon diagram technique	Sov. Phys. JETP 26 (1968) 414
8	D. d'Enterria	Hard scattering cross-sections at LHC in the Glauber approach: From pp to pA and AA collisions'', (2003). Originally published in CERN Yellow Report on ''Hard probes in heavy ion collisions at the LHC		nucl-ex/0302016
9	M. L. Miller, K. Reygers, S. J. Sanders, and P. Steinberg	Glauber modeling in high energy nuclear collisions	Ann. Rev. Nucl. Part. Sci. 57 (2007) 205	nucl-ex/0701025
10	D. d'Enterria et al.	Constraints from the first LHC data on hadronic event generators for ultra-high energy cosmic-ray physics	Astropart. Phys. 35 (2011) 98	1101.5596
11	R. Ulrich, R. Engel, and M. Unger	Hadronic multiparticle production at ultra-high energies and extensive air showers	PRD 83 (2011) 054026	1010.4310
12	R. D. Parsons, C. Bleve, S. S. Ostapchenko, and J. Knapp	Systematic uncertainties in air shower measurements from high-energy hadronic interaction models	Astropart. Phys. 34 (2011) 832	1102.4603
13	Pierre Auger Collaboration	Measurement of the proton-air cross-section at $ \sqrt{s}=57 $~TeV with the Pierre Auger Observatory	PRL 109 (2012) 062002	1208.1520
14	L. L. Frankfurt, M. I. Strikman, D. B. Day, and M. Sargsian	Evidence for short range correlations from high Q$ ^2 $ (e, e$ ' $) reactions	PRC 48 (1993) 2451
15	M. L. Good and W. D. Walker	Diffraction dissociation of beam particles	PR120 (1960) 1857
16	SELEX Collaboration	Total cross section measurements with $ \pi^- $, $ \Sigma^- $ and protons on nuclei and nucleons around 600~GeV/$ c $	Nucl. Phys. B 579 (2000) 277	hep-ex/9910052
17	G. Bellettini et al.	Proton-nuclei cross sections at 20~GeV	Nucl. Phys. 79 (1966) 609
18	R. P. V. Murthy et al.	Neutron total cross-sections on nuclei at Fermilab energies	Nucl. Phys. B 92 (1975) 269
19	J. Engler et al.	Neutron-nucleus total cross-sections between 8~GeV/$ c $ and 21~GeV/$ c $	PLB 32 (1970) 716
20	A. Babaev et al.	The neutron total cross section measurements on protons and nuclei in the energy range of 28-54~GeV	PLB 51 (1974) 501
21	C. Ciofi degli Atti et al.	Number of collisions in the Glauber model and beyond	PRC 84 (2011) 025205	1105.1080
22	M. Alvioli et al.	Nucleon momentum distributions, their spin-isospin dependence and short-range correlations	PRC 87 (2013) 034603	1211.0134
23	N. N. Kalmykov and S. S. Ostapchenko	The nucleus-nucleus interaction, nuclear fragmentation, and fluctuations of extensive air showers	Phys. Atom. Nucl. 56 (1993)346
24	V. Guzey and M. Strikman	Proton-nucleus scattering and cross section fluctuations at RHIC and LHC	PLB 633 (2006) 245	hep-ph/0505088
25	K. Werner, F.-M. Liu, and T. Pierog	Parton ladder splitting and the rapidity dependence of transverse momentum spectra in deuteron-gold collisions at RHIC	PRC 74 (2006) 044902	hep-ph/0506232
26	S. Ostapchenko	Total and diffractive cross sections in enhanced Pomeron scheme	PRD 81 (2010) 114028	1003.0196
27	S. Ostapchenko	Monte Carlo treatment of hadronic interactions in enhanced Pomeron scheme: I. QGSJET-II model	PRD 83 (2011) 014018	1010.1869
28	L. Frankfurt, G. A. Miller, and M. Strikman	Evidence for color fluctuations in hadrons from coherent nuclear diffraction	PRL 71 (1993) 2859	hep-ph/9309285
29	D. R. Harrington	Triple pomeron matrix model for dispersive corrections to nucleon nucleus total cross-section	PRC 67 (2003) 064904	nucl-th/0206032
30	CMS Collaboration	The CMS experiment at the CERN LHC	JINST 3 (2008) S08004	CMS-00-001
31	S. van der Meer	Calibration of the effective beam height in the ISR	Technical Report CERN-ISR-PO-68-31. ISR-PO-68-31, CERN
32	CMS Collaboration	Luminosity calibration for the 2013 proton-lead and proton-proton data taking	CDS
33	GEANT4 Collaboration	GEANT4---a simulation toolkit	NIMA 506 (2003) 250
34	F. W. Bopp, J. Ranft, R. Engel, and S. Roesler	Antiparticle to particle production ratios in hadron-hadron and d-Au collisions in the DPMJET-III Monte Carlo	PRC 77 (2008) 014904	hep-ph/0505035
35	X.-N. Wang and M. Gyulassy	HIJING: A Monte Carlo model for multiple jet production in pp, pA and AA collisions	PRD 44 (1991) 3501
36	A. J. Baltz et al.	The physics of ultraperipheral collisions at the LHC	PR 458 (2008) 1	0706.3356
37	O. Djuvsland and J. Nystrand	Single and double photonuclear excitations in Pb+Pb collisions at $ \sqrt{s_{NN}}=2.76 $ TeV at the CERN Large Hadron Collider	PRC 83 (2011) 041901	1011.4908
38	T. Sj\"ostrand, S. Mrenna, and P. Skands	PYTHIA 6.4 physics and manual	JHEP 05 (2006) 026	hep-ph/0603175
39	S. P. Denisov et al.	Absorption cross-sections for pions, kaons, protons and anti-protons on complex nuclei in the 6 to 60~GeV/$ c $ momentum range	Nucl. Phys. B 61 (1973) 62
40	V. V. Avakian et al.	Determining inelastic interaction cross-sections for nucleons and pions incident on carbon and lead nuclei at 0.5~TeV--5~TeV	Bull. Acad. Sci. USSR, Phys. Ser. 50 (1986)4
41	ALICE Collaboration	Measurement of visible cross sections in proton-lead collisions at $ \sqrt{s_{\rm NN}} $ = 5.02 TeV in van der Meer scans with the ALICE detector	JINST 9 (2014) P11003	1405.1849
42	COMPETE Collaboration	Benchmarks for the forward observables at RHIC, the Tevatron Run II and the LHC	PRL 89 (2002) 201801	hep-ph/0206172
43	TOTEM Collaboration	Luminosity-independent measurements of total, elastic and inelastic cross-sections at $ \sqrt{s}=7 $~TeV	Europhys. Lett. 101 (2013) 21004
44	E. Avsar, G. Gustafson, and L. Lonnblad	Energy conservation and saturation in small-x evolution	JHEP 07 (2005) 062	hep-ph/0503181
45	C. Flensburg, G. Gustafson, and L. Lonnblad	Inclusive and exclusive observables from dipoles in high energy collisions	JHEP 08 (2011) 103	1103.4321