

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SUS-16-034 | ||
| Search for new physics in final states with two opposite-sign, same-flavor leptons, jets, and missing transverse momentum in pp collisions at √s= 13 TeV | ||
| CMS Collaboration | ||
| March 2017 | ||
| Abstract: A search is presented for physics beyond the standard model in final states with two opposite-sign, same-flavor leptons, jets, and missing transverse momentum. The data sample corresponds to an integrated luminosity of 35.9 fb−1 of proton-proton collisions at √s= 13 TeV collected with the CMS detector at the LHC in 2016. The analysis uses the invariant mass of the lepton pair, searching for a kinematic edge or a resonant-like excess compatible with the Z boson mass. The search for a kinematic edge targets strong production while the resonance search targets both strongly and electroweakly produced new physics. Both search modes use several event categories, based on observables related to the lepton pair and the hadronic system, in order to increase the sensitivity to new physics. A fit is also employed to search for a possible kinematic edge position in the strong, non-resonant search. The observations in all signal regions are consistent with the expectations from the standard model, and the results are interpreted in the context of simplified models of supersymmetry. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JHEP 03 (2018) 076. The superseded preliminary plots can be found here. |
||
| Figures & Tables | Summary | Additional Figures & Tables | References | CMS Publications |
|---|
|
Additional information on efficiencies needed for reinterpretation of these results are available here.
Additional technical material for CMS speakers can be found here. |
| Figures | |
png pdf |
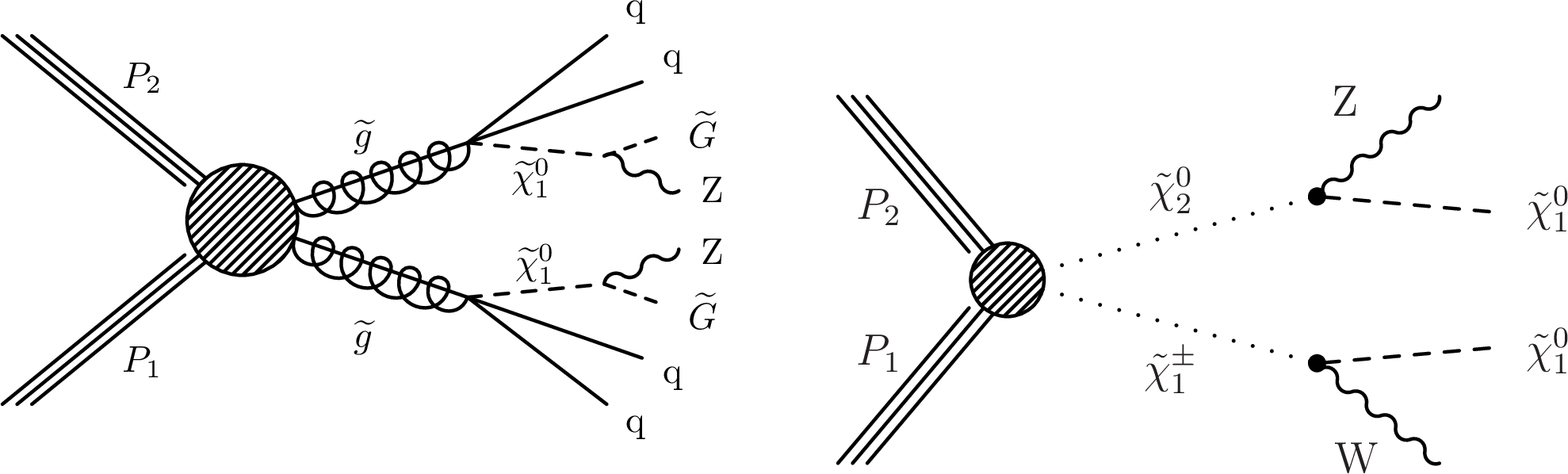
Figure 1:
Diagrams for models with decays containing at least one dilepton pair stemming from a Z decay are shown. The gluino GMSB model targeted by the strong on-Z search is shown in the left. The right diagram shows the chargino-neutralino production model resulting in a final state with a Z boson, a W boson, and two LSPs. In the gluino GMSB model, ˜G denotes the massless gravitino. |

png pdf |
Figure 1-a:
Diagram for the gluino GMSB model targeted by the strong on-Z search, where ˜G denotes the massless gravitino. |
png pdf |
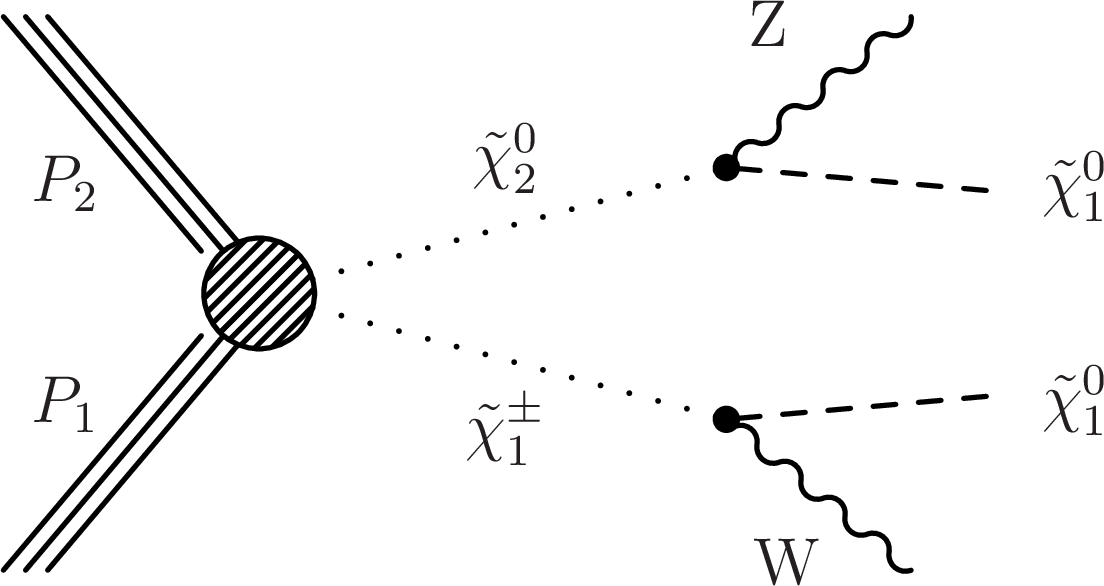
Figure 1-b:
The diagram shows the chargino-neutralino production model resulting in a final state with a Z boson, a W boson, and two LSPs. |

png pdf |
Figure 2:
A diagram showing a model in which bottom squarks are pair produced with subsequent decays that contain at least one dilepton pair. This model features a characteristic edge in the mℓℓ spectrum given approximately by the mass difference of the ˜χ02 and ˜χ01. |
png pdf |
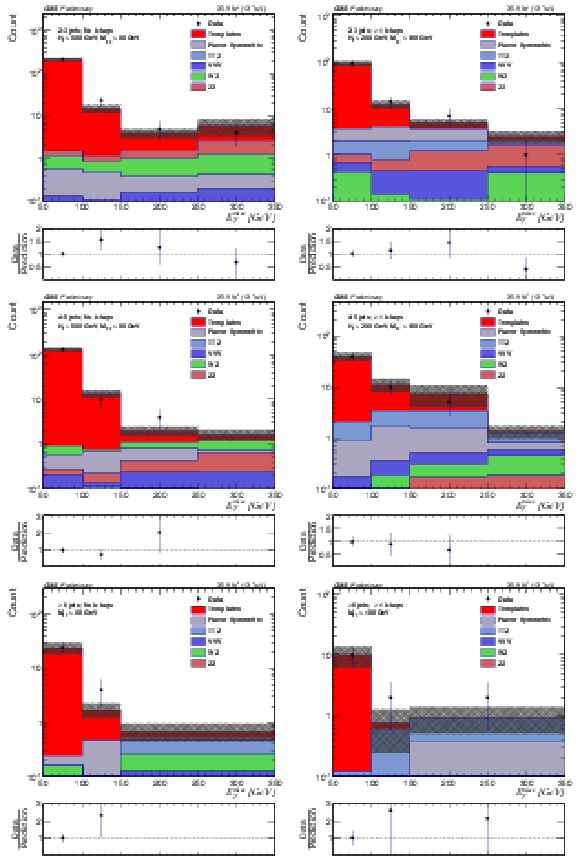
Figure 3:
The EmissT distribution is shown for data compared to the background prediction in the strong on-Z signal regions with Nb-jets= 0 (left) and Nb-jets≥ 1 (right). The rows show SRA (top), SRB (middle), and SRC (bottom). The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |

png pdf |
Figure 3-a:
The EmissT distribution is shown for data compared to the background prediction in the strong on-Z signal regions with Nb-jets= 0 for SRA. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |
png pdf |
Figure 3-b:
The EmissT distribution is shown for data compared to the background prediction in the strong on-Z signal regions with Nb-jets≥ 1 for SRA. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |

png pdf |
Figure 3-c:
The EmissT distribution is shown for data compared to the background prediction in the strong on-Z signal regions with Nb-jets= 0 for SRB. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |
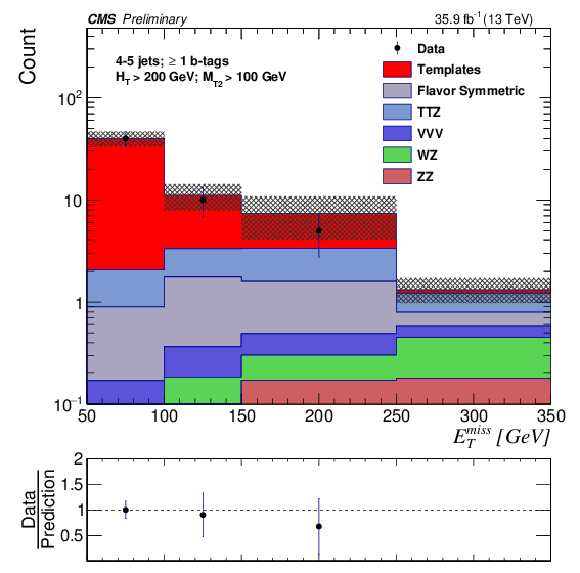
png pdf |
Figure 3-d:
The EmissT distribution is shown for data compared to the background prediction in the strong on-Z signal regions with Nb-jets≥ 1 for SRB. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |
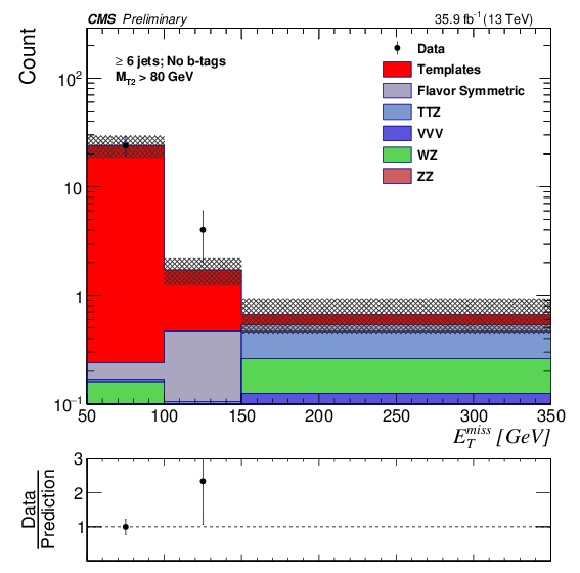
png pdf |
Figure 3-e:
The EmissT distribution is shown for data compared to the background prediction in the strong on-Z signal regions with Nb-jets= 0 for SRC. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |
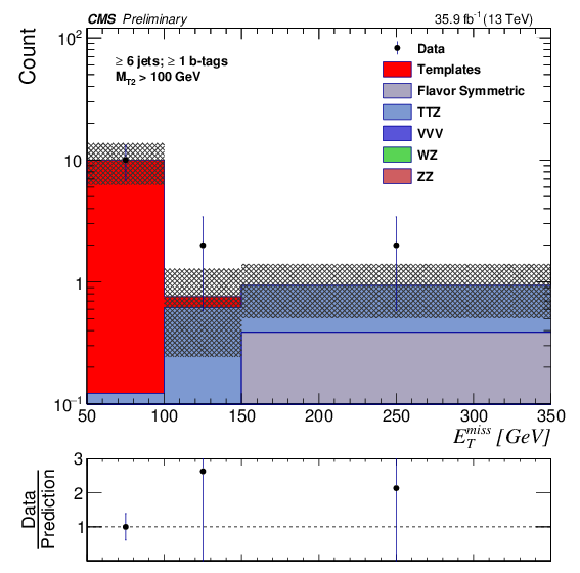
png pdf |
Figure 3-f:
The EmissT distribution is shown for data compared to the background prediction in the strong on-Z signal regions with Nb-jets≥ 1 for SRC. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |

png pdf |
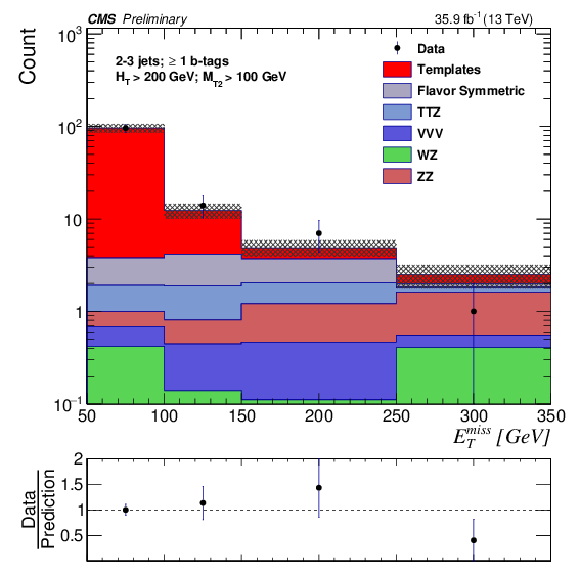
Figure 4:
The EmissT distribution is shown for data compared to the background prediction in the electroweak on-Z WZ/ZZ (left), and HZ (right) signal regions. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |

png pdf |
Figure 4-a:
The EmissT distribution is shown for data compared to the background prediction in the electroweak on-Z WZ/ZZ signal region. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |
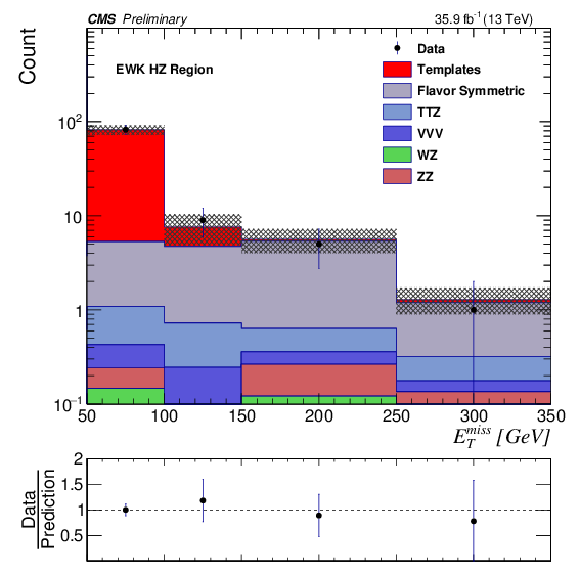
png pdf |
Figure 4-b:
The EmissT distribution is shown for data compared to the background prediction in the electroweak HZ signal region. The EmissT template prediction for each signal region is normalized to the first bin of each distribution, and therefore the prediction agrees with the data by construction. |

png pdf |
Figure 5:
Results of the counting experiment of the edge search. For each signal region, the number of observed events, shown as black data points, is compared to the total background estimate, shown as a blue line with a blue uncertainty band. The non flavor symmetric background component from instrumental EmissT is indicated as a green area while the non flavor symmetric background with neutrinos is shown as a violet area. |
png pdf |
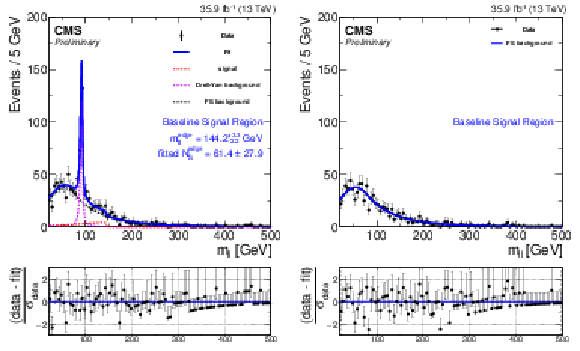
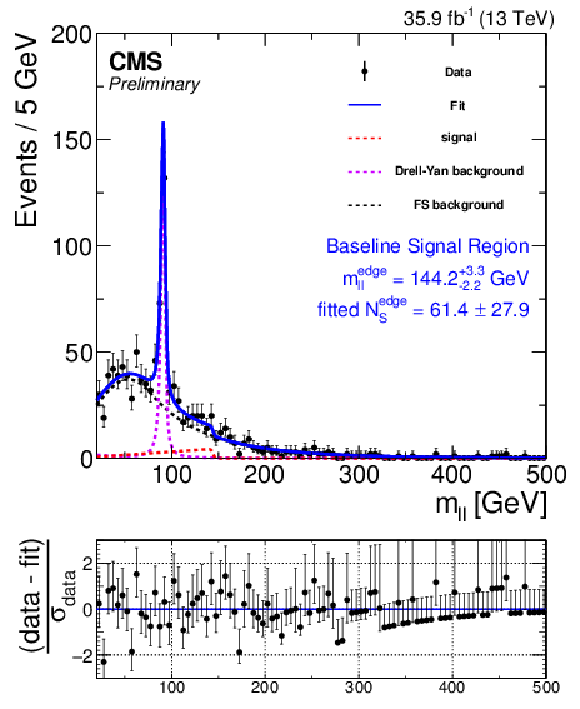
Figure 6:
Fit of the dilepton mass distributions to the signal-plus-background hypothesis in the baseline signal region, projected on the same-flavor (left) and opposite-flavor (right) event samples. The fit shape is shown as a blue, solid line. The individual fit components are indicated by dashed lines. The flavor-symmetric (FS) background is shown with a black dashed line. The Drell-Yan (DY) background is displayed with a purple dashed line. The extracted signal component is displayed with a red dashed line. |
png pdf |
Figure 6-a:
Fit of the dilepton mass distributions to the signal-plus-background hypothesis in the baseline signal region, projected on the same-flavor event sample. The fit shape is shown as a blue, solid line. The individual fit components are indicated by dashed lines. The flavor-symmetric (FS) background is shown with a black dashed line. The Drell-Yan (DY) background is displayed with a purple dashed line. The extracted signal component is displayed with a red dashed line. |
png pdf |
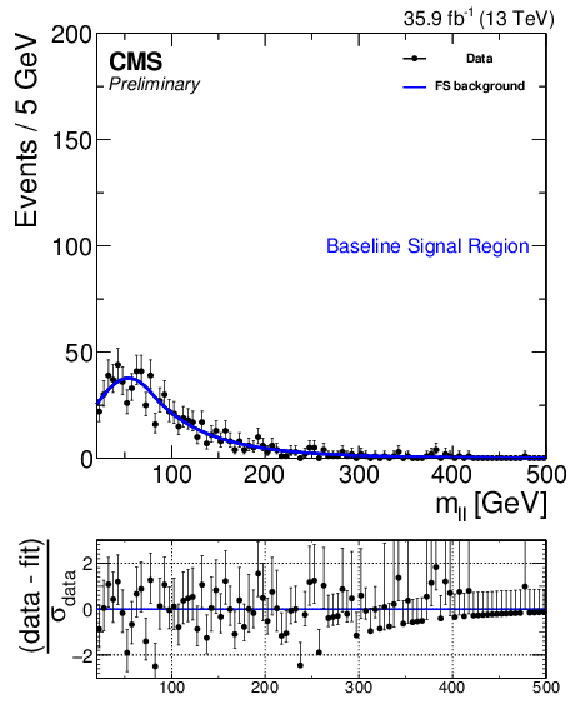
Figure 6-b:
Fit of the dilepton mass distributions to the signal-plus-background hypothesis in the baseline signal region, projected on the opposite-flavor event sample. The fit shape is shown as a blue, solid line. |
png pdf root |
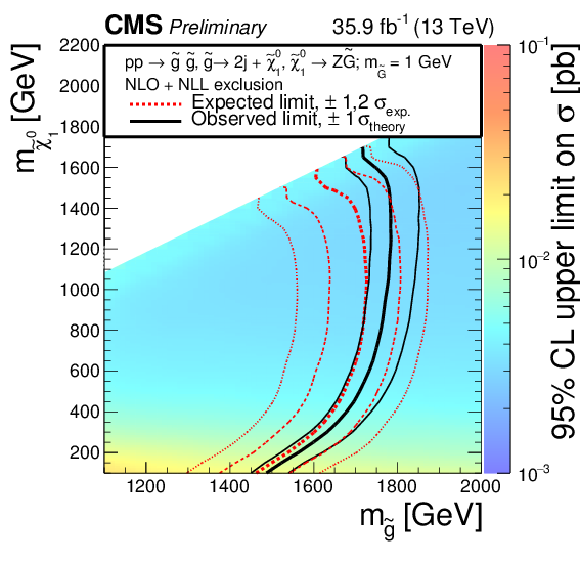
Figure 7:
Cross section upper limits and exclusions contours at 95% CL obtained from the results of the on-Z search interpreted in the gluino GMSB model. The region to the left of the red dotted (black solid) line shows the masses which are excluded by the expected (observed) limit. |
png pdf root |
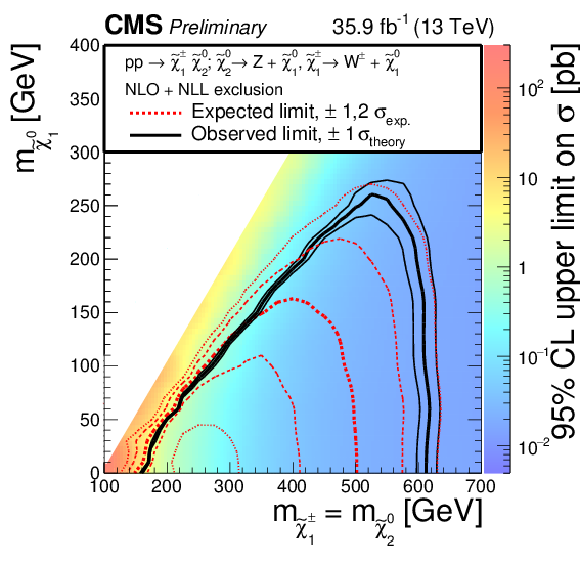
Figure 8:
Cross section upper limits and exclusions contours at 95% CL obtained from the results of the on-Z search interpreted in the electroweak WZ model. The region to the left of the red dotted (black solid) line shows the masses which are excluded by the expected (observed) limit. |

png pdf root |
Figure 9:
Cross section upper limits and exclusion contours at 95% CL obtained from the results of the edge search interpreted in the slepton-edge model. The region to the left of the red dotted (black solid) line shows the masses which are excluded by the expected (observed) limit. |

png pdf root |
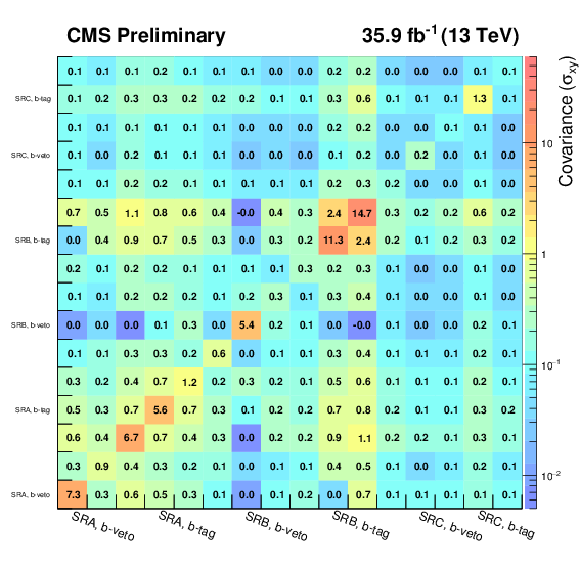
Figure 10:
The covariance (left) and correlation (right) matrices for the background predictions in the on-Z strong signal regions. Within each signal region, the individual EmissT bins are shown in increasing order starting from 100 GeV. |
png pdf root |
Figure 10-a:
The covariance matrix for the background predictions in the on-Z strong signal regions. Within each signal region, the individual EmissT bins are shown in increasing order starting from 100 GeV. |

png pdf root |
Figure 10-b:
The correlation matrix for the background predictions in the on-Z strong signal regions. Within each signal region, the individual EmissT bins are shown in increasing order starting from 100 GeV. |

png pdf root |
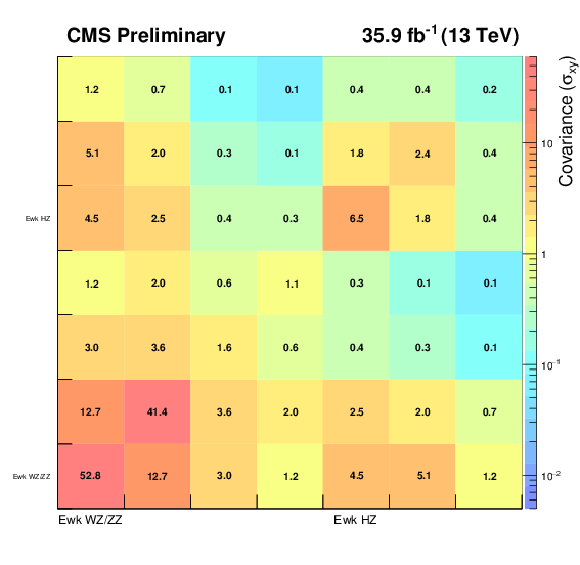
Figure 11:
The covariance (left) and correlation (right) matrices for the background predictions in the on-Z electroweak signal regions. Within each signal region, the individual EmissT bins are shown in increasing order starting from 100 GeV. |
png pdf root |
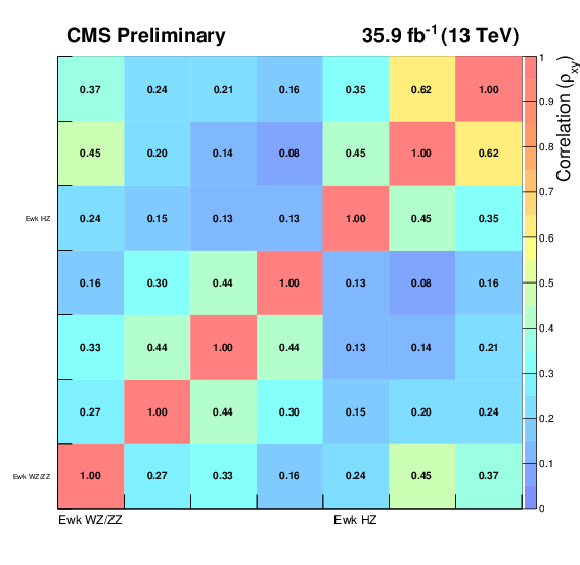
Figure 11-a:
The covariance matrix for the background predictions in the on-Z electroweak signal regions. Within each signal region, the individual EmissT bins are shown in increasing order starting from 100 GeV. |
png pdf root |
Figure 11-b:
The correlation matrix for the background predictions in the on-Z electroweak signal regions. Within each signal region, the individual EmissT bins are shown in increasing order starting from 100 GeV. |
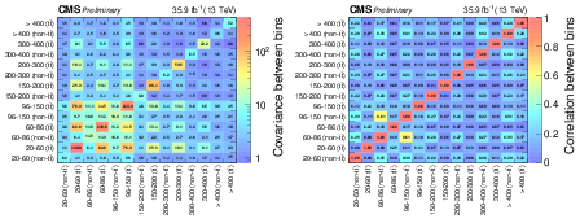
png pdf root |
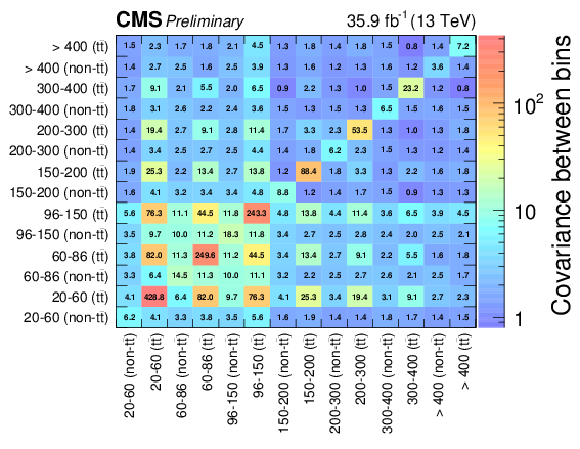
Figure 12:
The covariance (left) and correlation (right) matrices for the background predictions in the edge strong signal regions. |
png pdf root |
Figure 12-a:
The correlation matrix for the background predictions in the edge strong signal regions. |
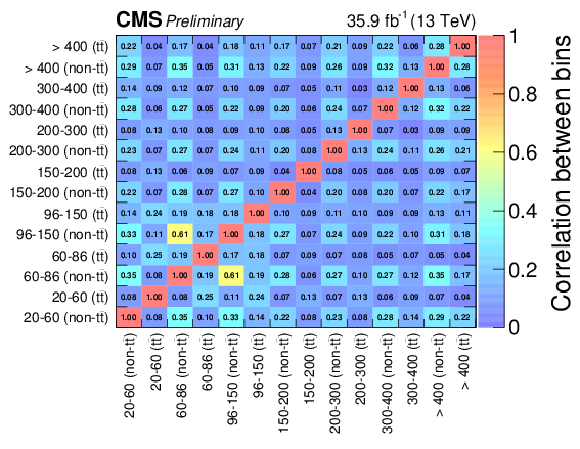
png pdf root |
Figure 12-b:
The covariance matrix for the background predictions in the edge strong signal regions. |
| Tables | |
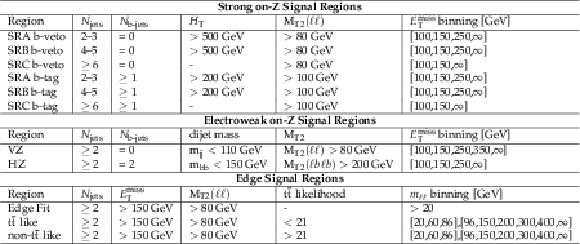
png pdf |
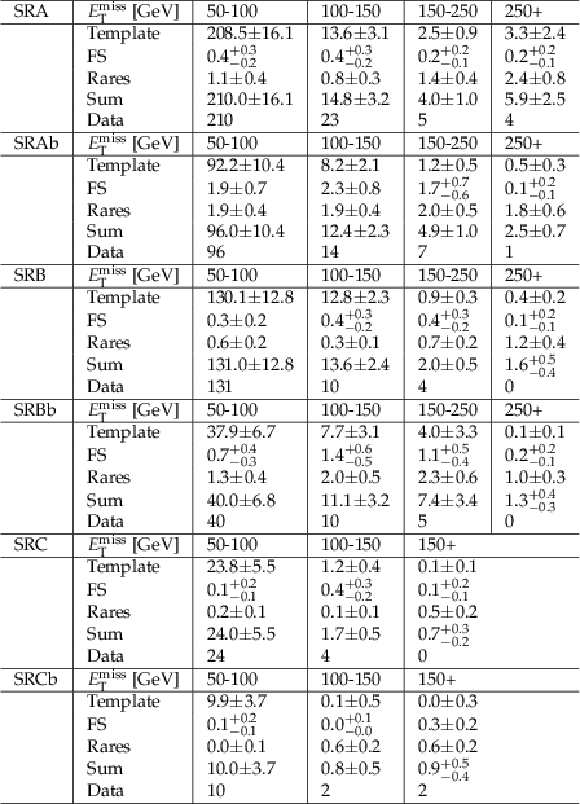
Table 1:
Summary of all signal region selections. |
png pdf |
Table 2:
Predicted and observed event yields are shown for the strong on-Z signal regions, for each region and EmissT bin defined in Table 1. The uncertainties shown include both statistical and systematic errors. |
png pdf |
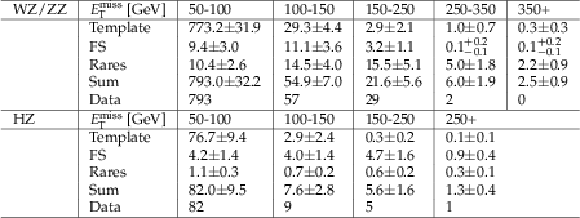
Table 3:
Predicted and observed event yields are shown for the electroweak on-Z signal regions, for each region and EmissT bin defined in Table 1. The uncertainties shown include both statistical and systematic errors. |
png pdf |
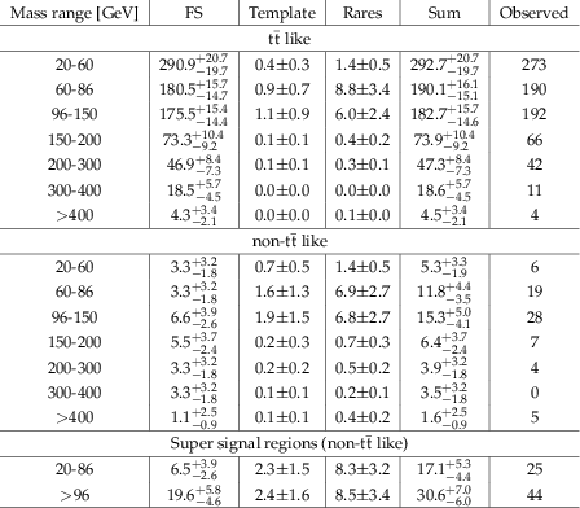
Table 4:
Results of the edge-search counting experiment for event yields in the signal regions. The statistical and systematic uncertainties are added in quadrature. |
png pdf |
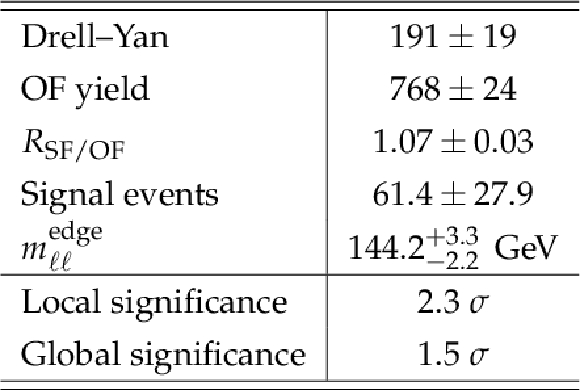
Table 5:
Results of the unbinned maximum likelihood fit for event yields in the signal region, including the DY and FS background components, along with the fitted signal contribution and edge position. The fitted value for RSF/OF and the local and global signal significances are also given. The quoted uncertainties account for both statistical and systematic sources. |
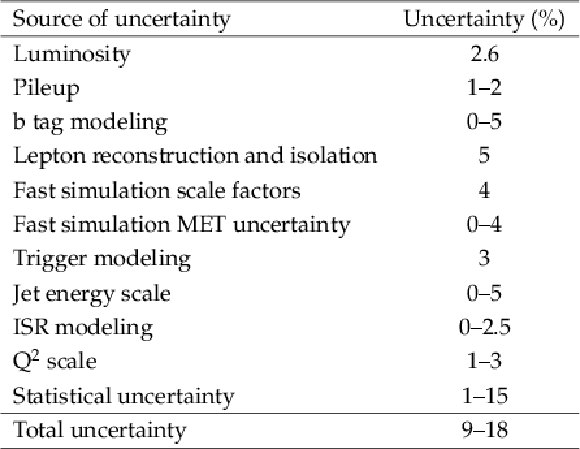
png pdf |
Table 6:
Systematic uncertainties taken into account for the signal yields and their typical values. |
| Summary |
|
A search for physics beyond the standard model has been presented in the opposite-sign, same-flavor lepton; jets; and EmissT final state using a data sample of pp collisions collected with the CMS detector in 2016 at a center-of-mass energy of 13 TeV, corresponding to an integrated luminosity of 35.9 fb−1. Searches are performed for signals that either produce a kinematic edge in the dilepton invariant mass, or use dilepton systems whose invariant mass is compatible with the decay of a Z boson. Comparing the observation to estimates for SM backgrounds obtained from data control samples, and no statistically significant evidence for a signal has been observed. The search for strongly produced new physics containing an on-shell Z boson is interpreted in a model of gauge-mediated supersymmetry breaking, where the Z bosons are produced in decay chains initiated through gluino pair production. Gluino masses below 1500-1770 GeV have been excluded, depending on the neutralino mass, extending the previous exclusion limits derived from the previous CMS publication by almost 500 GeV. The electroweak on-Z search has been interpreted in a simplified model of chargino-neutralino production where the neutralino decays to a Z boson and the LSP, and the chargino decays to a W boson and the LSP. In this model, we probe chargino masses in the range 160-610 GeV. The search for a kinematic edge in the mℓℓ distribution is interpreted in a simplified model based on bottom squark pair production, where dilepton mass edges are produced in decay chains containing the two lightest neutralinos and a slepton, where the branching ratios have been fixed to produce the desired topology. Bottom squark masses below 980 to 1200 GeV have been excluded, depending on the ˜χ02 mass. These limits extend previous exclusion limits by 400-600 GeV depending also on the ˜χ02 mass. |
| Additional Figures | |
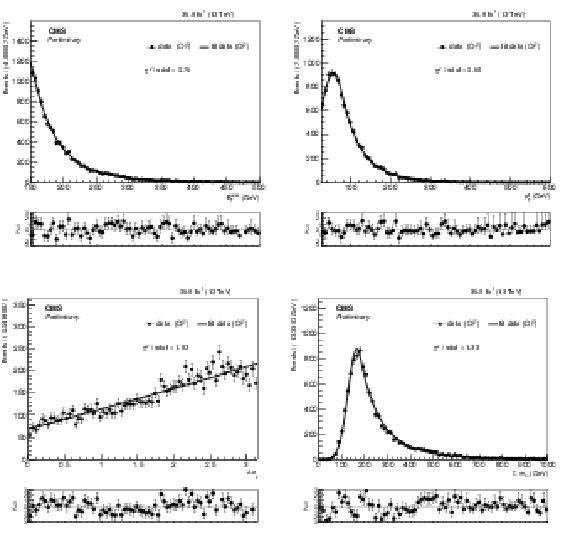
png pdf |
Additional Figure 1:
PDFs for the four input variables to the likelihood discriminant: EmissT (a), di-lepton pT (b), |Δϕ| between the leptons (c), and Σmℓb (d) for data in the OF region. |
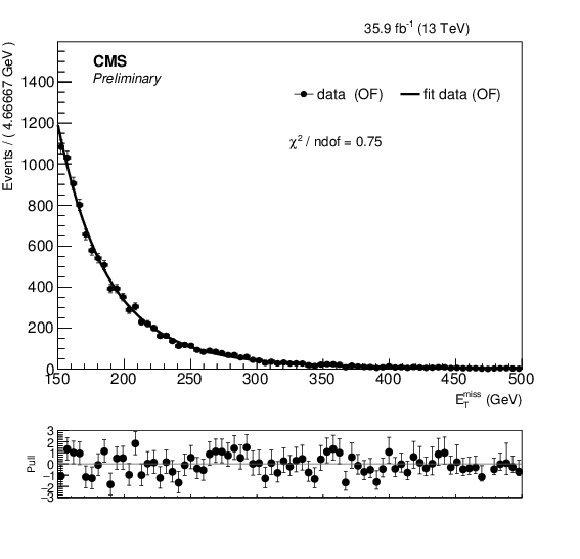
png pdf |
Additional Figure 1-a:
PDFs for one of the four input variables to the likelihood discriminant: EmissT for data in the OF region. |

png pdf |
Additional Figure 1-b:
PDFs for one of the four input variables to the likelihood discriminant: di-lepton pT for data in the OF region. |
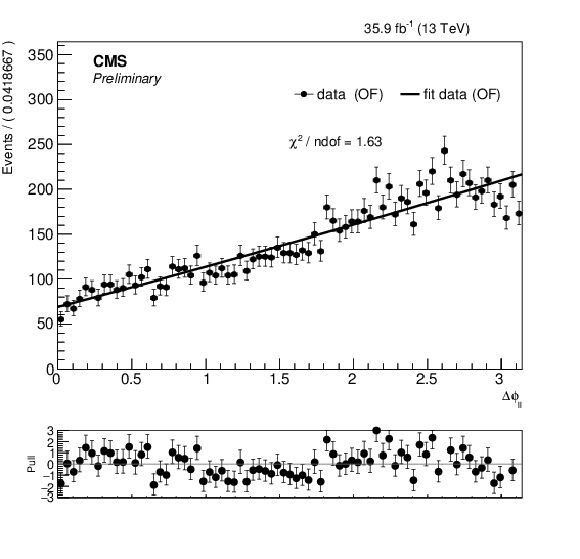
png pdf |
Additional Figure 1-c:
PDFs for one of the four input variables to the likelihood discriminant: |Δϕ| between the leptons for data in the OF region. |
png pdf |
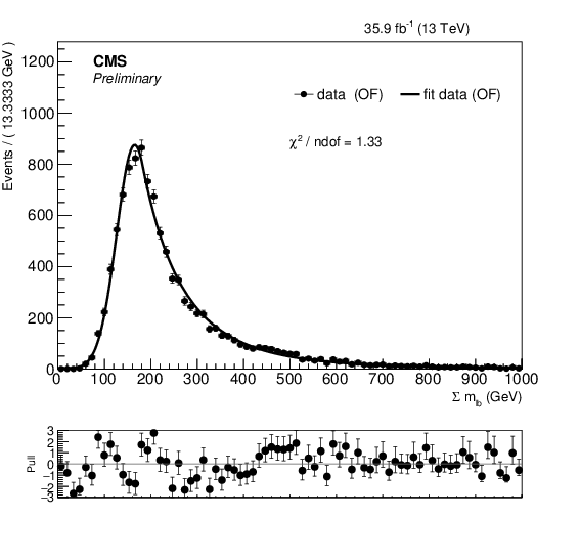
Additional Figure 1-d:
PDFs for one of the four input variables to the likelihood discriminant: Σmℓb for data in the OF region. |
png pdf |
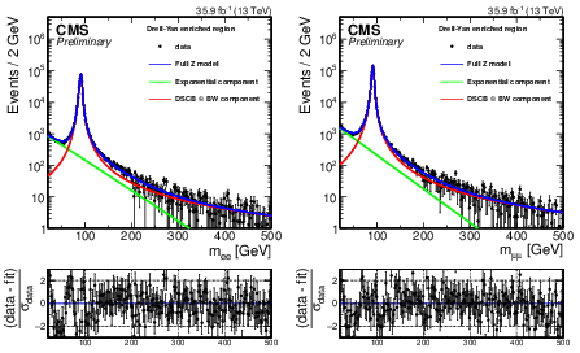
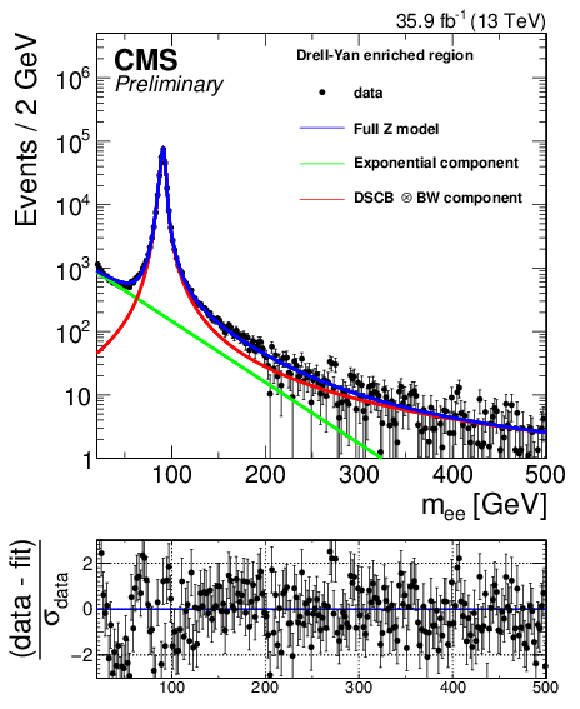
Additional Figure 2:
Fitted shape for backgrounds containing a Z boson for dielectron events (a) and dimuon events (b). The fitted shape consists of an exponential (green) and a Breit-wigner convolved with a double-sided Crystal-Ball (red), whose sum (blue) describes the backgrounds containing a Z boson. |
png pdf |
Additional Figure 2-a:
Fitted shape for backgrounds containing a Z boson for dielectron events. The fitted shape consists of an exponential (green) and a Breit-wigner convolved with a double-sided Crystal-Ball (red), whose sum (blue) describes the backgrounds containing a Z boson. |

png pdf |
Additional Figure 2-b:
Fitted shape for backgrounds containing a Z boson for dimuon events. The fitted shape consists of an exponential (green) and a Breit-wigner convolved with a double-sided Crystal-Ball (red), whose sum (blue) describes the backgrounds containing a Z boson. |

png pdf |
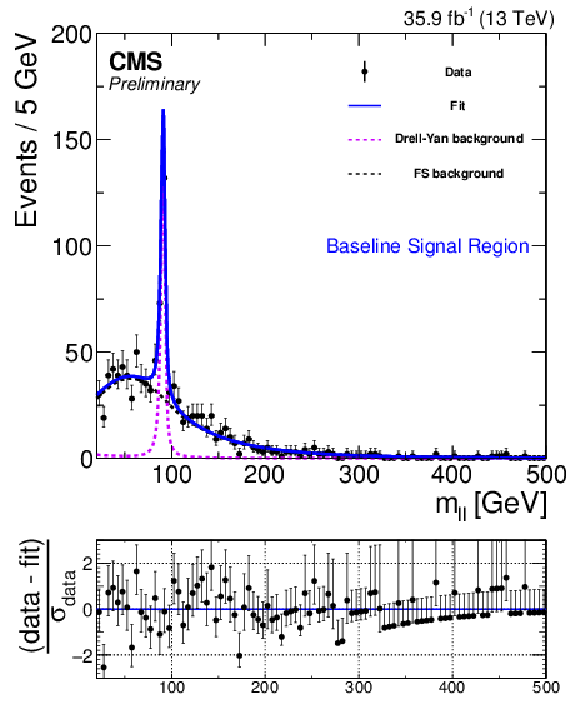
Additional Figure 3:
Result of fit in signal region for same-flavor (a) and opposite-flavor (b) events for data evaluating the null hypothesis. |
png pdf |
Additional Figure 3-a:
Result of fit in signal region for same-flavor events for data evaluating the null hypothesis. |
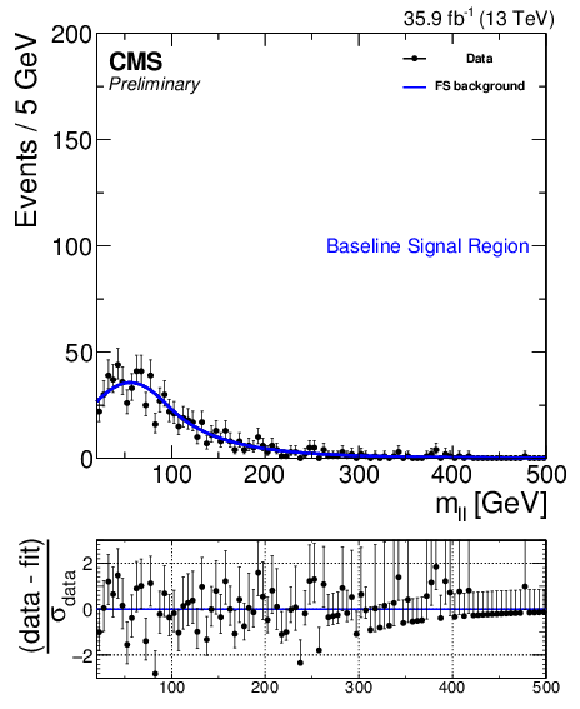
png pdf |
Additional Figure 3-b:
Result of fit in signal region for opposite-flavor events for data evaluating the null hypothesis. |
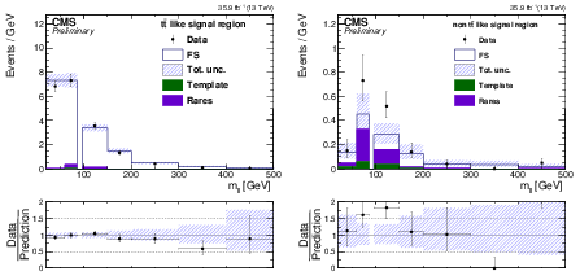
png pdf |
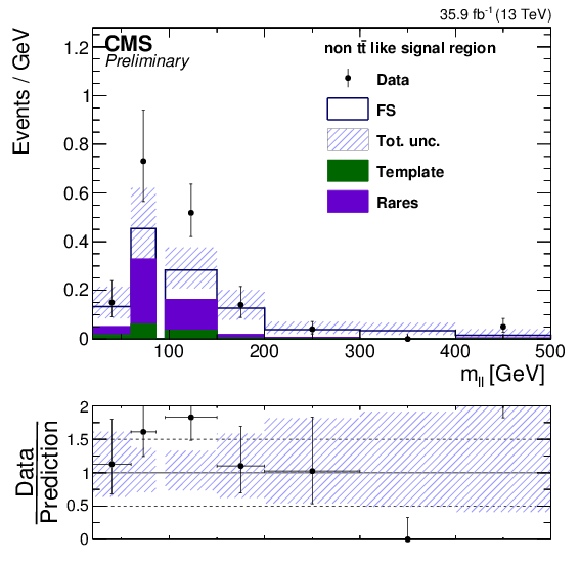
Additional Figure 4:
mℓℓ distribution in the tˉt like (a) and non tˉt like (b) edge signal regions.The number of observed events, shown as black data points, is compared to the total background estimate, shown as a blue line with a blue uncertainty band. The non flavor symmetric background component from instrumental EmissT is indicated as a green area while the non flavor symmetric background with neutrinos is shown as a violet area. |
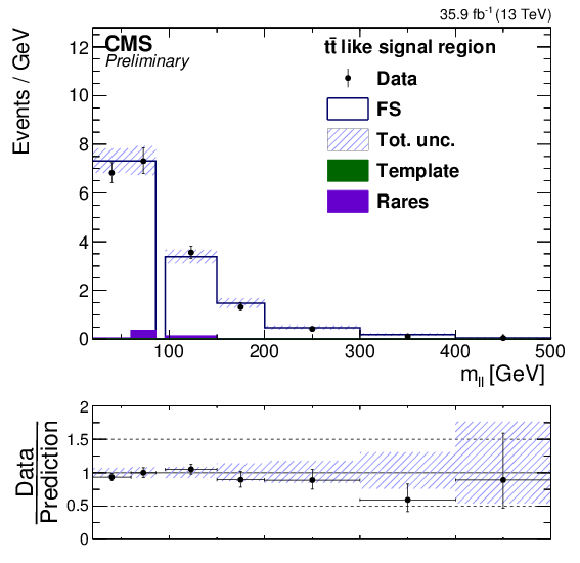
png pdf |
Additional Figure 4-a:
mℓℓ distribution in the tˉt like (a) and non tˉt like (b) edge signal regions.The number of observed events, shown as black data points, is compared to the total background estimate, shown as a blue line with a blue uncertainty band. The non flavor symmetric background component from instrumental EmissT is indicated as a green area while the non flavor symmetric background with neutrinos is shown as a violet area. |
png pdf |
Additional Figure 4-b:
mℓℓ distribution in the tˉt like (a) and non tˉt like (b) edge signal regions.The number of observed events, shown as black data points, is compared to the total background estimate, shown as a blue line with a blue uncertainty band. The non flavor symmetric background component from instrumental EmissT is indicated as a green area while the non flavor symmetric background with neutrinos is shown as a violet area. |
png pdf |
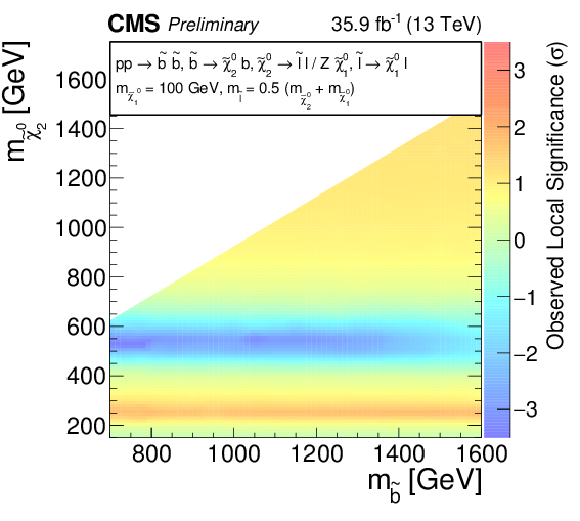
Additional Figure 5:
Two-dimensional distribution of the observed significances in the slepton-edge signal model. |
| Additional Tables | |
png pdf |
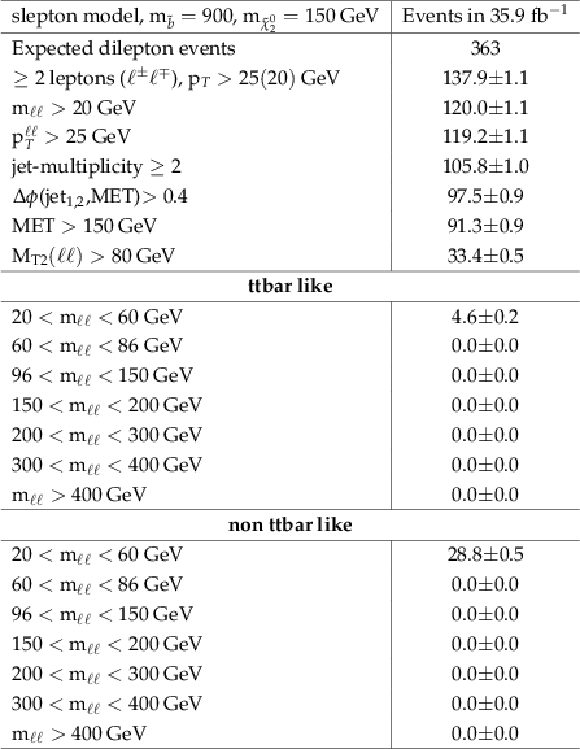
Additional Table 1:
Cut flow table for the edge signal model for a mass point at m˜b= 900 GeV and m˜χ02= 150 GeV. Expected dilepton events refers to luminosity×cross section×branching ratio. |

png pdf |
Additional Table 2:
Cut flow table for the edge signal model for a mass point at m˜b= 900 GeV and m˜χ02= 500 GeV. Expected dilepton events refers to luminosity×cross section×branching ratio. |
png pdf |
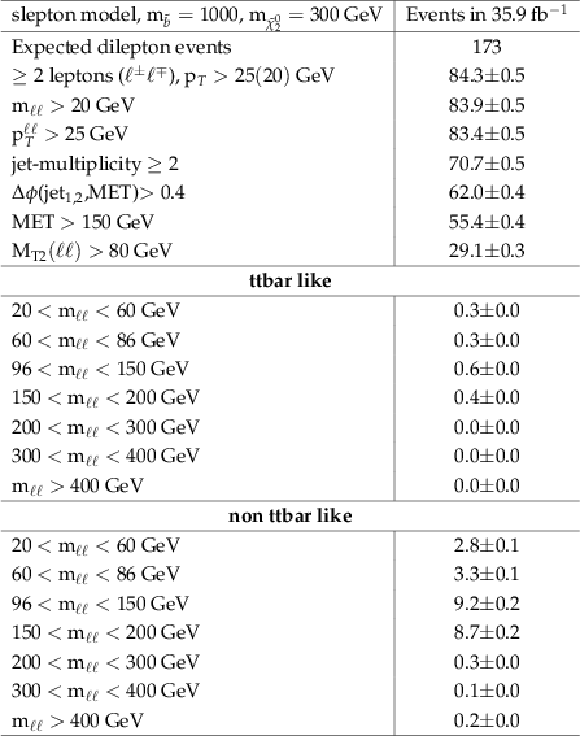
Additional Table 3:
Cut flow table for the edge signal model for a mass point at m˜b= 1000 GeV and m˜χ02= 300 GeV. Expected dilepton events refers to luminosity×cross section×branching ratio. |
png pdf |
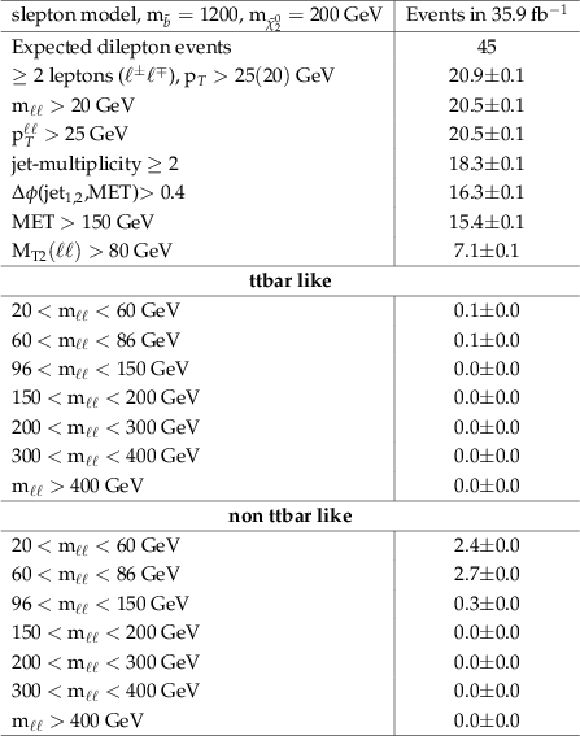
Additional Table 4:
Cut flow table for the edge signal model for a mass point at m˜b= 1200 GeV and m˜χ02= 200 GeV. Expected dilepton events refers to luminosity×cross section×branching ratio. |
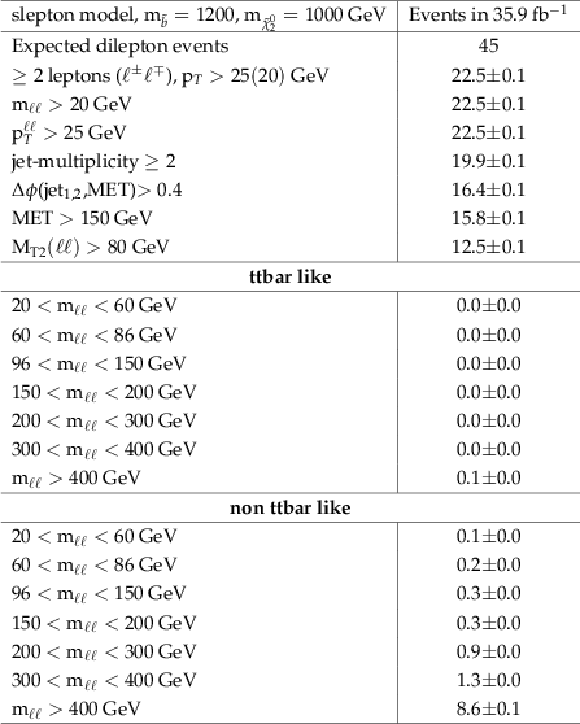
png pdf |
Additional Table 5:
Cut flow table for the edge signal model for a mass point at m˜b= 1200 GeV and m˜χ02= 1000 GeV. Expected dilepton events refers to luminosity×cross section×branching ratio. |
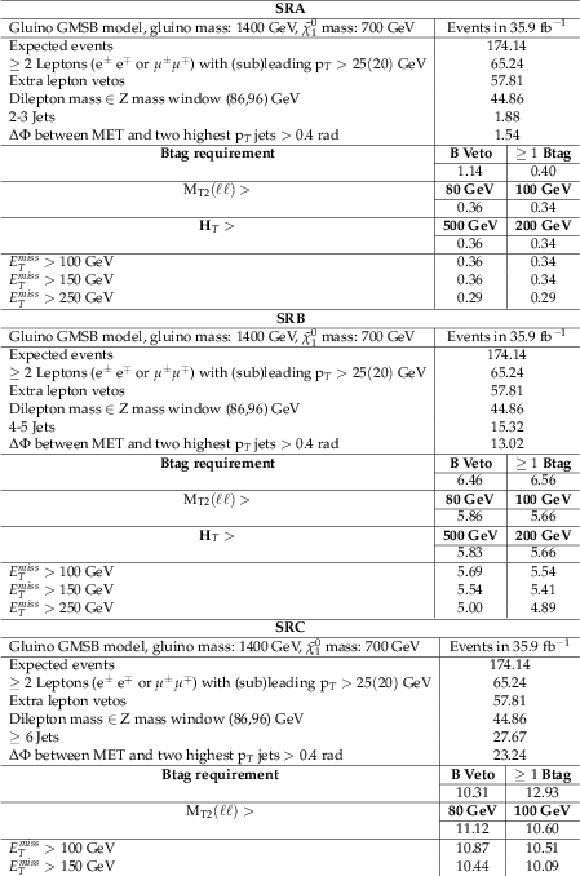
png pdf |
Additional Table 6:
Cut flow table for the strong on-Z signal region selections for the gluino GMSB signal model with the mass of the gluino and the ˜χ01 equal to 1400 and 700 GeV, respectively. The theoretical cross section for this signal is 25.3 fb and at least one Z boson was required to decay leptonically, for a branching fraction of 0.192. |

png pdf |
Additional Table 7:
Cut flow table for the electroweak on-Z signal region selections for the WZ signal model with the mass of the chargino and the LSP equal to 550 and 200 GeV, respectively. The theoretical cross section for this signal is 30.2 fb and the Z boson was required to decay leptonically, for a branching fraction of 0.10. |
|
The code for calculating the MT2 variable can be found here.
A macro for calculating the nll variable and the RooWorkSpace with the fitted pdfs used for the calculation is available here. |
| References | ||||
| 1 | P. Ramond | Dual theory for free fermions | PRD 3 (1971) 2415 | |
| 2 | Y. A. Golfand and E. P. Likhtman | Extension of the algebra of Poincare group generators and violation of P invariance | JEPTL 13 (1971)323 | |
| 3 | A. Neveu and J. H. Schwarz | Factorizable dual model of pions | Nucl. Phys. B 31 (1971) 86 | |
| 4 | D. V. Volkov and V. P. Akulov | Possible universal neutrino interaction | JEPTL 16 (1972)438 | |
| 5 | J. Wess and B. Zumino | A Lagrangian model invariant under supergauge transformations | PLB 49 (1974) 52 | |
| 6 | J. Wess and B. Zumino | Supergauge transformations in four dimensions | Nucl. Phys. B 70 (1974) 39 | |
| 7 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | Nucl. Phys. B 90 (1975) 104 | |
| 8 | H. P. Nilles | Supersymmetry, supergravity and particle physics | Phys. Rep. 110 (1984) 1 | |
| 9 | G. R. Farrar and P. Fayet | Phenomenology of the Production, Decay, and Detection of New Hadronic States Associated with Supersymmetry | PLB 76 (1978) 575 | |
| 10 | G. Buras, Ellis and Nanopoulos | Aspects of the grand unification of strong, weak and electromagnetic interactions | Nuclear Physics B 135 (1978), no. 1, 66 | |
| 11 | Haber and Kane | The search for supersymmetry: Probing physics beyond the standard model | Physics Reports 117 (1985), no. 2, 75 | |
| 12 | CMS Collaboration | Search for Physics Beyond the Standard Model in Events with Two Leptons, Jets, and Missing Transverse Momentum in pp Collisions at √s= 8 TeV | JHEP 04 (2015) 124 | CMS-SUS-14-014 1502.06031 |
| 13 | CMS Collaboration | Search for new physics in final states with two opposite-sign, same-flavor leptons, jets, and missing transverse momentum in pp collisions at √s = 13 TeV | JHEP 12 (2016) 013 | CMS-SUS-15-011 1607.00915 |
| 14 | CMS Collaboration | Search for new physics in events with opposite-sign leptons, jets, and missing transverse energy in pp collisions at√s= 7 TeV | Physics Letters B 718 (2013), no. 3, 815 | CMS-SUS-11-011 1206.3949 |
| 15 | CMS Collaboration | Search for physics beyond the standard model in opposite-sign dilepton events in pp collisions at√s= 7 TeV | Journal of High Energy Physics 2011 (2011), no. 6, 26 | CMS-SUS-10-007 1103.1348 |
| 16 | CMS Collaboration | Searches for electroweak production of charginos, neutralinos, and sleptons decaying to leptons and W, Z, and Higgs bosons in pp collisions at 8 TeV | The European Physical Journal C 74 (2014), no. 9, 1 | CMS-SUS-13-006 1405.7570 |
| 17 | CMS Collaboration | Searches for electroweak neutralino and chargino production in channels with Higgs, Z, and W bosons in pp collisions at 8 TeV | PRD 90 (Nov, 2014) 092007 | CMS-SUS-14-002 1409.3168 |
| 18 | ATLAS Collaboration | Search for supersymmetry in events containing a same-flavour opposite-sign dilepton pair, jets, and large missing transverse momentum in √s= 8 TeV pp collisions with the ATLAS detector | EPJC 75 (2015) 318, , [Erratum: \emphEur. Phys. J. C 75 (2015) 463] | 1503.03290 |
| 19 | ATLAS Collaboration | Search for the electroweak production of supersymmetric particles in √s= 8 TeV pp collisions with the ATLAS detector | PRD 93 (Mar, 2016) 052002 | 1509.07152 |
| 20 | ATLAS Collaboration | Search for new phenomena in events containing a same-flavour opposite-sign dilepton pair, jets, and large missing transverse momentum in √s= 13 TeV pp collisions with the ATLAS detector | 1611.05791 | |
| 21 | I. Hinchliffe et al. | Precision SUSY measurements at CERN LHC | PRD 55 (1997) 5520 | hep-ph/9610544 |
| 22 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 23 | CMS Collaboration | Particle-Flow Event Reconstruction in CMS and Performance for Jets, Taus, and MET | CDS | |
| 24 | CMS Collaboration | Commissioning of the Particle-flow Event Reconstruction with the first LHC collisions recorded in the CMS detector | CDS | |
| 25 | CMS Collaboration | Performance of electron reconstruction and selection with the CMS detector in proton-proton collisions at √s= 8 TeV | JINST 10 (2015) P06005 | CMS-EGM-13-001 1502.02701 |
| 26 | CMS Collaboration | Performance of photon reconstruction and identification with the CMS detector in proton-proton collisions at √s= 8 TeV | Journal of Instrumentation 10 (2015), no. 08, P08010 | |
| 27 | M. Cacciari, G. P. Salam, and G. Soyez | The anti-kt jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 28 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 29 | M. Cacciari and G. P. Salam | Dispelling the N3 myth for the kt jet-finder | PLB 641 (2006) 57 | hep-ph/0512210 |
| 30 | CMS Collaboration | Determination of Jet Energy Calibration and Transverse Momentum Resolution in CMS | JINST 6 (2011) P11002 | CMS-JME-10-011 1107.4277 |
| 31 | M. Cacciari and G. P. Salam | Pileup subtraction using jet areas | PLB 659 (2008) 119 | 0707.1378 |
| 32 | CMS Collaboration | Identification of b quark jets at the CMS Experiment in the LHC Run 2 | Technical Report CMS-PAS-BTV-15-001 | |
| 33 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 34 | S. Alioli, P. Nason, C. Oleari, and E. Re | NLO single-top production matched with shower in POWHEG: s- and t-channel contributions | JHEP 11 (2010) 111 | 0907.4076v2 |
| 35 | E. Re | Single-top Wt-channel production matched with parton showers using the POWHEG method | EPJC 71 (2011) 1547 | 1009.2450 |
| 36 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | FEWZ 2.0: A code for hadronic Z production at next-to-next-to-leading order | CPC 182 (2011) 2388--2403 | 1011.3540 |
| 37 | R. Gavin, Y. Li, F. Petriello, and S. Quackenbush | W Physics at the LHC with FEWZ 2.1 | CPC 184 (2013) 208--214 | 1201.5896 |
| 38 | M. Czakon and A. Mitov | Top++: A Program for the Calculation of the Top-Pair Cross-Section at Hadron Colliders | CPC 185 (2014) 2930 | 1112.5675 |
| 39 | C. Borschensky et al. | Squark and gluino production cross sections in pp collisions at √s= 13, 14, 33 and 100 TeV | EPJC 74 (2014), no. 12 | 1407.5066 |
| 40 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Gaugino production in proton-proton collisions at a center-of-mass energy of 8 TeV | JHEP 10 (2012) 081 | 1207.2159 |
| 41 | B. Fuks, M. Klasen, D. R. Lamprea, and M. Rothering | Precision predictions for electroweak superpartner production at hadron colliders with Resummino | EPJC 73 (2013) 2480 | 1304.0790 |
| 42 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 43 | S. Frixione, P. Nason, and C. Oleari | Matching NLO QCD computations with Parton Shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 44 | T. Sjostrand, S. Mrenna, and P. Z. Skands | A Brief Introduction to PYTHIA 8.1 | CPC 178 (2008) 852--867 | 0710.3820 |
| 45 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |
| 46 | GEANT4 Collaboration | GEANT4 --- a simulation toolkit | NIMA 506 (2003) 250 | |
| 47 | S. Abdullin et al. | The fast simulation of the CMS detector at LHC | J. Phys. Conf. Ser. 331 (2011) 032049 | |
| 48 | K. T. Matchev and S. D. Thomas | Higgs and Z boson signatures of supersymmetry | PRD 62 (2000) 077702 | hep-ph/9908482 |
| 49 | P. Meade, M. Reece, and D. Shih | Prompt decays of general neutralino NLSPs at the Tevatron | JHEP 05 (2010) 105 | 0911.4130 |
| 50 | J. T. Ruderman and D. Shih | General neutralino NLSPs at the early LHC | JHEP 08 (2012) 159 | 1103.6083 |
| 51 | C. G. Lester and D. J. Summers | Measuring masses of semiinvisibly decaying particles pair produced at hadron colliders | PLB 463 (1999) 99 | hep-ph/9906349 |
| 52 | A. Barr, C. Lester, and P. Stephens | A variable for measuring masses at hadron colliders when missing energy is expected; MT2 : the truth behind the glamour | JPG 29 (2003) 2343 | hep-ph/0304226 |
| 53 | M. J. Oreglia | PhD thesis, Stanford University, 1980 SLAC Report SLAC-R-236, see Appendix D | ||
| 54 | Olive et al. | Review of Particle Physics | CPC 38 (2014) 090001 | |
| 55 | T. Junk | Confidence level computation for combining searches with small statistics | NIMA 434 (1999) 435 | hep-ex/9902006 |
| 56 | A. L. Read | Presentation of search results: the CLs technique | JPG 28 (2002) 2693 | |
| 57 | ATLAS and CMS Collaborations | Procedure for the LHC Higgs boson search combination in summer 2011 | CMS-NOTE-2011-005 | |
| 58 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | EPJC 71 (2011) 1554 | 1007.1727 |
| 59 | CMS Collaboration | Simplified likelihood for the re-interpretation of public CMS results | CDS | |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|