

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-SMP-15-003 | ||
| Measurement of jet charge observables in dijet events at $\sqrt{s}=$ 8 TeV | ||
| CMS Collaboration | ||
| June 2016 | ||
| Abstract: Jet charge is an estimator for the electric charge of a quark, antiquark or gluon initiating a jet. It is based on the momentum-weighted sum of the measured electric charges of the jet constituents. A measurement of three different charge observables of the leading jet is performed in dijet events. The analysis is carried out with a data sample of 19.7 fb$^{-1}$ collected in proton-proton collisions at $\sqrt{s}=$ 8 TeV. The results are presented differentially in transverse momentum of the leading jet and compared to predictions from QCD-inspired leading order event generators. This is the first CMS measurement of jet charge observables unfolded for detector effects. | ||
|
Links:
CDS record (PDF) ;
inSPIRE record ;
CADI line (restricted) ;
These preliminary results are superseded in this paper, JHEP 10 (2017) 131. The superseded preliminary plots can be found here. |
||
| Figures | |
png pdf |
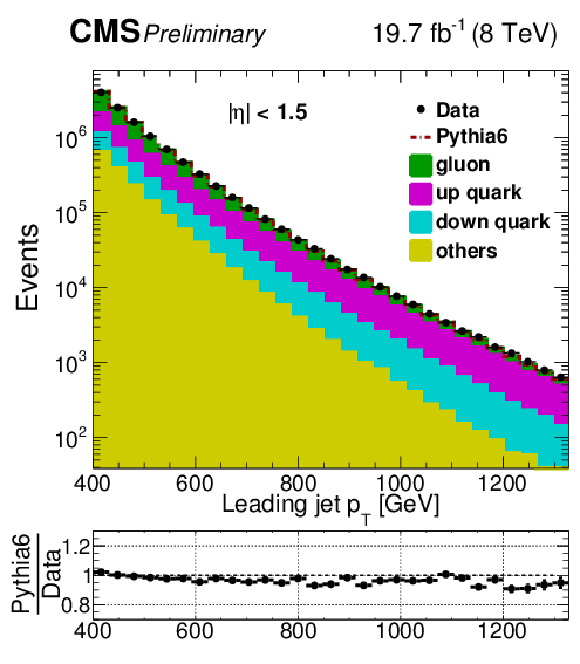
Figure 1:
Leading jet ${p_{\mathrm {T}}}$ distribution in data compared to PYTHIA 6 simulation. The fraction of events where the leading jet is matched to a generator quark or gluon are indicated as filled histograms. The ``others'' category represents those jets which are initiated by parton flavors including the anti-up quark ($\mathrm{ \bar{u} } $), the anti-down quark ($\mathrm{ \bar{d} } $), the charm, strange and bottom quarks ($\mathrm{c} $, $\mathrm{ \bar{c} } $, $\mathrm{ s } $, $\mathrm{ \bar{s} } $, $\mathrm{ b } $, $\mathrm{ \bar{b} } $) and the unmatched jets. |
png pdf |
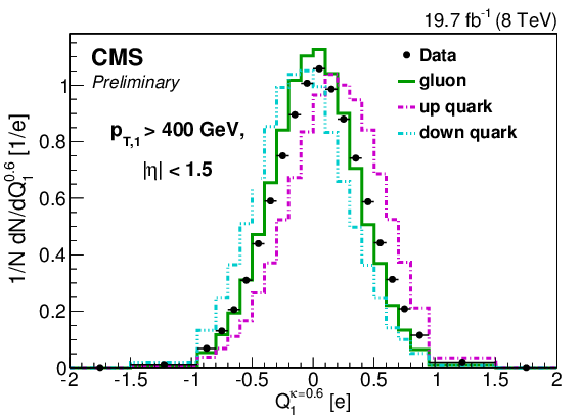
Figure 2-a:
Distribution of the jet charge (a and b) $Q^\kappa $, (c) $Q_{L}^\kappa $ and (d) $Q_{T}^\kappa $ in data compared to MC simulations. The (a) plot shows for the $\mathrm{ u } $, $\mathrm{ d } $ and $\gamma $ distributions in PYTHIA 6 in comparison with data where each distribution is normalized to its total number of events. The (b), (c) and (d) plots compare the sum of the contributions in PYTHIA 6 and HERWIG ++ to data where the flavor breakdown is carried out in PYTHIA 6. |

png pdf |
Figure 2-b:
Distribution of the jet charge (a and b) $Q^\kappa $, (c) $Q_{L}^\kappa $ and (d) $Q_{T}^\kappa $ in data compared to MC simulations. The (a) plot shows for the $\mathrm{ u } $, $\mathrm{ d } $ and $\gamma $ distributions in PYTHIA 6 in comparison with data where each distribution is normalized to its total number of events. The (b), (c) and (d) plots compare the sum of the contributions in PYTHIA 6 and HERWIG ++ to data where the flavor breakdown is carried out in PYTHIA 6. |
png pdf |
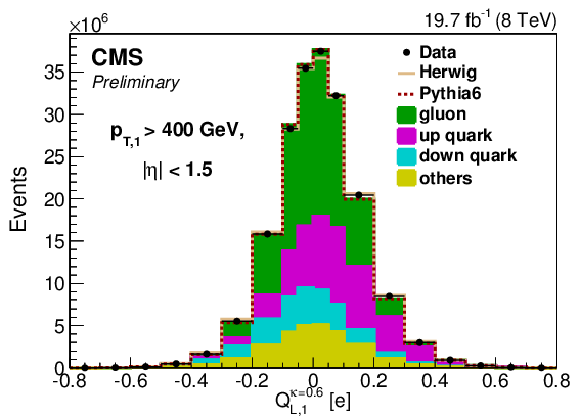
Figure 2-c:
Distribution of the jet charge (a and b) $Q^\kappa $, (c) $Q_{L}^\kappa $ and (d) $Q_{T}^\kappa $ in data compared to MC simulations. The (a) plot shows for the $\mathrm{ u } $, $\mathrm{ d } $ and $\gamma $ distributions in PYTHIA 6 in comparison with data where each distribution is normalized to its total number of events. The (b), (c) and (d) plots compare the sum of the contributions in PYTHIA 6 and HERWIG ++ to data where the flavor breakdown is carried out in PYTHIA 6. |

png pdf |
Figure 2-d:
Distribution of the jet charge (a and b) $Q^\kappa $, (c) $Q_{L}^\kappa $ and (d) $Q_{T}^\kappa $ in data compared to MC simulations. The (a) plot shows for the $\mathrm{ u } $, $\mathrm{ d } $ and $\gamma $ distributions in PYTHIA 6 in comparison with data where each distribution is normalized to its total number of events. The (b), (c) and (d) plots compare the sum of the contributions in PYTHIA 6 and HERWIG ++ to data where the flavor breakdown is carried out in PYTHIA 6. |
png pdf |
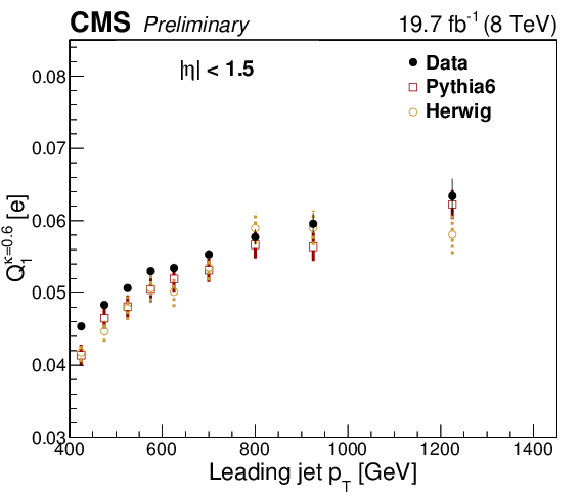
Figure 3:
Variation of the average leading jet charge in PYTHIA 6, HERWIG ++ and data as a function of leading jet ${p_{\mathrm {T}}} $. The error bars for the simulation indicate the uncertainty due to the MC simulation statistics. |

png pdf |
Figure 4-a:
Distributions of the jet charge of the leading jet at reconstructed level and generated level in PYTHIA 6 with $\kappa =$ 1.0 (a), 0.6 (b), 0.3 (c) respectively. |
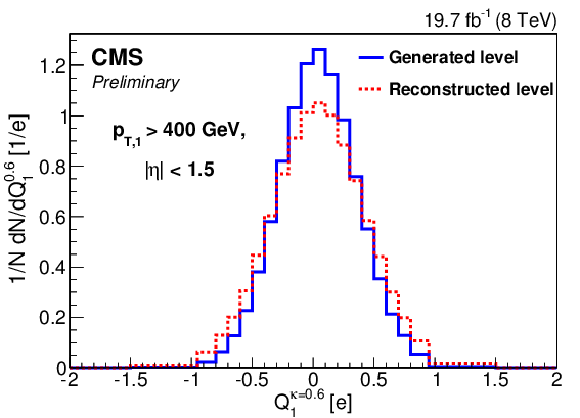
png pdf |
Figure 4-b:
Distributions of the jet charge of the leading jet at reconstructed level and generated level in PYTHIA 6 with $\kappa =$ 1.0 (a), 0.6 (b), 0.3 (c) respectively. |
png pdf |
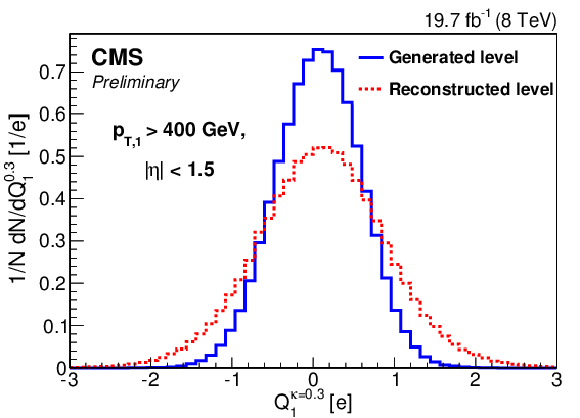
Figure 4-c:
Distributions of the jet charge of the leading jet at reconstructed level and generated level in PYTHIA 6 with $\kappa =$ 1.0 (a), 0.6 (b), 0.3 (c) respectively. |
png pdf |
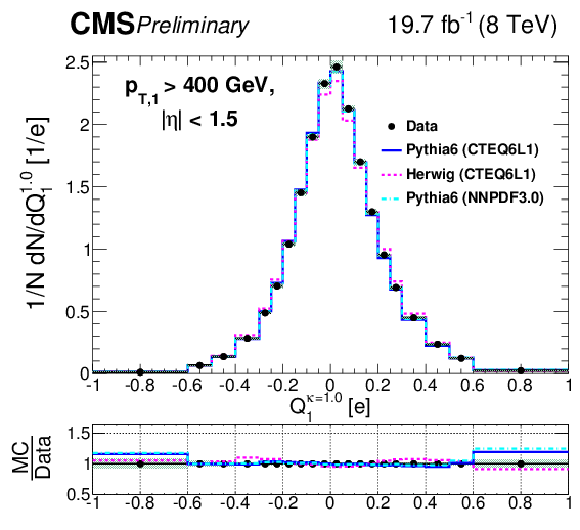
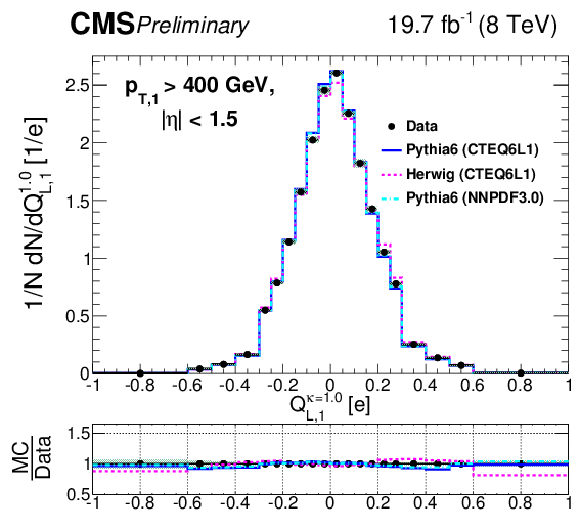
Figure 5-a:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators. The (a,c,e) plots show the distributions for the default jet charge definition ($Q^\kappa $) with all three different $\kappa $ values, while tthe (b,d,e) plots shows for the longitudinal jet charge definition ($Q_{L}^\kappa $) with all three different values of $\kappa $. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
Figure 5-b:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators. The (a,c,e) plots show the distributions for the default jet charge definition ($Q^\kappa $) with all three different $\kappa $ values, while tthe (b,d,e) plots shows for the longitudinal jet charge definition ($Q_{L}^\kappa $) with all three different values of $\kappa $. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
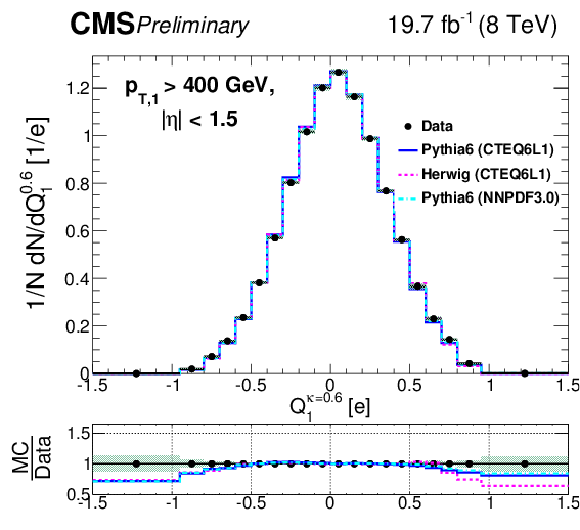
png pdf |
Figure 5-c:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators. The (a,c,e) plots show the distributions for the default jet charge definition ($Q^\kappa $) with all three different $\kappa $ values, while tthe (b,d,e) plots shows for the longitudinal jet charge definition ($Q_{L}^\kappa $) with all three different values of $\kappa $. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
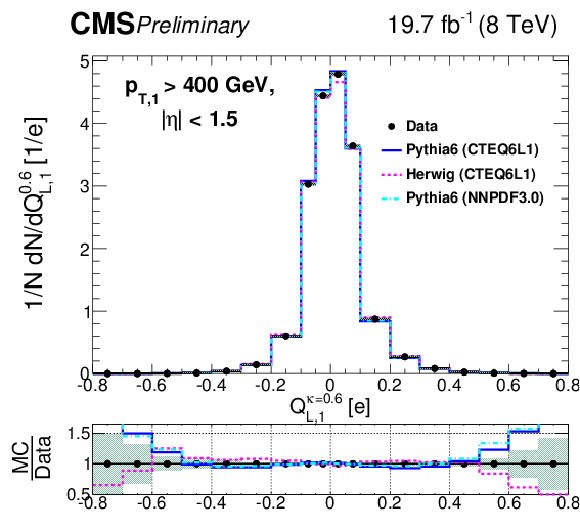
png pdf |
Figure 5-d:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators. The (a,c,e) plots show the distributions for the default jet charge definition ($Q^\kappa $) with all three different $\kappa $ values, while tthe (b,d,e) plots shows for the longitudinal jet charge definition ($Q_{L}^\kappa $) with all three different values of $\kappa $. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
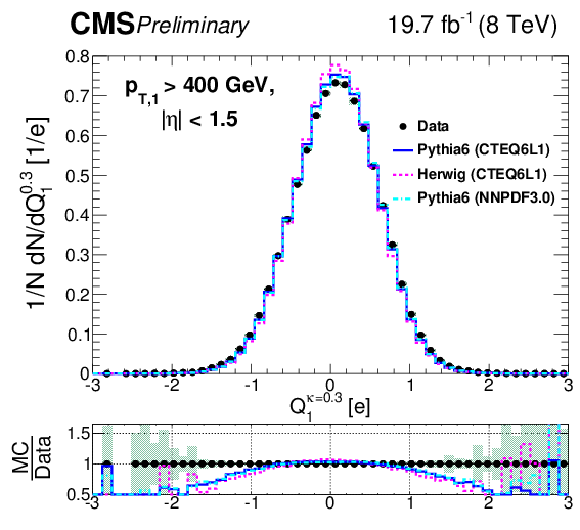
png pdf |
Figure 5-e:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators. The (a,c,e) plots show the distributions for the default jet charge definition ($Q^\kappa $) with all three different $\kappa $ values, while tthe (b,d,e) plots shows for the longitudinal jet charge definition ($Q_{L}^\kappa $) with all three different values of $\kappa $. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
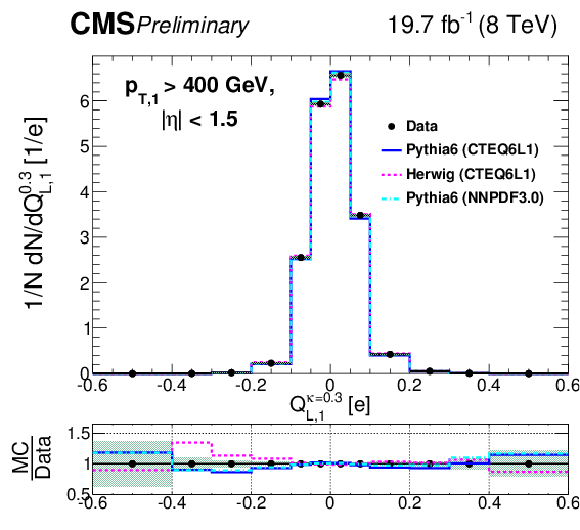
png pdf |
Figure 5-f:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators. The (a,c,e) plots show the distributions for the default jet charge definition ($Q^\kappa $) with all three different $\kappa $ values, while tthe (b,d,e) plots shows for the longitudinal jet charge definition ($Q_{L}^\kappa $) with all three different values of $\kappa $. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
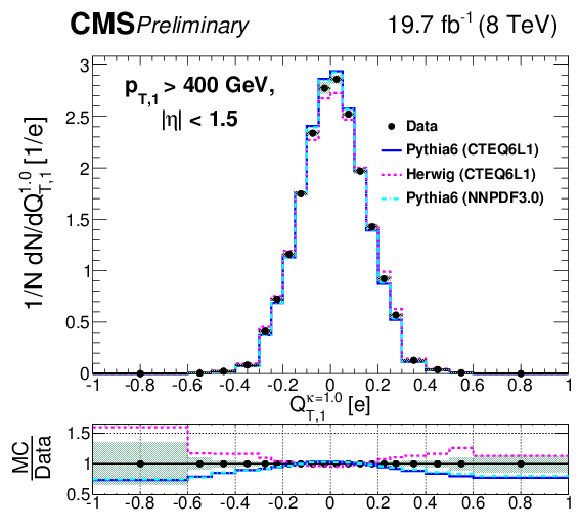
png pdf |
Figure 6-a:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators for transverse jet charge definition ($Q_{T}^\kappa $) with all different $\kappa $ values. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |

png pdf |
Figure 6-b:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators for transverse jet charge definition ($Q_{T}^\kappa $) with all different $\kappa $ values. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
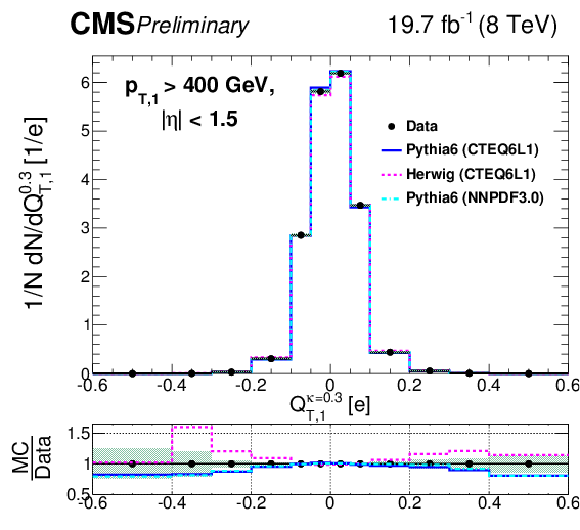
png pdf |
Figure 6-c:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators for transverse jet charge definition ($Q_{T}^\kappa $) with all different $\kappa $ values. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
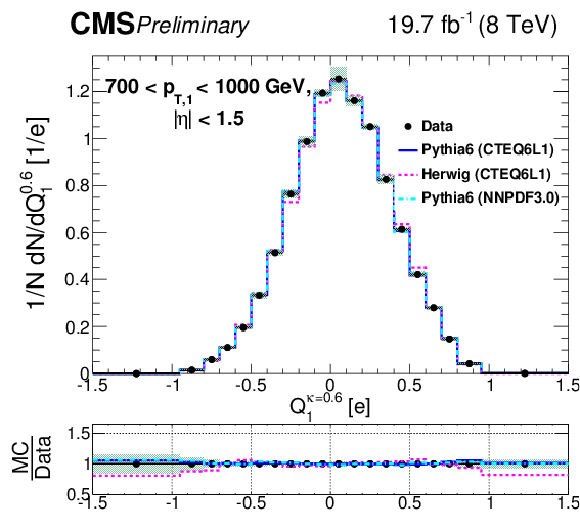
Figure 7-a:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}} $. Plots (a,c,e) show the jet ${p_{\mathrm {T}}}$ dependence for the default jet charge definition ($Q^\kappa $) with $\kappa $ = 0.6. Plots (b,d,f) shows the jet ${p_{\mathrm {T}}}$ dependence for the longitudinal jet charge definition ($Q_{L}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
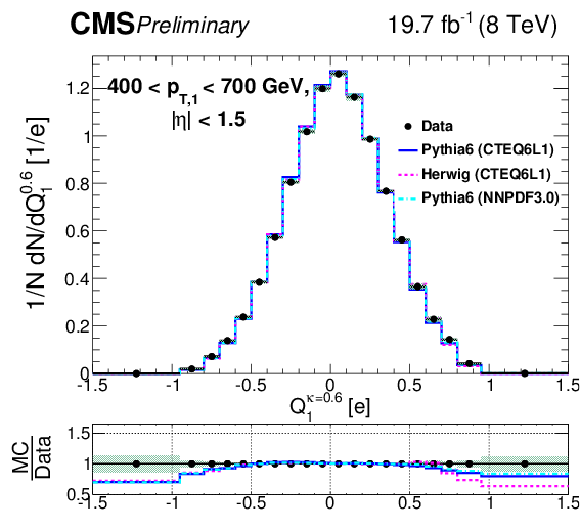
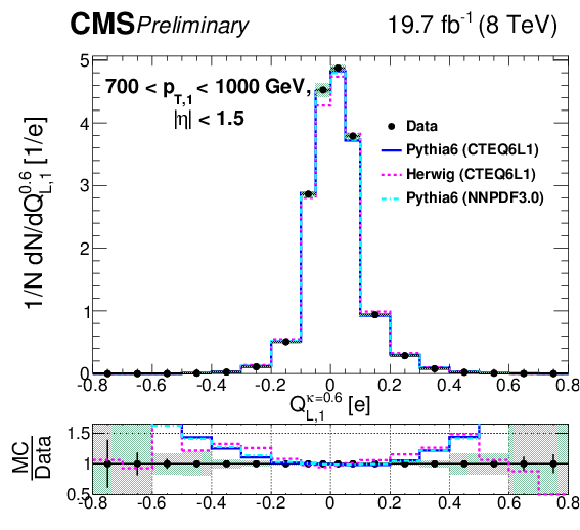
Figure 7-b:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}} $. Plots (a,c,e) show the jet ${p_{\mathrm {T}}}$ dependence for the default jet charge definition ($Q^\kappa $) with $\kappa $ = 0.6. Plots (b,d,f) shows the jet ${p_{\mathrm {T}}}$ dependence for the longitudinal jet charge definition ($Q_{L}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
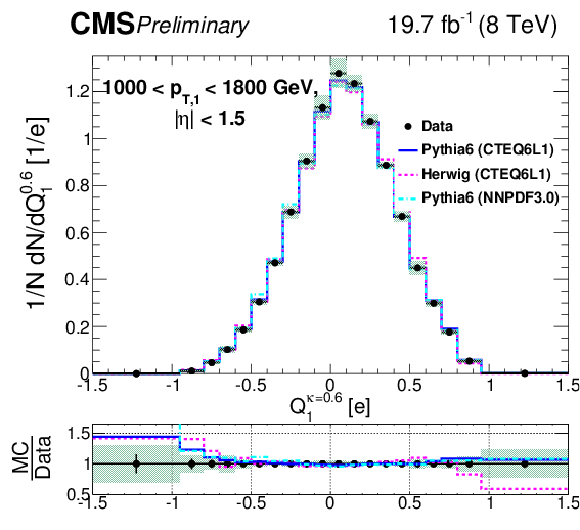
Figure 7-c:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}} $. Plots (a,c,e) show the jet ${p_{\mathrm {T}}}$ dependence for the default jet charge definition ($Q^\kappa $) with $\kappa $ = 0.6. Plots (b,d,f) shows the jet ${p_{\mathrm {T}}}$ dependence for the longitudinal jet charge definition ($Q_{L}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
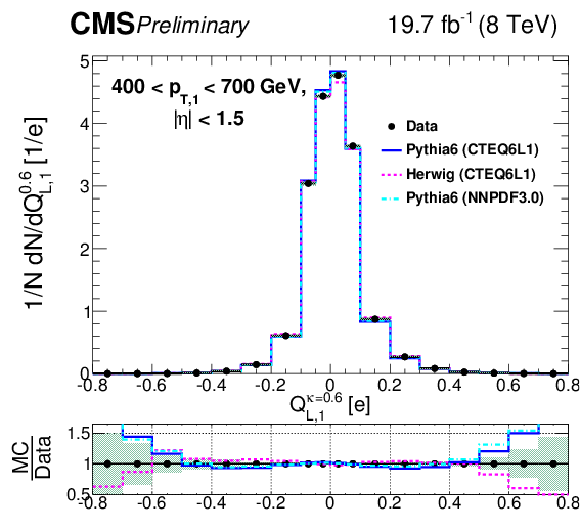
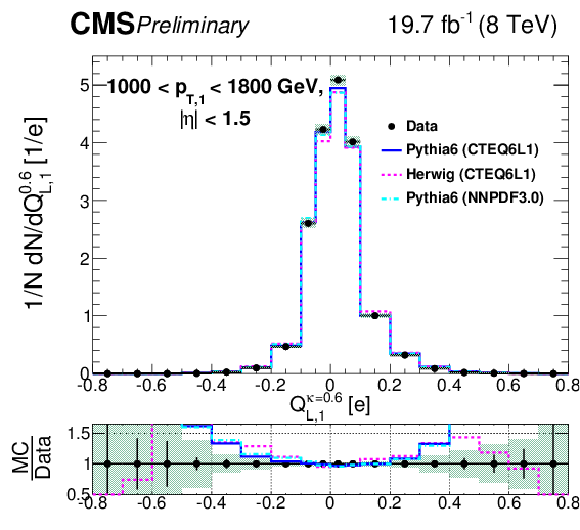
Figure 7-d:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}} $. Plots (a,c,e) show the jet ${p_{\mathrm {T}}}$ dependence for the default jet charge definition ($Q^\kappa $) with $\kappa $ = 0.6. Plots (b,d,f) shows the jet ${p_{\mathrm {T}}}$ dependence for the longitudinal jet charge definition ($Q_{L}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
Figure 7-e:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}} $. Plots (a,c,e) show the jet ${p_{\mathrm {T}}}$ dependence for the default jet charge definition ($Q^\kappa $) with $\kappa $ = 0.6. Plots (b,d,f) shows the jet ${p_{\mathrm {T}}}$ dependence for the longitudinal jet charge definition ($Q_{L}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
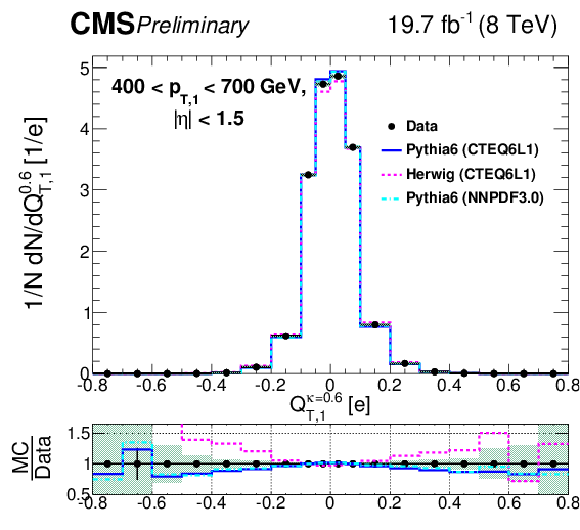
Figure 7-f:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}} $. Plots (a,c,e) show the jet ${p_{\mathrm {T}}}$ dependence for the default jet charge definition ($Q^\kappa $) with $\kappa $ = 0.6. Plots (b,d,f) shows the jet ${p_{\mathrm {T}}}$ dependence for the longitudinal jet charge definition ($Q_{L}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
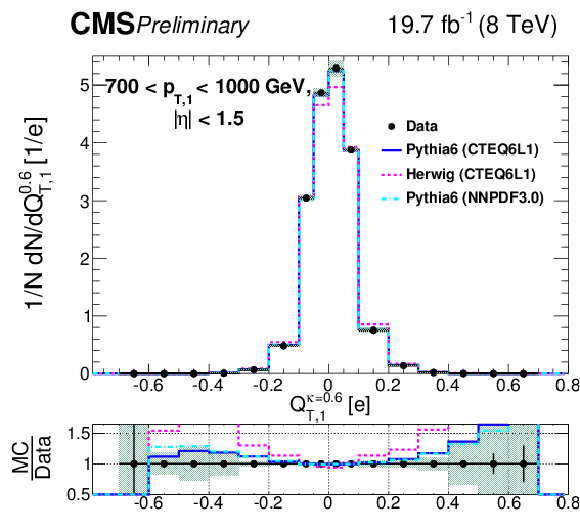
Figure 8-a:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}}$ for the transverse jet charge definition ($Q_{T}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
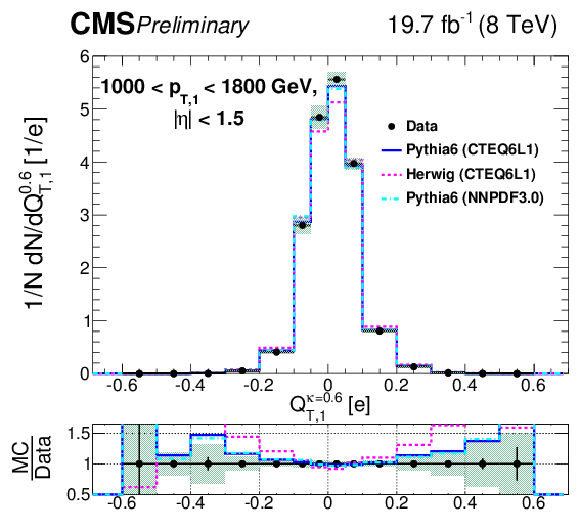
Figure 8-b:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}}$ for the transverse jet charge definition ($Q_{T}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
png pdf |
Figure 8-c:
Comparison of unfolded leading jet charge distributions with PYTHIA 6, HERWIG ++ generators in bins of leading jet ${p_{\mathrm {T}}}$ for the transverse jet charge definition ($Q_{T}^\kappa $) with $\kappa $ = 0.6. Shaded uncertainty bands include both statistical and systematic effects, added in quadrature. |
| Tables | |
png pdf |
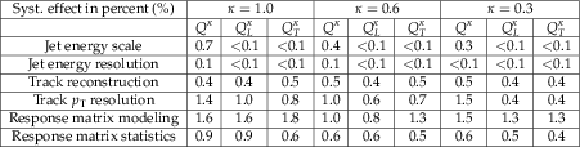
Table 1:
Various systematic effects and their corresponding error weighted mean of the fractional deviation in percent. |
| Summary |
|
In this paper we presented the first measurement of the jet charge distribution with the CMS experiment. Data distributions from dijet events unfolded for detector effects are provided for different definitions of jet charge and in different jet $p_{\mathrm{T}}$ bins. Three different definitions of jet charge provide different sensitivity to the fragmentation model. Three different $\kappa$ parameter choices provide different sensitivity to the softer and harder particles in the jet. We provided measurements in different leading jet $p_{\mathrm{T}}$ bins with sensitivity to the different composition of the quark and gluon jets in the dijet sample. In general the predictions from PYTHIA 6 and HERWIG++ generators show only mild discrepancies with the data distributions. However, the predictions from PYTHIA 6 and HERWIG++ generators are systematically different and could be constrained by this measurement. |
| References | ||||
| 1 | R. D. Field and R. P. Feynman | A Parametrization of the Properties of Quark Jets | Nucl. Phys. B 136 (1978) 1 | |
| 2 | Fermilab-Serpukhov-Moscow-Michigan Collaboration | Net Charge in Deep Inelastic anti-neutrino - Nucleon Scattering | PLB 91 (1980) 311--313 | |
| 3 | J. P. Berge et al. | Quark Jets from anti-neutrino Interactions. 1. Net Charge and Factorization in the Quark Jets | Nucl. Phys. B 184 (1981) 13--30 | |
| 4 | Aachen-Bonn-CERN-Munich-Oxford Collaboration | Multiplicity Distributions in Neutrino - Hydrogen Interactions | Nucl. Phys. B 181 (1981) 385--402 | |
| 5 | Aachen-Bonn-CERN-Munich-Oxford Collaboration | Charge Properties of the Hadronic System in Neutrino $ p $ and Anti-neutrino $ p $ Interactions | PLB 112 (1982) 88, .[,307(1982)] | |
| 6 | European Muon Collaboration | Quark Charge Retention in Final State Hadrons From Deep Inelastic Muon Scattering | PLB 144 (1984) 302--308 | |
| 7 | Amsterdam-Bologna-Padua-Pisa-Saclay-Turin Collaboration | Charged Hadron Multiplicities in High-energy Anti-muon Neutrino $ n $ and Anti-muon Neutrino $ p $ Interactions | Z. Phys. C 11 (1982) 283, .[Erratum: Z. Phys.C14,281(1982)] | |
| 8 | R. Erickson et al. | Charge Retention in Deep Inelastic Electroproduction | PRL 42 (1979) 822, .[Erratum: PRLett.42,1246(1979)] | |
| 9 | ALEPH Collaboration | Measurement of triple gauge boson couplings at 172-GeV | PLB 422 (1998) 369--383 | |
| 10 | D0 Collaboration | Experimental discrimination between charge 2e/3 top quark and charge 4e/3 exotic quark production scenarios | PRL 98 (2007) 041801 | hep-ex/0608044 |
| 11 | CDF Collaboration | The CDF Measurement of the Top Quark Charge using the Top Decay Products in Lepton+Jet channel | CDF note 10460 | |
| 12 | ATLAS Collaboration | Measurement of the top quark charge in $ pp $ collisions at $ \sqrt{s} = $ 7 TeV with the ATLAS detector | JHEP 11 (2013) 031 | 1307.4568 |
| 13 | W. J. Waalewijn | Calculating the Charge of a Jet | PRD 86 (2012) 094030 | 1209.3019 |
| 14 | D. Krohn, M. D. Schwartz, T. Lin, and W. J. Waalewijn | Jet Charge at the LHC | PRL 110 (2013), no. 21, 212001 | 1209.2421 |
| 15 | CMS Collaboration | Identification techniques for highly boosted W bosons that decay into hadrons | JHEP 12 (2014) 017 | CMS-JME-13-006 1410.4227 |
| 16 | ATLAS collaboration | Jet Charge Studies with the ATLAS Detector Using $ \sqrt{s} = 8 $ TeV Proton-Proton Collision Data | Technical Report ATLAS-CONF-2013-086 | |
| 17 | ATLAS Collaboration | Measurement of jet charge in dijet events from $ \sqrt{s} $=8 TeV pp collisions with the ATLAS detector | PRD 93 (2016), no. 5, 052003 | 1509.05190 |
| 18 | CMS Collaboration | Description and performance of track and primary-vertex reconstruction with the CMS tracker | JINST 9 (2014), no. 10, P10009 | CMS-TRK-11-001 1405.6569 |
| 19 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 20 | T. Sjostrand, S. Mrenna, and P. Z. Skands | PYTHIA 6.4 Physics and Manual | JHEP 05 (2006) 026 | hep-ph/0603175 |
| 21 | M. Bahr et al. | Herwig++ Physics and Manual | EPJC 58 (2008) 639--707 | 0803.0883 |
| 22 | R. Field | Min-Bias and the Underlying Event at the LHC | in Proceedings, 31st International Conference on Physics in collisions (PIC 2011) 2012 | 1202.0901 |
| 23 | B. Andersson, G. Gustafson, G. Ingelman, and T. Sjostrand | Parton Fragmentation and String Dynamics | PR 97 (1983) 31--145 | |
| 24 | T. Sjostrand | The Merging of Jets | PLB 142 (1984) 420--424 | |
| 25 | S. Gieseke, P. Stephens, and B. Webber | New formalism for QCD parton showers | JHEP 12 (2003) 045 | hep-ph/0310083 |
| 26 | B. R. Webber | A QCD Model for Jet Fragmentation Including Soft Gluon Interference | Nucl. Phys. B 238 (1984) 492--528 | |
| 27 | GEANT4 Collaboration | GEANT4: A Simulation toolkit | NIMA 506 (2003) 250--303 | |
| 28 | CMS Collaboration | Commissioning of the Particle-flow Event Reconstruction with the first LHC collisions recorded in the CMS detector | CDS | |
| 29 | M. Cacciari, G. P. Salam, and G. Soyez | The Anti-k(t) jet clustering algorithm | JHEP 04 (2008) 063 | 0802.1189 |
| 30 | M. Cacciari, G. P. Salam, and G. Soyez | FastJet user manual | EPJC 72 (2012) 1896 | 1111.6097 |
| 31 | CMS Collaboration | Determination of Jet Energy Calibration and Transverse Momentum Resolution in CMS | JINST 6 (2011) P11002 | CMS-JME-10-011 1107.4277 |
| 32 | CMS Collaboration | Jet Performance in pp Collisions at 7 TeV | CDS | |
| 33 | ALEPH Collaboration | Measurement of charge asymmetry in hadronic Z decays | PLB 259 (1991) 377--388 | |
| 34 | G. D'Agostini | A Multidimensional unfolding method based on Bayes' theorem | NIMA 362 (1995) 487--498 | |
| 35 | A. Hocker and V. Kartvelishvili | SVD approach to data unfolding | NIMA 372 (1996) 469--481 | hep-ph/9509307 |
| 36 | T. Adye | Unfolding algorithms and tests using RooUnfold | in Proceedings of the PHYSTAT 2011 Workshop, CERN, Geneva, Switzerland, January 2011, CERN-2011-006, pp. 313--318 2011 | 1105.1160 |
| 37 | CMS Collaboration | Jet Energy Resolution in CMS at sqrt(s)=7 TeV | CDS | |
| 38 | J. Pumplin et al. | New generation of parton distributions with uncertainties from global QCD analysis | JHEP 07 (2002) 012 | hep-ph/0201195 |
| 39 | NNPDF Collaboration | Parton distributions for the LHC Run II | JHEP 04 (2015) 040 | 1410.8849 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|