

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-HIG-16-035 | ||
| A search for beyond Standard Model light bosons decaying into muon pairs | ||
| CMS Collaboration | ||
| November 2016 | ||
| Abstract: A dataset corresponding to 2.8 fb$^{-1}$ of proton-proton collisions at $\sqrt{s} = $ 13 TeV was recorded by the CMS experiment at the CERN LHC. These data are used to search for new light bosons with a mass in the range 0.25-8.5 GeV/$c^2$ decaying into muon pairs. No excess is observed in the data, and a model-independent upper limit on the product of the cross section, branching fraction and acceptance is derived. The results are interpreted in the context of two benchmark models, namely, the next-to-minimal supersymmetric standard model, and dark SUSY models including those predicting a non-negligible light boson lifetime. | ||
| Links: CDS record (PDF) ; inSPIRE record ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
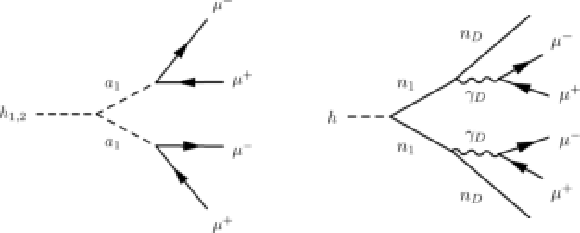
Figure 1:
Left: Feynman diagram of the NMSSM benchmark process $h_{1,2} \to 2a_1 \to 4\mu $. Right: Feynman diagram of the dark SUSY benchmark process $h \to 2n_1 \to 2n_D + 2\gamma _D \to 2n_D + 4\mu $. |
png pdf |
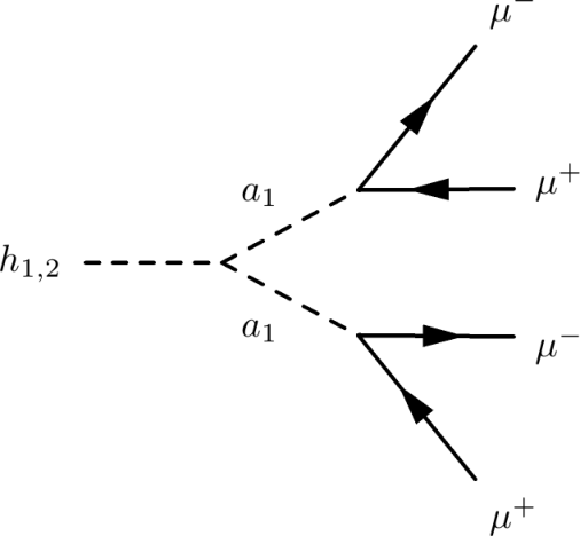
Figure 1-a:
Left: Feynman diagram of the NMSSM benchmark process $h_{1,2} \to 2a_1 \to 4\mu $. Right: Feynman diagram of the dark SUSY benchmark process $h \to 2n_1 \to 2n_D + 2\gamma _D \to 2n_D + 4\mu $. |
png pdf |
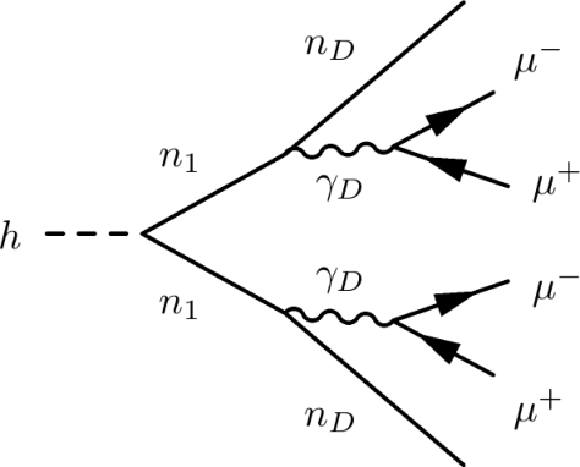
Figure 1-b:
Left: Feynman diagram of the NMSSM benchmark process $h_{1,2} \to 2a_1 \to 4\mu $. Right: Feynman diagram of the dark SUSY benchmark process $h \to 2n_1 \to 2n_D + 2\gamma _D \to 2n_D + 4\mu $. |
png pdf |
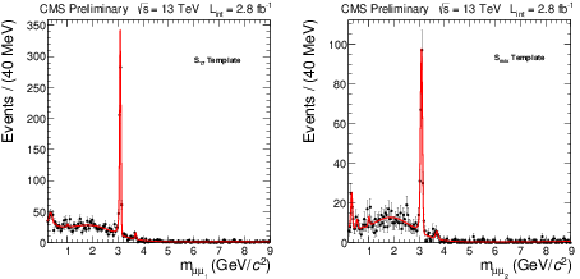
Figure 2:
The $S_{17}$ (left) and $S_{mix}$ (right) templates (solid lines) for dimuons obtained with background-enriched data (solid circles) samples. |
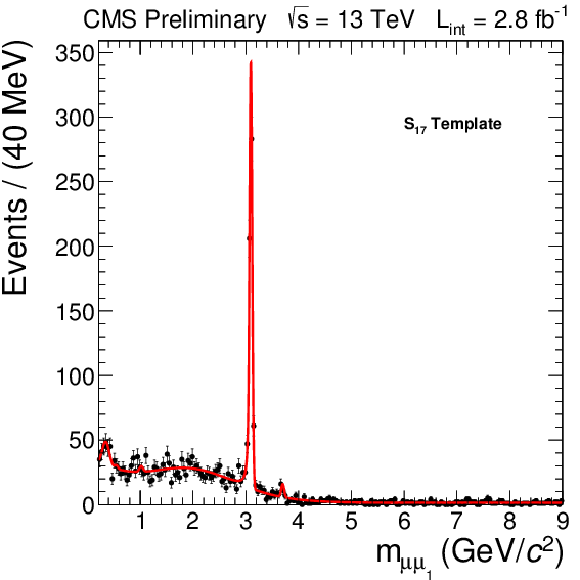
png pdf |
Figure 2-a:
The $S_{17}$ (left) and $S_{mix}$ (right) templates (solid lines) for dimuons obtained with background-enriched data (solid circles) samples. |
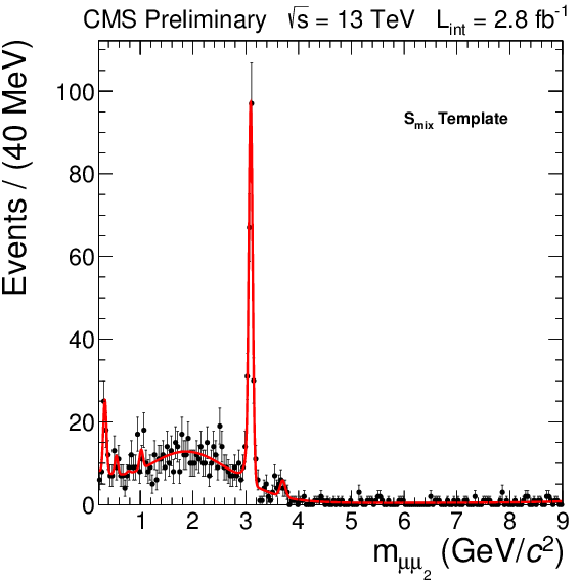
png pdf |
Figure 2-b:
The $S_{17}$ (left) and $S_{mix}$ (right) templates (solid lines) for dimuons obtained with background-enriched data (solid circles) samples. |
png pdf |
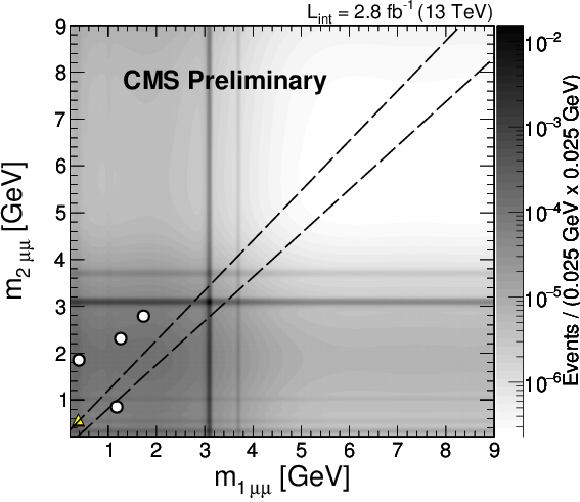
Figure 3:
Distribution of the invariant masses $m_{\mu \mu _1}$ vs. $m_{\mu \mu _2}$ for the isolated dimuon systems including the 4 events in the data (shown as empty circles) surviving all selections except for the requirement that these two masses fall into the diagonal signal region $m_{\mu \mu _1} \simeq m_{\mu \mu _2}$ (outlined with dashed lines). The triangle identifies the single event observed in the signal region. The intensity of the shading indicates the background expectation which is a sum of the $ {\mathrm{ b \bar{b} } } $ and the direct ${\mathrm{J}/\psi } $ pair production contributions. |
png pdf |
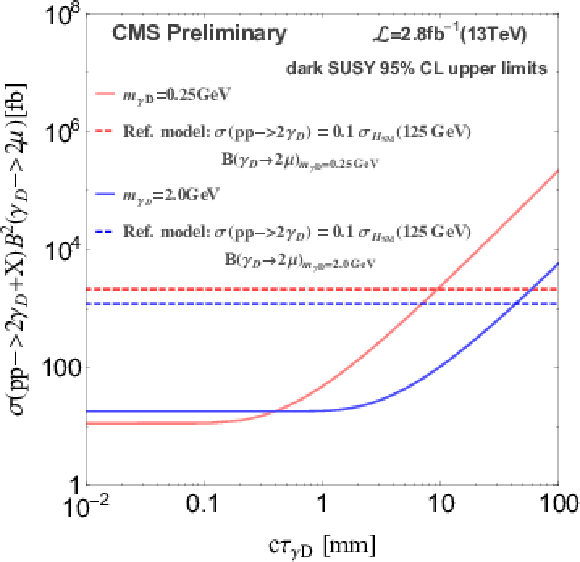
Figure 4:
95% CL upper Limit on $\sigma (\mathrm{ p } \mathrm{ p } \to 2 \gamma _D + \text {X}) \times \mathcal {B}^2(\gamma _D \rightarrow 2\mu )$ as a function of $c\tau _{\gamma _D}$ for two dark photon masses. The limits are compared to the predicted rate (dashed lines) obtained using a simplified scenario with $\sigma (\mathrm{ p } \mathrm{ p } \to 2 \gamma _D) = 0.1 \times \sigma _{SM}(125 GeV)$ and $\mathcal {B}(\gamma _D \rightarrow 2\mu )$ for 0.25 and 2 GeV mass points. |
png pdf |
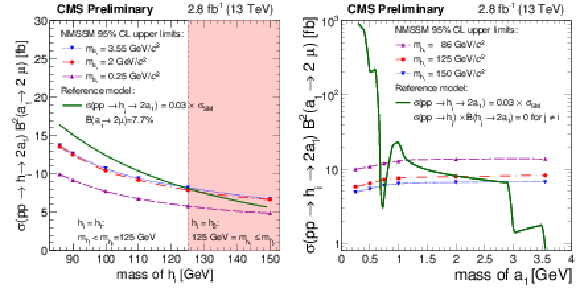
Figure 5:
Left: The 95% CL upper limits as functions of $m_{\text {h}_1}$, for the NMSSM case, on $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1,2} \to 2 \text {a}_1) \times \mathcal {B}^2(\text {a}_1 \to 2 \mu )$ with $m_{\text {a}_1}= $ 0.25 GeV/$c^2$ (dashed curve), $m_{\text {a}_1}= $ 2 GeV/$c^2$ (dash-dotted curve) and $m_{\text {a}_1}= $ 3.55 GeV/$c^2$ (dotted curve). As an illustration, the limits are compared to the predicted rate (solid curve) obtained using a simplified scenario with $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_1)=\sigma _\mathrm {SM}(m_{\text {h}_1})$ [69], $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_2) \times \mathcal {B}(\text {h}_{2} \rightarrow 2 \text {a}_1) = $ 0, $\mathcal {B}(\text {h}_1 \to 2 \text {a}_1) = $ 0.3%, and $\mathcal {B}(\text {a}_1 \to 2\mu ) = $ 7.7%. The chosen $\mathcal {B}(\text {a}_1 \to 2\mu )$ is taken from [28] for $m_{\text {a}_1} = $ 2 GeV/$c^2$ and NMSSM parameter $\tan\beta = $ 20. Right: The 95% CL upper limits as functions of $m_{\text {a}_1}$, for the NMSSM case, on $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1,2} \to 2 \text {a}_1) \times \mathcal {B}^2(\text {a}_1 \to 2 \mu )$ with $m_{\text {h}_1}= $ 86 GeV/$c^2$ (dashed curve), $m_{\text {h}_1}= $ 125 GeV/$c^2$ (dash-dotted curve), and $m_{\text {h}_1}= $ 150 GeV/$c^2$ (dotted curve). The limits are compared to the predicted rate (solid curve) obtained using a simplified scenario with $\mathcal {B}(\text {h}_{1} \to 2 \text {a}_1) = $ 0.3%, $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1})=\sigma _\mathrm {SM}(m_{\text {h}_{1}} = $ 125 GeV/$c^2$) [69], $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_2) \times \mathcal {B}(\text {h}_{2} \rightarrow 2 \text {a}_1) = $ 0, and $\mathcal {B}(\text {a}_1 \to 2\mu )$ as a function of $m_{\text {a}_1}$ which is taken from [28] for NMSSM parameter $\tan\beta = $ 20. |
png pdf |
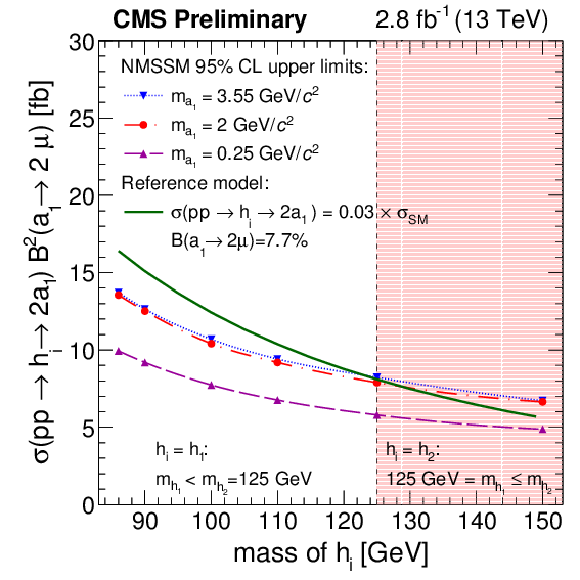
Figure 5-a:
Left: The 95% CL upper limits as functions of $m_{\text {h}_1}$, for the NMSSM case, on $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1,2} \to 2 \text {a}_1) \times \mathcal {B}^2(\text {a}_1 \to 2 \mu )$ with $m_{\text {a}_1}= $ 0.25 GeV/$c^2$ (dashed curve), $m_{\text {a}_1}= $ 2 GeV/$c^2$ (dash-dotted curve) and $m_{\text {a}_1}= $ 3.55 GeV/$c^2$ (dotted curve). As an illustration, the limits are compared to the predicted rate (solid curve) obtained using a simplified scenario with $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_1)=\sigma _\mathrm {SM}(m_{\text {h}_1})$ [69], $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_2) \times \mathcal {B}(\text {h}_{2} \rightarrow 2 \text {a}_1) = $ 0, $\mathcal {B}(\text {h}_1 \to 2 \text {a}_1) = $ 0.3%, and $\mathcal {B}(\text {a}_1 \to 2\mu ) = $ 7.7%. The chosen $\mathcal {B}(\text {a}_1 \to 2\mu )$ is taken from [28] for $m_{\text {a}_1} = $ 2 GeV/$c^2$ and NMSSM parameter $\tan\beta = $ 20. Right: The 95% CL upper limits as functions of $m_{\text {a}_1}$, for the NMSSM case, on $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1,2} \to 2 \text {a}_1) \times \mathcal {B}^2(\text {a}_1 \to 2 \mu )$ with $m_{\text {h}_1}= $ 86 GeV/$c^2$ (dashed curve), $m_{\text {h}_1}= $ 125 GeV/$c^2$ (dash-dotted curve), and $m_{\text {h}_1}= $ 150 GeV/$c^2$ (dotted curve). The limits are compared to the predicted rate (solid curve) obtained using a simplified scenario with $\mathcal {B}(\text {h}_{1} \to 2 \text {a}_1) = $ 0.3%, $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1})=\sigma _\mathrm {SM}(m_{\text {h}_{1}} = $ 125 GeV/$c^2$) [69], $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_2) \times \mathcal {B}(\text {h}_{2} \rightarrow 2 \text {a}_1) = $ 0, and $\mathcal {B}(\text {a}_1 \to 2\mu )$ as a function of $m_{\text {a}_1}$ which is taken from [28] for NMSSM parameter $\tan\beta = $ 20. |
png pdf |
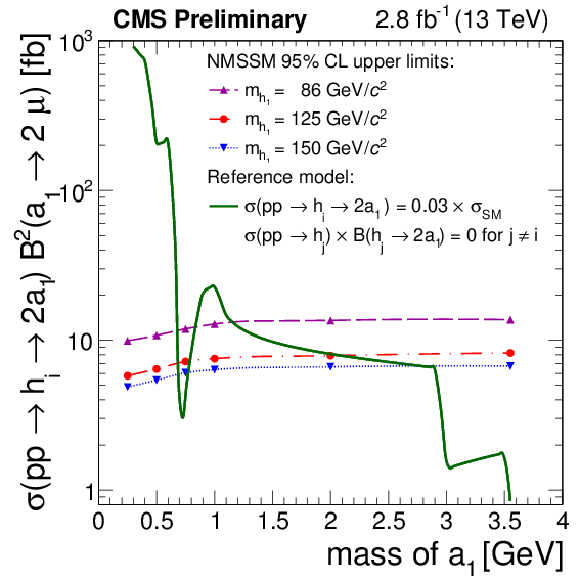
Figure 5-b:
Left: The 95% CL upper limits as functions of $m_{\text {h}_1}$, for the NMSSM case, on $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1,2} \to 2 \text {a}_1) \times \mathcal {B}^2(\text {a}_1 \to 2 \mu )$ with $m_{\text {a}_1}= $ 0.25 GeV/$c^2$ (dashed curve), $m_{\text {a}_1}= $ 2 GeV/$c^2$ (dash-dotted curve) and $m_{\text {a}_1}= $ 3.55 GeV/$c^2$ (dotted curve). As an illustration, the limits are compared to the predicted rate (solid curve) obtained using a simplified scenario with $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_1)=\sigma _\mathrm {SM}(m_{\text {h}_1})$ [69], $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_2) \times \mathcal {B}(\text {h}_{2} \rightarrow 2 \text {a}_1) = $ 0, $\mathcal {B}(\text {h}_1 \to 2 \text {a}_1) = $ 0.3%, and $\mathcal {B}(\text {a}_1 \to 2\mu ) = $ 7.7%. The chosen $\mathcal {B}(\text {a}_1 \to 2\mu )$ is taken from [28] for $m_{\text {a}_1} = $ 2 GeV/$c^2$ and NMSSM parameter $\tan\beta = $ 20. Right: The 95% CL upper limits as functions of $m_{\text {a}_1}$, for the NMSSM case, on $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1,2} \to 2 \text {a}_1) \times \mathcal {B}^2(\text {a}_1 \to 2 \mu )$ with $m_{\text {h}_1}= $ 86 GeV/$c^2$ (dashed curve), $m_{\text {h}_1}= $ 125 GeV/$c^2$ (dash-dotted curve), and $m_{\text {h}_1}= $ 150 GeV/$c^2$ (dotted curve). The limits are compared to the predicted rate (solid curve) obtained using a simplified scenario with $\mathcal {B}(\text {h}_{1} \to 2 \text {a}_1) = $ 0.3%, $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_{1})=\sigma _\mathrm {SM}(m_{\text {h}_{1}} = $ 125 GeV/$c^2$) [69], $\sigma (\mathrm{ p } \mathrm{ p } \to \text {h}_2) \times \mathcal {B}(\text {h}_{2} \rightarrow 2 \text {a}_1) = $ 0, and $\mathcal {B}(\text {a}_1 \to 2\mu )$ as a function of $m_{\text {a}_1}$ which is taken from [28] for NMSSM parameter $\tan\beta = $ 20. |
png pdf |
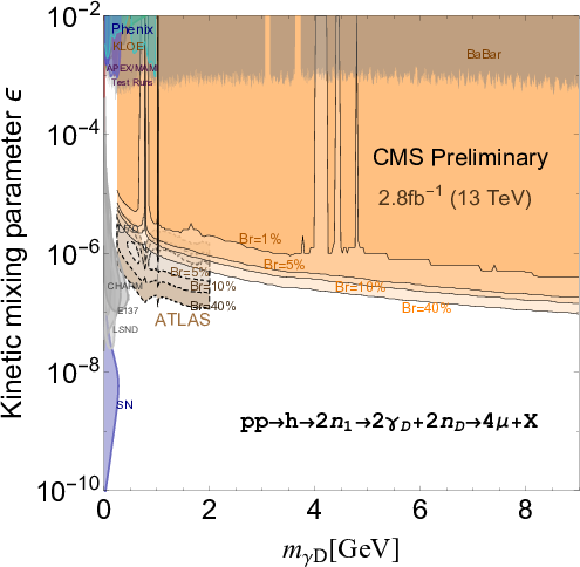
Figure 6:
95% CL upper limits (black solid curves) from this search on $\sigma (\mathrm{ p } \mathrm{ p } \to \mathrm{H} \to 2\gamma _{\mathrm {D}} + X) \mathcal {B}(\mathrm{H} \to 2\gamma _{\mathrm {D}} + X)$ (with $m_{\mathrm {n}_1}=10$ GeV , $m_{\mathrm {n}_{\mathrm {D}}}=1$ GeV ) in the plane of two of the parameters ($\varepsilon $ and $m_{\gamma _{\mathrm {D}}}$) for the dark SUSY scenarios, along with constraints from other experiments. The colored contours represent different values of $\mathcal {B}(\mathrm{H} \to 2\gamma _{\mathrm {D}} + X)$ in the range 1-40%. |
| Tables | |

png pdf |
Table 1:
Event selection efficiencies $\epsilon ^{MC}_{\text {full}}(m_{\text {h}_1}, m_{\text {a}_1})$, as obtained from the full detector simulation and the geometric and kinematic acceptances $\alpha _{\text {gen}}(m_{\text {h}_1}, m_{\text {a}_1})$ calculated using generator level information only with statistical uncertainties for the NMSSM benchmark model. The experimental data-to-simulation scale factors are not applied. |

png pdf |
Table 2:
Event selection efficiencies $\epsilon ^{MC}_{\text {full}}(m_{\text {h}}, m_{\gamma _D})$, as obtained from the full detector simulation and the geometric and kinematic acceptances $\alpha _{\text {gen}}(m_{\text {h}}, m_{\gamma _D})$ calculated using generator level information only with statistical uncertainties for a dark SUSY benchmark model with a dark photon lifetime of 2 mm as obtained from simulation. The experimental data-to-simulation scale factors are not applied. |
png pdf |
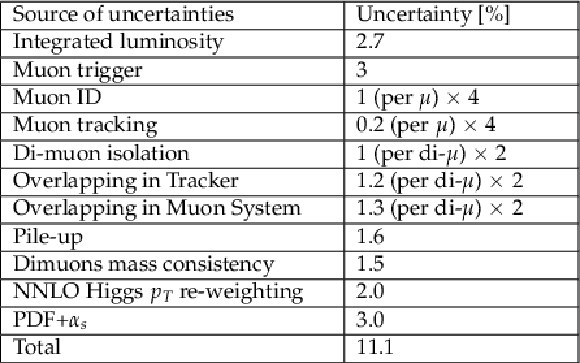
Table 3:
Summary of the magnitude of systematic uncertainties. |
| Summary |
| A search for beyond the standard model Higgs boson decays to pairs of new light bosons, which subsequently decay to pairs of oppositely charged muons ($\text{h} \to 2\text{a} + \text{X} \to 4 \mu + \text{X}$) has been presented. The search is based on a data sample corresponding to an integrated luminosity of 2.8 fb$^{-1}$ collected by the CMS experiment in proton-proton collisions at $\sqrt{s} = $ 13 TeV in 2015. One event with two dimuons of consistent single mass in the signal region was observed. The analysis has been designed as a model-independent search allowing interpretation of its results in the context of a broad range of new physics scenarios predicting the same type of final state signature. The results are interpreted in the context of the NMSSM and the dark SUSY benchmark models for $m_{\text{h}} < $ 150 GeV$c^2$. |
| References | ||||
| 1 | ATLAS Collaboration | Observation of a new particle in the search for the standard model Higgs boson with the ATLAS detector at the LHC | PLB 716 (2012) 1 | 1207.7214 |
| 2 | CMS Collaboration | Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC | PLB 716 (2012) 30 | CMS-HIG-12-028 1207.7235 |
| 3 | F. Englert and R. Brout | Broken symmetry and the mass of gauge vector mesons | PRL 13 (1964) 321 | |
| 4 | P. W. Higgs | Broken symmetries and the masses of gauge bosons | PRL 13 (1964) 508 | |
| 5 | G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble | Global conservation laws and massless particles | PRL 13 (1964) 585 | |
| 6 | P. Fayet | Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino | Nucl. Phys. B 90 (1975) 104 | |
| 7 | R. K. Kaul and P. Majumdar | Cancellation of quadratically divergent mass corrections in globally supersymmetric spontaneously broken gauge theories | Nucl. Phys. B 199 (1982) 36 | |
| 8 | R. Barbieri, S. Ferrara, and C. A. Savoy | Gauge models with spontaneously broken local supersymmetry | PLB 119 (1982) 343 | |
| 9 | H. P. Nilles, M. Srednicki, and D. Wyler | Weak interaction breakdown induced by supergravity | PL120 (1983) 346 | |
| 10 | J.-M. Frere, D. R. T. Jones, and S. Raby | Fermion masses and induction of the weak scale by supergravity | Nucl. Phys. B 222 (1983) 11 | |
| 11 | J.-P. Derendinger and C. A. Savoy | Quantum effects and SU(2)$ \times $U(1) breaking in supergravity gauge theories | Nucl. Phys. B 237 (1984) 307 | |
| 12 | M. Drees | Supersymmetric models with extended Higgs sector | Int. J. Mod. Phys. A 4 (1989) 3635 | |
| 13 | M. Maniatis | The next-to-minimal supersymmetric extension of the standard model reviewed | Int. J. Mod. Phys. A 25 (2010) 3505 | 0906.0777 |
| 14 | U. Ellwanger, C. Hugonie, and A. M. Teixeira | The next-to-minimal supersymmetric standard model | PR 496 (2010) 1 | 0910.1785 |
| 15 | H. P. Nilles | Supersymmetry, supergravity and particle physics | PR 110 (1984) 1 | |
| 16 | S. P. Martin | A Supersymmetry primer | Adv.Ser.Direct.High Energy Phys. 21 (2010) 1--153 | hep-ph/9709356 |
| 17 | D. J. H. Chung et al. | The soft supersymmetry breaking Lagrangian: theory and applications | PR 407 (2005) 1 | hep-ph/0312378 |
| 18 | J. E. Kim and H. P. Nilles | The $ \mu $-problem and the strong CP-problem | PLB 138 (1984) 150 | |
| 19 | J. A. Casas, J. R. Espinosa, and I. Hidalgo | The MSSM fine tuning problem: a way out | JHEP 01 (2004) 008 | hep-ph/0310137 |
| 20 | R. Dermisek and J. F. Gunion | Escaping the large fine tuning and little hierarchy problems in the next to minimal supersymmetric model and $ h \rightarrow aa $ decays | PRL 95 (2005) 041801 | hep-ph/0502105 |
| 21 | S. Chang, R. Dermisek, J. F. Gunion, and N. Weiner | Nonstandard Higgs boson decays | Ann. Rev. Nucl. Part. Sci. 58 (2008) 75 | 0801.4554 |
| 22 | J. Ellis et al. | Higgs bosons in a nonminimal supersymmetric model | PRD 39 (1989) 844 | |
| 23 | U. Ellwanger, M. Rausch de Traubenberg, and C. A. Savoy | Particle spectrum in supersymmetric models with a gauge singlet | PLB 315 (1993) 331 | hep-ph/9307322 |
| 24 | U. Ellwanger, M. Rausch de Traubenberg, and C. A. Savoy | Higgs phenomenology of the supersymmetric model with a gauge singlet | Z. Phys. C 67 (1995) 665 | hep-ph/9502206 |
| 25 | B. A. Dobrescu, G. L. Landsberg, and K. T. Matchev | Higgs boson decays to CP-odd scalars at the Tevatron and beyond | PRD 63 (2001) 075003 | hep-ph/0005308 |
| 26 | D. J. Miller, R. Nevzorov, and P. M. Zerwas | The Higgs sector of the next-to-minimal supersymmetric standard model | Nucl. Phys. B 681 (2004) 3 | hep-ph/0304049 |
| 27 | A. Belyaev et al. | LHC discovery potential of the lightest NMSSM Higgs in the $ h_1 \to a_1 a_1 \to 4 \mu $ channel | PRD 81 (2010) 075021 | 1002.1956 |
| 28 | R. Dermisek and J. F. Gunion | New constraints on a light CP-odd Higgs boson and related NMSSM ideal Higgs scenarios | PRD 81 (2010) 075003 | 1002.1971 |
| 29 | N. Arkani-Hamed, D. P. Finkbeiner, T. R. Slatyer, and N. Weiner | A theory of dark matter | PRD 79 (2009) 015014 | 0810.0713 |
| 30 | M. Baumgart et al. | Non-Abelian dark sectors and their collider signatures | JHEP 04 (2009) 014 | 0901.0283 |
| 31 | A. Falkowski, J. T. Ruderman, T. Volansky, and J. Zupan | Hidden Higgs decaying to lepton jets | JHEP 05 (2010) 077 | 1002.2952 |
| 32 | J. Hisano, S. Matsumoto, and M. M. Nojiri | Explosive dark matter annihilation | PRL 92 (2004) 031303 | hep-ph/0307216 |
| 33 | M. Cirelli, M. Kadastik, M. Raidal, and A. Strumia | Model-independent implications of the $ e^{\pm} $, $ \bar{p} $ cosmic ray spectra on properties of dark matter | Nucl. Phys. B 813 (2009) 1 | 0809.2409 |
| 34 | B. Holdom | Two U(1)'s and $ \epsilon $ charge shifts | PLB 166 (1986) 196 | |
| 35 | K. R. Dienes, C. F. Kolda, and J. March-Russell | Kinetic mixing and the supersymmetric gauge hierarchy | Nucl. Phys. B 492 (1997) 104 | hep-ph/9610479 |
| 36 | C. Cheung, J. T. Ruderman, L.-T. Wang, and I. Yavin | Kinetic mixing as the origin of light dark scales | PRD 80 (2009) 035008 | 0902.3246 |
| 37 | D0 Collaboration | Search for NMSSM Higgs bosons in the $ h \to aa \to \mu \mu \mu \mu, \mu \mu \tau \tau $ channels using $ p\bar{p} $ collisions at $ \sqrt{s} = 1.96 $~TeV | PRL 103 (2009) 061801 | 0905.3381 |
| 38 | J. Pivarski, A. Safonov, and A. Tatarinov | Search for collimated groups of muons | CMS Note 2010/462 (2010) | |
| 39 | CMS Collaboration | Search for light resonances decaying into pairs of muons as a signal of new physics | JHEP 07 (2011) 098 | CMS-EXO-11-013 1106.2375 |
| 40 | ATLAS Collaboration | Search for displaced muonic lepton jets from light Higgs boson decay in proton-proton collisions at $ \sqrt{s}=7 $ TeV with the ATLAS detector | , Submitted to PLB | 1210.0435 |
| 41 | Y. Pakhotin, A. Safonov, and A. Tatarinov | Search for New Light Bosons from the Higgs Boson Decays Using Multi-Muon Events at the LHC | CMS Note 2011/238 (2011) | |
| 42 | CMS Collaboration | Search for a non-standard-model Higgs boson decaying to a pair of new light bosons in four-muon final states | CMS-EXO-12-012 1210.7619 |
|
| 43 | ATLAS Collaboration Collaboration | Search for long-lived neutral particles decaying into lepton jets in proton--proton collisions at $ \sqrt{s} $ = 8 TeV with the ATLAS detector | 1409.0746 | |
| 44 | CMS Collaboration | A search for pair production of new light bosons decaying into muons | PLB752 (2016) 146--168 | CMS-HIG-13-010 1506.00424 |
| 45 | CLEO Collaboration | Search for very light CP-odd Higgs boson in radiative decays of $ \Upsilon(1S) $ | PRL 101 (2008) 151802 | 0807.1427 |
| 46 | BABAR Collaboration | Search for dimuon decays of a light scalar boson in radiative transitions $ \Upsilon \to \gamma A_0 $ | PRL 103 (2009) 081803 | 0905.4539 |
| 47 | BESIII Collaboration Collaboration | Search for a light exotic particle in $ J/ {\psi} $ radiative decays | PRD 85 (May, 2012) 092012 | |
| 48 | BESIII Collaboration Collaboration | Search for a light $ CP $-odd Higgs boson in radiative decays of $ J/ {\psi} $ | PRD 93 (Mar, 2016) 052005 | |
| 49 | CDF Collaboration | Search for a very light CP-odd Higgs boson in top quark decays from $ p \bar{p} $ Collisions at 1.96 TeV | PRL 107 (2011) 031801 | 1104.5701 |
| 50 | CMS Collaboration | Search for a light pseudoscalar Higgs boson in the dimuon decay channel in pp collisions at $ \sqrt{s} = 7 $~TeV | PRL 109 (2012) 121801 | CMS-HIG-12-004 1206.6326 |
| 51 | N. Jarosik et al. | Seven-year Wilkinson microwave anisotropy probe (WMAP) observations: sky maps,systematic errors, and basic results | Astrophys. J. Suppl. 192 (2011) 14 | 1001.4744 |
| 52 | OPAL Collaboration | Decay mode independent searches for new scalar bosons with the OPAL detector at LEP | EPJC 27 (2003) 311 | hep-ex/0206022 |
| 53 | OPAL Collaboration | Search for a low mass CP-odd Higgs boson in $ e^+ e^- $ collisions with the OPAL detector at LEP-2 | EPJC 27 (2003) 483 | hep-ex/0209068 |
| 54 | ALEPH, DELPHI, L3, OPAL, LEP Working Group for Higgs Boson Searches Collaboration | Search for neutral MSSM Higgs bosons at LEP | EPJC 47 (2006) 547 | hep-ex/0602042 |
| 55 | D0 Collaboration | Search for dark photons from supersymmetric hidden valleys | PRL 103 (2009) 081802 | 0905.1478 |
| 56 | D0 Collaboration | Search for events with leptonic jets and missing transverse energy in $ \text{p}\bar{\text{p}} $ collisions at $ \sqrt{s}=1.96 $~TeV | PRL 105 (2010) 211802 | 1008.3356 |
| 57 | CDF Collaboration | Search for anomalous production of multiple leptons in association with $ W $ and $ Z $ bosons at CDF | PRD 85 (2012) 092001 | 1202.1260 |
| 58 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 59 | CMS Collaboration | Performance of CMS muon reconstruction in $ \text{p} \text{p} $ collision events at $ \sqrt{s} = 7 $~TeV | JINST 7 (2012) P10002 | CMS-MUO-10-004 1206.4071 |
| 60 | T. Sj$\ddot\texto$strand, S. Mrenna, and P. Z. Skands | PYTHIA 6.4 physics and manual | JHEP 05 (2006) 026 | hep-ph/0603175 |
| 61 | J. Alwall et al. | MadGraph/MadEvent v4: the new web generation | JHEP 09 (2007) 028 | 0706.2334 |
| 62 | P. Meade and M. Reece | BRIDGE: Branching ratio inquiry / decay generated events | hep-ph/0703031 | |
| 63 | J. Allison et al. | Geant4 developments and applications | IEEE Trans. Nucl. Sci. 53 (2006) 270 | |
| 64 | S. Bernstein | Demonstration du theoreme de Weierstrass fondee sur le calcul des probabilities | Comm. Soc. Math. Kharkov 13 (1912) 1 | |
| 65 | M. J. Oreglia | PhD thesis, Stanford University, 1980 SLAC Report SLAC-R-236, Appendix D | ||
| 66 | CMS Collaboration | Studies of Higgs boson production in the four-lepton final state at $ \sqrt{s} $ = 13 TeV | CMS-PAS-HIG-15-004 (Mar, 2016) | |
| 67 | J. Butterworth et al. | PDF4LHC recommendations for LHC Run II | Journal of Physics G: Nuclear and Particle Physics 43 (2016), no. 2, 023001 | |
| 68 | J. M. Campbell and R. Ellis | Loops and Legs in Quantum Field Theory MCFM for the Tevatron and the LHC | Nuclear Physics B - Proceedings Supplements 205 (2010) 10 -- 15 | |
| 69 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 1. Inclusive Observables | 1101.0593 | |
| 70 | B. Batell, M. Pospelov, and A. Ritz | Probing a Secluded U(1) at B-factories | Phys.Rev. D79 (2009) 115008 | 0903.0363 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|