

Compact Muon Solenoid
LHC, CERN
| CMS-PAS-FTR-21-010 | ||
| Search for the nonresonant $\mathrm{t\bar{t}}$HH production in the semileptonic decay of the top pair and the Higgs pair decay into b quarks at the HL-LHC | ||
| CMS Collaboration | ||
| March 2022 | ||
| Abstract: This work describes a prospective search for the production of a top quark-antiquark pair associated to a pair of Higgs bosons with the upgraded CMS detector at the High-Luminosity LHC using proton-proton collisions at $\sqrt{s}= $ 14 TeV. The analysis is performed on dedicated samples simulated with the upgraded Phase-2 conditions. The candidate $\mathrm{t\bar{t}}$HH events are selected with criteria targeting the lepton plus jets decay channels of the $\mathrm{t\bar{t}}$ system and the decay of the double Higgs bosons into two bottom quark-antiquark pairs. In order to increase the sensitivity of the search, selected events are input to a multi-classifier deep neural network. The resulting discriminants are split into several b jet multiplicity categories with different expected signal and background rates. A simultaneous maximum likelihood fit is performed to evaluate the expected sensitivity reach. The analysis is expected to exclude $\mathrm{t\bar{t}}$HH production down to 3.14 times the SM cross section with 3000 fb$^{-1}$ of data. The sensitivity for Minimal Composite Higgs Model scenarios is also presented. | ||
| Links: CDS record (PDF) ; CADI line (restricted) ; | ||
| Figures | |
png pdf |
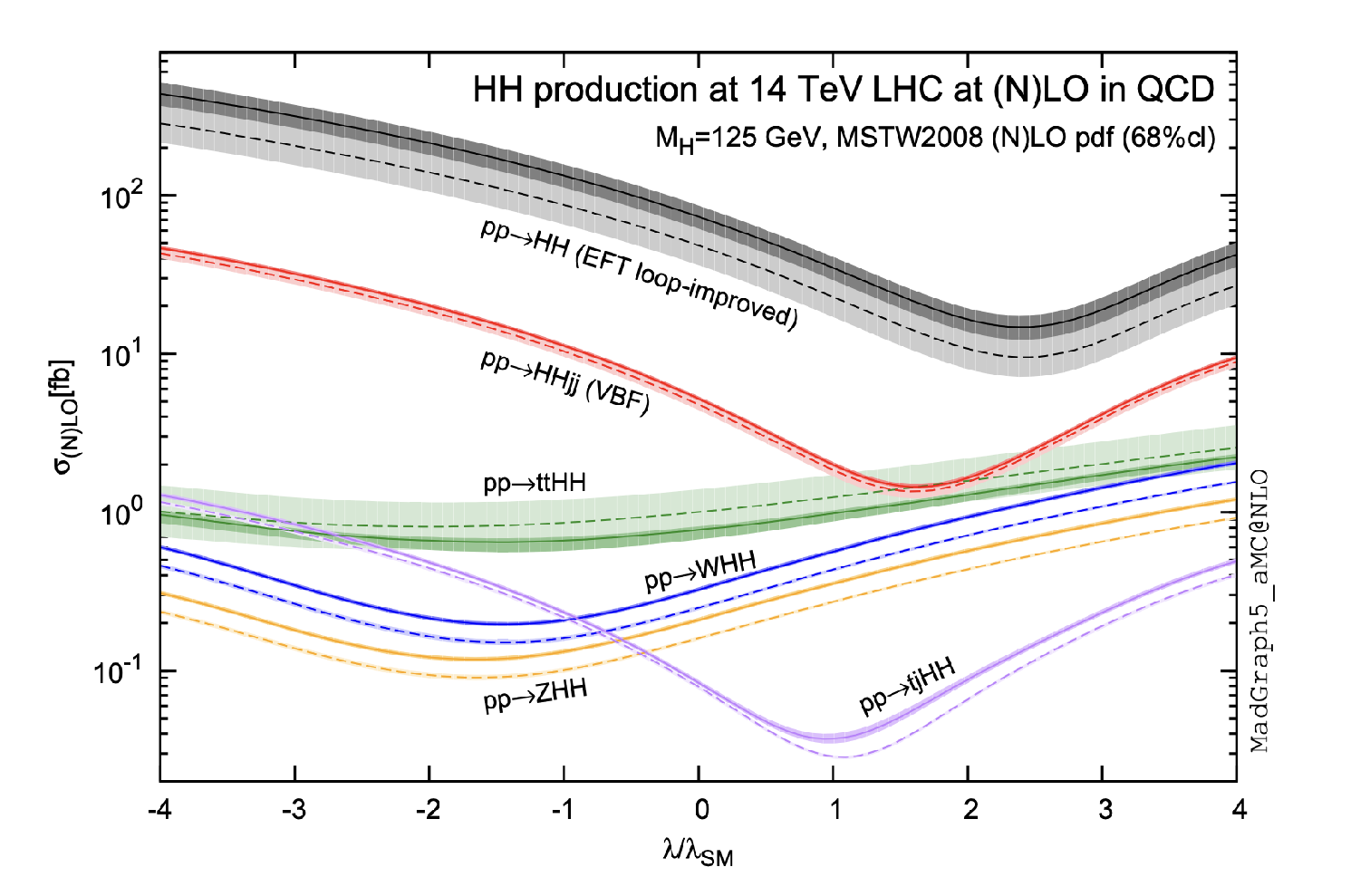
Figure 1:
Total cross sections at the LO and NLO in QCD for HH production channels, as a function of the self-interaction coupling $\lambda $ [5]. The dashed (solid) lines and light-(dark) colored bands correspond to the LO (NLO) results and to the scale of the PDF uncertainties added linearly. The SM values of the cross section are obtained at $\lambda /\lambda _{SM}=$ 1. |
png pdf |
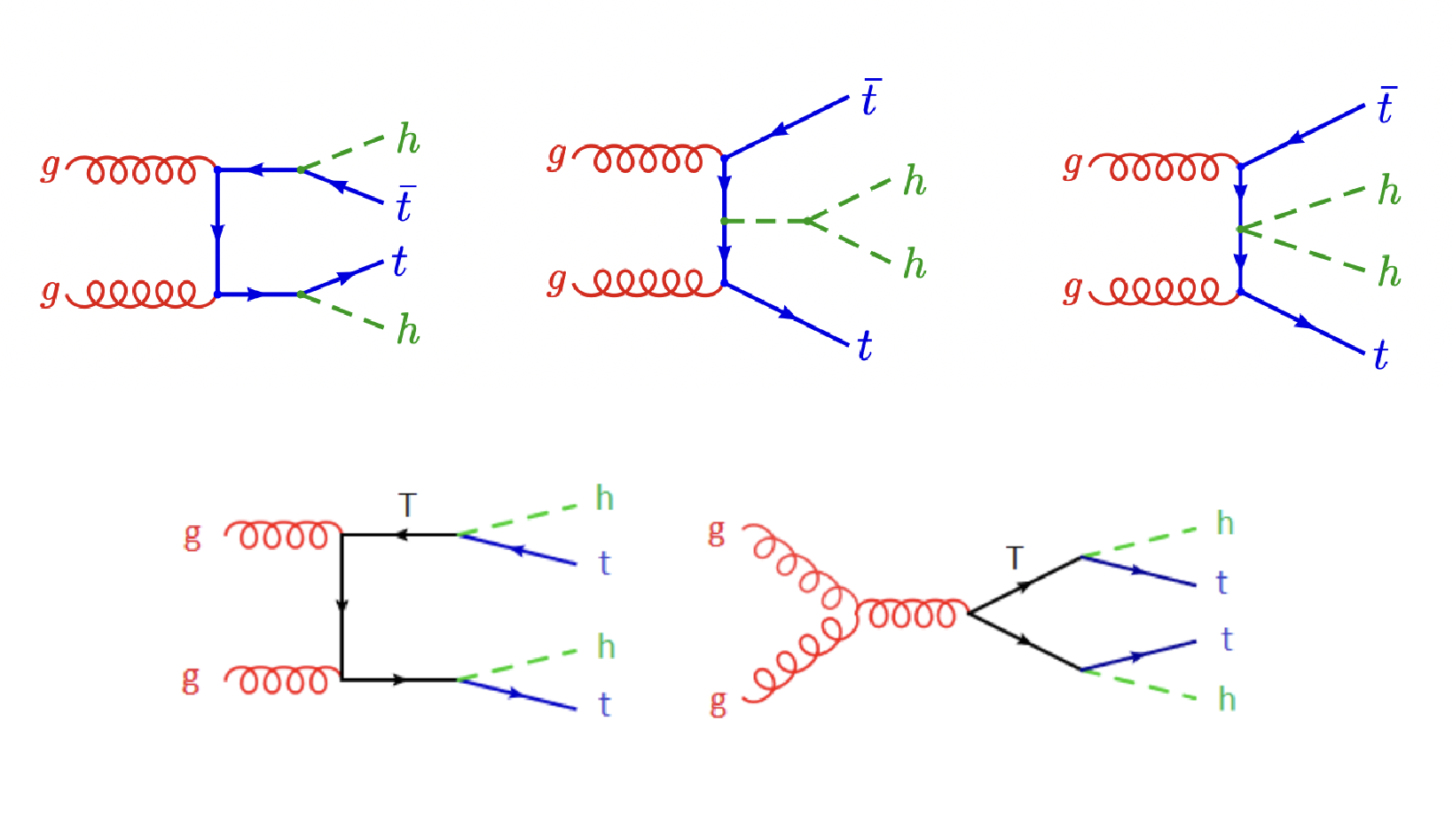
Figure 2:
Representative diagrams for the $\mathrm {t\bar{t}}$HH production process at LO within MCHM. Top: the non-resonant part of the $\mathrm {t\bar{t}}$HH production process, illustrating the three distinct physical subprocesses: the Yukawa vertex and the Higgs trilinear self-coupling, as in the SM case, and the "double Higgs" Yukawa vertex arising in Composite Higgs Models (CHM). Bottom: the resonant part illustrating the QCD pair production of the top heavy partners, with their top-Higgs decay. |
png |
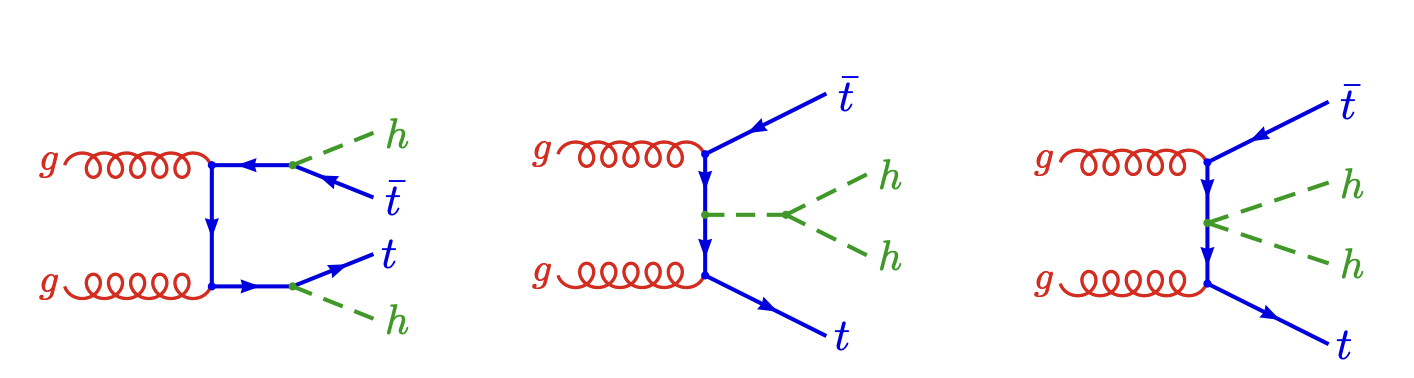
Figure 2-a:
Representative diagrams for the $\mathrm {t\bar{t}}$HH production process at LO within MCHM. Top: the non-resonant part of the $\mathrm {t\bar{t}}$HH production process, illustrating the three distinct physical subprocesses: the Yukawa vertex and the Higgs trilinear self-coupling, as in the SM case, and the "double Higgs" Yukawa vertex arising in Composite Higgs Models (CHM). Bottom: the resonant part illustrating the QCD pair production of the top heavy partners, with their top-Higgs decay. |
png |
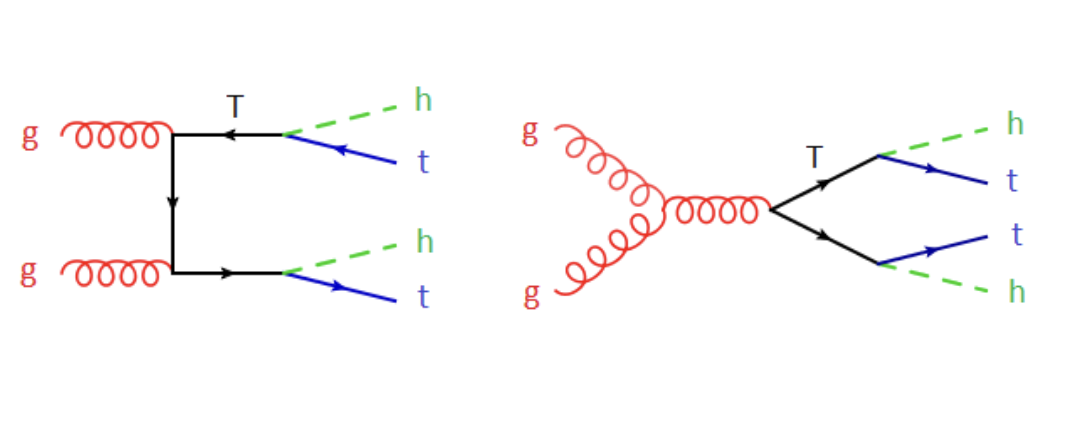
Figure 2-b:
Representative diagrams for the $\mathrm {t\bar{t}}$HH production process at LO within MCHM. Top: the non-resonant part of the $\mathrm {t\bar{t}}$HH production process, illustrating the three distinct physical subprocesses: the Yukawa vertex and the Higgs trilinear self-coupling, as in the SM case, and the "double Higgs" Yukawa vertex arising in Composite Higgs Models (CHM). Bottom: the resonant part illustrating the QCD pair production of the top heavy partners, with their top-Higgs decay. |
png pdf |
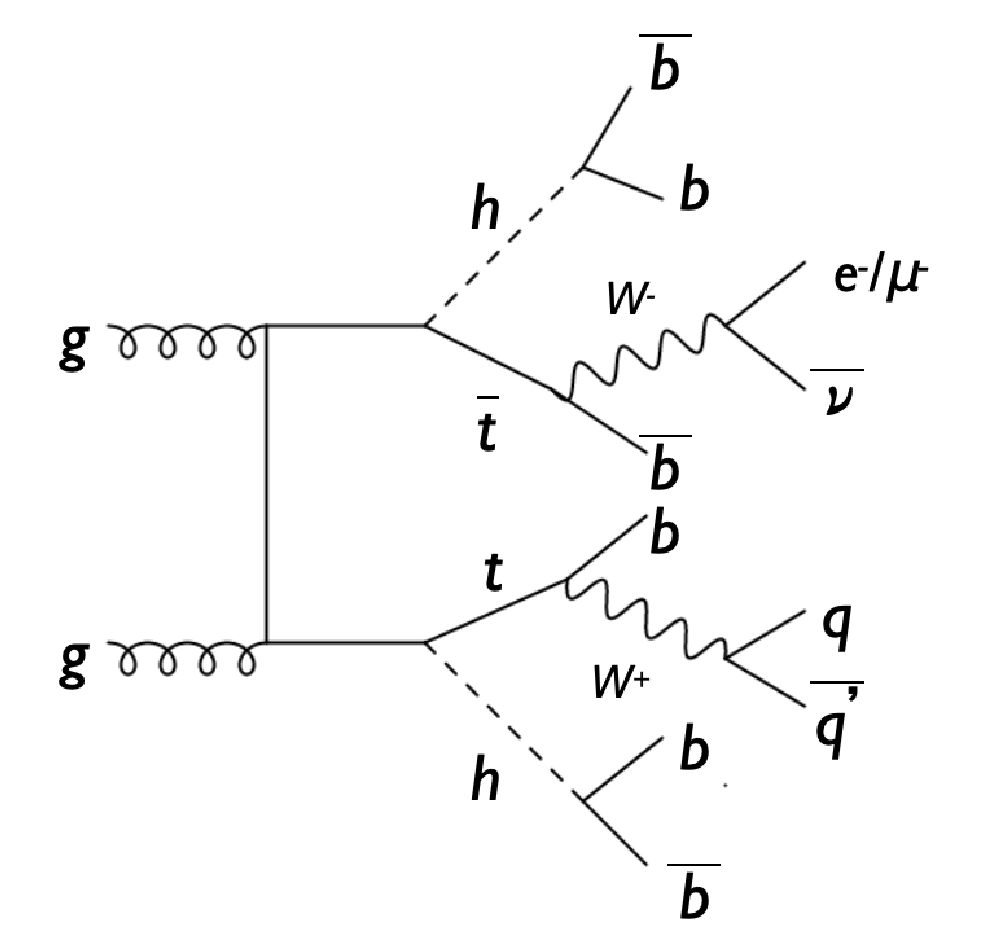
Figure 3:
Feynman diagram of the $\mathrm {t\bar{t}}$HH production process, the signal topology studied in this analysis. |
png pdf |
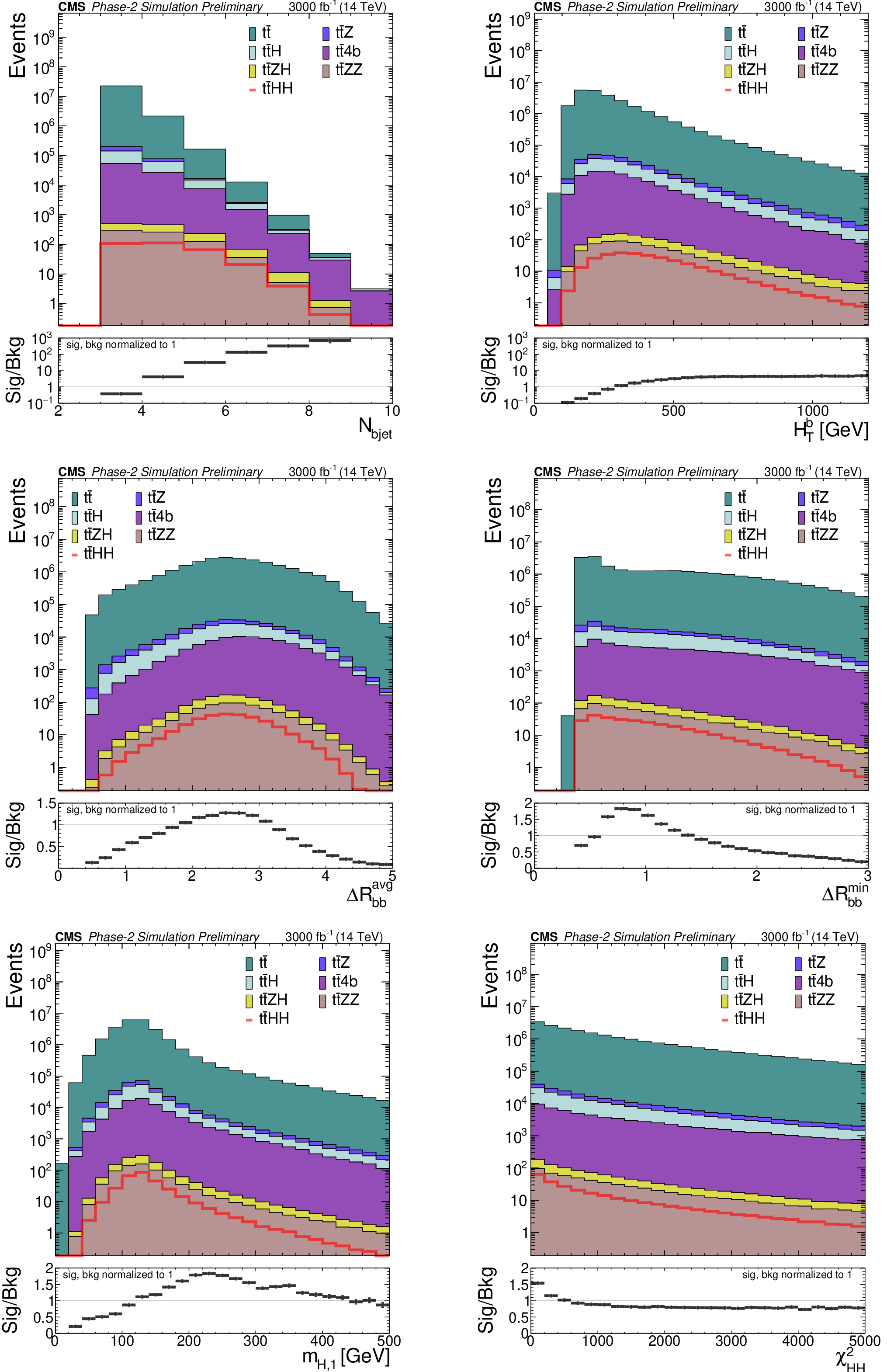
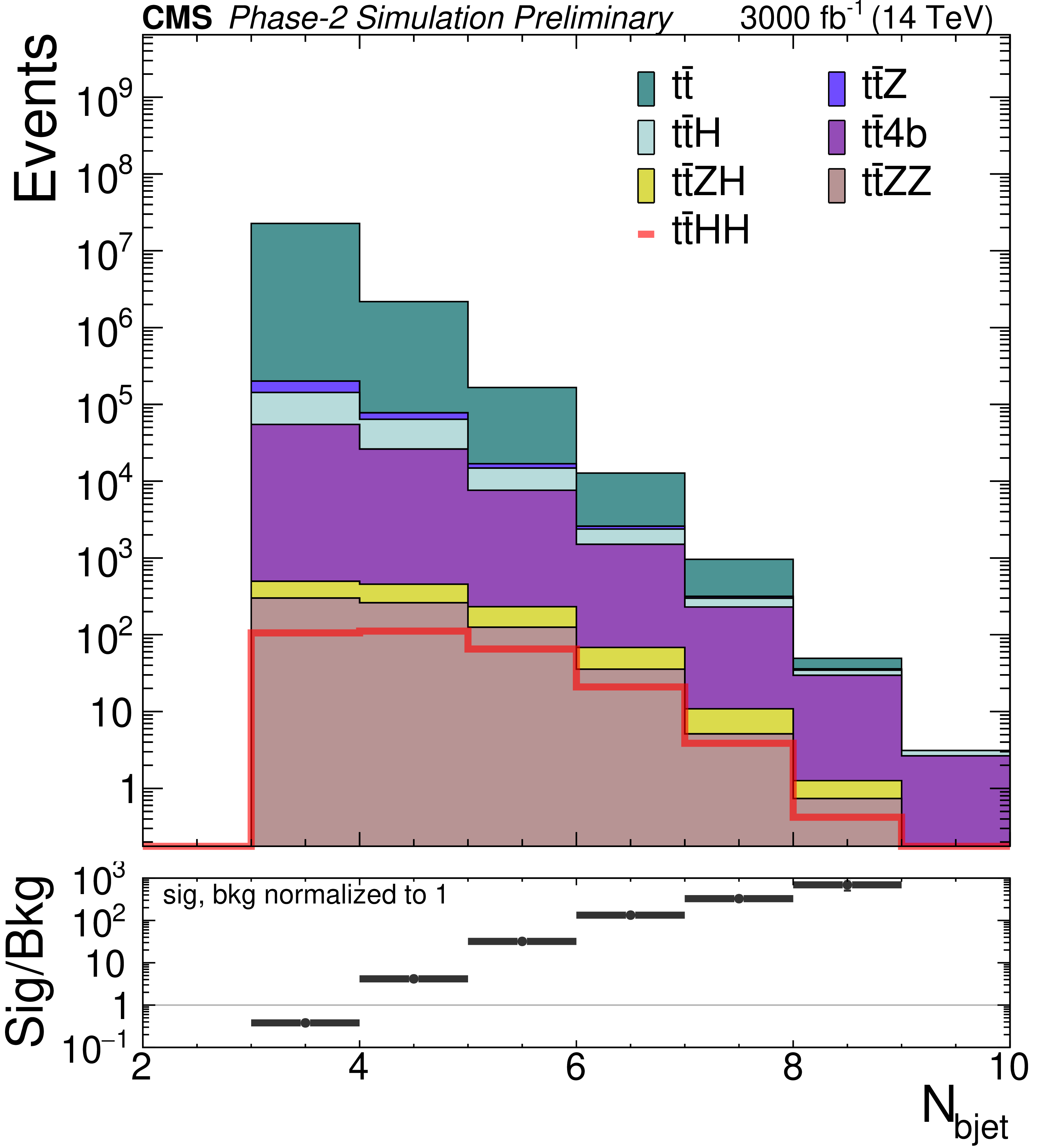
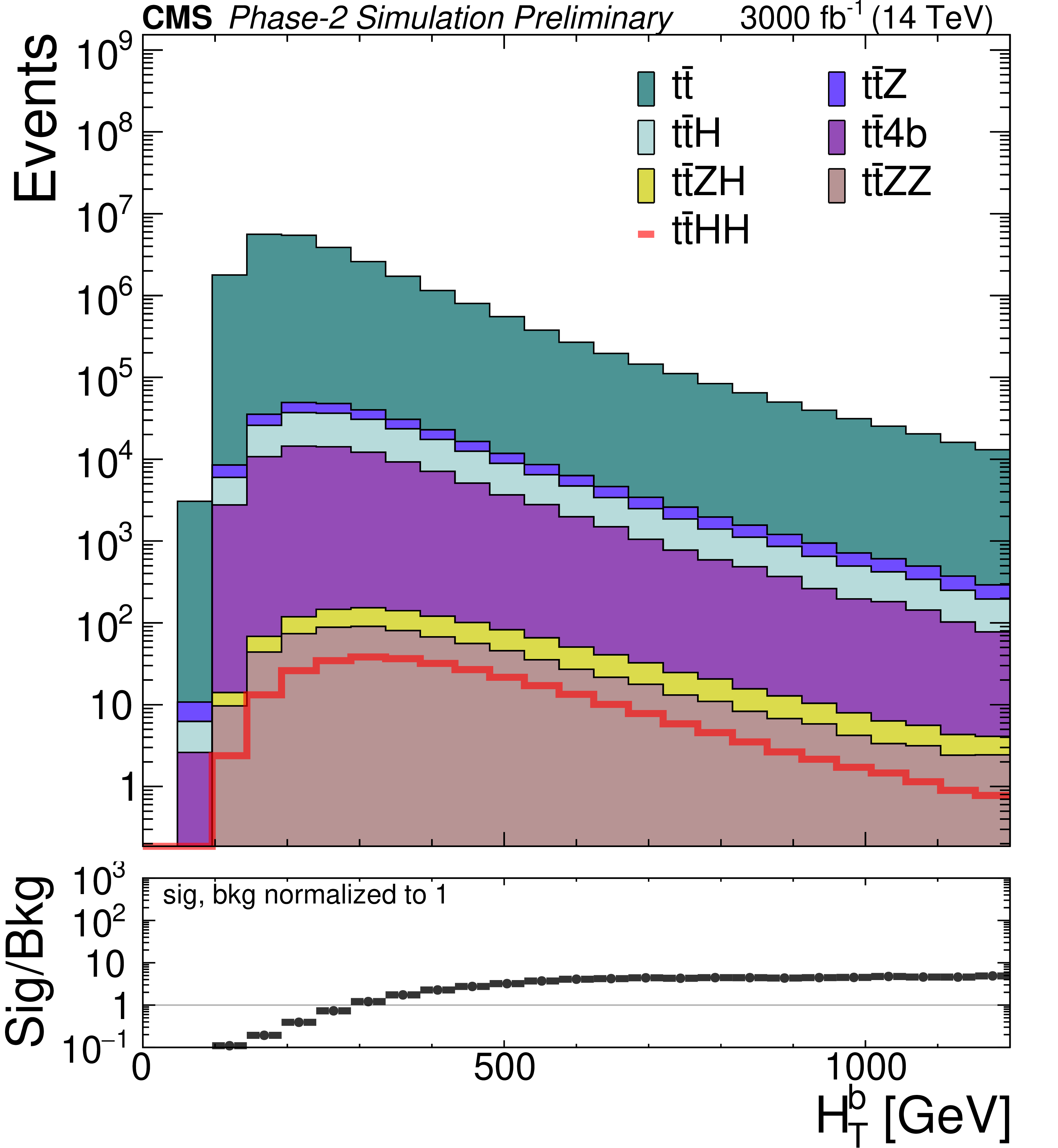
Figure 4:
Distributions of different discriminating variables after the baseline selection of the SM $\mathrm {t\bar{t}}$HH signal and the SM backgrounds, normalized to 3000 fb$^{-1}$ luminosity. The variables are: b jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and minimum (middle right) $\Delta R$ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). Background distributions are stacked. The ratio plots in the bottom panels are computed by taking signal and total background yields to be normalized to 1. |
png pdf |
Figure 4-a:
Distributions of different discriminating variables after the baseline selection of the SM $\mathrm {t\bar{t}}$HH signal and the SM backgrounds, normalized to 3000 fb$^{-1}$ luminosity. The variables are: b jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and minimum (middle right) $\Delta R$ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). Background distributions are stacked. The ratio plots in the bottom panels are computed by taking signal and total background yields to be normalized to 1. |
png pdf |
Figure 4-b:
Distributions of different discriminating variables after the baseline selection of the SM $\mathrm {t\bar{t}}$HH signal and the SM backgrounds, normalized to 3000 fb$^{-1}$ luminosity. The variables are: b jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and minimum (middle right) $\Delta R$ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). Background distributions are stacked. The ratio plots in the bottom panels are computed by taking signal and total background yields to be normalized to 1. |
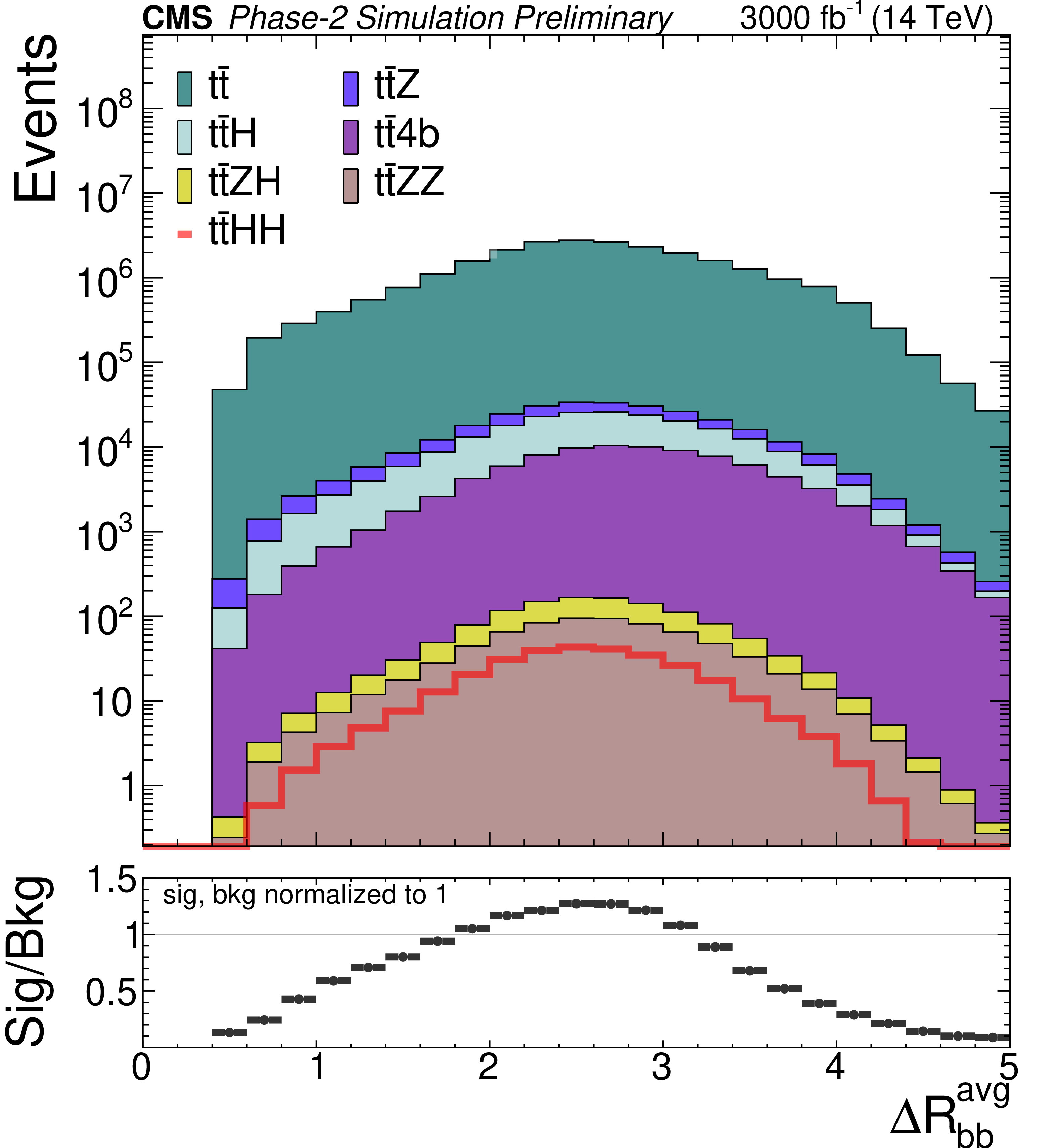
png pdf |
Figure 4-c:
Distributions of different discriminating variables after the baseline selection of the SM $\mathrm {t\bar{t}}$HH signal and the SM backgrounds, normalized to 3000 fb$^{-1}$ luminosity. The variables are: b jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and minimum (middle right) $\Delta R$ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). Background distributions are stacked. The ratio plots in the bottom panels are computed by taking signal and total background yields to be normalized to 1. |
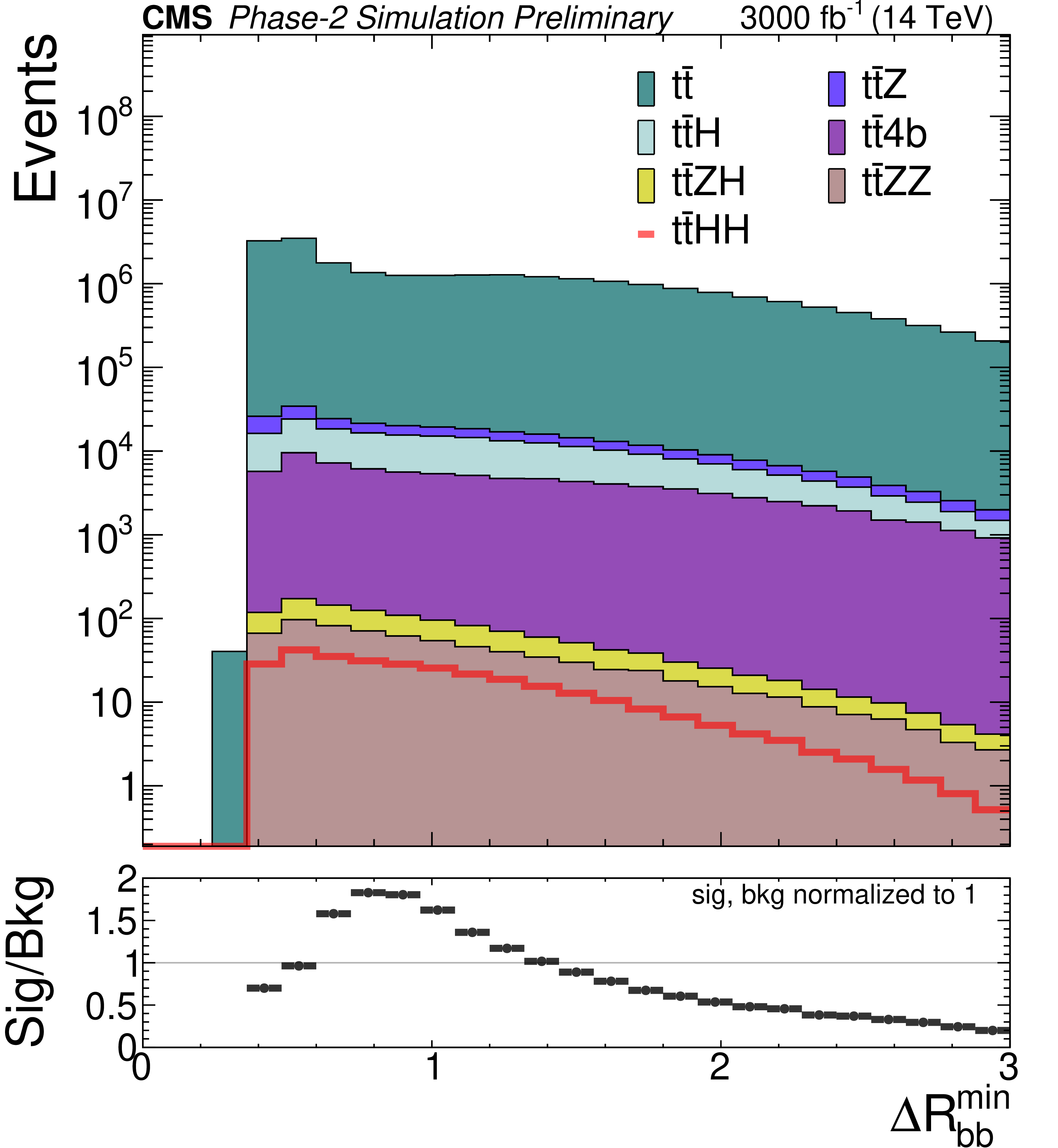
png pdf |
Figure 4-d:
Distributions of different discriminating variables after the baseline selection of the SM $\mathrm {t\bar{t}}$HH signal and the SM backgrounds, normalized to 3000 fb$^{-1}$ luminosity. The variables are: b jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and minimum (middle right) $\Delta R$ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). Background distributions are stacked. The ratio plots in the bottom panels are computed by taking signal and total background yields to be normalized to 1. |
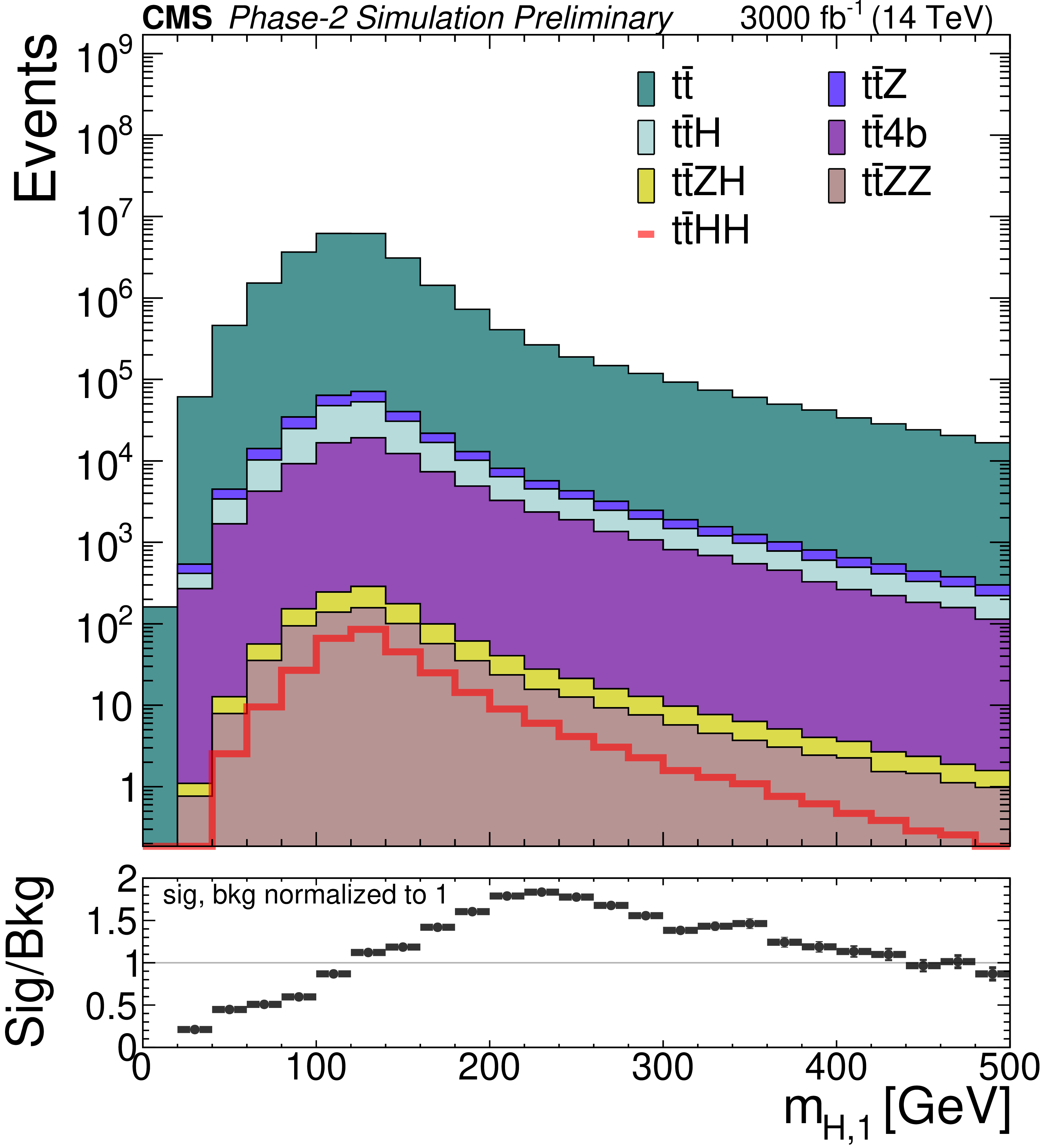
png pdf |
Figure 4-e:
Distributions of different discriminating variables after the baseline selection of the SM $\mathrm {t\bar{t}}$HH signal and the SM backgrounds, normalized to 3000 fb$^{-1}$ luminosity. The variables are: b jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and minimum (middle right) $\Delta R$ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). Background distributions are stacked. The ratio plots in the bottom panels are computed by taking signal and total background yields to be normalized to 1. |
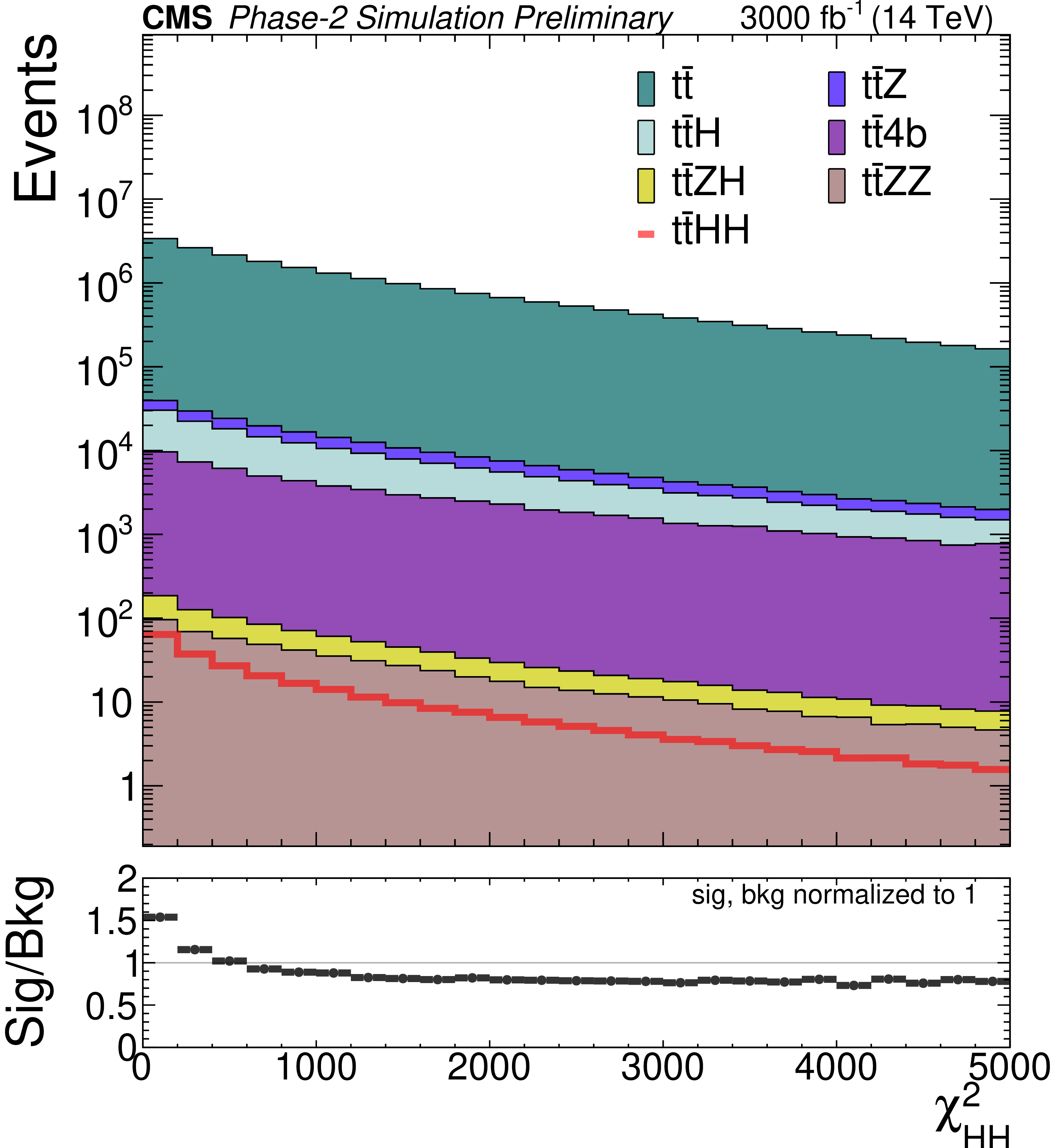
png pdf |
Figure 4-f:
Distributions of different discriminating variables after the baseline selection of the SM $\mathrm {t\bar{t}}$HH signal and the SM backgrounds, normalized to 3000 fb$^{-1}$ luminosity. The variables are: b jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and minimum (middle right) $\Delta R$ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). Background distributions are stacked. The ratio plots in the bottom panels are computed by taking signal and total background yields to be normalized to 1. |
png pdf |
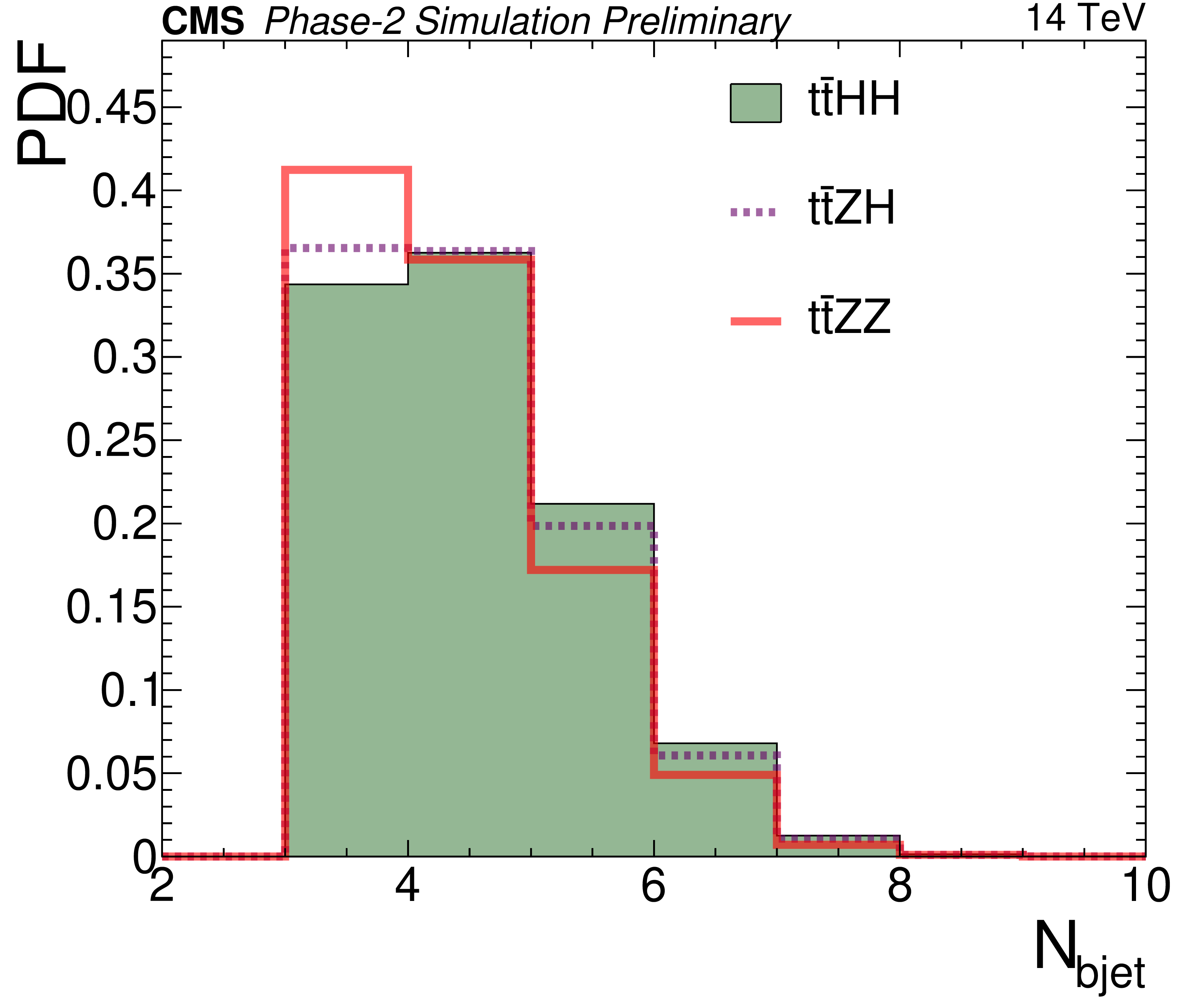
Figure 5-a:
Probability density functions for different discriminating variables after the baseline selection, comparing the SM $\mathrm {t\bar{t}}$HH signal shown as a filled histogram to two irreducible backgrounds : $\mathrm {t\bar{t}}$ZH and $\mathrm {t\bar{t}}$ZZ. The variables are: b-jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and maximum (middle right) $\Delta \eta $ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). |
png pdf |
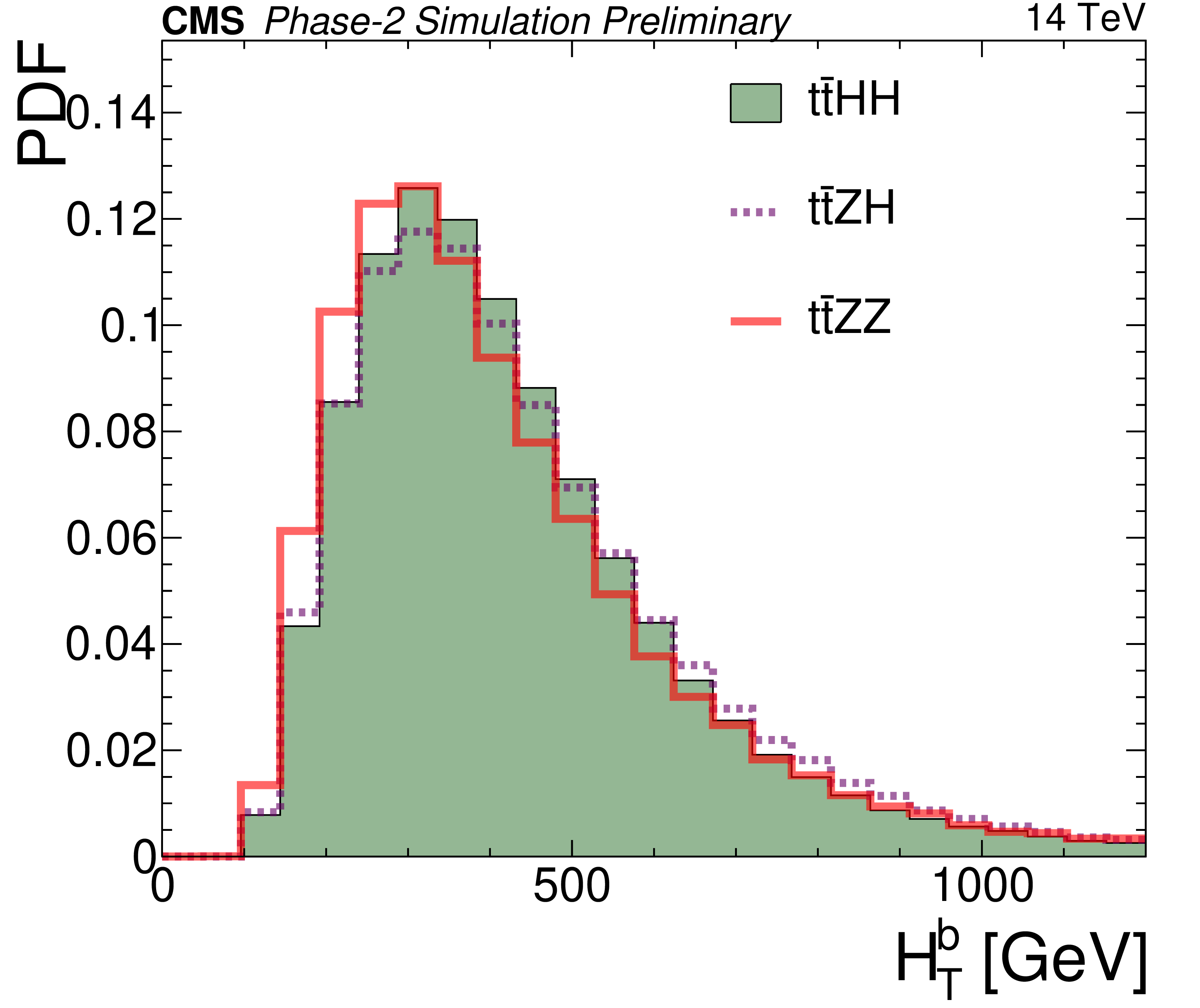
Figure 5-b:
Probability density functions for different discriminating variables after the baseline selection, comparing the SM $\mathrm {t\bar{t}}$HH signal shown as a filled histogram to two irreducible backgrounds : $\mathrm {t\bar{t}}$ZH and $\mathrm {t\bar{t}}$ZZ. The variables are: b-jet multiplicity (top left), hadronic transverse momentum built from b jets (top right), average (middle left) and maximum (middle right) $\Delta \eta $ between any two b jets, invariant mass of the reconstructed Higgs candidate with the closest mass to that of the Higgs boson (bottom left), and minimum $\chi ^2_{HH}$ (bottom right). |
png |
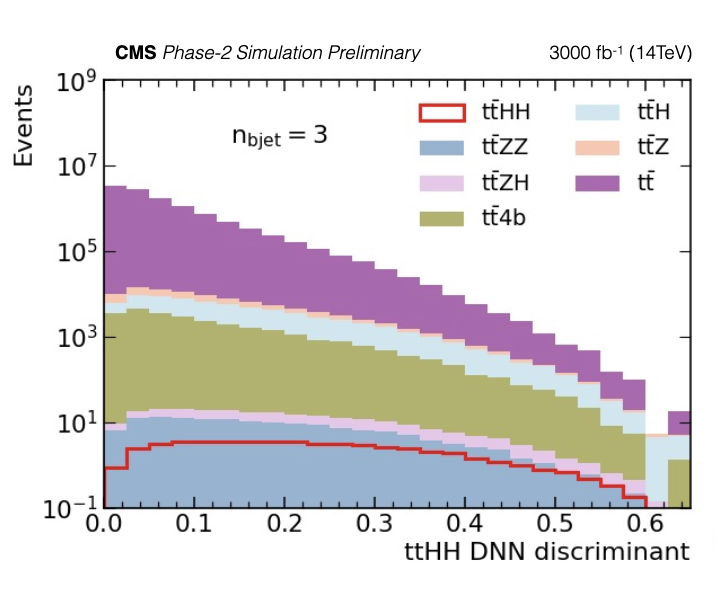
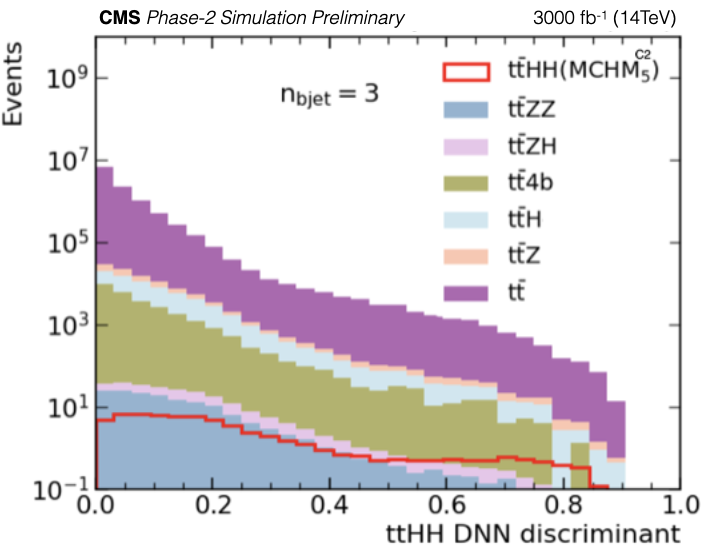
Figure 7-a:
Final discriminant distributions for SM $\mathrm {t\bar{t}}$HH are shown for three different $\mathrm {n_{b jet}}$ categories; $\mathrm {n_{b jet}}=$ 3 (top) $\mathrm {n_{b jet}}=$ 4 (middle), and $\mathrm {n_{b jet}} > $ 4 (bottom). The plots show the expected event yields. |
png |
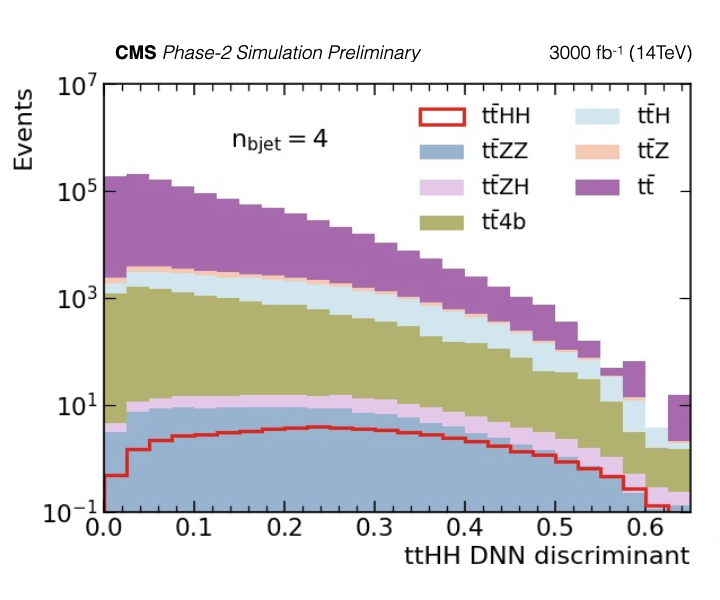
Figure 7-b:
Final discriminant distributions for SM $\mathrm {t\bar{t}}$HH are shown for three different $\mathrm {n_{b jet}}$ categories; $\mathrm {n_{b jet}}=$ 3 (top) $\mathrm {n_{b jet}}=$ 4 (middle), and $\mathrm {n_{b jet}} > $ 4 (bottom). The plots show the expected event yields. |
png |
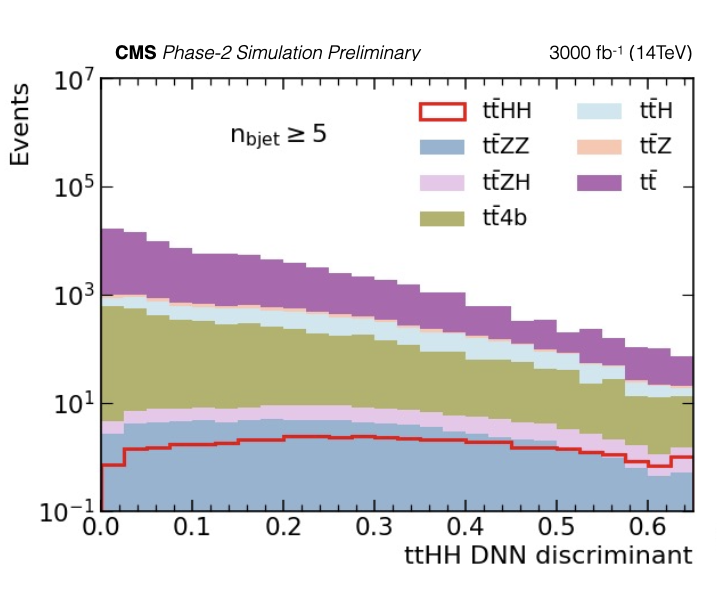
Figure 7-c:
Final discriminant distributions for SM $\mathrm {t\bar{t}}$HH are shown for three different $\mathrm {n_{b jet}}$ categories; $\mathrm {n_{b jet}}=$ 3 (top) $\mathrm {n_{b jet}}=$ 4 (middle), and $\mathrm {n_{b jet}} > $ 4 (bottom). The plots show the expected event yields. |
png |
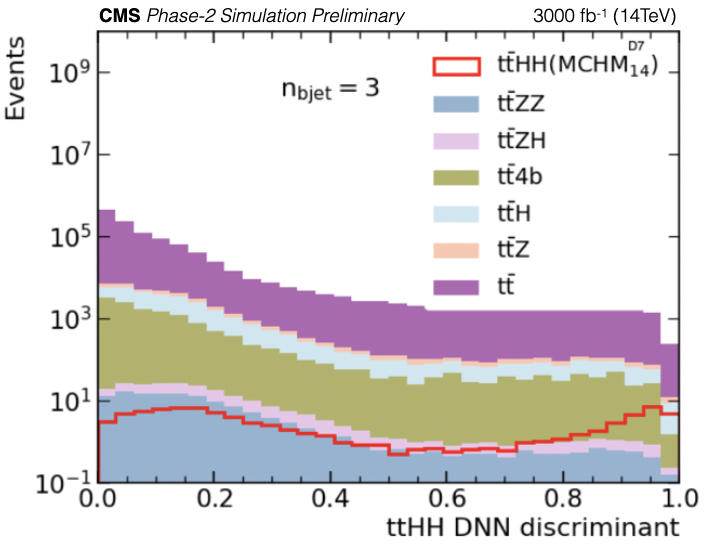
Figure 8-a:
Final discriminant distributions for the $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{5}^{C2}}$ benchmark point case (left) and $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{14}^{D7}}$ benchmark point case (right) are shown. The plots show the expected event yields. |
png |
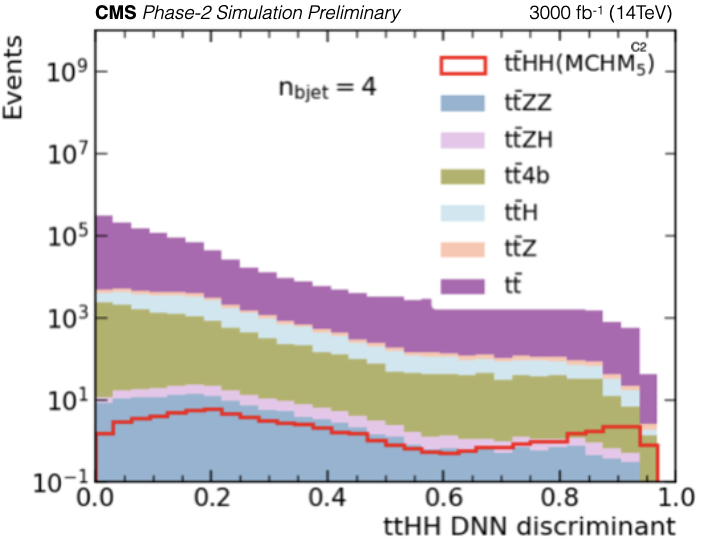
Figure 8-b:
Final discriminant distributions for the $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{5}^{C2}}$ benchmark point case (left) and $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{14}^{D7}}$ benchmark point case (right) are shown. The plots show the expected event yields. |
png |
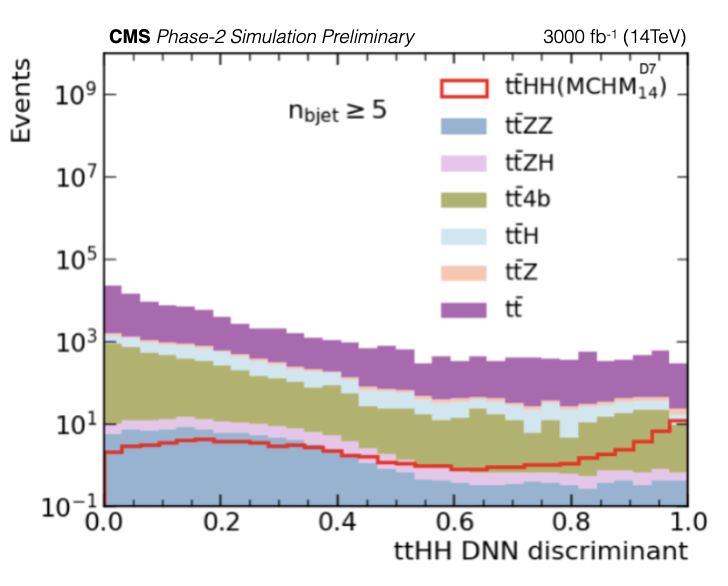
Figure 8-c:
Final discriminant distributions for the $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{5}^{C2}}$ benchmark point case (left) and $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{14}^{D7}}$ benchmark point case (right) are shown. The plots show the expected event yields. |
png |
Figure 8-d:
Final discriminant distributions for the $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{5}^{C2}}$ benchmark point case (left) and $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{14}^{D7}}$ benchmark point case (right) are shown. The plots show the expected event yields. |
png |
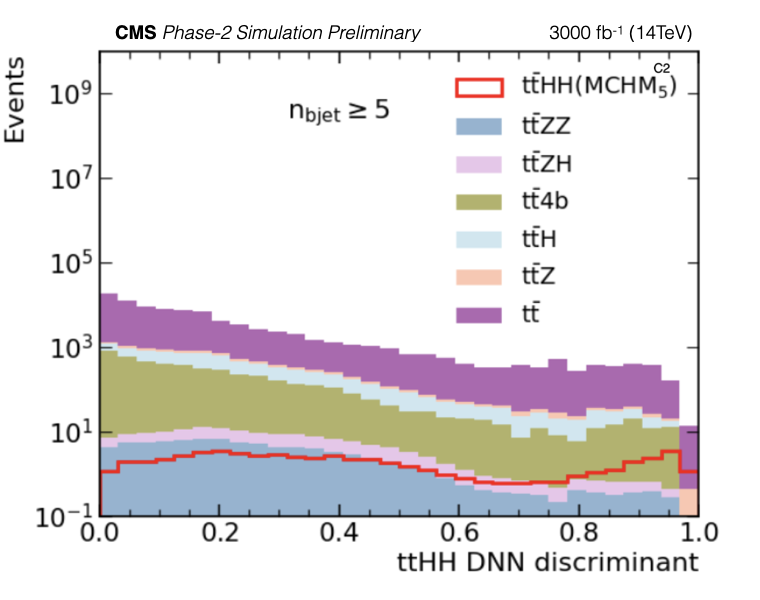
Figure 8-e:
Final discriminant distributions for the $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{5}^{C2}}$ benchmark point case (left) and $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{14}^{D7}}$ benchmark point case (right) are shown. The plots show the expected event yields. |
png |
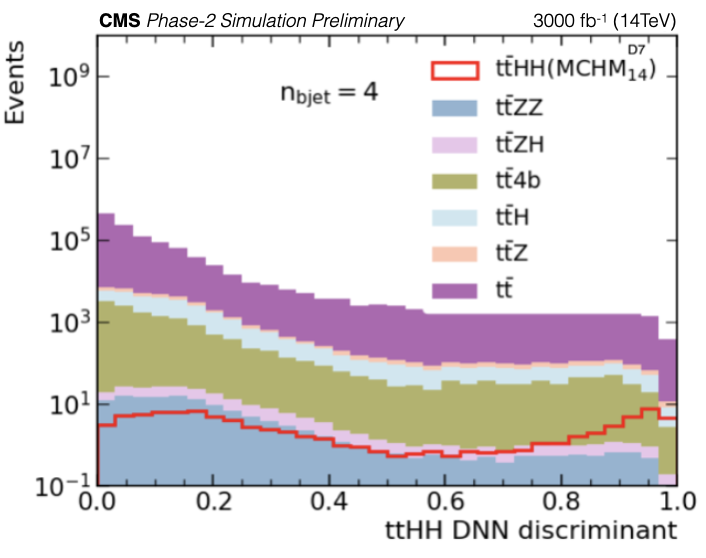
Figure 8-f:
Final discriminant distributions for the $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{5}^{C2}}$ benchmark point case (left) and $\mathrm {t\bar{t}}$HH MCHM$\mathrm {_{14}^{D7}}$ benchmark point case (right) are shown. The plots show the expected event yields. |
png pdf |
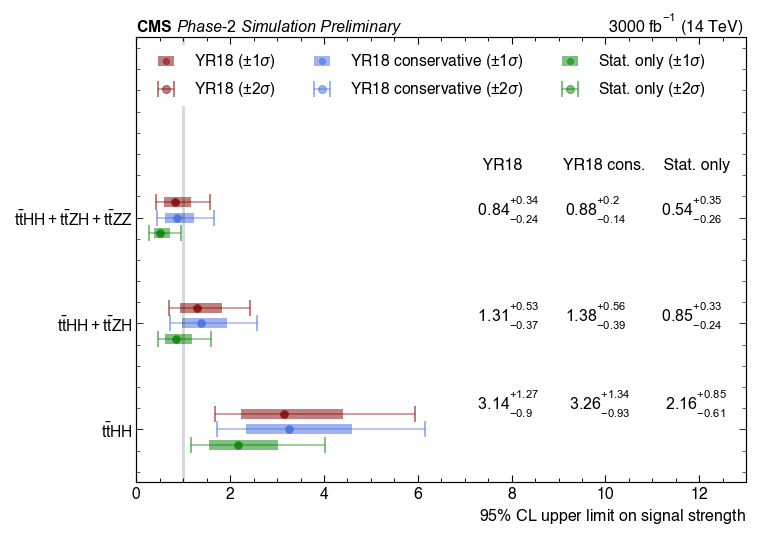
Figure 9:
The 95% upper limits on the signal strength shown for the SM $\mathrm {t\bar{t}}$HH, $\mathrm {t\bar{t}}$HH + $\mathrm {t\bar{t}}$ZH and $\mathrm {t\bar{t}}$HH +$\mathrm {t\bar{t}}$ZH + $\mathrm {t\bar{t}}$ZZ processes for different scenarios of systematic uncertainties. |
png pdf |
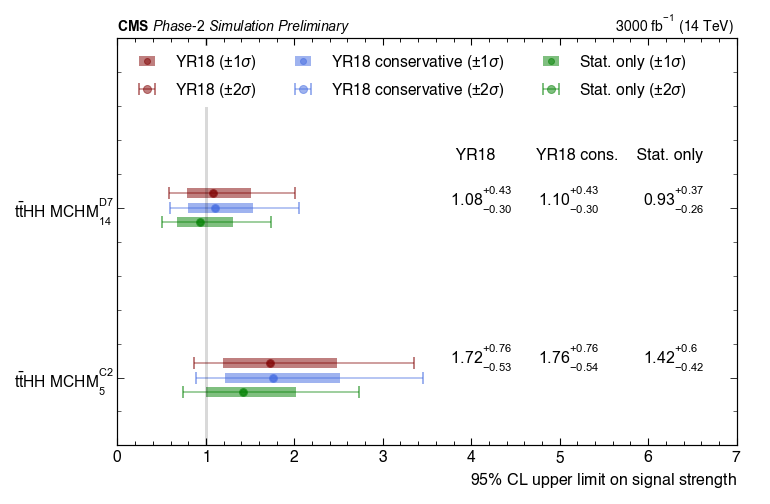
Figure 10:
The 95% upper limits on the signal strength shown for the $\mathrm {t\bar{t}}$HH MCHM$_{5}^{C2}$ and $\mathrm {t\bar{t}}$HH MCHM$_{14}^{D7}$ processes for different scenarios of systematic uncertainties. |
| Summary |
|
A study was performed to assess the sensitivity of the HL-LHC and the Phase-2 CMS detector to standard model di-Higgs production in association with a top-antitop quark pair ($\mathrm{t\bar{t}}$HH) for an integrated luminosity of 3000 fb$^{-1}$. The Higgs bosons are assumed to decay into b quark pairs while the $\mathrm{t\bar{t}}$ system is assumed to decay semileptonically. In addition, the study explored the HL-LHC sensitivity to beyond the standard model contributions to $\mathrm{t\bar{t}}$HH within the context of the Minimal Composite Higgs Models (MCHM). The analysis explored final states with exactly one electron or muon, multiple jets, multiple b-quark jets and moderate missing transverse energy, using Monte Carlo simulated events. Selected events were used for training deep neural networks that enhance signal by classifying events into signal and background categories. Dedicated networks were trained for the SM and MCHM signals. Events were partitioned into 3 search channels having number of b-quark jets equal to 3, equal to 4 and greater then or equal to 5. A statistical analysis was performed by simultaneously fitting the multi-classifier DNN discriminants in all available categories for the three b-jet multiplicity channels using a profile likelihood ratio method. Effects of various systematic uncertainties for the Phase-2 conditions are taken into account. With 3000 fb$^{-1}$ of data, and considering the YR18 systematic uncertainties, it is expected that the upper limit at the 95% CL on the combined $\mathrm{t\bar{t}}$ZZ+$\mathrm{t\bar{t}}$ZH+$\mathrm{t\bar{t}}$HH production cross section is $0.84^{+0.34}_{-0.24}$ times the SM prediction. If $\mathrm{t\bar{t}}$ZZ is taken as background, the upper limit on the combined $\mathrm{t\bar{t}}$ZH+$\mathrm{t\bar{t}}$HH production cross section is expected to be 1.31$^{+0.53}_{-0.37}$ times the SM prediction. If $\mathrm{t\bar{t}}$ZZ+$\mathrm{t\bar{t}}$ZH are taken as backgrounds, the upper limit on the $\mathrm{t\bar{t}}$HH production cross section alone is expected to become 3.14$^{+1.27}_{-0.9}$ times the SM prediction. For the MCHM case, the upper limits at the 95% CL $\mathrm{t\bar{t}}$HH cross sections are obtained as 1.72$^{+0.76}_{-0.53}$ times the MCHM$_{5}^{C2}$ prediction and 1.08$^{+0.43}_{-0.30}$ times the MCHM$_{14}^{D7}$ prediction, respectively. Moreover, the analysis demonstrated various kinematic characteristics of the MCHM scenarios that would discriminate them from the SM $\mathrm{t\bar{t}}$HH process. Overall, this exploratory work demonstrates the importance of studying $\mathrm{t\bar{t}}$HH as a key process in establishing the top-Higgs sector and its prospects, both on the SM and BSM fronts, in view of the expected progress within the next 2 decades, until the completion of the HL-LHC. |
| References | ||||
| 1 | CMS Collaboration | Technical Proposal for the Phase-II Upgrade of the CMS Detector | CDS | |
| 2 | LHC Higgs Cross Section Working Group Collaboration | Handbook of LHC Higgs Cross Sections: 4. Deciphering the Nature of the Higgs Sector | 1610.07922 | |
| 3 | C. Bautista et al. | Probing the Top-Higgs sector with Composite Higgs Models at present and future hadron colliders | JHEP 03 (2021) 049 | 2008.13026v1 |
| 4 | L. A. Fernandes do Prado | Exploring the Higgs sector beyond the standard model with the top Yukawa coupling: a phenomenological and experimental search | PhD thesis, Sao Paulo, IFT | |
| 5 | R. Frederix et al. | Higgs pair production at the LHC with NLO and parton-shower effects | Physics Letters B 732 (May, 2014) 142 | 1401.7340 |
| 6 | M. Cepeda et al. | Report from Working Group 2 | CERN Yellow Rep. Monogr. 7 (2019) 221 | 1902.00134 |
| 7 | K. Agashe, R. Contino, and A. Pomarol | The Minimal composite Higgs model | NPB 719 (2005) 165 | hep-ph/0412089 |
| 8 | G. Panico and A. Wulzer | The Composite Nambu-Goldstone Higgs | Lect. Notes Phys. 913 (2016) 1 | 1506.01961 |
| 9 | M. Carena, L. Da Rold, and E. Ponton | Minimal Composite Higgs Models at the LHC | JHEP 06 (2014) 159 | 1402.2987 |
| 10 | CMS Collaboration | The CMS Experiment at the CERN LHC | JINST 3 (2008) S08004 | |
| 11 | CMS Collaboration | The Phase-2 Upgrade of the CMS Tracker | CDS | |
| 12 | CMS Collaboration | The Phase-2 Upgrade of the CMS Barrel Calorimeters Technical Design Report | CDS | |
| 13 | CMS Collaboration | The Phase-2 Upgrade of the CMS Endcap Calorimeter | CDS | |
| 14 | CMS Collaboration | The Phase-2 Upgrade of the CMS Muon Detectors | CDS | |
| 15 | CMS Collaboration | A MIP Timing Detector for the CMS Phase-2 Upgrade | CDS | |
| 16 | CMS Collaboration | The Phase-2 Upgrade of the CMS Level-1 Trigger | CDS | |
| 17 | CMS Collaboration | The Phase-2 Upgrade of the CMS Data Acquisition and High Level Trigger | CDS | |
| 18 | CMS Collaboration | Expected performance of the physics objects with the upgraded CMS detector at the HL-LHC | CDS | |
| 19 | J. Alwall et al. | The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations | JHEP 07 (2014) 079 | 1405.0301 |
| 20 | S. Frixione et al. | Matching NLO QCD computations with parton shower simulations: the POWHEG method | JHEP 11 (2007) 070 | 0709.2092 |
| 21 | F. Buccioni, S. Kalweit, S. Pozzorini, and M. F. Zoller | NLO QCD predictions for ttbb production in association with a light jet at the LHC | JHEP 12 (2019) 015 | 1912.00068 |
| 22 | C. Englert, F. Krauss, M. Spannowsky, and J. M. Thompson | Di-higgs phenomenology in tthh: The forgotten channel | Physics Letters B 743 (2015) 93 | |
| 23 | NNPDF Collaboration | Parton distributions from high-precision collider data | EPJC 77 (2017), no. 10, 663 | 1706.00428 |
| 24 | T. Sjostrand et al. | An introduction to PYTHIA 8.2 | Computer Physics Communications 191 (2015) 159 | 1410.3012 |
| 25 | CMS Collaboration | Extraction and validation of a new set of CMS PYTHIA8 tunes from underlying-event measurements | EPJC 80 (2020), no. 1, 4 | 1903.12179 |
| 26 | DELPHES 3 Collaboration | DELPHES 3, A modular framework for fast simulation of a generic collider experiment | JHEP 02 (2014) 057 | 1307.6346 |
| 27 | S. Agostinelli et al. | GEANT4: A Simulation toolkit | NIM506 (2003), no. 3, 250 | |
| 28 | J. Allison et al. | Geant4 developments and applications | IEEE Trans. Nucl. Sci. 53 (2006) 270 | |
| 29 | CMS Collaboration | Particle-flow reconstruction and global event description with the CMS detector | JINST 12 (2017), no. 10, P10003 | CMS-PRF-14-001 1706.04965 |
| 30 | D. Bertolini, P. Harris, M. Low, and N. Tran | Pileup per particle identification | JHEP 10 (2014) 059 | 1407.6013 |
| 31 | CMS Collaboration | B-tagging performance of the CMS Legacy dataset 2018 | CDS | |
| 32 | Particle Data Group Collaboration | Review of Particle Physics | PTEP 2020 (2020), no. 8, 083C01 | |
| 33 | L. Li, Y.-Y. Li, and T. Liu | Anatomy of tthh physics at the HL-LHC | Physical Review D 101 (Mar, 2020) | 1905.03772 |
| 34 | F. Maltoni, D. Pagani, and I. Tsinikos | Associated production of a top-quark pair with vector bosons at NLO in QCD: impact on tth searches at the LHC | Journal of High Energy Physics 2016 (Feb, 2016) | 1507.05640 |
| 35 | A. M. Carrington et al. | Deep ROC analysis and AUC as balanced average accuracy, for improved classifier selection, audit and explanation | IEEE Transactions on Pattern Analysis and Machine Intelligence (2022) 1 | 2103.11357 |
| 36 | J. S. Conway | Incorporating nuisance parameters in likelihoods for multisource spectra | arXiv: Data Analysis, Statistics and Probability (2011) 115 | 1103.0354 |
| 37 | G. Cowan, K. Cranmer, E. Gross, and O. Vitells | Asymptotic formulae for likelihood-based tests of new physics | The European Physical Journal C 71 (Feb, 2011) | 1007.1727 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|