

Compact Muon Solenoid
LHC, CERN
| CMS-HIN-11-005 ; CERN-PH-EP-2013-196 | ||
| Measurement of higher-order harmonic azimuthal anisotropy in PbPb collisions at √sNN= 2.76 TeV | ||
| CMS Collaboration | ||
| 31 October 2013 | ||
| Phys. Rev. C 89 (2014) 044906 | ||
| Abstract: Measurements are presented by the CMS Collaboration at the Large Hadron Collider (LHC) of the higher-order harmonic coefficients that describe the azimuthal anisotropy of charged particles emitted in √sNN= 2.76 TeV PbPb collisions. Expressed in terms of the Fourier components of the azimuthal distribution, the n = 3-6 harmonic coefficients are presented for charged particles as a function of their transverse momentum (0.3 <pT< 8.0 GeV/c), collision centrality (0-70%), and pseudorapidity (|η|< 2.0 ). The data are analyzed using the event plane, multi-particle cumulant, and Lee-Yang zeros methods, which provide different sensitivities to initial state fluctuations. Taken together with earlier LHC measurements of elliptic flow (n= 2), the results on higher-order harmonic coefficients develop a more complete picture of the collective motion in high-energy heavy-ion collisions and shed light on the properties of the produced medium. | ||
| Links: e-print arXiv:1310.8651 [nucl-ex] (PDF) ; CDS record ; inSPIRE record ; Public twiki page ; CADI line (restricted) ; | ||
| Figures | |

png pdf |
Figure 1:
Event plane resolution correction factors Rn corresponding to different event plane angles Ψm used in the analysis, as discussed in the text, are shown as a function of centrality for event planes determined with HF− (open symbols) and HF+ (filled symbols). The R2{Ψ2} values are from Ref. [18] and are included for comparison purposes. Statistical uncertainties are smaller than the symbols. The heights of the open gray rectangles indicate the systematic uncertainties. |
png pdf |
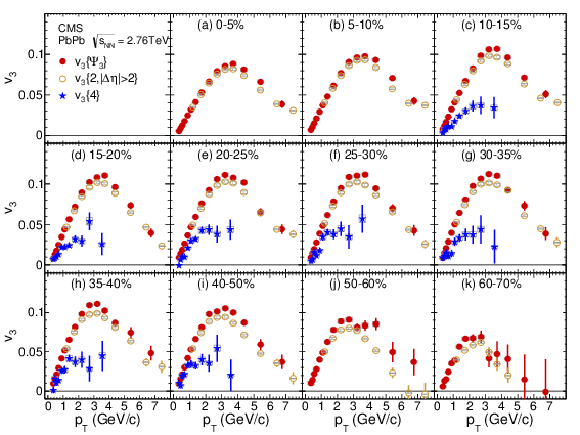
Figure 2:
Measurements of the azimuthal asymmetry coefficient v3 from three different methods as a function of pT for the indicated centrality bins, as specified in percent. The event plane (filled circles) and cumulant (filled stars) results are with |η|< 0.8 . The two particle correlation results (open circles) are from a previous CMS measurement [48]. Statistical (error bars) and systematic (light gray boxes) uncertainties are shown. |

png pdf |
Figure 3:
Measurements of the azimuthal asymmetry coefficient v4 from four different methods as a function of pT for the indicated centrality bins, as specified in percent. The event plane (filled circles and filled diamonds), cumulant (filled stars), and Lee-Yang zeros (open stars) analyses are with |η|< 0.8 . The two particle correlation results (open circles) are from a previous CMS measurement [48]. Statistical (error bars) and systematic (light gray boxes) uncertainties are shown. |

png pdf |
Figure 4:
Measurements of the azimuthal asymmetry coefficient v5 from two different methods as a function of pT for the indicated centrality bins, as specified in percent. The event plane analysis (filled circles) is with |η|< 0.8 . The two particle correlation results (open circles) are from a previous CMS measurement [48]. Statistical (error bars) and systematic (light gray boxes) uncertainties are shown. |

png pdf |
Figure 5:
Measurements of the azimuthal asymmetry coefficient v6 from the event plane (filled circles and filled diamonds) and Lee-Yang zeros (open stars) methods as a function of pT for the indicated centrality bins, as specified in percent. The results are for |η|< 0.8 . Statistical (error bars) and systematic (light gray boxes) uncertainties are shown. |
png pdf |
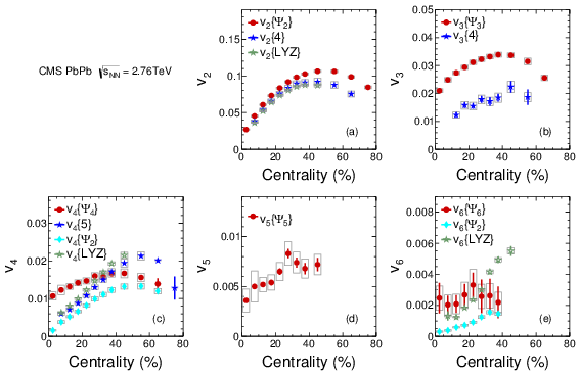
Figure 6:
Yield-weighted average azimuthal asymmetry coefficients vn, for n= 2-6, with 0.3 <pT< 3.0 GeV/c are shown for three different methods as a function of centrality. The v2 results are from Ref. [18] and included for completeness. Statistical (error bars) and systematic (light gray boxes) uncertainties are shown. The different results found for a given vn reflect the role of participant fluctuations and the variable sensitivity to them in each method, as discussed in the text. |
png pdf |
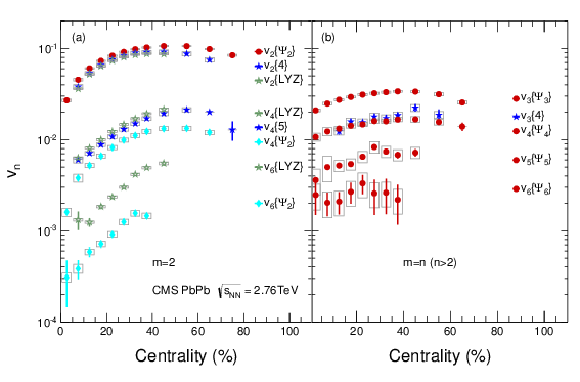
Figure 7:
(a) Yield-weighted average azimuthal asymmetry coefficients vn, for n= 2 , 4 and 6, with 0.3 <pT< 3.0 GeV/c and based on a second-order, m= 2 , reference frame are shown for three different methods as a function of centrality. The v2 results are from Ref. [18] and included for completeness. (b) Results for the event plane and cumulant analyses for distributions based on higher-order, m> 2 , reference distributions. Statistical (error bars) and systematic (light gray boxes) uncertainties are shown. |
png pdf |
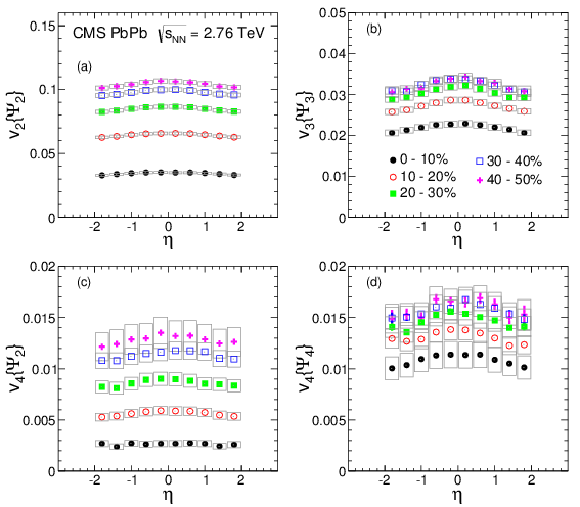
Figure 8:
Yield-weighted average azimuthal asymmetry coefficients vn, for n= 2-4, with 0.3 <pT< 3.0 GeV/c are shown as a function of pseudorapidity η for the indicated centrality ranges, as specified in percent. Statistical (error bars) and systematic (light gray boxes) uncertainties are shown. The v2 results are from Ref. [18] and included for completeness. |

png pdf |
Figure 9:
Comparison of the v3 results for PbPb collisions at √sNN= 2.76 TeV of the ALICE, ATLAS, and CMS Collaborations for the indicated centrality ranges, as specified in percent. The PHENIX results for AuAu collisions at √sNN= 200 GeV are also shown. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. References and experimental conditions are given in Table {tbl:expsum}. The predictions of the IP-Glasma+MUSIC model [62] for PbPb collisions at √sNN= 2.76 TeV are shown by the solid lines in the 0-5%, 10-20%, 20-30%, 30-40%, and 40-50% panels for 0 <pT< 2 GeV/c. |
png pdf |
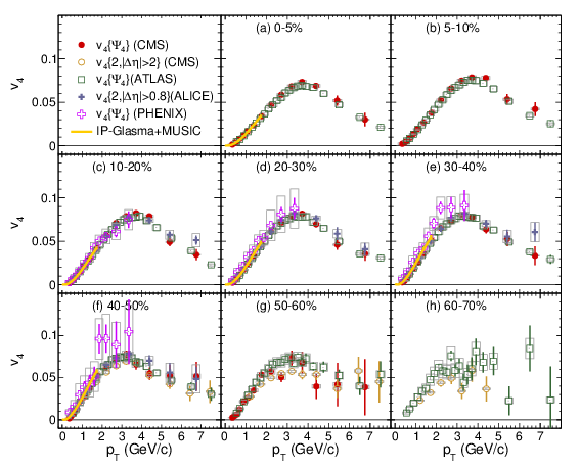
Figure 10:
Comparison of the v4 results for PbPb collisions at √sNN= 2.76 TeV of the ALICE, ATLAS, and CMS Collaborations for the indicated centrality ranges, as specified in percent. The PHENIX results for AuAu collisions at √sNN= 200 GeV are also shown. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. References and experimental conditions are given in Table {tbl:expsum}. The predictions of the IP-Glasma+MUSIC model [62] for PbPb collisions at √sNN= 2.76 TeV are shown by the solid lines in the 0-5%, 10-20%, 20-30%, 30-40%, and 40-50% panels for 0 <pT< 2 GeV/c. |

png pdf |
Figure 11:
Comparison of the v5 results of the ALICE, ATLAS, and CMS Collaborations for the indicated centrality ranges, as specified in percent. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. References and experimental conditions are given in Table {tbl:expsum}. The predictions of the IP-Glasma+MUSIC model [62] are shown by the solid lines in the 0-5%, 10-20%, 20-30%, 30-40%, and 40-50% panels for 0 <pT< 2 GeV/c. |
png pdf |
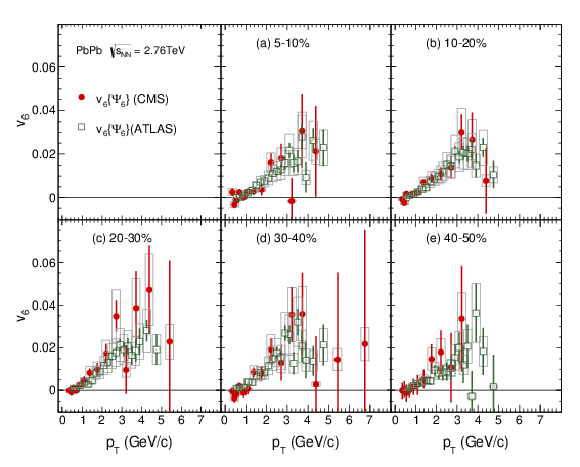
Figure 12:
Comparison of the v6 results of the ATLAS and CMS Collaborations for the indicated centrality ranges, as specified in percent. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. References and experimental conditions are given in Table {tbl:expsum}. |
png pdf |
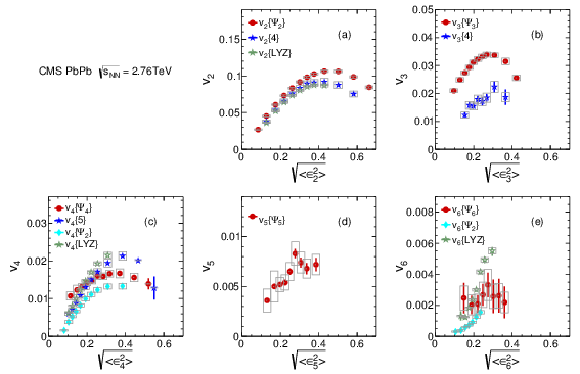
Figure 13:
Yield-weighted average azimuthal asymmetry parameters vn, for n= 2 -6 with 0.3 <pT< 3.0 GeV/c, as a function of the corresponding Glauber model rms anisotropy parameters √<ϵ2n>. The CMS v2 results are from Ref. [18] and included for completeness. The v4{Ψ2} and v6{Ψ2} results are plotted against √<ϵ24,2> and √<ϵ26,2>, respectively. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. |
png pdf |
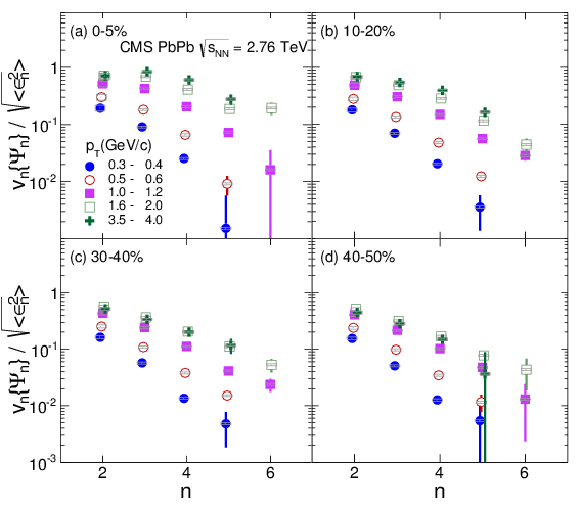
Figure 14:
The azimuthal asymmetry parameter vn, scaled by the corresponding Glauber model rms anisotropy parameter √ϵ2n for the indicated pT and centrality ranges, as specified in percent, as a function of harmonic number n. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. |

png pdf |
Figure 15:
Estimate of the event-by-event vn fluctuations in vn for n= 2 (filled circles) and 3 (filled stars) as discussed in the text. The results where the event plane v2 values are adjusted to their corresponding rms values, as discussed in the text, are indicated by the filled boxes and labelled n=2RMS. The results of event-by-event-fluctuation (E-by-E) analyses by the ATLAS Collaboration for the n = 2 and 3 harmonics [69] are also shown. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. The systematic uncertainties for the ATLAS results correspond to the mid-point of the uncertainty range indicated by the ATLAS Collaboration. |
png pdf |
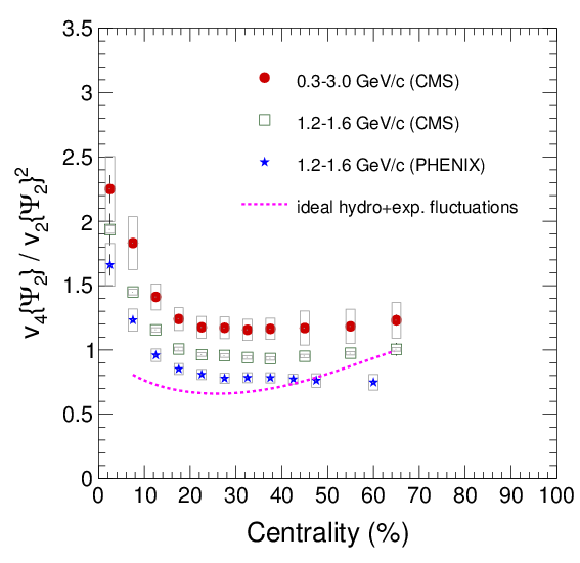
Figure 16:
The yield-weighted average values of the ratio v4/v22 as a function of centrality for 0.3 <pT< 3.0 GeV/c (filled circles) and 1.2 <pT< 1.6 GeV/c (open squares) are shown for PbPb collisions at √sNN= 2.76 TeV. The PHENIX results (stars) for 1.2 <pT< 1.6 GeV/c are also shown for AuAu collisions at √sNN= 200 GeV [22]. The dotted line is based on the method presented in Ref. [34] that allows the expected v4/v22 ratio for an event plane analysis to be calculated based on the ideal hydrodynamics limit of 0.5 and the observed relative fluctuation ratio \sigma /\delimiter "426830A v_n \delimiter "526930B , as discussed in the text. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. |
png pdf |
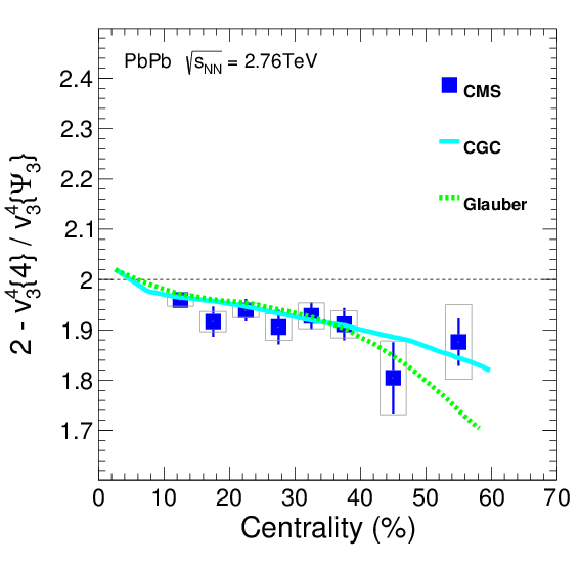
Figure 17:
Measurements of 2 - v_{3}^{4}\{4\}/v_{3}^{4}\{\Psi _{3}\} versus centrality. The CGC and Glauber model calculations are from Ref. [61]. Statistical (error bars) and systematic (light gray boxes) uncertainties are indicated. |
| Tables | |

png pdf |
Table 1:
The average number of participating nucleons and participant eccentricities, weighted by r^n, calculated using the Glauber model in bins of centrality. Systematic uncertainties resulting from the uncertainties in the Glauber-model parameters are indicated. |

png pdf |
Table 2:
Summary of experimental conditions for the data shown in this report. The Figure(s) column indicates the figures in this report where the data are shown. The {p_{\mathrm {T}}} range for previously published data corresponds to that shown in the original report. |
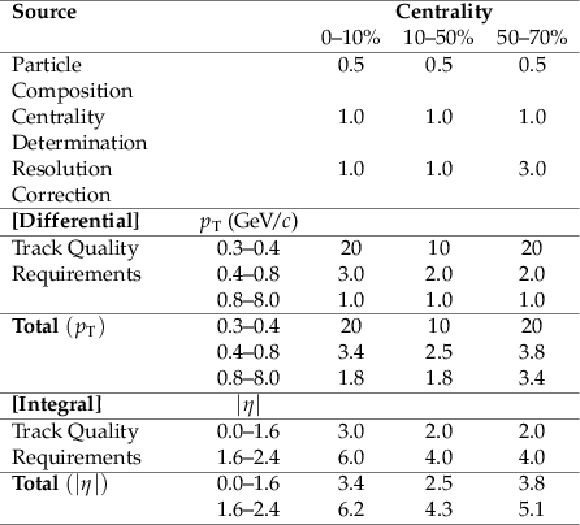
png pdf |
Table 3:
Systematic uncertainties in the v_{3}\{\Psi _{3}\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |

png pdf |
Table 4:
Systematic uncertainties in the v_{4}\{\Psi _{4}\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |
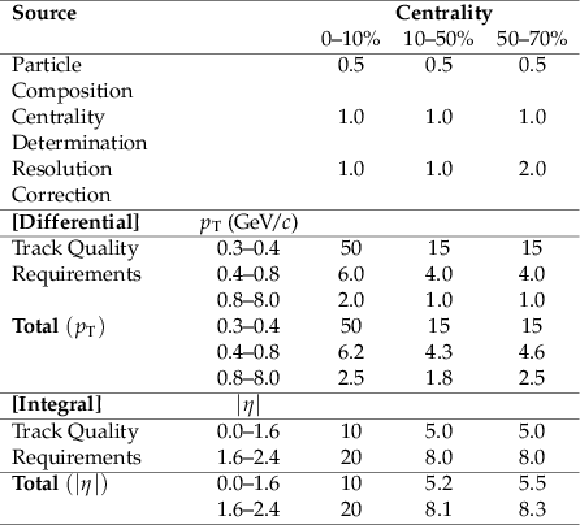
png pdf |
Table 5:
Systematic uncertainties in the v_{4}\{\Psi _{2}\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |

png pdf |
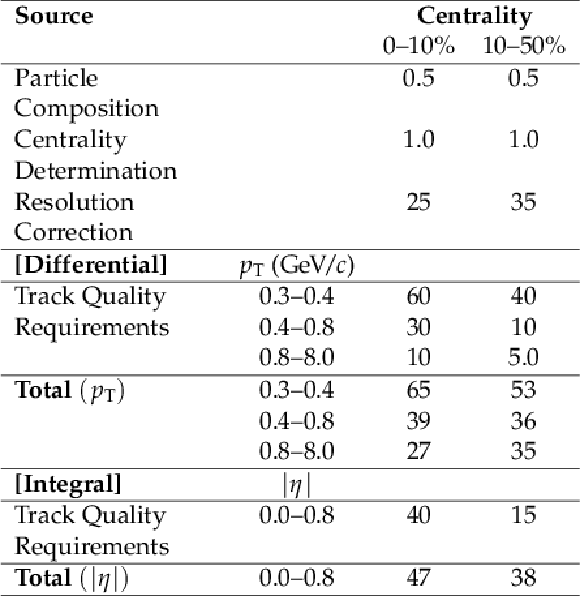
Table 6:
Systematic uncertainties in the v_{5}\{\Psi _{5}\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |
png pdf |
Table 7:
Systematic uncertainties in the v_{6}\{\Psi _{6}\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |

png pdf |
Table 8:
Systematic uncertainties in the v_{6}\{\Psi _{2}\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |

png pdf |
Table 9:
Systematic uncertainties in the v_{3}\{4\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |

png pdf |
Table 10:
Systematic uncertainties in the v_{4}\{5\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |

png pdf |
Table 11:
Systematic uncertainties in the v_{4}\{\mathrm {LYZ}\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |

png pdf |
Table 12:
Systematic uncertainties in the v_{6}\{\mathrm {LYZ}\} values as a function of centrality in percent. Common uncertainties are shown at the top of the table, followed by those specific to the differential ( {p_{\mathrm {T}}} dependent) and integral ( {| \eta | } dependent) measurements. |
| Summary |
|
Results from the CMS Collaboration have been presented on higher-order harmonic anisotropies of charged particles for PbPb collisions at \sqrt{s_{\mathrm{NN}}}= 2.76 TeV. The harmonic coefficients v_{n} have been studied as a function of transverse momentum (0.3 $ Comparisons of the event plane results with those of the cumulant and Lee-Yang zeros analyses suggest a strong influence of initial state fluctuations on the azimuthal anisotropies. The weak centrality dependence found for the event plane results based on event planes of harmonic order greater than two is also consistent with the presence of a strong fluctuation component. The pseudorapidity dependence of the higher-order azimuthal anisotropy parameters based on the event plane method is similar to that observed for elliptic flow, with only a modest decrease from the mid-rapidity values out to the limits of the measurement at \abs{\eta}= 2.0 . The mid-rapidity values are compared to those obtained by the ALICE [24,25] and ATLAS [26] Collaborations, and found to be in good agreement. A comparison is also done with lower-energy AuAu measurements by the PHENIX Collaboration at \sqrt{s_{\mathrm{NN}}}= 200 GeV, with only small differences found with the much higher energy LHC data. The results obtained for v_3 are compared to predictions from both the CGC and Glauber models. Both of these initial state models are found to be consistent with the data. It is noted that a calculation that employs IP-Glasma-model initial conditions for the early time evolution, followed by a viscous hydrodynamic development of the plasma, is quite successful in reproducing the observed v_{n}(p_{\mathrm{T}}) results in the low-p_{\mathrm{T}}, flow-dominated region [62]. The measurements presented in this paper help to further establish the pattern of azimuthal particle emission at LHC energies. Recent theoretical investigations have significantly increased our understanding of the initial conditions and hydrodynamics that lead to the experimentally observed asymmetry patterns. However, further calculations are needed to fully explain the method dependent differences seen in the data for the anisotropy harmonics. These differences can be attributed to the role of fluctuations in the participant geometry. Understanding the role of these fluctuations is necessary in order to establish the initial state of the created medium, thereby allowing for an improved determination of its properties. The current results are directly applicable to the study of the initial spatial anisotropy, time development, and shear viscosity of the medium formed in ultra-relativistic heavy-ion collisions. |
| References | ||||
| 1 | BRAHMS Collaboration | Quark-gluon plasma and color glass condensate at RHIC? The perspective from the BRAHMS experiment | Nucl. Phys. A 757 (2005) 1 | nucl-ex/0410020 |
| 2 | PHOBOS Collaboration | The PHOBOS perspective on discoveries at RHIC | Nucl. Phys. A 757 (2005) 28 | nucl-ex/0410022 |
| 3 | STAR Collaboration | Experimental and theoretical challenges in the search for the quark-gluon plasma: The STAR Collaboration's critical assessment of the evidence from RHIC collisions | Nucl. Phys. A 757 (2005) 102 | nucl-ex/0501009 |
| 4 | PHENIX Collaboration | Formation of dense partonic matter in relativistic nucleus-nucleus collisions at RHIC: Experimental evaluation by the PHENIX Collaboration | Nucl. Phys. A 757 (2005) 184 | nucl-ex/0410003 |
| 5 | M. Luzum and P. Romatschke | Conformal relativistic viscous hydrodynamics: Applications to RHIC results at \sqrt{s_{NN}} \ = \ 200~GeV | PRC 78 (2008) 034915, , Also erratum at \doi10.1103/PhysRevC.79.039903 | 0804.4015 |
| 6 | S. Gavin and M. Abdel-Aziz | Measuring Shear Viscosity Using Transverse Momentum Correlations in Relativistic Nuclear Collisions | PRL 97 (2006) 162302 | nucl-th/0606061 |
| 7 | PHENIX Collaboration | Energy loss and flow of heavy quarks in Au+Au collisions at \sqrt{s_{NN}} \ = \ 200~GeV | PRL 98 (2007) 172301 | nucl-ex/0611018 |
| 8 | H. J. Drescher, A. Dumitru, C. Gombeaud, and J. Y. Ollitrault | Centrality dependence of elliptic flow, the hydrodynamic limit, and the viscosity of hot QCD | PRC 76 (2007) 024905 | 0704.3553 |
| 9 | P. K. Kovtun, D. T. Son, and A. O. Starinets | Viscosity in Strongly Interacting Quantum Field Theories from Black Hole Physics | PRL 94 (2005) 111601 | hep-th/0405231 |
| 10 | J. Y. Ollitrault | Anisotropy as a Signature of Transverse Collective Flow | PRD 46 (1992) 229 | |
| 11 | H. Sorge | Highly Sensitive Centrality Dependence of Elliptic Flow: A Novel Signature of the Phase Transition in QCD | PRL 82 (1999) 2048 | nucl-th/9812057 |
| 12 | W. Reisdorf and H. G. Ritter | Collective flow in heavy-ion collisions | Ann. Rev. Nucl. Part. Sci. 47 (1997) 663 | |
| 13 | M. L. Miller, K. Reygers, S. J. Sanders, and P. Steinberg | Glauber modeling in high energy nuclear collisions | Ann. Rev. Nucl. Part. Sci. 57 (2007) 205 | nucl-ex/0701025 |
| 14 | L. D. McLerran | The Color Glass Condensate and Small x Physics: 4 lectures | in Lectures on quark matter. Proceedings, 40th Int. Universitaetswochen fuer Theoretische Physik, W. Plessas and L. Mathelitsch, eds., p. 291.\newblock Springer, 2002.\newblock | hep-ph/0104285 |
| 15 | B. Schenke, P. Tribedy, and R. Venugopalan | Event-by-event gluon multiplicity, energy density, and eccentricities in ultrarelativistic heavy-ion collisions | PRC 86 (2012) 034908 | 1206.6805 |
| 16 | ALICE Collaboration | Elliptic Flow of Charged Particles in Pb-Pb Collisions at \sqrt{s_{NN}} \ = \ 2.76~TeV | PRL 105 (2010) 252302 | 1011.3914 |
| 17 | ATLAS Collaboration | Measurement of the pseudorapidity and transverse momentum dependence of the elliptic flow of charged particles in lead-lead collisions at \sqrt{s_{NN}}\ =\ 2.76~{\rm TeV} with the ATLAS detector | PLB 707 (2012) 330 | 1108.6018 |
| 18 | CMS Collaboration | Measurement of the elliptic anisotropy of charged particles produced in PbPb collisions at \sqrt{s_{NN}} \ = \ 2.76~TeV | PRC 87 (2013) 014902 | CMS-HIN-10-002 1204.1409 |
| 19 | STAR Collaboration | Azimuthal anisotropy in Au+Au collisions at \sqrt{s_{NN}} \ = \ 200~GeV | PRC 72 (2005) 014904 | nucl-ex/0409033 |
| 20 | STAR Collaboration | Mass, quark-number, and \sqrt{s_{NN}} dependence of the second and fourth flow harmonics in ultrarelativistic nucleus-nucleus collisions | PRC 75 (2007) 054906 | nucl-ex/0701010 |
| 21 | STAR Collaboration | Azimuthal Anisotropy at the Relativistic Heavy Ion Collider: The First and Fourth Harmonics | PRL 92 (2004) 062301 | nucl-ex/0310029 |
| 22 | PHENIX Collaboration | Elliptic and Hexadecapole Flow of Charged Hadrons in Au+Au Collisions at \sqrt{s_{NN}} \ = \ 200~GeV | PRL 105 (2010) 062301 | 1003.5586 |
| 23 | PHENIX Collaboration | Measurements of Higher Order Flow Harmonics in Au+Au Collisions at \sqrt{s_{NN}} \ = \ 200~GeV | PRL 107 (2011) 252301 | 1105.3928 |
| 24 | ALICE Collaboration | Harmonic decomposition of two particle angular correlations in Pb-Pb collisions at \sqrt{s_{NN}}\ =\ 2.76~{\rm TeV} | PLB 708 (2012) 249 | 1109.2501 |
| 25 | ALICE Collaboration | Higher Harmonic Anisotropic Flow Measurements of Charged Particles in PbPb Collisions at \sqrt{s_{NN}} \ = \ 2.76~TeV | PRL 107 (2011) 032301 | 1105.3865 |
| 26 | ATLAS Collaboration | Measurement of the azimuthal anisotropy for charged particle production in \sqrt{s_{NN}}\ =\ 2.76~{\rm TeV} lead-lead collisions with the ATLAS detector | PRC 86 (2012) 014907 | 1203.3087 |
| 27 | A. M. Poskanzer and S. A. Voloshin | Methods for analyzing anisotropic flow in relativistic nuclear collisions | PRC 58 (1998) 1671 | nucl-ex/9805001 |
| 28 | PHOBOS Collaboration | Non-flow correlations and elliptic flow fluctuations in gold-gold collisions at \sqrt{s_{NN}}\ =\ 200 ~GeV | PRC 81 (2010) 034915 | 1002.0534 |
| 29 | PHOBOS Collaboration | Importance of correlations and fluctuations on the initial source eccentricity in high-energy nucleus-nucleus collisions | PRC 77 (2008) 014906 | 0711.3724 |
| 30 | B. Alver and G. Roland | Collision geometry fluctuations and triangular flow in heavy-ion collisions | PRC 81 (2010) 054905, , Also erratum at \doi10.1103/PhysRevC.82.039903 | 1003.0194 |
| 31 | R. S. Bhalerao and J. Y. Ollitrault | Eccentricity fluctuations and elliptic flow at RHIC | PLB 641 (2006) 260 | nucl-th/0607009 |
| 32 | W. Broniowski, P. Bo\.zek, and M. Rybczy\'nski | Fluctuating initial conditions in heavy ion collisions from the Glauber approach | PRC 76 (2007) 054905 | 0706.4266 |
| 33 | S. Gavin and G. Moschelli | Fluctuation probes of early-time correlations in nuclear collisions | PRC 85 (2012) 014905 | 1107.3317 |
| 34 | C. Gombeaud and J.-Y. Ollitrault | Effects of flow fluctuations and partial thermalization on v_{4} | PRC 81 (2010) 014901 | 0907.4664 |
| 35 | L. X. Han et al. | Initial fluctuation effect on harmonic flows in high-energy heavy-ion collisions | PRC 84 (2011) 064907 | 1105.5415 |
| 36 | J.-Y. Ollitrault, A. M. Poskanzer, and S. A. Voloshin | Effect of flow fluctuations and nonflow on elliptic flow methods | PRC 80 (2009) 014904 | 0904.2315 |
| 37 | G.-Y. Qin, H. Petersen, S. A. Bass, and B. M\"uller | Translation of collision geometry fluctuations into momentum anisotropies in relativistic heavy-ion collisions | PRC 82 (2010) 064903 | 1009.1847 |
| 38 | Z. Qiu and U. Heinz | Event-by-event shape and flow fluctuations of relativistic heavy-ion collision fireballs | PRC 84 (2011) 024911 | 1104.0650 |
| 39 | S. A. Voloshin, A. M. Poskanzer, A. Tang, and G. Wang | Elliptic flow in the Gaussian model of eccentricity fluctuations | PLB 659 (2008) 537 | 0708.0800 |
| 40 | B. H. Alver, C. Gombeaud, M. Luzum, and J.-Y. Ollitrault | Triangular flow in hydrodynamics and transport theory | PRC 82 (2010) 034913 | 1007.5469 |
| 41 | B. Schenke, S. Jeon, and C. Gale | Elliptic and Triangular Flow in Event-by-Event D=3+1 Viscous Hydrodynamics | PRL 106 (2011) 042301 | 1009.3244 |
| 42 | P. Staig and E. Shuryak | Fate of the initial state perturbations in heavy ion collisions. III. The second act of hydrodynamics | PRC 84 (2011) 044912 | 1105.0676 |
| 43 | B. Schenke, S. Jeon, and C. Gale | Higher flow harmonics from (3+1)D event-by-event viscous hydrodynamics | PRC 85 (2012) 024901 | 1109.6289 |
| 44 | M. Alvioli, H. Holopainen, K. J. Eskola, and M. Strikman | Initial state anisotropies and their uncertainties in ultrarelativistic heavy-ion collisions from the Monte Carlo Glauber model | PRC 85 (2012) 034902 | 1112.5306 |
| 45 | N. Borghini, P. M. Dinh, and J. Y. Ollitrault | Flow analysis from multiparticle azimuthal correlations | PRC 64 (2001) 054901 | nucl-th/0105040 |
| 46 | R. S. Bhalerao, N. Borghini, and J. Y. Ollitrault | Analysis of anisotropic flow with Lee-Yang zeroes | Nucl. Phys. A 727 (2003) 373 | nucl-th/0310016 |
| 47 | N. Borghini, R. S. Bhalerao, and J. Y. Ollitrault | Anisotropic flow from Lee-Yang zeroes: A practical guide | J. of Phys. G 30 (2004) S1213 | nucl-th/0402053 |
| 48 | CMS Collaboration | Centrality dependence of dihadron correlations and azimuthal anisotropy harmonics in PbPb collisions at \sqrt{s_{NN}}\ =\ 2.76 ~TeV | EPJC 72 (2012) 2012 | CMS-HIN-11-006 1201.3158 |
| 49 | CMS Collaboration | The CMS experiment at the CERN LHC | JINST 3 (2008) S08004 | CMS-00-001 |
| 50 | W. Adam, B. Mangano, T. Speer, and T. Todorov | Track reconstruction in the CMS tracker | CMS-NOTE-2006-041 | |
| 51 | O. Djuvsland and J. Nystrand | Single and double photonuclear excitations in Pb+Pb collisions at \sqrt{s_{NN}}\ =\ 2.76 ~TeV at the CERN Large Hadron Collider | PRC 83 (2011) 041901 | 1011.4908 |
| 52 | CMS Collaboration | Observation and studies of jet quenching in PbPb collisions at \sqrt{s_{NN}}\ =\ 2.76 ~TeV | PRC 84 (2011) 024906 | CMS-HIN-10-004 1102.1957 |
| 53 | CMS Collaboration | Dependence on pseudorapidity and centrality of charged hadron production in PbPb collisions at a nucleon-nucleon centre-of-mass energy of 2.76~TeV | JHEP 08 (2011) 141 | CMS-HIN-10-001 1107.4800 |
| 54 | D. Teaney and L. Yan | Nonlinearities in the harmonic spectrum of heavy ion collisions with ideal and viscous hydrodynamics | PRC 86 (2012) 044908 | 1206.1905 |
| 55 | I. P. Lokhtin and A. M. Snigirev | A model of jet quenching in ultrarelativistic heavy ion collisions and high- p_{\rm T} hadron spectra at RHIC | EPJC 45 (2006) 211 | hep-ph/0506189 |
| 56 | Z.-W. Lin et al. | Multiphase transport model for relativistic heavy ion collisions | PRC 72 (2005) 064901 | nucl-th/0411110 |
| 57 | PHENIX Collaboration | Identified Charged Particle Spectra and Yields in Au+Au Collisions at \sqrt{s_{NN}} = 200 GeV | PRC 69 (2004) 034909 | |
| 58 | B. Alver, M. Baker, C. Loizides, and P. Steinberg | The PHOBOS Glauber Monte Carlo | unpublished | 0805.4411 |
| 59 | H. De Vries, C. W. De Jager, and C. De Vries | Nuclear charge and magnetization density distribution parameters from elastic electron scattering | Atom. Data Nucl. Data Tabl. 36 (1987) 495 | |
| 60 | Particle Data Group, J. Beringer et al. | Review of Particle Physics | PRD 86 (2012) 010001 | |
| 61 | R. S. Bhalerao, M. Luzum, and J. Y. Ollitrault | Determining initial-state fluctuations from flow measurements in heavy-ion collisions | PRC 84 (2011) 034910 | 1104.4740 |
| 62 | C. Gale et al. | Event-by-Event Anisotropic Flow in Heavy-ion Collisions from Combined Yang-Mills and Viscous Fluid Dynamics | PRL 110 (2013) 012302 | 1209.6330 |
| 63 | R. A. Lacey et al. | Constraints on models for the initial collision geometry in ultrarelativistic heavy ion collisions | PRC 81 (2010) 061901 | 1002.0649 |
| 64 | R. A. Lacey et al. | Initial eccentricity fluctuations and their relation to higher-order flow harmonics | PRC 83 (2011) 044902 | 1009.5230 |
| 65 | B. Schenke, P. Tribedy, and R. Venugopalan | Fluctuating Glasma Initial Conditions and Flow in Heavy Ion Collisions | PRL 108 (2012) 252301 | 1202.6646 |
| 66 | F. G. Gardim, F. Grassi, M. Luzum, and J.-Y. Ollitrault | Mapping the hydrodynamic response to the initial geometry in heavy-ion collisions | PRC 85 (2012) 024908 | 1111.6538 |
| 67 | PHOBOS Collaboration | Event-by-Event Fluctuations of Azimuthal Particle Anisotropy in Au+Au Collisions at \sqrt{s_{NN}} \ = \ 200~GeV | PRL 104 (2010) 142301 | nucl-ex/0702036 |
| 68 | STAR Collaboration | Energy and system-size dependence of two and four particle v_2 measurements in heavy-ion collisions at RHIC and their implications on flow fluctuations and nonflow | PRC 86 (2012) 014904 | 1111.5637 |
| 69 | ATLAS Collaboration | Measurement of the distributions of event-by-event flow harmonics in lead--lead collisions at \sqrt{s_{NN}} \ = \ 2.76~TeV with the ATLAS detector at the LHC | Submitted to JHEP | 1305.2942 |
| 70 | P. F. Kolb | v(4): A small, but sensitive observable for heavy ion collisions | PRC 68 (2003) 031902 | nucl-th/0306081 |
| 71 | P. F. Kolb, L. W. Chen, V. Greco, and C. M. Ko | Momentum anisotropies in the quark coalescence model | PRC 69 (2004) 051901 | nucl-th/0402049 |
| 72 | R. S. Bhalerao, J. P. Blaizot, N. Borghini, and J. Y. Ollitrault | Elliptic flow and incomplete equilibration at RHIC | PLB 627 (2005) 49 | nucl-th/0508009 |
| 73 | R. S. Bhalerao, M. Luzum, and J. Y. Ollitrault | New flow observables | JPG 38 (2011) 124055 | 1106.4940 |
| 74 | STAR Collaboration | Third Harmonic Flow of Charged Particles in Au+Au Collisions at \sqrt{s_{NN}} \ = \ 200~GeV | PRC 88 (2013) 014904 | 1301.2187 |

|
Compact Muon Solenoid LHC, CERN |

|

|

|

|

|

|